Effects of the alkyl substituent in the π-donor heteroatom on the kinetic and thermodynamic acidities of Fischer thiocarbene complexes†
Martin Eduardo
Zoloff Michoff
,
Diego Marcelo
Andrada
,
Alejandro Manuel
Granados
* and
Rita Hoyos
de Rossi
*
Instituto de Investigaciones en Fisicoquímica de Córdoba, Departamento de Química Orgánica, Facultad de Ciencias Químicas, Universidad Nacional de Córdoba, Ciudad Universitaria, Córdoba, Argentina. E-mail: ale@mail.fcq.unc.edu.ar; ritah@mail.fcq.unc.edu.ar; Fax: +54 3514333030; Tel: +54 3514334170
First published on 24th August 2007
Abstract
Rate constants for the proton transfer reaction from Fischer thiocarbene complexes (CO)5M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(SR1)CH3 (M = Cr or W; R1 = n-butyl, isopropyl, tert-butyl, cyclohexyl) to OH– and various primary and secondary amines were determined in 50% acetonitrile–50% water at 25 °C. These measurements allowed the determination of the thermodynamic and kinetic acidities for these substrates. The results obtained show that there is a slight effect of the substituent on the thermodynamic acidity, which is governed by its hydrophobicity; whereas the effect on the kinetic acidity is more noticeable and is due to the steric effect of the substituent.
C(SR1)CH3 (M = Cr or W; R1 = n-butyl, isopropyl, tert-butyl, cyclohexyl) to OH– and various primary and secondary amines were determined in 50% acetonitrile–50% water at 25 °C. These measurements allowed the determination of the thermodynamic and kinetic acidities for these substrates. The results obtained show that there is a slight effect of the substituent on the thermodynamic acidity, which is governed by its hydrophobicity; whereas the effect on the kinetic acidity is more noticeable and is due to the steric effect of the substituent.
Introduction
The chemistry of Fischer carbene complexes, 1, has been largely developed since the first synthesis of one such complex by Fischer and Maasböl in 1964.1 Most of the investigations performed so far have aimed at applications in the area of organic synthesis.2 Their special electronic characteristics and multifunctional structure make these compounds very versatile synthons.Fischer carbene complexes have been shown to undergo a variety of reactions such as nucleophilic addition/substitution on the carbene carbon,3 interchange of ligands,4 insertion on C–H5 and C–C bonds6 and cycloadditions.7 Recently it has been reported that the carbene carbon can undergo an insertion on a S–S bond in a pseudo-aromatic heterocycle,8 and that these compounds are capable of reacting with electron transfer reagents or an electronspray source to form radical species with distinct reactivity.9
One of the major characteristics of these compounds is the high acidity of the hydrogens in the α-position with regard to the carbene carbon.10 This has opened the possibility of enlarging the range of carbene complexes that can be obtained,11 and has also inspired numerous synthetic studies in which the α-anions of acidic Fischer carbenes such as 2 have been successfully used as nucleophiles in, for example, stereoselective aldol additions to aldehydes and ketones,12 and asymmetric Michael additions to α,β-unsaturated ketones.13
Although most of the synthetic applications of these α-anions have been focused on alkoxycarbene and aminocarbene complexes, it has recently been reported that the corresponding carbanions obtained from thiocarbene complexes can undergo distinct reaction pathways leading to products that cannot be obtained from the isostructural alkoxycarbene complexes.14
Notwithstanding their usefulness as synthons in organic synthesis, it was not until recently that some of the mechanistic aspects of the reactions of these α-anions were reported. These studies were performed mainly by Bernasconi et al.3a,15 and deal with some of the factors that affect the thermodynamic and kinetic acidity of these compounds.
The findings of those studies can be summarized as follows: (i) the high acidity of these complexes is mainly due to the electron-withdrawing nature of the metal moiety. A wide range of acidities was found, spanning a pKa interval of 25 units. Some of the more important factors that affect the acidity of these compounds are the nature of the ligands L, and the heteroatom X. The nature of the substituents R2 and R3 also has some influence on the acidity constants of these compounds, but it is not as dramatic; (ii) the intrinsic rate constants, i.e. the rate constants extrapolated to a situation in which the thermodynamic driving force of the reaction is zero, for these reactions are typically low, usually lower than for other carbon acids. This is a consequence of the charge being delocalized into the metal moiety, combined with the fact that charge delocalization lags behind proton transfer. This causes the transition state for these reactions to be imbalanced which, according to the principle of non-perfect synchronization (PNS),16 leads to low intrinsic rate constants. Some of the factors that affect the intrinsic reactivity of acidic Fischer carbene complexes have also been evaluated.
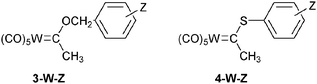
In the aforementioned studies, the effect of the nature of the R1 substituent has not been explored in depth. Only its electronic effect has been assessed from studies involving the benzoxy carbene complexes 3-W-Z and the thiophenoxy carbene complexes 4-W-Z.17
The only alkyl substituents studied so far are either methyl (with X = O18 and S19) or ethyl (with X = O20). However, it is known that the volume of an alkyl substituent in this position can alter the preferred conformation of these complexes,21 and that can also affect significantly the reactivity of these compounds against OH– or water as nucleophiles,22 but how it can influence the thermodynamic and kinetic acidities of ionizable Fischer carbenes has not yet been explored.
In this paper we report on the study of the proton transfer reaction from the Fischer thiocarbene complexes 5-M-R1 to KOH and a series of primary aliphatic and secondary alicyclic amines in order to assess how a change in the volume of the alkyl substituent can affect the thermodynamic and kinetic acidities of these compounds. The results obtained provide a new insight into how an alkyl substituent can influence the acidity of these compounds and suggest that the thermodynamic acidity is mainly affected by the hydrophobicity of the substituent, whereas the kinetic acidity is influenced by its steric effect.
Experimental
Materials
The Fischer carbene complexes were synthesized according to the procedure of Yamashita et al.23 The products were characterized by NMR spectroscopy (200 MHz and 400 MHz, CDCl3), FT-IR (KBr), HRMS (FAB) and UV-Vis spectrophotometry (see ESI for the full spectroscopic characterization of the Fischer carbenes 5-M-R1†).Acetonitrile was reagent grade and was used without further purification. Water was taken from a Milli-Q water purification system. The liquid amines were refluxed over Na and freshly distilled before use. TRIS was recrystallized from ethanol. Reagent grade potassium chloride was used as received. Stock solutions of KOH were prepared from solid KOH, reagent for analysis, with CO2-free water. These solutions were titrated and used to prepare the KOH solutions for the kinetic runs.
Kinetics and spectra
Stock solutions of the carbene complexes were prepared in pure acetonitrile, a medium in which they were relatively stable, and were used to make appropriate solutions in 50% MeCN–50% water prior to use. Typical concentrations of 5-M-R1 were (1.0–1.2) × 10–4 M. All kinetic experiments were performed on a stopped-flow spectrophotometer. The ionic strength was maintained at 0.1 M with KCl. Kinetic runs were monitored at the λmax of the carbene complexes. For the reactions run in the reverse direction, the anion was first generated in a solution containing 0.004 M KOH outside the stopped-flow apparatus and then immediately injected into one of the stopped-flow syringes for a subsequent stopped-flow experiment. For these experiments, solutions were prepared in a manner that they would neutralize the KOH used to generate the anions, and the remaining buffer is what we informed as reacting with the anions. The kOH1 values were obtained from 10 kinetic runs at [KOH] between 0.001–0.015 M. For the reactions with morpholine buffers, ten runs at total buffer concentrations ranging from 0.01 to 0.2 M were conducted at seven different pH values. The reactions with the other amines were run at only one pH, with 6–7 different total buffer concentrations ranging from 0.01 to 0.2 M.The absorption spectra were recorded on a diode array UV-Vis spectrophotometer.
pH and pKa measurements
The pH in 50% MeCN–50% water was calculated by adding 0.18 to the measured pH, according to Allen and Tidwell.24 The pKBHa values for the amines used were determined by measuring the pH of various buffer ratios and plotting log([B]/[BH+]) vs. pH according to the Henderson–Hasselbach equation, where the intercept is the pKa and the slope is unity. The pH of the reaction solutions for stopped-flow experiments were measured in mock-mixing experiments that mimicked the stopped-flow runs.Results
General features
The reactions were carried out in 50% MeCN–50% water at 25 °C. The primary amines employed were n-butylamine, furfurylamine, benzylamine, and 2-amino-2-(hydroxymethyl)propane-1,3-diol (TRIS), while the secondary amines were piperidine, piperazine, pyrrolidine and morpholine. When any of the thiocarbenes 5-M-R1 is placed into a KOH or amine buffer solution, a rapid conversion to the corresponding anion is observed. After the addition of a few drops of a concentrated HCl solution, the Fischer carbene is recovered. When this addition was done within 1–2 min after formation of the anion, recoveries were virtually quantitative, which indicates good reversibility of the proton transfer reaction (Fig. 1 is illustrative).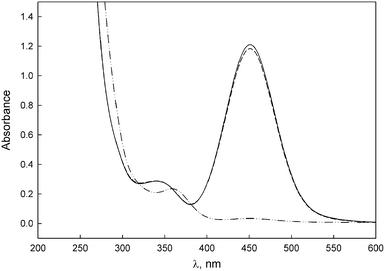 | ||
Fig. 1 UV-Vis spectra of (—) 1 × 10–4 M 5-Cr-iPr in 50% MeCN–50% water at 25 °C, (-··-) the corresponding anion obtained in 5 × 10–4 M KOH and (![[dash dash, graph caption]](https://www.rsc.org/images/entities/char_e091.gif) ) recovery after addition of acid. ) recovery after addition of acid. | ||
The reaction scheme for the reversible proton transfer from 5-M-R1 to a series of amine buffers and KOH consistent with the experiments described below is shown in Scheme 1.
 | ||
| Scheme 1 Reversible proton transfer for the carbene complexes 5-M-R1. | ||
The kinetic experiments were all carried out under pseudo-first order conditions with the Fischer carbenes as minor components. Hence, the general expression for the pseudo-first order rate constants is given by eqn (1).
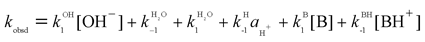 | (1) |
Spectrophotometric determination of the pKCHa values
For the chromium derivatives, various phosphate and borate buffers were used to measure the absorbances of mixtures of 5-Cr-R1 and 5-Cr-R1– in a pH range of 7–12. An illustrative example of the spectra obtained is shown in Fig. 2.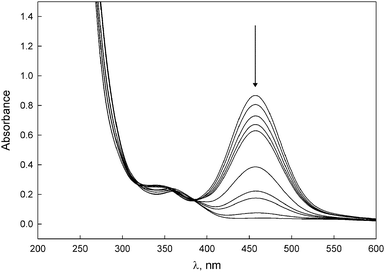 | ||
| Fig. 2 Spectra obtained for 5-Cr-tBu at different pH values. The arrow indicates the sense of increasing pH: 7.00, 8.00, 8.50, 8.75, 9.00, 9.75, 10.00, 10.50, 11.00, and 12.00. | ||
pKCHa (KCHa being the acidity constants of the Fischer carbene complexes studied) values were determined according to eqn (2), with ACH being the absorbance at pH ≪ pKCHa, A the absorbance at pH ∼ pKCHa and AC– the absorbance at pH ≫ pKCHa. Plots according to eqn (2) (not shown) were linear and yielded the pKCHa (spec) values summarized in Table 1.
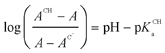 | (2) |
| Carbene complex | M = Cr | M = W | F + Rc | log Pd |
|
ν CH2R e |
|
|
|---|---|---|---|---|---|---|---|---|
| pKCHa (spec) | pKCHa (kin) | pKCHa (kin) | ||||||
| a The error reported is that of the linear fit, which underestimates the actual value. b Values taken from ref. 19. c Values taken for the alkyl substituent from ref. 25. d Calculated for the thiols R1SH according to Crippen and Ghose’s fragmentation method, see ref. 26. e Values taken from ref. 27. | ||||||||
| 5-M-Me b | 9.00 ± 0.21 | 9.05 ± 0.03 | 8.37 ± 0.06 | –0.17 | 0.56 | 1.0 | 0.56 | 1.0 |
| 5-M-tBu | 9.33 ± 0.03 | 9.17 ± 0.02 | 8.60 ± 0.05 | –0.20 | 1.43 | 2.6 | 1.34 | 2.4 |
| 5-M-iPr | 9.29 ± 0.03 | 9.18 ± 0.01 | 8.79 ± 0.05 | –0.15 | 1.21 | 2.2 | 0.98 | 1.8 |
| 5-M-nBu | 9.46 ± 0.04 | 9.24 ± 0.03 | 8.65 ± 0.01 | –0.16 | 1.80 | 3.2 | 0.68 | 1.2 |
| 5-M-cHex | 9.46 ± 0.04 | 9.35 ± 0.03 | 8.81 ± 0.08 | –0.15 | 2.10 | 3.8 | 0.97 | 1.7 |
Reactions with morpholine buffers. Kinetic determination of pKCHa
Rates of the reaction with morpholine buffers were determined in the pH range of 7.80–9.60. Most of the experiments were performed in the reverse direction, i.e. the anion was first generated in 0.004 M KOH, then these solutions were mixed with various morpholine buffers. Plots of kobsdvs. morpholinium ion concentration ([BH+]) were all linear with negligible intercepts (Fig. 3). This means that eqn (1) can be approximated by eqn (3), with KBHa being the acidity constant of BH+. | (3) |
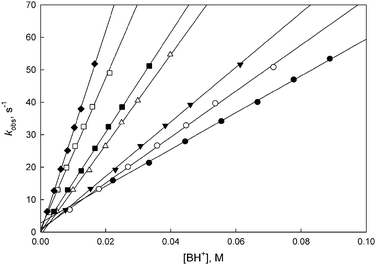 | ||
| Fig. 3 Representative plots for the proton transfer reaction of 5-W-iPr with morpholine buffers in 50% MeCN–50% water at 25 °C. (●) pH = 7.80, (○) pH = 8.30, (▼) pH = 8.50, (△) pH = 8.88, (■) pH = 9.00, (□) pH = 9.27, (◆) pH = 9.40. | ||
The slopes of the plots of kobsdvs. [BH+] are thus given by eqn (4). Fig. 4 shows representative plots of these slopes vs. 1/aH+, from which the kinetic acidity constants for the carbene complexes 5-M-R1 were obtained (pKCHa (kin) in Table 1). These plots also yield the kBH–1 values reported in Table 2; kB1 values were obtained as kBH–1KCHa/KBHa.
 | (4) |
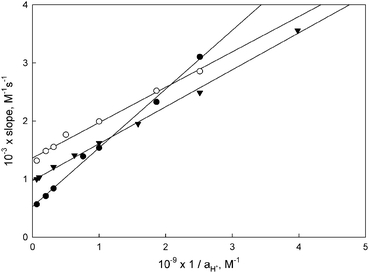 | ||
| Fig. 4 Slopes vs. 1/aH+ according to eqn (4) for the reactions of 5-Cr-cHex (○), 5-Cr-iPr (▼) and 5-W-iPr (●) with morpholine buffers. | ||
| M | R1 | k B1/M–1 s–1 | k BH–1/M–1 s–1 |
|---|---|---|---|
| a Standard deviation given for rate constants determined directly. b Values taken from ref. 19. | |||
| Cr | Methylb | 441 | 946 ± 30 |
| tert-Butyl | 260 | 820 ± 20 | |
| Isopropyl | 320 | 970 ± 20 | |
| n-Butyl | 370 | 1320 ± 30 | |
| Cyclohexyl | 300 | 1400 ± 30 | |
| W | Methylb | 927 | 414 ± 55 |
| tert-Butyl | 471 | 373 ± 23 | |
| Isopropyl | 476 | 592 ± 40 | |
| n-Butyl | 630 | 564 ± 5 | |
| Cyclohexyl | 500 | 641 ± 49 | |
Reaction with KOH and various amine buffers
For the chromium derivatives, rates of deprotonation by OH– and a series of primary aliphatic and secondary alicyclic amines were also determined.In KOH, rates were determined in the range [KOH] = 0.001–0.015 M. Plots of kobsdvs. [KOH] were linear with negligible intercepts (Fig. S1 in the ESI†). From the slopes kOH1 values were obtained and are reported in Table 3; whereas k–1H2O values were obtained as kOH1Kw/KCHa; where Kw is the solvent ionization constant. For the solvent used in this study pKw = 15.19.24
| B | pKBHa | K B1/M–1 s–1 | k BH–1/M–1 s–1 | k B1/M–1 s–1 | k BH–1/M–1 s–1 |
|---|---|---|---|---|---|
| a Standard deviation given for rate constants determined directly. b TRIS, 2-amino-2-(hydroxymethyl)propane-1,3-diol. c Rate constant values in s–1. | |||||
| 5-Cr-iPr | 5-Cr-tBu | ||||
| OH– | 16.64 | 872 ± 4 | 8.5 × 10–4 c | 809 ± 7 | 8.2 × 10–4 c |
| Pyrrolidine | 11.19 | 6814 ± 347 | 67 | 7261 ± 556 | 73 |
| Piperidine | 11.01 | 3273 ± 167 | 48 | 2937 ± 232 | 45 |
| Piperazine | 9.97 | 1035 ± 41 | 168 | 753 ± 58 | 126 ± 19 |
| n-BuNH2 | 10.40 | 927 ± 45 | 56 | 1007 ± 79 | 63 |
| Benzylamine | 9.12 | 346 | 403 ± 19 | 346 ± 53 | 420 ± 35 |
| Furfurylamine | 8.58 | 156 | 623 ± 33 | 156 ± 24 | 639 ± 56 |
| TRISb | 8.32 | 4.4 | 32 ± 2 | 2.8 ± 0.5 | 21 ± 2 |
| 5-Cr-nBu | 5-Cr-cHex | ||||
| OH– | 16.64 | 739 ± 10 | 8.7 × 10–4 c | 559 ± 8 | 8.6 × 10–4 c |
| Pyrrolidine | 11.19 | 7618 ± 624 | 89 | 6599 ± 482 | 101 |
| Piperidine | 11.01 | 4174 ± 324 | 74 | 3508 ± 230 | 82 |
| Piperazine | 9.97 | 1073 ± 78 | 209 | 805 ± 53 | 205 |
| n-BuNH2 | 10.40 | 1118 ± 81 | 81 ± 11 | 959 ± 62 | 91 ± 11 |
| Benzylamine | 9.12 | 395 ± 54 | 552 ± 41 | 335 ± 39 | 612 ± 39 |
| Furfurylamine | 8.58 | 163 ± 22 | 778 ± 57 | 141 ± 18 | 885 ± 64 |
| TRISb | 8.32 | 4.1 ± 0.6 | 36 ± 3 | 3.5 ± 0.5 | 40 ± 3 |
In amine buffer solutions, depending on the pKBHa, reactions were either run in the forward direction (for pKBHa > pKCHa) or in the reverse direction (for pKBHa < pKCHa). For any given amine, reactions were run at only one pH value. In all cases, the plots of kobsdvs. [B] or kobsdvs. [BH+] were linear, with slopes given by eqn (5) (plots vs. [B]) or eqn (4) (plots vs. [BH+]). The values of kB1 and kBH–1 were obtained from the slopes and the known pKCHa (kin) values.
 | (5) |
Discussion
Mechanism
We attribute the observed reaction to the proton transfer from the carbene complex to the various bases used, as depicted in Scheme 1 for several reasons: (i) nucleophilic substitution can be discarded in view of the virtually quantitative recovery of 5-M-R1 upon acidification. Nucleophilic substitution with amines is actually observed, but it occurs on a slower time scale. A detailed study of these reactions will be the subject of a future report; (ii) reversible nucleophilic addition to form tetrahedral adducts can also be excluded as the source of the observed kinetic process because these are intermediates in the substitution reactions and no accumulation of such intermediates is observed in the substitution reactions of 5-M-Me (M = Cr or W).28 Therefore, there is no reason to support the formation of a stable tetrahedral intermediate in the reactions reported here; (iii) there is great similarity in the behavior of the substrates 5-M-R1 with that of the previously studied carbene complexes 5-Cr-Me (M = Cr, R1 = methyl) and 5-W-Me (M = W, R1 = methyl).19Effects of R1 and the metal on the thermodynamic acidity
For the purpose of this discussion we will use the acidity constants determined from the kinetic experiments (labeled as pKCHa (kin) in Table 1) as they are not influenced by the decomposition of the conjugate base of the substrates, making them more reliable than the values determined spectrophotometrically. Nevertheless, it should be noted that the trends are the same whichever set is used for comparison purposes.29In principle the structural modification introduced can affect the stability of either the carbene complex, the corresponding anion or both.
Although the difference in pKCHa is not large (0.30 pK units for M = Cr and 0.44 pK units for M = W), there is a clear trend of decreasing acidity in the sense R1 = methyl > tert-butyl ∼ isopropyl ∼ n-butyl > cyclohexyl. The magnitude of the errors involved in the determination of the pKCHa values preclude a more clear-cut distinction in the order for the substrates that lie in the middle of the range, but the difference between the extremes is quite clear and beyond experimental uncertainties.
Since the resonance structure 5-M-R1± appears to play a dominant role in the stabilization of carbene complexes,30 the contribution from the combined inductive/field and resonance effects (F + R in Table 1) is expected to mostly stabilize 5-M-R1± and would not affect the anions, in which the negative charge is delocalized into the CO ligands relatively far away from the SR1 group.
This was the argument used to explain the difference in acidity between 6-Cr-Me (pKCHa = 12.50) and 6-Cr-Et (12.98).20
Considering the sum F + R as a measure of the electronic effect of R1, we can see in Table 1 that there is not a significant difference in the values for the series studied. So, from this point of view, all of the pKCHa values should be about the same. If there were any difference, 5-M-tBu should be the least acidic, but this does not correlate with the experimental findings.
One other factor that should not be set aside is the steric effect of SR1. In the resonance structure 5-M-R1± a planar conformation is required for optimum overlap of the sulfur d orbitals and the empty pz orbital in the carbene carbon. A bulkier R1 group will make this conformation less favorable, thus causing a less efficient π-donation by the heteroatom and destabilizing the carbene complex. This reduced π-overlap efficiency has been observed for a series of Fischer aminocarbene complexes by 53Cr-NMR studies, in which it was demonstrated that a bulkier substituent on the heteroatom causes a decrease in the charge density on the chromium atom.31 This steric interference on π-overlap also manifests itself in reduced C–O and C–N bond orders obtained from X-ray crystallography.30a For the carbene complexes 5-Cr-R1, there is a noticeable shift in λmax for the metal–ligand charge transfer band in the UV-Vis spectra. A ∼10 nm shift to the red is observed from R1 = methyl (448 nm) to R1 = tert-butyl (457 nm). A shift to longer wavelengths of this band is usually attributed to a lower bond order between the heteroatom and the carbene carbon.32 Thus, the steric effect of the bulkier isopropyl, cyclohexyl and tert-butyl substituents (νCH2R in Table 1) is expected to enhance the acidity of the corresponding carbene complexes.
Another factor that should be considered is the hydrophobicity of R1 (log P in Table 1). The more hydrophobic R1 becomes, the more disrupted would be the solvation sphere of the carbene complex and that of the corresponding anion. Since the latter bears a full charge, it is expected to be the most affected by this structural modification, hence making the carbene complex less acidic with increasing hydrophobicity.
We can see from the values listed in Table 1 that there is a significant change in log P for the series studied, with R1 = cyclohexyl being about four times more hydrophobic than R1 = methyl. While this and the other factors discussed above (steric and electronic effects) appear to compensate each other for R1 = tert-butyl, n-butyl and isopropyl, it seems to be the predominant factor decreasing the acidity for R1 = cyclohexyl.
Tungsten carbene complexes are slightly more acidic than the corresponding chromium analogs. This is reminiscent of previous observations for alkoxy20 as well as for thiocarbene complexes.19 The difference in pKCHa values is slightly higher for M = W (0.44 units) than for M = Cr (0.30 units). However, this difference is relatively small with respect to the experimental errors, so no interpretation of this small metal dependence will be attempted.
Effects of R1 and the metal on the kinetic acidity
There is a very good linear correlation between the catalytic rate constants for the deprotonation in KOH (see kB1 values for OH– entry in Table 3) of the substrates with M = Cr and their acidity constants (Fig. 5). The linear plot yields a slope of 1.09 ± 0.09.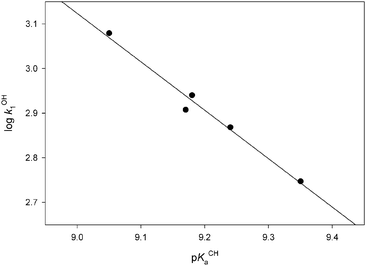 | ||
| Fig. 5 Correlation between the kinetic acidity in KOH (kOH1 = kB1 for OH– entry in Table 3) and the thermodynamic acidity for the chromium carbene complexes studied. | ||
Since these reactions have fairly large equilibrium constants, a relatively early transition state is expected according to the Hammond–Leffler postulate.33 The large value of the slope in the correlation of log kOH1vs. log KCHa, seems to contradict this assumption. The transition state seems to be affected by the change in the R1 substituent to the same extent as the corresponding carbanion. This is reflected in the unchanging k–1H2O values obtained for all the substrates.
This apparent contradiction is the result of the base bearing a negative charge. The transition state of these proton transfer reactions also has a full negative charge, so the hydrophobicity effect exerted by R1 will be ‘felt’ by the transition state to about the same extent as the carbanion that results from the reaction.
The steric effect of R1 seems to play an important role in the kinetic acidity of this series of carbene complexes in the reactions with amines. This is evidenced, on the one hand, by the abnormal reactivity of TRIS and pyrrolidine. TRIS is less reactive, whereas pyrrolidine is more reactive than expected from their pKBHa values. The fact that the relative reactivity between a relatively unhindered amine such as n-butylamine and TRIS is higher for the substrate with R1 = tert-butyl (360-fold) than for the substrate with R1 = n-butyl (270-fold), supports the notion that steric effects are important.
Unlike the other primary amines, TRIS has three bulky substituents on the carbon directly bonded to the nitrogen. So, in all of its possible conformations, one of the bulky hydroxymethylene substituents is placed towards the reaction center. Pyrrolidine is the only five-membered ring secondary amine used in this study. Its reduced size could contribute to a decreased steric hindrance in the transition state.
On the other hand, for the secondary 6-membered ring amines, 5-M-tBu are always less reactive than 5-M-cHex, although the former is more acidic and, hence, has a larger thermodynamic driving force. This fact points to a reduced intrinsic reactivity of the former substrates in these reactions.34
The steric effect seems to be more pronounced on the tungsten derivatives, as is evident from the comparison of the kB1(methyl)/kB1(tert-butyl) ratios. With B = morpholine, this ratio is 1.70 for M = Cr, while it increases to 1.97 with M = W. This could be explained in terms of a more advanced transition state, which is a consequence of a more favourable equilibrium constant towards deprotonation.
Intrinsic rate constants and transition states imbalances. Effects of R1 and the metal
Intrinsic rate constants for the chromium derivatives were determined from the corresponding Eigen plots. Fig. 6 shows a representative plot of kB1 and kBH–1vs. pKBHa – pKCHa + log (p/q).36 The intrinsic rate constants are extracted as log k0 from the intercepts of these plots. The values for log k0 and the Brønsted coefficients are summarized in Table 4. | ||
| Fig. 6 Eigen plot for the proton transfer reaction of 5-Cr-nBu. Filled symbols for kB1; open symbols for kBH–1. (●, ○) Primary amines; (■, □) secondary amines. | ||
| Carbene complex | pKCHa | Base type | α B b | β B c | log k0d |
|---|---|---|---|---|---|
| a Values taken from ref. 19. b Obtained as the slopes of the plots of log KBH–1vs. pKBHa – pKCHa + log(p/q). c Obtained as the slopes of the plots of log KB1vs. pKBHa – pKCHa + log(p/q). d Obtained as the intercepts of the plots of log kB1 or log kBH–1vs. pKBHa – pKCHa + log(p/q). | |||||
| 5-Cr-Me a | 9.05 | RNH2 | 0.52 ± 0.04 | 0.48 ± 0.04 | 2.09 ± 0.08 |
| R2NH | 0.55 ± 0.06 | 0.45 ± 0.06 | 2.61 ± 0.10 | ||
| 5-Cr-tBu | 9.17 | RNH2 | 0.58 ± 0.07 | 0.42 ± 0.07 | 2.31 ± 0.07 |
| R2NH | 0.54 ± 0.14 | 0.46 ± 0.14 | 2.39 ± 0.18 | ||
| 5-Cr-iPr | 9.18 | RNH2 | 0.59 ± 0.07 | 0.41 ± 0.07 | 2.30 ± 0.07 |
| R2NH | 0.56 ± 0.11 | 0.44 ± 0.11 | 2.50 ± 0.14 | ||
| 5-Cr-nBu | 9.24 | RNH2 | 0.57 ± 0.08 | 0.43 ± 0.08 | 2.37 ± 0.08 |
| R2NH | 0.53 ± 0.14 | 0.47 ± 0.14 | 2.58 ± 0.17 | ||
| 5-Cr-cHex | 9.35 | RNH2 | 0.57 ± 0.08 | 0.43 ± 0.08 | 2.36 ± 0.07 |
| R2NH | 0.52 ± 0.16 | 0.48 ± 0.16 | 2.53 ± 0.19 | ||
The Brønsted coefficient values are all within the usual range for the proton transfer from Fischer carbene complexes 17–19 and many other carbon acids,37 so no further comments will be made regarding these parameters.
The intrinsic rate constants are slightly lower for the reactions with primary amines than with secondary amines. In proton transfer reactions secondary amines are usually more reactive than primary amines. This is mainly due to a higher solvation energy of the ammonium ion for the primary amines, combined with the fact that solvation is only incipiently developed at the transition state. This leads to differences of log k0(R2NH) – log k0(RNH2) between 0.8–1.0 logarithmic units. Smaller differences imply the operation of steric effects.16c In the proton transfer reactions for the substrates 5-Cr-R1 this difference is much smaller than the usual values. Furthermore, there is a decrease in the sense R1 = methyl (0.52) ≫ n-butyl (0.21) ∼ isopropyl (0.20) > cyclohexyl (0.17) ≫ tert-butyl (0.08). This finding is a clear indication that steric effects are operating in the transition state of the proton transfer reaction.
Conclusions
The hydrophobicity of the R1 group plays a significant role in determining the thermodynamic acidity of the Fischer carbenes 5-M-R1, making these compounds slightly less acidic in the sense R1 = methyl > tert-butyl ∼ isopropyl ∼ n-butyl > cyclohexyl.On the other hand, the kinetic acidity is reduced in the following order: R1 = methyl > n-butyl > isopropyl ∼ cyclohexyl > tert-butyl. This result can be interpreted in terms of the steric effect exerted by the substituent, which is also manifested as a reduction in the intrinsic reactivity of secondary amines with respect to primary amines.
The greater stabilization of the negative charge by the W(CO)5 moiety compared to the Cr(CO)5 makes the former carbene complexes both thermodynamically and kinetically more acidic. With respect to the kinetic acidity, the steric bulkiness of R1 is manifested slightly stronger in the W carbene complexes due to a more advanced transition state.
Acknowledgements
This research was supported in part by the Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET), Fundación Antorchas, Agencia Nacional de Promoción Científica y Técnica (ANPCYT) and the Universidad Nacional de Córdoba, Argentina. M. E. Z. M. and D. M. A. are grateful recipients of fellowships from CONICET.References
- E. O. Fischer and A. Maasböl, Angew. Chem., Int. Ed. Engl., 1964, 3, 580–581 CrossRef.
- (a) J. Barluenga, M. A. Fernández-Rodríguez and E. Aguilar, J. Organomet. Chem., 2005, 690, 539–587 CrossRef CAS; (b) Y. T. Wu, M. Noltemeyer and A. de Meijere, Eur. J. Org. Chem., 2005, 2802–2810 CrossRef CAS; (c) V. Capriati, S. Florio, R. Luisi, F. M. Perna and J. Barluenga, J. Org. Chem., 2005, 70, 5852–5858 CrossRef CAS; (d) J. Barluenga, J. Santamaría and M. Tomás, Chem. Rev., 2004, 104, 2259–2283 CrossRef CAS; (e) M. A. Sierra, Chem. Rev., 2000, 100, 3591–3697 CrossRef CAS; (f) A. de Meijere, H. Schimer and M. Duetsch, Angew. Chem., Int. Ed., 2000, 39, 3964–4002 CrossRef CAS; (g) J. Barluenga and F. J. Fañañás, Tetrahedron, 2000, 56, 4597–4628 CrossRef CAS.
- (a) C. F. Bernasconi, Adv. Phys. Org. Chem., 2002, 37, 137–237 CAS; (b) C. F. Bernasconi, Chem. Soc. Rev., 1997, 26, 299–307 RSC; (c) J. Barluenga, J. Flórez and F. J. Fañañás, J. Organomet. Chem., 2001, 624, 5–17 CrossRef CAS.
- (a) C. P. Casey, N. W. Vollendrof and K. J. Haller, J. Am. Chem. Soc., 1984, 106, 3754–3764 CrossRef CAS; (b) K. H. Dötz and M. Popall, Tetrahedron, 1985, 41, 5797–5802 CrossRef; (c) K. H. Dötz, T. Schäfer, F. Kroll and K. Harms, Angew. Chem., Int. Ed. Engl., 1992, 31, 1236–1238 CrossRef; (d) C. A. Toledano, H. Rudler, J.-C. Daran and Y. Jeannin, J. Chem. Soc., Chem. Commun., 1984, 574–576 RSC.
- (a) J. Barluenga, F. Rodríguez, J. Vadecard, M. Bendix, F. J. Fañañás, F. López-Ortiz and M. A. Rodríguez, J. Am. Chem. Soc., 1999, 121, 8776–8782 CrossRef CAS; (b) M. A. Sierra, M. J. Mancheño, E. Sáez and J. C. del Amo, J. Am. Chem. Soc., 1998, 120, 6812–6813 CrossRef CAS.
- (a) M. Zora and J. W. Herndon, Organometallics, 1993, 12, 248–249 CrossRef CAS; (b) M. Zora, Y. Li and J. W. Herndon, Organometallics, 1999, 18, 4429–4436 CrossRef CAS.
- Recent selected references: (a) J. Barluenga, A. Gómez, A. de Prado, N. Panday, J. Santamaría and M. Tomás, Tetrahedron, 2007, 63, 6542–6547 CrossRef CAS; (b) J. Barluenga, S. Martínez, A. L. Suárez-Sobrino and M. Tomás, J. Organomet. Chem., 2005, 690, 5696–5700 CrossRef CAS; (c) A. de Meijere, H. Schirmer, F. Stein, F. Funke, M. Duetsch, Y.-T. Wu, M. Noltemeyer, T. Belgardt and B. Knieriem, Chem.–Eur. J., 2005, 11, 4132–4148 CrossRef CAS; (d) K. Kamikawa, Y. Shimizu, H. Matsuzaka and M. Uemura, J. Organomet. Chem., 2005, 690, 5922–5928 CrossRef CAS; (e) Y.-T. Wu, B. Flynn, H. Schirmer, F. Funke, S. Müller, T. Labahn, M. Nötzel and A. de Meijere, Eur. J. Org. Chem., 2004, 724–748 CrossRef CAS; (f) Y.-T. Wu, T. Labahn, A. Demeter, K. A. Zachariasse and A. de Meijere, Eur. J. Org. Chem., 2004, 4483–4491 CrossRef CAS; (g) J. Barluenga, M. A. Fernández-Rodríguez, F. Andina and E. Aguilar, J. Am. Chem. Soc., 2002, 124, 10978–10979 CrossRef CAS; (h) J. Barluenga, S. Martínez, A. L. Suárez-Sobrino and M. Tomás, J. Am. Chem. Soc., 2001, 123, 11113–11114 CrossRef CAS; (i) J. Barluenga, F. Aznar and M. A. Palomero, Chem.–Eur. J., 2001, 7, 5318–5324 CrossRef CAS; (j) J. Barluenga, M. A. Fernández-Rodríguez, E. Aguilar, F. Fernández-Marí, A. Salinas and B. Olano, Chem.–Eur. J., 2001, 7, 3533–3544 CrossRef CAS; (k) J. Barluenga, F. Fernández-Marí, R. González, E. Aguilar, G. A. Revelli, A. L. Viado, F. J. Fañañás and B. Olano, Eur. J. Org. Chem., 2000, 1773–1783 CrossRef CAS.
- A. M. Granados, J. Kreiker, R. H. de Rossi, P. Fuertes and T. Torroba, J. Org. Chem., 2006, 71, 808–810 CrossRef CAS.
- M. A. Sierra, M. Gómez-Gallego and R. Martínez-Álvarez, Chem.–Eur. J., 2007, 1, 736–744 CrossRef.
- C. G. Kreiter, Angew. Chem., Int. Ed. Engl., 1968, 7, 390–391 CrossRef CAS.
- (a) W. D. Wulff, B. A. Anderson and L. D. Isaacs, Tetrahedron Lett., 1989, 30, 4061–4064 CrossRef CAS; (b) Y.-C. Xu and W. D. Wulff, J. Org. Chem., 1987, 52, 3263–3275 CrossRef CAS; (c) C. P. Casey and W. R. Brunsvold, Inorg. Chem., 1977, 16, 391–396 CrossRef CAS; (d) C. P. Casey and W. R. Brunsvold, J. Organomet. Chem., 1976, 118, 309–323 CrossRef CAS; (e) C. P. Casey and W. R. Brunsvold, J. Organomet. Chem., 1975, 102, 175–183 CrossRef CAS; (f) C. P. Casey and R. L. Anderson, J. Organomet. Chem., 1974, 73, C28–C30 CrossRef CAS; (g) C. P. Casey and W. R. Brunsvold, J. Organomet. Chem., 1974, 77, 345–352 CrossRef CAS; (h) C. P. Casey, R. A. Boggs and R. L. Anderson, J. Am. Chem. Soc., 1972, 94, 8947–8949 CrossRef CAS.
- W. D. Wulff, B. A. Anderson, A. J. Toole and Y.-C. Xu, Inorg. Chim. Acta, 1994, 220, 215–231 CrossRef CAS.
- Y. Shi, W. D. Wulff, G. P. A. Yap and A. L. Rheingold, Chem. Commun., 1996, 2601–2602 RSC.
- F. Nitsche, R. Aumann and R. Frölich, J. Organomet. Chem., 2007, 692, 2971–2989 CrossRef CAS , and references cited therein.
- (a) C. F. Bernasconi, M. L. Ragains and S. Bhattacharya, J. Am. Chem. Soc., 2003, 125, 12328–12336 CrossRef CAS; (b) C. F. Bernasconi, V. Ruddat, P. J. Wenzel and H. Fischer, J. Org. Chem., 2004, 69, 5232–5239 CrossRef CAS; (c) C. F. Bernasconi and M. L. Ragains, J. Organomet. Chem., 2005, 690, 5616–5624 CrossRef CAS.
- (a) C. F. Bernasconi, Tetrahedron, 1985, 41, 3219–3233 CrossRef CAS; (b) C. F. Bernasconi, Acc. Chem. Res., 1987, 20, 301–308 CrossRef CAS; (c) C. F. Bernasconi, Adv. Phys. Org. Chem., 1992, 27, 119–237 CAS; (d) C. F. Bernasconi, Acc. Chem. Res., 1992, 25, 9–16 CrossRef CAS.
- C. F. Bernasconi and V. Ruddat, J. Am. Chem. Soc., 2002, 124, 14968–14976 CrossRef CAS.
- C. F. Bernasconi and W. Sun, J. Am. Chem. Soc., 1993, 115, 12526–12532 CrossRef CAS.
- C. F. Bernasconi and M. Ali, J. Am. Chem. Soc., 1999, 121, 3039–3045 CrossRef CAS.
- C. F. Bernasconi and W. Sun, Organometallics, 1997, 16, 1926–1932 CrossRef CAS.
- (a) M. Cases, G. Frenking, M. Duran and M. Solà, Organometallics, 2002, 21, 4182–4191 CrossRef CAS; (b) H. Jacobsen and T. Ziegler, Organometallics, 1995, 14, 224–230 CrossRef CAS.
- M. E. Zoloff Michoff, R. H. de Rossi and A. M. Granados, J. Org. Chem., 2006, 71, 2395–2401 CrossRef CAS.
- A. Yamashita, A. Toy, N. B. Ghazal and C. R. Muchmore, J. Org. Chem., 1989, 54, 4481–4483 CrossRef CAS.
- A. D. Allen and T. T. Tidwell, J. Am. Chem. Soc., 1987, 109, 2774–2780 CrossRef CAS.
- C. Hansch, A. Leo and R. W. Taft, Chem. Rev., 1991, 91, 165–195 CrossRef CAS.
- A. K. Ghose and G. M. Crippen, J. Chem. Inf. Comput. Sci., 1987, 27, 21–35 CrossRef CAS.
- M. Charton, J. Am. Chem. Soc., 1975, 97, 1552–1556 CrossRef CAS.
- (a) M. Ali, New J. Chem., 2003, 27, 349–353 RSC; (b) M. Ali and D. Maiti, J. Organomet. Chem., 2004, 689, 3520–3527 CrossRef; (c) M. Ali, S. Gangopadhyay and Md. Mijanudin, J. Organomet. Chem., 2005, 690, 4878–4885 CrossRef CAS.
- The thermodynamic pKCHa of 5-W-R1 were not determined due to the rapid decomposition of the corresponding anions, so that precise values could not be obtained.
- (a) K. H. Dötz, H. Fischer, P. Hofmann, F. R. Schubert and K. Weiss, Transition Metal Complexes, Verlag Chemie, Deerfield Beach, FL, 1983 Search PubMed; (b) U. Schubert, Coord. Chem. Rev., 1984, 55, 261–286 CrossRef CAS.
- A. Hafner, L. S. Hegedus, G. deWeck, B. Hawkins and K. H. Dötz, J. Am. Chem. Soc., 1988, 110, 8413–8421 CrossRef CAS.
- J. A. Connor and E. M. Jones, J. Chem. Soc. A, 1971, 1974–1978 RSC.
- (a) G. S. Hammond, J. Am. Chem. Soc., 1955, 77, 334–338 CrossRef CAS; (b) J. E. Leffler, Science, 1953, 117, 340–341 CrossRef CAS.
- This observation becomes evident when inspecting the simplest version of the Marcus equation:35 log k0 = log k1 – 0.5 log K1, where k0 refers to the intrinsic rate constant for a one step reaction, k1 refers to the forward rate constant and K1 to the reaction equilibrium constant. In our case K1 = KCHa/KBHa, which is a measure of the thermodynamic driving force of the reaction, and k1 is the kinetic acidity. When comparing, for example, 5-Cr-tBu and 5-Cr-cHex reacting with any secondary 6-member ring amine, both ratios KtBu1/KcHex1 (> 1) and ktBu1/kcHex1 (< 1) contribute to a decrease in the intrinsic reactivity of the tert-butyl derivative with respect to the cyclohexyl substituted carbene complex, i.e. ktBu0/kcHex0 < 1.
- (a) R. A. Marcus, J. Chem. Phys., 1965, 43, 679–701 CrossRef CAS; (b) R. A. Marcus, J. Phys. Chem., 1968, 72, 891–899 CrossRef CAS.
- q and p are statistical factors: q is the number of equivalent basic sites on B, while p is the number of equivalent protons on BH+.
- (a) R. P. Bell, The Proton in Chemistry, Chapman and Hall Ltd, London, 1973 Search PubMed; (b) A. J. Kresge, The Brønsted Relation; Significance of the Exponent, in Proton-Transfer Reactions, ed. E. Caldin and V. Gold, Chapman and Hall Ltd, London, 1975, pp. 179–199 Search PubMed; (c) C. F. Bernasconi and P. Paschalis, J. Am. Chem. Soc., 1986, 108, 2969–2977 CrossRef CAS; (d) C. F. Bernasconi and F. Terrier, J. Am. Chem. Soc., 1987, 109, 7115–7121 CrossRef CAS; (e) C. F. Bernasconi, D. A. V. Kliner, A. S. Mullin and J. X. Ni, J. Org. Chem., 1988, 53, 3342–3351 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Fig. S1, plots of kobsdvs. [KOH] for 5-Cr-R1; Table S1 containing the kobsd values for the reactions of 5-W-iPr in morpholine buffers. Characterization and IR, 1H and 13C NMR spectra of carbene complexes 5-M-R1. See DOI: 10.1039/b709504j. |
| This journal is © The Royal Society of Chemistry and the Centre National de la Recherche Scientifique 2008 |