Multiple calcium binding sites make calmodulin multifunctional†
Najl V.
Valeyev
*a,
Pat
Heslop-Harrison
b,
Ian
Postlethwaite
a,
Nicolai V.
Kotov
c and
Declan G.
Bates
a
aSystems Biology Lab, Department of Engineering, University of Leicester, University Road, Leicester, UK LE1 7RH. E-mail: nv28@le.ac.uk; Tel: +44 (0) 7817 068953
bSystems Biology Lab, Department of Biology, University of Leicester, University Road, Leicester, UK LE1 7RH
cBiophysics & Bionics Lab, Department of Physics, Kazan State University, Kazan, 420008, Russia
First published on 30th October 2007
Abstract
Protein –protein or protein –ion interactions with multisite proteins are essential to the regulation of intracellular and extracellular events. There is, however, limited understanding of how ligand–multisite protein interactions selectively regulate the activities of multiple protein targets. In this paper, we focus on the important calcium (Ca2+) binding protein calmodulin (CaM), which has four Ca2+ ion binding sites and regulates the activity of over 30 other proteins . Recent progress in structural studies has led to significant improvements in the understanding of Ca2+–CaM-dependent regulation mechanisms. However, no quantitative model is currently available that can fully explain how the structural diversity of protein interaction surfaces leads to selective activation of protein targets. In this paper, we analyze the multisite protein –ligand binding mechanism using mathematical modelling and experimental data for Ca2+–CaM-dependent protein targets. Our study suggests a potential mechanism for selective and differential activation of Ca2+–CaM targets by the same CaM molecules, which are involved in a variety of intracellular functions. The close agreement between model predictions and experimental dose–response curves for CaM targets available in the literature suggests that such activation is due to the selective activity of CaM conformations in complexes with variable numbers of Ca2+ ions. Although the paper focuses on the Ca2+–CaM pair as a particularly data rich example, the proposed model predictions are quite general and can easily be extended to other multisite proteins . The results of the study may therefore be proposed as a general explanation for multifunctional target regulation by multisite proteins .
Introduction
Protein molecules with multiple ligand binding sites regulate a vast range of intracellular components. Despite the ubiquity of multisite interaction-dependent protein regulation, the exact mechanism through which multisite proteins differentially regulate the activity of intracellulareffectors , and thereby participate in a diverse range of physiological processes, is still not clearly understood. In this paper, we adopt a structural systems biology approach1 to address this question. We have chosen to use CaM, a protein that binds four Ca2+ ions, as a data rich example of an important multifunctional protein in our study. Ca2+ bindingproteins constitute an important class of multi-ligand proteins because they are involved in more than 50 Ca2+-dependent regulation mechanisms2 mediated through more than 30 interacting proteins . Ca2+–calmodulin complexes and other proteins with multiple Ca2+ binding sites themselves bind to and modulate many targets, so Ca2+–multisite protein interactions are crucial for understanding Ca2+-dependent physiology. It has been shown that helix–loop–helix structures (EF-hand motifs) bind Ca2+ ions, and Ca2+ and EF-hand protein interactions are believed to transduce Ca2+ alterations in intracellular space and time into a wide variety of intracellular signals.3 The most ubiquitous Ca2+-dependent protein , CaM (Fig. 1A), contains four EF-hand motifs.4 The EF-hand domains share high overall sequence homology (about 75%) and structural similarity, both in the presence and absence of Ca2+ ions. NMR characterization of calmodulin has revealed significant differences in dynamics between N- and C-terminal domains, which appeared to influence their independent function.5 | ||
| Fig. 1 Alternative mechanisms for Ca2+–CaM-dependent target activation selectivity. The mechanism of Ca2+–CaM protein (1CLL8) (A) dependent regulation is shown in (B–D). The ligand concentration-dependent profiles for the apo (1DMO6) and saturated Ca2+–CaM (1CLL8) states are usually the only CaM conformations analyzed in the Ca2+–CaM-dependent studies (B). However, the number of possibilities for selective activation of different targets by the same multisite proteins is limited if the second messenger proteins are governed by a fully bound multisite protein only (C). The ligand concentration-dependent distribution of intermediate Ca2+–CaM conformations allows a higher degree of multisite protein -dependent selective regulation (D). | ||
The traditional model for CaM activation suggests that the CaM structure undergoes conformational changes upon Ca2+ ions binding to the EF-hand domains. It is frequently assumed that the apo- conformation6 is inactive whereas CaM becomes activated in a fully Ca2+ bound state.7 A conventional explanation for cooperative multiple binding is to ensure a steep slope/switch for the on–off response of the target in response to a gradually changing ligand concentration. Fig. 1B illustrates the Ca2+ concentration-dependent profiles for apo- (1DMO6) and fully Ca2+-bound (Ca2+)4 CaM (1CLL8) conformations. This graph shows that the concentration of apo-CaM decreases as the level of Ca2+ increases, whereas the (Ca2+)4–CaM complexes have a progressively higher probability of formation. Selective target activation by the same (Ca2+)4–CaM molecules is believed to be due to the unique CaM–target binding interface.9
Studies of the structure of CaM provide fundamental information for understanding multisite Ca2+–CaM interactions and consequent target activation.9,10 However, it is still unclear how activation selectivity can be achieved if targets are activated only by fully ligand bound CaM. To illustrate this point, Fig. 1C depicts a schematic range of dose–response curves for three hypothetical targets all activated by the same fully ligand bound multisite protein . The ligand concentration ranges, L1 to L4, where the target activities can differ are shown. When the ligand concentration varies within the range L1 all three target proteins are inactive. The target 2 becomes active as ligand concentration increases to L2. In the ligand range L3 the target 2 is at the highest saturating degree of activity, whereas target proteins 1 and 3 have variable activities. Finally, when the ligand reaches the highest L4 concentration level, all three proteins are at their highest activity states. It follows from this diagram that there is a range of ligand concentration for which target 2 can be active while targets 1 and 3 remain near their basal levels. On the other hand, it is impossible to activate target 3 without activating targets 1 and 2. Biologically meaningful modulation of selectivity with this type of mechanism for target activation is thus clearly quite limited.
In addition, a significant amount of experimental evidence is now available that also casts doubt on the view that only saturated multisite proteins can activate targets: the shape of some concentration–response profiles is not sigmoid for some multisite-dependent proteins . In fact, the concentration-dependent profiles for several Ca2+–CaM-dependent protein targets exhibit quite a diverse range of behaviour. Plasma membraneCa2+ pump (PMCA) and phosphodiesterase (PDE) protein concentrations in the active state, for example, reveal “Hill-shape”-like curves, whereas ryanodine receptor (RyR) is inhibited by increasing Ca2+ concentration.11Adenylate cyclase I (ACI) isoforms, on the other hand, exhibit bell-shaped concentration-dependent profiles.12,13 It has also been shown that CaMPKII,14 as well as the K+ channel from paramecium,15 are activated by CaM with two bound Ca2+ ions.
To investigate why Ca2+–CaM binding to a target molecule leads to essentially different Ca2+-dependent profiles, we developed a model of multisite Ca2+ binding to CaM and CaM-dependent regulation of target proteins . The main biochemical prediction that follows from our analysis of this model is that intermediate Ca2+–CaM complexes, with variable numbers of bound Ca2+ ions, i.e. (Ca2+)0–CaM, (Ca2+)1–CaM, (Ca2+)2–CaM, (Ca2+)3–CaM, and not only (Ca2+)4–CaM, can selectively activate a target or a combination of target proteins . The results suggest that the selectivity is largely due to the differences in ligand concentrations where targets are activated. This prediction qualitatively distinguishes the current work from previously published papers describing mechanisms of selective activation. The Ca2+–CaM system is considered in this study due to the vast amount of reliable experimental data available in the literature. However, the proposed mechanism for Ca2+–CaM-dependent differential regulation can clearly be extended to other multisite protein -dependent targets, and may, therefore, provide a general explanation for the mechanisms underlying multifunctional regulation by multisite proteins .
Materials and methods
Multisite proteins with n independent sites
In our study, the model described below is used as a tool to analyze multisite protein -dependent target activity. It predicts the probability for a multisite protein to be in a particular conformation with a given number of bound ligands, as a function of ligand concentration. We first considered ligand binding to a protein or a protein complex with independent and identical binding sites. Next, we varied the binding centre affinities and studied what impact binding constants have on target regulation. The multisite protein –ligand interactions are shown to constitute the primary mechanism for selective target regulation.The number of combinations of ligand molecules on a multisite protein is given by:
 | (1) |
We will denote multisite protein conformations by L(j), j = 0, 1, …, M – 1. L(0) is a conformation with no bound ligand molecules and L(1) is a conformation with one bound ligand molecule. The concentration of a multisite protein being in a conformation with a given number of bound ligand molecules as a function of ligand concentration is given by:
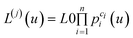 | (2) |
To find the probabilities for binding sites being occupied p1i(u) or not being occupied p0i(u) as a function of ligand concentration u, we consider protein –ligand interaction for a protein with one binding site:
The corresponding model for this scheme is given by:
 | (3) |
The steady-state solution of this system is:
 | (4) |
 .
.
Normalizing both equations by L0, one obtains probabilities for a binding site to be not occupied or occupied as a function of ligand concentration:
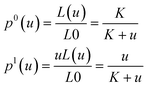 | (5) |
Substituting the probabilities eqn (5) for a single binding site into eqn (2) one can obtain the probability for a multisite protein to be in a given molecular mode as a function of ligand concentration. For example, the probabilities for a protein with two binding sites to be in an apo state or in the fully bound state are:
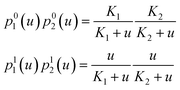 | (6) |
The probabilities for one site to be free and at the same time for another one to be occupied are given by:
 | (7) |
Thus, the multiplication of probabilities from eqn (5) gives an equation for a fully bound protein with n independent binding sites:
 | (8) |
Other well-known models for multisite ligand binding have been published by Hill,16 Adair17 and Weiss:18
 | (9) |
A detailed discussion of the similarities and differences between the above models and the one used in this study is provided in the ESI.†
The concentration of a multisite protein bound to ligand as a function of ligand concentration is given by:
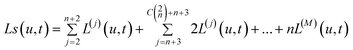 | (10) |
If all the binding sites are independent, the total amount of multisite protein bound to ligand u as a function of ligand concentration (eqn (10)) reduces to:
 | (11) |
The equations for the amount of bound ligand can be important for interpretation of experimental binding data, since it is the amount of bound ligand that is usually being measured in a typical experiment.
Multisite proteins with identical ligand binding sites
We next consider the properties of a multisite protein L with n identical binding sites. According to eqn (1) there are M possible protein –ligand complex combinations in total, where all binding sites are structurally identical (as, for example, in multimeric protein complexes). Then all protein conformations with equal numbers of bound ligands have the same activity and can be described by the same equations. The combination of eqn (2) and (11) provides the concentration of a molecular form for a multisite protein bound to i ligand molecules as a function of ligand concentration: | (12) |
 | (13) |
The magnitudes Lmaxi of the intermediate conformations Li corresponding to umaxi values are:
 | (14) |
Multisite proteins with different ligand binding sites
In this section we analyze a multisite protein with four different binding sites. We assume that all association (K1, K2, K3, K4) and dissociation (K–1, K–2, K–3, K–4) rates are unique for each binding centre. Let us assume for example that (K1 > K2 > K3 > K4) and (K–1 > K–2 > K–3 > K–4). We will further introduce the variable x = u/K1 and dimensionless constants: k1 = 1, k2 = K2/K1, k3 = K3/K1, k4 = K4/K1, k–1 = K–1/K–1, k–2 = K–2/K–1, k–3 = K–3/K–1, k–4 = K–4/K–1.Eqn (12) can then be applied to the case of a multisite protein containing four binding centres with slightly (k1 = 1, k2 = 0.9, k3 = 0.8, k4 = 0.7) and substantially (k1 = 1, k2 = 0.6, k3 = 0.2, k4 = 0.1) different binding affinities. Fig. 3C and 3E show the steady-state dependence of intermediate protein complexeskmi = KMi/KM0 as a function of ligand concentration x = u/K1. The dotted lines indicate the ligand concentration for the maximum amounts of intermediate multisite protein –ligand complexes. The ligand concentrations corresponding to the maximum values are given by:
 | (15) |
Multisite protein -dependent target regulation
There are multiple mechanisms for how multisite proteins can modulate activities of protein targets. In our model we assume that multisite protein L forms a complex with a target molecule (N) only when ligand molecules are bound to certain specific binding sites (Li). All the ligand binding sites on protein L change their affinities upon L–N complex formation. At the same time, the activity of the governed molecule N is altered. Another important biological fact is that the affinity of the governing multisite protein L to N is altered when the ligand occupation of binding sites on L has changed. In the most general case the regulation and control of a target molecule N by a multisite protein L can be represented as shown in Fig. 2E.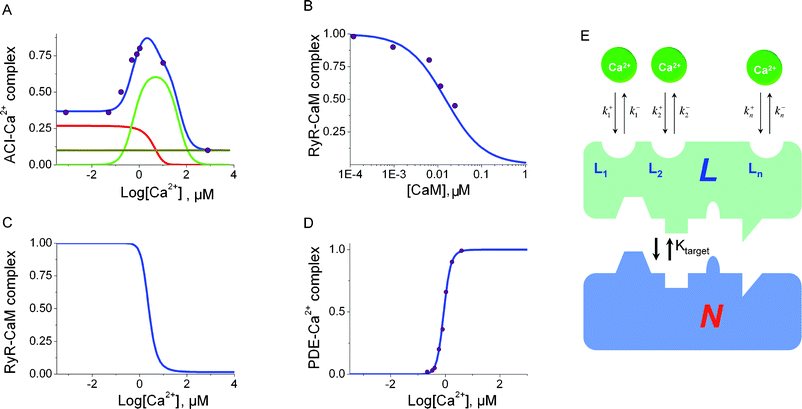 | ||
| Fig. 2 Normalized steady-state activities of ACI isoform (A), RyRI isoform (B) and (C), PDE (D) Data for ACI activity (A) from ref. 12, RyRI(B) and (C) from ref. 11 are shown as circles. Data points for the activated form of PDE (D) are taken from ref. 41. The blue solid line in each case shows the model predictions. (A) The red and green lines show CaM species with 0 and 2 Ca2+ ions, respectively, whereas the brown line indicates the steady-state basal activity of ACI. (B) The experimental data and model comparison of RyRI inhibition by Ca2+ bound CaM. The validated model prediction is further extended to RyRI dependence on Ca2+ (C). The separate and selective Ca2+–CaM-dependent activation of ACI isoform, RyRI and PDE is schematically illustrated for the ligand–multisite protein -dependent mechanism for protein target activation (E). A combination of bound ligand molecules causes the multisite protein to adopt the conformation complementary to a regulatory protein . A particular multisite protein conformation (specific to a target molecule) becomes dominant at a given ligand concentration. The described ligand-dependent selectivity mechanism complements the structural selective target activation theory through the CaM-target interaction surfaces.9 | ||
Suppose that N0 is the total number of molecules of a target protein and L0 is the total number of a governing multisite protein . Let us consider a simplified case when L0 ≫ N0. We also assume that all ligand binding sitesLi on a multisite protein do not change their states when L is bound to N. In that case k+1i = 0, k–1i = 0, k–1i = 0, k–1k = 0. In addition, the maximal time constant max (τi) for ligand–multisite protein L interaction is much lower that the time constant for L–N complex formation τk: max (τi) ≪ τk.
In this case the multisite protein -dependent regulation can be described as an L–N complex formation process according to the Michaelis–Menten formalism and multisite protein –ligand interactions as described by eqn (12). The steady-state concentration of the complexes L–N as a function of ligand concentration is given by:
 | (16) |
These equations have been employed to model the Ca2+–CaM-dependent activation of CaM-dependent PDE, RyR and AC isoforms shown in Fig. 2.
Results
Ca2+–CaM-dependent selective target regulation
Fig. 1B and 1D show the ligand dependent distribution of the free, intermediate complexes and the fully Ca2+ bound CaM species predicted by our model. This model assumes that there are all complexes ((Ca2+)0–CaM, 4 × (Ca2+)1–CaM, 6 × (Ca2+)2–CaM, 4 × (Ca2+)3–CaM, and (Ca2+)4–CaM) present inside any living cell at any given physiological Ca2+ concentration. Their proportion at any given time depends on the current Ca2+ concentration. If the Ca2+ concentration is low, most of the CaM molecules are in the apo state. With an increase in the free Ca2+ concentration, the number of (Ca2+)0–CaM complexes decreases, while the concentration of the intermediate (Ca2+)1–CaM complexes becomes dominant. As the Ca2+ concentration continues to rise, the number of (Ca2+)1–CaM complexes diminishes and the (Ca2+)2–CaM conformations become dominant. Next the (Ca2+)3–CaM conformations take over from (Ca2+)2–CaM, until eventually the (Ca2+)4–CaM conformation becomes dominant and the majority of the CaM molecules are fully Ca2+ bound. The intermediate (Ca2+)1–CaM, (Ca2+)2–CaM, and (Ca2+)3–CaM states exhibit bell-shaped dose–response curves (shown in a logarithmic scale in Fig. 1D).We compared our model predictions for ligand concentration-dependent profiles with experimental data for three important CaM targets, ACI, RyRI and PDE. ACs are important signal transduction molecules that convert ATP to 3′,5′-cyclic AMP.13PDE is an enzyme that degrades the phosphodiester bond in cAMP and cGMP molecules,19 while ryanodine receptors form a class of calcium receptors that mediate the release of calcium ions from the sarcoplasmic reticulum.20 The model predictions for apo, intermediate and fully bound conformations of the multisite protein are superimposed on the experimental dose–response curves in Fig. 2. This figure shows the Ca2+-dependent profiles of concentrations for the ACI isoform (A), RyRI (B,C) and PDE (D). The presented Ca2+ concentration-dependent activation curves comprise Ca2+, CaM and the target protein only.
The experimental data points shown in Fig. 2 highlight the limitations of some models of Ca2+–CaM-dependent target activation that rely on saturation of binding sites, where the dose–response curves with (Ca2+)4–CaM-dependent activation would always be similar to those in Fig. 1C. However, the dose–response curves for the ACI isoform and RyRI (Fig. 2A, 2B, and 2C) cannot be described by the AC and RyR dependence on the (Ca2+)4–CaM conformation only, for any possible combination of model parameters. It therefore appears to be unlikely that only the (Ca2+)4–CaM conformation activates ACI and RyRI. The seeming contradiction between the experimental data and the standard model predictions for fully Ca2+ bound CaM molecules is resolved in our model by allowing selective activation of ACvia the intermediate (Ca2+)1–CaM, (Ca2+)2–CaM or (Ca2+)3–CaM conformations. Our model makes excellent predictions for the steady-state target protein dose–response curves , as shown in Fig. 2. The model predicts that the activity of each Ca2+–CaM-dependent target is determined by a combination of the different CaM conformation concentrations bound to a certain number of Ca2+ ions. It appears that the unique binding interface to the CaM targets9 is necessary, but not sufficient for Ca2+–CaM-dependent selective target activation. The sum of Ca2+–CaM species provides a mechanism for selective target regulation over a range of Ca2+ concentrations. The dose–response curves for the intermediate species (Fig. 1D), in addition to only free and fully bound states (Fig. 1B), allow a much greater variety of target activation modes and provide a fully-parameterized explanation of the Ca2+ concentration-dependent profiles for CaM-dependent proteins shown in Fig. 2.
Differences in binding affinities mainly affect magnitudes of the intermediate conformations
In the analysis described above, we modelled a multisite protein with identical binding sites, a frequent situation in multimeric proteins including two or more identical protein subunits. To examine the implications of variations in the binding site affinity on the predicted concentration–response profiles we extended our model to incorporate non-identical binding sites. The concentration-dependent curves for a protein with identical binding sites were compared with a protein which has different, but similar affinities (k1 = 1, k2 = 0.9, k3 = 0.8, k4 = 0.7) and with a protein which has four substantially different binding centres (k1 = 1, k2 = 0.6, k3 = 0.2, k4 = 0.1).Fig. 3 shows the ligand concentration-dependent ligand–protein complexes for a protein with identical binding sites (Fig. 3A), for a protein with similar binding sites (Fig. 3C) and for a protein with significantly different binding sites (Fig. 3E). The main result that follows from the analysis of the intermediate conformation curves is that the affinities of the binding sites mainly affect the magnitude of the corresponding protein conformation. For example, the conformation of a multisite protein corresponding to the one ligand-bound state is present in lower concentration if the affinity of the binding centre is lower. However, the shape of the concentration-dependent profile has not changed; the only parameter which is affected is the magnitude. The dose–response curve of the one ligand–multisite protein conformation complex has not undergone shifts along the ligand concentration axis. Similar effects in terms of modulated magnitudes are also observed for the two ligand- and three ligand-bound conformations. The binding affinity variation has insignificant impact on the apo and fully saturated conformations (Fig. 3B, 3D, 3F). On the other hand, a wide variation in affinities changes both the magnitude of the concentration-dependent curves as well as the maximum position on the concentration axis. For example, if all the affinities are changed simultaneously, the intermediate species reach their maximum at a different ligand concentration. The example described in this section holds if the binding site with the lowest equilibrium constant remains the same, whereas the variation of affinities (within one or two orders of magnitude) for other sites would mainly affect the magnitudes of intermediate species.
 | ||
| Fig. 3 The ligand concentration-dependent profiles for apo, intermediate and fully bound multisite proteins The selectivity mechanism emerging from CaM with a variable number of Ca2+ ions (A) as well as in apo and fully saturated conformations (B) is analyzed when the macroscopic binding constants were altered. (C) and (D) represent the variations in the magnitudes of the multisite protein species with slightly varied binding site affinities. (E) and (F) show a multisite protein with significantly varied binding site affinities. | ||
Underlying assumptions and limitations of the model
The canonical CaM–target interaction involves one CaM molecule and one target protein . Examples of multiprotein complex associations include one CaM and two anthrax AC molecule complex assemblies, as well as two CaM molecules with two Ca2+-gated K+ channels.9 In this study we focus on the canonical mode only and do not consider effects associated with the multimolecule complex formation.It has been reported that the CaM–target interactions may alter CaM affinity to Ca2+ ions. Any modulation of multisite protein –ligand binding affinities because of the multisite protein –target interactions is not included into this study in order to keep the model equations analytically tractable.
The Michaelis–Menten , Hill, Adair and a number of other models represent the activity or the rate of an enzyme as a function of a (substrate) ligand concentration. This rate is a product of the enzyme catalytic constant, total enzyme concentration and the (substrate) ligand dependent fraction. In order to extend the model to non-enzymatic multisite proteins we formulated equations for the protein concentrations rather than the activity rates of the individual protein species. Given that the activities of enzymes are proportional to the enzyme concentrations in the active states, the mathematical consideration of protein concentrations rather than activities remains valid for describing both enzymatic and other non-enzymatic multisite protein examples.
We have applied the mathematical model for multisite binding to the particular example of Ca2+–CaM-target interactions. Some reports have suggested that CaM independently binds Ca2+ ions,21,22 whereas other studies suggest that Ca2+–CaM binding is a cooperative process.23,24 In order to assess whether the cooperativity of Ca2+ binding to CaM would influence the proposed hypothesis of selective target regulation by proteins with variable numbers of ligand molecules, we compared Ca2+–CaM species in the presence and in the absence of cooperative binding . Fig. 4 shows the Ca2+-dependent distribution of Ca2+–CaM species in the apo state, with two Ca2+ ions and fully bound CaM. This figure shows that although cooperative binding may somewhat shift the distribution of multisite protein species, it still allows the selective regulation of target protein by a multisite protein in a complex with variable numbers of ligand molecules.
 | ||
| Fig. 4 The comparison of independent and cooperative Ca2+ binding to CaM (A) The Ca2+ concentration-dependent apo and fully saturated CaM species shown in the absence (green lines) and presence (blue lines) of cooperativity. (B) The intermediate CaM conformations are shown as a function of Ca2+ concentration. CaM with one, two and three Ca2+ ions is highlighted in red, green and blue, respectively. The thin curves indicate CaM species profiles in the absence of cooperative binding whereas the thick lines show the Ca2+ binding to CaM in the presence of cooperativity. Both (A) and (B) reveal that the existence of cooperativity shifts the CaM dependence on Ca2+ towards lower Ca2+ concentrations and also alters the magnitudes of the intermediate complexes. However, both independent as well as cooperative binding mechanisms allow selective target activation by a specific conformation. | ||
Discussion
This work introduces a plausible explanation for the mechanism underlying selective target activation by multisite proteins . The proposed model extends previously developed models for multisite binding reactions25–30 and for Ca2+–CaM interactions31–36 that increases our understanding of how concentration alterations of one ligand may selectively activate multiple targets.Multifunctional intracellular regulation is largely due to differential target modulation. The main conclusion from our study is that the selective protein activity can be governed by a multisite protein in conformations with variable numbers of bound ligand molecules. This idea is supported by the comparison of the model predictions with experimental concentration-dependent profiles for Ca2+–CaM-dependent AC, RyR and PDE. Eqn (16) in the Materials and methods section is a general formula that represents the activity of a multisite protein -dependent target as a function of ligand concentration. Indeed, in a generalized model of cellular signalling that involves regulation through multisite-binding proteins , incorporation of this formula will ensure that the model behaves correctly under diverse conditions, particularly under situations where ligand concentration may be finely regulated.
It has been suggested in previous studies that CaM translates Ca2+ alterations into the changed activity of Ca2+–CaM-dependent proteins by undergoing conformational changes.37–39 The differential target activation by Ca2+–CaM is exclusively attributed to the structural diversity of CaM interactions with its targets.9 Previous structural studies of the Ca2+-loaded CaM molecules and the application of the Hill equation for modelling Ca2+-dependent CaM activation suggest the existence of the apo or Ca2+-loaded states only. Recent experimental data, however, support the hypothesis that intermediate complexes can also be biologically active. One study, for example, reported that CaMPKII is activated by CaM with two bound Ca2+ ions,14 while the results reported in15 showed that the K+ channel of paramecium is also activated by CaM with two bound Ca2+ ions. Also, the skeletal muscle ryanodine receptor is activated by a Ca2+-free and inhibited by a Ca2+-bound CaM conformation.40
Our analysis of the effect of variations in binding affinities allows us to propose that allosteric modulators could be involved in the mechanism of selective regulation. Proteins activated by a specific intermediate multisite protein conformation (or by a combination of conformations) as the current study proposes can be selectively turned on or off by the modulators of the intermediate species magnitudes as shown in Fig. 3A, 3C, and 3E. Selective variation of a target protein activity within two orders of magnitude at a specific ligand concentration could provide yet another means for efficient multisite protein -dependent control of intracellular events. The proposed mathematical model may have another application in understanding the complex effects of drugs that may have multisite interaction mechanisms with target proteins , but it is not trivial to understand how protein function alters under such conditions. The mechanism of selective effector protein activation by a multisite protein at a given ligand concentration is complemented by the regulation of intermediate conformation amplitudes with or without significant shifts from the ligand “activation” concentration. It appears that when evolution engineered multiple binding sites on proteins , it allowed for greater complexity while keeping tight control on every single activation event. This study provides a plausible explanation for the mechanism underlying this selective control.
Acknowledgements
This work was carried out under an EPSRC platform grant (EP/D029937/1), a BBSRC grant (BB/D015340/1) and by RFBR grant.References
- P. Aloy and R. B. Russell, Nat. Rev. Mol. Cell Biol., 2006, 7, 188–197 CrossRef CAS.
- J. Robison and R. J. Colbran, in Encyclopedia of Biological Chemistry, ed. W. Lennarz and M. D. Lane, Elsevier, 2004, vol. 1, pp. 281–286 Search PubMed.
- M. J. Berridge, M. D. Bootman and P. Lipp, Nature, 1998, 395, 645–648 CrossRef CAS.
- K. L. Yap, J. B. Ames, M. B. Swindells and M. Ikura, Proteins: Struct., Funct., Genet., 1999, 37, 499–507 CrossRef CAS.
- S. Bhattacharya, C. G. Bunick and W. J. Chazin, Biochim. Biophys. Acta, 2004, 1742, 69–79 CrossRef CAS.
- M. Zhang, T. Tanaka and M. Ikura, Nat. Struct. Biol., 1995, 2, 758–767 CrossRef CAS.
- H. Ishida, K. Takahashi, K. Nakashima, Y. Kumaki, M. Nakata, K. Hikichi and M. Yazawa, Biochemistry, 2000, 39, 13660–13668 CrossRef CAS.
- R. Chattopadhyaya, W. E. Meador, A. R. Means and F. A. Quiocho, J. Mol. Biol., 1992, 228, 1177–1192 CAS.
- K. P. Hoeflich and M. Ikura, Cell (Cambridge, MA, U. S.), 2002, 108, 739–742 Search PubMed.
- S. W. Vetter and E. Leclerc, Eur. J. Biochem., 2003, 270, 404–414 CrossRef CAS.
- N. Yamaguchi, C. Xin and G. Meissner, J. Biol. Chem., 2001, 276, 22579–22585 CrossRef CAS.
- J. L. Guillou, H. Nakata and D. M. Cooper, J. Biol. Chem., 1999, 274, 35539–35545 CrossRef CAS.
- D. M. Cooper, Biochem. J., 2003, 375, 517–529 CrossRef CAS.
- J. M. Shifman, M. H. Choi, S. Mihalas, S. L. Mayo and M. B. Kennedy, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 13968–13973 CrossRef CAS.
- C. Kung, R. R. Preston, M. E. Maley, K. Y. Ling, J. A. Kanabrocki, B. R. Seavey and Y. Saimi, Cell Calcium, 1992, 13, 413–425 CrossRef CAS.
- A. Hill, J. Physiol. (Oxford, U. K.), 1910, 40, 4–7 Search PubMed.
- G. Adair, J. Biol. Chem., 1925, 63, 529–545 CAS.
- J. N. Weiss, FASEB J., 1997, 11, 835–841 CAS.
- B. Weiss, Adv. Cyclic Nucleotide Res., 1975, 5, 195–211 Search PubMed.
- R. Zucchi and S. Ronca-Testoni, Pharmacol. Rev., 1997, 49, 1–51 CAS.
- M. P. Walsh, F. C. Stevens, K. Oikawa and C. M. Kay, J. Biochem. (Tokyo), 1980, 57, 267–279 Search PubMed.
- J. R. Dedman, J. D. Potter, R. L. Jackson, J. D. Johnson and A. R. Means, J. Biol. Chem., 1977, 252, 8415–8422 CAS.
- M. C. Kilhoffer, J. G. Demaille and D. Gerard, Biochemistry, 1981, 20, 4407–4414 CrossRef CAS.
- M. C. Kilhoffer, D. Gerard and J. G. Demaille, FEBS Lett., 1980, 120, 99–103 CrossRef CAS.
- J. Gunawardena, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 14617–14622 CrossRef CAS.
- J. P. Changeux and M. M. Rubin, Biochemistry, 1968, 7, 553–561 CrossRef CAS.
- S. J. Edelstein and W. G. Bardsley, J. Mol. Biol., 1997, 267, 10–16 CrossRef CAS.
- M. M. Rubin and J. P. Changeux, J. Mol. Biol., 1966, 21, 265–274 CrossRef CAS.
- C. Salazar and T. Hofer, FEBS J., 2007, 274, 1046–1061 Search PubMed.
- F. Ortega, J. L. Garces, F. Mas, B. N. Kholodenko and M. Cascante, FEBS J., 2006, 273, 3915–3926 Search PubMed.
- S. Mirzoeva, S. Weigand, T. J. Lukas, L. Shuvalova, W. F. Anderson and D. M. Watterson, Biochemistry, 1999, 38, 14117–14118 CrossRef CAS.
- O. Minowa and K. Yagi, J. Biochem. (Tokyo), 1984, 96, 1175–1182 Search PubMed.
- O. B. Peersen, T. S. Madsen and J. J. Falke, Protein Sci., 1997, 6, 794–807 CAS.
- T. Porumb, Anal. Biochem., 1994, 220, 227–237 CrossRef CAS.
- R. Y. Tan, Y. Mabuchi and Z. Grabarek, J. Biol. Chem., 1996, 271, 7479–7483 CrossRef CAS.
- J. F. Maune, C. B. Klee and K. Beckingham, J. Biol. Chem., 1992, 267, 5286–5295 CAS.
- M. Ikura, Trends Biochem. Sci., 1996, 21, 14–17 CAS.
- M. R. Nelson and W. J. Chazin, Protein Sci., 1998, 7, 270–282 CAS.
- M. R. Nelson, E. Thulin, P. A. Fagan, S. Forsen and W. J. Chazin, Protein Sci., 2002, 11, 198–205 CrossRef CAS.
- G. G. Rodney, C. P. Moore, B. Y. Williams, J. Z. Zhang, J. Krol, S. E. Pedersen and S. L. Hamilton, J. Biol. Chem., 2001, 276, 2069–2074 CAS.
- R. K. Sharma and J. Kalra, Biochem. J., 1994, 299(Pt 1), 97–100 CAS.
Footnote |
| † Electronic supplementary information (ESI) available: A comparison of different multisite binding models. See DOI: 10.1039/b713461d |
| This journal is © The Royal Society of Chemistry 2008 |

