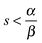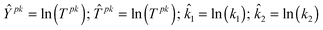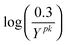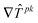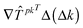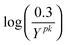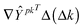Proximate parameter tuning for biochemical networks with uncertain kinetic parameters†
Stephen J.
Wilkinson
ab,
Neil
Benson
c and
Douglas B.
Kell
*ab
aSchool of Chemistry, Princess St, Manchester, UK M1 7DN. E-mail: stephen.wilkinson@manchester.ac.uk; dbk@manchester.ac.uk; Fax: +44 (0)161![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 306
306![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4556; Tel: +44 (0)161
4556; Tel: +44 (0)161![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 306
306![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4492
4492
bThe Manchester Centre for Integrative Systems Biology, Manchester Interdisciplinary Biocentre, The University of Manchester, Princess St, Manchester, M1 7DN, UK
cPfizer Central Research, Ramsgate Road, Sandwich, Kent, UK CT13 9NJ. E-mail: neil.benson@pfizer.com
First published on 9th October 2007
Abstract
It is commonly the case in biochemical modelling that we have knowledge of the qualitative ‘structure’ of a model and some measurements of the time series of the variables of interest (concentrations and fluxes), but little or no knowledge of the model's parameters. This is, then, a system identification problem, that is commonly addressed by running a model with estimated parameters and assessing how far the model's behaviour is from the ‘target’ behaviour of the variables, and adjusting parameters iteratively until a good fit is achieved. The issue is that most of these problems are grossly underdetermined, such that many combinations of parameters can be used to fit a given set of variables. We introduce the constraint that the estimated parameters should be within given bounds and as close as possible to stated nominal values. This deterministic ‘proximate parameter tuning’ algorithm turns out to be exceptionally effective, and we illustrate its utility for models of p38 signalling, of yeast glycolysis and for a benchmark dataset describing the thermal isomerisation of α-pinene.
Introduction
Various types of computational modelling are being used both to understand biochemical systems and to make sense of existing (often omics) data, especially as part of iterative experimental design programmes aimed at the serial generation of new data and hypotheses.1–9We consider initially the problem of tuning a detailed kinetic model of a signalling pathway whose stoichiometric structure is known but in which most of the parameter values have not been experimentally determined and are therefore highly uncertain. We assume that very limited time course data of a few (perhaps only one) participatory species are available. We would like to ‘fit’ our model to the available data. In this context, traditional parameter estimation techniques10–12 are of limited utility13 given the large number of undetermined model parameters and the relatively few measured variables. Put another way, the models are typically grossly underdetermined and many combinations of parameters can fit the measured variables.
The above problem is a very common one for biochemical and other models, and a common remedy is to use a greatly reduced model in which the number of unknown parameters does not swamp the number of measured variables.14–17 This approach can provide valuable insights but model reduction techniques often make big structural simplifications to the original kinetic scheme, thereby discarding the considerable biological knowledge that went into building them in the first place. In this paper, therefore, we adopt an alternative approach in which we retain the detailed kinetic structure of the model. We navigate the uncertain parameter space using local sensitivity information in order to match the model with measured output features. In such an under-defined system there may well be many distinct parameter combinations that fit the measured data but we seek those that are closest to the nominal parameter values rather than those at the extremes of the parameter space. This turns out to be an extremely effective method.
One can separate the information required to construct a detailed ‘forward’ kinetic model of a signalling network into two types: structural data and kinetic data. Structural data describe the nodes and links of the signalling network, i.e. the species, reactions and the stoichiometric quantities of each species consumed and produced by each reaction together with effector interactions. Kinetic data consist of the functional form of the rate equation for each reaction and the values of the associated kinetic parameters. For many well-studied signalling networks the structural data are known with a comparatively high level of confidence but the kinetic parameters are known with far less certainty. The proximate tuning method presented in this paper can use very limited output data to find reasonable values for the model parameters.
In the next sections we develop the mathematical framework before presenting some results.
Background
A typical model of a biochemical network consists of a set of ordinary differential equations that govern the temporal evolution of the variable species.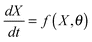 | (1) |
| X(t0) = X0 | (2) |
Here, X represents the vector of n species concentrations and θ is the vector of m parameters:
| X = [x1x2…xi…xn]T | (3) |
| θ = [k1k2…kj…km]T | (4) |
In general, the rate of change of species concentration variable xi depends on a non-linear function of the concentration variables and the model parameters.
Parameter uncertainty is taken into account by assigning each parameter value a nominal value k0j, a lower bound kminj and an upper bound kmaxj
 | (5) |
In the absence of experimental measurements, these values can be arrived at using biological prior knowledge. The nominal value corresponds to the most likely value whereas the bounds are reasonable estimates of the smallest and largest values that the parameter could take. For such intuitive estimates the bounds are likely to be rather wide, perhaps spanning several orders of magnitude. However, the lower bound for a rate constant is constrained by the known flux through a pathway if metabolic, and cannot be larger than the diffusion-controlled limit, for instance. Measured parameters, on the other hand, will have tighter bounds corresponding to the experimental error. In the unlikely event of a parameter value being known exactly, the upper and lower bounds can be assigned the same value ± the noise level, without loss of generality.
Suppose also that we have some measured concentration time series that we would like our model to reproduce. We characterize these time profiles by features (peak value, time to peak, area under curve etc.) that we can write as a general function of the concentration profiles and the parameters.
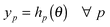 | (6) |
Here yp is the value of feature simulated by the model for parameter set θ represented by the implicit function hp(θ). This is a sensible strategy since measured data are typically limited and uncertain such as those illustrated in Fig. 1. It might be the case that the emphasis is on getting a model output with a peak value of species A of 0.5 at 60 min. In this case we could use these two features (i.e. peak value and time to peak, as in ref. 18,19) to drive the parameter tuning. If on the other hand, a best fit to the raw time series data is sought, we could define a separate feature for each measured value at each time point which the tuning process will seek to match simultaneously. Examples of both approaches are given later.
 | ||
| Fig. 1 Typical time series data for a hypothetical species A. | ||
In this paper we label the features that we are trying to get the model to match as ‘target’ features. Whilst these will usually be measured values, as previously discussed, it may also be the case that they are simply values that we would intuitively like the model to emulate (e.g. as in metabolic engineering11,20–26). Many signalling networks, for example, have quite well known characteristic response times. Here we use ‘response time’ in an informal sense meaning the time for the signalling species of interest to reach peak activation (e.g. 10 min). The modeller would then seek to tune the initial model to this target value even though it is not (yet) a measured value.
In general, a model run using the nominal parameter values will give off-target output features since the parameters have been estimated without regard either to their measured values or to those of the output measurements. We would therefore like to adjust these values so that the simulated target output feature values of the model are closer to the measured (target) values. In order to achieve this we propose an iterative scheme in which the local sensitivity of the required model outputs with respect to all the parameters is evaluated at each iteration. This information is then used to predict the smallest step to take in the parameter space in order to minimize the error between the model outputs and their target values. The parameters are then updated to these new predicted best values and the ODE model re-run to determine the actual simulated values of the output features. This iterative loop is then repeated as the algorithm steps through the parameter space until the error between the simulated values and the target values is reduced to a specified tolerance, or stops decreasing, or the maximum number of iterations is reached. We can list the key components of the proximate parameter tuning (PPT) algorithm as follows.
General PPT algorithm
1. Initialise each parameter to its most likely (nominal) value
2. Run model at current parameter values and compare outputs to target values
3. If convergence achieved or iteration limit reached then terminate.
4. Otherwise, calculate sensitivities of model outputs to each parameter.
5. Use sensitivities to calculate better fitting parameter values that are proximate to current values and within minimum/maximum bounds
6. Update current parameters to new values
7. Go to 2.
The key steps above are 4. and 5. which can be implemented in a number of different ways, as briefly discussed below, to give alternative implementations of the PPT algorithm.
In step 4 we could certainly calculate the first order sensitivities of the desired model output features with respect to each parameter. This gives a local linear approximation of how each varies in the neighbourhood of the current point in the parameter space. However, for highly non-linear systems, we may also wish to capture interactions between parameters via higher order effects. For example, a second order approximation would be superior to the linear (first order) approximation, although this improved accuracy would come at a much greater computational expense. The second order model would require an estimate of the Hessian matrix giving the sensitivity of each parameter sensitivity to changes in that parameter and each of the other parameters in the model.
Another key consideration in step 4 of the PPT algorithm is how to calculate the sensitivities. The most general method is to treat the model equations as a black box and estimate the sensitivities using small perturbations to the model parameters and performing a complete simulation after each perturbation. This has the advantage that it will work for any type of model and any type of output feature. On the other hand, it may be possible to calculate sensitivities analytically or using short-cut methods for certain types of model output without the need to perform repeated numerical simulations.
Once we have estimated or calculated the sensitivities in step 4 we also have considerable flexibility as to how we use them in step 5 to calculate a better set of model parameters. This is the key part of the PPT algorithm and in general we will need to solve some sort of optimisation sub-problem in order to minimize the fitting errors and also stay as close as possible to the nominal parameter values. In general this will be a constrained, multi-variable optimisation problem.
For the rest of this paper we use a specific implementation of the general scheme described above which we call ‘linear programming-based proximate parameter tuning’ or LP-PPT. As its name suggests, this implementation involves the solution of a linear programming (LP) sub-problem27 to calculate better parameter values (step 5 of the general PPT algorithm described above). Each sub-problem uses first-order sensitivities and therefore assumes that the contributions of each parameter to each output feature are linear and independent. We estimate these sensitivities (step 4) using perturbed simulations of the full model. Despite the assumptions of linearity implicit in the formulation of each LP sub-problem the method performs well in the examples discussed below. This is because of its iterative nature whereby the sensitivity information is repeatedly updated at each iteration. The steps taken in the parameter space generally decrease after a handful of iterations as the algorithm converges on good local solutions.
We now provide an illustration of how the LP-PPT algorithm navigates the uncertain parameter space with the aim of bringing the model into closer agreement with the target feature values. In general the parameter space is large since the upper and lower bounds for each parameter may span several orders of magnitude. We therefore use variables that describe the logarithmic (base 10) deviation of each parameter from its nominal value. Fig. 2 shows how the iterative scheme would adjust a single parameter in order to match a single target output feature. For the initial or nominal parameter value (Iteration 0), the model gives an output feature which is higher than the target value. In order to find the direction in which to adjust the parameter, the gradient is calculated (the start of Iteration 1) and this is used to calculate a new parameter value. The model is then run at this new parameter value and, if convergence to the target value has not occurred, the gradient is calculated at this new parameter value (the start of Iteration 2) and this cycle is repeated until convergence on the target value is achieved. This process is very similar to Newton's method for solving non-linear equations except that in our case we evaluate the gradients numerically and, in general, we have multiple targets to meet.
 | ||
| Fig. 2 Hypothetical logarithmic plot of output feature vs. parameter value to illustrate iterative use of local scaled sensitivity to move towards target value. | ||
The idea of solving a sequence of linear programming sub-problems (known as successive linear programming) is also well a established technique for tackling large-scale non-linear programming problems arising from engineering applications in power systems planning and refining scheduling.28,29 It should also be mentioned that the problem presented in this paper is a specific instance of a much wider class of ill-posed inverse problems which have been extensively studied in applied mathematics. The unique numerical solution of these problems requires regularization i.e. some additional assumptions constraining the decision variables. In this case we penalize the amount that the parameters deviate from the nominal values which biases the estimation towards our prior knowledge. There is a considerable body of work regarding the theoretical properties of different regularization functions and the choice of weightings to use30 but detailed discussion of this is beyond the scope of this paper. The technique has been applied in biochemical modelling applications in order to reduce the effect of insensitive parameters during the parameter estimation.31
The linear programming (LP) sub-problem solved at each iteration r is:
Minimise:
 | (7) |
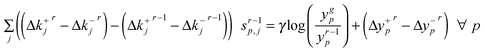 | (8) |
Subject to:
 | (9) |
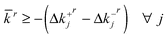 | (10) |
 | (11) |
 | (12) |
 | (13) |
 | (14) |
Note that this is a linear programming problem since it has an objective function and constraints that are linear with respect to the decision variables. The logarithmic terms appearing in some of the equations involve only constant values for each problem instance and these therefore evaluate to constant values (right hand sides) for all constraints.
We solve a sequence of sub-problems in which the coefficients and right hand sides are iteratively varied. The decision variables for the rth linear programming sub-problem are:
Δk+ir, Δk–ir: the positive and negative components of the logarithm of the fractional deviation of parameter j from its nominal value after iteration r. So the value of each parameter j after each iteration r is given by:
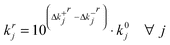 | (15) |
Note that we need to include each positive and negative term explicitly and independently in the LP problem statement. This is because they have opposite signs in all constraints but have the same sign in the objective function which seeks to minimize their sum.
![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) r: the maximal absolute logarithmic fractional deviation from the nominal value of all parameters.
r: the maximal absolute logarithmic fractional deviation from the nominal value of all parameters.
Δy+nr, Δy–nr: the positive and negative components of the ‘predicted’ logarithmic fractional error of the fitted value compared to its target value for feature p after iteration r. Note that the LP sub-problem solves for these quantities exactly but they are only the predicted actual values. This is because the LP assumes that parameter sensitivities are locally constant and have no higher order or interaction terms. Generally this is not the case and the actual errors between the fitted and target values after iteration r are calculated by a full simulation of the original ODE model at the updated parameter values.
ȳr: the maximal absolute logarithmic fractional error of all fitted feature values compared to their target values.
The parameters in the linear programming sub-problem (as opposed to the ODE parameters which are, of course, variables in the fitting process) are:
ygp: the target value of feature p
k 0 i , kmini, kmaxi: the nominal, minimum and maximum values for parameter j respectively.
srp,j: the scaled sensitivity of the simulated value (yp) of feature p with respect to parameter j at iteration r. This value is calculated numerically by solving the system of ODEs for each parameter with its value perturbed slightly (0.1%) from the current value.
ᾱ: the penalty associated with the maximal logarithmic fractional deviation of all parameters from their nominal values.
αj: the penalty associated with the logarithmic fractional deviation of each individual parameter j from its nominal value.
β: the penalty associated with the maximal logarithmic fractional error of the fitted value compared to its target value for all features.
βp: the penalty associated with the logarithmic fractional error of the fitted value compared to its target value for feature p.
γ: the step length for the feature improvement factor during each iteration 0 < γ < 1.
In the linear programming formulation summarized above, the objective function (7) is designed to minimize a linear combination of four terms. The first two terms seek to restrict the search to proximate points in the parameter space by applying a penalty to the maximal parameter deviation (first term) and also including a weighted sum penalizing the individual parameter deviations (second term). The third and fourth terms penalize the error between the simulated and target feature values. The third term penalizes the maximal error and the fourth term is a weighted sum of the individual errors which can be to penalize features differentially depending on the certainty of their measurement or their perceived importance.
Note the symmetry with which this representation treats the parameter deviations and the fitting errors. We do not need to include all the terms but we need one or both of the first two terms and one or both of the third and fourth terms. In the examples used in this paper we do not include the second term ( nor the third term (β = 0). In any case the objective function defines a trade-off between minimizing the errors and not straying too far from the nominal parameter values and the relative values of the penalty coefficients should reflect this. Usually the former is more important than the latter so we use
nor the third term (β = 0). In any case the objective function defines a trade-off between minimizing the errors and not straying too far from the nominal parameter values and the relative values of the penalty coefficients should reflect this. Usually the former is more important than the latter so we use  . For the examples presented in this paper we use:
. For the examples presented in this paper we use: .
.
The key constraint is eqn (8) which uses local parameter sensitivities to adjust the feature values closer to their targets. This can be seen as a generalization to multiple parameters of the update formula given in Fig. 2 which was for a single parameter. The constraint assumes that each parameter contributes independently and multiplicatively (additively in the logarithmic space) to each output feature. It ensures that the optimizer uses first order sensitivity information in order to adjust the parameters in such a way as to minimize the predicted penalty at the new point in parameter space. For multiple features, the optimizer may not be able to match all the features exactly and therefore seeks the best compromise parameter adjustment. Note that the actual penalty calculated at the new point (by direct simulation of the ODEs) is not likely to be equal to the predicted penalty because of variations in first order sensitivity and interactions between parameters (higher order terms). This is the reason for the iterative approach as exemplified in Fig. 2. For all examples presented in this paper, the step length improvement factor is unity (γ = 1) so we are always taking full steps. For other problems, however, it may be advantageous to employ an adaptive strategy whereby the step length is reduced as the error between the predicted and actual penalties is found to increase. Taking full steps as we do in all the examples in this paper is an aggressive ‘un-damped’ strategy and may result in the non-convergence of the PPT algorithm to a final unique point. Although this behaviour is observed in both examples 3 and 4. the limiting oscillations are very small and therefore bracket the final solution within a very tight tolerance (Table 1).
| Itn. | Predicted Obj. | Actual Obj. | Sum squared errors | Parameter values | ||||
|---|---|---|---|---|---|---|---|---|
| p1 | p2 | p3 | p4 | p5 | ||||
| 0 | — | 39.3765 | 19.870 | 5.9300e–05 | 2.9600e–05 | 2.0500e–05 | 2.7500e–04 | 4.0000e–05 |
| 1 | 30.8827 | 30.8827 | 42.5283 | 5.8098e–05 | 2.9291e–05 | 3.7170e–05 | 3.2769e–04 | 5.3651e–05 |
| 2 | 30.5283 | 30.6602 | 46.3047 | 5.8104e–05 | 2.9385e–05 | 3.8635e–05 | 3.5188e–04 | 6.0138e–05 |
| 3 | 30.4823 | 30.5778 | 40.5213 | 5.8096e–05 | 2.9797e–05 | 3.6648e–05 | 3.2380e–04 | 5.3777e–05 |
| 4 | 30.5072 | 30.6574 | 46.2321 | 5.8111e–05 | 2.9394e–05 | 3.8630e–05 | 3.5206e–04 | 6.0176e–05 |
| 5 | 30.4809 | 30.5778 | 40.5183 | 5.8097e–05 | 2.9797e–05 | 3.6648e–05 | 3.2378e–04 | 5.3775e–05 |
| 6 | 30.5071 | 30.6574 | 46.2318 | 5.8111e–05 | 2.9394e–05 | 3.8630e–05 | 3.5206e–04 | 6.0176e–05 |
| 7 | 30.4809 | 30.5778 | 40.5183 | 5.8097e–05 | 2.9797e–05 | 3.6648e–05 | 3.2378e–04 | 5.3775e–05 |
| 8 | 30.5071 | 30.6574 | 46.2318 | 5.8111e–05 | 2.9394e–05 | 3.8630e–05 | 3.5206e–04 | 6.0176e–05 |
| 9 | 30.4809 | 30.5778 | 40.5183 | 5.8097e–05 | 2.9797e–05 | 3.6648e–05 | 3.2378e–04 | 5.3775e–05 |
| 10 | 30.5071 | 30.6574 | 46.2318 | 5.8111e–05 | 2.9394e–05 | 3.8630e–05 | 3.5206e–04 | 6.0176e–05 |
| 11 | 30.4809 | 30.5778 | 40.5183 | 5.8097e–05 | 2.9797e–05 | 3.6648e–05 | 3.2378e–04 | 5.3775e–05 |
| 12 | 30.5071 | 30.6574 | 46.2318 | 5.8111e–05 | 2.9394e–05 | 3.8630e–05 | 3.5206e–04 | 6.0176e–05 |
Constraints eqn (9) and eqn (10) ensure that ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ris greater than or equal to the absolute deviation of any parameter from its nominal value. It is important to note that our choice of maximum deviation as the proximity metric keeps the sub-problem as a linear programming problem and therefore simple to solve. There are, however, other choices for the proximity metric which may be considered more appropriate for other applications. These depend on the prior probability distributions of the parameter values and are elaborated on in the discussion.
ris greater than or equal to the absolute deviation of any parameter from its nominal value. It is important to note that our choice of maximum deviation as the proximity metric keeps the sub-problem as a linear programming problem and therefore simple to solve. There are, however, other choices for the proximity metric which may be considered more appropriate for other applications. These depend on the prior probability distributions of the parameter values and are elaborated on in the discussion.
Constraints eqn (11) and eqn (12) ensure that ȳr is greater than or equal to the absolute logarithmic fractional error of all fitted feature values compared to their target values.
Constraints eqn (13) and eqn (14) are simple bounds on how far each parameter can change without violating its minimum or maximum values.
The properties of the formulation—particularly those relating to the penalties on the parameter deviations—are illustrated graphically in Appendix A.
Another point to note with regard to the mathematical formulation presented above is that this method relies on local sensitivities and therefore has no guarantee of convergence to a global minimum of the objective function (eqn (7)). If however, the parameter space is relatively smooth and convex it will always be possible to obtain good solutions. This is illustrated in the examples below.
Results
Four examples are presented below. Example 1 is a very simple ‘toy’ pathway of two reactions and three species that has an analytical solution and that we use to illustrate the proximate tuning methodology. In Example 2 we apply the technique to a model of the p38 MAP kinase signalling pathway for which very little measured data exist and which is therefore highly under-constrained. Conversely, in Example 3 we investigate the performance of the algorithm in a much more constrained application in which we seek to fit most of the steady state concentrations in a well-known glycolysis model. This example also demonstrates the convergence of the method starting from different nominal points in the parameter space. Finally, in Example 4 we apply the algorithm to an extensively studied parameter estimation problem that enables us to compare it to existing approaches. All examples were solved using Sentero, a software tool for the modeling and analysis of biochemical networks that includes the LP-PPT algorithm as one of its analysis modules. Sentero uses Matlab as the simulation engine and a third party solver to solve the linear programming sub-problems.Example 1
For this illustrative example we consider two irreversible reactions (Reaction 1 and Reaction 2) in series that carry out the conversion of Species 1 to Species 3 via an intermediate Species 2. Fig. 3 shows the data for this example. Species 1 has an initial concentration = 1 µM whereas Species 2 and Species 3 have zero initial concentration. The system is closed with no external fluxes and no fixed concentrations. The reactions conform to mass-action kinetics with first order rate constants k1 and k2. The minimum, maximum and nominal values for these two constants are also shown in Fig. 3. | ||
| Fig. 3 Network structure and data for illustrative example. | ||
Suppose we have carried out time course measurements on Species 2 and found the following output feature values:
| Ypk: Height of peak value of Species2 = 0.30 µM |
| Tpk: Time of peak value of Species2 = 80 s |
When we perform the simulation at the nominal parameter values, however, we find that Ypk = 0.774 µM and Tpk = 25.7 s (Fig. 4). The nominal parameter values are therefore incorrect and we use the proximate tuning algorithm to adjust them in order to fit the model to the measured outputs. The progress of the algorithm is shown in Table 2. At the start of each iteration the model simulation is run at the current point in the parameter space and the simulated output values are compared with the measured values. If convergence of the simulated and measured values (within a pre-specified tolerance) has been achieved the algorithm terminates. Otherwise the sensitivities of each output feature with respect to each parameter are evaluated and this information is used to formulate an LP sub-problem as described earlier. The optimal solution to the LP sub-problem defines a step in the parameter space to a new (hopefully better) point in the parameter space and the next iteration then begins. It can be seen that the algorithm converges to the measured output values in just 3 iterations.
 | ||
| Fig. 4 Simulated concentration profiles for the nominal (i.e. initial estimate) vs. fitted parameter sets in Example 1. The final fit is exact. | ||
| Itn | Objective value | Parameter Values | Outputs | Sensitivities (Dynamic Control Coefficients) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Predicted | Actual | k 1 | k 2 | Ypk | Tpk | dYpk/dk1 | dYpk/dk2 | dTpk/dk1 | dYpk/dk2 | |
| 0 | — | 9.0572 | 0.1000 | 0.0100 | 0.774 | 25.7 | 0.173 | –0.173 | –0.646 | –0.354 |
| 1 | 2.6403 | 3.9164 | 0.0100 | 0.0270 | 0.206 | 58.8 | 0.659 | –0.659 | –0.406 | –0.594 |
| 2 | 0.9871 | 1.1749 | 0.0103 | 0.0158 | 0.293 | 78.5 | 0.569 | –0.569 | –0.470 | –0.530 |
| 3 | 0.9854 | 0.9864 | 0.0103 | 0.0152 | 0.300 | 80.0 | 0.563 | –0.563 | –0.473 | –0.527 |
It is interesting to observe qualitatively the performance of the algorithm for this simple example. At the nominal point (Iteration 0), for example, the sensitivities of Tpk with respect to k1 and k2 are both negative which suggests that either or both could be decreased in order to increase the model Tpk value towards the measured Tpk value. However, the sensitivities of Ypk with respect to k1 and k2 are of opposite sign and therefore, in order to decrease Ypk to its measured value, a decrease in k1 (positive sensitivity) and an increase in k2 (negative sensitivity) could be used. This is in fact what the algorithm chooses to do, thus moving towards the measured value of Ypk. However, the net effect on Tpk is also in the right direction (i.e.Tpk is increased) since the LP sub-problem chooses a larger fractional change in k1 than in k2. Thus the LP-sub-problem chooses a step that is the best compromise in order to move towards all the measured values while minimizing the maximum distance moved from the nominal point. The effect of the varying sensitivities can be also be observed qualitatively in Table 2. At the nominal point the sensitivities of Ypk with respect to k1 and k2 are comparatively low (± 0.173) and the consequence of this is that the LP sub-problem prescribes the largest possible reduction of k1 down to its minimum value of 0.01 s–1. However, the magnitude of the Ypk sensitivities increase strongly to (± 0.659) at the next point (Iteration 1). This is indicated by the fact that the algorithm overestimates that required step and the value of Ypk at the new point (0.206 µM) is less than its measured value (0.300 µM). During the next step (Iteration 2) the algorithm corrects this by slightly increasing the value of k1 from its minimum value.
The progress of the algorithm through this 2-dimensional parameter space is conveniently represented in graphical form in Fig. 5. Note that the final two points (Iterations 2 and 3) are difficult to distinguish since they are in close proximity.
 | ||
| Fig. 5 Graphical illustration of proximate tuning algorithm for Example 1. | ||
Another fact that is evident from Table 2 is that the Ypk sensitivities are always equal and opposite. This is a demonstration of the summation theorems for dynamic metabolic control analysis.18 These state that all the Ypk sensitivities must sum to zero and the all Tpk sensitivities must sum to minus one (as can also be verified from Table 2).
Finally, it should also be noted that Example 1 is completely defined in terms of parameter estimation in that there is a single unique point in the parameter space that gives the measured outputs for this case. An analytical treatment of this example is given in Appendix B. For real networks, however, there are likely to be far more uncertain parameters than measured outputs, leading to a grossly under-defined problem for traditional parameter estimation methods that treat each point in the parameter space as equally probable. In general there will be infinite points in the parameter space that fit the model to the measured outputs. The use of the nominal point by the proximate tuning algorithm is the key feature that enables an under-defined problem to be converted into one that is much better defined—perhaps with a unique solution—since not all the points fitting the measured values are likely to be equidistant from the nominal point.
Example 2
In this case study we apply the proximate tuning algorithm to a model of the p38 MAP kinase signalling pathway. The p38 MAP kinases regulate the expression of inflammatory cytokines and are therefore a target for treating chronic inflammatory diseases. Some sixteen p38 inhibitors are in development32 for the treatment of rheumatoid arthritis, inflammation, Crohn's disease, chronic obstructive pulmonary disease and psoriasis. The model has 89 reactions and 59 species and mass-action kinetics are assumed. The network stoichiometry is shown in Fig. 6. The full set of ordinary differential equations and the SBML33 file for this model are given in the ESI.†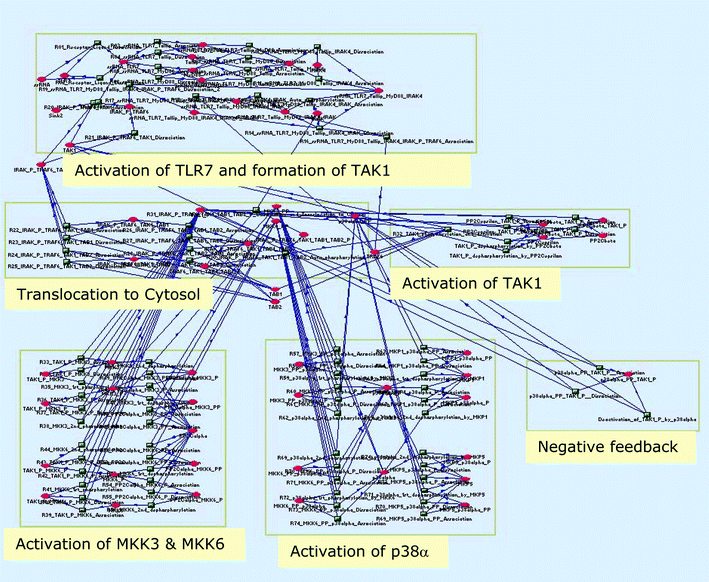 | ||
| Fig. 6 p38 MAP kinase signalling network. | ||
None of the 89 rate constant values has been published in the literature so we decided to group the reactions into families and use order of magnitude estimates for their nominal, minimum and maximum values as listed in Table 3. One assertion we make is that the on rates of aqueous reactions at room temperature proceed at approximately 107 M–1 s–1. This is derived from estimates that the limiting rate of such reactions is of the order of 7.109 M–1 s–1.34 Observed rates are often two orders of magnitude less than this limiting value and it has been argued that this is due to the productive contact surface on a typical protein being only ca. 1%,35 although unfavourable electrostatic forces may also contribute.36 In addition, due to natural selection pressures, biomolecule–partner interactions tend not to be less than nM,37 leading in turn to typical estimates of off rates of the order of not greater than 1 s–1. e.g. dissociation rates for enzyme–substrate reactions tend to vary between 10–4–1 s–1.38
| Reaction Type | Schoeberl ERK MAP kinase model parameters | Example 2 parameters | ||||||
|---|---|---|---|---|---|---|---|---|
| No. reactions | Units | Average | Min | Max | Nominal | Min | Max | |
| Complex Association | 28 | µM–1 s–1 | 8.483 | 0.100 | 30.000 | 10.00 | 0.01 | 100.00 |
| Complex Dissociation | 28 | s–1 | 0.277 | 0.002 | 1.300 | 10.00 | 0.01 | 100.00 |
| Phosphatase Association | 5 | µM–1 s–1 | 21.150 | 0.250 | 71.700 | 10.00 | 0.01 | 100.00 |
| Phosphatase Dissociation | 5 | s–1 | 0.520 | 0.200 | 0.800 | 10.00 | 0.01 | 100.00 |
| Phosphatase Catalysis | 5 | s–1 | 0.337 | 0.058 | 1.000 | 0.100 | 0.001 | 10.000 |
| Kinase Association | 4 | µM–1 s–1 | 5.605 | 0.110 | 11.100 | 10.00 | 0.01 | 100.00 |
| Kinase Dissociation | 4 | s–1 | 0.026 | 0.018 | 0.033 | 10.00 | 0.010 | 100.00 |
| Kinase Catalysis | 4 | s–1 | 7.025 | 2.900 | 16.000 | 0.100 | 0.001 | 10.00 |
| Complex Auto-Catalysis (forward reaction) | 1 | s–1 | 6.000 | 6.000 | 6.000 | 0.100 | 0.001 | 10.00 |
| Receptor-ligand Association | 1 | µM–1 s–1 | 30 | 30 | 30 | 10.00 | 0.100 | 100.00 |
| Receptor-ligand Dissociation | 1 | s–1 | 0.0038 | 0.0038 | 0.0038 | 0.010 | 0.001 | 10.00 |
In Table 3 we also compare our values with those from a well known model of the closely related ERK MAP kinase pathway.39 It can be seen that the values are in broad agreement except for protein dissociation rates which we choose to be equal to the association rates. There is therefore no forward bias along the pathway at our nominal point and we were interested in how the PPT algorithm would adjust these parameters in order to fit the model to the data.
We also assume that all species are initially present in their uncomplexed and inactive form at a concentration = 1 µM (see Appendix D). It should be noted that these initial concentrations are also parameters in the ODE model and could be fitted to the data in exactly the same way as the rate constants. In this study, however, none of these initial concentrations is allowed to vary in the fitting process.
In addition to the complete lack of kinetic data, there has been very little published dynamic measurements of p38α phosphorylation. We can, however, use what little output data are available to tune the model. Unpublished studies suggest that around half of the total p38α MAP Kinase is doubly-phosphorylated to p38αPP after stimulation. So we assume Ypk(p38αPP) = 0.5. Other experiments on MAPKAP2—a substrate of p38αPP—suggest that the peak value of phosphorylated MAPKAP2 occurs 30 min after stimulation. MAPKAP2 is not considered in our model, but using it as a surrogate for p38αPP we shall assume Tpk(p38αPP) = 1800 s.
As illustrated in Table 4, the proximate tuning algorithm gave convergence to these measured values in just 6 iterations occupying around 10 min of CPU time on an Intel Pentium 4. The fitted p38αPP profile is shown in Fig. 7. Note that the maximal fractional change in any parameter required to tune the model was only 2.34 (up or down)— i.e. the optimal value of ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) = log10 (2.34) = 0.369. Thus a perhaps surprisingly small change is required to increase the simulated value of Ypk by some 23 orders of magnitude. However, it should be remembered that there are 89 parameters that can vary up or down by this amount. If, for example, Ypk had a sensitivity of ±1 to each parameter, and we choose to increase those parameters with a positive sensitivity and decrease those with a negative sensitivity by the same factor, then the predicted value of Ypk would be increased by a factor of (2.34)89 = 7 × 1032.
= log10 (2.34) = 0.369. Thus a perhaps surprisingly small change is required to increase the simulated value of Ypk by some 23 orders of magnitude. However, it should be remembered that there are 89 parameters that can vary up or down by this amount. If, for example, Ypk had a sensitivity of ±1 to each parameter, and we choose to increase those parameters with a positive sensitivity and decrease those with a negative sensitivity by the same factor, then the predicted value of Ypk would be increased by a factor of (2.34)89 = 7 × 1032.
 | ||
| Fig. 7 Fitted profile with Ypk = 0.5 and Tpk = 30 min. | ||
| Itn. | Max Fractional Parameter Change | Ypk/µM | Tpk/s |
|---|---|---|---|
| 0 | 1 | 6.78e–24 | 2.40e+02 |
| 1 | 2.08 | 7.40e–04 | 3.60e+03 |
| 2 | 2.14 | 5.14e–02 | 2.51e+03 |
| 3 | 2.24 | 2.65e–01 | 2.04e+03 |
| 4 | 2.31 | 4.26e–01 | 1.86e+03 |
| 5 | 2.34 | 4.89e–01 | 1.84e+03 |
| 6 | 2.34 | 5.00e–01 | 1.81e+03 |
The fitted ODEs for this model are given in Appendix D. It can be seen that these equations, unlike the original ODEs, have a forward bias leading to much stronger activation of p38. The activating reactions such as kinases associating to their substrate proteins and phosphorylating them are increased—usually by a factor of 2.34. Conversely, the deactivating reactions such as phosphatase association/catalysis are decreased by the same amount.
It is also instructive to look at how the sensitivities vary during each step of the proximate tuning algorithm (Table 5 and Fig. 8, 9). The average absolute Ypk sensitivity decreases monotonically as the iterations proceed from an initial value of 0.966 down to a final value of 0.099. In addition, only 7 out of 90 parameter sensitivities change in sign during the course of the iterations—i.e. have plots that cross the abscissa in Fig. 8. Even these 7 parameters do not undergo large changes in sign but rather stay within 4 × 10–4 of the abscissa once they have crossed it (Fig. 8 inset). This suggests that the Ypk output feature space is fairly well behaved, smooth, and convex in most directions. In addition, the decreasing trend in most of the sensitivities means that we are unlikely to take overly large steps. We can therefore be confident that the proximate tuning algorithm takes us to the most proximate point that matches our measured Ypk value.
 | ||
| Fig. 8 Variation of Ypk sensitivities during proximate tuning for Example 2. | ||
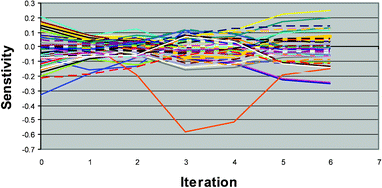 | ||
| Fig. 9 Variation of Tpk sensitivities during proximate tuning for Example 2. | ||
| Feature | Sensitivities changing sign | Average Absolute Sensitivity | ||||||
|---|---|---|---|---|---|---|---|---|
| Itn. 0 | Itn. 1 | Itn. 2 | Itn. 3 | Itn. 4 | Itn. 5 | Itn. 6 | ||
| Ypk | 7 | 0.966 | 0.715 | 0.523 | 0.265 | 0.140 | 0.104 | 0.099 |
| Tpk | 50 | 0.055 | 0.033 | 0.041 | 0.057 | 0.054 | 0.057 | 0.062 |
Unfortunately the same is not true for the Tpk output feature space. There is no decreasing trend in the sensitivities (Fig. 9) and 50 out of the 90 parameter sensitivities undergo a change of sign. Unlike the Ypk sensitivities, many of these sensitivity sign changes are significant—i.e. the sensitivities have sizeable negative and positive values during the search. (This is plausibly due to the different summation theorems for the peak value and peak time, see above).
Example 3
We have applied the LP implementation of the PPT algorithm to the glucose-derepressed glycolysis model initially described by Teusink and colleagues.40 This is a detailed ODE model comprising 25 metabolites and 19 reactions. Many of these reactions are regulated by multiple metabolites and have quite complex rate equations. Most of these equations are modified Michaelis–Menten in form and are therefore pre-multiplied by a Vmax parameter that specifies the maximal rate of the corresponding reaction. The kinetic constants appearing in these rate equations have been measured in vitro separately for each step in the pathway but there is still a discrepancy between the model predictions and metabolite concentrations observed in vivo.Pritchard and Kell41 subsequently investigated one likely cause of this discrepancy, namely, variations of the expression levels of intra-cellular enzymes as quantified by the Vmax parameters. They used evolutionary programming to fit the model to the in vivo data by adjusting Vmax for 14 of the 20 reactions. As we noted with the p38 example above, they found that only minor adjustments in these parameters are needed to remove the aforementioned discrepancy almost completely and achieve a very close fit to the metabolite concentrations measured in vivo. They also explored a large parameter space in which each of the 14 Vmax parameters was independently set to a value between one half of or twice its best-fit value in all combinations. Their analysis showed that only 50% of these combinations reached a steady state. The steady-state solutions could be assigned to one of 3 regimes depending on their patterns of flux control.
This parameter space, together with the requirement to fit 12 steady-state variables represents a challenging landscape and we decided to use it to test the PPT algorithm. We were interested in whether the algorithm could start at randomly selected points within the parameter space and navigate to the best fit point that matches the target metabolite concentrations. We randomly sampled 20 points from within the same parameter space as considered by Pritchard and Kell.41 Note that they were exploring the vertices of the parameter space hypercube whereas we sampled uniformly from its interior.
We found that 12 out of the 20 (60%) sampled nominal points achieved a steady state, which is in broad agreement with the figure of 50% reported by Pritchard and Kell although they were sampling from the edge of the parameter space rather then uniformly from its interior as in this work. The LP-PPT algorithm achieved a reasonable fit for 11 out of the 20 sampled nominal points. The failure of the remaining 9 samples was due to unsteady solutions encountered during the course of each fitting run since the PPT algorithm explores a new intermediate point at each iteration. This is illustrated in Fig. 10. For all the 9 fitting runs that fail, at least a third of their iterations are unsteady, even though 4 of these are initially steady (i.e. at Iteration 0). Equally, of the 11 runs that give acceptable fitting, 3 were not initially steady but still succeeded due to subsequent steady iterations. Thus the PPT algorithm demonstrates a degree of robustness in the presence of unsteady (and therefore for this model unattainable) solutions.
 | ||
| Fig. 10 Impact of unsteady solutions on the algorithm performance. | ||
Table 6 shows the parameter values and steady state concentrations for the 11 runs that gave good performance (objective function decreased by at least 90%). The objective function represents the degree to which the simulated steady state concentrations differ from the target values. The samples are ordered from left to right in order of descending objective function decrease. It should be noted that the number of iterations for each run was limited to 10 and that the lowest objective function is not necessarily the last one since in some cases the objective function increased, indicating a worse fit than the previous iteration. This is due to the linearity assumptions implicit in the optimisation sub-problem combined with the fact that we used a fully ‘optimistic’ step length (γ = 1).This ‘un-damped’ variant of the algorithm is prone to give oscillatory behaviour in this challenging landscape. More sophisticated methods such as those with adaptive step lengths would most likely achieve smoother convergence but in this case we decided simply to let the algorithm run its course for a fixed number of iterations and report the iteration with the closest fit for each run in Table 6.
| Sample # | 17 | 8 | 18 | 16 | 4 | 14 | 1 | 12 | 11 | 7 | 2 | Mean | Std/Mean (%) | Base Values | Fitting Error (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| % Obj. Improvement | 99.4 | 98.8 | 97.5 | 96.6 | 94.7 | 93.2 | 93.2 | 93.1 | 93.1 | 91.8 | 91.0 | 94.8 | 2.9 | — | — |
| Initial Obj. | 64.7 | 71.8 | 37.2 | 31.9 | 18.2 | 55.4 | 70.8 | 31.7 | 108.8 | 37.9 | 131.8 | 60.0 | 55.5 | — | — |
| Fitted Obj. | 0.4 | 0.87 | 0.94 | 1.09 | 0.96 | 3.74 | 4.83 | 2.18 | 7.54 | 3.1 | 11.91 | 3.415 | 99.1 | — | — |
| Max Frac. Change | 1.997 | 1.559 | 1.571 | 1.685 | 1.792 | 1.743 | 1.675 | 1.808 | 1.923 | 1.638 | 1.895 | 1.753 | 7.8 | — | — |
| V max(HXT)/mM min–1 | 114.2 | 102.8 | 108.8 | 101.3 | 105.1 | 103.7 | 102.6 | 101.6 | 102.0 | 101.6 | 103.5 | 104.3 | 3.6 | 103.3 | –0.99 |
| V max(HK)/mM min–1 | 202.5 | 431.8 | 243.8 | 670.5 | 311.9 | 275.4 | 608.0 | 807.1 | 807.1 | 806.0 | 740.8 | 536.8 | 43.9 | 403.5 | –33.02 |
| V max(PGI)/mM min–1 | 1929 | 1898 | 1909 | 1933 | 1919 | 1897 | 1709 | 1881 | 1839 | 1917 | 1631 | 1860 | 5.1 | 1937.6 | 3.99 |
| V max(PFK)/mM min–1 | 121.6 | 121.5 | 122.2 | 121.5 | 121.7 | 120.2 | 125.1 | 121.3 | 101.9 | 122.1 | 108.4 | 118.8 | 5.6 | 121.7 | 2.32 |
| V max(ALD)/mM min–1 | 101.1 | 101.0 | 100.8 | 101.0 | 100.8 | 98.7 | 97.9 | 100.4 | 102.4 | 100.4 | 96.2 | 100.1 | 1.7 | 101.2 | 1.11 |
| V max(PGK)/mM min–1 | 801 | 642 | 2278 | 2291 | 1362 | 642 | 1013 | 2568 | 1258 | 1769 | 1003 | 1421 | 47.0 | 1283.8 | –10.66 |
| V max(PGM)/mM min–1 | 2466 | 2434 | 2419 | 2423 | 2430 | 2430 | 2428 | 2445 | 2529 | 2473 | 2530 | 2455 | 1.6 | 2429.2 | –1.07 |
| V max(ENO)/mM min–1 | 333.1 | 227.1 | 254.0 | 240.4 | 320.9 | 214.4 | 206.3 | 211.4 | 242.7 | 211.0 | 218.6 | 243.6 | 17.2 | 220.6 | –10.43 |
| V max(PYK)/mM min–1 | 476.1 | 790.1 | 624.9 | 700.5 | 482.2 | 985.1 | 1572.8 | 1267.6 | 660.4 | 1055.0 | 1195.6 | 891.8 | 37.7 | 952.3 | 6.35 |
| V max(PDC)/mM min–1 | 875.3 | 870.2 | 871.1 | 869.9 | 874.3 | 877.6 | 888.3 | 875.5 | 894.3 | 883.9 | 908.8 | 880.8 | 1.3 | 874.3 | –0.75 |
| V max(ADH)/mM min–1 | 50.2 | 50.3 | 50.2 | 50.2 | 50.0 | 50.3 | 51.2 | 50.5 | 51.5 | 50.6 | 52.1 | 50.6 | 1.2 | 50.1 | –1.02 |
| V max(G3PDH)/mM min–1 | 47.2 | 47.2 | 47.2 | 47.2 | 47.0 | 46.8 | 46.6 | 47.3 | 47.2 | 47.2 | 46.9 | 47.1 | 0.5 | 47.4 | 0.62 |
| V max(GAPDHr)/mM min–1 | 7449 | 5665 | 3298 | 3298 | 3298 | 3424 | 12429 | 4690 | 11180 | 7325 | 3298 | 5941 | 53.1 | 6596.2 | 9.93 |
| V max(GAPDHf)/mM min–1 | 3973 | 3562 | 2393 | 2336 | 2541 | 2794 | 4740 | 2666 | 4653 | 3297 | 2302 | 3205 | 27.1 | 3419.5 | 6.27 |
| [ATP]ss/mM | 2.534 | 2.529 | 2.532 | 2.521 | 2.531 | 2.450 | 2.567 | 2.550 | 2.578 | 2.544 | 2.606 | 2.540 | 1.5 | 2.536 | –0.18 |
| [G6P]ss/mM | 2.346 | 2.358 | 2.370 | 2.353 | 2.365 | 2.076 | 2.634 | 2.520 | 4.472 | 2.484 | 4.462 | 2.767 | 29.3 | 2.346 | –17.94 |
| [ADP]ss/mM | 1.276 | 1.279 | 1.278 | 1.284 | 1.278 | 1.327 | 1.257 | 1.267 | 1.249 | 1.271 | 1.232 | 1.273 | 1.8 | 1.276 | 0.23 |
| [F6P]ss/mM | 0.596 | 0.598 | 0.601 | 0.598 | 0.600 | 0.526 | 0.659 | 0.638 | 1.143 | 0.631 | 1.120 | 0.701 | 29.3 | 0.596 | –17.56 |
| [F16bP]ss/mM | 5.377 | 5.478 | 5.692 | 5.592 | 5.602 | 4.892 | 8.242 | 6.132 | 5.432 | 6.302 | 12.029 | 6.434 | 30.4 | 5.358 | –20.07 |
| [AMP]ss/mM | 0.289 | 0.291 | 0.290 | 0.294 | 0.291 | 0.323 | 0.277 | 0.283 | 0.272 | 0.286 | 0.262 | 0.287 | 5.1 | 0.289 | 0.54 |
| [DHAP]ss/mM | 0.790 | 0.801 | 0.808 | 0.816 | 0.806 | 0.750 | 0.860 | 0.815 | 0.808 | 0.837 | 0.899 | 0.817 | 4.5 | 0.788 | –3.65 |
| [GAP]ss/mM | 0.036 | 0.036 | 0.036 | 0.037 | 0.036 | 0.034 | 0.039 | 0.037 | 0.036 | 0.038 | 0.041 | 0.037 | 4.5 | 0.035 | –3.66 |
| [NAD]ss/mM | 1.161 | 1.166 | 1.168 | 1.172 | 1.160 | 1.168 | 1.180 | 1.171 | 1.176 | 1.178 | 1.197 | 1.172 | 0.9 | 1.161 | –0.99 |
| [NADH]ss/mM | 0.429 | 0.424 | 0.422 | 0.418 | 0.430 | 0.422 | 0.410 | 0.419 | 0.414 | 0.412 | 0.393 | 0.418 | 2.4 | 0.429 | 2.67 |
| [P3G]ss/mM | 0.886 | 0.908 | 0.885 | 0.874 | 0.902 | 0.835 | 0.924 | 0.895 | 0.951 | 0.957 | 0.885 | 0.900 | 3.7 | 0.882 | –2.10 |
| [P2G]ss/mM | 0.124 | 0.127 | 0.123 | 0.122 | 0.126 | 0.117 | 0.129 | 0.125 | 0.134 | 0.135 | 0.124 | 0.126 | 4.0 | 0.123 | –2.57 |
| [PYR]ss/mM | 1.857 | 1.862 | 1.863 | 1.862 | 1.857 | 1.820 | 1.852 | 1.863 | 1.846 | 1.851 | 1.841 | 1.852 | 0.7 | 1.859 | 0.36 |
It can be seen from the rightmost column that the error between the mean fitted concentrations and the actual concentrations is less than 4% for all species except G6P, F6P and F16bP for which the error is 20%. However, it can be noticed from the third to right column that the standard deviations of these three concentrations are also much larger than the others at around 30% of the mean value which indicates that fitting errors are not in this sense statistically significant. The higher scatter for these concentrations indicates that they interact with the parameters in a strongly non-linear manner—i.e. their sensitivity to the parameters has significant higher order terms. A similar argument can be applied to the scatter in the fitted Vmax values. Even for those parameters that seem to be poorly estimated (e.g.Vmax(HK)), the fitting error of their mean value lies well within the scatter in the values across all the runs.
We use this example to compare the PPT algorithm with 5 other established algorithms for parameter estimation that are available in COPASI.42 The results are given in Table 7 which gives the sum of squared residuals with mean square weighting. The last row gives the average number of function evaluations used for each method. This corresponds to the number of times the original set of ODEs is integrated. We group the algorithms into gradient based methods versus sampling methods. Levenberg–Marquardt, steepest descent and PPT itself fall into the category of gradient based methods in that they all generate a single deterministic trajectory in the search space with each new step depending on the gradient information at the current point on the trajectory. Hooke & Jeeves, genetic algorithms and evolutionary programming use sampled function evaluations to generate improved solutions rather than relying on gradient calculations.
| Run | PPT | LevenbergMarquardt | Steepest descent | Hooke & Jeeves | Genetic algorithm | Evolutionary programming | Best performing algorithm overall | Best performing gradient based algorithm |
|---|---|---|---|---|---|---|---|---|
| 1 | 5.697e–02 | 3.247e–01 | 1.909e–02 | 6.909e–03 | 1.375e–02 | 6.0542e–02 | Hooke & Jeeves | Steepest descent |
| 2 | 3.798e–01 | 1.805e–01 | 1.687e+00 | 1.191e–01 | 3.994e–02 | 7.5641e–02 | Genetic algorithm | Levenberg-marquardt |
| 3 | 1.133e+01 | 2.436e+03 | 2.459e–01 | 2.089e–02 | 1.667e–02 | 3.3798e–02 | Genetic algorithm | Steepest descent |
| 4 | 4.338e–04 | 1.208e–02 | 1.849e–02 | 1.284e–02 | 6.930e–02 | 8.0994e–02 | PPT | PPT |
| 5 | 2.819e–01 | 2.360e–01 | 1.457e–01 | 1.127e–02 | 4.629e–02 | 1.0499e–01 | Hooke & Jeeves | Steepest descent |
| 6 | 7.431e+00 | #INF | #INF | 5.040e–01 | 3.102e–02 | 8.4930e–02 | Genetic algorithm | PPT |
| 7 | 6.686e–03 | 2.193e–01 | 2.193e–01 | 2.501e–02 | 1.263e–02 | 5.2787e–02 | PPT | PPT |
| 8 | 1.420e–04 | #INF | #INF | 9.002e–02 | 4.082e–02 | 8.5003e–02 | PPT | PPT |
| 9 | 5.769e–01 | 8.046e–01 | 1.302e+00 | 8.179e–02 | 2.232e–02 | 6.7386e–02 | Genetic algorithm | PPT |
| 10 | 7.115e–01 | 1.585e+00 | 1.466e+00 | 7.459e–01 | 1.717e–02 | 2.5531e–02 | Genetic algorithm | PPT |
| 11 | 8.654e–02 | 1.672e+00 | 1.624e+00 | 6.193e–01 | 2.384e–02 | 4.9066e–02 | Genetic algorithm | PPT |
| 12 | 4.591e–03 | 8.591e–01 | 4.753e–02 | 7.777e–03 | 2.293e–02 | 2.5364e–02 | PPT | PPT |
| 13 | 5.803e–01 | 4.512e–01 | 3.467e–01 | 8.876e–02 | 9.162e–02 | 9.7494e–02 | Genetic algorithm | Steepest descent |
| 14 | 3.375e–03 | 9.649e+00 | 6.764e–02 | 7.168e–03 | 3.589e–02 | 8.5433e–02 | PPT | PPT |
| 15 | 3.444e–01 | 1.848e+00 | 1.835e+00 | 6.667e–02 | 2.977e–02 | 1.0630e–01 | Genetic algorithm | PPT |
| 16 | 4.234e–04 | 1.235e+00 | 3.944e–02 | 2.459e–03 | 5.157e–02 | 5.3368e–02 | PPT | PPT |
| 17 | 4.105e–06 | 3.235e–01 | 3.244e–01 | 1.470e–01 | 2.915e–02 | 6.9475e–02 | PPT | PPT |
| 18 | 7.733e–04 | 1.209e+00 | 1.183e–02 | 2.399e–02 | 4.910e–02 | 5.1171e–02 | PPT | PPT |
| 19 | 5.984e–01 | 4.871e–01 | 1.233e+00 | 4.871e–01 | 2.557e–02 | 7.1215e–02 | Genetic algorithm | Levenberg-marquardt |
| 20 | 5.794e–01 | 2.874e+02 | 1.700e+00 | 2.848e–02 | 1.623e–02 | 1.6233e–02 | Genetic algorithm | PPT |
| Ave. function evals. per run | 140 | 180 | 182 | 277 | 216 | 216 | — | — |
It can be seen from Table 7 that PPT was the best performing algorithm of all the methods in 8 of the runs, surpassed only by the genetic algorithm which gave the best solution for 10 runs. Hooke & Jeeves was the only other algorithm to dominate the others—but only for 2 of the runs. Out of the 3 gradient based methods, PPT proved to be easily the best performer, beating the other two methods in 14 runs, with steepest descent and Levenberg-Marquardt winning for 4 and 2 of the runs respectively. Given the somewhat pathological nature of this model (i.e. the absence of a steady state for around half of the parameter combinations) one would expect the sampling based methods to be more robust than those using gradients. It is therefore encouraging that the proximate tuning algorithm is the only gradient based method that is competitive with the sampling based methods.
Example 4
The previous examples have demonstrated that the proximate parameter tuning algorithm can be an effective method for adjusting parameters in order to fit a model to limited target output features. In this example we change tack somewhat in order to compare the algorithm with others that represent the current state-of-the-art in parameter estimation. We apply the algorithm to estimate the kinetic parameters for the thermal isomerisation of α-pinene for which detailed time course measurements been made available by Fuguitt & Hawkins.43 The fact that this 60-year-old example is still one of the most data-rich examples cited in the field of biochemical parameter estimation is indicative of the paucity of time series data being generated to fuel systems biology research and hence the need for approaches—such as that presented here—that can work with very little data.The reactions with the five rate constants (p1 to p5) to be estimated are given in Fig. 11 along with the measured concentrations of the 5 species (y1 to y5). This challenging benchmark parameter estimation problem has been studied extensively (e.g.ref. 44,45) and most recently by Rodriguez-Fernandez et al46 who used a novel scatter search methodology to detect the globally optimal solution reliably in a fraction of the computational time required by previous methods. The objective function that is minimized is the unweighted sum of the squared residual errors for between the measured and simulated concentrations for each of the 5 species at each of the 8 time points:
 | (16) |
 | ||
| Fig. 11 Reaction scheme for the thermal isomerisation of α-pinene and measured time series data. | ||
Rodriguez-Fernandez and colleagues46 report the global minimum to be J = 19.87 which occurs at: p1=5.926e–5, p2=2.963e–5, p3=2.047e–5, p4=2.745e–4, p5=3.998e–5. Under the assumption that the residuals are normally distributed with the same variance, the minimum sum of squared residuals represents the maximum likelihood estimator. On the other hand, the proximate tuning algorithm treats each measured data point  as a separate feature and, if all terms except the first in the objective function eqn (7) are neglected, seeks to minimize a radically different objective, viz:
as a separate feature and, if all terms except the first in the objective function eqn (7) are neglected, seeks to minimize a radically different objective, viz:
 | (17) |
What is the relationship between the PPT objective and the standard sum of squares residuals (SSR) objective? In order to answer this question we ran the PPT algorithm using the global minimum SSR solution as the nominal point with all minimum parameter values = 10–8 and all maximum parameter values = 0.5. We found that the global minimum SSR solution is not the minimiser of the PPT objective since the PPT algorithm adjusts the parameter values and smoothly moves to a nearby location in the parameter space where it oscillates between two new points which are superior with respect to the PPT objective but are obviously not the SSR objective. The progress of the algorithm in moving away from the SSR best fit solution and the limiting oscillations are shown in Table 1 and Fig. 12 (Run 1). Thus, as expected, the PPT and SSR objectives have different local minima (for this example the SSR local minimum is also thought to be the global SSR minimum.). It can be seen in Table 1 that the PPT algorithm does make significant adjustments for some parameters (e.g. 88% for parameter p3) in order to minimize the PPT objective. The PPT and SSR solutions are, nevertheless, relatively close (‘proximate’) when the large size of the parameter space is taken into account (±3 orders of magnitude from the nominal point).
 | ||
| Fig. 12 Least squares fitting performance of the PPT algorithm for 4 runs using different nominal points, feature types and penalty weightings. | ||
The quality of the fit of the PPT adjusted solution is compared to that of the original best fit SSR solution in Fig. 13. It can be seen that the profiles are in good agreement except for species y4 which is plotted with magnified vertical scaling in the inset. For species y4, it can be seen that the PPT solution has chosen to fit the earlier time points more closely at the expense of a poor fit to the final two points whereas the SSR solution gives a better overall compromise fit to all the points. This is because, in the SSR objective, the penalty incurred by each error increases as its square, so it will tend to give a good compromise fit with many smaller errors rather then fewer larger errors. This is nearly always a desirable feature for curve fitting. In addition, the unweighted SSR fit penalizes the fractional error in larger value points more heavily than smaller ones.
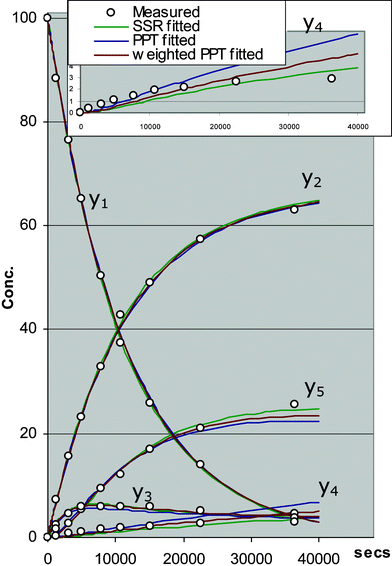 | ||
| Fig. 13 Comparison of weighted/unweighted PPT fit to measured points versus SSR best fit. | ||
Conversely, each term in the PPT objective penalizes the fractional error of the fitted versus the target value irrespective of its magnitude meaning that points of smaller magnitude carry equal weight to larger ones. Also, the logarithmic form of each penalty term implies that the penalty incurred by a large error is proportionately less than that for a smaller error which is also in direct contrast to the SSR fitting. A consequence of this is that minimization of the sum of these logarithmic terms can give a poorer fit, both intuitively and probabilistically. Given these differences (summarized in Table 8), it is perhaps surprising but certainly encouraging that the PPT and SSR fits are in close agreement. The different form of the PPT objective as compared to the SSR objective gives slightly different results but both give a good approximation to the true maximum likelihood solution. It is important to note that even the SSR solution represents an approximation since it use the assumption that the residual errors are normally distributed which implies a non-zero probability of negative concentrations which is obviously impossible.
| Un-weighted SSR objective | Un-weighted PPT objective | |
|---|---|---|
| Different errors | Penalises fractional errors in large target values more heavily than those for small target values | Penalises fractional errors in all target values by the same amount |
| Same error | The larger the fractional error, the larger the proportionate penalty. | The larger the fractional error, the smaller the proportionate penalty. |
The first of these differences listed in Table 8 can be reduced by applying variable feature weightings in PPT whereby the fractional errors for larger points are penalized more heavily than those for smaller points. This is shown by Run 2 (Table 9 and Fig. 12) where we use weightings to improve the SSR fit achieved by the PPT algorithm. The weightings we used in this case were simply the target value for each feature (βp = ygp). This is a rather arbitrary choice but it does have the effect of penalizing bigger feature values and improving the SSR score of the PPT (see Fig. 11) fit so we also used it for Run 3.
| Run | Nominal parameter set | Feature type | Feature penalty weighting | Parameter set | PPT Obj. | Sum squared errors | Parameter values | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| p 1 | p 2 | p 3 | p 4 | p 5 | |||||||
| 1 | SSR best fit | Points | Uniform: βp=10 | Nominal | 39.4 | 19.8 | 5.93e–05 | 2.96e–05 | 2.05e–05 | 2.75e–04 | 4.00e–05 |
| Fitted (12 itns.) | 30.7 | 46.2 | 5.81e–05 | 2.94e–05 | 3.86e–05 | 3.52e–04 | 6.02e–05 | ||||
| 2 | SSR best fit | Points | Target value: βp=ypg | Nominal | 11.4 | 19.8 | 5.93e–05 | 2.96e–05 | 2.05e–05 | 2.75e–04 | 4.00e–05 |
| Fitted (12 itns.) | 10.4 | 26.0 | 5.85e–05 | 2.94e–05 | 2.61e–05 | 2.98e–04 | 5.09e–05 | ||||
| 3 | Minimum: pi=1e–08 | Points | Target value: βp=ypg | Nominal | 1970.3 | 45558.6 | 1.00e–08 | 1.00e–08 | 1.00e–08 | 1.00e–08 | 1.00e–08 |
| Fitted (12 itns.) | 14.7 | 24.8 | 5.85e–05 | 2.95e–05 | 2.69e–05 | 2.80e–04 | 4.28e–05 | ||||
| 4 | Maximum: pi=0.5 | Areas | Uniform: βp=10 | Nominal | 125.5 | 48210.0 | 5.00e–01 | 5.00e–01 | 5.00e–01 | 5.00e–01 | 5.00e–01 |
| Fitted (12 itns.) | 4.4 | 116.4 | 5.93e–05 | 2.96e–05 | 2.60e–05 | 4.24e–01 | 1.17e–01 | ||||
The second of the differences summarized in Table 8 can perhaps be addressed in some instances by the introduction of a penalty for the maximum fractional error (β > 0), although this did not help for this example and so we kept this penalty at zero. One can, however, readily envisage many other situations in which the minimization of the maximum fractional error is a strong driver and this penalty would be helpful in this context.
Next we wanted to test the performance of the PPT algorithm starting from nominal points that were a long way from the SSR best fit values. The results are shown in Fig. 12 and Table 9 (Runs 3 and 4).
Run 3 started from the maximum value for all parameters but, rather than fitting to the points as for the other runs, we were obliged instead to fit to the areas under the profiles. The reason that PPT is unable to fit to the points is that the nominal parameter values are so large (dynamics so rapid) that the system reaches steady state in under 30 s. It can be seen by inspection from the reaction scheme (Fig. 11) that the steady state concentrations of y1, y3 and y5 are zero for any positive set of parameters. It therefore proves impossible to calculate sensitivities numerically even for the first measured time point (1020 s) since the steady state has long since been reached. The concentrations of y1, y3 and y5 are all zero at this time and a perturbation in any parameter value has no detectable effect (i.e. their concentrations remain zero). This is all due to a very poor choice of nominal point.
However, the areas under the concentration profiles have finite values and sensitivities could be calculated for all of these species profile areas. We therefore decided to use the total area under each SSR best fit profile as target features for the PPT to try and fit the model to. The results are shown in Table 9 and Fig. 12 (Run 3). Note that we report the progress of this run in terms of the sum-of-squared errors of the points (not the areas) in order to facilitate comparison with the other runs. Although it can be seen that the sum-of-squared errors for the 40 points does not decrease monotonically, the equivalent error for the 5 areas being actually driving the fitting does decrease monotonically and, after 12 iterations, the PPT algorithm matches the areas almost exactly which is the reason why the final PPT objective is small.
However, it can be seen that the actual points are poorly fitted for y4 (Fig. 14) as the algorithm converges to an incorrect point in the parameter space with very much larger values of p4 and p5 than the best fit values (Table 9). It can be seen directly from the reaction scheme (Fig. 11) that these latter two parameters comprise the forward and backward rate constants of the same reversible reaction. The effect of an increase in one on the net flux through this reaction is therefore offset by an increase in the other and they therefore form a correlated subset. This lack of identifiability is thought to result in multiple local minima which is the major reason why this is a challenging problem. Nevertheless, the fact that values of p1, p2 and p3 close to the best fit values are obtained and the fact that the fit is good for most of the points show that there is merit in this approach. The PPT algorithm is able to reduce the sum-of-squares error by over 2 orders of magnitude. This example shows the flexibility of the PPT approach presented here whereby different features can be selected to drive the fitting process. It may be the case that certain feature spaces are smoother and more convex than others and these should be selected if appropriate. It would also be worthwhile to investigate transformations from one feature space to another. As an example, we could extend the use of areas as features to use one or more higher order ‘moments’ of area which might give better convergence than that obtained by considering the points individually.
 | ||
| Fig. 14 Comparison of best SSR fit with Run 4 fit (starting at maximum parameter values and fitting on areas under best fit profiles rather than measured points). | ||
In Run 4 we used the minimum parameter values as the nominal point and went back to using the points as the target features (as for Runs 1 and 2) since there was no difficulty in calculating sensitivities for these. The algorithm performed impressively, converging to a point very close to that found in Run 2 (which started at the SSR best fit) and with a slightly better SSR objective (Table 9 and Fig. 12). Thus, the PPT algorithm is able to traverse this large parameter space and reduce the SSR objective by over 3 orders of magnitude. It can be seen that the final PPT objective for Run 4 is higher than that for Run 2 even though the SSR objective is lower. This is because, as well as the error penalty, the PPT objective includes a penalty for the maximum logarithmic parameter deviation which, in the case of Run 4, is higher because the final point is much further away from the nominal point. This is also the reason why Run 4 finds ends up at a slightly different point in the parameter space compared to Run 2—i.e. because both are balancing the error penalties with those for the maximal parameter deviation. In this case, this happens to give a slightly lower final SSR objective for Run 4 than for Run 2.
The results from this example demonstrate that the PPT algorithm presented here can be effectively applied to standard parameter estimation problems. It should be remembered that the determination of the SSR best fit for this example is a challenging benchmark problem and only recently has a global sampling algorithm (SSm) been devised that can efficiently solve it with non-local starting points. PPT, on the other hand, is a deterministic and essentially local search algorithm that still manages to achieve a good fit from some distant starting points. In some cases, such as for Run 3 of this example, some manual intervention may be necessary to define alternative features. This, however, demonstrates a key strength of the PPT approach, namely that any target feature can be defined based on the measured time series data and used to drive the fitting process. In addition, the fact that the PPT algorithm is not computationally expensive means that it can be solved multiple times as part of an algorithm that globally samples the parameter space.
Discussion
Until this point we have addressed the problem of uncertainty but have deliberately avoided mention of ‘probability’—i.e. how that uncertainty should be quantified. We have both parameter uncertainty and measurement uncertainty. In our approach, parameter uncertainty is represented by a minimum and maximum value and also a nominal value which is the most likely value in the absence of any measured values. In a Bayesian sense, these values implicitly suggest a prior probability distribution for each parameter in the same way that a gaussian probability distribution would explicitly achieve. By looking for proximate values that fit the measured data (i.e. values close to the nominal values), the PPT algorithm finds fitted parameter values that are most probable with respect to the prior distributions. In addition, the penalty weightings αj for each parameter j can be used to model the spread of the prior distribution about the nominal point; the higher the value the smaller the implied standard deviation. In the same way, measurement uncertainty can be included by the penalties for each target feature error which reflect the relative confidence bounds for each measured value.Overall, this ability of the PPT algorithm to make use of a priori knowledge to inform the fitting process is crucial when the measured data are scarce. Future work will aim to integrate the PPT approach into a truly Bayesian framework that produces full posterior distributions for each fitted parameter and will therefore deliver confidence bounds on the final fitted parameter values. It is hoped that PPT could provide a computationally efficient alternative to existing methods for Bayesian parameter estimation, such as Markov Chain Monte Carlo (MCMC),47 that have proved to be intractable for some systems with many unknown parameters.
The analysis presented here does not consider the important questions of identifiability and confidence intervals on the fitted parameter values. The emphasis of our work is on tuning a model made up of an ensemble of parameters rather than uniquely estimating each and every parameter value. To illustrate this we can return to Example 2 in which PPT provided an ensemble parameter fit to the very limited output data. The final fitted parameter values should not be viewed in isolation but instead should be viewed as giving the correct overall model behaviour in combination. There are likely to be countless other parameter combinations within the parameter space that give the same fit—possibly some that are closer to the nominal values since PPT does not guarantee finding the global optimum. While more data to discriminate them is anticipated, the PPT solution provides a fit to the existing data.
In this paper we offer no theoretical guarantees of convergence for the PPT algorithm. In fact, as can be seen in examples 3 or 4, it can exhibit divergent or oscillatory behaviour in which the size of the steps taken in the parameter space do not vanish to zero. This has not been a problem for these examples—we just used a preset number of iterations and choose the minimum objective of all of them as the final solution which was good enough. There may, however, be more pathological systems of ODEs in which LP-PPT fails to find a reasonable solution at all. Ultimately, the convergence of the algorithm depends on the accuracy of the linear approximation that is used by the LP sub-problem to predict that point in the parameter space that will minimize the objective function. An analysis of this error for Example 1 is given in Appendix B. If there are significant higher order terms and/or strong correlations between parameters then the discrepancy between the predicted feature errors and the actual errors at each point in the parameter space may grow to such an extent that LP-PPT fails. In this case we would need to reduce the step length or else switch to QP-PPT (Appendix C) which takes account of second order terms. The error between predicted and actual errors can be monitored as the algorithm proceeds and appropriate action can be taken if it gets too high (switch to QP-PPT, reduce step length etc.)
Despite the potential limitations of LP-PPT caused by its use of a local linearization at each step, this same approximation results in a very efficient algorithm in computational terms since the small linear programming sub-problems can be solved very quickly. The main computational burden in the current implementation occurs in Step 4 in which the sensitivities are estimated numerically therefore requiring at least one simulation per parameter to be estimated. For the results reported in this paper we have made no efforts to make this step more efficient since the longest of our runs took less than 10 min of CPU time. However, there is certainly scope to do significantly improve efficiency if, for example, the algorithm were to be repeatedly solved a part of an intensive sampling strategy. We use two simulations per parameter since we estimate the local sensitivity by perturbing each parameter value upwards and downwards by 0.1% and take the average; however one perturbation would probably suffice. It may also be possible to take other short-cuts to reduce the calculation time. We found that many of the sensitivities do not vary much from one step to another since the region of feature space is locally quite flat or the only small steps are being made in the direction of some parameters. Under these circumstances, the algorithm could use simple interpolation to approximate the sensitivities in parameter directions that are only weakly varying and only perform full updates using perturbed simulations when necessary. This is analogous to projected Hessian approximations used in quasi-Newton methods for nonlinear programming.48
We introduced the PPT algorithm as being applicable for networks whose structure and kinetics are known with the only uncertainty residing in the kinetic constants and initial concentrations. However, PPT can be applied in exactly the same way to networks in which we do not known the form of the kinetic equations because we can use lin-log49,50 or other generalized kinetics51 that can give good approximations over a wide range. It may also be possible to extend the approach further problems in which the structure of the biochemical network is uncertain. In this case, we could postulate a ‘super-structure’ of all possible interactions and allow the algorithm to select the smallest subset that best explains the measured data. To do this exactly would require the solution of a mixed integer linear programming (MILP) problem in step 5 of the general PPT algorithm since it requires binary variables to model the inclusion of each candidate parameter in the fitted model (see Appendix C). However, we could generate approximate solutions using the existing LP-PPT implementation described here. In order to do this the lower bounds on the rate constant for each uncertain reaction would be set to a negligible value; small enough to represent the absence of an interaction (note that we cannot use a lower bound of zero because the LP-PPT algorithm uses the logarithms of these quantities). The algorithm would then start from a nominal point with all rate constants at their minimum values—i.e. the lower extreme of their ranges rather than at intermediate values - and, by increasing parameter values, would introduce the minimal subset of interactions to fit the model to the data. This would necessitate the use of positive values for the αj parameters that penalize the inclusion of each parameter j. This approach has some similarities with the recent work of Papadopoulos and Brown52 which uses the sum of the parameter deviations as a proximity metric in order to obtain ‘sparse’ models containing the fewest number of parameters.
A key feature of the LP-PPT algorithm as presented in this paper is that it is deterministic. For a given starting point and a pre-set step length, the algorithm will end up at a unique point in the parameter space after a certain number of iterations. The only circumstances in which different implementations of the algorithm might terminate at different end points would be if there is degeneracy in an LP sub-problem (more than one solution that gives the optimal objective). In this case different LP solvers might make different choices about which solution to select and therefore which direction to step next in the parameter space. For the LP solver this choice is arbitrary since all the predicted solutions are equally good but this will effect the trajectory of the algorithm as a whole is likely to lead to a different end point. One could easily eliminate this arbitrary choice by requiring the algorithm to consider all degenerate LP solutions by performing a simulation at each predicted step in the parameter space. The algorithm would then select the predicted point that gave the best actual objective.
In summary the proximate parameter tuning algorithm is a novel approach for adjusting biochemical models to fit target output values using prior knowledge about the parameter values. The algorithm can use any type of output feature and scales well with the number of output features to be fitted and the number of uncertain parameters to be adjusted. The examples presented demonstrate that the algorithm performs well on a diverse problem set. The approach is deterministic and is therefore complimentary to those based on random sampling or evolutionary algorithms.
Conclusions
Parameter estimation has been an area of intense activity—sometimes more because of its mathematical interest than its immense practical importance. Theoretically rigorous treatments of sensitivity, identifiability etc. are certainly valuable but not if they make the techniques opaque to a large portion of the modeling and experimental community. We believe that the proximate tuning algorithm presented here is a practical approach with the ability to transform the vast array of dormant biochemical knowledge into ‘first guess’ dynamic models and thus kick start the cycle of model prediction, testing and refinement that will deliver the true potential of systems biology.Appendix A: Properties of the LP-PPT algorithm
The linear programming sub-problem of LP-PPT algorithm is given by eqn (7) to (14). Eqn (7) gives the general objective that involves the four terms:1. The infinity norm of the (absolute value of the logarithmic) parameter deviations
2. The (weighted) 1-norm of the parameter deviations
3. The infinity norm of the (absolute value of the logarithmic) feature errors
4. The (weighted) 1-norm of the feature errors
For all the case studies presented this paper we use only the first and fourth terms above 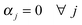 ,β = 0. We now explore the properties of the solutions to this LP problem. In particular, we use a simple graphical example to show how the relative penalties effect the solution obtained. Finally, we shall prove two results relating to feasible and optimal solutions.
,β = 0. We now explore the properties of the solutions to this LP problem. In particular, we use a simple graphical example to show how the relative penalties effect the solution obtained. Finally, we shall prove two results relating to feasible and optimal solutions.
Consider the simplest possible problem with a single parameter and a single output feature. In this case only the 1-norms (i.e. second and fourth terms above) are included in the objective and we therefore ignore the maximum deviation and error variables and the constraints that they appear in (eqn (9)–(12)). We have 4 variables representing positive and negative parameter deviations and positive and negative target feature errors respectively. However, we only have a single constraint (eqn (8)) and so there is an optimal solution to the LP-subproblem that lies at an extreme point of feasible region and has only one of these 4 variables as basic (potentially non-zero). The other 3 variables must all be non-basic i.e. at their bounds—zero valued since there are no upper bounds in this problem so all non-basic variables must be at their lower bounds of zero.
This is illustrated in Fig. 15 which represents the constraints and objective for the simplest possible problem introduced above. For this two dimensional representation we have dropped the j and p subscripts and also the r superscript since we only have one parameter, one feature and are only considering the first iteration. We also amalgamate the positive and negative components of the parameter deviation and the feature error into two free variables that can be positive or negative (Δk = Δk+jr + Δk–jr and Δy = Δy+pr + Δy–pr).
 | ||
| Fig. 15 Illustration of optimality conditions for the case of one feature and one parameter with only 1-norms considered in the objective and the upper bound on the parameter deviation not limiting. | ||
For the case shown above we have assumed that the right hand side of the constraint is positive—i.e:
and the optimal solution would switch to the vertical axis corresponding to zero parameter deiviation at the expense of a non zero feature error. In this case, there is no point changing the parameter from its nominal value because it will be penalised more in the objective than the gain from the reduction in feature error.
Note that if the constraint is parallel to the objective contours—i.e:
Note also that for Fig. 15 we assume that any upper bound on Δk is not limiting. If the upper bound is active at the optimal solution we get the situation illustrated in Fig. 16 in which both Δk and Δy are non-zero but only Δy is non-basic since Δk is non-basic at its upper bound. As this upper bound is made tighter the optimal solution gets worse (higher).
 | ||
| Fig. 16 As for Fig. 15 but with upper bound on parameter deviation now limiting. | ||
We can now turn our attention to a slightly more complex case in which we add another parameter to the example above (Fig. 17). This enables us to give a similar geometric representation for the optimal solution for the case when we now penalise the maximum parameter deviation (infinity norm on the parameter deviations) rather than the 1-norm. This is what we actually do for all the case studies presented in this paper.
 | ||
| Fig. 17 Two parameters (with only their infinity norm penalised) and one feature. | ||
In this case the feature constraint is a 2-D plane in the 3-D space and an optimal solution to the problem must lie at a vertex of the contour surface (i.e. either Δk1 = Δk2 > 0, Δy = 0 or Δk1 = Δk2 = 0,Δy > 0. If there are limiting upper bounds on the parameters then the second case should be replaced by the following: Δk1 ∈ {0,Δkmax1}Δk2 ∈ {0,Δkmax2}Δy > 0.
Note that when we map this back into the original variable space in which we track the positive and negative parameter deviations and feature errors we have 5 constraints (1 × eqn (8) + 2 × eqn (9) + 2 × eqn (10)) therefore 5 of the variables (including the slack variables in inequalities eqn (9) and eqn (10) must be basic in the optimal solution.
We can also show the effect of penalising the 1-norm on the parameter deviations as well as the infinity norm as illustrated in Fig. 18. The effect of this is to add four more vertices along the Δk axes and so now the optimal solution can have a zero valued parameter (e.g. Δk2 in Fig 18).
 | ||
| Fig. 18 Two parameters (with penalties on both the infinity norm and weighted 1-norm of their deviations from their nominal values) and one feature. | ||
In general the LP sub-problem will involve more than two parameters and have several features to be matched resulting in a high dimensional variable space. However, the same principles as discussed above will apply. The optimal solution will always lie at a one of a finite number of points in the solution space corresponding to the vertices of the objective surface or upper bounds on the parameter deviations.
Although we are unable to visualise the general case we can use the established properties of linear programming problems to prove two useful properties.
Property 1 (Feasibility)
Any set of parameter values that are within their maximum and minimum values correspond to a point that is feasible with respect to the LP sub-problem.This result follows directly from examination of the LP constraints whereby it can be seen that the Δy variables are really only slack variables in eqn (8) and feasibility is assured provided the positive and negative parameter deviation variables are within their bounds.
Property 2 (Basic solutions when the objective function only involves the maximum (infinity norm) of the parameter deviations and the weighted sum (1-norm) of the feature errors)
The number of distinct parameter adjustments (that are not at their maximum limit) specified by any basic feasible solution to the LP sub-problem (i.e. a vertex solution) cannot be more than the number of features specified to be matched exactly by that solutionThis property follows from the directly from the fact that the number of basic variables (i.e. not at their bounds) is equal to the number of constraints for any LP extreme point solution as we now demonstrate for the LP sub-problem of the proximate parameter tuning algorithm.
If we have n parameters and m features then we have a total of 4n + 2m + 1 variables and 2n + m constraints as detailed in Table 10. For each basic solution, therefore, exactly 2n + m variables are not at their lower bounds (all zero) or upper bounds (only for the parameter deviations). For any basic solution we can split the parameters into the following subsets:
| n = nmax + nless + nbound |
| Variables | |
|---|---|
| Δk+jr,Δk–jr Positive and negative parameter deviations | 2n |
![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) r Maximum parameter deviation r Maximum parameter deviation |
1 |
| Slack variables in eqn (9) & (10) | 2n |
| Δy+pr,Δy–pr Positive and negative feature errors | 2m |
| Total variables | 4n + 2m + 1 |
| Constraints | |
|---|---|
| Eqn (8) | m |
| Eqn (9) & (10) | 2n |
| Total constraints | 2n + m |
n max = the number of parameters whose non-zero positive or negative deviation is equal to the maximum deviation
n less = the number of parameters whose non-zero positive or negative deviation is less the maximum deviation maximal but not at their upper bound
n bound = the number of parameters whose positive or negative deviation is at their upper bound or else are both zero.
Similarly we can split the features into the following two subsets:
| m = mexact + merror |
m exact = the number of features with zero positive and negative error
m error = the number of parameters with a non-zero positive or negative error
For any vertex solution we can express the number of basic variables in terms of the above subsets. Table 11 shows how these subsets give rise to basic variables in a vertex solution. It can be seen that the number of basic variables is 1 + 2nmax + 3nbound + merror but this is equal to the number of constraints so we can write:
| 1 + 2nmax + 3nless + 2nbound + merror = 2n + m = 2(nmax + nless + nbound) + mexact + merror |
| 1 | Maximum parameter deviation variable ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) r r |
| n max | Positive (Δk–jr) or negative (Δk+jr) parameter deviation variables for those variables that are equal to the maximum deviation |
| n max | Slack variables for whichever constraint (eqn (9) or (10)) is inactive for the maximal parameter deviation variables above |
| n less | Positive (Δk–jr) or negative (Δk+jr) parameter deviation variables for those non-zero variables that are less than the maximum deviation but not at their upper bound |
| 2nless | Slack variables for constraints (eqn (9) and (10)) which are both inactive for the non-maximal parameter deviation variables above |
| 2nbound | Slack variables for constraints (eqn (9) and (10)) which are both inactive for any parameter deviation variables that are zero or at their upper bounds |
| m error | Positive (Δy+pr) or negative (Δy–pr) feature error variables for those features that are not matched exactly |
Which can be simplified to give:
| nless + 1 = mexact (mexact > 0) |
The right hand side of the above equation must be greater than or equal to the number of distinct non-zero parameter adjustments not at their upper bound since there is one maximal adjustment and potentially a different adjustment value for each parameter that is adjusted less than this maximal amount. Hence Property 2 follows directly from the above equality. Note that this equality only applies where there is at least one zero feature error otherwise the ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) r variable is non-basic and we should therefore subtract unity from the left hand side to reflect this i.e.:
r variable is non-basic and we should therefore subtract unity from the left hand side to reflect this i.e.:
| nless = 0 (mexact = 0) |
The example in Fig. 17 illustrates Property 2 since it can be seen that each vertex solution in the horizontal plane only specifies a single distinct parameter adjustment (i.e. the maximal adjustment).
In the implementation of the LP-PPT algorithm used for the examples in this paper we construct an initial feasible basis for each LP sub-problem by making all parameter deviations zero and, depending on the sign of the initial error of each feature, making either the positive or negative feature error variables basic as appropriate. Finally we instantiate each slack variable in eqn (9) and (10) to be basic.
Pivoting in the LP optimization procedure then consists of choosing a parameter deviation variable to enter the basis. This parameter deviation variable may increase up to the maximum value (thereby rendering active the appropriate inequality (eqn (9) or (10) and thus eliminating the corresponding slack variable from the basis). Alternatively, the entering variable may be prevented from increasing up to the maximum value by: the feature error variable becoming zero and leaving the basis; or by another parameter deviation variable being driven to its bound; or else the by same parameter deviation variable as chosen to enter the basis immediately leaving the basis corresponding to a simple bound swap for that variable.
The key significance of Property 2 is that each optimal solution is also a basic feasible solution so we know that the final parameter adjustments at the termination of the algorithm also obey this property. The number of distinct parameter adjustments must always be less than the number of features fitted exactly. So, if there are far fewer features than parameters, most of the parameters will be adjusted by the same amount—even if all the features are fitted exactly. In this way the LP-PPT algorithm can be thought of as performing a form of implicit reduction of the dimensionality of the parameter space such that changes of only a few different magnitudes are made.
Finally it should be noted that that the analysis carried out here is limited to the linear programming implementation of the PPT algorithm. However, some of the same principles apply for other implementations and the same graphical interpretation can be applied in order to analyse optimality conditions in these cases as well. If, for example, 2-norms are used in the objective function, it can be shown that the objective contours are hyper-ellispsoids.
Appendix B: Analytical solution of example 1
Using the following standard result that the differential equation: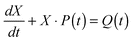 | (B1) |
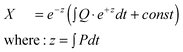 | (B2) |
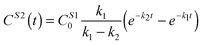 | (B3) |
Differentiating and setting equal to zero to locate the time of the maximum of the above function we get the following expressions for Tpk and Ypk:
 | (B4) |
 | (B5) |
It can be seen that Ypk depends only on the ratio of the rate constants (Cs10 = 1 µm). For Ypk = 0.3 µm we can solve for the ratio in eqn (B3) numerically (e.g. by successive substitution) to get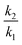 = 1.4674. Substituting back into eqn (B2) yields the analytical solution: k1 = 0.01026, k2 = 0.01505. The fact that these values are slightly different from the values given in Example 1 is merely indicative of the error of our quadratic interpolation routine for detecting the time of the peak concentration.
= 1.4674. Substituting back into eqn (B2) yields the analytical solution: k1 = 0.01026, k2 = 0.01505. The fact that these values are slightly different from the values given in Example 1 is merely indicative of the error of our quadratic interpolation routine for detecting the time of the peak concentration.
We now continue the analysis to look at the error of the linear approximation used by the LP-PPT algorithm.
We can approximate a general function F(x) by a Taylor expansion around the point x = x*:
 | (B6) |
Here:
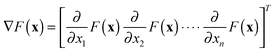 | (B7) |
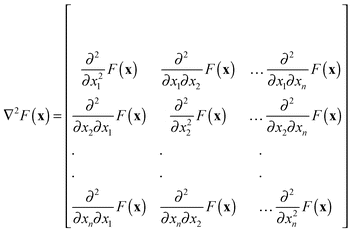 | (B8) |
For Example 1 we derive analytical expressions for the above quantities for the two output features. For convenience we can write (B4) and (B5) above in terms of logarithmic transformed variables
 | (B9) |
 | (B10) |
Below we differentiate eqn (B9) and eqn (B10) once to give  ; then a second time to give
; then a second time to give  . We then show how the second order error varies as the algorithm proceeds.
. We then show how the second order error varies as the algorithm proceeds.
Differentiation of eqn (B4) and eqn (B5) yields the gradient vectors of the logarithmically transformed variables which are the scaled sensitivities of the original features with respect to the parameters:
 | (B11) |
 | (B12) |
The summation theorems for Tpk and Ypk can easily be verified for the expressions above since the sum of the two elements of the vector in eqn (B11) can be readily seen to be equal to –1 thus implying that the two elements of the vector in eqn (B12) must sum to zero.
Further differentiation of eqn (B11) and eqn (B12) yields the Hessian matrices:
 | (B13) |
 | (B14) |
Table 12 gives the analytically calculated derivatives at the nominal point. The first derivatives are equivalent to the numerically calculated sensitivities that are used to calculate the first step in the parameter space (Δ(Δk) is the change in the parameter deviation). Because the LP-PPT sub-problem only uses first order information, there will be an error between the predicted outputs/objective and the actual outputs/objective. Table 13 shows that the second order term of the Taylor expansion helps to reduce the error between the predicted first order change and the actual change—but only by 50% or less. So, certainly for this example, use of QP-PPT (which incorporates a second order approximation—see Appendix C) would require considerably more computational effort for very limited payback in terms of reducing the number of iterations for convergence.
|
|
|
Δ(Δk) |
|
|
|
|
|---|---|---|---|---|---|---|
| 0.495 | –0.412 |

|

|
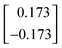
|

|
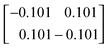
|
|
|
Predicted change (1st order)
|
2nd order correction
|
Actual Change |
|
Predicted change (1st order)
|
2nd order correction
|
Actual Change |
|---|---|---|---|---|---|---|---|
| 0.495 | 0.494 | –0.067 | 0.359 | –0.412 | –0.247 | –0.103 | –0.575 |
| 0.132 | 0.132 | –0.002 | 0.124 | 0.160 | 0.160 | –0.004 | 0.152 |
| 0.008 | 0.008 | –1.4e–5 | 0.008 | 0.011 | 0.011 | –2.9e–5 | 0.010 |
Appendix C: alternative PPT algorithms QP-PPT and MILP-PPT
QP-PPT
The LP-PPT presented in the main body of this paper is just one implementation of the general algorithm using, as it does, a linear approximation of the dependence of the output features on the parameters for the optimization sub-problem (Step 5). If it is necessary to improve the accuracy of the sub-problem we could move to a second order approximation that takes some account of the curvature (i.e. variation in the gradients/sensitivities) and also the interactions between parameters. This is achieved by solving a quadratically constrained quadratic programming (QP) problem in Step 5 as part of a QP-PPT algorithm. The other benefit of using a QP is that the we can directly penalize the Euclidean distance from the nominal point thereby facilitating an exact representation of the probability of a given solution in the parameter space for normally distributed parameters.The mathematical formulation of the optimisation sub-problem used in QP-PPT is best explained in terms of second-order Taylor approximations for each output feature.
Consider a point in the parameter space (Δk*1,Δk*2,…,Δk*m) as referenced as a deviation from the nominal point. We can use first and second order derivatives to approximate the logarithm value  of each output feature in the neighbourhood of that point.
of each output feature in the neighbourhood of that point.
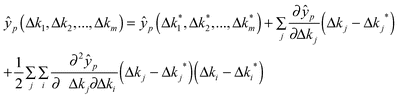 | (C1) |
Where Δkj(= Δk+j – Δk–j) is the total parameter deviation from the nominal point—i.e. the sum of the positive and negative components used in LP-PPT, but we do not need to split these variables into their positive and negative parts for QP-PPT. So these are now free variables that can be positive or negative. The key constraint (eqn (8)) in LP-PPT ignores the last term in the eqn (C1) above and is therefore based on a linear approximation. Comparing the above equation to eqn 8 we can recognize the following:
Δk*j = Δk+jr–1 – Δk–jr–1—the parameter deviations from the previous iteration;
Δkj = Δk+jr – Δk–jr—the new parameter deviations to be calculated in the current iteration;
 —the first order sensitivity coefficient;
—the first order sensitivity coefficient;
 =log((yr–1p)—the current feature value;
=log((yr–1p)—the current feature value;
 =log(ygp)—the target feature value.
=log(ygp)—the target feature value.
The only other variables that need to be introduced to convert the above into eqn (8) are the target error variables reflect that fact that, in general, we are trying to match multiple features and are therefore unlikely to be able to match all of them exactly. As for the parameter deviation variables, we do not need to keep track of the positive and negative target errors individually in QP-PPT.
Based on the above discussion we can write down the mathematical formulation of QP-PPT in which the last term in eqn (C1) is retained to give a second order approximation. Since we have introduced bilinear terms into the constraints, we can also (without increasing problem difficulty) introduce similar terms into the objective function in order to penalize the Euclidean distance of the parameter deviation and the sum-of-square target errors to give a maximum likelihood solution. Minimise:
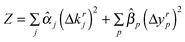 | (C2) |
Subject to:
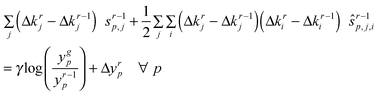 | (C3) |
 | (C4) |
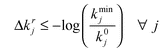 | (C5) |
The first and second order derivatives (sensitivity coefficients) can be calculated numerically by using central difference approximations for a small perturbation ε as follows:
 | (C6) |
 | (C7) |
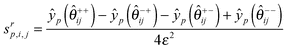 | (C8) |
The QP-PPT formulation is more computationally demanding than the LP-PPT formulation in two ways. Firstly, it requires the calculation of the second order sensitivity coefficients which requires 2n(n + 1) separate numerical simulations (where n is the number of parameters) rather than 2n for the first order sensitivity coefficients. Secondly, the quadratically constrained optimization problem is inherently more difficult to solve than its linear counterpart. However, efficient techniques exist for solving these problems to optimality53 making the QP-PPT algorithm perfectly tractable in principle.
MILP-PPT
When adjusting parameter values to fit the model to the data it may be desirable to adjust a parameter only if this makes a significant impact in order to keep as many of the insensitive parameters at their original nominal values. In order to do this we need to introduce binary variables as follows:zrj = 1 if parameter j is adjusted away from its nominal value after iteration r,
zrj = 0 if parameter j remains at its nominal value after iteration r.
We use these variables in the following constraints that force them to take the value of unity if either there is either a positive or negative logarithmic deviation of a parameter from its nominal value.
 | (C9) |
 | (C10) |
Note that these constraints force the parameter deviation to be zero unless the corresponding binary variable is unity. They replace the bounding constraints (eqn (13) and eqn (14)) of the original LP-PPT formulation. The introduction of the binary variables allow us to include a fixed cost α′j penalizing the adjustment of parameter j (whatever its magnitude) into the objective function:
The full MILP-PPT formulation is made up of constraints eqn (C9)–(C11) above as well as constraints eqn (8)–(12) from the original LP-PPT formulation.
 | (C11) |
Like QP-PPT the optimization subproblem in MILP-PPT is computationally more demanding than LP-PPT but, again, efficient algorithms exist such as those using branch-and-bound search.
The two formulations presented in this Appendix are but two examples to illustrate the flexibility of the PPT approach for incorporating better approximations or different objectives in the estimation process. Several other possibilities exist and, indeed, the two formulations described above could be combined to give a second order approximation that also incorporates fixed penalties (MIQP-PPT).
Acknowledgements
We thank Pfizer Ltd and the BBSRC for financial support, and Dr Martin Brown and Dr Dicky Dimelow for useful discussions.References
- D. B. Kell, Metabolomics and systems biology: making sense of the soup, Curr. Opin. Microbiol., 2004, 7, 296–307 CrossRef CAS.
- R. D. King, Functional genomic hypothesis generation and experimentation by a robot scientist, Nature, 2004, 427, 247–252 CrossRef CAS.
- D. B. Kell, Metabolomics, machine learning and modelling: towards an understanding of the language of cells, Biochem. Soc. Trans., 2005, 33, 520–524 CrossRef CAS.
- E. Klipp, R. Herwig, A. Kowald, C. Wierling and H. Lehrach, Systems biology in practice: concepts, implementation and clinical application, Wiley/VCH, Berlin, 2005) Search PubMed.
- Computational systems biology, ed. A. Kriete and R. Eils, Academic Press, New York, 2005 Search PubMed.
- D. B. Kell and J. D. Knowles, in System modeling in cellular biology: from concepts to nuts and bolts, ed. Z. Szallasi, J. Stelling and V. Periwal, MIT Press, Cambridge, 2006, 3–18 Search PubMed.
- U. Alon, An introduction to systems biology: design principles of biological circuits, Chapman and Hall/CRC, London, 2006) Search PubMed.
- B.Ø. Palsson, Systems biology: properties of reconstructed networks, Cambridge University Press, Cambridge, 2006 Search PubMed.
- D. J. Wilkinson, Stochastic modelling for systems biology, Chapman and Hall/CRC, London, 2006 Search PubMed.
- L. Ljung, System identification: theory for the user, Prentice Hall, Englewood Cliffs, NJ, 1987 Search PubMed.
- P. Mendes and D. B. Kell, Non-linear optimization of biochemical pathways: applications to metabolic engineering and parameter estimation, Bioinformatics, 1998, 14, 869–883 CrossRef CAS.
- E. J. Crampin, S. Schnell and P. E. McSharry, Mathematical and computational techniques to deduce complex biochemical reaction mechanisms, Prog. Biophys. Mol. Biol., 2004, 86, 77–112 CrossRef CAS.
- J. Bongard and H. Lipson, Automated reverse engineering of nonlinear dynamical systems, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 9943–9948 CrossRef CAS.
- K. Edwards, T. F. Edgar and V. I. Manousiouthakis, Kinetic model reduction using genetic algorithms, Comp. Chem. Eng., 1998, 22, 239–246 Search PubMed.
- M. S. Okino and M. L. Mavrovouniotis, Simplification of Mathematical Models of Chemical Reaction Systems, Chem. Rev., 1998, 98, 391–408 CrossRef CAS.
- C. Brochot, J. Tóth and F. Y. Bois, Lumping in pharmacokinetics, J. Pharmacokinet. Pharmacodyn., 2005, 32, 719–736 Search PubMed.
- W. Liebermeister, U. Baur and E. Klipp, Biochemical network models simplified by balanced truncation, FEBS J., 2005, 272, 4034–4043 Search PubMed.
- J. J. Hornberg, Principles behind the multifarious control of signal transduction. ERK phosphorylation and kinase/phosphatase control, FEBS J., 2005, 272, 244–258 Search PubMed.
- H. Yue, Insights into the behaviour of systems biology models from dynamic sensitivity and identifiability analysis: a case study of an NF-kappaB signalling pathway, Mol. Biosyst., 2006, 2, 640–649 RSC.
- D. B. Kell and H. V. Westerhoff, Metabolic control theory: its role in microbiology and biotechnology, FEMS Microbiol. Rev., 1986, 39, 305–320 CrossRef CAS.
- J. E. Bailey, Toward a science of metabolic engineering,, Science, 1991, 252, 1668–1675 CrossRef CAS.
- L. J. Sweetlove, R. L. Last and A. R. Fernie, Predictive metabolic engineering: a goal for systems biology, Plant Physiol., 2003, 132, 420–425 CrossRef CAS.
- K. R. Patil, M. Akesson and J. Nielsen, Use of genome-scale microbial models for metabolic engineering, Curr. Opin. Biotechnol., 2004, 15, 64–69 CrossRef CAS.
- K. R. Patil, I. Rocha, J. Förster and J. Nielsen, Evolutionary programming as a platform for in silico metabolic engineering, BMC Bioinformatics, 2005, 6, 308 CrossRef.
- L. Wang and V. Hatzimanikatis, Metabolic engineering under uncertainty. I: framework development, Metab. Eng., 2006, 8, 133–141 CrossRef CAS.
- L. Wang and V. Hatzimanikatis, Metabolic engineering under uncertainty--II: analysis of yeast metabolism, Metab. Eng., 2006, 8, 142–159 CrossRef CAS.
- H. P. Williams, Model building in mathematical programming, Wiley, New York, 1993 Search PubMed.
- T. E. Baker and L. S. Lasdon, Successive linear programming at Exxon, Management Sci., 1985, 31, 264–274 Search PubMed.
- M. Olofsson, G. Andersson and L. Soder, Linear-programming based optimal power flow using 2nd-order Sensitivities, IEEE Trans. Power Syst., 1995, 10, 1691–1697 CrossRef.
- T. A. Johansen, On Tikhonov regularization, bias and variance in nonlinear system identification, Automatica, 1997, 33, 441–446 CrossRef.
- F. Lei and S. B. Jørgensen, Estimation of kinetic parameters in a structured yeast model using regularisation, J. Biotechnol., 2001, 88, 223–237 CrossRef CAS.
- J. Saklatvala, The p38 MAP kinase pathway as a therapeutic target in inflammatory disease, Curr. Opin. Pharmacol., 2004, 4, 372–377 CrossRef CAS.
- M. Hucka, The systems biology markup language (SBML): a medium for representation and exchange of biochemical network models, Bioinformatics, 2003, 19, 524–531 CrossRef CAS.
- S. H. Northrup and H. P. Erickson, Kinetics of protein-protein association explained by Brownian dynamics computer simulation, Proc. Natl. Acad. Sci. U. S. A., 1992, 89, 3338–3342 CrossRef CAS.
- H. Gutfreund, Reflections on the kinetics of substrate binding, Biophys. Chem., 1987, 26, 117–121 CrossRef CAS.
- G. Schreiber and A. R. Fersht, Rapid, electrostatically assisted association of proteins, Nat. Struct. Biol., 1996, 3, 427–431 CrossRef CAS.
- J. R. Knowles and W. J. Albery, Perfection in enzyme catalysis - energetics of triosephosphate isomerase, Acc. Chem. Res., 1977, 10, 105–111 CrossRef CAS.
- A. Fersht, Structure and mechanism in protein science : a guide to enzyme catalysis and protein folding, W. H. Freeman, San Francisco, 1999 Search PubMed.
- B. Schoeberl, C. Eichler-Jonsson, E. D. Gilles and G. Muller, Computational modeling of the dynamics of the MAP kinase cascade activated by surface and internalized EGF receptors, Nat. Biotechnol., 2002, 20, 370–375 CrossRef.
- B. Teusink, Can yeast glycolysis be understood in terms of in vitro kinetics of the constituent enzymes? Testing biochemistry, Eur. J. Biochem., 2000, 267, 5313–5329 CrossRef CAS.
- L. Pritchard and D. B. Kell, Schemes of flux control in a model of Saccharomyces cerevisiae glycolysis, Eur. J. Biochem., 2002, 269, 3894–3904 CrossRef CAS.
- S. Hoops, COPASI: a COmplex PAthway SImulator, Bioinformatics, 2006, 22, 3067–3074 CrossRef CAS.
- R. Fuguitt and J. E. Hawkins, Rate of thermal isomerization of a-pinene in the liquid phase, J. Am. Chem. Soc., 1947, 69, 461.
- G. E. P. Box, W. G. Hunter, J. F. MacGregor and J. Erjavec, Some problems associated with the analysis of multiresponse data, Technometrics, 1973, 15, 33–51 CrossRef.
- I. B. Tjoa and L. T. Biegler, Simultaneous solution and optimization strategies for parameter estimation of differential algebraic equation systems, Ind. Eng. Chem. Res., 1991, 30, 376–385 CrossRef CAS.
- M. Rodriguez-Fernandez, P. Mendes and J. R. Banga, A hybrid approach for efficient and robust parameter estimation in biochemical pathways, Biosystems, 2006, 83, 248–265 CrossRef CAS.
- W. R. Gilks, S. Richardson and D. J. Spiegelhalter, Markov chain Monte Carlo in practice, Chapman and Hall, London, 1996 Search PubMed.
- S. J. Wright, Convergence of projected Hessian approximations in quasi-Newton methods for the nonlinear programming problem, IMA J. Numer. Anal., 1986, 6, 463–474 Search PubMed.
- L. Wu, W. Wang, W. A. van Winden, W. M. van Gulik and J. J. Heijnen, A new framework for the estimation of control parameters in metabolic pathways using lin-log kinetics, Eur. J. Biochem., 2004, 271, 3348–3359 CrossRef CAS.
- M. T. A. P. Kresnowati, W. A. van Winden and J. J. Heijnen, Determination of elasticities, concentration and flux control coefficients from transient metabolite data using linlog kinetics, Metab. Eng., 2005, 7, 142–153 CrossRef CAS.
- M. Savageau, Biochemical systems analysis: a study of function and design in molecular biology, Addison-Wesley, Reading, MA, 1976 Search PubMed.
- G. Papadopoulos and M. Brown, Feature sensitivity of biochemical signalling pathways, IEEE Symp. Comp. Intell. Bioinf. Comput. Biol., 2007, 373–380 Search PubMed.
- S. Boyd and L. Vandenberghe, Convex optimization, Cambridge University Press, Cambridge, 2004 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: SBML models. See DOI: 10.1039/b707506e |
| This journal is © The Royal Society of Chemistry 2008 |