The role of hydrodynamics, matrix and sampling duration in passive sampling of polar compounds with Empore™ SDB-RPS disks

Abstract

There is an increasing need to monitor concentrations of polar organic contaminants in the aquatic environment. Integrative passive samplers can be used to assess time weighted average aqueous concentrations, provided calibration data are available and sampling rates are known. The sampling rate depends on environmental factors, such as temperature and water flow rate. Here we introduce an apparatus to investigate the sampling properties of passive samplers using river-like flow conditions and ambient environmental matrices: river water and treated sewage effluent. As a model sampler we selected Empore™ SDB-RPS disks in a Chemcatcher housing. The disks were exposed for 1 to 8 days at flow rates between 0.03 and 0.4 m s^–1. Samples were analysed using a bioassay for estrogenic activity and by LC-MS-MS target analysis of the pharmaceuticals sulfamethoxazole, carbamazepine and clarithromycin. In order to assess sampling rates of SDB disks, we also measured aqueous concentrations of the pharmaceuticals. Sampling rates increased with increasing flow rate and this relationship was not affected by the environmental matrix. However, SDB disks were only sampling in the integrative mode at low flow rates <0.1 m s^–1 and/or for short sampling times. The duration of linear uptake was particularly short for sulfamethoxazole (1 day) and longer for clarithromycin (5 days). At 0.03 m s^–1 and 12–14 °C, the sampling rate of SDB disks was 0.09 L day^–1 for clarithromycin, 0.14 L day^–1 for sulfamethoxazole and 0.25 L day^–1 for carbamazepine. The results show that under controlled conditions, SDB disks can be effectively used as passive sampling devices.

---

Introduction

Assessing concentrations of pollutants in the aquatic environment is an integral part of risk assessment and environmental regulation. Within this diverse research area there has been a lot of focus, in the past, on metals and persistent organic chemicals. Recently, more interest has been directed towards polar organic chemicals, which include many pesticides, pharmaceuticals and endocrine disruptors. Although polar compounds do not have a high bioaccumulation potential, they constitute a risk to aquatic organisms, as these substances are often continuously released into the environment, resulting in pseudo-persistence.¹ This is particularly well established for environmental estrogens, for which effects on aquatic organisms have been shown.² Consequently, many countries have set water quality criteria for pesticides and other micropollutants.³ In addition, a recent amendment of the list of priority pollutants in the EU includes a fair number of polar compounds, among them carbamazepine and various antibiotics.⁴ These regulatory developments generate a need for cost-effective monitoring tools.

Sampling the aquatic environment for pollutants is often a challenging task. Water bodies are rarely well mixed and consequently chemicals are not evenly distributed.⁵ Concentrations of pollutants often fluctuate and small river catchments can pose additional challenges, as they are often hydrologically very dynamic.⁶ These circumstances may thwart the use of grab sampling to determine chemical loads. For example, in long term monitoring studies that aim to link exposure to chemicals with effects in organisms, grab sampling is only practicable when concentrations of the target chemicals are fairly stable. In dynamic ecosystems that receive a dynamic input, grab sampling is inadequate. On the other hand, time or flow proportional sampling is very costly. In order to circumvent these difficulties, and to produce a simple, biologically relevant and economical sampling method, passive samplers have been developed.^7,8

Passive sampling is described by diffusion processes in, and partitioning between, the aqueous phase and a sampling phase. Under conditions of constant aqueous concentrations, the concentration of a compound in the sampler increases nearly linearly with time, after which the increase flattens and ultimately the concentrations in the water and sampler reach equilibrium.^9,10 The main attraction of passive sampling, when employed over the linear uptake phase, is that the technique provides an integrated measure of the presence of chemicals at a sampling site. A major drawback of the method, is that it is not straightforward to calculate time weighted average concentrations from passive sampling data. The main reason for this is that the diffusion and partitioning processes are influenced by temperature, turbulence around the passive sampler/water interface and fouling of the sampler.^11–13

A major part of our work deals with polar organic contaminants that occur in rivers and various stages within the sewage treatment process. The present study focuses on two aspects that are important in driving the passive sampling process in these aquatic systems: flow regime and matrix (i.e. river water and treated sewage effluent). To our knowledge, the interaction between these two parameters has not been investigated yet. One previous study looked at the effect of turbulence (fluid stirring rate) on the sampling rate of a passive sampler for polar compounds.¹⁴ Alvarez and co-workers¹⁴ showed that a change from “not stirring” the sampled water to “stirring” leads to an increase in sampling rate of four- to nine-fold (depending on the substance). More such studies exist for samplers for non-polar compounds. For example, Vrana et al.¹⁵ looked at the effect of flow rate on the sampling rates of semi permeable membrane devices (SPMDs). However, flow rates in their study were very low, only up to 14 mm s^–1, and consequently not comparable with conditions in rivers and wastewater treatment plants. Using Empore™ C₁₈ disks saturated with octanol, also targeting hydrophobic substances, Vrana et al.¹⁶ investigated the effect of water turbulence on the passive sampling process. All three studies^14–16 used controlled media-tap water spiked with chemicals—and not environmental matrices.

Here, we monitored the performance of a passive sampler for polar compounds under controlled, yet very close to environmental, conditions. To achieve this, we constructed two simple and robust channel systems that were fed with either river water containing treated sewage effluent or undiluted effluent. The design of this new system is described in detail together with first applications. We collected 24 h composite water samples to link aqueous concentrations with passive sampling data and to provide information on field sampling rates. The main question was how environmentally relevant flow regimes and matrices affect sampler performance. To evaluate if the samplers were operating in the integrative mode, we exposed the samplers sequentially and concomitantly for 1 to 8 days.

As a passive sampler model to test in our channel systems, we selected Empore™ SDB-RPS (poly(styrenedivinylbenzene) copolymer, modified with sulfonic acid groups), for several reasons. First, polar compounds can effectively be sampled by the receiving phase when used without a diffusion limiting membrane^17,18 (own unpublished work). Second, SDB disks were shown to be operating in an integrative sampling mode for at least 5 days in a lab study¹⁸ and a field trial.¹⁹ Third, recently a streamlined polycarbonate Empore™ disk holder, i.e. Chemcatcher body, has become available that suits the deployment of these disks in our experimental system.²⁰

With respect to the analyses of samples, we focused on environmental estrogens using a receptor based bioassay (the yeast estrogen screen, YES).²¹ In addition, we selected three pharmaceuticals with different substance properties that were measured using LC-MS-MS: a macrolide (clarithromycin) and a sulfonamide antibiotic (sulfamethoxazole), as well as an anticonvulsant/analgesic (carbamazepine).

Experimental

Channel systems to generate stable flow rates

We constructed two channel systems; each system was made up of a set of four Plexiglass channels, a Plexiglass dispenser box and a polyester basin. The channels were 1.80 m long, 0.10 m wide and 0.15 m high. One end of each channel was closed; the other end had a PVC partition with multiple holes. A box (0.70 × 0.40 × 0.45 m) with four steel vents (2 inch diameter) at the bottom served as a water dispenser and was set on top of the channels. On the inside of the dispenser box, each vent was fitted with a PVC screw cap with a round hole. The outflow of each vent was inserted near the closed end of a channel. The holes in each PVC partition were designed to ascertain a stable water level of 0.10 m and a homogeneous flow profile across the width and depth of each of the four channels. The channels were mounted on a table and when the box was filled with water, the water ran through the holes in the PVC caps, through the vents and into and through the channels. Finally, the water passed through the partitions and dropped out of the channels and into the polyester basin (0.7 by 0.8 by 0.6 m, water depth 0.5 m). This basin housed a pump (Hilge, Schötz, Switzerland) that took the water back to the dispenser box at a rate of approximately 6.1 L s^–1 (Fig. 1; see ESI for photos†).

Fig. 1 Channel system to investigate the effect of flow rate on the sampling performance of passive sampling devices.

The dispenser box was dimensioned in such a way that there was always some overflow. Thus, the hydraulic head at the holes of the vents remained constant (0.30 m). Surplus water could leave the dispenser box via a large slit, the overflowing water also drained into the basin.

The water in the basin was continuously refreshed at a rate of approximately 1.9 L s^–1. Mixing in the system was such that more than 95% of the water was renewed within 10 min. We assessed this by letting the system run without refreshing for a couple of hours. This caused the water temperature to increase, as heat produced by the pump was transferred to the water. Using a temperature logger, we then monitored how quickly the ambient temperature was reached after refreshing was started.

To plan the size of the holes in the caps on the vents, we ran a series of preliminary tests. We tested four hole sizes and we measured the volume of water that was discharged through a hole of a given size. There was a linear relationship between the area of the hole and the amount of water discharged through the hole. The following diameters were selected for the trials: 12, 17, 27 and 46 mm. They corresponded to the following volumetric flow rates: 0.26, 0.55, 1.5 and 3.7 L s^–1. Given a water depth in the channels of 0.1 m, this produced flow rates of: 0.026, 0.055, 0.15 and 0.37 m s^–1. We checked the accuracy of this calculation in two ways: (1) by simply measuring the flow with a flow meter (MiniAir2, Schiltknecht, Gossau, Switzerland), and (2) by measuring the time for small particles to travel a distance of 0.5 m. These measurements agreed well with the calculated velocities.

One channel system was placed at the Eawag, Dübendorf (Switzerland) and was run with water from the river Chriesbach, which flows through the site. This river contains treated sewage effluent from the sewage treatment works (STW) Bassersdorf, located 6 km upstream. The other channel system was placed at STW Wüeri in Regensdorf (Switzerland) and used effluent that was taken just after sand filtration. During experiments, river water and effluent temperatures were logged inside the channels (Hobo Pendant; Bakrona, Zürich, Switzerland). Experiments were run in the dark, and no visible fouling was observed (see ESI for photos†).

Typical values of general water parameters for the Chriesbach are: pH, 8.0; and conductivity 600–700 µSi cm^–1. For sand filtered effluent at STW Wüeri these values are: pH, 7.7; and conductivity, 800–900 µSi cm^–1.

Preparation of Empore™ SDB-RPS disks

Empore™ SDB-RPS disks (Infochroma AG, Zug, Switzerland) were dipped into methanol and were placed on the bottom half of a polycarbonate Empore™ disk holder (Chemcatcher bodies; AlControl AB, Linköping, Sweden). The top half of the holder was then fastened onto the bottom half, and the whole device immersed in methanol for 30 min, followed by nanopure water for at least 30 min.

A Chemcatcher body has three holes in its rim. Using these holes, two samplers (i.e. duplicates) were fastened onto an aluminium sheet using cable ties. The aluminium sheet was suspended into the water from the top of the channels so that it was parallel to the water flow.

After the exposure period, the SDB disks were rolled up and transferred to a 8.5 mL vial filled with 7 mL of acetone. The vials were transported to the lab and sonicated for 5 min. Subsequently, the acetone was transferred to a new vial and the SDB disk sonicated again, this time with 7 mL methanol. The methanol was added to the acetone and the combined solvents were filtered through a 0.47 µm PTFE membrane in a polypropylene housing (Sartorius AG, Göttingen, Germany), evaporated under a stream of nitrogen to ca. 100 µL and taken up to 500 µL with methanol. The extract was divided in two parts, 100 µL was used for biological analysis, the remainder for chemical analysis.

Two channel trials

In two trials, we exposed SDB disks to effluent for 5 days and to river water for 8 days. During Trial I (starting on November 15, 2006), an additional set of samplers were placed in one of the channels (0.15 m s^–1) for the first 2 and the last 3 days (effluent) and the first 4 and the last 4 days (river) of the sampling period. This test was designed to address the issue of whether or not sampling occurred in an integrative mode over the 5 and 8 day periods.

During Trial II (starting on January 21, 2007), additional sets of SDB disks were placed in the four channels with effluent. These disks were exchanged each day; again, to address the issue of integrative (or equilibrium) sampling. In the second trial we also took 24 h composite samples (100 mL every 20 min) in parallel to the 24 h SDB disk exposures (see Table 1 for further details of the sampling regimes).

Table 1 Passive sampling regimes of Trial I and Trial II

Flow speed/m s^–1	Effluent		River water
a Every 20 min, 100 mL of water was pumped from the collection basin and pooled to obtain a 24 h composite effluent sample on each of 5 days.
Trial I
0.026	0–5 d		0–8 d
0.055	0–5 d		0–8 d
0.15	0–5 d	0–2 and 3–5 d	0–8 d	0–4 and 5–8 d
0.37	0–5 d		0–8 d
Trial II
0.026	0–5 d	5 times 1 d^a	0–8 d
0.055	0–5 d	5 times 1 d^a	0–8 d
0.15	0–5 d	5 times 1 d^a	0–8 d
0.37	0–5 d	5 times 1 d^a	0–8 d

---

Solid phase extraction of 24 h composite effluent samples

The composite effluent samples were filtered (glass fibre filter, pore size ∼1 µm; Schleicher & Schuell MicroScience GmbH, Dassel, Germany) and adjusted to a pH of 7.5. One hundred mL of sample was spiked with the internal standards sulfamethoxazole-d₄, dihydro-carbamazepine and oleandomycine at a final concentration of 1000 ng L^–1. Subsequently, the samples were enriched using 200 mg OASIS® HLB cartridges (Waters, Milford, MA, USA) and eluted with 8 mL methanol, reduced to approximately 100 µL under a stream of nitrogen, transferred to vials with a PTFE-lined cap and filled up to 500 µL with 5 mM ammonium acetate in HPLC grade water with 10% acetonitrile. The recoveries of the internal standard over the SPE step (including ion suppression, i.e. matrix effects, in the chemical analysis; n = 10), were: sulfamethoxazole-d₄, 68 ± 8%; dihydro-carbamazepine, 65 ± 4%; and oleandomycine, 43 ± 4%. The concentrations of the analytes were corrected based on the recoveries in each sample.

Biological analysis of estrogenic activity

We used the YES, a recombinant yeast assay, based on the methods described by Routledge and Sumpter.²¹ From each SDB disk extract, four different amounts were pipetted onto 96-well plates and the extract was left to evaporate to dryness. Duplicate SDB disks for each sampling point were split between two plates (“A” and “B”) for each of the extract amount that was tested. The estrogenicity of an extract (17β-estradiol equivalents, EEQ; ng SDB^–1) was then interpolated from the average of the standard curves on the “A” and “B” plates.⁶

Chemical analysis of pharmaceuticals

The extracts of the SDB disks were spiked with internal standards, sulfamethoxazole-d₄, dihydro-carbamazepine and oleandomycine, and analysed with LC-MS-MS. Separation of the pharmaceuticals was achieved on a 150 × 2.1 mm C₁₈-column (3 µm particle size, YMC, Kyoto, Japan) combined with a 10 × 2.1 mm precolumn containing the same sorbent; the flow rate was 200 µL min^–1. The mobile phases were: 5 mM ammonium acetate containing 10% acetonitrile (A); and 80% acetonitrile and 20% of phase A (B). The gradient started with 10 min of phase A followed by a 5 min linear gradient to 26% of phase B, a 2 min linear gradient to 38% of phase B which was then kept constant for 7 min. After a 6 min linear gradient to 100% phase B, this level of phase B was kept constant for 4 min. Finally, the system was equilibrated to phase A.

MS-MS detection (API 4000; Applied Biosystems, Ontario, Canada) was performed in the selected reaction mode (SRM), with positive electrospray ionisation using a source voltage of 5 kV, and an ion transfer capillary temperature of 390 °C. The monitored transitions of the pharmaceuticals and their internal standards are reported elsewhere²² (transition of carbamazepine; 237.1 to 194.2 (quantifier), 237.1 to 192.1 (qualifier); see Table 2 for further details of the analysed compounds). Limits of quantitation for sulfamethoxazole, carbamazepine and clarithromycin were: 9, 2 and 4 ng L^–1 for SPE samples and 3, 11 and 1 ng per SDB disk (based on a signal-to-noise ratio >10). The amounts of the analytes per SDB disk were corrected based on the recoveries of the internal standards in each sample.

Table 2 Chemicals collected by Empore™ SDB-RPS disks and analysed by LC-MS-MS

Compound	Therapeutic class	CAS	Chemical structure	Molecular weight	pKa^34	LogKOW
Sulfamethoxazole	Sulfonamide- antibiotic	723-46-6		253	1.8 5.7	0.89
Carbamazepine	Anticonvulsant/analgesic	298-46-4		236	<1 13.9	2.45
Clarithromycin	Macrolide-antibiotic	81103-11-9		748	8.9	3.16

---

Results

Different temperature profiles for effluent and river water

Effluent temperature was fairly stable in both trials, except for a sharp drop at the end of Trial I (figure provided in the ESI†). This temperature drop was due to a local rain event that occurred on November 19 2006. Average effluent temperature was 16.7 °C in Trial I and 13.1 °C in Trial II. River water temperature was more variable and associated with diurnal cycles. Average river water temperature was 11.7 °C in Trial I and 8.2 °C in Trial II.

Repeatable flow rate and SDB uptake relationships for pharmaceuticals

Biological analysis—estrogenic activity. Fig. 2 shows the relationship between flow rate and the accumulation of estrogenic activity by SDB disks. Extracted estrogenicity increased with increasing flow rate. In order to illustrate the relationship between accumulated analytes and the flow rate, the data were fitted with an empirical model which we derived from the “standard” passive sampling equation:^9,15where C_SDB and C_W are concentrations in SDB disk (ng L^–1) and in water (ng L^–1), K_SDB represents the partition coefficient of a given chemical between the SDB disk and the water at equilibrium. We express the data in amount per SDB disk (m_SDB) and not in terms of the concentration in the disk (C_SDB). Consequently, we multiplied both sides of eqn (1) by the volume of the SDB disks. The product of C_W and K_SDB was constant for all treatments (i.e. all flow rates). Thus, we replaced all these constants by a fit parameter “a”. The overall exchange rate “k_e” is a complex term, including, amongst other parameters, the flow rate “v”.¹⁵ However, with the exception of v, all other parameters in the overall exchange rate were constant within each experiment; also, the exposure time “t” was the same for all flow rates. A theoretical/empirical correlation between dimensionless numbers (the Sherwood number, Sh; and the Reynolds number, Re) can be used to evaluate the effects of the flow rate on the mass transfer coefficient. Sh is proportional to “k_e” and Re is proportional to “v”. Their correlation is generally given by Sh ∝ Reⁿ.^23,24 The exponent “n” is equal to 0.5 when a chemical diffuses through the laminar boundary layer to a semi-infinite flat surface and disappears as soon as it touches that surface.²⁴ These assumptions may be applicable to a passive sampler if it operates in the integrative mode. Therefore, we exchanged k_et with the product of a constant “b” and v^c. As the shape of the passive sampler does not exactly satisfy the theoretical restrictions, we introduced the additional parameter “c”. Following the modifications to eqn (1), we fitted the data with the following empirical model: This model describes the relationship between flow rate and sampled amounts very well within the experimental flow range (0.026 to 0.37 m s^–1) in all experiments.

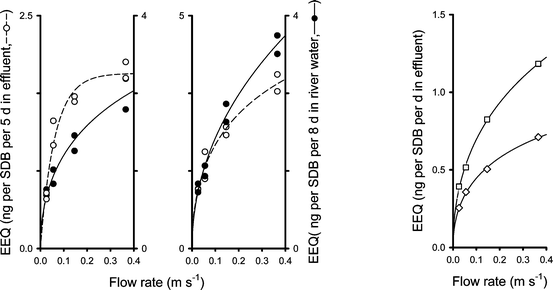Fig. 2 The association between water flow rate and the estrogenic activity (EEQ) on SDB disks exposed to effluent (left Y-axes) and river water (right Y-axes). Data from Trial I are shown on the left and data from Trial II in the middle. The right panel shows the comparison between a 5 day sampling block (repeated from the middle panel and divided by 5 to get a daily average value; diamonds) and the average of five subsequent 24 h samplings (squares). Data were fitted with eqn (2) (lines).

In Trial I, the plot of EEQ against flow rate flattened off sooner for effluent than for river water. In Trial II the EEQ plots were more similar, though again, at higher flow rates, the relationship remained steeper for river water compared to effluent. One has to note, however, that there were two different sampling times, thus a direct comparison is not possible.

The average daily EEQs sampled (ng per SDB disk) were between 44% (at 0.055 m s^–1) and 66% (at 0.37 m s^–1) higher for the daily SDB samples compared to the disks that sampled the full 5 day period (indicating that the integrative sampling phase was exceeded).

Chemical analysis—pharmaceuticals. In contrast to the estrogenic activity, the amounts of accumulated analytes differed markedly between effluent and river water (Fig. 3). Nevertheless, the relationships between flow rate and sampled amounts (eqn (2)) were remarkably similar. For example, for sulfamethoxazole, sampled amounts in the effluent in Trial I surpassed 60 ng per SDB, whereas for river water they reached approximately 5 ng per SDB disk. Despite this 12-fold difference, the relationship between flow rate and the amounts of sulfamethoxazole sampled differed only by the scale (fit parameter a) but not the shape (fit parameters b and c) for the two matrices. In Trial II, there was a more than five-fold increase in sulfamethoxazole sampled in river water compared to Trial I. Again, this large change did not affect the relationship between flow rate and sampled amounts. The situation is similar for the other substances. SDB disks in effluent showed about four-fold higher levels of carbamazepine and clarithromycin compared to river water; levels were three-fold higher in Trial II compared to Trial I.

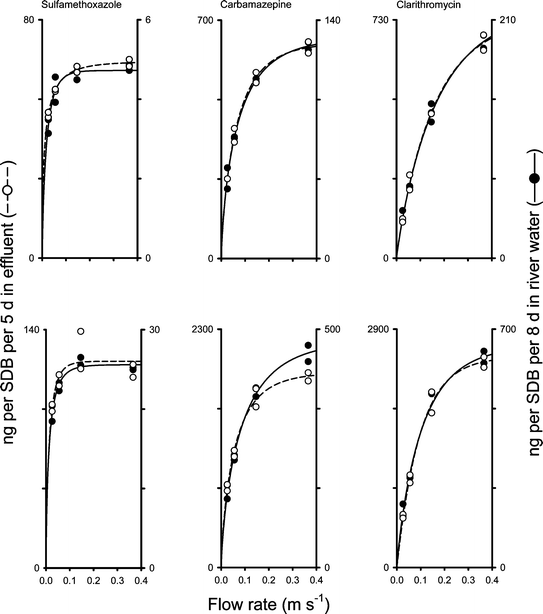Fig. 3 The association between water flow rate and the amounts of three pharmaceuticals on SDB disks exposed for 5 days in effluent (left Y-axes) and 8 days in river water (right Y-axes). Top panels, data from Trial I; lower panels, data from Trial II. Data were fitted with eqn (2) (lines).

Fig. 4 shows that the SDBs that were changed on a daily basis collected more pharmaceuticals compared to the disks that were left for the full 5 day period. The discrepancy was largest for sulfamethoxazole, from 72% at 0.026 m s^–1 to 250% at 0.37 m s^–1; intermediate for carbamazepine, from 47% to 227%; and smallest for clarithromycin, from 7% to 53% (indicating that, at the lower flow rates, clarithromycin was sampled in a nearly integrative mode).

Fig. 4 Daily average amounts of three pharmaceuticals sampled by SDB disks over a 5 day sampling window (diamonds) and over the five subsequent 1 day samplings that comprise the 5 day window (squares). The data were fitted with eqn (2) (lines).

Aqueous concentrations correlate with passive sampling data

Effluent concentrations of carbamazepine in Trial II were very stable over the 5 day sampling period (626 ± 25 ng L^–1; Fig. 5). For both antibiotics, concentrations gradually increased; sulfamethoxazole levels rose from 172 to 246 ng L^–1, clarithromycin went from 351 ng L^–1 on the first day to 599 ng L^–1 on the last day of sampling (Fig. 5).

Fig. 5 Left: concentrations of pharmaceuticals in five 24 h composite samples of treated sewage effluent. Right: concentrations of the pharmaceuticals in 24 h composite samples offset against the amount of each pharmaceutical adsorbed onto SDB disks over the corresponding 24 h period. The data were fitted with linear regressions (eqn (3)).‡

When the daily concentrations of a substance varied over the 5 day period, these concentrations tended to correlate with the amounts of that substance found on SDB disks exposed at 0.026 m s^–1 over the same 24 h period (Fig. 5). These data were fitted with linear regression lines (with the intercept set to zero) to get an approximation of the apparent sampling rates R_S.

We obtained the following sampling rates: sulfamethoxazole, 0.14 L day^–1 (P = 0.073); carbamazepine, 0.25 L day^–1; and clarithromycin, 0.09 L day^–1 (P = 0.056).

Discussion

An environmentally relevant flow through system to evaluate passive samplers

One of our aims was to test the effects of flow rate on passive samplers in an environmentally relevant situation. The newly designed channel system appears to be highly suitable and robust to study the effects of flow rate on the performance of passive samplers. Also, the matrices that we tested suited this purpose, i.e. estrogens and various pharmaceuticals were found both in river water and the effluent. The main advantage of this set-up is that any aspect of the passive sampler deployment, including housing or sampler position in the flow, can be assessed in a relevant and complex matrix under a controlled flow regime.

The pharmaceutical concentrations in the effluent (Trial II) were in line with what has previously been reported.^22,25 Considerably higher amounts of pharmaceuticals were sampled by SBD disks in Trial II compared to Trial I. This difference between the two trials may reflect the increased use of pharmaceuticals, especially antibiotics, during the winter.²⁵ Additionally, changes in the efficiency of the treatment process can affect the load of pharmaceuticals in the effluent.^22,25,26

Compared to the effluent, between four to 12-fold lower amounts of pharmaceuticals were sampled per SDB disk from river water. This result can be expected, as the river contains effluent that is considerably diluted. It is intriguing, however, that in both trials, a higher estrogenicity was found in river water compared to the effluent. This contrasts with the data on the pharmaceuticals and may point to an unknown emission of estrogens into the river, or a particularly poor estrogen removal rate at STW Bassersdorf, the STW that discharges into the river Chriesbach.

No interaction between flow rate and matrix for pharmaceuticals sampled by SDB disk

The relationship between flow rates and the sampled amounts of pharmaceuticals was strikingly similar for the two matrices and the two trials. Still, it has to be noted that no direct comparisons can be made as the sampling windows differed (effluent 5 days, river water 8 days). Then again, even with identical sampling windows, the temperature of the two matrices would have been different. Obviously, using ambient environmental conditions, identical situations simply cannot be generated. Regardless of this given variation, we often observed identical patterns for river water and effluent. This supports the assumption that there are no significant effects of the matrix.

The biological results show a slightly different picture, however. This may be explained by the fact that the estrogenicity data incorporate the effect of a mixture of compounds that react with the human estrogen receptor. In addition, the bioassay is susceptible to matrix components that modify the results.²⁷ Therefore, if the estrogenic cocktail differs over time or between the matrices, different relationships can be expected. As the various components of the cocktail are likely to differ in their relationship between flow rate and sampled amounts—analogous to the differences observed between individual pharmaceuticals. Therefore, it is important to consider that bioassay results are much less amenable to modelling than single compounds, particularly when bioassay results depend on mixtures of (unknown) compounds with differing chemical properties.

In our figures we illustrate the relationship between flow rate and sampled amounts with an empirical model (eqn (2)). If the sampling rate is dominated by aqueous boundary layer diffusion under a laminar flow regime, an increase flow rate (v) should lead to an increase in the sampling rate according to v^0.5, as previously stated. The average value for the parameter “c” (in v^c) was 0.7, which is slightly higher than the theoretical value. This implies that the effect of flow rate on the overall exchange rate is more significant for the “real” sampler than for an “ideal” flat sampler. Although the Chemcatcher body is streamlined, there is a rim around the SDB disk that may affect the flow conditions over the SDB disk. Increased flow rates will increase the intensity of turbulent eddies near the rim and will eventually increase the overall transfer rate more than expected by the theoretical laminar flow assumption. Moreover, fitting the empirical model to the four experimental data points results in only one degree of freedom. Consequently, any quantitative interpretation of the fitted parameters is not possible.

SDB disks deliver time weighed average concentrations for short sampling windows only

For our first trial we selected a sampling window of 5 days for the treated sewage effluent matrix; this choice based on published experiences with SDB disks. Stephens and co-workers¹⁸ state that the kinetic phase for diuron sampled by SDB disks is just over 10 days; Escher et al.¹⁹ observed a good association between grab sample and SDB disk data over a 5 day field trial. As we conducted our experiments in autumn/winter, we knew that the temperatures in our trials would be lower than the 22 °C described in Stephens et al.¹⁸ Sampling rates are lower at reduced temperatures¹⁶ (own unpublished work), so we expected to be well within the integrative period with a 5 day sampling window. Following the same argument, and as we expected the temperature of river water to be considerably lower than that of the effluent, we opted for a slightly longer sampling window for the river water matrix, i.e. 8 days.

In Trial I, the temperatures matched our expectations. However, data from Trial I indicated that the sampling window of 5 or 8 days was too long. At a flow of 0.15 m s^–1 we compared the amount sampled over a 5 or 8 day sampling window (effluent and river water, respectively) with the sum of the amounts sampled in two sampling slots within these windows (see Experimental section for details). For sulfamethoxazole and carbamazepine, the sum of the two slots exceeded the amounts sampled over 5 or 8 days (data not shown). To address the issue of the length of the integrative sampling phase in more detail, we included a daily sequential sampling protocol for all four effluent channels in Trial II. It emerged that the daily average amount sampled per SDB disk in the 5 day sampling window was below the average of the 5 individual days for most compounds and most flow rates (Fig. 4). For example, at 0.026 m s^–1, the daily average amount of clarithromycin sampled over 5 days agreed well with the average amount sampled on the five subsequent days with a difference of 7%. At higher flow rates, up to 35% less clarithromycin was sampled over 5 days compared to the sum of the 24 h sampling periods. Thus, the samplers were in the integrative uptake mode at the lowest flow rate but not at higher flow rates. While for clarithromycin the sampling mode was integrative at 0.026 m s^–1, sulfamethoxazole never showed agreement between the average of the five 24 h sampling periods and the average daily amounts calculated for the 5 day period. In fact, the samplers exposed for 5 days collected similar amounts of sulfamethoxazole between 0.055 and 0.37 m s^–1. This indicates that equilibrium was reached under these conditions, corresponding to 116 ng of sulfamethoxazole per SDB disk.

It is generally assumed that passive samplers are integrative to up to 50% of the equilibrium.⁹ For sulfamethoxazole, the maximum for the 24 h samples was 58 ng SDB^–1, this is exactly 50% of the equilibrium amount after 5 days. Consequently, the 24 h sulfamethoxazole data meet the criterion for an integrative sampling window. For carbamazepine, all 24 h sampler data (maximum: 840 ng SDB^–1) were below 50% of equilibrium amount (>1900 ng SDB^–1), also indicating an integrative uptake mode. This is also the case for clarithromycin. Moreover, the sampled amount of clarithromycin over 5 days at 0.026 m s^–1 was only 620 ng SDB^–1, well below 25% of the equilibrium amount (>2500 ng SDB^–1). This indicates that clarithromycin should have been in the linear uptake phase over 5 days at this flow rate. This assumption is supported by the fact that, at the lower flow rates, the data for the 24 h samplings and the 5 day sampling window matched rather well (Fig. 4).

As expected, there is a direct relationship between the hydrophobicity of the compounds, expressed as octanol–water partition coefficient K_OW, and the uptake kinetics. Sulfamethoxazole, with its low logK_OW (0.89),²⁸ reaches equilibrium fast, while the most hydrophobic compound of our test set, chlarithromycin (logK_OW 3.16),²⁹ remains in the integrative phase longest. Carbamazepine has an intermediate logK_OW (2.45)³⁰ and shows an intermediate uptake kinetic. This situation is analogous to samplers for more non-polar compounds, where the time to equilibrium increases with the K_OW of the sampled substance.^9,31

Overall, we can conclude that the investigated compounds were sampled in an integrative manner over 24 h. For a longer exposure period, integrative sampling cannot be assured, especially at high flow rates and for compounds of low hydrophobicity. The integrative sampling window in our experiments is shorter compared to previous studies.^17–19 This may be explained by the fact that we used newly developed and streamlined Chemcatcher bodies.²⁰ In the older design, the Empore™ disk is surrounded by a 20 mm deep Teflon rim; this slows down sampling rates.³² Obviously, slower sampling rates provide for a longer integrative sampling window. Should longer integrative sampling periods be required, diffusion-limiting membranes can be used to slow down sampling rates.^17,20,33

Consistent sampling rates for three pharmaceuticals

The sampled amounts of pharmaceuticals by SDB disks over 24 h in the channel with the slowest flow (0.026 m s^–1) was between 5% (clarithromycin) and 28% (sulfamethoxazole) of amounts sampled over 5 days at 0.37 m s^–1 (carbamazepine: 12%). As discussed in more detail above, these amounts indicate that the samplers were operating in the integrative mode. For this reason, we used these data to correlate them with the measured effluent concentrations in 24 h composite samples. Provided there was some variability in the data, this approach resulted in good correlations. Also for carbamazepine, with virtually constant aqueous concentrations, the coefficient of variation of the five sampling rates calculated for the five 24 h samplings was only 5% (sulfamethoxazole 7%; clarithromycin 14%).

What needs to be addressed in future studies is whether identical sampling rates can be achieved in different matrices (different rivers and different effluents). This would involve collecting multiple SDB disk and SPE combinations at a large number of sites.

Conclusions

In two trials we show that Empore™ SDB-RPS disks can be applied effectively as passive samplers to monitor various polar pharmaceuticals, as well as environmental estrogens. However, the integrative sampling window of SDB disks is fairly short (1 to 5 days) and this holds only at low water flow rates (<0.1 m s^–1); the ability of SDB disks to provide an integrative measure of fluctuating aqueous concentrations diminishes appreciably at higher flow rates. We observed that the sampling rate increases with increasing flow rate. However, some of our observations are complicated by the fact that flow rate effects occurred over a time period where the sampling was not always in the linear uptake phase. Consequently, only for selected samplings do our results reflect sole effects of flow rate on the sampling rate.

The shape of the relationship between flow rate and sampled amounts is highly repeatable over time for individual pharmaceuticals. Furthermore, this relationship appears to be unaffected by the two matrices that we tested in our trials (i.e. treated sewage effluent and river water containing effluent). Given this reproducibility and the good association between aqueous concentrations and accumulated pharmaceuticals on SDB disks, our data show that SDB disks can be used as passive samplers in the integrative mode, but only when a low flow rate can be maintained at a fairly constant level. The prospect of using SDB disks as equilibrium samplers for selected—fast responding—compounds or under conditions of high flow-rate is an interesting topic that requires more study.

Acknowledgements

We thank Pius Niederhauser, Peter Spohn (both AWEL; Amt für Abfall, Wasser, Energie und Luft, Zürich) and Markus Gassmann (STW Effretikon-Illnau) for their help in finding a location for our channel systems. Arthur Wanner and colleagues assisted at STW Wüeri in Regensdorf. Miguel Sibila (University of Cadiz, Spain) helped to process some of the samples. This study was funded by the Swiss National Science Foundation, NRP50 Programme: Endocrine disruptors, Relevance to Humans, Animals and Ecosystems (4050-111386). Additional funding was provided by FOEN (Federal Office for the Environment) within the framework “Strategy MicroPoll”.

References

1. C. G. Daughton, Lancet, 2002, 360, 1035–1036.
2. J. P. Sumpter and A. C. Johnson, Environ. Sci. Technol., 2005, 39, 4321–4332.
3. D. J. Hamilton, Á. Ambrus, R. M. Dieterle, A. S. Felsot, C. A. Harris, P. T. Holland, A. Katayama, N. Kurihara, J. Linders, J. Unsworth and S.-S. Wong, Pure Appl. Chem., 2003, 75, 1123–1155.
4. A. Laperrouze, Proposal for a directive, Committee on the Environment, Public Health and Food Safety PE 386.558v01-00, Brussels, 2007.
5. S. Pawlowski, T. A. Ternes, M. Bonerz, A. C. Rastall, L. Erdinger and T. Braunbeck, Toxicol. in Vitro, 2004, 18, 129–138.
6. E. L. M. Vermeirssen, M. J.-F. Suter and P. Burkhardt-Holm, Environ. Toxicol. Chem., 2006, 25, 2413–2422.
7. J. N. Huckins, M. W. Tubergen and G. K. Manuweera, Chemosphere, 1990, 20, 533–552.
8. G. A. Mills, B. Vrana, I. Allan, D. A. Alvarez, J. N. Huckins and R. Greenwood, Anal. Bioanal. Chem., 2007, 387, 1153–1157.
9. J. N. Huckins, J. D. Petty, C. E. Orazio, J. A. Lebo, R. C. Clark, V. L. Gibson, W. R. Gala and K. R. Echols, Environ. Sci. Technol., 1999, 33, 3918–3923.
10. P. Mayer, J. Tolls, L. Hermens and D. Mackay, Environ. Sci. Technol., 2003, 37, 184A–191A.
11. K. Booij, H. M. Sleiderink and F. Smedes, Environ. Toxicol. Chem., 1998, 17, 1236–1245.
12. K. Booij, H. E. Hofmans, C. V. Fischer and E. M. van Weerlee, Environ. Sci. Technol., 2003, 37, 361–366.
13. K. Booij, R. van Bommel, A. Mets and R. Dekker, Chemosphere, 2006, 65, 2485–2492.
14. D. A. Alvarez, J. D. Petty, J. N. Huckins, T. L. Jones-Lepp, D. T. Getting, J. P. Goddard and S. E. Manahan, Environ. Toxicol. Chem., 2004, 23, 1640–1648.
15. B. Vrana and G. Schüürmann, Environ. Sci. Technol., 2002, 36, 290–296.
16. B. Vrana, G. A. Mills, E. Dominiak and R. Greenwood, Environ. Pollut., 2006, 142, 333–343.
17. J. K. Kingston, R. Greenwood, G. A. Mills, G. M. Morrison and L. B. Persson, J. Environ. Monit., 2000, 2, 487–495.
18. B. S. Stephens, A. Kapernick, G. Eaglesham and J. Mueller, Environ. Sci. Technol., 2005, 39, 8891–8897.
19. B. I. Escher, P. Quayle, R. Muller, U. Schreiber and J. Mueller, J. Environ. Monit., 2006, 8, 456–464.
20. R. Greenwood, D. A. Mills and B. Vrana, Passive Sampling Techniques in Environmental Monitoring, Elsevier, Amsterdam, 2007, p. 486.
21. E. J. Routledge and J. P. Sumpter, Environ. Toxicol. Chem., 1996, 15, 241–248.
22. A. Göbel, C. S. McArdell, M. J.-F. Suter and W. Giger, Anal. Chem., 2004, 76, 4756–4764.
23. R. B. Bird, W. E. Stewart and E. N. Lightfoot, Transport Phenomena, John Wiley & Sons Inc., New York, 2nd edn, 2002, p. 895.
24. V. G. Levich, Physicochemical Hydrodynamics, Prentice-Hall Inc., Engelwood Cliffs, 1962, p. 700.
25. C. S. McArdell, E. Molnar, M. J.-F. Suter and W. Giger, Environ. Sci. Technol., 2003, 37, 5479–5486.
26. A. Joss, E. Keller, A. C. Alder, A. Göbel, C. S. McArdell, T. Ternes and H. Siegrist, Water Res., 2005, 39, 3139–3152.
27. E. L. M. Vermeirssen, R. Burki, C. Joris, A. Peter, H. Segner, M. J.-F. Suter and P. Burkhardt-Holm, Environ. Toxicol. Chem., 2005, 24, 2226–2233.
28. C. Hansch, A. Leo and D. Hoekman, Exploring QSAR. Hydrophobic, Electronic and Steric Constants, American Chemical Society, Washington, 1995, p. 348.
29. J. W. McFarland, C. M. Berger, S. A. Froshauer, S. F. Hayashi, S. J. Hecker, B. H. Jaynes, M. R. Jefson, B. J. Kamicker, C. A. Lipinski, K. M. Lundy, C. P. Reese and C. B. Vu, J. Med. Chem., 1997, 40, 1340–1346.
30. A. Dal Pozzo, G. Donzelli, L. Rodriquez and A. Tajana, Int. J. Pharm., 1989, 50, 97–101.
31. B. Vrana, G. A. Mills, M. Kotterman, P. Leonards, K. Booij and R. Greenwood, Environ. Pollut., 2007, 145, 895–904.
32. T. Lobpreis, B. Vrana, E. Dominiak, K. Dercová, G. A. Mills and R. Greenwood, Environ. Pollut., 2007 DOI:10.1016/j.envpol.2007.09.011.
33. A. T. K. Tan, R. V. Hyne and P. Doble, Environ. Toxicol. Chem., 2007, 26, 435–443.
34. T. A. Ternes and A. Joss, Human Pharmaceuticals, Hormones and Fragrances: The challenge of micropollutants in urban water management, IWA Publishing, London, 2007, p. 468.

---

Footnotes

† Electronic supplementary information (ESI) available: Photos of channel system and temperature profiles of treated sewage effluent and river water. See DOI: 10.1039/b710790k

‡ For clarithromycin we had to reanalyse the samples after storage. We observed a significant reduction of the values for both the SDB disks and the water samples, which may be explained by the use of oleandomycine as the surrogate internal standard (see Experimental section for details). Results of aqueous concentrations and SDB disks were similarly affected.

---