Using first-principles calculations to accelerate materials discovery for hydrogen purification membranes by modeling amorphous metals
Shiqiang
Hao
ab and
David S.
Sholl
*c
aDepartment of Chemical Engineering, Carnegie Mellon University, Pittsburgh, PA 15213, USA
bNational Energy Technology Laboratory, Pittsburgh, PA 15236, USA
cSchool of Chemical and Biomolecular Engineering, Georgia Institute of Technology, Atlanta, GA 30332-0100, USA. E-mail: david.sholl@chbe.gatech.edu
First published on 3rd July 2008
Abstract
Efficient purification of hydrogen from high temperature mixed gas streams can potentially play a critical role in the large-scale production of hydrogen from gasification of coal or biomass. Dense metal membranes have many favorable properties for this kind of purification, but existing membranes based on crystalline metal alloys have a number of limitations. The use of amorphous metal films as membranes has potential to overcome at least some of the disadvantages of crystalline metal membranes. We present new modeling methods that make it possible for the first time to quantitatively predict the performance of amorphous metal films as hydrogen purification membranes. These methods are introduced by examining amorphous Fe3B, a material where comparisons can be made to a crystalline material with the same composition. A membrane made from the amorphous material is predicted to have a hydrogen permeability 1.5–2 orders of magnitude higher than a crystalline membrane. The methods we introduce here will be useful in accelerating the development of amorphous membranes for practical applications.
1 Introduction
Hydrogen has the potential to play an important role in creating large-scale changes to the mix of energy sources currently used by our global society, particularly in transport applications that currently are entirely dependent on liquid hydrocarbons. In the most utopian setting, hydrogen could be produced by electrolysis of water from a truly renewable energy source (e.g. solar). In the nearer term, a time still likely to be measured in decades, large-scale hydrogen production will involve gasification of hydrocarbon resources, including coal and biomass. If the syngas produced from these gasification processes can be effectively separated into (nearly pure) hydrogen and concentrated CO2, then an overall process that is carbon-neutral (for coal) or carbon-negative (for biomass) can be envisioned.1,2 This concept of course assumes that the resulting CO2 is sequestered in some long term manner. As with any scenario for large-scale energy use, this scheme has a number of negative aspects and faces serious technological, infrastructure and policy hurdles.3One of the key technological challenges associated with large-scale production of hydrogen via gasification is the need to economically purify H2 from syngas and other feeds. If the resulting H2 is to be used in fuel cell applications, extremely high levels of purity are desirable.4,5 It is of course important to perform this separation economically. In gasification applications, feed streams are typically at high temperatures; temperatures of 300–500 °C.6,7 Membrane-based separations provide an excellent general strategy for achieving separations with these requirements.8 Ockwig and Nenoff recently produced an extensive review of membrane technologies for hydrogen purification, which include a large range of materials.9 For high temperature applications, dense metal membranes are in many cases the most promising membrane materials.
Dense metal membranes function by allowing the diffusion of individual H atoms through a dense membrane layer via interstitial diffusion; a process that effectively excludes atoms of all elements except H.9 This allows these membranes to have potentially “perfect” selectivity for H2. This observation has led to a large body of work aimed at developing durable, cost-effective dense membranes with large permeabilities for H2. Multiple reviews of this field have appeared in recent years.9–14 The materials used for these membranes can be broadly divided into elemental metals, crystalline metal alloys and amorphous metal alloys. The fundamental properties of essentially all elemental metal membranes are known, with Pd being by far the most widely studied. When alloys are considered, it becomes difficult to systematically consider all the possible compositions that can be considered as potential membranes. Large numbers of binary crystalline alloys and a smaller number of ternary and other multi-component alloys have been examined experimentally, but the search for materials that are durable, cost-effective, poison tolerant and exhibit high permeability for H continues to be an active area.
Using thin films of amorphous metals, that is, metals without long range structural order, offers significant opportunities for fabrication of membranes that outperform existing Pd-based metal membranes based on crystalline alloys. Dolan et al. have recently provided a detailed review of hydrogen-selective amorphous alloy membranes,11 and Ockwig and Nenoff highlighted recent progress with these materials as part of their comprehensive review of membranes for hydrogen production.9 Perhaps the single most important observation from these two reviews is that amorphous metal membranes have been tested by multiple groups, so the methods required for creating pinhole-free membranes are now well developed. As is the case with crystalline membranes, the number of distinct alloy compositions that can be considered as candidates for amorphous film membranes is vast. Ockwig and Nenoff noted that development of these membranes is “still an entirely open field”, and this is in large part due to the huge number of materials that could be used. Among the limited number of materials that have been tested as membranes, a number have shown promising permeabilities relative to well known crystalline membranes. Inoue and coworkers have reported several films involving Zr, Ni and other metals that have H2 permeabilities comparable to pure Pd.15–18
The use of amorphous metal films as membranes can address several of the difficulties associated with crystalline membranes. In general, concerns about hydrogen embrittlement and sintering are greatly reduced in amorphous materials when compared to crystalline materials.11 The cost of the membrane materials in amorphous films can potentially be far less than in Pd-based alloys. Many of the amorphous films studied to date have been based on low-cost materials such as Zr, Ni, Cu and Al. Another positive feature of these films is that the glass-forming requirements of materials for amorphous films are much less stringent than for bulk samples of the same materials. The glass forming ability of an alloy is typically characterized by the minimum cooling rate that must be used to avoid crystallization.19,20 Flow casting methods exist for films as thin as 20 μm that give cooling rates up to 1010 °C s−1;21 this cooling rate is much larger than the critical cooling rate for most alloys.
In this paper, we consider how the development of amorphous metal membranes for hydrogen purification could be accelerated by making quantitative theoretical predictions about the performance of these membranes. Although the properties of interstitial H in amorphous metals has been studied for at least 30 years,22–24 previous theoretical work on these materials has been phenomenological rather than quantitative. Below, we introduce a new approach based on quantum chemistry calculations that gives quantitative information about the flux of hydrogen through amorphous metal films. These methods should be useful in seeking amorphous alloys that are worth intensive experimental investigation and device development.
The paper is structured as follows. In section 2, we discuss several general principles regarding the use of theoretical models to screen materials for practical applications, and describe why metal membranes are one area to which theoretical calculations are well suited. In section 3, we introduce our new methods for using quantum chemistry and statistical mechanics to predict the solubility, diffusion and permeation of H through amorphous metals. We illustrate our approach for a specific material, amorphous Fe3B, that can be directly compared to a crystalline material with the same composition. Comparing these two materials provides an example of how an amorphous structure can lead to permeation rates through a membrane that are greatly enhanced relative to a crystalline material. In section 4, we summarize the methods we have introduced in relation to the principles listed in section 2, with a particular emphasis on discussing the limitations of our current approach and areas where experimental efforts are required to provide a complete description of membrane performance.
2 Using theoretical predictions to screen materials for hydrogen purification membranes
The consideration of amorphous metals as hydrogen purification membranes is one of a large class of applied science problems where a very large number of possible materials can be considered for a particular application. An obvious goal for work on any problem of this type is to rapidly consider many candidate materials to identify the materials with the highest performance for intensive development. In this section, we briefly consider the question of how theoretical predictions can play a useful role in this kind of screening process.We suggest five principles that should be considered in any planned application of theory for materials screening:
(i) Theoretical predictions must be made for multiple materials on time scales shorter than the same materials can be assessed experimentally.
(ii) Theoretical predictions should require minimal input from experimental data.
(iii) Theoretical predictions must be made about the quantities relevant to end-use applications, not about microscopic properties that are inaccessible experimentally.
(iv) Theoretical predictions need to have sufficient quantitative accuracy that confident judgments can be made separating promising and unpromising materials (although precision going beyond this semi-quantitative standard is frequently not necessary).
(v) The assumptions and caveats associated with theoretical methods should be clearly stated to allow judgements to be made about the potential impact of these factors on “real world” performance of materials.
If modeling methods cannot satisfy principles (i) and (ii), then it will almost certainly be more productive to directly screen materials experimentally. Principle (iii) may seem self-evident, but it is important to remember that almost all screening activities occur for applications where the performance of a material cannot be described by a single number. Instead, it is typical to have a long list of objectives that a material or process must satisfy. A key goal in any effort to screen materials is to identify a small number of properties, perhaps just one, that are the critical limitations of known materials and to use this as the basis for considering new materials. A useful metric for anyone considering using theoretical methods in this situation is to ask what properties will be important in the long-term application of interest that are not captured in any way in the proposed calculations. If a convincing answer to this question cannot be given, the value of the calculations is, at best, uncertain. This issue is also addressed by principle (v) above.
Principle (iv) above addresses the temptation that often faces theorists to use the most sophisticated methods available to provide high precision data. A strong trade-off almost always exists between the precision of a theoretical calculation and the time required to complete it. It is important that strenuous efforts be made to make theoretical predictions precise enough that their predictions can be trusted. But when the aim is to identify materials that will then be tested in a more comprehensive way via experiments, increasing the level of a theoretical description beyond what might be called the minimal acceptable level rapidly enters the realm of diminishing returns.
The development of thin metal membranes for hydrogen purification has multiple characteristics that make it an area where quantitative theoretical calculations can play an important role. The time and resources required to comprehensively test experimentally even a single alloy composition as a thin film membrane are considerable; even after many years of work in this area, only a tiny fraction of the conceivable alloy compositions for crystalline films have been studied.9,10 This situation is even worse when a new class of materials, such as amorphous metals, is being considered, because the fabrication methods needed to make thin film membranes from these materials are not yet widely known. As a result, quantitative predictions can be made about the performance of even a handful of amorphous metals as membranes could provide important motivation and focus for experimental efforts with these materials.
Our current work on amorphous metal films is motivated by our previous theoretical treatments of crystalline metal films, which we feel measure up well against the five principles listed above.25–31 The aim of these calculations is to predict the flux of H2 through a defect-free membrane when the membrane is exposed to pure H2. While multiple other criteria are important in the final application of a membrane (resistance to chemical poisons, durability under thermal cycling, ease of manufacture etc.), no material that can only lead to extremely low H2 fluxes will be useful, regardless of its other merits.
The ingredients of a continuum-level description of H2 transport through crystalline metal alloys are well known.10,29,32 In many instances, net transport of H2 across a membrane is rate-limited by interstitial diffusion of H through the bulk material. In that case, the flux can be related to the membrane's operating conditions once the solubility of interstitial H and the diffusion coefficient of interstitial H are known. Detailed descriptions that incorporate the other microscopic processes that are also necessary for net transport of H through a membrane are available that make it possible to determine when these processes cause a membrane to deviate from being diffusion limited.29,32
To use this continuum description in a predictive sense, methods to quantitatively predict H solubility and diffusivity in metal alloys must be used. These tasks can be performed effectively by appropriate use of density functional theory (DFT) calculations. Plane-wave DFT calculations are well suited to describing the local properties of interstitial H in metals. Examples where direct comparisons with experimental data have been used to establish the accuracy of these methods include the binding energies, vibrational frequencies and diffusion properties of interstitial H in simple metals such as Pd and in ordered intermetallics,27,33–36 and the thermodynamics of complex metal hydrides for reversible storage of hydrogen.37–39
The crystalline materials usually considered for use in membrane applications are typically solid solutions of multiple atomic components. A strong limitation on using DFT calculations to describe alloys of this kind is that they are made up from a huge range of compositionally distinct interstitial sites. A practical way to approach this issue is to perform a large number of DFT calculations characterizing the local properties of a range of interstitial sites and to use the information from these calculations to parameterize a model that defines the properties of an H atom in terms of the arrangement of metal atoms around the site being considered.25,27,31 Once this model has been defined, H solubility can be readily calculated via statistical mechanics methods. Similarly, H diffusion can be calculated via a kinetic Monte Carlo technique that rigorously defines the net diffusion coefficient once the local site-to-site hopping rates are known.27,40
In order for first-principles methods to be applied to H transport through amorphous metals, several technical challenges must be overcome that do not exist for crystalline alloys. First, a detailed model of the atomic coordinates of the amorphous material must be generated. Once this model is available, the sites that can be occupied by interstitial H and the transition states for hopping of H atoms between these sites must be identified. All of these tasks can be greatly simplified by symmetry considerations in crystalline materials but not amorphous materials. Because the solubility of H in amorphous materials is frequently considerably stronger than in crystalline materials,11,22,23,41 modeling of H solubility in amorphous films must consider the effects of H concentration. Concentration effects can have important implications for interstitial diffusion in amorphous films. Experiments and empirical models of H diffusion in amorphous films have shown that H diffusivities can increase greatly as the concentration of interstitial H increases.22,23 As a result, models of these films must consider not only the dilute concentrations of H that are all that is needed in describing crystalline membranes, but also the effects of interstitial H concentration. In the remainder of this paper, we show that we have developed methods to address each of these challenges for the first time.
3 First-principles calculations of H solubility and transport in amorphous Fe3B
To introduce our new methods for predicting H transport through amorphous metal films, we have chosen an amorphous material whose structure (in the absence of hydrogen) has been studied in previous DFT calculations by Widom and co-workers,42,43 namely Fe3B. This material has the interesting property that a crystalline phase with exactly the same composition exists with similar energy to the amorphous phase, namely crystalline Fe3B with Pearson symbol oP16. We take advantage of this situation to directly compare the predicted membrane properties of the amorphous and crystalline phases of Fe3B, which we denote a-Fe3B and c-Fe3B, respectively. It is important to note that this material was not chosen because we anticipated that it would have favorable membrane properties relative to known crystalline membrane materials, such as Pd. Rather, our calculations are designed to illustrate the principle that quantitative predictions can be made about membranes made from amorphous materials using methods that could reliably be extended to other amorphous alloys of interest.All DFT calculations were performed with the generalized gradient approximation using the PW91 functional and PAW potentials as implemented in VASP.44 Spin polarization with VWN spin interpolation was used in all calculations; this approach introduces additional computational expense but is required because of the magnetic properties of Fe. In all energy minimizations, all atoms were relaxed until the forces exerted on every atom are less than 0.03 eV Å−1. The amorphous structure was created by simulating a representative liquid-like sample of Fe3B containing 100 atoms in the computational supercell with ab-initio molecular dynamics, followed by a rapid temperature quench and then energy minimization.43 Calculations with this material sampled k-space at the Γ-point only. Unfortunately, the computational expense associated with these systems means that it is currently impractical for us to explore multiple realizations of this material. Calculations for c-Fe3B used a supercell with 32 atoms and sampled k-space using 7 × 5 × 4 k-points placed using the Monkhorst–Pack scheme. Test calculations showed that individual H atoms in these structures caused only small changes in their lattice constants, so in all subsequent calculations we fixed the supercell size and volume.
3.1 H solubility in Fe3B
Our DFT-based results assessing H solubility in Fe3B have been presented elsewhere,45 but because they play a crucial role in our treatment of Fe3B membranes, we summarize the key results here. To predict the solubility of interstitial H in a metal, the binding energy of H atoms in each interstitial site in the material must be known. Finding these sites is usually straightforward in crystalline materials, but this is not the case for amorphous materials. We developed a method to identify all interstitial sites in an amorphous metal without introducing bias into this process.45 The key to our method is to first find all local minima for H atoms defined using empirical pair potentials for interactions between H atoms and the host atoms, then to use the distinct local minima found in this way as starting points for DFT calculations in which all atoms are allowed to relax. The DFT calculations performed starting from the minima found from the empirical potentials gave 4 structurally distinct interstitial sites in c-Fe3B and 174 sites in a-Fe3B. The binding energy of H in each site was defined by25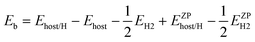 | (1) |
In the crystalline material, H binding in the octahedral Fe6 sites gives Eb ≈ 0. The other three distinct interstitial sites are tetrahedral sites with binding energies > 0.5 eV larger than the octahedral site. The amorphous material has the characteristics that have been identified in previous experimental studies of amorphous alloys:22,46,47 a broad range of binding energies is observed with a significant fraction of the sites having H binding energies that are much more favorable than the crystalline material. Approximately 40% of the interstitial sites in the amorphous material have Eb < 0. We refer to the distribution of interstitial site energies as the site energy density of states (DOS). Further details on the site energy DOS and the characteristics of the favorable binding sites are available in our previous report.45
To illustrate the number of interstitial sites that were characterized in the amorphous material, Fig. 1 shows the calculated vibrational density of states (VDOS) of amorphous and crystalline Fe3B in terms of the zero point energy of individual interstitial H atoms. For visualization purposes, the results for each site in the amorphous material were plotted using a Gaussian with standard deviation 0.005 eV. Our results are consistent with the qualitative trends seen experimentally in materials such as amorphous TiCu, where measurements have been performed at high H loadings;48 the VDOS in the amorphous material covers a broader range of energies than the crystalline material. In crystalline materials it is not unusual to find that interstitial sites with more favorable binding energies have lower vibrational frequencies for H than other sites.26 In c-Fe3B we find that the most favored site does have the lowest vibrational frequency. As shown in the inset in Fig. 3, however, there is no clear correlation in the amorphous material between the binding energy and the vibrational frequencies of interstitial H.
 | ||
| Fig. 1 The calculated vibrational density of states of interstitial H in a-Fe3B (solid curve) and c-Fe3B (arrows). The zero point energies for H in each interstitial site in a-Fe3B are plotted as a function of their classical binding energy in the inset. | ||
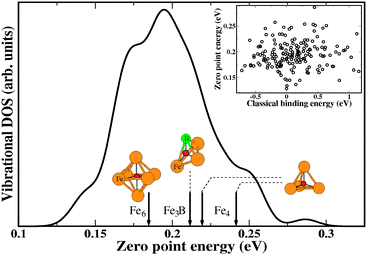
As we show below, interactions between interstitial H atoms in Fe3B play a crucial role in the overall solubility and diffusion of H in this material. To characterize H–H interactions in a-Fe3B, DFT calculations in which all atoms were allowed to relax were performed for a large number of interstitial H–H pairs. The interaction energy for a pair of H atoms was defined by
| ΔEH–H = Ehost/2H + Ehost − Ehost/H,1 − Ehost/H,2 | (2) |
 | ||
| Fig. 2 Calculated H–H interaction energies for 35 distinct H–H pairs in a-Fe3B. The parameters for the solid line are a0 = 5.68 eV and a1 = 1.61 Å−1. Pairs for which one or both of the H atoms has a binding energy < −0.2 eV as an individual interstitial atom are shown as favorable sites. The Westlake criterion is described in the text. | ||
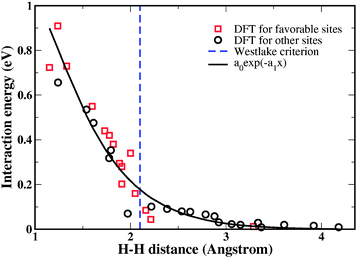
We used the site energies and H–H interaction energies described above to predict the solubility of H in a-Fe3B and c-Fe3B using grand canonical Monte Carlo calculations that defined the chemical potential of H by treating H2 as an ideal gas.29 Because these calculations used atomic structures identical to the material examined in our DFT calculations, there is no requirement that the site energy DOS is fitted in any way. The dashed curves in Fig. 3 show the calculated H solubility at 400 K from these calculations. Here and below, solubility is characterized using the ratio of H atoms to host atoms, H/M. Fig. 3 also shows results for the equilibrium between the amorphous phase and gaseous D2 and T2. The predicted isotope effects are qualitatively similar to experimental observations in crystalline Pd, where the heavier isotopes have reduced solubility.49
 | ||
| Fig. 3 The predicted solubility of H in a-Fe3B as a function of H2 pressure at 400 K. Symbols connected by dashed curves show data for H2, D2, and T2. Other symbols show results for the approximate treatments of H2 as explained in the text. | ||
Fig. 3 shows two approximate treatments of H–H interactions in a-Fe3B. First, H solubility was calculated without any H–H interactions. This approach strongly overestimates the H solubility. The second approximation in Fig. 3 is to describe H–H interactions using the Westlake criterion,50 a rule of thumb that states that pairs of interstitial sites closer to 0.21 nm cannot be simultaneously occupied by H atoms. This criterion amounts to approximating the H–H interaction energy with a hard wall potential, as indicated by the vertical line in Fig. 2. This simple model of interactions gives results in reasonable agreement with the more detailed approach of describing H–H interactions using the exponential curve in Fig. 2. Using the Westlake criterion in this way slightly overestimates the H solubility because it neglects the repulsive interactions that exist for H–H atoms with distances > 0.21 nm. At p = 1 atm, the approximate treatment based on the Westlake criterion gives a solubility 9% larger than our detailed calculation.
The predicted solubility of interstitial H in amorphous and crystalline Fe3B is compared as a function of temperature and H2 pressure in Fig. 4. The most striking aspect of this comparison is that H solubility in the amorphous material is far larger than in the crystalline material. At 600 K, for example, the solubility of H in amorphous Fe3B is predicted to be 2–3 orders of magnitude larger than for the crystalline material. The broad distribution of site energies in the amorphous material causes the qualitative dependence of the solubility on temperature to differ strongly from the simple behavior seen in the crystalline case.
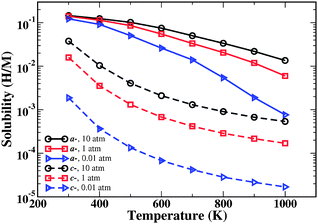 | ||
| Fig. 4 Calculated H solubility in a-Fe3B (solid curves) and c-Fe3B (dashed curves) as a function of temperature and H2 pressure. Lines are guides to the eye. | ||
3.2 H diffusion in Fe3B
We now turn to the diffusion of interstitial H atoms in Fe3B. We approached this task by first finding all the transition states that control the hopping of H atoms between adjacent interstitial sites in each material we considered. Similar to our methods for finding all interstitial sites in these complex materials, our characterization of transition states was greatly assisted by finding reasonable approximations for the positions of these states before beginning computationally expensive DFT calculations. Specifically, we noted that the transition states for interstitial diffusion are located with the H atom close to the geometric center of the polyhedral face connecting the two interstitial sites. Using this position as an initial estimate, a quasi-Newton optimization algorithm that converges to critical points on the energy surface was used. When our initial estimate is sufficiently close to the true transition state, this calculation finds the transition state with roughly the same level of computational effort as optimizing the geometry of a single interstitial site. This approach was successful for ∼90% of the transition states we examined. If the initial estimate is not close enough to the true transition state, the H atom will converge to a nearby interstitial site. In this case a standard chain-of-states method such as the Nudged Elastic Band (NEB) method can be applied.51 NEB calculations require much larger computational resources than individual geometry optimizations, so reducing the number of NEB calculations needed to fully characterize a sample is crucial to the success of our calculations. We used these methods to characterize all 462 transition states in our computational supercell for a-Fe3B. Similar calculations for c-Fe3B identified 77 transition states. For each transition state, the energy of the state was defined using eqn (1) and the vibrational frequencies (two real and one imaginary) of H were computed within the harmonic approximation. The imaginary frequencies at the transition states are important at very low temperatures where quantum tunneling can contribute to H–H hopping,33,35 but this effect is negligible at the temperatures we consider below.We examined the long-range mobility of H atoms using kinetic Monte Carlo (KMC) simulations.27 In these simulations, the hopping rates for H atoms leaving an interstitial site were defined using quantum corrected transition state theory using the energies and vibrational frequencies of H found from our DFT calculations for the relevant interstitial site and transition state. This approach accurately describes the local hopping rates in the temperature regime we examine below.33 Once these local rates are known, KMC is an efficient way to simulate the motion of H atoms on long time scales. Within our KMC simulations, we first determine the hopping rate associated with the fastest process among all possible hops in the simulation volume, kfast. At each step in our KMC algorithm, an interstitial H atom is selected randomly from all H atoms in the simulation volume and a move direction for hopping out of the current site is selected randomly. After defining the rate associated with the selected hop, k, the hop is accepted with probability (nk)/(nfastkfast), where n and nfast are the total number of hopping directions for the selected site and the site that defines the fastest possible rate, respectively. Regardless of the outcome of the attempted hop, time is incremented by Δt = (nfastkfastN)−1, where N is the total number of interstitial atoms in the simulation volume. For both the amorphous and crystalline materials, we defined simulation volumes for replicating the supercells used in our DFT calculations using periodic boundary conditions. At the beginning of each simulation, H atoms were distributed randomly among the simulation volume's interstitial sites according to a Boltzmann weighted energy distribution. This allowed us to equilibrate the initial state for the KMC simulation using a relatively small number of MC events, typically 5000 MC events per H atom.
It is clear from Fig. 4 that a description of H diffusion in amorphous Fe3B under conditions relevant for practical membranes must include interstitial H at non-dilute concentrations. As an initial effort to examine these effects, we used the Westlake criterion to characterize H–H interactions. With this approach, if the destination site for an attempted hop in our KMC simulation was within a radius of 0.21 nm of another interstitial H, this hop was not allowed to occur (although time was still incremented in the simulation as defined above). The Westlake criterion was also enforced during the initial placement of H atoms in interstitial sites in these calculations.
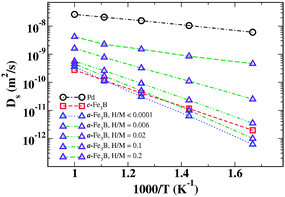
After equilibration, a further 6 million (20 million) MC events per H atom were performed while collecting data on the trajectory of each atom in crystalline phase (amorphous phase). The tracer diffusivity (also known as the self diffusivity) of the H atoms was then obtained using the usual Einstein expression
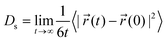 | (3) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (t) is the position of an H atom and the angled brackets indicate an average over all H atoms.
(t) is the position of an H atom and the angled brackets indicate an average over all H atoms.
Fig. 5 shows the tracer diffusivity of dilute H in c-Fe3B and a-Fe3B. The results for a-Fe3B in this limit were obtained from a KMC simulation of a small number of H atoms diffusing in a simulation volume containing >1.5 × 106 Fe and B atoms. As expected, the temperature dependence in c-Fe3B can be represented by an Arrhenius expression, Ds = Dexp(−Eeff/kBT), where D and Eeff are the diffusion prefactor and effective activation barrier, respectively. Fitting our calculated results in this way gives D = 5.84×10−7 m2 s−1 and Eeff = 0.66 eV. This effective activation energy is entirely consistent with the barrier that would be expected from examining the energies required for H atoms to hop between nearby Fe6 sites in this material. Fitting the calculated diffusivities for dilute H in the amorphous phase gives a somewhat higher effective activation energy of 0.78 eV. DFT-based calculations analogous to ones we have presented here have been shown previously to agree quantitatively with H diffusivities in crystalline Pd and Pd–Cu alloys.27Fig. 5 shows the DFT-based results for pure Pd. As shown in Fig. 5, the diffusivity of H at dilute concentrations in crystalline Pd is 2–4 orders of magnitude faster than in either of the Fe3B materials we have considered here.
 | ||
| Fig. 5 The calculated diffusion coefficients of dilute H in c-Fe3B and a range of H concentrations in a-Fe3B. The diffusion coefficients in pure Pd are also shown. | ||
Fig. 5 also shows the effect of increasing the interstitial H concentration on the tracer diffusion coefficient in amorphous Fe3B. The concentration dependence of this diffusion coefficient at 600 K is also shown in Fig. 6. It is clear from these results that the concentration of H strongly influences the overall diffusion coefficient. Our observations are consistent with a variety of previous experiments and phenomenological theories22–24 in that the diffusivity increases markedly as the H concentration increases. At 600 K, our calculations indicate that the diffusion coefficient increases by roughly three orders of magnitude as the interstitial H concentration is increased from H/M = 0 to 0.2. The physical origin of this behavior is not difficult to understand. At dilute concentrations, H atoms are essentially always found in the sites associated with the strongest binding energies, so long-range diffusion is dominated by the large barriers that exist to moving H atoms away from these sites. At higher concentrations, however, the most favorable sites are populated by some fraction of the population of H atoms, allowing the remaining H atoms to occupy and hop among less favored sites. The latter population moves far more rapidly than atoms trapped in the most favored sites, so they dominate the overall diffusion coefficient. At sufficiently high concentrations this effect is countered by site blocking effects that make it difficult for individual atoms to move through the material. The influence of these effects is evident in the highest concentrations examined in Fig. 6.
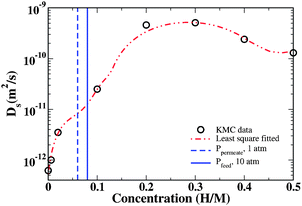 | ||
| Fig. 6 The diffusion coefficient as a function of H concentration in a-Fe3B at 600 K. | ||
3.3 H permeation through Fe3B membranes
Having made quantitative predictions for the solubility and diffusivity of interstitial H in two Fe3B materials, we can now examine the issue that would be relevant to using these materials as membranes for hydrogen purification, predicting the permeation of H through these materials. We will examine the situation where net transport across a membrane is dominated by diffusion through the membrane. The flux through a membrane of this kind is52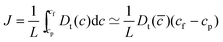 | (4) |
![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) = (cf − cp)/2. For the purposes of comparing with well characterized membrane materials such as crystalline Pd, we report our results below in terms of membrane permeability,10,25k = JL/(√Pf−√Pp), where Pf and Pp are the H2 pressures on the feed and permeate sides of the membrane, respectively. Previous comparisons of DFT-based predictions for membrane permeance with pure Pd have been found to provide predictions that lie within a factor of two of experimental observations over a wide range of temperatures;25 this level of agreement is within the range of uncertainties in permeability deduced from comparing multiple experimental studies.
= (cf − cp)/2. For the purposes of comparing with well characterized membrane materials such as crystalline Pd, we report our results below in terms of membrane permeability,10,25k = JL/(√Pf−√Pp), where Pf and Pp are the H2 pressures on the feed and permeate sides of the membrane, respectively. Previous comparisons of DFT-based predictions for membrane permeance with pure Pd have been found to provide predictions that lie within a factor of two of experimental observations over a wide range of temperatures;25 this level of agreement is within the range of uncertainties in permeability deduced from comparing multiple experimental studies.
It is important to note that the tracer diffusivity that we calculated with our KMC simulations, Ds and the Fickian diffusion coefficient, Dt, are only equal for dilute H concentrations.53–56 In general, however, Dt(c) ≥ Ds(c). This observation means that if we use Ds to approximate the diffusion coefficient on the right hand side of eqn (4), the resulting flux is a lower bound to the actual membrane flux. All results shown below were calculated using this approximation. For the amorphous material, the value of the diffusion coefficient for each case we considered was established by fitting a continuous curve to our KMC-calculated diffusivities as shown in Fig. 6.
Our predicted permeabilities for crystalline and amorphous Fe3B are shown in Fig. 7 for membranes with a feed pressure of 10 atm and a permeate pressure of 1 atm. These conditions are highlighted with vertical lines in Fig. 6. The permeability for crystalline Pd derived from DFT-based calculations25 is also shown. It should not be surprising after examining the solubility and diffusivity of the amorphous and crystalline materials that the permeability of H through the amorphous material is very different from the crystalline phase. Under the conditions shown in Fig. 7, the permeability of the amorphous material is 1.5–2 orders of magnitude larger than crystalline Fe3B.
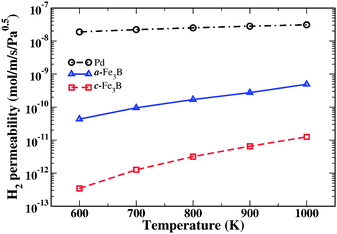 | ||
| Fig. 7 The calculated permeability of H2 in a-Fe3B and c-Fe3B at different temperatures. For comparison, the permeability of pure Pd is also shown. | ||
Because this is the first example that has ever been presented where a quantitative prediction for the performance of an amorphous metal as a hydrogen purification membrane, we reiterate that we did not select Fe3B because we anticipated it would have excellent properties as a membrane. Fig. 7 indicates that the amorphous material would have poor properties as a membrane in practical applications because its permeability is far lower than crystalline Pd.
4 Discussion and outlook
Dense metal membranes are in many ways ideal for purifying hydrogen in applications where energy efficiency in the separation process and purity in the product are important. Amorphous metal films have considerable potential to avoid some of the limitations inherent to using crystalline metals as membranes. Advances in the development of amorphous membranes are limited by the small number of alloy compositions that have been tested experimentally. We have developed a new approach to describe H solubility and diffusion in amorphous metals using quantum chemical DFT calculations that makes it possible to quantitatively predict the performance of amorphous metal films as hydrogen purification membranes. Prior to this work, no methods existed that were suitable for this task. Our methods create interesting opportunities to accelerate experimental efforts to develop effective membranes based on amorphous films.To conclude, we revisit the five principles we introduced in section 2 that affect the impact of theoretical methods on materials screening for practical applications. Although the quantum chemical methods we have used require significant computational resources, the time scale for examining multiple materials with our methods is almost certainly shorter than the time required for thorough experimental testing of the same number of materials (principle (i)). Our methods require no input at all from experimental data (principle (ii)), although it would be wise to concentrate attention on alloys that are known experimentally to be good glass-formers. Our calculations make explicit predictions for the net permeability of hydrogen through amorphous films—this is the main performance metric used experimentally in comparing different membrane materials (principle (iii)). Although we do not know of experimental data to which we can compare our predictions for the amorphous Fe-B material we have considered here, the DFT-based methods we have used are known to give quantitatively accurate information for a wide range of properties associated with interstitial H in metals and metal alloys. It is therefore reasonable to expect that our calculations have sufficient quantitative accuracy to distinguish between promising materials, that is, membranes with high permeability for H, and less promising materials (principle (iv)).
To satisfy the fifth of our principles, we need to discuss the limitations and approximations within our theoretical predictions. The most important among these are:
(i) Our results make no predictions about the performance of a membrane in the presence of chemical contaminants in the feed stream. This issue can be crucial in real applications, although the nature and level of contaminants may depend strongly on the details of the application.
(ii) At sufficiently high temperatures, amorphous metals recrystallize into crystalline alloys. This phenomenon would have disastrous consequences for any membrane whose operation depends on the film being in an amorphous state. Our methods make no predictions about the temperatures at which recrystallization would become problematic. Although many amorphous metals are known that are stable up to temperatures as high as 500 °C,9 it is likely that the specific amorphous material we have considered here is not stable against recrystallization at the highest temperatures for which we reported permeabilities in Fig. 7.
(iii) Our calculations were performed for materials by assuming the volume of the amorphous material was not substantially increased by interstitial H. Direct calculations showed that this assumption is appropriate for H/M = 0.01, but under membrane operating conditions for which much higher concentrations of H are relevant, expansion of the membrane due to interstitial H may affect the overall permeation of H through a membrane.
(iv) Our calculations for the membrane permeability of the amorphous material used the tracer diffusivity rather than the Fickian diffusivity. As stated above, this approximation means that our results define a lower bound on the permeability defined by eqn (4). Well defined simulation methods exist for determining the Fickian diffusivity once particle trajectories are known from a dynamical simulation such as kinetic Monte Carlo,55,57,58 and we plan to use these methods in the future to remove this approximation from our calculations.
(v) Our results are appropriate only for membranes where diffusion through the bulk material is the rate-limiting step. In experimental studies of amorphous films, a thin layer of a catalytically active material such as pure Pd is often used to enhance H2 dissociation rates on the membrane's surface.9,11 When this is the case, the situations in which the performance of a membrane deviates from being diffusion dominated are likely to be similar to those for crystalline membranes where this issue has been carefully characterized.29,32
Acknowledgements
This work was supported by the U.S. Department of Energy through the National Energy Technology Laboratory under grant No. 41817M2044.References
- A. Newcomer and J. Apt, Environ. Sci. Technol., 2007, 41, 7974 CrossRef CAS
.
- E. S. Rubin, C. Chen and A. B. Rao, Energy Policy, 2007, 35, 4444 CrossRef
.
-
V. Smil, Energy at the Crossroads: Global Perspectives and Uncertainties, MIT Press, Cambridge, MA, USA, 2005 Search PubMed
.
- L. Schlapbach and A. Züttel, Nature, 2001, 414, 353 CrossRef
.
- J. P. Trembly, R. S. Gemmen and D. J. Bayless, J. Power Sources, 2007, 169, 347 CrossRef CAS
.
- M. Amelio, M. P. Morrone, P. F. Galucci and A. Basile, Energy Conversion Manage., 2007, 48, 2680 Search PubMed
.
- M. J. Prins, K. J. Ptasinski and F. J. J. G. Janssen, Energy, 2007, 32, 1248 CrossRef CAS
.
-
J. M. S. Henis, Commercial and Practical Aspects of Gas Separation Membranes, CRC Press, Boca Raton, FL, USA, 1994 Search PubMed
.
- N. W. Ockwig and T. M. Nenoff, Chem. Rev., 2007, 107, 4078 CrossRef CAS
.
- S. N. Paglieri and J. D. Way, Sep. Purif. Methods, 2002, 31, 1 CrossRef CAS
.
- M. D. Dolan, N. C. Dave, A. Y. Ilyushechkin, L. D. Morpeth and K. G. McLennan, J. Membr. Sci., 2006, 285, 30 CrossRef CAS
.
- J. W. Phair and R. Donelson, Ind. Eng. Chem. Res., 2006, 45, 5637
.
- D. S. Sholl and Y. H. Ma, MRS Bull., 2006, 31, 770 CAS
.
- S. Adhikari and S. Fernando, Ind. Eng. Chem. Res., 2006, 45, 875 CrossRef CAS
.
- S. Hara, K. Sakaki, N. Itoh, H. M. Kimura, K. Asami and A. Inoue, J. Membr. Sci., 2000, 164, 289 CrossRef CAS
.
- S. Hara, N. Hatakeyama, N. Itoh, H. M. Kimura and A. Inoue, J. Membr. Sci., 2003, 211, 149 CrossRef CAS
.
- S. I. Yamaura, Y. Shimpo, H. Okouchi, M. Nishida, O. Kajita and A. Inoue, Mater. Trans., 2004, 45, 330 CrossRef CAS
.
- Y. Shimpo, S. Yamaura, H. Okouchi, M. Nishida, O. Kajita, H. Kimura and A. Inoue, J. Alloys Compd., 2004, 372, 197 CrossRef CAS
.
- A. Inoue, Acta Mater., 2000, 48, 279 CrossRef CAS
.
- W. H. Wang, C. Dong and C. H. Shek, Mater. Sci. Eng., 2004, R44, 45 CAS
.
- H. A. Davies, Phys. Chem. Glasses, 1976, 17, 159 CAS
.
- R. Kirchheim, Prog. Mater. Sci., 1988, 32, 261 CrossRef CAS
.
- R. Kirchheim, Phys. Scripta, 2001, 94, 58 Search PubMed
.
- N. Eliaz and D. Eliezer, Adv. Perform. Mater., 1999, 6, 5 CrossRef CAS
.
- P. Kamakoti, B. D. Morreale, M. V. Ciocci, B. H. Howard, R. P. Killmeyer, A. V. Cugini and D. S. Sholl, Science, 2005, 307, 569 CrossRef CAS
.
- P. Kamakoti and D. S. Sholl, J. Membr. Sci., 2003, 225, 145 CrossRef CAS
.
- P. Kamakoti and D. S. Sholl, Phys. Rev. B, 2005, 71 Search PubMed
014301.
- P. Kamakoti and D. S. Sholl, J. Membr. Sci., 2006, 279, 94 CrossRef CAS
.
- C. Ling and D. S. Sholl, J. Membr. Sci., 2007, 303, 162 CrossRef CAS
.
- B. D. Morreale, B. H. Howard, O. Iyoha, R. M. Enick, C. Ling and D. S. Sholl, Ind. Eng. Chem. Res., 2007, 46, 6313 CrossRef CAS
.
- L. Semidey-Flecha and D. S. Sholl, J. Chem. Phys., 2008, 128, 144701 CrossRef
.
- T. L. Ward and T. Dao, J. Membr. Sci., 1999, 153, 211 CrossRef CAS
.
- D. S. Sholl, J. Alloys Compd., 2007, 446, 462 CrossRef
.
- B. Bhatia, X. J. Luo, C. A. Sholl and D. S. Sholl, J. Phys.: Condens. Matter, 2004, 16, 8891 CrossRef CAS
.
- B. Bhatia and D. S. Sholl, Phys. Rev. B, 2005, 72, 224302 CrossRef
.
- D. E. Jiang and E. Carter, Phys. Rev. B, 2004, 70 Search PubMed
064102.
- S. V. Alapati, J. K. Johnson and D. S. Sholl, J. Phys. Chem. B, 2006, 110, 8769 CrossRef CAS
.
- S. V. Alapati, J. K. Johnson and D. S. Sholl, J. Phys. Chem. C, 2007, 111, 1584 CrossRef CAS
.
- A. R. Akbarzadeh, V. Ozolins and C. Wolverton, Adv. Mater., 2007, 19, 3233 CrossRef CAS
.
- B. P. Uberuaga, A. F. Voter, K. K. Sieber and D. S. Sholl, Phys. Rev. Lett., 2003, 91, 105901 CrossRef
.
- D. S. dos Santos and P. E. V. Miranda, J. Mater. Sci., 1997, 32, 6311 CrossRef CAS
.
- M. Mihalkovič and M. Widom, Phys. Rev. B, 2004, 70, 144107 CrossRef
.
- P. Ganesh and M. Widom, Phys. Rev. B, 2008, 77 Search PubMed
014205.
- G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15 CrossRef CAS
.
- S. Hao, M. Widom and D. S. Sholl, Phys. Rev. Lett., 2008 Search PubMed
, submitted.
- H. Wu, W. Zhou, T. J. Udovic and J. J. Rush, Chem. Mater., 2007, 19, 329 CrossRef CAS
.
- R. Kirchheim, T. M. Otschele, W. Kieninger, H. Gleiter, R. Birringer and T. D. Koble, Mater. Sci. Eng., 1988, 99, 457 CrossRef CAS
.
- J. J. Rush, J. M. Rowe and A. J. Maeland, J. Phys. F: Met. Phys., 1980, 10, L283 CrossRef CAS
.
- R. Lässer, Phys. Rev. B, 1984, 29, 4765 CrossRef
.
- D. G. Westlake, J. Less-Common Met., 1983, 91, 1 CrossRef CAS
.
- G. Henkelman, B. P. Uberuga and H. Jonsson, J. Chem. Phys., 2000, 113, 9901 CrossRef CAS
.
- D. S. Sholl, Ind. Eng. Chem. Res., 2000, 39, 3737 CrossRef CAS
.
- K. W. Kehr and O. Paetzold, Physica A, 1992, 190, 1 CrossRef
.
- K. W. Kehr and T. Wichmann, Mater. Sci. Forum, 1996, 223, 151 Search PubMed
.
- D. S. Sholl, Acc. Chem. Res., 2006, 39, 403 CrossRef
.
- F. J. Keil, R. Krishna and M. O. Coppens, Rev. Chem. Eng., 2000, 16, 71 Search PubMed
.
- A. I. Skoulidas and D. S. Sholl, J. Phys. Chem. B, 2001, 105, 3151 CAS
.
- A. I. Skoulidas and D. S. Sholl, J. Phys. Chem. B, 2005, 109, 15760 CrossRef CAS
.
| This journal is © The Royal Society of Chemistry 2008 |
