Systems chemistry
R. Frederick
Ludlow
and
Sijbren
Otto
*
Department of Chemistry, University of Cambridge, Lensfield Road, Cambridge, UK CB2 1EW. E-mail: so230@cam.ac.uk; Fax: +44 (0)1223 336017; Tel: +44 (0)1223 336509
First published on 3rd September 2007
Abstract
The study of complex mixtures of interacting synthetic molecules has historically not received much attention from chemists, even though research into complexity is well established in the neighbouring fields. However, with the huge recent interest in systems biology and the availability of modern analytical techniques this situation is likely to change. In this tutorial review we discuss some of the incentives for developing systems chemistry and we highlight the pioneering work in which molecular networks are making a splash. A distinction is made between networks under thermodynamic and kinetic control. The former include dynamic combinatorial libraries while the latter involve pseudo-dynamic combinatorial libraries, oscillating reactions and networks of autocatalytic and replicating compounds. These studies provide fundamental insights into the organisational principles of molecular networks and how these give rise to emergent properties such as amplification and feedback loops, and may eventually shed light on the origin of life. The knowledge obtained from the study of molecular networks should ultimately enable us to engineer new systems with properties and functions unlike any conventional materials.
 R. Frederick Ludlow | Fred Ludlow was born in England in 1982. He received his MChem from the University of Oxford in 2004, spending the final year of the course working with Paul Beer on anion templated rotaxanes. He is currently a third year PhD student at the University of Cambridge working in the field of supramolecular chemistry in Sijbren Otto's group. His research interests include molecular recognition in aqueous solution and the use of dynamic combinatorial chemistry to extract information about host–guest systems. |
 Sijbren Otto | Sijbren Otto received his MSc (1994) and PhD (1998) degrees cum laude from the University of Groningen in the Netherlands, where he worked on physical organic chemistry in aqueous solutions in the group of Jan Engberts. In 1998, he moved to the United States for a year as a postdoctoral researcher with Steve Regen (Lehigh University, Bethlehem, Pennsylvania) investigating synthetic systems mediating ion transport through lipid bilayers. In 1999, he received a Marie Curie Fellowship and moved to the University of Cambridge where he worked for two years with Jeremy Sanders on dynamic combinatorial chemistry. He started his independent research career in 2001 as a Royal Society University Research Fellow at the same university. His current research interests involve molecular recognition at biomembranes and dynamic combinatorial/systems chemistry in water. |
Introduction
Complex systems are all around us. Think of stock markets, distribution networks, the world wide web, metabolic pathways, ecosystems, and even scientific co-authorship networks. Research into complex networks1,2 is well established in most major scientific disciplines including engineering, economics, computer science, biology, mathematics and physics, but not in chemistry. Most chemists have been conditioned to study substances in isolation and have a tendency to dislike mixtures of molecules. There used to be a very good reason for this: for a long time complex mixtures were simply intractable. Yet, with the recent rapid development of analytical tools this situation has changed and the study of complex mixtures has already resulted in some useful applications. For example, protein sequencing is now routinely performed through the analysis of the diverse product mixtures resulting from enzymatic digests and combinatorial chemistry has become an established tool in drug discovery.†We believe that the time has come for chemists to firmly embrace complexity and we make a case for systems chemistry3 as a new discipline that looks at complex mixtures of interacting molecules. Complex mixtures can give rise to interesting and desirable emergent properties—properties that result from the interactions between components and cannot be attributed to any of these components acting in isolation. Complementary to this, a complex mixture contains information about all its constituents and the study of the complete mixture should in principle allow us to obtain properties of interest of all these molecules simultaneously, provided we can find a way of deconvoluting the results of such investigations. Furthermore, there is considerable interest in uncovering the organisational principles behind complex networks in order to understand their workings and eventually be able to modify and engineer networks.
We will discuss some selected examples of pioneering experimental work on systems chemistry covering a wide range of subjects, including dynamic combinatorial libraries, oscillating reactions, replicating networks and self-assembling systems. First though, we provide a concise summary of the state of the art in systems biology, which is a field to which systems chemistry is intimately related and which currently struggles with issues that may perhaps be more conveniently addressed by a more chemical approach.
The term systems chemistry is potentially very broad. For example, the fields of heterogeneous catalysis as well as atmospheric and environmental chemistry deal with large systems of interacting chemical species. We will restrict this review to cover work on synthetic systems in solution, and apologise to anyone whose favourite subject is glossed over or ignored altogether. Nevertheless, we hope our paper will spark interest in what is, for many chemists, an unconventional subject.
A brief overview of systems biology
Biology is immensely complex at almost every level: for a start, there is the network of atomic interactions that determine the conformation or folding of biomacromolecules such as proteins. Superimposed on this, there is the organisation of biomolecules into cells, which, in turn, can be organised to give higher organisms. Finally, a network of interactions exists between the numerous different organisms and their surroundings, which defines the field of ecology. Systems biology4,5 deals with the second of these levels of complexity by addressing how the function of a biological system (a cell or a specific cellular process) is related to the interactions between the various molecular components. Study of the subject has become possible with the coming on stream of high throughput data acquisition methods (DNA sequencers, microarray analysis and mass spectrometry) that have resulted in the emergence of genomics, proteomics and metabolomics. The vast amounts of data produced by these disciplines boosted the development of bioinformatics (including visualisation tools) in an attempt to make sense of it all. However, how to get from data to understanding is still very much an unmet challenge. Problems that have sprung up include the not always reliable quality of very large data sets, the fact that the nature of the interactions between the various components in the system is often poorly characterised and that the effects of the interactions are mostly not quantified. This lack of quantitative information makes the computational modelling of biological systems very difficult. Notwithstanding, the first attempts at creating “silicon cells” are being made.6While the ultimate aim of systems biology is being able to predict, repair, control and eventually design a biological system, most of the current work is more down to earth and focussed on improving the understanding at systems level. At present, the main challenges are to drill down from the global picture of a network to identify the basic network motifs7 and to determine the way these are interlinked.8,9 Possible approaches include tinkering with existing networks to identify some of the organisational principles or even engineering new functional networks in living organisms.10 However, biological organisms are relatively fragile: too much tinkering will result in death, limiting the use of this top-down approach. This calls for an alternative bottom-up approach; an area where systems chemistry may provide new fundamental insights.
Systems chemistry3,11,12
Contrary to the reductionist approach that inspires most research in chemistry, systems chemistry is about the study of multiple variables simultaneously. Research in this area is in its infancy and still fragmented. A number of nuclei of interest can be identified, which will be discussed in more detail below. The last decade has seen an increased interest in the study of mixtures of molecules that are connected through exchange of components under thermodynamic control, most notably in the area of dynamic combinatorial chemistry. Also kinetically controlled chemical systems have gained popularity. Driven by the mystery of the origin of life, considerable efforts are being made in developing self-replicating systems. In addition, sparked by the serendipitous discovery of oscillating reactions, a vibrant community has sprung up investigating the intriguing behaviour of such systems. Recently, relatively simple chemical systems have appeared that successfully model much more elaborate biological networks. Finally, self-assembly can be considered as a means to construct complex chemical systems.Dynamic combinatorial libraries: molecular networks under thermodynamic control
In dynamic combinatorial chemistry,13 a dynamic combinatorial library (DCL) of oligomers is generated from a set of building blocks. The bond formation between these building blocks is reversible, allowing exchange of blocks between oligomers and the establishment of a network of interconverting compounds. Under thermodynamic control, the library distribution depends on the relative free energies of each oligomer, so anything which can alter these free energies will affect the distribution of the material in the network.This behaviour has been successfully exploited for the discovery of new compounds that are good at molecular recognition (synthetic receptors for small molecule guests, or ligands for biomacromolecules). If a template molecule is added to a DCL, those oligomers which can form favourable interactions with it are stabilised, and so the equilibrium shifts to favour those library members which bind the template. Under the right experimental conditions, the strongly binding oligomers are amplified at the expense of the weaker binders.
The development of this field has been driven by the need for improved methods for developing synthetic receptors and ligands for biomolecules. The approach hinges on the intuitive hypothesis that there should be a correlation between binding affinity and amplification. However, subsequent theoretical work revealed that dynamic libraries can show some not immediately intuitive deviations from this behaviour, reflecting the fact that the product distributions in DCLs are dictated by the interplay of binding equilibria and mass balance equations involving all the species in the network. Theoretical and experimental studies by Severin et al. revealed two situations where the correlation between host–guest binding affinity and amplification can break down, or even reverse.14,15
For the first case, consider a library containing a single building block, A, which can form a dimer or trimer. We shall assume that both dimer and trimer bind to the template, T, with the trimer having a higher affinity. At low relative template concentration, the trimer will be amplified as expected, but if the template concentration is high, this will not necessarily be the case. As shown in Fig. 1a, forming two trimer–guest complexes requires the disruption of three dimer–guest complexes, so the trimer must be a significantly stronger binder for it to be amplified. If the dimer is only slightly weaker, it may still be preferentially amplified.
 | ||
| Fig. 1 Equilibria representing the competition between oligomers in a DCL. | ||
The second case involves competition between homo-oligomers and hetero-oligomers. Consider a library containing three building blocks, A, B and C, which form all possible trimers. The A3homotrimer and ABC heterotrimer can both bind to a template, T, which is present in excess. In this case, the relevant equilibrium is that shown in Fig. 1b: in order for one A3·T complex to form, three ABC·T complexes must be disrupted. Therefore the homotrimer, A3, must have a much higher affinity for the template than ABC in order for the amplification to reflect their relative association constants.
These examples serve to highlight the danger of thinking in terms of individual molecules, when it is the free energy of the entire system that is important. In both cases, the problem arises because many weak host–guest complexes need to be disrupted to form one strong host–guest complex. One way to negate this is to lower the template concentration so that fewer of the weak host–guest complexes form in the first place.
These principles apply not only to the relatively simple systems of Fig. 1 but also to much larger DCLs. Fig. 2 shows two examples of the correlation between binding affinity and amplification in a simulated 322-component library at two different concentrations of template.16
![The relationship between amplification (AF; the ratio between the concentration of a library member in the presence of a template compared to that in the absence of the template) and free energy of binding for all binders in two simulated DCLs that differ only in the concentration of the template T: (a) [T] = 10 mM; (b) [T] = 1 mM.](/image/article/2008/CS/b611921m/b611921m-f2.gif) | ||
| Fig. 2 The relationship between amplification (AF; the ratio between the concentration of a library member in the presence of a template compared to that in the absence of the template) and free energy of binding for all binders in two simulated DCLs that differ only in the concentration of the template T: (a) [T] = 10 mM; (b) [T] = 1 mM. | ||
Another solution is to ensure there is a reservoir of building blocks, only a fraction of which can exist in active oligomers. Severin et al. have reported a library with an unusual network topology that achieves this.17 The library is based on metal–ligand exchange, with two different self-sorting ligands. One ligand forms active receptors, while the other forms a library of non-receptor complexes which acts as a metal ion reservoir. A better correlation is observed between binding constant and amplification factor than for the system containing only the active ligand.
As we have seen, a DCL is a complicated and sometimes non-intuitive system. However, it is not as complex as systems such as stock markets, fluid flows or cellular automata, because the final state is not dependent on the history of the system. For a given set of building block and template concentrations, the same equilibrium will be reached whatever the starting point, and this equilibrium point can be exactly calculated from quantitative knowledge of all the individual interactions within the system. It is this relative simplicity which allows us to be confident that, given careful experiment design, the amplified species in a templated library is likely to be a strong binder. In most instances, studying the behaviour of the library does not give us any information that we could not have obtained by studying its parts in isolation; however, a DCL is an efficient short cut to this information. Two examples will be discussed which demonstrate the wealth of information present in a DCL and how it can be accessed using only relatively simple analytical techniques.
Recently, we have shown that quantitative information about library members' affinities for a guest can be determined directly from the library distribution.18 This enables host–guest interactions to be quantified without the need for isolation and purification of individual library members. To demonstrate the potential of this method, we simulated the composition of a 31-component DCL based on fixed host–guest binding constants at a number of different template concentrations to serve as an “experimental” data set. The library distribution was modelled computationally at each template concentration using a set of trial values for the template-binding affinities of each oligomer and the error between simulated and “experimental” concentrations was determined. The trial values were then varied so as to minimize the error using a standard algorithm. Good fits could be obtained for the majority of the compounds in the mixture, with a particularly good agreement for the more strongly binding oligomers (Fig. 3).
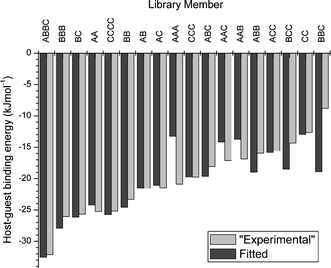 | ||
| Fig. 3 Comparison of the “experimental” and fitted values of the host–guest binding energies in a simulated 31-component dynamic combinatorial library. | ||
We have also tested the method on a truly experimental system and obtained good agreement between fitted binding constants and those obtained by microcalorimetry.
The majority of work on DCLs has focused on methods for the identification and characterisation of good binders, either to form one part of a host–guest system or as catalysts.13 Severin and co-workers have described a different application of DCLs in which the library's guest-induced adaptation is used to determine the identity of an unknown guest. Any molecule that interacts with a DCL will cause a perturbation to its composition that is characteristic of the particular molecule. Thus, it should be possible to work backwards from the adaptation of a library to the identity of the guest. As a proof of principle study, a DCL based on two metal ions and three coordinating dye compounds (Fig. 4) was used.19
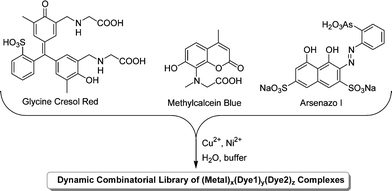 | ||
| Fig. 4 Generation of a DCL of metal–dye complexes by mixing three dyes with CuCl2 and NiCl2 in buffered aqueous solution. | ||
Addition of a dipeptide guest caused the library to re-equilibrate, resulting in a change to the UV/vis spectrum. Initially, DCLs were prepared with one of the six dipeptides, Val–Phe, Gly–Ala, His–Ala, Ala–His, Phe–Pro and Pro–Gly, as guests. The UV/vis spectra of these solutions confirmed that this method could distinguish between the six dipeptides. To test the sensitivity of this method, a further experiment was carried out using the five structurally similar dipeptides, Gly–Ala, Val–Phe, Ala–Phe, Phe–Ala and D-Phe–Ala. In this case, the differences between the UV/vis spectra of the libraries were much smaller, and so linear discriminant analysis (LDA)20 was used to classify the compounds. Fifteen spectra were recorded for each peptide, at slightly varying peptide concentration. Eight wavelengths were then selected from the spectra, and the absorption at these wavelengths formed the input.
Using the entire data set as a training set generated Fig 5. A clear separation can be seen between the different peptides. In another experiment, 50% of the observations were randomly selected and used as the training set, 97% of the remaining observations were correctly classified. This is particularly impressive given the similarity of the peptides.
 | ||
| Fig. 5 Linear discriminant analysis score plot showing clear separation of a series of closely related dipeptide analytes. | ||
In a separate study, a sensor was developed for distinguishing Gly–Gly–His from either His–Gly–Gly or from Gly–His–Gly.21 The experimental simplicity of the system allowed a large number of libraries to be set up and compared for their ability to distinguish between isomers. Using this approach, optimised DCL sensors were discovered for a variety of sensing applications in addition to sequence differentiation, including concentration quantification and identifying the proportions of components in a mixture.
Molecular networks under kinetic control
While thermodynamically controlled molecular networks are probably easier to study and understand, kinetically controlled networks have greater relevance to biology. Most biological systems operate far from equilibrium and even though they may sometimes appear to be stable, this usually results from a balance between two or more processes that are kinetically controlled. In the words of Pross: life can be thought of as ‘a kinetic state of matter’.22 Below we show some selected examples of kinetically controlled molecular networks, starting with a kinetically controlled equivalent of dynamic combinatorial chemistry, followed by a series of examples that feature autocatalytic or cross-catalytic networks.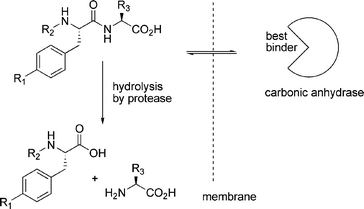 | ||
| Fig. 6 Carbonic anhydrase selectively protects those library members that bind to it from being hydrolysed. | ||
In a further publication, Gleason and Kazlauskas et al. described a pseudo-dynamic combinatorial library (pDCL).24 Again, the system contained separated screening and hydrolysis chambers, but this time a synthesis chamber was added in which the peptides could be regenerated by reaction of the amine hydrolysis product with solid-supported active esters (Fig. 7). Four different activated esters 2a–2d were combined with two amines to produce eight potential CA inhibitors. The concentration of these peptides was monitored over a number of days with periodic addition of fresh activated ester. Again a large amplification in the selectivity was observed—the final concentration ratio of the two best inhibitors was greater than 100 ∶ 1, despite an affinity ratio of only 2.2 ∶ 1.
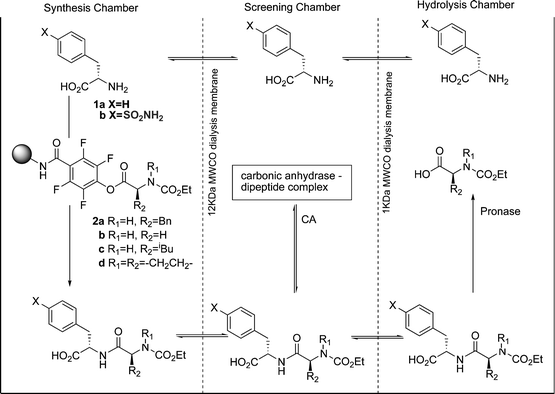 | ||
| Fig. 7 The experimental setup of the pseudo-dynamic combinatorial library developed by Gleason and Kazlauskas et al. | ||
This pDCL bears an intriguing resemblance to the model for pre-biotic peptide synthesis and degradation proposed by Wächtershäuser and co-workers.25 Under conditions similar to those found around volcanic vents (CO and colloidal transition-metal sulfides), peptide synthesis and degradation were found to occur simultaneously. The authors speculate that the resulting dynamic chemical libraries may well become self-selecting if the constituents are differentially stabilised by binding as ligands to the transition-metal centres that are involved in their production. This may give rise to positive feedback loops that could well have played a role in the emergence of life.
Self-replicators have been developed by a number of groups, based on a variety of chemistries, including RNA, peptides and purely synthetic compounds.28,29 Work carried out by Ghadiri and co-workers in the late 1990s on self-replicating peptides provided two examples of how complex behaviour such as symbiotic cooperation30 and dynamic error correction31 can emerge from networks of interacting self-replicators.
More recently, von Kiedrowski et al. reported on a system first described by Wang and Sutherland32 for which they established the presence of several simultaneous autocatalytic and cross-catalytic pathways,33 while Philp and Kassianidis have described a reciprocal replicating system in which two molecules catalyse the other's formation but not their own.34
Larger systems have also been studied; Ghadiri and co-workers have reported the behaviour of a network arising from a series of nine self-replicating, coiled-coil forming peptides.35 The basic reaction underpinning this system is shown in Fig. 8 The reaction between an electrophilic (E) and a nucleophilic (N) peptide fragment can be accelerated by a full-length template peptide (T) via the quaternary complex [ENTT]. The efficiency of this templated reaction depends on the stability of the quaternary complex, which can be estimated from the structure of the peptides. This allowed Ghadiri to construct a graph of the reactions in which the nodes represent the templates and the edges the predicted catalytic pathways (Fig. 9).
![Schematic mechanism of templated peptide formationvia the quarternary coiled-coil complex [Ej·N·Ti·Ti].](/image/article/2008/CS/b611921m/b611921m-f8.gif) | ||
| Fig. 8 Schematic mechanism of templated peptide formationvia the quarternary coiled-coil complex [Ej·N·Ti·Ti]. | ||
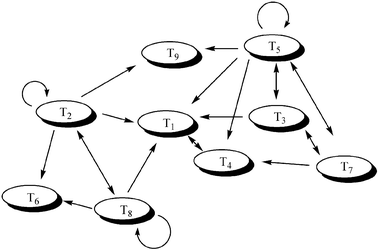 | ||
| Fig. 9 The predicted network of auto and cross-catalytic reactions in Ghadiri's peptide replicator system. | ||
When a subsection of this graph containing nine peptides was selected and investigated experimentally, some of the predicted reactions were not observed. They went on to demonstrate that all the “missing” pathways were indeed active when studied in isolation, but were suppressed in the larger system due to competition with more favourable reactions. This system is simple by biological standards, containing only 10 reactants and 9 products, yet it is still capable of complex dynamic behaviour, arising from the interaction of several sub-systems. The peptide networks can be exploited in the design of molecular Boolean logic gates.36 By varying the input concentrations (templates and fragments), and monitoring the formation of a particular product, various subsections of the network could be shown to express OR, NOR and NOTIF logic, which constitute basic elements of molecular computing.
One of the advantages of molecular computing is the potential for parallelisation, particularly when applied to large combinatorial search problems. For example, DNA computers have been used to solve the travelling salesman problem,37 a task that involves generating and testing many candidate solutions in order to determine the optimum. Whilst an electronic computer must work through these sequentially, the enormous number of molecules in a DNA computer allows many solutions to be searched simultaneously. Work on these systems is described in more detail in a recent review by Ezziane.38
 | ||
| Fig. 10 Turing patterns (a–c) from simulations of cellular behaviour arising through coupling of an intracellular autocatalytic reaction to differential trans-membrane signal transduction rates of activator and inhibitor messengers. (d) Emergence of pattern a over time from a homogeneous starting state. Reproduced with permission of J. Theor. Biol.40 | ||
The most well-known oscillating process is the Belousov–Zhabotinsky reaction, discovered by Belousov in 1950, who experienced great difficulty in getting his results published. In fact, only after Zhabotinsky got involved a decade later did the first reports of this reaction appear in the Russian literature. It took another decade before the oscillatory behaviour was understood mechanistically41,42 and another before oscillating reactions could be systematically designed.43 For the Belousov–Zhabotinsky reaction, the oscillations result from the complex interplay between 18 different transformations, many of which feature the same species as reactants or products. The overall reaction is the Ce(IV) catalysed oxidation of citric acid by BrO3– to give bromide, CO2 and water. A key feature in the mechanism of this and many other oscillators is the autocatalytic production of an intermediate, in this case HBrO2. For the complete mechanism, the reader is referred to ref. 42.
In order to sustain oscillations, a continuous conversion of starting material into product must occur, requiring an open system into which starting material is fed and from which the product is removed. This is the situation in flow reactors and oscillating behaviour is now well recognised by chemical engineers.
For more detail on the subject of oscillating reactions and pattern formation the reader is referred to three excellent recent reviews.39,44,45
| S2O32– + 2ClO2– + 3H2O → 2SO42– + 2H3O+ + 2Cl– |
At the same time H3O+ is consumed through:
| 4S2O32– + ClO2– + 4H3O+ → 2S4O62– + 6H2O + Cl– |
A series of elegant experiments were carried out with this system, including one in which a microfluidic device was used, which mimics the human circulatory system in which large inlet (artery) and outlet (vein) channels connect a set of smaller capillaries. When one of the capillaries was punctured, gelation (clotting) occurred and propagated within the damaged capillary without affecting any of the other channels. What triggered this spontaneous initiation is not fully understood. Intriguingly, the authors found that the extent to which gelation propagated through the system was dependent on the nature of the connection between the capillaries' inlet and outlet channels. While no propagation took place when the connections mimicked those found in nature, other connections were found to give catastrophic propagation of clotting into ‘veins’ and ‘arteries’. In a later study, the authors found a good correspondence between the spatiotemporal dynamics of clotting initiation between their chemical model system and experiments with human blood plasma.47
Self-assembling systems
The organisation and function of a system is governed by the interactions between its components. At the simplest level, noncovalent interactions between molecules can lead to the emergence of larger structures resulting from self-assembly processes. An extensive body of literature exists describing how the structure of the resulting aggregates depends on the nature of the constituent molecules. Recently reports have started to appear aiming at creating functional assemblies. For example, Luisi and Szostak have investigated the replication of vesicles which can be considered as models for primitive cell growth and division.48 For example, it was found that vesicles made from oleate containing RNA were able to grow at the expense of similar vesicles devoid of RNA. The driving force is provided by the difference in osmotic stress induced by the presence of a charged nucleic acid polymer inside one of the vesicle populations. This suggests that protocells in which RNA replication takes place would recruit lipid material from less prolific counterparts which comes close to Darwinian selection.49 In another example, Luisi and co-workers have reported a chemical model for homeostasis, maintaining a steady state through two reactions in a flow system: one which produces a vesicle forming surfactant (oleate) through the hydrolysis of its anhydride while an oxidation reaction hydroxylates the oleate to a non-vesicle forming compound.50 Depending on the rates of the two reactions, a stable but dynamic state can be maintained or vesicle growth or death can be induced.More elaborate control over a chemical network can be exerted through establishing interactions between molecules (in network terminology: through creating the vertices between nodes). The selectivity of these interactions is important if vertices need to be created between specific nodes only. Isaacs and co-workers have addressed this issue by mixing a series of molecules well known to recognise themselves or pair up with a complementary partner. The authors observed a strong preference for thermodynamically controlled self-sorting; i.e. the various interacting pairs formed the expected complexes, essentially ignoring the other molecules present in the solution.51 In a more recent paper, Isaacs et al. investigated self-sorting in a small 4-component system containing two cucurbituril hosts and two guests, each with multiple binding sites. Different host–guest pairings were observed under kinetic and under thermodynamic control.52
Conclusions and outlook
Research into networks of interacting molecules is gaining popularity. The analytical capabilities are in place that will enable a rapid growth of the field, which should be further stimulated by the rapid expansion of research in systems biology. Looking ahead, a number of areas in which systems chemistry is likely to make an impact can be identified.Systems chemistry may contribute to developing an improved understanding of the organisational principles of biological networks and how these are related to function. Model systems that reflect the behaviour of the real biological network may be used to make predictions of their behaviour and may lead to the discovery of new ways of manipulating and controlling biological systems. It complements activities aimed at assembling unnatural systems from interchangeable biological elements taken from existing organisms.53
Unravelling the origin of life will, in all likelihood, involve a systems chemistry approach.27 The work on the development of replicators and self-assembling membranes can be seen as the first steps in this direction.
Molecular computing, particularly DNA computing, has the potential to out-perform silicon based computers for several combinatorial search problems. As well as these, calculations in chemico could be advantageous in the sense that it is not necessary to lay every circuit down on a device: computation may be performed in a self-regulating communicating solution of molecules.
One of the unique capabilities of chemists is their ability to design and create new molecules. Extending this creativity from isolated molecules to molecular networks is bound to give rise to many new molecular systems with unique and exciting properties.
References
- S. H. Strogatz, Nature, 2001, 410, 268 CrossRef CAS.
- R. Albert and A. L. Barabasi, Rev. Mod. Phys., 2002, 74, 47 CrossRef.
- This term was used by von Kiedrowski to describe the chemical origins of biological organisation. See: J. Stankiewicz and L. H. Eckardt, Angew. Chem., Int. Ed., 2006, 45, 342 Search PubMed.
- A. Aderem, Cell, 2005, 121, 511 CrossRef CAS.
- Special issue devoted to systems biology: Science, 2002, 295, 1661 Search PubMed.
- J. L. Snoep, F. Bruggeman, B. G. Olivier and H. V. Westerhoff, BioSystems, 2006, 83, 207 CrossRef CAS.
- S. S. Shen-Orr, R. Milo, S. Mangan and U. Alon, Nat. Genet., 2002, 31, 64 CrossRef CAS.
- E. Alm and A. P. Arkin, Curr. Opin. Struct. Biol., 2003, 13, 193 CrossRef CAS.
- D. Bray, Science, 2003, 301, 1864 CrossRef CAS.
- M. B. Elowitz and S. Leibler, Nature, 2000, 403, 335 CrossRef CAS.
- G. M. Whitesides and R. F. Ismagilov, Science, 1999, 284, 89 CrossRef CAS.
- D. Newth and J. Finnigan, Aust. J. Chem., 2006, 59, 841 CrossRef CAS.
- P. T. Corbett, J. Leclaire, L. Vial, K. R. West, J.-L. Wietor, J. K. M. Sanders and S. Otto, Chem. Rev., 2006, 106, 3652 CrossRef CAS.
- Z. Grote, R. Scopelliti and K. Severin, Angew. Chem., Int. Ed., 2003, 42, 3821 CrossRef.
- K. Severin, Chem.–Eur. J., 2004, 10, 2565 CrossRef CAS.
- P. T. Corbett, S. Otto and J. K. M. Sanders, Chem.–Eur. J., 2004, 10, 3139 CrossRef CAS.
- B. Saur, R. Scopelliti and K. Severin, Chem.–Eur. J., 2006, 12, 1058 CrossRef CAS.
- R. F. Ludlow, J. Liu, H.-X. Li, S. L. Roberts, J. K. M. Sanders and S. Otto, Angew. Chem., Int. Ed., 2007, 46, 5762 CrossRef CAS.
- A. Buryak and K. Severin, Angew. Chem., Int. Ed., 2005, 44, 7935 CrossRef CAS.
- Essentially, LDA generates one or more discriminant functions, which are linear combinations of the input variables (in this case wavelengths). New points can be classified by comparing the value this function generates for the new point to the values for known points in the training set. For a more detailed description see: P. C. Jurs, G. A. Bakken and H. E. McClelland, Chem. Rev., 2000, 100, 2649 Search PubMed and references therein.
- A. Buryak and K. Severin, J. Comb. Chem., 2006, 8, 540 CrossRef CAS.
- A. Pross, Pure Appl. Chem., 2005, 77, 1905 CrossRef CAS.
- J. D. Cheeseman, A. D. Corbett, R. Shu, J. Croteau, J. L. Gleason and R. J. Kazlauskas, J. Am. Chem. Soc., 2002, 124, 5692 CrossRef CAS.
- A. D. Corbett, J. D. Cheeseman, R. J. Kazlauskas and J. L. Gleason, Angew. Chem., Int. Ed., 2004, 43, 2432 CrossRef CAS.
- C. Huber, W. Eisenreich, S. Hecht and G. Wächtershäuser, Science, 2003, 301, 938 CrossRef CAS.
- D. H. Lee, K. Severin and M. R. Ghadiri, Curr. Opin. Chem. Biol., 1997, 1, 491 CrossRef CAS.
- S. A. Kauffman, The origins of order, Oxford University Press, Oxford, 1993 Search PubMed.
- A. Robertson, A. J. Sinclair and D. Philp, Chem. Soc. Rev., 2000, 29, 141 RSC.
- N. Paul and G. F. Joyce, Curr. Opin. Chem. Biol., 2004, 8, 634 CrossRef CAS.
- D. H. Lee, K. Severin, Y. Yokobayashi and M. R. Ghadiri, Nature, 1997, 390, 591 CrossRef CAS.
- K. Severin, D. H. Lee, J. A. Martinez, M. Vieth and M. R. Ghadiri, Angew. Chem., Int. Ed., 1998, 37, 126 CrossRef CAS.
- B. Wang and I. O. Sutherland, Chem. Commun., 1997, 1495 RSC.
- M. Kindermann, I. Stahl, M. Reimold, W. M. Pankau and G. von Kiedrowski, Angew. Chem., Int. Ed., 2005, 44, 6750 CrossRef CAS.
- E. Kassianidis and D. Philp, Chem. Commun., 2006, 4072 RSC.
- G. Ashkenasy, R. Jagasia, M. Yadav and M. R. Ghadiri, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 10872 CrossRef CAS.
- G. Ashkenasy and M. R. Ghadiri, J. Am. Chem. Soc., 2004, 126, 11140 CrossRef CAS.
- L. M. Adleman, Science, 1994, 266, 1021 CrossRef CAS.
- Z. Ezziane, Nanotechnology, 2006, 17, R27 CrossRef CAS.
- G. Biosa, S. Bastianoni and M. Rustici, Chem.–Eur. J., 2006, 12, 3430 CrossRef CAS.
- E. M. Rauch and M. M. Millonas, J. Theor. Biol., 2004, 226, 401 CrossRef CAS.
- R. M. Noyes, R. J. Field and E. Koros, J. Am. Chem. Soc., 1972, 94, 1394 CrossRef CAS.
- R. J. Field, R. M. Noyes and E. Koros, J. Am. Chem. Soc., 1972, 94, 8649 CrossRef CAS.
- P. De Kepper, I. R. Epstein and K. Kustin, J. Am. Chem. Soc., 1981, 103, 2133 CrossRef CAS.
- I. R. Epstein, J. A. Pojman and O. Steinbock, Chaos, 2006, 16, 037101 CrossRef.
- I. R. Epstein and K. Showalter, J. Phys. Chem., 1996, 100, 13132 CrossRef CAS.
- M. K. Runyon, B. L. Johnson-Kerner and R. F. Ismagilov, Angew. Chem., Int. Ed., 2004, 43, 1531 CrossRef CAS.
- C. J. Kastrup, M. K. Runyon, F. Shen and R. F. Ismagilov, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 15747 CrossRef CAS.
- M. M. Hanczyc and J. W. Szostak, Curr. Opin. Chem. Biol., 2004, 8, 660 CrossRef CAS.
- I. A. Chen, R. W. Roberts and J. W. Szostak, Science, 2004, 305, 1474 CrossRef CAS.
- H. H. Zepik, E. Blochliger and P. L. Luisi, Angew. Chem., Int. Ed., 2001, 40, 199 CrossRef CAS.
- P. Mukhopadhyay, A. X. Wu and L. Isaacs, J. Org. Chem., 2004, 69, 6157 CrossRef CAS.
- P. Mukhopadhyay, P. Y. Zavalij and L. Isaacs, J. Am. Chem. Soc., 2006, 128, 14093 CrossRef CAS.
- S. A. Benner and A. M. Sismour, Nat. Rev. Genet., 2005, 6, 533 CrossRef CAS.
Footnote |
| † While combinatorial chemistry has traditionally included making compound libraries as mixtures, there has been a shift towards high-throughput parallel screening of pure compounds because mixtures of molecules frequently showed ‘false positives’ i.e. activity that arises from a combination of different compounds and that disappears upon deconvolution. Although perhaps undesirable in a drug discovery process, such behaviour provides clear evidence of the added value of complex mixtures that remains largely unexplored. |
| This journal is © The Royal Society of Chemistry 2008 |
