Experimental and theoretical study of the microsolvation of sodium atoms in methanol clusters: differences and similarities to sodium–water and sodium–ammonia

Abstract

Methanol clusters are generated in a continuous He-seeded supersonic expansion and doped with sodium atoms in a pick-up cell. By this method, clusters of the type Na(CH₃OH)_n are formed and subsequently photoionized by applying a tunable dye-laser system. The microsolvation process of the Na 3s electron is studied by determining the ionization potentials (IPs) of these clusters size-selectively for n = 2–40. A decrease is found from n = 2 to 6 and a constant value of 3.19 ± 0.07 eV for n = 6–40. The experimentally-determined ionization potentials are compared with ionization potentials derived from quantum-chemical calculations, assuming limiting vertical and adiabatic processes. In the first case, energy differences are calculated between the neutral and the ionized cationic clusters of the same geometry. In the second case, the ionized clusters are used in their optimized relaxed geometry. These energy differences and relative stabilities of isomeric clusters vary significantly with the applied quantum-chemical method (B3LYP or MP2). The comparison with the experiment for n = 2–7 reveals strong variations of the ionization potential with the cluster structure indicating that structural diversity and non-vertical pathways give significant signal contributions at the threshold. Based on these findings, a possible explanation for the remarkable difference in IP evolutions of methanol or water and ammonia is presented: for methanol and water a rather localized surface or semi-internal Na 3s electron is excited to either high Rydberg or more localized states below the vertical ionization threshold. This excitation is followed by a local structural relaxation that couples to an autoionization process. For small clusters with n < 6 for methanol and n < 4 for water the addition of solvent molecules leads to larger solvent–metal-ion interaction energies, which consequently lead to lower ionization thresholds. For n = 6 (methanol) and n = 4 (water) this effect comes to a halt, which may be connected with the completion of the first cationic solvation shell limiting the release of local relaxation energy. For Na(NH₃)_n, a largely delocalized and internal electron is excited to autoionizing electronic states, a process that is no longer local and consequently may depend on cluster size up to very large n.

---

Introduction

Solvation is a universal phenomenon playing a crucial role in a wide range of chemical and biochemical processes. It is closely connected to the energetics, structure, and dynamics of weakly-bound clusters.¹ If size-selective detection methods are available, studies on clusters reveal the evolution of spectroscopic features from small complexes to macroscopic solutions. This paves the way for a microscopic understanding of macroscopic solution properties. There are fundamental differences between neutral and ionic solutions due to the long range of the Coulomb potential. Perhaps the most exotic and certainly the least classical ionic solute is the electron itself. Liquid alkali–ammonia solutions and excess electrons in water clusters are examples of such systems where much progress has been made in recent years in resolving their microstructure.^2–4 Both systems have in common that they are largely governed by the molecular-level interaction of the excess electron with the H-bond network topologies. Alkali-doped clusters of solvent molecules provide a bridge from neutral solvent clusters to both negatively-charged clusters of solvent molecules with a solvated excess electron and positively-charged alkali cation–solvent clusters. In the case of sodium, water and ammonia clusters have been extensively studied with diverse spectroscopic methods.^2,3,5–10 Photoionization experiments combined with mass spectrometric detection have proven to be a suitable approach to study the coupled sodium–electron solvation process in hydrogen-bonded clusters.^3,8 These experiments revealed that the water–sodium and the ammonia–sodium systems show remarkable differences in the size-dependent evolution of their ionization potentials (IPs). The IPs of Na(H₂O)_nclusters decrease from n = 1 to n = 4 and stay constant for n≥ 4 while the Na(NH₃)_n IPs show a stepwise decrease to the bulk value, as measured by Steinbach and Buck³ up to n = 1500. These qualitative differences are surprising and have been discussed theoretically in various studies,^11–15 assuming either a one-center solvation state with the electron trapped around the cation or a two-center state with a separated electron placed either at the surface or inside the cluster in a cavity-like structure surrounded by solvent molecules. Photoionization experiments with Cs- and Li-doped water clusters have also been carried out.^16,17 In both studies the evolution of the IPs agrees qualitatively and quantitatively with the sodium system. New insights into the interaction of sodium with polar solvents are expected from studies of the sodium–methanol system which has received less attention. Methanol has a simpler hydrogen-bond topology than water, lending itself very well to a detailed understanding of the competition between sodium solvation and hydrogen-bonding. For sodium–methanol, size-selected ionization potentials have not yet been published but some studies have been performed focusing on the sodium–methanol interaction. In the work of Borodinet al. the reactivity of Na with thin methanol films at low temperatures was examined.⁹ The energies of electrons emitted from the film were measured using metastable impact-electron spectroscopy (MIES). In the same study similar experiments were performed for sodium with water and ammonia. In the same work a structure of the neutral Na(CH₃OH)₆cluster was predicted using density-functional theory (DFT).¹⁸ The structures of cationic Na(CH₃OH)_n⁺clusters (n = 1–6) were characterized by García-Muruais et al.,¹⁹ also using DFT. Cézard et al. presented an extensive study on cationic alkali–solvent clusters employing a combined Monte-Carlo-growth method/model-potential approach.²⁰ Further studies focused on charged methanol clusters due to protonation²¹ or addition of an excess electron.^22,23

In the present study we investigate experimental Na(CH₃OH)_n ionization potentials for n = 2–40. These data are expected to provide valuable information about the alkali/polar solvent solvation process, especially when compared with the much better examined water and ammonia systems.

In a very recent DFT study by Gao and Liu it is demonstrated that the IP evolution of sodium-doped water clusters in photoionization experiments can be explained by an adiabatic autoionization process²⁴ contrasting earlier studies where a vertical process was assumed.^7,14 This motivated us to use DFT on the same level of approximation for an exploratory quantum-chemical characterization of the sodium–methanol system. MP2 single-point calculations for the optimized structures were additionally performed. From the structures and energies of neutral and cationic Na(CH₃OH)_nclusters for n = 1–7, we derive vertical and adiabatic ionization potentials that are compared with the experimental data. The results provide new information on the microsolvation of the Na 3s electron in methanol and have implications for the understanding of the photoionization of sodium-doped polar-solvent clusters in general.

Experiment

The experiments have been carried out in a molecular beam machine with a reflectron time-of-flight mass spectrometer (RETOF) which is described elsewhere in detail.²⁵ Therefore only a brief description of the basic setup is given. A He-seeded methanol-cluster beam is skimmed and crosses an atmosphere of sodium vapour created in a pick-up cell. The products are detected by photoionization, mass-resolved in the RETOF with a mass resolution of m/Δm = 1300, and sampled by a multi-channel plate. The methanol clusters are generated in a continuous expansion of methanol at temperatures of 313 K and 331 K. The stagnation pressure is 3 bar. With these expansion conditions, bimodal size distributions are produced that allow a sensitive detection of ion signals for both small and large clusters. The mole fractions of methanol in the expanding gas are x = 0.11 for 313 K and x = 0.25 for 331 K. The nozzle is kept at 319 K for the 313 K expansion and at 347 K for the 331 K expansion. The conical nozzle has a diameter of 76 μm and an aperture angle of 20.1°. Following the results obtained for pure methanol hexamers, we estimate a cluster temperature of about 120 K.⁵² The sodium pick-up cell is heated to 443 K which results in a pressure of 0.016 mPa. This leads to the capture of at most one sodium atom for each cluster size.

For the photoionization of the products, a pulsed excimer laser (Lambda Physics LPX200i) is used for pumping a dye laser (Lambda Physics LPD3000). For the determination of the IPs of cluster sizes 3 ≤n≤ 50 the wavelength is tuned in steps of 1 nm from 348 to 420 nm. Additionally a mass spectrum is measured at 308 nm with the excimer-laser light. The measured spectra are analyzed in terms of the wavelength-dependent ion yield for the different cluster sizes.

The pulse energy at the ionizing volume is at most 4 mJ per pulse corresponding to a fluence of 150 mJ cm⁻² at a repetition rate of 20 Hz. These conditions are also ensured for the experiment at 308 nm. In this range, conditions for single-photon ionization are fulfilled, which implies that a linear dependence of the yield on the pulse energy is obtained. Therefore, the ion yields in each mass spectrum are weighted with the respective wavelength-dependent pulse energies. The ion signals are recorded using a multi-channel scaler.

Computational method

The hybrid density-functional approach on the unrestricted B3LYP/6-31+G** level has been identified in a number of studies^18,24,26 on similar systems as being suitable for determining optimized geometries and their relative energies at acceptable computational costs. Clearly, such a simple approach must profit from significant error compensation,²⁷ but it provides a meaningful starting point for the interpretation of the experimental spectra. Diffuse functions on heavy atoms are mandatory for the neutral clusters, although they lead to an overestimated dipole moment for methanol¹⁹ and thus affect ion solvation and hydrogen-bond strength. In several studies, geometry optimization on the B3LYP/6-31+G** level was accompanied by optimizations or single-point calculations using correlated methods such as MP2.^14,28,29 The importance of the inclusion of correlated calculations is pointed out by Feller et al.: for cationic alkali-metal–water clusters (n = 1–8) they systematically explored structures and binding energies using various methods and extended basis sets.^28a Their study revealed that even for cationic systems, whose interactions are largely electrostatic in nature, correlated methods are needed for a balanced description of all interactions when hydrogen-bonds are present.

We took these findings into account for our exploratory study of the potential-energy surface of neutral and ionic clusters of the type Na(CH₃OH)_n and Na(CH₃OH)_n⁺ for 1 ≤n≤ 7. The robust minima which we found for Na(CH₃OH)₃/Na(CH₃OH)₄ are assumed to be energetically very close to the global minimum, but zero-point energy aspects are important as we will see. For n = 5–7, different types of hydrogen-bond patterns and Na–methanol interactions start to compete and have been explored by testing different trial structures. For the neutral clusters, the sodium atom is either attached at various positions to an optimized structure of pure methanol clusters or embedded into differently-oriented solvent molecules. The latter geometry resembles the cationic minima. The n = 6 structure presented in ref. 18 was included. Geometries obtained after the first optimization cycle were further modified by changing the relative numbers and orientations of hydrogen-bonds and Na–CH₃OH interactions. The procedure was iterated until further modifications did not lead to structures with lower energies. This strategy has proven suitable to identify representative structures in the very floppy systems of neutral sodium–polar-solvent clusters. In a recent, more systematic study,²⁴ a large number of isomers separated by small energy differences were identified even for moderate cluster sizes with n = 5 and 6 in the sodium–water and the sodium–ammonia systems. Stochastic sampling methods such as the ab initio molecular dynamics (AIMD) approach²⁴ are imperative beyond n = 7, but we consider our trial approach acceptable up to n≈ 7 in view of the limited quality of the underlying electronic-structure approach. The structures of the cationic systems have been characterized in the same manner. Starting structures are either the optimized geometries of the neutral system or those with the sodium atom placed in a central position surrounded by methanol molecules. Vibrational frequencies are calculated for all optimized structures to verify their local-minimum nature. No correction for the basis-set superposition error was applied to the quoted energies.

Results and discussion

Mass spectra

In Fig. 1, typical mass spectra of sodium-doped methanol clusters Na(CH₃OH)_n measured with photon energies at and above the photoionization threshold are shown as a function of the mass to charge ratio (m/z) in atomic mass units (u). The clusters with n = 5 and 6 are marked and it is seen that the relative ion yield for n = 5 is drastically reduced at the lower photon energy, indicating the higher ionization potential of Na(CH₃OH)₅. A prerequisite for the IP determination is the absence of fragmentation effects. The signal increase for n = 5 should not be due to fragments from n≥ 6. Therefore the influence of fragmentation was systematically examined by comparing ion-yield profiles recorded under different expansion conditions. With a nozzle temperature of 347 K the formation of larger clusters is largely suppressed and the relative signal intensities of smaller clusters are changed. The wavelength-dependent ion yields for the detectable small clusters with n = 3–10 remain unaffected by this change in cluster-size distribution. This indicates that the signals are not distorted significantly by fragmentation in accordance with previous studies.^3,7,8,10 For small clusters the possible influence of fragmentation on the data analysis is further reduced by the shape of the cluster-size distribution. The drop in cluster abundance from n = 5 to 10 is even sharper than suggested by Fig. 1 because the ionization cross-section is enhanced for larger clusters.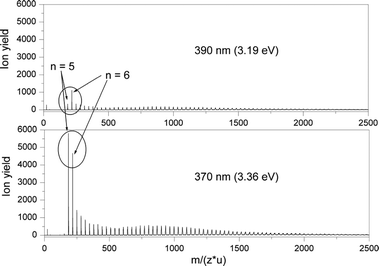

Fig. 1 TOF mass spectra of Na(CH₃OH)_n⁺clusters produced by photoionization of a supersonic expansion at 3 bar and a temperature of 313 K at 370 and 390 nm. The ion yields are normalized by the laser-pulse power density.

In Fig. 2, ion yields relative to the maximum signal at 308 nm are shown as a function of photon energy for selected cluster sizes. The initial decline of the ionization barrier comes to a halt for n > 6. The inserted plot further demonstrates that the signal onset (absolute ion yields) is almost the same for n = 3 and 4 but the increase is much steeper for n = 4. Calculated vertical IPs discussed in the next sections indicate that the appearance of Na(CH₃OH)₃ around 3.35 eV with a weak signal increase is possibly due to the unstable structure of the methanol three-ring.

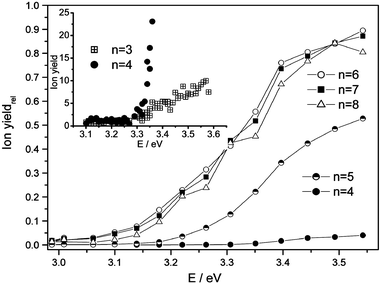Fig. 2 Relative power-normalized ion yields as a function of the photon energy of the ionization laser for Na(CH₃OH)_nclusters with 4 ≤n≤ 8. The ion yields are normalized by the signal intensity at 308 nm. Inserted plot: Absolute ion yields for n = 3 and 4.

In general the gradual increase of the ion yields with increasing photon energies is typical for clusters and is in contrast to the sharper rise observed for atoms and molecules. Therefore the ionization onset in most cases cannot be derived by a simple extrapolation of the steepest ion-signal gradient to the baseline. The photoionization process in clusters is complicated by the structural differences among isoenergetic isomers. A broadening due to signal contributions from autoionization must also be considered. For small Li(NH₃)_nclusters, Salter and Ellis²⁹ relate sharp and slow signal rises to small and substantial amounts of structural change upon ionization.

These complications make a unique determination of the ionization threshold difficult. Steinbach and Buck³ successfully used Watanabe-type plots^30b to determine photoionization thresholds of sodium–ammonia clusters in a very broad size range (n = 10–1500). In this method, the lowest break in the logarithmic plot of ion yields versus photon energy is assigned to the ionization threshold.³⁰ Results for selected cluster sizes based on this method are shown in Fig. 3 and the resulting set of IPs is listed in Table 1. Their relative trends are certainly more robust than their absolute values. The larger uncertainties for n = 4 and notably for n = 3 are due to the 3.57 eV limit of the current dye laser system which could only partially be compensated by a single measurement at 4.03 eV, the pump-laser energy. Clusters with n = 2 also appear at 4.03 eV providing at least an upper limit and a basis for a rough estimation of their IP. For larger clusters the experiments show a constant IP up to n = 40. Measurements under different expansion conditions suggest that the same threshold is found even for clusters as large as n = 80. These results clearly indicate that the evolution of IPs of sodium–methanol clusters is very similar to that in the sodium–water system but much different from sodium solvated in ammonia as illustrated in Fig. 4. Even the absolute photoionization energy of 3.19 ± 0.07 eV for n≥ 6 is within error margins of the value of 3.17 eV found for sodium in water for n≥ 4. These results agree with studies on the interaction of sodium with thin films of solid methanol and water,^9,32 where the binding energies of the Na 3s electrons measured by MIES spectroscopy show similar values for water and methanol.

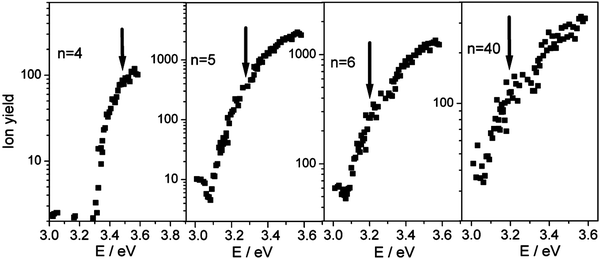Fig. 3 Dependence of the logarithm of the ion yield of selected Na(CH₃OH)_nclusters on the photon energy. The position of the lowest break associated with the ionization potential is marked by an arrow.

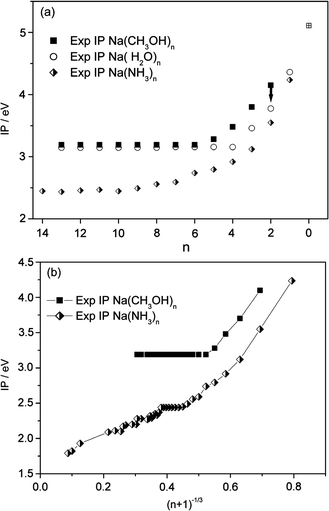Fig. 4 (a) Experimental ionization potentials for Na(CH₃OH)_n, (2 ≤n≤ 14; the arrow indicates the large uncertainty for n = 2), Na(H₂O)_n, (1 ≤n≤ 14) (ref. 8) and Na(NH₃)_n, (1 ≤n≤ 14) (ref. 3 and 8). (b) Experimental ionization potentials for Na(CH₃OH)_n and Na(NH₃)_n plotted against (n + 1)^−1/3 (ref. 3 and 8).

Table 1 Ionization threshold IPs of Na(CH₃OH)_nclusters in eV

n	IP	n	IP
a IP of Na from ref. 31.
0	5.139^a	6	3.19 ± 0.05
1	—	7	3.19 ± 0.05
2	4.15 > IP > 3.85	8	3.19 ± 0.05
3	3.8 ± 0.15	10	3.19 ± 0.05
4	3.48 ± 0.07	20	3.19 ± 0.06
5	3.28 ± 0.05	40	3.19 ± 0.07

---

Quantum-chemical characterization

Various theoretical studies have aimed at a molecular-level characterization of the experimental results of photoionization experiments for sodium attached to water and ammonia. The measured IPs were compared to theoretically-derived IPs using different approaches. The application of pseudo-potentials^8,13 led to qualitative agreement for small cluster sizes for the water and ammonia system but failed to describe the evolution for large ammonia clusters. In later studies quantum-chemical methods have been applied at different levels of approximation. In the first studies, geometry optimization was often performed at the Hartree–Fock level.¹² In several more recent studies, structures and energies have been calculated using the unrestricted B3LYP/6-31+G** approach.^18,24,26

In these quantum-chemical studies of alkali–solvent systems, the ionization potentials were derived by calculating the energies of the neutral and cationic clusters with the same nuclear framework. The energy difference was assigned to the ionization potential assuming a vertical transition. The reasonable agreement of those calculations with the experiments in case of water and ammonia suggested that a vertical-ionization picture is adequate.^14,15 In an extensive theoretical study, Tsurusawa and Iwata³³ relate the constant IP of sodium/lithium–water clusters for n = 4–6 to ion-pair complexes that are vertically ionized. However, a recent comparative study of the sodium–water and –ammonia interactions²⁴ questions the vertical-ionization picture for Na(H₂O)_n. For cluster sizes n≥ 5, many isomers appear within an energy window of a few kJ mol⁻¹ and their corresponding vertical ionization potentials differ by as much as 1 eV. Their calculations for larger n (up to n = 20) show that trends seen for 3 ≤n≤ 6 cannot simply be extrapolated to larger n. Interestingly, energy differences between neutral and cationic clusters calculated with the unrestricted MP2 method tend to be 0.2–0.3 eV below those calculated by applying DFT.^24,29,33 These differences have significant consequences for the interpretation of theoretical studies: for Na(H₂O)_n (n = 4–6), Gao and Liu²⁴ find vertical ionization potentials (DFT) of all considered isomers that are significantly above the experimental threshold and postulate an adiabatic ionization process involving Rydberg states, while Tsurusawa and Iwata³³ explain, based on MP2 energies, the constant experimental IP with vertical transitions and ion-pair structures. These aspects are considered in the present study for the optimization of geometries for Na(CH₃OH)_n/Na(CH₃OH)_n⁺clusters and the derivation of the ionization potentials.

Structures

Representative neutral and cationic structures of Na(CH₃OH)_n are presented in Fig. 5 together with a notation to characterize the structures, which we will use below. We first discuss the neutral clusters. To explore the expected differences between MP2 and B3LYP energies we performed single-point MP2/6-311++G** calculations for structures optimized with the B3LYP/6-31+G** approach. Moreover, harmonic zero-point energy (ZPE) aspects are examined using B3LYP/6-31+G**. Neglecting a ZPE correction, the minimum energy structures have in common that for n≥ 3 the formation of hydrogen-bonds is preferred over neutral sodium–O-atom interactions and that the sodium atom is located in exterior positions. Only for n = 2 is a structure without H-bonds, where the sodium atom is coordinated by two methanol molecules, favoured. For n≥ 3 all minima are rings, the larger ones with a side chain of one (n = 6) and two (n = 7) methanol molecules, forming a lasso structure.³⁴ However, if harmonic ZPE corrections are applied, the results are different—especially when starting geometries are used that correspond to the lowest minima of cationic clusters: fewer H-bonds are formed and for most of the clusters with n≥ 4 the sodium atom sits in an interior position where it is coordinated by four O atoms. The ZPE-corrected B3LYP energies of these interior structures for n > 5 are below the energies of the exterior structures mentioned above. However, with respect to MP2 energies, all interior structures are less stable than the exterior ones, regardless of whether a ZPE correction is performed. We examined these aspects systematically for n = 4: relative B3LYP(6-31+G** and 6-311++G** basis) and MP2(6-311++G** basis) energies are calculated for the exterior ring structure (4⁴₁), the interior structure (4⁰₄) and a “mixed” structure (4²₃) with both H-bonds and Na–O interactions. The results are listed in Table 2. The first observation is that the exterior structure is the most stable one for all applied levels of approximation. Secondly, MP2 calculations significantly favor the exterior structures. A third observation is that ZPE corrections systematically stabilize interior complexes. These results also hold for the larger clusters with n = 5–7. All energies given below are ZPE-corrected. Relative electronic energies are used to calculate vertical ionization potentials as explained in the next section. Here ZPE is not defined for cations with geometries of neutral minima.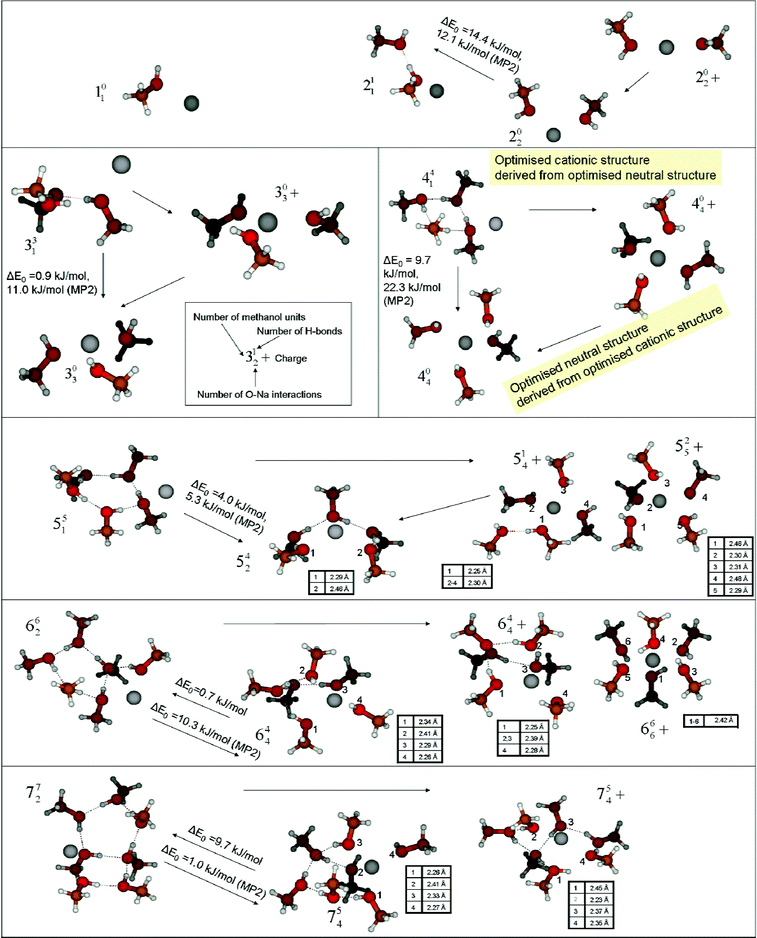

Fig. 5 Representative structures for Na(CH₃OH)_n/Na(CH₃OH)_n⁺ (1 ≤n≤7): the most stable neutral, “exterior” (left) and cationic (right) structures are shown together with neutral structures with an “interior” Na that are derived from cationic starting configurations (lower/middle positions). For n = 5 and 6, energetically-competing cationic structures with 5 and 6 molecules in the first solvation shell are also shown. Arrows relate structures derived from each other. The structures are characterized by their interaction patterns: the large number stands for the number of methanol molecules, the upper index for the number of hydrogen bonds (O–H distance below 2.5 Å) and the lower index for the number of Na–O-atom interactions (Na–O distance below 2.5 Å). The Na–O distances of interacting atoms are given for selected interior structures in Tables. B3LYP- (no label) and MP2-energy differences between the most stable “exterior” and the “interior” neutral structures including B3LYP ZPE correction are also given.

Table 2 Energy of Na(CH₃OH)₄ complexes with an “interior” 4⁰₄ and a “mixed” 4²₃ geometry relative to the “exterior” 4⁴₁ complex

Level of approximation	4^04/kJ mol^−1	4^23/kJ mol^−1
B3LYP/6-31+G**	22.1	12.9
B3LYP/6-31+G** (ZPE)	9.7	6.9
B3LYP/6-311++G**	18.5	10.7
B3LYP/6-311++G** (ZPE)	6.0	4.7
MP2/6-311++G**	32.6	22.5
MP2/6-311++G** (ZPE)	20.2	16.5

---

For n = 6, an optimized structure was presented by Allouche et al.¹⁸ It is an interior structure where the sodium atom is bound to four methanol O-atoms with distances of 2.3–2.5 Å. We reconstructed this structure and obtained a B3LYP energy 0.7 kJ mol⁻¹ below the energy of the most stable optimized lasso-structure found in the present study (see Fig. 5). As expected from the findings for n = 4, the MP2 energy is 10.3 kJ lower for the exterior structure. For n = 7 we found a minimum with interior geometry that is 9.7 kJ more stable than the exterior one, but 1 kJ mol⁻¹ less stable based on the MP2 calculation. One should view the discrepancies between MP2 and B3LYP as well as between electronic and zero-point-corrected energies as a rough measure of the degree of accuracy with which the energies of these neutral radical structures are modeled.

The competition we see between solvent–solvent and solvent–sodium interactions can be rationalized as follows: the formation of solvent–solvent interactions is favoured for n≥ 3 when the exterior structures start to be stabilized by cooperative H-bonds.³⁵ Clearly, the importance of cooperative stabilization fades away with decreasing hydrogen-bonded ring strain and increasing flexibility of the solvent clusters. Beyond n≈ 6 (n = 6 B3LYP, n = 7 MP2) the results indicate that both types of interaction can be maximized simultaneously. We note that the competitiveness of structures with optimized solute–solvent and solvent–solvent interactions and the indecisive B3LYP and MP2 results have major implications for the derivation and interpretation of vertical ionization potentials. This aspect will be discussed in the next section. Therefore, both the optimized interior and exterior structures are shown in Fig. 5 with relative B3LYP and MP2 energies.

For the cationic clusters a different interaction pattern is found. Here, many of the most stable structures show a sodium atom that is bound to four methanol O-atoms. Obviously, Coulomb interaction between the cation and the methanol molecules dominates the tendency to maximize the number of hydrogen-bonds. Even without sophisticated global minimization techniques, it is seen that this dominance persists up to n = 4, which is in good agreement with earlier studies on the sodium–cation solvation.^19,20 For n≥ 5, further methanol molecules can start to form a H-bonded network while the sodium atom remains coordinated by only four O-atoms. However, we also found almost isoenergetic structures for n = 5 and 6 where the sodium atoms are coordinated by 5 (5²₅+) and 6 (6⁶₆+) O-atoms respectively. These structures strongly resemble the results of García-Muruais et al. who found a square pyramid for n = 5 and an octahedral structure for n = 6. We optimized these structures at the B3LYP/6-31G* level applied in ref. 19 to explore the sensitivity of the relative energies of these structures to the applied level of theory. Single-point calculations were additionally performed at the B3LYP/aug-cc-pVTZ and the MP2/6-31+G** level. The results are presented in Table 3. It is seen that with the 6-31G* basis set for B3LYP and with the MP2 method in general, the higher-coordinated clusters show the lower energy. The remaining B3LYP predictions including diffuse functions show a higher stability of the 5¹₄+ and 6⁴₄+ structures. Zero-point-energy corrections have only a minor effect on the calculations (≤0.7 kJ mol⁻¹). The increased stability of the H-bond-optimized complexes could be caused by the overestimated dipole moment of CH₃OH in calculations at the B3LYP/6-31+G** level (μ = 2.0 D, see also ref. 19). However, the single-point calculations with the aug-cc-pVTZ basis (μ = 1.8 D) indicate that B3LYP calculations may favor the low coordination independent of the overestimated dipole moment. Interestingly, this is opposite to the neutral open-shell-system results discussed above. Earlier experimental and theoretical studies^36,37 suggest the first Na solvation shell accommodates 6 methanol molecules in line with the MP2 predictions. As pointed out above, Feller et al. found that even for cationic systems well correlated methods are needed for a balanced description of electrostatic interactions and dispersion forces when hydrogen bonds are present.^28a

Table 3 Energy of Na(CH₃OH)_n⁺ ions with a maximized sodium-ion interaction (5²₅+, 6⁶₆+) relative to ions with optimized H-bond interactions (5¹₄+, 6⁴₄+) for n = 5 and 6

Level of approximation	5^25+/kJ mol^−1	6^66+/kJ mol^−1
a Single-point energy. b Structure optimized at B3LYP/6-31G* level. c Structure optimized at B3LYP/6-31+G** level.
B3LYP/6-31G*	−0.5	−0.7
B3LYP/6-31+G**	4.6	8.1
B3LYP/aug-cc-pVTZ ^a^,^b	5.2	4.7
B3LYP/aug-cc-pVTZ ^a^,^c	5.0	7.8
MP2/6-31+G**^a^,^b	−2.0	−1.7
MP2/6-31+G**^a^,^c	−3.1	−1.1

---

The present study allows no final conclusions on the Na-coordination in the most stable cationic Na(CH₃OH)_n⁺ structures for n = 5 and 6 but indicates that Na(CH₃OH)_n complexes with the sodium atom coordinated by 4 O-atoms are competitive with 5- and 6-coordinated complexes. However, considering the extensive theoretical study of Feller et al.^28a and the experiment of Selegueet al.³⁶ we expect the higher-coordinated structures to be more stable for n = 5 and 6. In any case, the quantum-chemical description of the ionic systems is more robust than that of the neutral clusters.

Comparison with experiment

We used the optimized neutral and cationic cluster geometries to predict ionization potentials, assuming limiting vertical and adiabatic processes. In the vertical case, energy differences were calculated between the neutral and the ionized cationic clusters of the same structure. In the adiabatic limit, the ionized clusters were used with their optimized relaxed structure. For the adiabatic IPs we used the most stable neutral and cationic structures. Since their relative stability strongly depends on the quantum-chemical approach used we discuss DFT and MP2 results. Within their error margins, different interpretations of the ionization process are possible. Therefore, we develop and discuss two limiting scenarios: an isomer-specific vertical ionization with little structural change and an indirect adiabatic process where significant structural rearrangement is expected. Both scenarios are linked to the vertical and adiabatic IPs of interior and exterior complexes that are compared with the experimental values based on MP2 energies in Fig. 6a and based on B3LYP energies in Fig. 6b. Finally, the results are discussed with respect to the experimental and theoretical findings for the related Na(H₂O)_n and Na(NH₃)_n systems.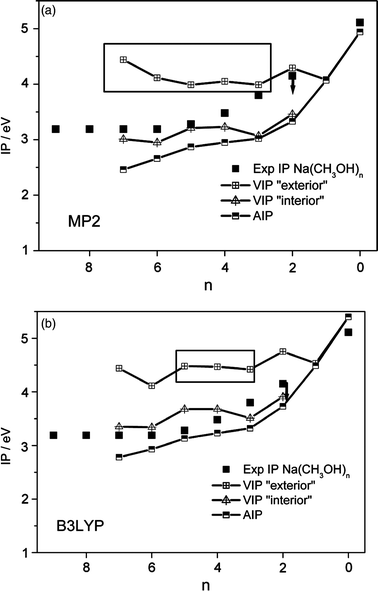

Fig. 6 Experimental ionization potentials for Na(CH₃OH)_n (3 ≤n≤ 9) compared to calculated vertical ionization potentials of “interior” and “exterior” structures as well as adiabatic ionization potentials of Na(CH₃OH)_n (0 ≤n≤ 7) (a) MP2 6-311++G** and (b) B3LYP 6-31+G**. Vertical IPs within the boxes belong to “exterior” isomers that are the most stable ones found for the corresponding n.

Vertical ionization

The vertical ionization potential (VIP) is very sensitive to the cluster structure, in particular when solute–solvent and solvent–solvent interactions are in close competition: the sensitivity of the VIPs to the neutral starting structure for Na(CH₃OH)_n is illustrated in Fig. 6 and 7, where VIPs of representative interior structures are compared to those of exterior structures. The former are naturally closer to the ionic structures and hence are expected to have much smaller VIPs. Based on B3LYP calculations, the VIPs of the interior structures correlate almost as well with experimental data as the adiabatic ionization potentials (AIP) of the most stable structures (Fig. 6, squares within boxes). Based on MP2 calculations (Fig. 6a) the experimental values are better predicted by vertical IPs of internal structures compared to adiabatic IPs which are considerably lower. However, for n = 3–5 the MP2 and B3LYP calculations consistently predict that the most stable structures are exterior ones and their corresponding VIPs are significantly above the experimental results. Therefore, a vertical ionization process out of the most stable neutral cluster structures is incompatible with experiment in the intermediate cluster-size range. If we take a closer look at Na(CH₃OH)₄ we see that the exterior 4-ring is much more stable than the “mixed” and interior geometries considered (see Table 2) which would be needed to explain the experimental ionization threshold by a strict vertical transition. The finite temperature of these clusters of approx. 120 K does not change this picture significantly.⁵² Based on the result for the methanol hexamers we expect that different configurations with an energy difference of 4 kJ mol⁻¹ just start to be populated in this temperature range. If heating of the methanol clusters by Na-attachment is considered, we still find that the energy to produce interior structures is substantial for selected clusters (see Fig. 5): it is comparable to the adiabatic attachment energy of neutral Na to neutral methanol clusters (≈20 kJ mol⁻¹ for n = 4 and 5; but very uncertain at B3LYP level). Part of this energy may still be present in the clusters when they cross the ionization laser beam, but barriers for isomerization into internal structures are sizable. A significant barrier is expected for n = 4 because the initially-formed 4-ring structures originate from hydrogen-bonded methanol 4-rings³⁵ picking up sodium atoms. Additionally, the study of Raveendran et al. illustrates the exceptional stability of methanol 4-rings.³⁸ It was shown in supersonic jet expansions that eucalyptol can stabilize chain conformations of (CH₃OH)_n for n = 3 with respect to the fully-cooperative ring formation but not for n = 4. Furthermore, selective ionization of special cluster isomers is expected to lead to magic numbers in the mass spectra (see for example ref. 39 and references therein), which are not observed experimentally (Fig. 1). For n = 3 the difference in energy (B3LYP) between the interior and the most stable exterior structure (ΔE₀ = 0.8 kJ mol⁻¹) is small and the vertical IP is lower than for n = 4. Assuming an isomer-selective vertical ionization of Na(CH₃OH)_n, the clusters with n = 3 should consequently appear at a lower ionization threshold than those with n = 4. But at 308 nm n = 4 is the cluster with the second-highest intensity and n = 3 shows a comparably weak peak. Assuming for a moment that B3LYP better predicts relative energies of neutral isomers and MP2 better captures the energetic difference of neutral and cationic clusters, most experimental thresholds can be explained by vertical ionization of interior structures. However, for n = 4, both the calculations and the consideration of the experimental conditions suggest that exterior 4-ring structures are already ionized at an energy that cannot be explained by a strict vertical process.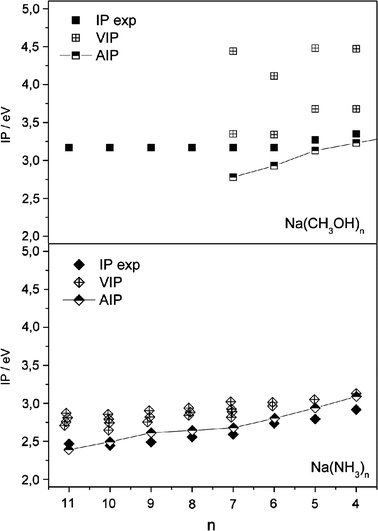

Fig. 7 Comparison of experimental ionization potentials for Na(CH₃OH)_n, and Na(NH₃)_n (3 ≤n≤ 11, ref. 3 and 8) with calculated (B3LYP) adiabatic and vertical ionization potentials (ref. 24).

Adiabatic ionization

Calculations with both methods suggest that predicted AIPs are somewhat below the experimental values (Fig. 6). On the other hand, the most stable neutral structures in the intermediate size range clearly have an exterior sodium (in particular at MP2 level) and thus a much higher VIP, incompatible with the experimentally-identified thresholds. This calls for a substantial adiabatic character of the threshold ionization process, equivalent to major rearrangement of the solvent network during ionization. Due to the mismatch of timescales, this requires an intermediate state for the photoelectron. Given such a state, the predicted AIPs are compatible with experiment, in particular considering that the process is unlikely to be fully adiabatic. However, any non-adiabaticity can lead to fragmentation of the ion and must be quite limited according to the experimental finding. There are further indications that support this picture when the related sodium–water system is considered.

It goes beyond the scope of the present study to systematically search the potential-energy surface for local minima with all conceivable solute–solvent and solvent–solvent interaction patterns. However, it is obvious from Fig. 6 and 7 that for n≥ 2 local minimum structures can be generated for each cluster size that show IPs close to and more than 1 eV above the adiabatic IPs (especially if MP2 energies are used). The corresponding structures exhibit between one (exterior configuration) and up to four (interior configuration) sodium–methanol interactions. For the sodium–water system, Gao and Liu²⁴ nicely illustrated this effect: for local minimum structures (ΔE≤ 10 kJ mol⁻¹) vertical IPs differ by up to 1 eV for various cluster sizes (n≥ 4). The reason for this effect is the same as in the methanol system: competing solute–solvent and solvent–solvent interactions lead to exterior and interior cluster geometries which are close in energy but vary strongly in their vertical IPs. In their study, vertical IPs (B3LYP) of all Na(H₂O)_n isomers with n≤ 8 are significantly above the experimental threshold.

Gao and Liu conclude that an adiabatic ionization process via vertical excitation to a high Rydberg state followed by structural reorganisation and autoionization explains the observed evolution of IPs. An adiabatic interpretation is also applied to photoionization experiments with Li(NH₃)_n (n = 1–5) clusters²⁹ where the experimental thresholds are characterized by calculated adiabatic ionization energies (B3LYP and MP2).

There is another experimental finding that indicates signal contributions of autoionization: recently Steinbach and Buck reported size-selected IR spectra of Na(H₂O)_nclusters.⁴⁰ These measurements are based on the effect that the absorption of IR photons in the OH-stretch region (ca. 0.4 eV) prior to the UV-vis laser pulse results in a signal increase and thus a reduced photoionization threshold. No fragmentation or water evaporation due to the deposited vibrational energy is observed indicating that Na(H₂O)_nclusters are comparably stable. Assuming an autoionization process, where the energy released by structural relaxation is coupled to the excitation of Rydberg photons into the continuum, additional vibrational photons are expected to facilitate ionization via the same coupling. This corresponds to the phenomenon of vibrational autoionization in polyatomic molecules.⁴¹ At the ionization threshold an absorbed IR photon increases the internal energy of the cluster. Together with the local relaxation energy after e⁻ excitation, a larger amount of energy can effectively couple to autoionization, thus lowering the ionization threshold.

A further indication for the partial adiabatic character of the ionization process is the broad transition region of sodium–methanol clusters (n≥ 3) at the ionization threshold. This is a typical autoionization effect in large polyatomic molecules.⁴¹ It was also observed for pure sodium clusters (Na_n, n≥ 3) and attributed to autoionization.⁴² The Watanabe approach used to derive the ionization thresholds in the previous section is considered appropriate to such systems.^3,30 Additionally, the slow signal growth is observed for all evaluated ion yield profiles (see Fig. 3) which indicates that no change in the ionization process takes place for n≥ 3.

However, the calculated adiabatic IPs for Na(CH₃OH)_n tend to underestimate the experimental threshold for larger clusters (n > 5), especially at MP2 level. This is in line with the findings of Gao and Liu for Na(H₂O)_n where ionization potentials are calculated up to n = 20. Thus both the experimental and computational results indicate that neither a direct vertical nor a simple adiabatic picture is adequate. The slow signal increase at the ionization threshold and the high vertical ionization potential of the exceptionally-stable Na(CH₃OH)₄cluster give evidence that for n≥ 3 indirect autoionization may contribute significantly. The results also shed light on the difficulties that arise when experimental photoionization thresholds are characterized quantum-chemically. As long as it is not clear which method (MP2 or B3LYP) and which basis set (certainly beyond the ones used here) allows reliable predictions of energy differences of neutral isomers and neutral/cationic systems, interpretations that relate experimental IP evolutions with structural motifs in neutral sodium–solvent clusters provide only limited evidence. Despite the addressed difficulties, the comparison of findings for the less complicated Na(CH₃OH)_n system with the much better examined sodium–water and sodium–ammonia systems provides valuable information on Na 3s electron microsolvation.

Comparison with Na(H₂O)_n and Na(NH₃)_n

The present study clearly shows that the experimental ionization-threshold trends of Na(CH₃OH)_n and Na(H₂O)_n are similar while they are qualitatively different for Na(CH₃OH)_n and Na(NH₃)_n. The discussion of the previous section has shown that an interpretation of this observation based on quantum-chemical calculations is complicated because the experimental thresholds cannot simply be assigned to calculated energy differences that result from limiting adiabatic and vertical ionization processes.

These difficulties are partially reflected in the theoretical study of Gao and Liu,²⁴ who give an explanation for the different behaviour of Na(H₂O)_n and Na(NH₃)_n that involves different ionization processes. As already stated above for Na(H₂O)_n, the constant IP for n≥ 4 is explained by an adiabatic ionization process via vertical excitation to a high Rydberg state followed by structural reorganisation and autoionization. They argue that the excitation to Rydberg states is no longer cluster-size dependent when the first cationic solvation shell is filled. This proposal is supported by a recent study on electronic excitation from the singly-occupied molecular orbital (SOMO) to the lowest unoccupied molecular orbital (LUMO) of Na(H₂O)_nclusters. The excitation energy is only significantly red-shifted for the addition of the first four water molecules while further addition produces only very small shifts.⁴³ This corresponds to a general pattern of the size dependence of the first electronic excitation in predissociation experiments with cationic clusters. Here, significant red-shifts are only observed when the first solvation shell is filled.^44,45 However, it is not clear if the trend seen in studies of small clusters and excitations to energetically-lower states generally applies to larger clusters and excitations to high Rydberg states.

The related Na(CH₃OH)_n system shows the same features as Na(H₂O)_n: the IP drops stepwise with the addition of methanol molecules to sodium and stays constant from a certain cluster size even up to very large clusters. The cluster size from which a constant IP is observed is reached when n = 6 for methanol compared to n = 4 for water. As discussed in the previous section the present study, as well as previous theoretical and experimental studies, indicate that the first solvation shell of the sodium cation is filled with up to 6 methanol molecules,^19,36,37 whereas it is complete at n = 4 for water.^24,28 The proposal of Gao and Liu that the excitation to high Rydberg states determines the experimentally-observed ionization thresholds can explain the similar behaviour of Na(CH₃OH)_n. However, the interpretation is based on assumptions that need further evidence. At the present stage, for example, it is not clear whether the density distribution of the excited electron has a rather Rydberg-type or a more localized character. Neumark et al. studied the dynamics of the related solvated excess electron in (H₂O)_n⁻clusters by time-resolved photoelectron imaging.⁴⁶ Their results are in agreement with the picture that the excited hydrated electron is described by a localized p-type orbital.

The question arising at this point is how the findings of the present study can be related to Na(NH₃)_n which is characterized by a stepwise decrease of the IP to the bulk value in accordance with the (n + 1)^−1/3 rule for the transition of properties from clusters to the bulk (see Fig. 4b). Gao and Liu explain the difference between ammonia and water by their different local relaxation energies leading to different ionization mechanisms, though autoionization was not ruled out for Na–ammonia. They define the local relaxation energy by the energy difference between the optimized neutral structure and the relaxed local cationic minimum. We note that in the present study most cationic clusters are derived directly from the neutral clusters. This means that local and global minima are identical for these small systems.

Na(NH₃)_n topologies are governed by much weaker and less-directed hydrogen-bonds between ammonia molecules compared to those in water and methanol. Thus for smaller clusters, first the Na–NH₃ interaction is maximized. With growing cluster size the first solvation shell is filled and solvent–solvent interaction becomes more and more important. This leads to much simpler cluster-structure patterns with Na embedded by NH₃ molecules resembling the cationic structures.²⁴ The consequences are much less fluctuation in vertical IPs and much lower relaxation energies compared to Na(CH₃OH)_n and Na(H₂O)_n. Does this provide evidence that a different ionization process for Na(NH₃)_n is the reason for the different IP evolutions? In Fig. 7 we compare for Na(CH₃OH)_n and Na(NH₃)_n the calculated (B3LYP) adiabatic IPs with vertical ones and the experimental data. For both systems the adiabatic curves show much better agreement with experiments. The fluctuation of vertical IPs is much less pronounced for Na(NH₃)_n but the vertical IPs are consistently 0.1–0.2 eV above the experimental data, which is almost exactly matched by the adiabatic IPs. Although the accuracy of the quantum-chemically-calculated energies should not be overestimated, this observation suggests that even for Na(NH₃)_n autoionization has to be taken into account. This is in line with the slow signal rises that are observed for larger Na(NH₃)_nclusters and selected smaller Li(NH₃)_nclusters.^3,29 We see in Fig. 7 that for n≤ 10 the calculated adiabatic ionization potentials for Na(NH₃)_n are slightly higher than the experimental values. These findings are similar to Li(NH₃)_n, where Salter and Ellis find adiabatic IPs calculated with B3LYP slightly above and those calculated with MP2 below the experimental values.²⁹ Considering the slow signal rise where the first ions are seen significantly below the threshold, MP2 seems to capture better the energy difference of neutral and cationic clusters, at least for alkali–ammonia systems.

But how can one rationalize the fact that IPs measured by photoionization obey the (n + 1)^−1/3 rule for Na(NH₃)_n but not for Na(CH₃OH)_n and Na(H₂O)_n? CH₃OH, H₂O and NH₃ show very different reactivities with Na. Water and methanol react to form NaOH in exothermic reactions while NH₃ forms a stable solution with its famous blue colour. Ferro et al. relate the different reactivity to the much different degree of Na 3s electron delocalisation.¹⁸ In methanol and water it is localized at the cluster surface or in cavities whereas the 3s electron is broadly delocalized in ammonia solutions. In Fig. 8 the total spin density is shown for the two isoenergetic Na(CH₃OH)₇clusters and representative structures of Na(H₂O)₇ and Na(NH₃)₇ reconstructed from geometries given in ref. 18 and 26. The spin density largely represents the electron density of the singly-occupied molecular orbital (SOMO). For Na(CH₃OH)₇ and Na(H₂O)₇ the same cut-off for the spin density is used which is a factor of 2 above the value for Na(NH₃)₇ (Fig. 8d). The characteristic feature of Na(CH₃OH)₇ is that the highest spin density is localized at the surface of the clusters for both the interior and the exterior structure. This is in line with a recent experimental study on excess electron solvation in large anionic methanol clusters, where two isomers have been observed using photoelectron imaging.²³ It has been proposed that besides internal solvation the excess electron can exist in a dipole-bound surface state. Na(H₂O)₇ also exhibits a high electron density at the surface, which is slightly lower than that for Na(CH₃OH)₇. Different from the systems with oxygen–hydrogen bonds, the 3s electron is smeared over a large part of the Na(NH₃)_ncluster, which is reflected by a lower cut-off value for the electron density needed to obtain a connected domain. A slightly higher cut-off value reveals that the highest spin density is located in the frontier orbitals of three N-atoms (Fig. 8e). Ferro et al.¹⁸ relate the reactivity of H₂O and CH₃OH to the localized electron that can be transferred to initiate the chemical reaction. An explanation for the ionization-threshold evolution could go along the following lines: in photoionization experiments, the rather localized electron is excited to highly-excited states of Rydberg or more localized character below the vertical ionization threshold. This excitation is followed by a local relaxation that couples to an autoionization process. For small clusters with n < 6 the addition of methanol molecules leads to larger relaxation energies, which consequently lead to lower ionization thresholds. For n = 6 this effect comes to a halt since the first cationic solvation shell is filled, which limits the locally-available amount of relaxation energy that effectively couples to autoionization. For n > 6 the global relaxation energies, and consequently the calculated adiabatic IPs, further drop but the resulting larger global energy differences between the most stable neutral and cationic clusters do not influence the experimentally-observed ionization thresholds because the extra energy due to global structural change does not couple to the autoionization process. Therefore, the energy of the cation after ionization increases for larger n, which can lead to the evaporation of one or two methanol molecules, almost impossible to detect in the photoionization experiments. This mechanism also applies to Na(H₂O)_n because of the similar electron-density distribution discussed above. Tsurusawa and Iwata identified semi-internal but also surface electrons in their extensive SOMO analysis, which is in line with our limited straightforward approach.³³ With respect to the related system of electron solvation in neutral water, an extensive theoretical study up to n = 200 indicates that the solvated excess electron can be characterized by surface-bound states.⁴⁷

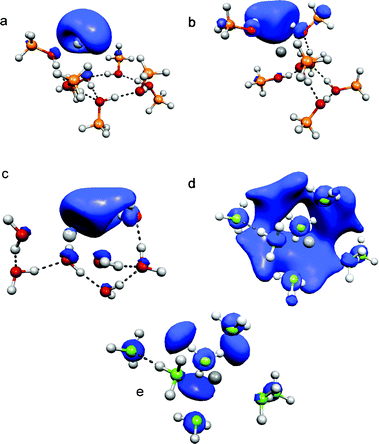Fig. 8 Total spin density distribution (B3LYP) in Na(CH₃OH)₇: (a) exterior structure, (b) interior structure, (c) Na(H₂O)₇, (d) Na(NH₃)₇, and (e) showing frontier orbitals of Na(NH₃)₇ with a higher cut-off value.

In Na(NH₃)_n the Na 3s interaction with the hydrogen-bonded NH₃ topology is of a very different nature. In this system an interior, largely-delocalized electron is excited. Therefore, if a similar mechanism involving autoionization applies, the process is expected to be much less local. By excitation to a highly-excited state, the electron density is reduced in a much larger volume of the clusters. Therefore, autoionization can couple to the energy release induced by structural change in large volume fractions of the clusters and it will consequently depend on cluster size up to very large n, which can give an explanation for the IP evolution of Na(NH₃)_n. This assumption is supported by a recent theoretical study of Shkrob⁴⁸ on excess electron solvation in ammonia. He explains the typical effects of the ammoniated electron by solvent-stabilized multimer radical anions where the excess electron density is shared among the ammonia molecules residing in the frontier orbitals of N-atoms (see Fig. 8e). But the study is limited to ammonia clusters with n = 18 and it is conceivable that for very large clusters two-center states,³ which show a growing distance between the sodium atom and the electron-density peak, also play a role. The calculations of Gao and Liu up to n = 11 show that the local relaxation energies of Na(NH₃)_n isomers grow significantly with increasing n though they fluctuate less than in Na(H₂O)_n or Na(CH₃OH)_n. Interestingly, the agreement of the AIPs with the experimental values is excellent and becomes better for larger n and higher relaxation energies of vertically-ionized isomers (Fig. 7). This supports the assumption that the mechanism pointed out above for Na(CH₃OH)_n also applies for sodium–ammonia where it is no longer local. The studies of electronic spectra of Na(NH₃)_n by Schulz et al. and of NH₄(NH₃)_n by Nonoseet al. support this assumption.^49,50 In both studies the electronic spectra are red-shifted as the first solvation shell is filled, and stay constant or are slightly blue-shifted for larger n (up to n = 22 in ref. 49). The findings for Na(NH₃)_n are similar to Na(H₂O)_n in the study of Schulz et al. discussed above, suggesting that this similarity also holds for excitations to higher excited states. Schulz et al. found an increasing Rydberg-type nature of the solvated electron for both systems with increasing cluster size that they relate to the red-shifts in the excitation spectra. This is different from the hydrated excess electron, the electronic excited states of which are of localized p-type nature.⁴⁶ Similar time-resolved experiments for Na(H₂O)_n or Na(CH₃OH)_n could help to identify common motives and differences in their excitation dynamics but size selection is difficult to obtain for the neutral metal–solvent systems.

The general slow signal rise of Na(NH₃)_n in the photoionization experiments of Steinbach and Buck³ gives further evidence for significant indirect signal contributions at the threshold. However, the theoretical basis for such an interpretation is not robust yet. The methodological difficulties of many quantum-chemical studies are discussed above. Moreover, at present we cannot distinguish what causes the size-dependent IP evolution: the excitation to highly-excited states, the following autoionizing process or the coupling of both. Especially for Na(NH₃)_n, theoretical studies that go beyond n = 20 are needed. They potentially reveal electron-solvation features that can be related to the regions of constant IP found in the experiment.³ As suggested above, both largely-delocalized electrons but also two-center, ion-pair-like states are conceivable.

Conclusions

The processes involved in the photoionization of sodium-doped clusters of hydrogen-bonded solvents are complex. We found strong variations of the ionization potential with the cluster structure, vertical pathways and non-vertical pathways involving autoionization. The remarkable differences between experimental results for ammonia^3,8 and water^7,8 call for a systematic exploration of related solvents. Here we initiate this exploration with methanol and find that its behaviour is close to that of water. The theoretical characterization of Na(CH₃OH)_n with standard quantum-chemical methods reveals that the relative energies of neutral isomers and the energy differences of neutral and cationic clusters depend substantially on the applied methods (B3LYP, MP2). For a detailed comparison of theory with experiment studies at far higher levels of electron correlation treatment are therefore needed. However, the present study indicates that a substantial contribution of indirect ionization at the threshold can explain the difference in Na microsolvation between methanol/water and ammonia. In photoionization experiments with Na(CH₃OH)_n and Na(H₂O)_n, a rather localized electron at or close to the surface is excited to either high Rydberg or more localized states below the vertical ionization threshold. This excitation is followed by a relaxation that couples to an autoionization process. This mechanism is local for Na(CH₃OH)_n and Na(H₂O)_n and depends on the size of the first solvation shell in the cations, which limits the amount of the released local relaxation energy. Therefore the IP evolution stops for n = 6 in Na(CH₃OH)_n and for n = 4 in Na(H₂O)_n because at these n the first cationic solvation shells are complete. Studies with different solvents are needed to test this simple picture. For Na(NH₃)_n, a largely delocalized electron is excited to autoionizing electronic states close to the threshold. This process is no longer local and depends on cluster size up to very large n (n = 1500). To validate the hypothesis, theoretical studies on neutral and cationic Na(NH₃)_nclusters that go well beyond n = 20 are needed. For larger clusters, both a widely delocalized electron or two center states, which show a growing distance between the sodium atom and the electron-density peak, are conceivable. Photoionization experiments for related solvents such as methylamine and ethanolamine will help to further elucidate the solvent–solvated-electron interaction in N–H and O–H hydrogen-bonded clusters. In favourable cases, MATI/ZEKE approaches may provide more detailed information on the ionization threshold.⁵¹ Moreover, size-resolved vibrational data (see ref. 40) would provide valuable information, especially with respect to characterizing the influence of isomer selectivity in photoionization experiments.

Acknowledgements

We thank Prof. Zhi-Feng Liu for fruitful discussions and for providing ref. 24 prior to publication. This project was supported by the DFG research training group GRK 782 (www.pcgg.de). We gratefully acknowledge the help of Dr Christof Steinbach.

References

1. U. Buck and F. Huisken, Chem. Rev., 2000, 100, 3863.
2. G. Lepoutre, Colloque Weyl VI: The Sixth International Conference on Excess Electrons and Metal–Ammonia Solutions, J. Chem. Phys., 1984, 88, 3699.
3. C. Steinbach and U. Buck, J. Chem. Phys., 2005, 122, 134301.
4. N. I. Hammer, J.-W. Shin, J. M. Headrick, E. G. Diken, J. R. Roscioli, G. H. Weddle and M. A. Johnson, Science, 2004, 306, 675.
5. R. Quinn and J. Lagowski, J. Phys. Chem., 1969, 73, 2326.
6. D. A. Copeland, N. R. Kestner and J. Jortner, J. Chem. Phys., 1970, 53, 1189.
7. C. P. Schulz, R. Haugstätter, H.-U. Tittes and I. V. Hertel, Z. Phys. D, 1988, 10, 279.
8. I. V. Hertel, C. Hüglin, C. Nitsch and C. P. Schulz, Phys. Rev. Lett., 1991, 67, 1767.
9. A. Borodin, O. Höfft, U. Kahnert, V. Kempter, Y. Ferro and A. Allouche, J. Chem. Phys., 2004, 120, 8692.
10. C. Bobbert, S. Schütte, C. Steinbach and U. Buck, Eur. Phys. J. D, 2002, 19, 183.
11. J. Jortner, Z. Phys. D, 1992, 24, 247.
12. K. Hashimoto, S. He and K. Morokuma, Chem. Phys. Lett., 1993, 206, 297.
13. R. N. Barnett and U. Landman, Phys. Rev. Lett., 1993, 70, 1775.
14. K. Hashimoto and K. Morokuma, J. Am. Chem. Soc., 1994, 116, 11436.
15. K. Hashimoto and K. Morokuma, J. Am. Chem. Soc., 1995, 117, 4151.
16. F. Misaizu, K. Tsukamoto, M. Sanekata and K. Fuke, Chem. Phys. Lett., 1992, 188, 241.
17. R. Takasu, F. Misaizu, K. Hashimoto and K. Fuke, J. Phys. Chem. A, 1997, 101, 3078.
18. Y. Ferro, A. Allouche and V. Kempter, J. Chem. Phys., 2004, 120, 8683.
19. A. García-Muruais, E. M. Cabaleiro-Lago, J. M. Hermida-Ramón and M. A. Ríos, Chem. Phys., 2000, 254, 109.
20. C. Cézard, B. Bouvier, V. Brenner, M. Defranceschi, Ph. Millié, J. M. Soudan and J. P. Dognon, J. Phys. Chem. B, 2004, 108, 1497.
21. A. Fujii, S. Enomoto, M. Miazaki and N. Mikami, J. Phys. Chem., 1986, 50, 79.
22. L. Turi, J. Chem. Phys., 1999, 110, 10364.
23. A. Kammrath, J. R. R. Verlet, G. B. Griffin and D. M. Neumark, J. Chem. Phys., 2006, 125, 171102.
24. B. Gao and Zhi-Feng Liu, J. Chem. Phys., 2007, 126, 084501.
25. S. Schütte and U. Buck, Int. J. Mass Spectrom., 2002, 220, 183.
26. Y. Ferro and A. Allouche, J. Chem. Phys., 2003, 118, 10461.
27. J. M. Herbst and M. Head-Gordon, J. Phys. Chem. A, 2005, 109, 5217.
28. (a) D. Feller, E. D. Glendening, D. E. Won and M. W. Feyereisen, J. Chem. Phys., 1995, 103, 3526; (b) H. M. Lee, P. Tarakeshwar, J. Park, M. R. Kolaski, Y. J. Yoon, H.-B. Yi, W. J. Kim and K. S. Kim, J. Phys. Chem. A, 2004, 108, 2949.
29. T. E. Salter and A. M. Ellis, J. Phys. Chem. A, 2007, 111, 4922.
30. (a) S. D. Elliot, R. Ahlrichs, O. Hampe and M. M. Kappes, Phys. Chem. Chem. Phys., 2000, 2, 3415; (b) K. Watanabe, J. Chem. Phys., 1954, 22, 1564.
31. A. Radzig and B. Smirnov, Reference Data on Atoms, Molecules and Ions: Springer Series in Chemical Physics, Springer, Berlin, vol. 31, 1985.
32. A. Borodin, O. Höfft, U. Kahnert, V. Kempter and A. Allouche, Phys. Surf. Eng., 2003, 1, 146.
33. T. Tsurusawa and S. Iwata, J. Phys. Chem. A, 1999, 103, 6134.
34. D. Zimmermann, T. Häber, H. Schaal and M. A. Suhm, Mol. Phys., 2001, 99, 413.
35. R. W. Larsen, P. Zielke and M. A. Suhm, J. Chem. Phys., 2007, 126, 194307.
36. T. J. Selegue, N. Moe, J. A. Draves and J. M. Lisy, J. Chem. Phys., 1992, 96, 7268.
37. C. J. Weinheimer and J. M. Lisy, J. Phys. Chem., 1996, 100, 15305.
38. P. Raveendran, D. Zimmermann, T. Häber and M. A. Suhm, Phys. Chem. Chem. Phys., 2000, 2, 3555.
39. B. Hartke, A. Charvat, M. Reich and B. Abel, J. Chem. Phys., 2002, 116, 3588.
40. C. Steinbach and U. Buck, J. Phys. Chem. A, 2006, 110, 3128.
41. J. H. D. Eland, Photoelectron Spectroscopy, Wiley, New York, 1974.
42. K. I. Peterson, P. D. Dao, R. W. Farley and A. W. Castleman, Jr, J. Chem. Phys., 1984, 80, 1780.
43. C. P. Schulz, C. Bobbert, T. Shimasato, K. Daigoku, N. Miura and K. Hashimoto, J. Chem. Phys., 2003, 119, 11620.
44. F. Misaizu, M. Sanekata, K. Fuke and S. Iwata, J. Chem. Phys., 1994, 100, 116.
45. J. I. Lee, D. C. Sperry and J. M. Farrar, J. Chem. Phys., 2001, 114, 6180.
46. A. E. Bragg, J. R. R. Verlet, A. Kammrath, O. Cheshnovsky and D. M. Neumark, Science, 2004, 306, 669.
47. L. Turi, W.-S. Sheu and P. J. Rossky, Science, 2005, 309, 914.
48. I. A. Shkrob, J. Phys. Chem. A, 2006, 110, 3967.
49. P. Brockhaus, I. V. Hertel and C. P. Schulz, J. Chem. Phys., 1999, 110, 393.
50. S. Nonose, T. Taguchi, F. Chen, S. Iwata and K. Fuke, J. Phys. Chem. A, 2002, 106, 5242.
51. X. Peng and W. Kong, J. Chem. Phys., 2002, 117, 9306.
52. C. Steinbach, M. Farnik, I. Ettischer, J. Siebers and U. Buck, Phys. Chem. Chem. Phys., 2006, 8, 752.

---