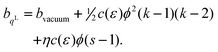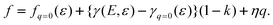Dependence of surface stress, surface energy and surface tension on potential and charge†
Received
18th July 2007
, Accepted 19th October 2007
First published on 16th November 2007
Abstract
A toy model and simple model functions are used to exemplify the relation between surface tension, surface energy and surface stress given by Shuttleworth’s equation. Variations of the surface tension of charged interfaces must obey Lippmann’s equation. Variations Δf of the surface stress of electrodes would be either equal to or proportional to and smaller than those variations Δγ of the surface tension, if the potential of zero charge (pzc) did not depend on the surface strain ε. However, since the pzc E0 is a function of strain ε, the basic dependence of the surface stress on the charge, f(q), is described by a sum of three terms: the first one is the surface stress of the uncharged surface. The second one varies linearly with the surface tension, γ(q), as long as the amount of specific adsorption remains constant, and is quadratic in E and q for a potential-independent double layer capacitance. The third summand that contributes to f(q) is linear in q and is a direct consequence of the potential dependence E0(ε) of the pzc. This result should help to resolve the seeming discrepancy between previous work on the surface stress changes of electrodes: Most experimental and theoretical results supported either the view that the variations of surface stress are identical or similar to that of surface tension, i.e. have essentially a quadratic dependence on the electrode potential, or that the basic dependence is a linear function of the charge. The more comprehensive model description presented here allows an explanation of the different results and their seeming discrepancies without assuming experimental errors or fundamental thermodynamic problems. Furthermore, an estimate of the potential dependence of the surface modulus can be obtained.
1. Introduction
Surface stress changes can be investigated e.g. by the cantilever bending method1 or by measuring the expansion of nanomaterials.2 For electrodes, measurements of surface stress changes have been conducted for decades, starting with the work of Gokhshtein (ref. 3 and references therein) and Beck.4 Although their interpretation was advanced by recent publications on the thermodynamics5 and on ab initio calculations of charged surfaces and their strain,6,7 even the simple question of the basic dependence of the surface stress f on the electrode potential E or on the charge q has not been answered conclusively yet. The community seems split: Many publications, especially most of those published before 1998, describe the dependence of f(E) as comparable to that of the surface tension, γ(E). According to Lippmann’s classical equation8–10| | 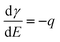 | (1) |
which is important for and confirmed by wetting phenomena at the solid–liquid interface,10 it is expected that γ varies with the square of the charge density q or of the potential E| |  | (2) |
if the double layer capacity c0 is potential-independent, giving q = c0(E−E0) with the potential of zero charge E0.
Eqn (1) neglects a possible potential-dependent strain dε/dE of solid electrodes, but it is valid for massive solid electrodes since dε/dE≈ 0 in that case.11
Often, f(E) parabolas have been shown, e.g. in ref. 4, 12–24 (see Table S1† for details). Accordingly, the function f(E) was described as analogous to γ(E): “The similarity to electrocapillary curves for mercury may be noted”.4 In addition, it has been shown in a theoretical analysis based on Shuttleworth’s equation that the variations of surface stress Δf and that of the tension Δγ can be equal if certain conditions are met.12,14,25 On the other hand, the principal differences between surface stress and tension have been often emphasized, e.g. in ref. 18, 26.
With respect to the fundamental dependence, a paradigm shift occurred in the late 1990’s: Whereas most earlier publications emphasized the parabolic parts of f(E) curves, the linear dependence f(q) was highlighted in later publications. The work of Haiss et al.27–30 is the most important contribution to that paradigm shift, in particular the publication of 1998 that demonstrates a linear dependence of f(q) of a gold electrode over a large potential range28 and that highlights this observation in the title of the work.28 In the following years, the linear f(q) behaviour was confirmed for gold and platinum.2,31–35 Sometimes, the variation Δf was larger than Δγ calculated using the Lippmann equation.21,34,36–38 A remarkable consequence of df/dq = const is that the derivative df/dE of the surface stress change measured during a cyclic voltammogram is proportional to the current I, which means that a graph of df/dE vs. E (“voltstressogram” = derivative of the Δf(E) curve) looks very similar to the voltammogram I(E) itself.18,39 The main features of the df/dE curves shown in ref. 28, 30, 40 are indeed analogous to those of the voltammograms, supporting the underlying linear f(q).39
According to a calculation using the jellium model, the variation of the surface stress is much larger than that of the interfacial tension, but the shape of both curves is parabolic in both cases.20 A similar relation was obtained for the contribution of chloride adions to the stress of an Au(111) surface calculated using statistical thermodynamic theory.41 In contrast to that, essentially linear functions have been predicted for gold clusters6 and for Au(111) and Au(100) surfaces,7 but a parabolic curve for Au(110).7
Haiss demonstrated that the observation of a parabolic behaviour f(E) can be due to experimental artefacts: Parabolic curves with the maximum in the vicinity of the potential of zero charge (pzc) during substrate curvature experiments can be the result of weakening of the adhesion between the thin film electrode and the substrate.30 In that case, the magnitude of the variation of Δf calculated is much smaller than that obtained with optimum conditions.30 According to Haiss, another possible source of difference is the use of rough electrodes, e.g. those obtained by sputtering.30 Another point which is very critical for the investigation of solid electrodes is the adsorption of contamination; it has been demonstrated that dirt can cause a parabolic appearance of f(E).34 In, ref. 12 changes of the surface stress with time have been explained by adsorption of organic impurities, i.e. contamination was mentioned explicitly as a disturbing factor of the surface stress measurement. However, none of these possible interferences alone can explain the striking qualitative difference between the results reported. In particular, it should be mentioned that the extensometer method of Beck4 and the estance technique of Gokhshtein3 have been used with bulk metal electrodes (e.g. with a 0.25 mm thick gold plate42), ruling out film adhesion problems. Although the results of some of the very early publications might suffer from contamination, and although the routine use of high purity chemicals and ultrapure water does not automatically guarantee a contamination-free measurement, it is not likely that all of the more recent measurements are affected. Therefore, the question remains whether the observation of both linear and parabolic shapes of f(q) can be considered as experimental results. In particular, we would like to mention that almost perfect linear curves of derivatives of f have been observed, e.g. the q-estance (df/dq) curves of gold shown in ref. 42.
Here we use a simple model and Lippmann’s classical equation to discuss the basic dependences f(E) and f(q). In principle, f(E) is given by the well known39 Gokhshtein equation
| | 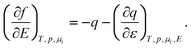 | (3) |
However, the value of the second term d
q/d
ε, the dependence of the charge density
q on the strain
ε, and its potential dependence can be considered as unknown since only very few independent experiments have been done to determine them, giving contradictory results. Often, it was assumed that d
q/d
ε can be neglected,
e.
g. in
ref. 43. Stretching experiments under potentiostatic conditions seem to support that view.
44 However, the difference between the potential of the surface stress maximum and
pzc observed by Valincius demonstrates that d
q/d
ε≠ 0.
42 Here, we would like to base our arguments on the latter publication of Valincius, because it is the only work which used a direct comparison of the surface stress and the
pzc measured for the same electrode in the same electrolyte; in many other cases, literature values have been used for comparison.
2. Surface stress and surface tension. The Shuttleworth equation
2.1 Nomenclature, definitions and basic relations
The surface tension is mechanical work per area of formation of the surface in a reversible process, and at a constant number density n of atoms at the surface;26 it is the superficial work σ in the nomenclature of Linford.45 Here, we define surface stress f as a function of the surface tension γ, according to Shuttleworth’s equation.46 To simplify matters, we use a scalar parameter f for the surface stress as in ref. 26, which is sufficient in the case of isotropic strain and high symmetry surfaces or if mean values are considered, although we emphasize once more that stress and strain are tensorial quantities. For an electrode/electrolyte interface and laboratory coordinates, f is given by Shuttleworth’s equation in its non-tensorial form26,39,45,46| | 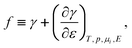 | (4) |
with the strain ε being a true areal strain defined by | |  | (5) |
By integration, this gives | |  | (6) |
γ = γ(ε,E) is a function that gives the surface tension for all possible conditions of ε and E. In the following, we will extract information on the elastic response from the derivatives of the state function γ, cf. ref. 26.
For comparison, we will also consider quantities, especially surface stress fL, surface tension γL and charge density qL, measured using Lagrangian coordinates which are attached to a given piece of matter. In that case, Shuttleworth’s equation reads26,39,47
| | 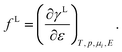 | (7) |
Using
| |  | (8) |
the relations between the quantities measured using different reference frames are obtained:
| |  | (9) |
For any dependence
γL(
ε), the corresponding function in Eulerian coordinates is
γ(
ε) =
γLexp(−
ε), which means that d
γ/d
ε = exp(−
ε) d
γL/d
ε−
γ = exp(−
ε)
fL(
ε) −
γ. Therefore, the difference between
eqn (4) and
(7), the additional first term +
γ in
eqn (4), is just necessary to compensate the −
γ of d
γ/d
ε to obtain
f = exp(−
ε)
fL as expected, which confirms that both forms of Shuttleworth’s equation have the same meaning,
cf. the discussion in
ref. 26.
2.2 Simple model in vacuum
The simple model that we use has been introduced in ref. 26. It uses a solid where the free energy is due to bonds between neighbouring atoms. Let a surface be created, for instance by cleavage, so that there is extra energy, for instance due to broken bonds. A specific surface free energy u can be defined as the extra energy per area. It is identical with the surface tension, provided that there is no adsorption or excess charge. Interatomic bond forces, where they are of interest, will be represented by springs, assuming that each atom has bonds to all of its nearest neighbours. In section 3.2. of ref. 26 the simplest case of the dependence of the surface tension on the strain, γ(ε) = γ0 exp(−ε), has been discussed. In that case, no surface stress occurs.
2.3 Variant with surface stress
Let us consider that the bonds between the surface atoms favour a slightly different lateral interatomic spacing than those in the bulk. We represent the bonds by linear elastic springs of spring constant C, and let the springs in the surface differ from those in bulk by their length. Thus, when the solid is laterally strained, so that the bond length changes from its value a0 in the reference state to a new value a, the energies of the lateral bonds in the bulk and at the surface are ½C (a−a0)2 and ½C (a−aS)2. The difference in the bond energies results in a surface excess energy per bond of ½C (aS−a0) (aS + a0− 2a). Since a = a0 exp(ε/2), we obtain (assuming 4/2 in-plane bonds per atom and a square lattice with n0 = a0−2) | |  | (10) |
For Lagrangian coordinates, we have | | 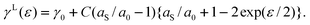 | (11) |
In the two reference frames, we then obtain | | 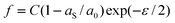 | (12) |
and | | 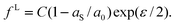 | (13) |
Eqn (12) is obviously correct—which can be used to depict the validity of Shuttleworth’s equation—because the excess force per surface atom is F = C (a0−aS), which gives the surface stress using f = F/a.
The difference between eqn (12) and (13), which is only noticeable at finite strain, arises from the fact that f is an energy per unit area, and that the area differs by a factor of exp(ε) depending on the frame.
The discussion emphasizes here again that the values of γ and of f relate to different microscopic processes at the surface (here, broken out-of-plane bonds versus change of in-plane bond forces). At any given value of the strain, the state function γ(ε) takes on a value which is unrelated to the value f of its strain-derivative.
Calculations of f using the simple model combined with the Lippmann equation are discussed in Section 4.
3. The Lippmann equation
Severe doubts have been raised on the validity of the Lippmann equation for solids.48–51 Therefore, we will shortly reproduce a deduction, cf. ref. 8. In the following, we use the potential ϕ measured with respect to the uncharged surface, | | 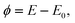 | (14) |
i.e. ϕ is zero at the potential of zero charge.
Let us consider an electrode with an initial state, which is the pzc and a surface area of A0, and a second state with a potential ϕ, the surface tension γ and an area A1, cf. Fig. S1.† One possible way to bring it to the second state is to charge the electrode first, followed by a reversible area increase at the potential ϕ. Since the area increase could be done by cleaving of a solid electrode, the following conclusions are valid for solids as well. The total work required is
| |  | (15) |
with
ω =
ω(
ϕ) being the electrical work per area of charging of the surface starting from
q = 0.
An alternative way to the second state is to do the reversible area change first, and to do the charging afterwards:
| |  | (16) |
Since
WA =
WB due to conservation of energy, we obtain for (
A1−
A0) ≠ 0
| |  | (17) |
This result is a consequence of the fact that surface tension and surface free energy
u (superficial Helmholtz energy
45) are state functions.
8 In the absence of
adsorption considered here,
u is given by
| | 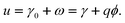 | (18) |
The general relation is the fundamental surface thermodynamic equation45
| |  | (19) |
From
eqn (17), we obtain the classical Lippmann equation by using d
ω/d
ϕ =
ϕc and
c = d
q/d
ϕ. It reads, if the boundary conditions of the derivation, constant temperature, pressure, chemical potential of the components and given surface structure, which also means a constant strain, are added explicitly,
| |  | (20) |
It is clearly valid for liquid electrodes.
8–10,45 The considerations given above show that it is valid for solid electrodes as well, except if there is a potential-dependent strain,
i.e. a variation of the surface density of the atoms if
E is varied. If such a strain occurs in the general case of an arbitrary (non-rigid)
electrode, the generalized Lippmann equation or Couchman(–Davidson) equation has to be used
11,39| | 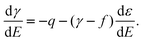 | (21) |
This equation can be derived
11,39 from
eqn (4) (Shuttleworth’s equation). As mentioned in the introduction, d
ε/d
E can be neglected for flat electrodes;
11 in the following part, we assume planar semi-infinite electrodes so that the potential-dependent strain d
ε/d
E can be omitted,
i.e. the classical Lippmann equation is used.
For the special case of a double layer capacitance which is independent of potential, c(E) = c0, the parabola of eqn (2) is obtained
| |  | (22) |
4. Dependence of the surface stress on charge—model calculations
4.1 The dependence of the surface stress on the charge in the case of a strain-independent pzc
Let us use the simple model of Sections 2.2 and 2.3 to consider the effect of surface charge. It is instructive to consider the variant of 2.2 first, where the surface tension of the (charge-neutral) surface is only due to broken bonds, so that there is no surface stress for q = 0.
In our model, the effect of charging on the surface stress is governed by two effects, i) the strain-dependence of c, c(ε), and ii) the strain-dependence of the pzc, E0(ε). For c(ε), we consider two (a priori hypothetical) limiting cases, and arbitrary intermediate functions. In case 1 the charging is via adsorption of ions at specific sites on the surface, with a strain-independent adsorption enthalpy. It has been shown in Section 4.2. of ref. 26 that f is independent of E in that case. A strain-independent adsorption energy is likely to be valid only if the adsorbate–substrate interactions are much stronger than the adsorbate–adsorbate forces; this requires low coverage and/or a significant charge transfer during ion adsorption with a considerable fraction of covalent bonding to the metal. A substantial covalent contribution occurs e.g. for the halide–metal bonds;52 halides form ordered overlayers in-registry with the substrate.52
In case 2 we consider double-layer charging of an electrode in a diluted electrolyte (diffuse double layer charging) with a charge density q which is a function of potential alone. Accordingly, the capacitance per area in laboratory coordinates is independent of ε:26
| | 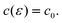 | (23) |
This means that
γ (in laboratory coordinates) has an extra term which is independent of
ε, if
E0 is independent of
ε,
| |  | (24) |
With Shuttleworth’s equation, we find that
| |  | (25) |
In this case, the variations of
f and
γ with
E or
q are identical, and d
f/d
ε = 0.
The same result, Δf = Δγ, was obtained in ref. 12 assuming that df/dε = b, with a potential-independent surface modulus b. In that case f and γ fulfil Shuttleworth’s equation if12
| |  | (26) |
Eqn (26) must satisfy the Lippmann equation; accordingly,
f must be a function of potential and of the capacitance. The function
γ−
γϕ=0, which is a function of the potential
E and of a potential-dependent capacitance
c(
E) in the more general case, does not depend on the strain if
E0,
b and
c(
E) (
i.e. if
adsorption can be neglected) are independent of
ε and if
b is independent of
E. Therefore, the conclusion,
12 that the potential dependence of
γ should be practically identical to that of
f, would be correct if these conditions would be met.
As case 3, let us use an arbitrary function like
| | 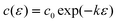 | (27) |
to illustrate simultaneous charging including both the inner Helmholtz layer and the diffuse layer, with typical values of
k between 0 (capacitive charging) and 1 (specific
adsorption), which gives
| |  | (28) |
| |  | (29) |
This illustrates that Δ
f is proportional to Δ
γ and less than it due to the factor (1 −
k) < 1, if the
E0 is constant. Within this simple model, d
f/d
ε = −
k f(
ϕ), which gives a first hint that the potential dependence of
b must not be neglected and that the scenario of
ref. 12 is not the most relevant for electrodes.
4.2 The pzc as a function of the strain
In the following, we take into account the fact that the potential of zero charge E0 depends on the strain, because the work function of the metal depends on ε.5,28,30,53 Based on the experimental results, it was suggested in ref. 53 that the potential is a linear function E0 = E00 + ηlinεlin of the linear strain, εlin = Δl/l0. Since ε = 2 ln (εlin + 1), this gives | |  | (30) |
However, alternative functions might be used to describe the data of ref. 53, using the true areal strain ε as the natural strain parameter. Approximately, E0 is a linear function of the strain: | |  | (31) |
Another possible model function E0(ε) which is analogous to the other exponential strain-dependent functions like eqn (9) or (27) is | | 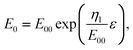 | (32) |
taking into account that the slope dE0/dε should not depend on the value of E00 which changes if it is referred to another reference electrode.
Instead of these three model functions E0(ε) eqn (30)–(32), the general function
| |  | (33) |
will be considered in the following, and the definition
| |  | (34) |
will be used. If
eqn (31) were valid,
η would be a constant, but in the general case,
η is a function
η(
ε) of the strain,
e.
g.
η(
ε) =
ηlin exp(
ε/2) from
eqn (30) or
η(
ε) =
η1 exp(
η1ε /
E00) from
eqn (32).
The strain dependence E0(ε) is expected due to the relation between pzc and the work function which depends on the strain as well.6,54 Within the picture of Smoluchovski, which emphasizes the importance of the surface dipole as the origin of the work function,55 it is easy to visualize a strain dependence of the surface dipole moment by assuming a contraction in the surface normal direction as a consequence of a positive surface strain.
4.3 Surface tension and surface stress
For case 4 of the model calculations, we use the arbitrary function c(ε) = c0 exp(−kε) of case 3 again, the resulting γ(ε) is | |  | (35) |
| |  | (36) |
and | |  | (37) |
Note that the first term is minus half of {the electrical work per area qϕ(1 −k)} which is done by the potentiostat if the surface is strained at constant potential. For potential-independent capacity, the change of γ with ϕ is also minus half of {the electrical work per area qϕ} for charging at constant potential, e.g. during surface area increase by cleavage of a crystal. γ is reduced by only half of qϕ (more precisely, by ω−qϕ in the general case, see eqn (17)) because the other part is still available as useful electrical energy stored in the double layer. The second term of eqn (37) is the electrical work that would be required to charge the surface at a constant potential η; it is the change of electrostatic surface energy due to the change of the pzc. In contrast to the −q2/2 shift which is always negative, the sign of ηq will change for a given η if the polarity of q changes: the energetic consequence of a potential shift η on a surface charge density depends on the sign of q.
For case 5, we omit the restriction of a potential-independent double layer capacity. As an example, we assume that the differential capacitance can be represented by a polynomial:
| | 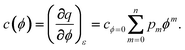 | (38) |
We find by integration at constant strain
| |  | (39) |
We assume that the dependence on the strain is given by
| | 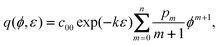 | (40) |
which means that we assume that the dependence on the strain is independent of the charge and that the functional dependence on the strain,
q(
ϕ),
i.e. the coefficients
pm, are independent of the strain.
By integration of the Lippmann equation, we obtain
| |  | (41) |
using again the simple model of
γϕ=0 being proportional to the number of broken bonds.
With Shuttleworth’s equation and dϕ/dε = −η we find that
| | 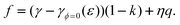 | (42) |
Since we assume flat, rigid non-nanoscaled solid surfaces with d
ε /d
E≈ 0, we can safely neglect the dependencies
γϕ=0(
ε) and
η(
ε) on the strain if we consider the potential dependence
f(
E) (but not if derivatives are considered, see below). In a potential range with a constant amount of
adsorption (
i.e. constant
k),
| |  | (43) |
The ‘error’ of the latter equation is smaller than that of the previous one, which neglects that for actual solids,
f is not zero at the
pzc.
For case 6, we use the simple spring model of Section 2.3. to introduce surface stress at q = 0. In view of the model it might seem obvious that the spring constant or the surface reference lattice parameter aS or both should depend on the potential. However, since the surface tension of a rigid solid must adhere strictly to the classical Lippmann eqn (1), it is possible to argue that all potential-dependent terms are already included if we integrate the charge to obtain γ−γϕ=0. Therefore, in the context of the simple model discussed here, it is sufficient to assume that the strain dependence given by eqn (10) is valid for γϕ=0 of the surface in the electrolyte, i.e. we assume that the surface tension at q = 0 is identical to that in vacuum, and that the dependence on both ε and ϕ can be represented by the sum
| | 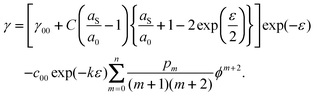 | (44) |
The resulting
f(
ε,
ϕ)is
| |  | (45) |
or
| | 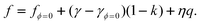 | (46) |
4.4 Alternative model functions
Instead of eqn (27) which was just chosen as a function in between the cases 1 and 2, a function should be considered by assuming that the diffuse double layer capacity and the specific adsorption act as parallel circuit parts of the total capacity, e.g. by presuming that the strain dependence of the sum c = cdiffuse + cspecific could be represented by | | 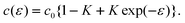 | (47) |
Eqn (42) and (46) remain for stiff surfaces with dε /dE≈ 0, if 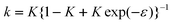 .
.
The assumption of a potential-independent k is not very realistic. In particular, it is expected that the amount of specific adsorption of anions is completely different from that of cations. To test the effect of a potential-dependent strain-capacity parameter k, the approximation exp(−kε) ≈ 1 −εk was used as a starting point, and the function
| | 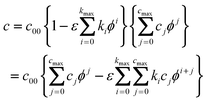 | (48) |
was considered.
The results are
| |  | (49) |
and
| |  | (50) |
It is remarkable that the components
ηq and (
γ−
γϕ=0) still remain as a part of
f which are exactly linear in
q and
γ, although the linearity in
γ might be hidden due to the additional term if
k is not independent of potential.
4.5 General consideration
If we assume—independent of any model considerations—that any of the parameters c, q, or (γ−γq=0) can be written as a product of a function which depends on strain only and another function which depends on the potential only, it is clear that all of these parameters c, q, or (γ−γq=0) can be written as such a product. For example, if we assume that | |  | (51) |
we obtain  and
and  , whereas
, whereas 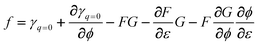 or
or 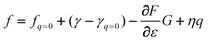 . The summand ηq is a direct consequence of the fact that both q and f are derivatives of γ.
. The summand ηq is a direct consequence of the fact that both q and f are derivatives of γ.
5. Discussion and comparisons using the Maxwell equation and Gokhshtein’s equation
Eqn (43), (44), (46) and (50) are important results since they reproduce central features of γ and f. The underlying physical picture and the related eqn (27) or (47) for c(ε) and (30)–(32) for E0(ε) are realistic in the sense that they catch main characteristics of the changes of f in an electrolyte, although they are as simplistic as the naïve assumption of a potential-independent c0 that is often used to illustrate the basic potential dependence of γ. The equations demonstrate that a linear dependence of f(q), with a slope of η can be expected if η≫½(E−E0) (1 −k), i.e. for potentials close to the pzc. The fundamental dependence is parabolic, but the maximum is shifted to the potential E0 + η/(1 −k), see Fig. 1. Since |η| is in the order of 1 V,7,53 this is a considerable shift, and the maximum can be outside of a typical electrochemical window used for surface stress measurements, e.g. in ref. 28–33.
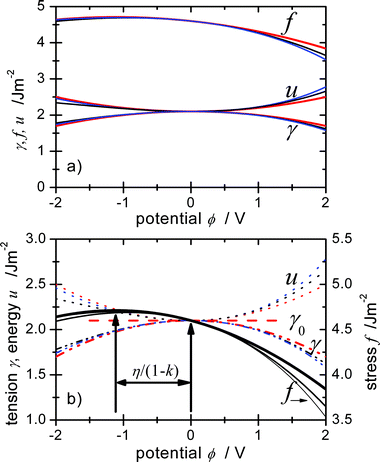 |
| | Fig. 1 Dependence of surface tension γ, surface stress f and surface energy u on the electrode potential, calculated for different double layer capacities (e.g. 20 μF cm−2 and {20 + 6 ϕ/V} μF cm−2) and assuming that the charging is mainly capacitive. γ and u are obtained using Lippmann eqn (20) and eqn (18), i.e. the ∑μiγi terms of eqn (19) which include the superficial amounts of substances γi are neglected here. f follows from eqn (46) based on the simple model functions with typical values: η = −1 V, cf. the values of df/dq of −0.91 V for Au(111) in HClO430 or −1.9 V for platinum in NaF.33 The values of γ0 = 2.1 J m−2 and f0 = 4.6 J m−2 have been chosen after calculating mean values of γ and f given in ref. 30 for different metals and surfaces, to obtain a typical picture. To consider mainly double layer charging, k = 0.1 was applied, neglecting a possible potential dependence. (a) Overview showing that the absolute values remain quite constant even for the very large potential window displayed. (b) Comparison between f and γ demonstrating the large shift of the extrema of η/(1−k) and that the variation Δf is much larger than Δγ at the pzc and for ϕ > 0. | |
Close to the pzc, the quadratic contribution is still a component of f which contributes to the phenomena in real experiments; however, the linear response given by ηq dominates the dependencies f(E) and f(q). This is illustrated in Fig. 2, S2 and S3,† which use eqn (46) to predict the surface stress of Au surfaces in perchloric acid.
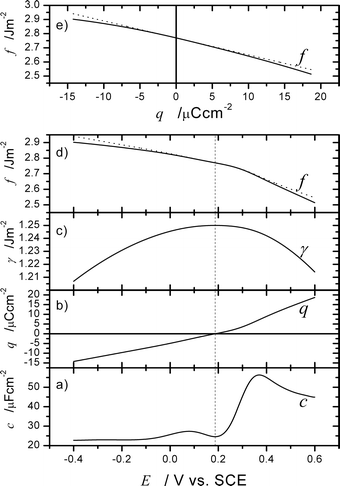 |
| | Fig. 2 Illustration of the use of eqn (46) to predict surface stress curves based on electrochemical data. (a) Double layer capacity of the non-reconstructed Au(111) surface in 10 mM HClO4. Data taken from Fig. 3(b) of ref. 56. (b) Charge density q obtained by integration of (a) and by assuming that the minimum indicates the pzc. (c) Surface tension γ obtained by integration of (b) and by taking γ0 = 1.25 J m−2.30 (d) and (e) Surface stress as predicted by eqn (46) by assuming k = 0.1 to indicate the weak adsorption of perchlorate56 and η = −1.2 V. The dotted line indicates the predicted value of f if the surface tension contribution, (γ−γ0)(1 −k) is neglected, demonstrating that the ηq contribution dominates the variation of f. This is also apparent by a comparison of (b) and (d). Note the large variation of f compared to the variation of γ. | |
The linear contribution ηq is a direct consequence of the shift of the potential of zero charge ΔE0 with the strain ε. At the same time, it is a consequence of the linear response of f on the changes of the lateral bonding in the metal due to changes in q.6 The microscopic origin of this linear contribution to f in metals is a consequence of the charge dependence of the stretch,6 which is a displacement of the atoms in the normal direction: The change of the surface stress reflects “the transverse contraction tendency by which the matter at the surface responds to the stretch”.6 The picture suggested in Section 4.2 above, the contraction of the surface dipole during straining, which results in a reduction of the work function and therefore in a shift of the pzcΔE0 = ηε, gives the result that the slope of f(q) is dominated by η. The arguments in ref. 6 are the reverse of that, since the starting point is the normal displacement of the surface atoms caused by the charge, but both lines of argument are analogous since they are based on a response in the normal direction. In the simplest case, the surface dipole and the work function will be reduced due to strain, which means that η is expected to be negative in the case of metals.
In ref. 6, the quadratic term is considered negligible for metal surfaces in an electrolyte, but it contributes noticeably to the relaxation behaviour of metal clusters charged in a vacuum.
The surface-stress charge density coefficient ς is defined as the derivative of f with respect to the charge density at constant strain,5,33
| |  | (52) |
The Maxwell equation
5,30,42,48–50| |  | (53) |
derived first by Gokhshtein, relates the surface stress derivatives
ς or
ςL with the variation of the potential at constant charge density
qL. Lagrange coordinates are indicated with the
L,
ς =
ςL. During straining of an electrode,
qL is constant if the total charge
Q is constant,
i.e. qL is a very useful quantity which is relevant for experiments.
We obtain from eqn (37)
| |  | (54) |
This result is as expected: the first term,
η, describes the potential shift due to the change of the
pzc, d
E0/d
ε. The second one is the shift of
E due to the change of charge density,
q =
qLexp(−
ε) at constant
qL (in contrast to constant
E conditions with
q =
qε=0 exp(−
kε)).
From eqn (53) and (54), it is obvious that the value of η is identical to the surface-stress charge density coefficient ς at the pzc. The value of ς has been shown to get smaller with increasing bond strength;30 therefore, the observation of the surface stress maximum in 0.1 M KCl in ref. 4, 18 and 21 might be a result of the relatively strong adsorption of chloride ions and a small value of η. The latter case, with η≈ 0, is expected for the Au(110) surface.7
If ς is measured using potential modulation with high frequency, it is identical to the q-estance,42 as measured by Gokhshtein.3 Within the assumptions above, ς is a linear function of the charge and of the potential, eqn (54). Therefore, it is not surprising that an almost perfectly linear dependence of ς vs. E was observed in q-estance experiments, e.g. by Gokhshtein for a lead surface,57,58 also shown in ref. 48–50 and 59, or for gold in perchloric acid.42 There is no contradiction to the experimental observations of an almost linear f(q) in ref. 27, 31–33 and 35.
The experimental result that Δf can be larger than Δγ21,36–38 and that f(q) is often linear can not be explained within the framework of cases 1–3 in Section 4.1 above, but they are an obvious possibility for the conditions of the model cases 4–6. This demonstrates the significance of the pzc shift with respect to an explanation of the properties of f. An additional consequence of the pzc shift is that  is to be expected as a rule rather than the exception; this has sometimes been overlooked, e.g. in eqn (20) of ref. 60. For the model,
is to be expected as a rule rather than the exception; this has sometimes been overlooked, e.g. in eqn (20) of ref. 60. For the model,  , eqn (3) is fulfilled. For purely capacitive charging of the diffuse layer, k = 0, and
, eqn (3) is fulfilled. For purely capacitive charging of the diffuse layer, k = 0, and  . It is remarkable that this materials parameter of the interface26 is the product of η which is dominated by the behaviour of the metal, and of c, which depends strongly on the electrolyte, e.g. on the concentration.
. It is remarkable that this materials parameter of the interface26 is the product of η which is dominated by the behaviour of the metal, and of c, which depends strongly on the electrolyte, e.g. on the concentration.
If k would have a negligible potential dependence for a large interval (which might be the case for weakly adsorbing conditions), it would be possible to determine the parameters k and η from high quality experimental f and q data by using eqn (43) and a fitting procedure. The pzc E0 is an additional parameter of such a fit, but it is not independent of η: For any suggested value of η, the corresponding pzc can be determined, e.g. as the potential of the maximum of an f−qη plot. Therefore, the combination of a surface stress measurement with such a fit can be considered as a possible independent means of determining the pzc, e.g. for concentrated solutions for which a determination from the double layer capacitance is not possible. This is remarkable due to the importance of this parameter for the interface.‡
Finally, we would like to consider the surface modulus b, b = df /dε, i.e. the derivative of the surface stress with strain. In principle, several different moduli are possible for charged surfaces. Probably bE = (df/dε)E measured at constant potential is the most important one, but the value bqL = (df/dε)Q for a constant total surface charge Q (constant Lagrangian charge density qL) is accessible in experiments as well. To calculate the moduli, it is necessary to specify the function η(ε). Again, an arbitrary model function, for example
| |  | (55) |
is used. According to the model functions used here (
eqn (27), (37), (46)), the moduli are
| |  | (56) |
and (for a potential-independent capacitance)
| | 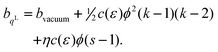 | (57) |
The moduli
bE and
bqL depend strongly on potential and on charge, with a contribution which is linear in charge and which is dominant if
η is of the order of 1 V. The variations of the modulus Δ
bE are approximately identical to the variations Δ
f of the stress, about 1 J m
−2 for Δ
E = 1 V (
Fig. 1). This was neglected in
ref. 12, causing the mostly incorrect result Δ
γ = Δ
f. Even at
q = 0, the modulus
bE of a surface in an electrolyte differs from that in a vacuum (
c≈ 0) by the −
η2c contribution, which might take typical values between −0.01 J m
−2 and −2 J m
−2.
6. Summary
A simple model has been used to describe the surface tension. The following assumptions have been made:
i) Simple model functions such as c(ε) = c0 exp(−kε) or c(ε) = c0 {1 −K+K exp(−ε)} describe the dependence of the capacity c on the strain ε. This is simplistic, but it is a reasonable general model since it gives a correct description of the limiting cases of strong specific adsorption (k→ 1 and K→1) and diffuse double layer charging (k→ 0 and K→1).
ii) There is no additional dependence of the charge function q(ϕ) on strain, i.e. q(ϕ) is given by the product of eqn (39).
iii) The potential of zero charge E0 is a function of the strain, and we define η(ε) as the derivative dE0 /dε, eqn (34).
iiii) The charge-induced strain and the corresponding dε/dE term in eqn (21) can be neglected, e.g. because the electrode is a rigid or massive, flat solid.
Since the surface tension must obey Lippmann’s eqn (1), its dependence on charge q or on potential E is known if c(E) is known. By using Shuttleworth’s equation, the dependence of the surface stress on strain and on potential was obtained. The following conclusions can be made:
1. According to the model, the surface stress f of an electrode is given as
Its variations with the potential are not identical to the variations of
γ, most notably due to the
ηq term. Δ
f > Δ
γ is possible for |
η| > 0, which is to be expected for metals.
2. The basic dependence of surface stress on potential—which is obtained by making the additional assumptions that the strain parameter k and the capacity c are potential-independent—is parabolic:
f as a function of potential or of charge
q contains the sum of a linear and a quadratic term, which are of comparable magnitude.
3. On the potential scale, the f(E) curve is shifted compared to that of γ(E) by η /(1 −k). Therefore, both types of experimental results of f(E) or f(q) curves can be correct depending on the potential window used for their measurement: parabolic curves f(E) with a visible maximum are expected if f would be investigated near E0 + η /(1 −k). A linear dependence f(q) is expected close to E0.
4. Although we emphasize that parabolic curves are to be expected in general, which means that such curves reported in the literature might be correct and not an experimental artefact as suggested previously, we would like to point out that the shift η/(1 −k) of the maximum on the potential scale can be large, since η is comparable to the surface stress-charge density coefficient ς, which has values as large as −1.9.33 For such large shifts, the corresponding maximum of f is likely to be outside the measurable potential window.
From a work function point of view, η values of the order of −1 V seem reasonable for metals. η might be smaller for carbon, which means that the surface stress of carbon electrodes might vary similar to the surface tension. Parabolic shapes of f(E) have been observed indeed for carbon,16,17 and if we assume that η is small, the maxima would be close to the potential of zero charge.
5. The equation given is derived from γ fulfilling the original Lippmann equation. The linear term ηq is a direct consequence of the dependence of the pzc on the stain which must not be neglected since the experimental result of Δf > Δγ can not be explained for η = 0.
6. The derivative of the charge density with respect to strain, dq/dε, has the same order of magnitude as the charge density; dq/dε might be even larger than q. It must not be neglected during the use of the Gokhshtein eqn (3). From the model,
d
q/d
ε≠ 0 is the rule and not an exception.
7. The surface moduli of electrodes depend strongly on potential; see eqn (56) and (57).
Although the model functions are simplistic, it seems reasonable to assume that the result is meaningful, not only because the conclusions can be made independent of the detailed model—alternative functions like eqn (47), c(ε) = c0 {1 −K + K exp(−ε)}, instead of c(ε) = c0 exp(−kε) give practically the same result—but rather because the basic assumptions—the validity of Shuttleworth’s equation and Lippmann’s equation—must be met at least for surfaces of rigid solids. In particular, it is noted that the result of a linear contribution ηq is obtained for all functions E0(ε), including the simple linear relation E0 = E00 + ηε and exponential functions like eqn (30) and (32), and for the case of a capacity function c(ε) with a potential-dependent response to straining according to eqn (48).
For the discussion of adsorption-induced stress, a simple model has been developed as well,61 clearly demonstrating the demand of easy models to understand surface stress effects. In contrast to the model functions of surface parameters like c or q used here, the model of ref. 61 is based on atomistic interactions which are treated using the Lennard-Jones potential formula, which introduces two known parameters into the model.
Finally, we would like to mention that a change in the adsorption regime can result in a ‘sudden’ change of the slope of a f(q) curve, resulting in several linear intervals, e.g. as shown in ref. 35 and 62. This might be influenced by a pronounced potential dependence k(E), but the even more important effect is a possible change of the value of η.35 The model results in several intersecting parabolas then, and segments of different slope occur. In such a case, the maximum value of the measured surface stress curve can represent an intersection point which does not coincide with the maximum of a parabola.
Acknowledgements
Thanks to Maxim Smetanin for helpful discussions and for pointing out some relevant publications. Thanks to Dr Huiling Duan and to Dr Jörg Weissmüller for helpful discussions.63–66
References
- H. Ibach, The role of surface stress in reconstruction, epitaxial growth and stabilization of mesoscopic structures, Surf. Sci. Rep., 1997, 29, 193–263 CrossRef CAS.
- J. Weissmüller, R. N. Viswanath, D. Kramer, P. Zimmer, R. Würschum and H. Gleiter, Charge-Induced Reversible Strain in a Metal, Science, 2003, 300, 312–315 CrossRef CAS.
- A. Y. Gokhshtein, Investigation of surface tension of solid electrodes at several frequencies simultaneously, Electrochim. Acta, 1970, 15, 219–223 CrossRef CAS.
- T. R. Beck, “Electrocapillary Curves” of Solid Metals Measured by Extensometer Instrument, J. Phys. Chem., 1969, 73, 466–468 CrossRef CAS.
- J. Weissmüller and D. Kramer, Balance of Force at Curved Solid Metal–Liquid Electrolyte Interfaces, Langmuir, 2005, 21, 4592–4603 CrossRef CAS.
- F. Weigend, F. Evers and J. Weissmüller, Structural Relaxation in Charged Metal Surfaces and Cluster Ions, Small, 2006, 2, 1497–1503 CrossRef CAS.
- Y. Umeno, C. Elsässer, B. Meyer, P. Gumbsch, M. Nothacker, J. Weissmüller and F. Evers,
Ab initio study of surface stress response to charging, Europhys. Lett., 2007, 78, 13001-p1–13001-p5.
- G. Lippmann, Relations entre les phénomènes électriques et capillaires, Ann. Chim. Phys., 1875, 5, 494–549 Search PubMed.
- D. C. Grahame, The electrical double layer and the theory of electrocapillarity, Chem. Rev., 1947, 41, 441–501 CrossRef CAS.
- F. Mugele and J.-Ch. Baret, Electrowetting: from basics to applications, J. Phys.: Condens. Matter, 2005, 17, R705–R774 CrossRef CAS.
- J. Lipkowski, W. Schmickler, D. M. Kolb and R. Parsons, Comments on the thermodynamics of solid electrodes, J. Electroanal. Chem., 1998, 452, 193–197 CrossRef CAS.
- R. A. Fredlein and J. O’M. Bockris, An “electrocapillary” study of the gold-perchloric acid solution interface, Surf. Sci., 1974, 46, 641–652 CrossRef CAS.
- R. A. Fredlein, A. Damjanovic and J. O’M. Bockris, Differential Surface Tension Measurements at Thin Solid Metal Electrodes, Surf. Sci., 1971, 25, 261–264 CrossRef CAS.
- K. F. Lin and T. R. Beck, Surface Stress Curves for Gold, J. Electrochem. Soc., 1976, 123, 1145–1151 CrossRef CAS.
- N. Pangarov and G. Kolarov, “Electrocapillary” curve on solid metal obtained by holographic interferometry, J. Electroanal. Chem., 1978, 91, 281–285 CrossRef CAS.
- Y. Oren and A. Soffer, The electrical double layer of carbon and graphite electrodes: Part III. Charge and dimensional changes at wide potential range, J. Electroanal. Chem., 1986, 206, 101–114 CrossRef CAS.
- D. Golub, Y. Oren and A. Soffer, Electroadsorption, the electrical double layer and their relation to dimensional changes of carbon electrodes, Carbon, 1987, 25, 109–117 CrossRef CAS.
- R. Raiteri and H.-J. Butt, Measuring Electrochemically Induced Surface Stress with an Atomic Force Microscope, J. Phys. Chem., 1995, 99, 15728–15732 CrossRef CAS.
- G. Láng and K. E. Heusler, Changes of the specific surface energy of gold due to the chemisorption of sulfate, J. Electroanal. Chem., 1995, 391, 169–179 CrossRef CAS.
- W. Schmickler and E. Leiva, A note on the surface stress and tension of solid metal electrodes, J. Electroanal. Chem., 1998, 453, 61–67 CrossRef CAS.
- K. Ueno and M. Seo, Study of Adsorption of Iodide Ions on Gold Electrode by a Laser-Beam Deflection Method Compared with a Piezoelectric Technique, J. Electrochem. Soc., 1999, 146, 1496–1499 CrossRef CAS.
- S. J. O'Shea, M. E. Welland, T. A. Brunt, A. R. Ramadan and T. Rayment, Atomic force microscopy stress sensors for studies in liquids, J. Vac. Sci. Technol., B, 1996, 14, 1383–1385 CAS.
- T. A. Brunt, E. D. Chabala, T. Rayment, S. J. O'Shea and M. E. Welland, Measuring surface stress induced by electrode processes using a micromechanical sensor, J. Chem. Soc., Faraday Trans., 1996, 92, 3807–3812 RSC.
- G. G. Láng, M. Seo and K. E. Heusler, Simultaneous oscillations of surface energy, superficial mass and electrode potential in the course of galvanostatic oxidation of formic acid, J. Solid State Electrochem., 2005, 9, 347–353 CrossRef CAS.
- D. M. Mohilner and T. R. Beck, Thermodynamic Theory of Electrocapillarity for Solid Metal Electrodes, J. Phys. Chem., 1979, 83, 1160–1166 CrossRef CAS.
- D. Kramer and J. Weissmüller, A note on surface stress and surface tension and their interrelation via Shuttleworth’s equation and Lippmann’s equation, Surf. Sci., 2007, 601, 3042–3051 CrossRef CAS.
- W. Haiss and J. K. Sass, Adsorbate-induced surface stress at the solid|electrolyte interface measured with an STM, J. Electroanal. Chem., 1995, 386, 267–270 CrossRef CAS.
- W. Haiss, R. J. Nichols, J. K. Sass and K. P. Charle, Linear correlation between surface stress and surface charge in anion adsorption on Au(111), J. Electroanal. Chem., 1998, 452, 199–202 CrossRef CAS.
- R. J. Nichols, T. Nouar, C. A. Lucas, W. Haiss and W. A. Hofer, Surface relaxation and surface stress of Au(111), Surf. Sci., 2002, 513, 263–271 CrossRef CAS.
- W. Haiss, Surface stress of clean and adsorbate-covered solids, Rep. Prog. Phys., 2001, 64, 591–648 CrossRef CAS.
- H. Ibach, Stress in densely packed adsorbate layers and stress at the solid–liquid interface—is the stress due to repulsive interactions between the adsorbed species?, Electrochim. Acta, 1999, 45, 575–581 CrossRef CAS.
- D. Kramer, R. N. Viswanath and J. Weissmüller, Surface-Stress Induced Macroscopic Bending of Nanoporous Gold Cantilevers, Nano Lett., 2004, 4(5), 793–796 CrossRef CAS.
- R. N. Viswanath, D. Kramer and J. Weissmüller, Variation of the Surface Stress-Charge Coefficient of Platinum with Electrolyte Concentration, Langmuir, 2005, 21, 4604–4609 CrossRef CAS.
-
V. Tabard-Cossa, Microcantilever Actuation Generated by Redox-induced Surface Stress, PhD Thesis, McGill University, Montréal, 2005.
- R. N. Viswanath, D. Kramer and J. Weissmüller, Adsorbate Effects on the Surface Stress-Charge Response of Platinum Electrodes, Electrochim. Acta, 2007 DOI:10.1016/j.electacta.2007.10.049.
- H. Ibach, C. E. Bach, M. Giesen and A. Grossmann, Potential-induced stress in the solid–liquid interface; Au(111)and Au(100) in an HClO4 electrolyte, Surf. Sci., 1997, 375, 107–119 CrossRef CAS.
- R. N. Viswanath, J. Weissmüller, R. Würschum and H. Gleiter, Charge-Influenced Structural Properties of Electrically Connected Platinum Nanoparticles, Mater. Res. Soc. Symp. Proc., 2001, 676 Search PubMed , Y6.10.
- M. Seo and Y. Serizawa, Changes in Surface Stress of Platinum Electrode in Acidic and Alkaline Sulfate or Alkaline Fluoride Solutions, J. Electrochem. Soc., 2003, 150, E472–E476 CrossRef CAS.
- J. Proost, Thermodynamic issues associated with combined cyclic voltammetry and wafer curvature measurements in electrolytes, J. Solid State Electrochem., 2005, 9, 660–664 CrossRef CAS.
- W. Haiss and J.-K. Sass, Quantitative Surface Stress Measurements on Au(111) Electrodes by Scanning Tunneling Microscopy, Langmuir, 1996, 12, 4311–4313 CrossRef CAS.
- R. Xie, D. Chen, X. Wang, T. He and F.-C. Liu, Adsorbate-Induced Surface Stress of Chloride Monolayer on Au(111) Electrode, J. Phys. Chem. B, 2002, 106, 12948–12956 CrossRef CAS.
- G. Valincius, Elastic Electrocapillary Properties of Polycrystalline Gold, Langmuir, 1998, 14, 6307–6319 CrossRef CAS.
- M. Seo and K. Ueno, Piezoelectric Detection of Changes in Surface Energy of Gold Electrode in Perchlorate Solutions Containing Iodide Ions, J. Electrochem. Soc., 1996, 143, 899–904 CrossRef CAS.
- T. Agladze and A. Podobayev, The study of specific adsorption of a polar solvent at solid electrodes by means of step elastic stretching under potentiostatic conditions, Electrochim. Acta, 1991, 36, 859–867 CrossRef CAS.
- R. G. Linford, The derivation of thermodynamic
equations for solid surfaces, Chem. Rev., 1978, 78, 81–95 CrossRef CAS.
- R. Shuttleworth, The Surface Tension of Solids, Proc. Phys. Soc., London, Sect. A, 1950, 63, 444–457 CrossRef.
-
J. W. Cahn, in Interfacial Segregation, ed. W. C. Johnson and J. M. Blakely, ASM, Metals Park, OH, 1979, p. 3 Search PubMed.
- V. A. Marichev, Methodological Aspects of the Partial Charge Transfer in the Adsorption of Anions. Part I, Protect. Met., 2003, 39(6), 505–520 Search PubMed (translation of V. A. Marichev, Zashch. Met., 2003, 39, 565–582 Search PubMed ).
- V. A. Marichev, Partial charge transfer during anion adsorption—Methodological aspects, Surf. Sci. Rep., 2005, 56, 277–324 CrossRef CAS.
- V. A. Marichev, Structure–mechanical approach to surface tension of solids, Surf. Sci., 2006, 600, 4527–4536 CrossRef CAS.
- V. A. Marichev, Plastic deformation and surface tension of solids, Chem. Phys. Lett., 2007, 434, 218–221 CrossRef CAS.
- O. M. Magnussen, Ordered Anion Adlayers on Metal Electrode Surfaces, Chem. Rev., 2002, 102, 679–725 CrossRef CAS.
- Á. Horváth and R. Schiller, The effect of mechanical stress on the potential of the Ag/Ag+ electrode, Phys. Chem. Chem. Phys., 2001, 3, 2662–2667 RSC.
- W. Li and D. Y. Li, Effects of elastic and plastic deformations on the electron work function of metals during bending tests, Philos. Mag., 2004, 84, 3717–3728 CrossRef CAS.
- R. Smoluchowski, Anisotropy of the Electronic Work Function of Metals, Phys. Rev., 1941, 60, 661–674 CrossRef CAS.
- D. Eberhardt, E. Santos and W. Schmickler, Impedance studies of reconstructed and non-reconstructed gold single crystal surfaces, J. Electroanal. Chem., 1996, 419, 23–31 CrossRef CAS.
- A. Ya. Gokhshtein, Elektrokhimiya (Engl. Transl.), 1971, 7, 3 Search PubMed.
-
A. Ya. Gokhshtein, in Poverkhnostnoe natyazhenie tverdykh tel i adsorbtsiya (Surface Tension of Solids and Adsorption), ed. A. N. Frumkin, Nauka, Moscow, 1976, p. 400 Search PubMed.
- I. Morcos, The electrocapillary phenomena of solid electrodes, J. Electroanal. Chem., 1975, 62, 313–340 CrossRef.
- C. Friesen, N. Dimitrov, R. C. Cammarata and K. Sieradzki, Surface Stress and Electrocapillarity of Solid Electrodes, Langmuir, 2001, 17, 807–815 CrossRef CAS.
- D. W. Dareing and T. Thundat, Simulation of adsorption-induced stress of a microcantilever sensor, J. Appl. Phys., 2005, 97, 043526 CrossRef (5 pages).
- M. Seo and M. Yamazaki, Changes in Surface Stress of Gold Electrode during Underpotential Deposition of Pb, J. Electrochem. Soc., 2004, 151, E276–E281 CrossRef CAS.
- I. O. Efimov and K. E. Heusler, Electrocapillary curves of polycrystalline gold in aqueous solutions of pyridine, J. Electroanal. Chem., 1996, 414, 75–80 CrossRef CAS.
- L. Jaeckel, G. Láng and K. E. Heusler, A new interferometric method to investigate surface energies at solid electrodes, Electrochim. Acta, 1994, 39, 1031–1038 CrossRef CAS.
- M. Seo, X. C. Jiang and N. Sato, Piezoelectric Response to Surface Stress Change of Gold Electrode in Sulfate Aqueous Solutions, J. Electrochem. Soc., 1987, 134, 3094–3098 CAS.
- R. E. Malpas, R. A. Fredlein and A. J. Bard, The piezoelectric measurement of electrocapillary curves, J. Electroanal. Chem., 1979, 98, 339–343 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: Table S1 (with ref. 63–66), Fig. S1, Fig. S2 and Fig. S3. See DOI: 10.1039/b710065e |
| ‡ The practical value of this proposed pzc determination method is limited by the difficulty of predicting the behaviour of k. Furthermore, a large potential window and a very high accuracy in the determination of f(q) are required, because the method relies on the deviation of the f(q) from a straight line. This deviation is very small, see Fig. 2. |
|
| This journal is © the Owner Societies 2008 |
Click here to see how this site uses Cookies. View our privacy policy here. 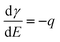

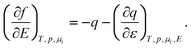
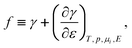


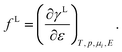



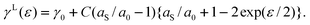
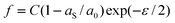
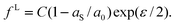
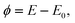



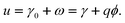


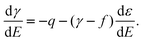

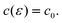



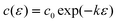




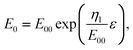





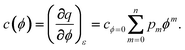

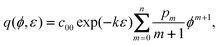

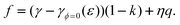

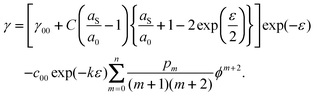

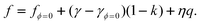
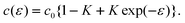
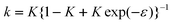 .
.
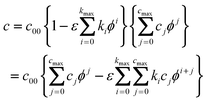



 and
and  , whereas
, whereas 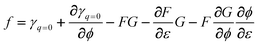 or
or 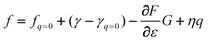 . The summand ηq is a direct consequence of the fact that both q and f are derivatives of γ.
. The summand ηq is a direct consequence of the fact that both q and f are derivatives of γ.





 is to be expected as a rule rather than the exception; this has sometimes been overlooked, e.g. in eqn (20) of ref. 60. For the model,
is to be expected as a rule rather than the exception; this has sometimes been overlooked, e.g. in eqn (20) of ref. 60. For the model,  , eqn (3) is fulfilled. For purely capacitive charging of the diffuse layer, k = 0, and
, eqn (3) is fulfilled. For purely capacitive charging of the diffuse layer, k = 0, and  . It is remarkable that this materials parameter of the interface26 is the product of η which is dominated by the behaviour of the metal, and of c, which depends strongly on the electrolyte, e.g. on the concentration.
. It is remarkable that this materials parameter of the interface26 is the product of η which is dominated by the behaviour of the metal, and of c, which depends strongly on the electrolyte, e.g. on the concentration.