Investigation of entrance and exit effects on liquid transport through a cylindrical nanopore

Abstract

The entrance and exit effects on liquid transport through a nano-sized cylindrical pore under different solid wall–liquid interactions were studied by comparing molecular dynamics (MD) results of a finite length nanopore in a membrane with those of an infinite length one. The liquid transport through a finite length nanopore in a membrane was carried out by using a pressure-driven non-equilibrium molecular dynamics (NEMD) method proposed by Huang et al. [C. Huang, K. Nandakumar, P. Choi and L. W. Kostiuk, J. Chem. Phys., 2006, 124, 234701]. The fluid motion through an infinite length nanopore, which had the same cross-stream dimension as the finite length channel in the membrane, but with periodic boundary conditions in the stream-wise direction, was carried out by using the external-field driven NEMD approach [J. Koplik, J. R. Bavanar and J. F. Willemsen, Phys. Rev. Lett., 1988, 60, 1282]. The NEMD results show that the pressure and density distributions averaged over the channel in the radial direction in both finite and infinite length channels are similar, but the radial distributions of the stream-wise velocity were significantly different when the solid wall was repulsive. The entrance and exit effects lead to a decrease in flow rate at about 39% for the repulsive wall and 6% for the neutral-like wall.

---

1. Introduction

Transport of materials through a finite length nano-channel is an important problem common to a variety of natural phenomena and industrial processes such as protein translocation, DNA transfer across nuclear pores, gene swapping between the guest and host bacteria through pili,^1–9membrane separation of mixtures,^10,11 electrokinetic channel battery,¹² molecular transport in crystalline nanochannels¹³ and silicalite,¹⁴etc. For fluid transport in such small confined channels, the classical continuum approach may not be valid.^15–18 To gain insights into such problems, molecular dynamics (MD) simulation is probably the best choice as the length scale of systems of interest is comparable to the size of molecules. In many earlier MD works, such as Couette^19–24 and Poiseuille flow,^{17,18,20,22,25–29} periodic boundary conditions were usually used. The results correspond to a steady state flow through an infinitely long channel. Such an approach, however, is not suitable to describe the process of fluid transport through a finite length nanopore due to the fact that entrance and exit effects of the channel and changes of fluid properties in the flow direction on fluid transport are not taken into account. Zhang et al.¹⁰ indicated that the entrance effect of fluids into pores plays an important role in mass transfer and separation processes for membrane separation. However, to the best of our knowledge, such influence for a pressure driven flow through a nanoscale channel has not been studied.

The algorithms commonly used to study fluid transport through a finite length nanopore include the external-field driven non-equilibrium molecular dynamics (NEMD) simulation^30,31 and the dual-control-volume grand-canonical molecular dynamics (DCV-GCMD) simulation.^10,32–39 In the first method, a constant external force is exerted on all or partial liquid molecules. The pressure fields in the reservoirs (located at the front and back of the nanopore), generated by this method, are not constant. Rather, they are a function of distance in the force direction. In the second method, particle insertion and deletion are required to maintain a constant density or chemical potential difference between the inlet and outlet of the channel. The inserting and deleting of particles, especially for a dense system, can significantly disturb the dynamic field. Differing from these methods, Huang et al.⁴⁰ recently proposed an alternative approach which uses two self-adjusting plates on which two external forces are exerted to generate constant pressure fields in the front and back reservoirs that are connected to the inlet and outlet of the nanopore. This method has been used to study monatomic flows,⁴¹ but it is anticipated that it could also be used to investigate multi-component flows, such as diluted DNA or polymer molecules suspending in a solvent transport through a nanopore in a membrane driven by a constant pressure difference or a combination of electrical field and pressure difference. In this paper, we applied an improved version of the method of Huang et al. to study liquid transport through a finite length nanopore in a membrane under two different solid wall–liquid interactions (i.e., neutral-like and hydrophobic-like solid wall–liquid interactions) and compared such results with those of an infinite length channel with the same diameter (i.e., a channel with a periodic boundary condition in stream-wise direction) driven by an external-field. This comparison is used to isolate the entrance and exit effects of the channel. The organization of this paper is as follows: we will first introduce the molecular model and simulation methodology; then, present and discuss our NEMD simulation results and finally give some conclusions.

2. Molecular dynamics simulation and methodology

Two systems are studied in the present paper. The first one is a cylindrical nanopore that has a finite length. Two ends of the nanopore connect to two semi-infinite reservoirs in which the pressure was maintained at fixed but different levels to cause steady flow through the nanopore. The nanopore was modeled by an aligned cylinder with an inside diameter of 2.2 nm and a length of 6 nm, respectively. Fig. 1(a) depicts a snapshot of such a system. The liquid used in this system was made up of 15 088 argon molecules. The solid substrate that defines the boundaries of the system was constructed from two layers of molecules (a total of 2132 molecules) that had the same size as the liquid molecules but interacted with different energy scales. The solid molecules were fixed at their respective lattice positions using a very stiff spring constant. Two different energy scales for the solid substrate, i.e., ε_s = 0.1ε_l and ε_s = ε_l, were used to investigate the effect of solid wall–liquid interaction on the difference between the liquid transport through the finite length nanopore under a constant pressure difference and that through an infinitely long nanopore with the same diameter. Here, ε_s and ε_l are the solid wall molecule and liquid energy scales, respectively. For NEMD simulations performed in this system, periodic boundary conditions were exerted in the x and y-directions, but not the z-direction. Therefore, the system can be thought of as the building unit of a membrane in which an array of nanopores are arranged regularly. The two reservoirs are considered to be semi-infinite, which allows the use of far field boundary conditions, i.e., 1-D uniform velocity and pressure, at locations far away from the inlet and outlet of the nanopore. In our previous paper,⁴⁰ we addressed how to model these far field boundary conditions by using two self-adjusting plates. In the old version, the self-adjusting plates were two rigid plates. In order to reduce the effect of rigid plates on the molecular motions near them in the reservoirs, we changed the two rigid self-adjusting plates into two self-adjusting frames in which molecules can move freely in the x and y directions but cannot escape from the frames in the z direction. The molecules in each frame have the uniform velocity component in the z direction. This modification lets molecules in these self-adjusting boundaries have quasi three dimensional properties. To remain consistent with our previous paper, the far field boundary conditions modeled by two self-adjusting frames in this article are still called self-adjusting plates. In this study, the size of the rectangular reservoirs in the x- and y-directions were set at L_x = L_y = 7 nm. The pressures (P_f and P_b) exerted on the front and back self-adjusting plates were selected to be 80 MPa and 40 MPa; the distances (L_zf and L_zb) for the front and back self-adjusting plates to the inlet and outlet of the nanopore, respectively, were controlled to be larger than 8 nm and 4 nm in order to minimize the influence on the channel flow. For details of this method and parameter selections, please refer to ref. 40.

Fig. 1 (a) Snapshot of a finite length nanopore in a membrane, (b) snapshot of nanopore with periodical boundary condition in its axial direction and (c) cross-section of the nanopore.

To compare the difference between the fluid transport through finite and infinite length channels, the second system is a cylinder with periodic boundary condition in its axial direction, as shown in Fig. 1(b). The formation and geometry of the cylinder used in the second system is the same with the cylinder used in the first system. Instead of having a pressure gradient as used in the first system, an external gravity-like force in the second system was applied to drive molecules moving in the channel, a method commonly applied in the literature.^18,25,26 To make the results of two systems comparable, the molecules inside the channel in both systems and the total external forces exerted on both systems should be set to be the same, i.e.,

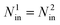where N¹_in and N²_in express the numbers of molecules inside the channel in the first and second systems, respectively; ΔP is the pressure drop over the channel in the first system; A is the inside cross-section area of the channel; a_ext is the external gravity exerted on each liquid molecule in the second system and m is the mass of liquid molecule.

The method for establishing initial conditions in the first system is similar to that applied in our previous work, i.e., a rigid and impenetrable plate with zero thickness was crossly located at the mid-length of the channel to separate the system into upstream and downstream parts, then the two self-adjusting plates and the molecules in the system were allowed to move until the thermodynamic equilibrium was reached. After that, the separation plate was removed and the molecules from the two sides were allowed to transport by the pressure difference. During this period, the Berendsen thermostats^42–44 were coupled to adjust the temperature of the system as Tk_b/ε_l = 1.1 (T = 133 K), where k_b is the Boltzmann constant. The method for establishing initial conditions in the second system is that the liquid molecules were packed in the channel. The initial velocities that had a Maxwellian distribution (corresponding to the liquid with an average temperature of T = 133 K) were assigned to the molecules. Then molecules in the channel were released to move without the external force until the equilibrium state was reached. After that, a constant external force, a_extm, was exerted on each liquid molecule until a steady state flow was established. During this period, two Berendsen thermostats were coupled to liquid molecules and wall molecules separately to maintain the system temperature constant.

The motion of liquid molecules inside the channel in the first system is governed only by the intermolecular force. While the motion of liquid molecules in the second system is dominated by both the intermolecular force and external force. The interaction between two molecules separated by a distance r_ij is governed by a truncated and shifted Lennard-Jones 12–6 potential:

where ϕ(r_c) is the truncated Lennard-Jones potential at r_ij = r_c; σ_ij and ε_ij are the characteristic length and energy scales. The truncated distance used in this paper was 2.2σ.^21,26 In the above equation, ϕ(r_ij) = 0 if r_ij > r_c. If molecules i and j are different types (e.g., one is solid and the other is liquid), σ_ij and ε_ij are calculated by using the Lorentz–Berthelot combining rule.⁴⁵ In this article, liquid argon was chosen as the working medium. Its length and energy scales are σ_l = 0.34 nm and ε_l = 1.67 × 10⁻²¹ J,⁴⁶ respectively.

For each molecule in the wall, a stiff Hookean spring attaches it to its lattice position with a potential of ϕ_spring = 12k_wR², where K_w is the stiffness of the spring and R is the distance of the wall molecules from their respective lattice sites. To keep the displacement of the wall molecules at a low level, a large stiffness constant, K_w = 6000ε_lσ_l⁻²,⁴⁷ was chosen.

The equations of motion were integrated using a Velocity Verlet algorithm. In all simulations, two criteria for the time step were adopted. One is dt = a×τ, where a is a coefficient and τ = (mσ_l²/ε_l)^1/2 is the characteristic time of the Lennard-Jones potential (m is the mass of molecule). The other is dt = b× (σ_min/ν_max), where b is a constant and was selected between 0.001–0.01; ν_max is the maximum relative velocity between two interacting molecules. The second criterion guarantees no interacting molecules overlapping or passing through each other directly in one iteration. In our simulations, the smaller one was chosen as the effective time step, which was 0.1–1 fs.

The stress tensor for a microscopic system of particles consists of a kinetic part and a virial part, which can be expressed by Irving–Kirkwood equation⁴⁸ as,

where is the volume of the computational box defined; N is the total number of molecules, including those in the images if the system has periodic boundary conditions; m_i is the mass of ith molecule; μ_iα and μ_iβ are the peculiar velocity components of molecule i in the α and β directions; r_ijα is the component of the distance vector between molecules i and j in the α direction; and F_ijβ is the component of the force between molecules i and j in the β direction. In NEMD simulations carried out in this study, N is a molecular number in an enlarged volume by extending the computational box in each direction one cutoff distance due to the truncating algorithm used. In our previous work,⁴⁰ when we calculated the virial part of the pressure, we did not include the interactions between the molecules in the computation box and those outside the computational box in the axial direction but within the cutoff distance used. This bug in our original code was fixed.

The constitutive pressure is defined as the trace of the stress tensor:

3. Results and discussion

In each system, two cases with different solid wall–liquid interactions, i.e., one with a hydrophobic-like (ε_s = 0.1ε_l) and the other with a neutral-like (ε_s = ε_l) solid wall–liquid interaction, were carried out. In all simulations, temperature was controlled to be Tk_b/ε_l = 1.1. In a rigorous sense, one should distinguish the streaming kinetic energy from the thermal kinetic energy when the thermostat is applied. Fortunately, the streaming kinetic energy in all simulations is only a small fraction of the thermal energy (e.g., the largest streaming velocity as shown in Fig. 8 contributes less than 2% of the thermal kinetic energy). Therefore, we ignored the effect of the streaming kinetic energy on temperature.

The liquid transport through the finite length nanopore in the first system is more complicated than the liquid flow in the second system. The fluid properties (e.g., pressure, density, velocity, etc.) in the first system vary not only in the radial direction, but also in the stream-wise direction due to the entrance and exit effects, while the fluid properties in the second system only change with respect to the radial distance because of the periodic boundary condition applied in the axial direction of the channel. To demonstrate the fluid variation in the first system clearly, the case with the hydrophobic-like solid wall–liquid interaction was taken as an example and the results are discussed in the following subsection in detail.

3.1 Liquid transport through a finite length channel

The objective of the improved method used in the first system is to produce constant pressure fields with different levels in the front and back reservoirs to induce liquid transport through the nanopore. Pressures in the nanopore and two reservoirs were calculated by the Irving–Kirkwood equation. The computational box for pressure calculation is a moving window that has a width of 2 nm in the z-direction, 7 nm in x and y-directions in the reservoirs, 0.1 nm in the radial direction in the nanopore. In the kinetic part of the Irving–Kirkwood equation (i.e.eqn (4)), the streaming kinetic energy should be distinguished from the thermal kinetic energy. As discussed previously, the streaming kinetic energy in all simulations is only a small fraction of the thermal kinetic energy. Therefore, the influence of streaming kinetic energy on pressure was ignored. Fig. 2 shows the pressure and the distributions of its two components (averaged over the corresponding cross-sections) in the z direction. In this figure, the short vertical dash lines signify the entrance and exit of the nanopore; the long horizontal dash lines denote the pressures externally exerted on the front and back self-adjusting plates. The lines with the symbols of ▲, ●, and ◆ represent the kinetic component, virial component and total pressure, respectively. The kinetic component varies slightly in the z direction due to the fact that temperature was constant throughout system and the density change in the z-direction is small (see Fig. 4). But the virial component in the nanopore changes significantly in the flow direction and dominates the variation of the total pressure. Two points are noteworthy. First, the calculated pressures in the front and back reservoirs are constant and equal to the pressures exerted on the front and back self-adjusting plates. Here, we demonstrate, for the first time, using the Irving–Kirkwood equation to capture this characteristic which is physically observed in macroscopic system (e.g., liquid pressure in a cylinder is equal to the pressure externally exerted on a piston if the effect of liquid density and the weight of piston are negligible). Secondly, the pressure averaged in each cross-section in this small nanopore decreases monotonically, just like a pressure distribution of a pressure-driven flow in a macroscopic channel, for this case with weak solid wall–liquid interaction. Fig. 3 shows the pressure distributions in the radial direction at locations 0.5 nm away from the inlet and outlet and in the nanopore. Pressure distributions at both inlet and outlet have a small change when r≤ 0.75 nm, especially for the pressure at the outlet. But variation of pressure distributions intensifies strongly when r≤ 0.75 nm. Pressure distribution in the nanopore shows a wavelike pattern, and the amplitude of the wave increases when the radial distance approaches the solid substrate. The reason for this distribution is mainly due to the layered distribution of the liquid molecules and the interaction between the solid and liquid.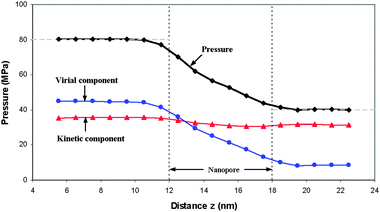

Fig. 2 Pressure and its components (kinetic and virial parts) distributions under solid wall–liquid with a hydrophobic-like interaction (ε_s = 0.1ε_l) averaged over the whole cross-section as a function of axial distance z.

Fig. 3 Pressure distribution under solid wall–liquid with a hydrophobic-like interaction (ε_s = 0.1ε_l) with respect to the radial distance at the inlet, nanopore and outlet.

Fig. 4 shows the density and streaming velocity distributions (averaged over the whole cross-section) with respect to the axial distance z for case with ε_s = 0.1ε_l. In this figure, the solid lines with ▲ and ■ symbols express the number density and streaming velocity, respectively. It is noted that the number density and the streaming velocity in both front and back reservoirs remain constant, but the values in the two reservoirs are slightly different. Density in the channel decreases monotonically in the stream-wise direction and reaches a lower value at the exit of the channel than that in the back reservoir due mainly to the wall effect. When molecules approach and enter the channel, they accelerate and the streaming velocity increases dramatically due to contraction of pass-through area. In the nanopore, the streaming velocity increases slightly because of small decrease in density, as shown by the line with ▲ symbols in Fig. 4. When molecules leave the nanopore and enter into the back reservoir, the streaming velocity drops to a low level due to the pass-through area change.

Fig. 4 Density and streaming velocity distributions under solid wall–liquid with a hydrophobic-like interaction (ε_s = 0.1ε_l) versus the axial distance z. The solid line with ▲ symbols is the density distribution; the solid line with ■ symbols is the streaming velocity distribution.

Fig. 5 and its inset show the pressure, number density and streaming velocity distributions in the stream-wise direction obtained for a solid wall–liquid with a neutral-like interaction (ε_s = ε_l). From this figure, one sees that the pressure fields in the upstream and downstream reservoirs are also equal to the pressures exerted on the front and back self-adjusting plates, which implies that the method used in the study works well and it can be used to create a target pressure difference between two reservoirs easily. The pressure distribution in the channel in this case displays the same pattern as that shown in Fig. 2. While there exist slight differences between the pressures in both cases, e.g., pressure in the stream-wise direction in the channel for the case with ε_s = ε_l decreases slightly faster than pressure in the case with ε_s = 0.1ε_l. The profiles of density and the streaming velocity distributions in the stream-wise direction, as shown in the inset of this figure, are similar to those shown in Fig. 4. The difference between the density distributions in the stream-wise direction in two cases is that the densities at the inlet and outlet for the case with ε_s = ε_l are slightly higher than the densities in the upstream and downstream reservoirs, while this phenomenon was not observed in the case with ε_s = 0.1ε_l. Other than a small difference of the density distributions in both cases, the streaming velocity in the nanopore for the case with the neutral-like solid wall–liquid interaction is much lower than that for the case with the hydrophobic-like solid wall–liquid interaction (e.g., the streaming velocity at the middle of the nanopore was 4.9 m s⁻¹ when ε_s = ε_l, 17.6 m s⁻¹ when ε_s = 0.1ε_l), which indicates that the solid wall–liquid interactions strongly impact a fluid transport through a nanopore. The effect of solid wall–liquid interactions on pressure, density and streaming velocity distributions in the radial direction in the channel will be addressed in following subsection.

Fig. 5 Pressure distribution averaged over the whole cross-section as a function of axial distance z obtained under solid wall–liquid with a neutral-like interaction (ε_s = ε_l). The inset of the figure is the distributions of number density and streaming velocity with respect to the axial distance z obtained under the same solid wall–liquid interaction.

3.2 Comparison of liquid transports through a finite and an infinite length nanopore

For liquid motion in an infinite length nanopore (i.e., a nanopore with periodic boundary condition in the stream-wise direction), an implementable approach, at present, is the external-field driven method. In this approach, a constant, gravitational-like force is exerted on all liquid molecules to induce the liquid motion in the channel. As mentioned in the previous section, the number of molecules in the channel and the total external force exerted on those molecules in two systems should be set to be same in order to make the results in the two systems comparable. Under these conditions, the parameters (e.g., density, pressure and streaming velocity) calculated from the second system would be equivalent to the values averaged over the channel in the first system. The simulation results obtained from the first system show that the numbers of molecules in the nanopore are 376 when ε_s = 0.1ε_l and 423 when ε_s = ε_l. According to eqn (2), the external gravities exerted on each liquid molecule in the second system (i.e., a_ext) should be 6.24 × 10¹² m s⁻² when ε_s = 0.1ε_l and 5.42 × 10¹² m s⁻² when ε_s = ε_l. In this section, three major parameters (i.e., pressure, density and streaming velocity) obtained from the two different systems were compared to isolate the impact of the entrance and exit on liquid transport through a nanochannel.

Fig. 6 shows the comparison of pressure distributions versus the radial distance obtained under two different solid wall–liquid interactions in the two different systems. In the figure, two solid lines represent the pressure-driven NEMD results obtained in the finite length system; two dashed lines with ▲ and ■symbols show the results calculated in the infinite length channel and the error bars are the standard deviation. Comparing the distributions obtained in the two different systems, one sees that all results exhibit similar characteristics, i.e., the pressure distributes in the radial direction in an oscillatory pattern. For each system, the amplitude of the fluctuation depends on the interaction between solid and liquid. The stronger the solid wall–liquid interaction, the larger the amplitude of the pressure wave. To determine the consistence between the two systems under the same solid–liquid interaction, the standard deviations were calculated. In the case of the hydrophobic-like interactions, the standard deviations for both systems are small and are in a size similar to that of the error bar symbols. In the case of the neutral-like interactions, the largest standard deviations for both systems occurred at the first peak next to the solid wall, which were 7.33 MPa for the finite length system and 5.56 MPa for the infinite length system. One sees that the pressure difference between the two systems were within the uncertainties.

Fig. 6 Comparison of pressure distributions (averaged over the channel) versus the radial distance under two different solid wall–liquid interactions in two different systems. The two solid lines show the results obtained in the finite length channel; the dashed lines with ▲ and ■ symbols are results calculated in the infinite length channel and error bars are the standard deviation.

To obtain the density and streaming velocity distributions along the radial direction in the nanopore, the domain (r≤ 1.5 nm) was divided into 30 sections in the radial direction. To quickly obtain statistical values in a small system with limited number of molecules passing through the nanopore during a short period of time, each molecule was divided into several pieces by the grid (in radial direction). Each piece for a counted molecule has different volume fractions but the same velocity in different sections. Fig. 7 shows the density distributions in the radial direction under the two different solid wall–liquid interactions in the two different systems. It is noted that the density distributions in the radial direction in both systems are oscillatory in the nanopore, and the amplitude of the oscillation is dependent on the strength of solid wall–liquid interaction. In particular, the stronger the interaction, the larger the amplitude. Moreover, the six-peak structure of the density profile implies that there were three circular liquid layers formed in this small channel with a size of 6.5 molecules. Comparing the results obtained in the two different systems, one sees that the density distributions in the channel for both systems are excellently agreeable, except for the value at the first valley close to the solid wall when ε_s = ε_l. This deviation between two systems is probably a statistical error because the density at this valley point had about ±0.3 (nm⁻³) uncertainty for each system.

Fig. 7 Comparison of number density distributions (averaged over the channel) with radial distance under different solid wall–liquid interactions in two different systems. Two solid lines are the results obtained in the finite length channel; the dashed lines with ▲ and ■ symbols are results calculated in the infinite length channel. The vertical dash lines are the internal surface of the nanopore.

Fig. 8 shows the comparison of the radial distributions of streaming velocity under the two different solid wall–liquid interactions in the two different systems. Similar to the expressions used in the Fig. 6 and 7, the two solid lines are the results obtained in the finite length system; two dashed lines with symbols express the results calculated in the infinite system. All curves in the figure show that the velocity distributions in the nanopore are characterized by having a maximum velocity at the center of the nanopore. For a solid wall–liquid with the hydrophobic-like interaction, the profile of the streaming velocity in the two systems are similar, but the values are significantly different, i.e., the streaming velocity obtained in the infinite length channel is essentially larger than that obtained in the finite length channel. We believe that the major reason causing this phenomenon is that the solid molecules located at around entrance of the channel repulse liquid molecules in the front reservoir to enter the channel due to the solid wall’s repulsive property. However, for a neutral-like solid wall, the streaming velocities in two systems show nearly the same results, except for a slight difference in a central region of r < 0.5 nm. This result means that the entrance and exit have a slight impact on liquid transport through a nanochannel if the solid wall–liquid has a neutral-like interaction. Actually, solid molecules around the entrance and exit in this case play a neutral-like role (neither significant repulsive force nor essential attractive force) to the liquid molecules around them. From Fig. 8, one sees that the effect of the entrance and exit plays a major role in liquid transport through a nanopore if the solid wall is repulsive (or hydrophobic-like).

Fig. 8 Comparison of streaming velocity distributions (averaged over the channel) versus radial distance under different solid wall–liquid interactions in two different systems. Two solid lines are the results obtained in the finite length channel; the dashed lines with ▲ and ■ symbols are results calculated in the infinite length channel. The vertical dashed lines are the internal surface of the nanopore.

For an incompressible flow in a macroscopic system, the volumetric flow rate can be used to express the transport ability of a channel. But in a confined small system, the density distribution in the radial direction is not uniform. As a result, the transport ability (flow rate) of a channel can only be calculated by integrating the product of the local density and velocity over the whole cross-area of the channel. In this study, the number flow rates per nanosecond in the finite channel were 1111 when ε_s = 0.1ε_l and 345 when ε_s = ε_l, respectively. The number flow rates in the infinite channel were 1829 when ε_s = 0.1ε_l and 367 when ε_s = ε_l. Comparing the number flow rates in the two different systems, one sees that the entrance and exit effects lead to a decrease of about 39% when ε_s = 0.1ε_l and 6% when ε_s = ε_l in the liquid transport ability of the channel. This result clearly shows that entrance and exit effects play an important role in the liquid transport through a finite length nanochannel if the solid wall is repulsive.

4. Conclusions

The entrance and exit effects on liquid transport through a cylindrical nanopore were studied by comparing the NEMD simulation results obtained from a finite length channel with those of an infinite length channel with the same diameter. The NEMD simulation results indicate that the entrance and exit effects of a nanopore decrease the liquid transport ability through a nanopore made up of a repulsive wall.

Acknowledgements

The financial support from NSERC for K. N, P. C. and L. W. K. is gratefully acknowledged. C. H. thanks the financial support from the PhD Scholarship of the University at Alberta and the Postgraduate Scholarship from NSERC.

References

1. M. Muthukumar, Phys. Rev. Lett., 2001, 86, 3188.
2. A. Aksimentiev and K. Schulten, Biophys. J., 2005, 88, 3745.
3. M. Akeson, D. Branton, J. J. Kasianowicz, E. Brandin and D. W. Deamer, Biophys. J., 1999, 77, 3227.
4. I.-C. Yeh and G. Hummer, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 12177.
5. S. E. Henrickson, M. Misakian, B. Robertson and J. Kasianowicz, Phys. Rev. Lett., 2000, 85, 3057.
6. A. Aksimentiev, J. B. Heng, G. Timp and K. Schulten, Biophys. J., 2004, 87, 2086.
7. E. A. Marzio and J. J. Kasianowicz, J. Chem. Phys., 2002, 117, 4063.
8. W. Sung and P. J. Park, Phys. Rev. Lett., 1996, 77, 783.
9. E. Slonkina and A. B. Kolomeisky, J. Chem. Phys., 2003, 118, 7112.
10. Q. Zhang, J. Zheng, A. Shevade, L. Zhang, S. H. Gehrke, G. S. Heffelfinger and S. Jiang, J. Chem. Phys., 2002, 117, 808.
11. P. Keblinski, W. Ma, A. Maritan, J. Koplik and J. R. Banavar, Phys. Rev. E, 1993, 47, R2265.
12. J. Yang, F. Lu, L. W. Kostiuk and D. Y. Kwok, J. Micromech. Microeng., 2003, 13, 963.
13. J. Marti-Rujas, A. Desmed, K. D. M. Harris and F. Guillaume, J. Am. Chem. Soc., 2004, 126, 11124.
14. G. K. Papadopoulos, H. Jobic and D. N. Theodorou, J. Phys. Chem. B, 2004, 108, 12748.
15. R. Allen and J. P. Hansen, J. Chem. Phys., 2003, 119, 3905.
16. G. E. Karniadakis and A. Beskok, Micro Flows: Fundamentals and Simulation, Springer, New York, 2002.
17. K. P. Travis, B. D. Todd and D. J. Evans, Phys. Rev. E, 1997, 55, 4288.
18. K. P. Travis and K. Gubbins, J. Chem. Phys., 2000, 112, 1984.
19. P. A. Thompson and S. Troian, Nature, 1997, 389, 360.
20. J. Koplik, J. R. Banavar and J. F. Willemsen, Phys. Fluids A, 1989, 5, 781.
21. M. Cieplak, J. Koplik and J. R. Bavanar, Phys. Rev. Lett., 2001, 86, 803.
22. J. L. Barrat and L. Bocquet, Phys. Rev. Lett., 1999, 82, 4671.
23. A. Jabbarzadeh, J. D. Atkinson and R. I. Tanner, Phys. Rev. E, 2000, 61, 690.
24. P. A. Thompson and M. O. Robbins, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 41, 6830.
25. J. Koplik, J. R. Bavanar and J. F. Willemsen, Phys. Rev. Lett., 1988, 60, 1282.
26. M. Cieplak, J. Koplik and J. R. Bavanar, Physica A, 2000, 287, 153.
27. K. P. Travis and D. J. Evans, Phys. Rev. E, 1997, 55, 1566.
28. G. Nagayama and P. Cheng, Int. J. Heat Mass Transfer, 2004, 47, 501.
29. V. P. Sokhan, D. Nicholson and N. Quirke, J. Chem. Phys., 2002, 117, 8531.
30. J. Dzubiella, R. J. Allen and J. P. Hansen, J. Chem. Phys., 2004, 120, 5001.
31. F. Zhu, E. Tajkhorshid and K. Schulten, Biophys. J., 2002, 83, 154.
32. G. S. Heffelfinger and F. Swol, J. Chem. Phys., 1994, 100, 7548.
33. M. Lisal, W. R. Brennan and F. R. Siperstein, J. Chem. Phys., 2004, 121, 4901.
34. M. Firouzi, K. M. Nezhad, T. T. Tsotsis and M. Sahimi, J. Chem. Phys., 2004, 120, 8172.
35. D. R. Wheeler and J. Newman, J. Phys. Chem. B, 2004, 108, 18362.
36. M. G. Martin and A. P. Thompson, J. Chem. Phys., 2001, 114, 7174.
37. G. Arya, H. Chang and E. J. Maginn, J. Chem. Phys., 2001, 115, 8112.
38. R. F. Cracknell, D. Nicholson and N. Quirke, Phys. Rev. Lett., 1995, 74, 2463.
39. L. Xu, M. G. Sedigh, M. Sahimi and T. T. Tsotsis, Phys. Rev. Lett., 1998, 80, 3511.
40. C. Huang, K. Nandakumar, P. Choi and L. W. Kostiuk, J. Chem. Phys., 2006, 124, 234701.
41. C. Huang, P. Choi, K. Nandakumar and L. W. Kostiuk, J. Chem. Phys., 2007, 126, 224702.
42. H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNila and J. R. Haak, J. Chem. Phys., 1984, 81, 3684.
43. J. B. Freund, J. Chem. Phys., 2002, 116, 2194.
44. R. Qiao and N. R. Aluru, J. Chem. Phys., 2003, 118, 4692.
45. G. C. Maitland, M. Rigby, E. B. Smith and W. A. Wakeham, Intermolecular Forces: Their Origin and Determination, Clarendon Press, Oxford, 1981.
46. J. Weng, S. Park, J. R. Lukes and C. Tien, J. Chem. Phys., 2000, 113, 5917.
47. A. Jabbarzadeh, J. Atkinson and R. Tanner, J. Non-Newtonian Fluid Mech., 1997, 69, 169.
48. J. H. Irving and J. G. Kirkwood, J. Chem. Phys., 1950, 18, 817.

---

Footnote

† The HTML version of this article has been enhanced with colour images.

---