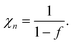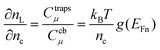Physical electrochemistry of nanostructured devices
Received
19th June 2007
, Accepted 24th July 2007
First published on 8th August 2007
Abstract
This Perspective reviews recent developments in experimental techniques and conceptual methods applied to the electrochemical properties of metal-oxide semiconductor nanostructures and organic conductors, such as those used in dye-sensitized solar cells, high-energy batteries, sensors, and electrochromic devices. The aim is to provide a broad view of the interpretation of electrochemical and optoelectrical measurements for semiconductor nanostructures (sintered colloidal particles, nanorods, arrays of quantum dots, etc.) deposited or grown on a conducting substrate. The Fermi level displacement by potentiostatic control causes a broad change of physical properties such as the hopping conductivity, that can be investigated over a very large variation of electron density. In contrast to traditional electrochemistry, we emphasize that in nanostructured devices we must deal with systems that depart heavily from the ideal, Maxwell–Boltzmann statistics, due to broad distributions of states (energy disorder) and interactions of charge carriers, therefore the electrochemical analysis must be aided by thermodynamics and statistical mechanics. We discuss in detail the most characteristic densities of states, the chemical capacitance, and the transport properties, specially the chemical diffusion coefficient, mobility, and generalized Einstein relation.
 Juan Bisquert Juan Bisquert | Juan Bisquert studied his PhD at the University of Valencia in mathematical physics. He joined Universitat Jaume I in 1991 and now is full professor of applied physics. He leads a research group of 8 physicists and chemists working on photovoltaic and electrooptic materials and devices based on nanostructured metal oxides and organic conductors. Current research activity is focused on dye-sensitized solar cells, organic LEDs, electrochromic displays, batteries and supercapacitors. He is specialist in theoretical modeling and interpretation of impedance spectroscopy of electroactive films, transport in disordered materials, interfacial charge-transfer, and the glass transition. |
1. Introduction
The increasing need for the replacement of conventional energy sources in favor of carbon-neutral energies has boosted the research on new materials and devices for the production and storage of clean energies. Solar cells are able to directly convert sunlight into electricity. A great effort of research is currently devoted to develop solar cells that could lower considerably the production costs of current photovoltaic devices (mostly silicon-based) while maintaining a reasonable efficiency and stability. Also important would be devices able to produce hydrogen by splitting water with sunlight. But even if the production of huge amounts of clean energy, either in the form of electricity or hydrogen, would be reached, it is still necessary to store and transport the energy for solving the demands of energy use in society. Convenient hydrogen-storage systems currently constitute a bottleneck for the realization of the hydrogen economy. Cheaper fuel cells, and devices for energy storage with both a high energy and power density, like batteries and supercapacitors, are needed for electric cars, and also for leveling off the intermittent nature of several renewable energy sources. Other advances, such as large area light-emitting diodes (LEDs) for solid-state lighting, would also contribute significantly to the efficient use of energy.
The early 1990s witnessed a great development of a series of electrochemical devices.1 The lithium ion battery entered the market, to soon become an essential component of portable electronics, and the group of M. Grätzel developed a successful dye-sensitized solar cell (DSC) based on nanocrystalline TiO2.2,3 These breakthroughs showed the great potential of devices based on electroactive materials for energy production and storage applications. In addition, the demonstration of efficient LEDs with organic semiconductors4 (that have become a technological reality) showed that electroactive and optically active films for devices could be formed from either inorganic or organic materials, or with a combination of both. Research on nanostructured electrochemical devices has exploded in recent years, in relation with DSC, high-energy batteries, photocatalysis, chemical and biochemical sensors, and electrochromic devices.
This paper will focus on combined methods of physics and electrochemistry for analyzing the properties of electrochemical nanostructured devices in which a semiconductor nanostructure can be electronically addressed from a conducting substrate. Since organic, hole transport media are usually a key element of such devices, their properties will be addressed as well. The paper presents an introduction to the subject exposing an array of experimental methods and theoretical concepts that have emerged in recent years while studying such devices, particularly around the subjects of Fermi level displacement and electron transport. Recent reviews on physical properties of DSC,5,6 electrochemical gating,7 and the electrochemical determination of the density of states (DOS),8 describe these related issues in more detail, and in another paper9 I discuss a broad range of applications of metal-oxide nanoparticles in electrochemical devices. Here, emphasis is made to relating the macroscopic quantities measured by physical–electrochemical methods to the electronic and ionic properties of nanostructured devices and in particular of DSC. First some introductory remarks will be made about nanoparticles, nanostructures and their application in electrochemical, photoelectrochemical and all-solid devices. Next, in section 2 the electrochemical measurement of the DOS and its shape in a variety of relevant materials is described. Section 3 considers the basic concepts of macroscopic transport in a semiconductor nanostructure, with several particular models that illustrate the general concepts. We finish with the conclusions and outlook in section 4.
There is a wide variety of nanostructures currently investigated for electronic and electrooptic devices with different morphology, size and composition. We will be mostly concerned with physical electrochemical properties of semiconductor nanoparticles and nanostructures that are prepared by wet chemical methods. These methods lead to colloidal nanocrystals present in dispersion, which are the basic building blocks for the preparation of larger architectures.10
Quantum dots are nanocrystals of size roughly between 1 and 10 nm. In these crystals, for example of CdSe, the electron wave functions are strongly confined, so that the electron energy levels are discrete and their separation is determined by the crystal size. Accordingly, electronic and electrooptic properties of quantum dots can be tailored by the dimensions.
Colloidal nanocrystals, in the range 10–50 nm, do not generally show the acute confinement effect, but are important for many applications, because they allow for electrochemical gating, i.e., an increase in electronic density compensated by ionic density at the surface. Examples are metal oxides used in DSC such as TiO2, ZnO and SnO2.11–15
Colloidal nanocrystals are usually deposited over a conducting substrate and thermally treated to form a connected array of nanoparticles that can be used as electroactive electrodes. Structures can be more or less ordered, and interparticle connection can also be controlled with molecular ligands, which can be used to promote the self-assembly of special architectures.16
Another approach towards electroactive nanostructured electrodes consists on growing nanofibers or nanowires with columnar, tubular, dendritic or other structures over a substrate, see Fig. 1 and 2. These structures have the advantage of providing long and uninterrupted paths for electron transport while maintaining a high area density as that found in random nanoparticulate films.20–23 There has been recent progress in obtaining highly ordered transparent TiO2nanotube arrays of the type shown in Fig. 1 for DSC with high electron lifetimes and excellent pathways for electron percolation.17,18 Vertically aligned ZnO nanorods, formed by electrodeposition on a transparent conducting oxide,24,25 as those shown in Fig. 2, have also attracted much attention for applications in solar cells20,26–28 and optoelectronic devices such as light emitting and laser diodes.24,29,30
 |
| | Fig. 2
SEM microgaph of electrodeposited ZnO nanowire array. Image courtesy of R. Tena-Zaera. | |
An important step of nanostructuring is an additional treatment of colloidal nanoparticles or nanorods for governing the electronic properties at the surface. This can be realized, for example, with strategies of conformal coating of sintered nanoparticulate films. Insulating layers ca. 2 nm thick have been deposited over TiO2nanoparticles in DSC.31–37 It was shown that alumina coating improves considerably the electron lifetime by an almost complete passivation of surface trap states.23,38 Absorption of molecules with different dipole moment modifies the energy level of a nanostructured semiconductor immersed in solution, as shown in Fig. 3 and discussed later.39 Besides shifting the conduction band of the semiconductor, adsorbed molecules also are able to reduce recombination and increase the efficiency of DSC.40,41
Finally some architectures require the combination of different elements with specific photophysical, physical or electrochemical functions. For example nanostructured solar cells are envisioned with a matrix of TiO2 nanoparticulate film sensitized with surface-attached quantum dots42 in order to exploit the opportunities arising from discretization of energy levels in quantum dots, which could greatly enhance the photocurrent by multiple exciton generation from a single high energy photon.43–46 Devices such as photocapacitor47 and self-driven photoelectrochromic window48 have been formed by combining in direct contact several nanoparticulate layers with different functions.
1.2 Basic features of nanostructured electrochemical devices
Prompted by key applications such as the Li battery and DSC, the widespread investigation of electroactive materials started with electrochemical configurations. The basic structure of such devices is shown in Fig. 4. It is composed of a nanoparticulate electroactive electrode, a counterelectrode and an ionic (liquid or solid electrolyte) or hole conductor that joins both films. The first electrode is “active” in the sense that it realizes the main steps in the function in the device, such as sunlight conversion to electricity, or energy storage. Usually in realizing such function the material undergoes a huge change in the concentration of some species, either electrons or ions, or both, with the consequent change of the electrochemical potential.
 |
| | Fig. 4 Scheme of an electroactive device formed by a nanostructured film and counterelectrode joined by an electrolyte (or hole transport material). | |
The process of electrochemical charging is shown in more detail for the DSC in Fig. 5. In this system the change in electron density in the TiO2nanoparticles by photoinjection from surface-adsorbed dye molecules is facilitated by positive but inert ions at the nanoparticles surface, in order to maintain electrical charge neutrality. Electron density may vary from nearly zero, in the insulator state, to 100 electrons per 10 nm diameter nanoparticle. Here a main point of contrast with solid-state semiconductor devices must be emphasized. In semiconductor devices many device properties are ruled by electrical fields in space–charge regions at the interfaces. In general, whether the internal field can be built or not into an object of nanometric dimensions, depends on the relationship of the object size to the Debye screening length. In the case of the DSC indicated in Fig. 5, long range electrical fields do not govern the properties of the device. In fact if the particle is low-doped and not too large there is no room to build internal electrical fields in the nanoparticles49 and the conduction band remains homogeneous in the major part of the nanostructure (the opposite situation will be treated in section 2.4).
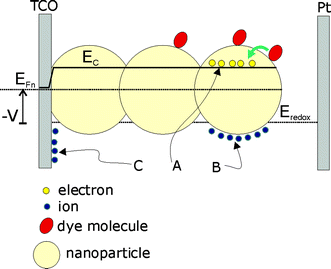 |
| | Fig. 5 Schematics of a dye-sensitized solar cell, consisting on dye molecules adsorbed on nanoparticulate TiO2 that is deposited over a transparent conducting oxide (TCO). Photoinjection increases the chemical potential (concentration) of electrons in the TiO2 phase (A). The electron Fermi level, EFn, is displaced with respect to the lower edge of the conduction band, Ec. The electrode potential, V, is given by the difference between EFn and the redox level Eredox. The increasing negative charge in the semiconductor nanoparticles is compensated by positive ionic charge at the surface (B). With the change of EFn also changes the electrostatic potential of the Helmholtz layer and semiconductor bandbending at the interface between the exposed surface of the transparent conducting oxide substrate and the electrolyte (C). | |
When the TiO2electrode in Fig. 4 contains a significant concentration of electrons, it is in an out-of-equilibrium situation and is able to do work as it returns to equilibrium. In fact the device is arranged in such a way that the only path for electrons is the external circuit (except for recombination due to interfacial charge transfer), because the electrolyte only conducts ions in batteries, and holes in solar cells. The amount of work that this system can do is described by the free energy per carrier, which is the electrochemical potential (η), also known as the quasi-Fermi level (EF), in the case of electrons in a solid, and as the redox potential (Eredox), in the case of ionic species in solution. These different denominations refer to the same thermodynamic quantity.50
Considering the energy diagram in Fig. 6, we assume that the species injected in phase A with number density nA, is distributed in equivalent sites with total density NA, hence the fractional occupancy of sites is xA = nA/NA. The electrochemical potential, ηA = ηA(xA) has two basic components
| |  | (1) |
The first one,
EA, is the energy level, it is the energy gained when the system acquires one carrier. For noninteracting species, the energy level
EA is independent of the concentration, and
ηA(
xA) is equivalent to the Langmuir isotherm. The energy level for electrons can be associated with
ϕA, the Galvani (electrostatic) potential with respect to some suitable reference level, as follows
| | 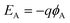 | (2) |
where
q is the positive elementary charge.
 |
| | Fig. 6 Basic energy diagram for the systems of Fig. 4 and 5, showing the applied potential V, the electrochemical potentials η, the chemical potential μ of electrons in phase A, and the energy level EA in the phase A. (a) Equilibrium situation without applied potential. (b) Equilibrium situation under an applied potential. | |
The second component in eqn (1), μA, the chemical potential, is an entropic contribution that accounts for the dispersion of the carriers over all the available sites. If the species is distributed randomly in the available sites the following expression holds:
| |  | (3) |
where
kB is Boltzmann’s constant and
T the absolute temperature.
If the semiconductor nanocrystallites are wide enough to neglect confinement effects, they will have a transport band similar to that for carriers in macroscopic materials. Let us assume that electrons have been injected to the conduction band with density nc. The lower edge of the conduction band Ec is related to the potential in the semiconductor phase with respect to the electron at rest in vacuum, as Ec = −qϕ.51Nc is the effective density of conduction band states. Usually the Fermi level remains below the conduction band level Ec−EFn≫kBT, hence nc≪Nc and the electrochemical potential or Fermi level, can be expressed as
| |  | (4) |
The cell potential in
Fig. 5 corresponds to the difference of electrochemical potential of electrons between the contacts,
52 as indicated in the scheme of
Fig. 6| |  | (5) |
In equilibrium the electrochemical potential is homogeneous through the device,
ηA =
ηC and
V = 0 as shown in
Fig. 6(a). The quasi-equilibrium situation under a nonzero potential is represented in
Fig. 6(b). Note that the chemical potential in A (
μA =
ηA−
EA), and hence the concentration of electrons, increases with respect to the situation
V = 0, while the electrochemical potential in the electrolyte,
ηc, remains stationary.
The distinction between the chemical and electrostatic potential of species in a given phase, stated in eqn (1), is entirely conceptual. A priori the contributions cannot be separated experimentally without making non-thermodynamic assumptions.53 Furthermore, this distinction is lost for carriers strongly interacting with their neighbors, as in examples discussed further on. Nonetheless, the statistics of independent particles is broadly used and applies in a great variety of electrochemical systems (e.g., low-doped nanostructured semiconductors and electronically conducting polymers). When the DOS at the Fermi level is low, the potential has the effect of displacing the Fermi level ηA with respect to the energy level EA. In these situations there is a significant change in the concentration of carriers that can be interpreted as a change in the chemical potential (see for example ref. 54). Additionally changes may occur in the local electrostatic level associated with self-charging of the phase or interaction of the carriers.55 In contrast, for metals and highly doped semiconductors, the DOS at the Fermi level is very high. Significant changes in the density of carriers, as an effect of an applied potential, are not possible, because the Fermi level is pinned at a fixed energy level.
When the Fermi level of electrons, determining the cell potential V, changes, not only the chemical potential is modified, but variation of electrostatic potential between the electrodes occurs as well inside the cell. However it may be confined by shielding to a short region at the substrate surface, as indicated by the step of the conduction band level in Fig. 5.49 Therefore in many situations the diagrams of Fig. 6 constitute a good approximation to describe the device.
For electrochemical measurements, the potential of the active electrode (the working electrode WE in the electrochemical cell, Fig. 7(a)) is recorded with respect to a reference electrode RE, while the current flows between working and counterelectrode CE.56 In devices where WE and CE need to be close to each other special precautions are needed for using a RE. For example in DSC an internal photo-reference electrode is proposed with the cell structured as indicated in Fig. 7(b).57
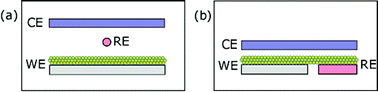 |
| | Fig. 7 Scheme of an electrochemical cell for measuring a nanoparticulate film as working electrode (WE), indicating the reference electrode (RE) and counterelectrode (CE). (a) Normal electrochemical cell. (b) The RE is formed of the same material as the WE by introducing an insulating gap in the conducting substrate. | |
Instead of photoinjecting the electrons in a DSC, as indicated in Fig. 5, the change of electron Fermi level can be induced by applied voltage using a potentiostat in the configuration of Fig. 7(a). It is important to recognize that the manipulation of the Fermi level induces a huge change in an array of physical properties related to the electron density in the nanostructure. Therefore, the electrochemical configuration constitutes an excellent tool for studying the physical properties of nanoparticles and nanoparticulate films. One can monitor properties such as the electronic conductivity over many orders of magnitude in a very simple way.58,59 In addition, interesting devices are formed, based on the manipulation of electronic density in the nanostructure by potential control. For instance molecules attached at the metal-oxide surface as in Fig. 5 can be oxidized and reduced, changing the optical transmission of the film as a whole, which yields an electrochromic device.60 It is even possible to electronically address from the substrate the molecular layer absorbed in the surface of the mesoporous structure.61,62
Since the changes in electrode potential modify the properties of the electrode, very often we are interested in characterizing the nanostructured electrode as a function of the steady-state Fermi level or electrochemical potential. To this end one uses a measurement based on a general principle that involves two levels of perturbation. A large one establishes a steady state in the semiconductor, for instance by a certain level of photon irradiation or steady-state bias potential, while a small perturbation probes the properties of that particular steady state, usually by time transient or frequently resolved means. The small perturbation produces differential quantities such as a resistance or capacitance. Studies of macroscopic assemblies of semiconductor nanoparticles often utilize such techniques, including electrochemical impedance spectroscopy (EIS),62–67intensity-modulated photocurrent spectroscopy (IMPS),68–72 and intensity-modulated photovoltage spectroscopy (IMVS).73 Recently, many studies have determined the properties of DSC using EIS.40,64,66,74–78 This technique has the advantage of identifying different types of operational elements, consisting either in electronic or ionic processes, in photoelectrochemical devices.
An important measurement of this class is the determination of electronic conductivity as a function of electrode potential and it uses a conducting substrate that is divided in two separated regions, bridged by the nanostructured film, Fig. 8(a).7,58,79 These regions can be controlled as independent working electrodes. Then it is possible to govern the Fermi level in the film with a bias U1≅U2 as in Fig. 8(b), while maintaining a small potential difference between the two sides, ΔU = U2−U1, which causes a current flow ΔI between WE1 and WE2 that enables to measure the electronic conductivity, σ, related to ΔI/ΔU by the geometry of the film.58,59,80,81 An example of the application of this technique is shown in Fig. 3 for measurements of the conductivity of nanostructured TiO2 with different surface treatments. Changes in the conductivity are obtained by a shift of the conduction band of TiO2 due to the different dipole moments of the molecular absorbed species.39
 |
| | Fig. 8 (a) Electrochemical transistor measurement configuration. The conducting substrate over which the film is deposited is divided into two regions, separated by an insulating gap. The separated regions serve as two working electrodes WE1 and WE2. (b) Equivalent circuit of the electrochemical transistor configuration. When WE1 and WE2 are shorted the film can be operated as in normal electrochemical cell with potential Ubias. The two working electrodes can also be operated independently with potentials U1 and U2 with respect to the reference electrode (RE). | |
Other electrochemical techniques scan the properties of the nanostructured electrode using a single large perturbation. For example in cyclic voltammetry (CV) the current is recorded while the electrode potential is varied at a constant rate. CV has the advantage of providing a global view of the properties of the electrode in a swift measurement.82 When a thin film is voltage-scanned close to equilibrium, CV provides the DOS of the film material, as discussed later.82,83
In electrochemical devices, the counterelectrode may require special properties, for example for storing a large amount of ions expelled from the active film. High-energy density of the Li battery necessitates, in addition to high specific capacity, that the difference in equilibrium potentials between positive and negative electrodes be large, so that both anode and cathode must be optimized. For anode, Li metal can be replaced by some appropriate hosts capable of Li-ion insertion at a potential not far from the equilibrium potential of Li electrode, e.g.graphite and some other carbonaceous materials. Therefore two active films may be coupled in a device, and electrochemical potentials will change in both.
Liquid electrolytes have the benefit of realizing a perfect junction whatever the morphology of the active film, so that a huge active area, addressable from the macroscopic contacts, is readily obtained. In addition, liquid electrolytes provide a very large ionic (or hole) conductivity and a wide potential window of operation. But liquids are not generally convenient for all devices, due to technical problems of sealing and volatility. Consequently, a major trend of current research in DSC aims at solid or quasi-solid electrolytes (such as conducting polymers and room-temperature ionic liquids) with good ionic or hole conducting properties for replacing the liquid electrolytes.84,85 Conversion efficiencies exceeding 8% have been achieved with non-volatile electrolytes in combination with specially designed dyes, standing 1000 h accelerated test at 80 °C without decay of performance.86
It is appreciated that devices, which can be solar cells, supercapacitors, batteries, and others, formed with nanostructured semiconductor films filled with a convenient “soft” conducting medium (able to fill the solid nanostructure), rely on the separation of Fermi levels or electrochemical potentials in at least two phases that are separately connected to the outer electrodes, as indicated in Fig. 6. The voltage generated by the device is determined by the ability of the different phases to maintain the excess carriers. In batteries, the electrolyte must be a perfect electronic insulator for maintaining the stored energy over extended periods of time. In solar cells an electronic connection exists necessarily between the two phases, otherwise the process of photogeneration would be impossible.3 So the kinetics of the reciprocal process (recombination) must be very slow. The surface of nanoparticles and quantum dots is therefore a critical aspect for most applications, it is where carriers in separate phases meet each other and eventually recombine. If the electrons are lost across the particle’s surface the voltage in the solar cell device will be very low. Furthermore, often at the surface bandgap electronic states (surface states) are formed that modify the expected physical properties of quantum dots.
During operation, charge carriers in each phase must be well connected to the respective electrode, and therefore efficient electron or hole transport in each medium is a necessary requirement. Indeed, the work per carrier described by the electrochemical potentials as commented above, is restricted to a near equilibrium situation, i.e. when the current is close to zero. Devices such as solar cells and supercapacitors need to supply a significant power, and this is determined both by the voltage and current that the device generates. A solar cell with a very high open-circuit voltage may be a useless device if it cannot supply the electrons due to a low conductivity in the semiconductor nanostructure.
Summarizing, in the nanostructured electrochemical devices the classical, metal/solution interface of electrochemistry has been largely extended in several ways. Microporous or nanoporous films up to 10 μm and larger are used on top of the metal contact. Besides the interfacial processes at the contact of the nanoparticles and the solution, a variety of electronic and ionic processes occur in the material itself. It is necessary to use an array of chemical, electrochemical and physical methods and techniques for understanding the behavior of such materials and improving the performance of devices.
2. The density of states
One important question for the analysis of electronic properties of a given nanostructured film is the relationship between the average electron density and the electrochemical potential. Theoretically this is a problem amenable to the methods of thermodynamics and statistical mechanics. If the electrons can be treated as non interacting entities, the question is related to finding the one-particle DOS. When there are interactions between the electrons and with surrounding media, for example through polarization effects, the question becomes a many-body problem that is much more complex from a theoretical point of view. Examples of systems with interacting carriers will be presented in section 3.
2.1 The electrochemical capacitance
Let us consider first the case in which the energy of a state does not depend on electrochemical potential, i.e. we neglect many particle effects. One of the methods for determination of DOS is based on the measurement of the variation of the density of electrons (holes) caused by a variation of Fermi energy.8 As an example in Fig. 9 a possible DOS for the nanostructured TiO2electrode discussed before in Fig. 5 is indicated. As already commented on before, as a result of ionic charge compensation the electronic density can be varied as a univocal function of a homogeneous Fermi level EFn.
 |
| | Fig. 9 Electron energy diagram illustrating the behavior of a nanostructured TiO2electrode (shown in the top scheme) when a variation dV of the electrochemical potential of electrons ηn (Fermi level) is applied, assuming that conduction band energy (Ec) remains stationary with respect to the redox level, Eredox. Changes of occupancy both of conduction band, dnc, and trapped electrons in localized levels, dnL (shaded region of the bandgap), are indicated. | |
We consider one specific electronic state characterized by the energy E. This energy is defined to be increasingly negative for states deeper in the gap. The average occupancy is described by the Fermi–Dirac distribution function
| | 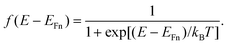 | (6) |
A displacement of the Fermi level causes a variation of the state occupancy in the following way
| |  | (7) |
Let us introduce the concept of the electrochemical capacitance. We consider in
Fig. 10 two basic mechanisms of accumulating charge with respect to voltage in electrochemical systems. The first one,
Fig. 10(a), is a standard dielectric capacitor where energy is stored in the electrical field, related to spatial charge separation. This capacitance is ubiquitous at interfaces with space charge such as Schottky barriers and Helmholtz layers. In general the dielectric capacitance is associated with charging the spatially separated plates of the capacitor with a displacement current. The second one,
Fig. 10(b), consists of increasing the chemical potential of the species in a bulk material by increasing their number. Here the “plate” of the capacitor is charged by conduction current. This second case can be called the chemical capacitor
85,87 and it is specially relevant for intercalation batteries and solar cells.
85
 |
| | Fig. 10 Schematic representation of (a) electrostatic capacitor and (b) chemical capacitor. | |
As commented before, it may not always be possible to separate electrostatic and chemical potential contributions in the electrochemical potential. In the general case one defines the electrochemical capacitance, that relates the change of concentration to the change of electrochemical potential
| | 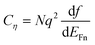 | (8) |
where the capacitance is given per unit volume using the volume density of the state,
N.
In the case of Fig. 9, it has already been discussed that the voltage variation is absorbed at the TCO/TiO2 electrolyte interface, hence the relationship −qdV = dEFn. The Fermi level inside the TiO2nanostructure is displaced towards the conduction band, i.e., the change of electrochemical potential implies a change of the chemical potential of electrons: dEFn = dμn. Eqn (8) gives a purely chemical capacitance
| |  | (9) |
For a single state the capacitance peaks at the energy level of that state, see below (Fig. 17(b)).
In Fig. 9 the nanostructured electrode is treated as a continuum in which the DOS, constitutes a probability of finding a number of electronic states g(E)dE in the energy interval dE. An exponential distribution of localized states in the bandgap is described by the expression
| |  | (10) |
Here
NL is the total density and
T0 is a parameter with temperature units that determines the depth of the distribution. Also a band of transport states at the energy level
Ec is indicated in
Fig. 9.
When we consider the distribution of bandgap states g(E), the chemical capacitance is obtained integrating all the contributions through the bandgap
| |  | (11) |
Using d
f(
E−
EFn)/d
EFn = −d
f(
E−
EFn)/d
E and integrating
eqn (11) by parts, we arrive at
| |  | (12) |
A simple solution to
eqn (12) is obtained by the zero-temperature limit of the Fermi function,
i.e. a step function at
E =
EFn separating occupied from unoccupied states. Then it follows that
| |  | (13) |
In this approximation,
eqn (13), the charging related to the perturbation d
V corresponds to filling a slice of traps at the Fermi level. Note that in
eqn (13) the thermal spread of the distribution function is completely neglected. Near room temperature this approximation is justified to some extent if the DOS is smoothly varying as a function of the energy. However, detailed features of the DOS are rounded off, so for a more exact determination the thermal effect of the distribution should be taken into account. An iterative method to derive the DOS from charging data has been developed.
88,89
On the other hand, for the transport states at the energy level Ec, and for potentials such that EFn≪Ec (f≪ 1), the chemical capacitance of the conduction band (cb) states is given by the tail of the Boltzmann distribution indicated in eqn (4)
| |  | (14) |
Let us mention that the total capacitance can take negative values in nanostructured devices, provided that the system is far from equilibrium by applied bias.
67,90
2.2 Factors affecting the chemical capacitance
According to eqn (13) in a first approximation the chemical capacitance is simply proportional to the DOS. This method has been applied in many works for investigation of DOS in conducting polymers,54,91quantum dots,59 and porous semiconductors.13,82,92–94 The electrochemical determination of the DOS in metal-oxide nanostructures and organic conductors has been reviewed recently,8 and are only briefly commented on here.
For the case of nanostructured TiO2 the capacitance–voltage relationship, according to the traps distribution in eqn (10), is exponential
| | 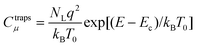 | (15) |
with a slope 1/
kBT0 in log–linear representation, a fact that has been observed many times in the literature, using
EIS,
CV13,40,66,82 and electron
extraction as a function of open-circuit potential.
92,95,96
In organic conductors, disorder or structural correlations with correlation lengths of a few intermolecular distances (fluctuation in the local conjugation length) lead to a dispersion of energies. It is widely agreed that the distribution of electronic states in disordered organic conductors has a Gaussian shape, and this is observed by capacitance measurements.83,91 When a conducting polymer is oxidized electrochemically, the excess carriers (holes) in the polymer chains usually lead to a molecular deformation, which causes a lowering in energy for the excess carrier. Such a carrier together with its produced molecular deformation is called a polaron (P). If two charge carriers share the same molecular deformation a bipolaron (B) is formed; the energy gained by forming only one deformation may outweigh the increased Coulomb repulsion energy.97 It has been pointed out that the relative stability of one Bversus two P may depend on the experimental conditions such as solvent and type of counterions.98
The statistics of P and B in conjugated polymers are well known,99,100 and from these expressions the chemical capacitance can be calculated. In addition, the effect of the Gaussian disorder on the statistics of carriers has been described.54Fig. 11 shows the predictions of the model54 for the chemical capacitance with the successive formation of P and B, in the presence of Gaussian disorder. Initially, at low oxidation potentials, only P are formed, but since the B energy is lower than that of two P (in this example), in the simulation the P readily recombine to form B. Therefore, the P peak in the chemical capacitance, Fig. 11(b), is quite small, and the CV is dominated by the B peak. Experimental examples are found in ref. 8. Note also the negative capacitance of polarons. This is due to the decrease in their number, when the B formation is dominant, despite the increase in the thermodynamic driving force.
 |
| | Fig. 11 Simulation of the charging experiment for a polymer with site density Ns = 1020 cm−3. The polaron levels are centered at εP = 1.5 eV with dispersion σP = 0.2 eV, and the bipolaron levels are centered at εB = 2.8 eV with dispersion εB = 0.15 eV. (a) Number density of polarons and bipolarons. (b) Chemical capacitance of polarons, CPμ, bipolarons, CBμ, and total capacitance, as a function of Fermi level. | |
In ion-intercalation materials the cell voltage variation with the amount of inserted ions (fractional occupancy of lattice sites x) is an essential characteristic for applications such as Li ion batteries. For example modification of composition in metal oxides LixMO determines the chemical potential variation, μ(x), with respect to the Li/Li+ potential (μref). The observed capacitance is dominated by chemical capacitance, eqn (8), which can be written, with respect to N, the number density of intercalation sites, as
| |  | (16) |
Obviously, the chemical capacitance can be determined as the inverse derivative of the equilibrium voltage–composition curve. This derivative parameter is widely used in insertion studies because it provides a detailed view of the features of the thermodynamic function. Many studies of
crystalline intercalation systems used the mean-field (Bragg–Williams
101) approximation, corresponding to the Frumkin isotherm,
102 to describe the voltage–composition and equilibrium capacitance curves.
102–106 We should also remark that in diffusion control the CV departs from the capacitive behavior. Numerical methods are required for explaining detailed features of
voltammetry in the presence of the phase transitions that are characteristic of Li intercalation.
107
In contrast, in amorphous intercalation materials, in particular in LixWO3, phase transitions are absent and the voltage–composition curve shows a monotonic characteristic that was first described in terms of a Gaussian distribution of states related to energetic disorder.108 Recently, it was shown that contributions to the chemical potential of Li+ inside the amorphous film caused by host distortions play a central role both in the voltage–composition curve and in the ion diffusion effects.109–112 In this approach the electrochemical potential takes the form
| |  | (17) |
The first term
E0 in
eqn (17) corresponds to a constant energy level, the second one (1 +
γ)
Gxγ relates to the dependence of the intercalant–host interaction with the insertion level. For
G > 0 additional energy is needed to deform the host. A power-law dependence with composition with
γ < 1 was reported.
109 The last summand accounts for the entropic term. Chemical capacitance results in
| |  | (18) |
where
C0 =
q2N/
kBT is a constant of the order 20 kF cm
−3 depending on
N.
Measurements of the chemical capacitance in a-WO3 films of different thickness agree well with eqn (18), as shown in Fig. 12. Remarkably, the effect of elastic interactions is a strong function of the film thickness. For the thinnest film (100 nm), the ideal statistics of a dilute solution (corresponding to non-interacting lattice gas model), given in eqn (3), is observed, while the Gxγ term becomes increasingly dominant for larger thickness.111 Further studies112 related the intercalation thermodynamics with the models for elastic interactions due to film expansion.113,114
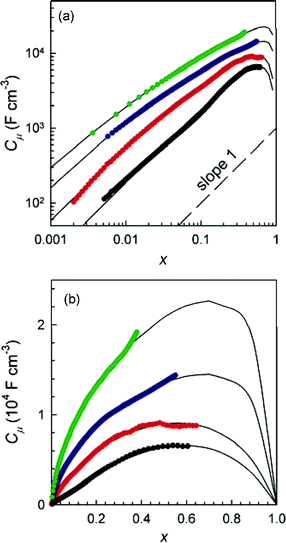 |
| | Fig. 12 Equilibrium (chemical) film capacitance Cμ as a function of the composition (molar fraction) x for a-LixWO3 film thickness (in nm, from bottom to top): 100, 200, 300, and 400. Fine solid lines correspond to fits. Capacitance is multiplied by 2, 4 and 8 for thicknesses 200, 300 and 400 nm, respectively, to improve the clarity of the graph. A reference line of slope 1 is shown. Reprinted with permission from ref. 112, copyright 2006 American Chemical Society. | |
2.3 Depletion capacitance in nanowires
Nanowires and nanotubes are drawing a tremendous attention due to their potential applications in various nanoscale devices. In particular ZnO can be easily induced to grow in the form of rods with high aspect ratio and nanometric dimensions. Recently, some papers have addressed the electrochemical properties of electrodes formed by an array of ZnO rods.115–117 So far we have considered in the previous section capacitance models where both the Fermi level and conduction band level are homogeneous inside the semiconductor nanostructure. However, when the semiconductor is highly doped and/or the minimal size increases, the Debye screening length shrinks well bellow the nano-object dimensions, and an internal field distribution, associated with band bending, is obtained. As in classical photoelectrochemistry,118 the Fermi level in the semiconductor equilibrates with the redox level in solution, resulting in surface depletion layer that is manifest in the Mott–Schottky (MS) formula of the capacitance | | 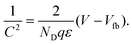 | (19) |
Here ND is the donor density in the n-type semiconductor with dielectric constant ε, V is the voltage and Vfb is the flatband potential, that may be displaced due to the Helmholtz layer at the solution side of the interface.119
When an array of semiconductor nanorods as that shown in Fig. 2 is immersed in solution, the outer surface of the rods is depleted of carriers, forming surface bandbending in the radial direction, while the central region of the rods is a conducting (quasi-neutral) tubular region connected to the substrate, as indicated in Fig. 13. Note that the structure shown in Fig. 13 is ideal for channeling electrons towards the collecting contact, avoiding recombination at the surface, in DSC-type solar cells. Since the whole surface of the rods is an equipotential, the surface barrier can be manipulated by modifying the voltage of the substrate with respect to solution. Further, the depletion layer has a circular shape, Fig. 13, and this introduces a strong modification to the standard MS relationship, eqn (19).115
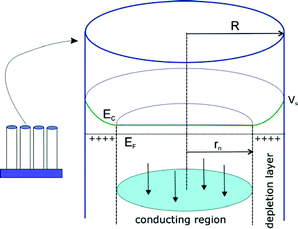 |
| | Fig. 13 Electrical field and carrier distribution in a semiconductor rod of radius R in contact with electrolyte. Ec is the conduction band energy, EF is the Fermi level and Vs the electric potential at the surface. The surface depletion layer and the central conducting region (radius rn) are indicated. | |
In order to calculate the capacitance of the depletion layer in the geometry of Fig. 13, we consider the charge outside a cylinder of radius r
| |  | (20) |
Applying Gauss law, the electrical field is
| | 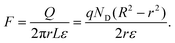 | (21) |
Let
rn be the radius of the quasi-neutral region. The potential across the depletion layer
V =
Vn−
Vs =
Vapp−
Vfb is
| | 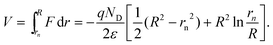 | (22) |
Now we take the derivatives in
eqn (20) and (22)| |  | (23) |
| |  | (24) |
therefore the capacitance of the rod wall is given by
| |  | (25) |
and the specific capacitance per unit surface is
| |  | (26) |
Now
eqn (22) and (26) when combined provide the voltage-dependence of the capacitance, which is illustrated in
Fig. 14 for different levels of doping. For the less-doped sample,
Fig. 14(a), the MS plot shows a large curvature due to the restriction of the depletion layer in the tubular geometry. As the doping increases,
Fig. 14(b), the depletion layer is confined in a short region close to the surface and the straight MS line,
eqn (19), is recovered. Experimentally, it has been found that electrochemically grown ZnO rod arrays show a very high doping of the order 10
20 cm
−3, which decreases considerably by thermal
annealing.
115Fig. 14(c) shows a characteristic MS plot of the capacitance measured in the ZnO
nanorods array. Note that the good fit to the model is expected in highly monodisperse samples. Carrier densities of 10
19 cm
−3 have also been found for the ZnO
nanorods prepared by chemical bath.
117
 |
| | Fig. 14 (a) and (b) Simulation of a Mott–Schottky plot for the specific surface capacitance of a semiconductor rod with R = 50 nm, ε = 10 ε0, and different donor densities as indicated. (c) Experimental data of electrodeposited ZnO rods array on TCO, after annealing 30 min in air, rod dimensions R = 105 nm, L = 950 nm, density 2.40 × 109 cm−2. The line is a fit to the model described in text that gives ND = 1.78 × 1018 cm−3. Data courtesy of I. Mora-Seró. | |
3.
Transport properties
The electronic transport properties of assemblies of colloidal particles vary strongly depending on the individual properties of the nanoparticles, the extent of contacting or electronic coupling between the particles, and the overall geometrical configuration of the assembly.
In the nanostructures formed by sintering of low-doped colloidal nanoparticles, electronic continuity is formed at the contact between adjacent particles. The assembly could be treated in principle as a conventional semiconductor with a band of extended states. The salient difference with respect to monolithic semiconductors, is that the electron density can be varied easily in the whole nanostructure by potential control from the substrate, or photoinjection, as already explained in previous sections, while in compact semiconductors, only the surface density can be varied. In addition, in nanostructured semiconductors the large ratio of surface to volume usually produces a large amount of surface states in the bandgap. The presence of impurities and other factors not totally clear as yet, also cause bulk trap states in the inner part of the nanoparticles, as described above in relation to the DOS in different systems. Therefore the influence of traps on the transport must be considered.
The simplest approach to take trapping into account is the classical multiple trapping (MT) framework.120–123 In this approach transport through extended states is slowed down by trapping–detrapping events, while direct hopping between localized states is neglected. The mobility decreases rapidly below a certain value of energy defining the transport states, so that the motion of a bound electron is limited by the rate of thermal excitations to E≥Ec.
Detailed information on the physical parameters related to transport in DSC has been obtained using small perturbation techniques at a fixed steady state such as IMPS72,73 and EIS.38,65,66,78 Short range electron displacement in nanoporous semiconductors and DSC has been described in terms of the continuous time random walk (CTRW) formalism,124 but the most widely used approach to long range electronic motion, involving macroscopic transport equations, is the MT model, which has been described in a number of papers.68,72,125–127 It was found that both the effective electron diffusion coefficient, Dn, and the effective electron lifetime, τn,128,129 that are measured become a function of the steady state.13,68,72,129–135 Using quasi-equilibrium arguments, the variations of both diffusion coefficient and lifetime were attributed to the statistics of electrons in the material, which deviates from dilution, as described by thermodynamic factors.136 The varying Dn was recognized as a chemical diffusion coefficient,55,127 and the correlation between variations of Dn and τn,135 was explained by a common origin of their variations in an exponential distribution in the bandgap.95,136 The application of the multiple trapping model in DSC will be described in detail in section 3.4.
There are many situations in which it is necessary to consider the transitions between localized levels as the main transport mechanism. Wave functions of localized states decay with the increase of the distance from localization center r. This decay occurs at some characteristic distance a and can be often approximated by:
| |  | (27) |
Therefore, the tunnelling probability decreases exponentially with increasing distance. On the other hand the probability of phonon-activated transitions towards higher energy levels also depends exponentially on the energy difference. When the distribution is very wide in the energy scale, it is necessary to consider the combination of probabilities for hopping at different distances and hopping at different levels, as is well established in the theories of hopping conductivity for bulk amorphous semiconductors,
137,138 and this will be summarily discussed below.
The extent of disorder is an important aspect for characterizing the electronic properties of nanostructured materials, first because of the dispersion of energy of charge carrier within quantum dots, but also due to the influence on long range paths for electron transport. Nanoparticulate film architectures vary from spatially regular to random nanoparticulate networks that form highly disordered structures. Geometrical disorder may become increasingly important for more open structures, due to the existence of highly branched particle structures that influence electron transport dynamics. Studies of electron percolation139,140 show that for compact TiO2 films (40% porosity) used in DSC, the average coordination number is about 6.6, whereas for open-structured films (80% porosity), the average number of particle interconnections is as low as 2.8. Therefore, increasing the porosity has the effect of increasing the average number of particles visited by electrons by 10-fold, from 106 to 107 during their respective transit through 50 and 75% porous 10 μm thick films.140Fig. 15 shows the reported141 evolution of the diffusion coefficient of electrons in nanostructured TiO2, as a function of the excess porosity above the critical value for transport. Samples of different porosity are achieved by consecutively pressing the TiO2 film, from 7 to 4 μm thickness. Therefore energy distribution and trapping factors are not significantly changed for different porosity samples. The results show a change of the diffusion coefficient due to the geometrical effect of the coordination between nanoparticles.
 |
| | Fig. 15 Plot of the effective (chemical) diffusion coefficient of electrons, obtained from transient photocurrents, as a function of the porosity of TiO2 layers. The critical porosity was set to 0.76. Reprinted with permission from ref. 141. Copyright 2006, American Institute of Physics. | |
In the following we will consider in more detail some basic concepts that are important for the interpretation of measurements of transport in a connected array of nanoparticles. First the influence of non-ideal statistics on the measured quantities such as the diffusion coefficient will be described, and also the deviation from standard Einstein relationship due to thermodynamic factors. Then, a number of specific models will be reviewed in detail, in order to show the effects of the DOS and interactions between carriers, on the measurable macroscopic transport coefficients, when the Fermi level is displaced in the nanostructure by potentiostatic control from a substrate. The range of models investigated is summarized in Fig. 16. Free (non-interacting) carriers are considered in a first instance and then the effects of interactions are explored. The hopping conductivity in a broad DOS will be also commented.
 |
| | Fig. 16 Schematic representation of several transport models in an array of quantum dots or in a distribution of electronic states. (a) Hopping transport through a unique level. (b) Transport in a single level affected by trapping in a deeper level. (c) Hopping transport in a two-level system. (d) Transport between discrete energy levels in an array of quantum dots. (e) Conduction band transport affected by trapping in a wide distribution of states in the bandgap. (f) Hopping transport in a wide distribution of states in the bandgap. EFn is the Fermi level, Ec the conduction band energy, and Ei are the energies of discrete levels. | |
3.1 Diffusion and chemical diffusion coefficient
The diffusion of carriers in disordered and nanostructured media is affected by several factors: the available states for hopping, the interactions between carriers, the extent of shielding by surrounding media, etc. Therefore, the relationship between the microscopic hopping mechanisms and the macroscopic transport coefficients is not always straightforward and must be carefully defined. In the following we present a useful framework that dates back to the statement by Onsager and Fuoss of the thermodynamic component of the diffusion coefficient in non-ideal solutions.142 These ideas have been vastly applied in surface diffusion143 and in the simulation of model systems consisting of interacting particles diffusing on the lattice.144,145 Recently, the chemical diffusion coefficient has been found quite useful for rationalizing the transport of electrons in metal-oxide nanostructures,55,127 and it allows also the formulation of the generalized Einstein relation in a very clear way, as discussed later. All these concepts have been well known for a long time in the field of electrochemistry of inorganic solids.51 It was pointed out146 that thermodynamic factors play an important role in Li diffusion in intercalation materials, and a correlation of chemical capacitance and the Li chemical diffusion coefficient is often observed in such materials.147 In nanostructured semiconductor and organic conductors, a broad DOS may cause dominant effects on transport coefficients. It is therefore important to adapt these concepts to electron transport in the presence of energy disorder, and to show the application with examples.
When an electronic or ionic species with concentration n diffuses in a material, the true driving force for diffusion is the gradient of its chemical potential. In the Onsager form of the diffusion law, a linear relationship is assumed142 between the diffusive flux and the gradient of the chemical potential
| |  | (28) |
The prefactor
Ln =
nun/
q is known as the Onsager coefficient. On another hand, diffusion is also formulated in terms of the
concentration gradient in Fick’s form,
| |  | (29) |
The coefficient
Dn in
eqn (29) is called the
chemical diffusion coefficient.
144,148 It is given by
| |  | (30) |
Dn contains two components: (i) a phenomenological coefficient
un (the mobility) and (ii) the term
n∂μn/
∂n, that accounts for the difference between a gradient in concentration, and a gradient in chemical potential. This last term is expressed in dimensionless form as the
thermodynamic factor introduced by Darken
149| |  | (31) |
Note that
χn = 1 in the case of Maxwell–Boltzmann distribution of
eqn (4). Let us introduce the jump (or kinetic) diffusion coefficient,
143 which is simply proportional to mobility
| |  | (32) |
Now we can write the chemical diffusion coefficient as the product
| | 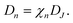 | (33) |
Alternatively, we have
| |  | (34) |
The phenomenological quantities introduced so far can be given more precise meaning in terms of statistical concepts. The thermodynamic factor can be expressed with respect to the chemical capacitance as
| |  | (35) |
and the chemical capacitance is related to the mean-square fluctuation of the particle number
N in a volume
V by the formula
150| |  | (36) |
where 〈〉 denotes a statistical average. Therefore the thermodynamic factor is
| |  | (37) |
The chemical diffusion coefficient
Dn in
eqn (33) can be derived from a microscopic approach using Green–Kubo theory.
144,145 The jump diffusion coefficient has the form
| |  | (38) |
where Δ
ri is the displacement of the
ith particle at time
t. In a regular lattice of spacing
l,
DJ can often be expressed as
| | 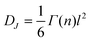 | (39) |
in terms of a mean effective jump frequency
Γ(
n), that varies with the occupancy of the lattice.
143,148
It is important to remark that routine electrochemical methods, based on a step of the voltage (either in time or frequency domain), measure the chemical diffusion coefficient, see e.g.ref. 151 and 152. In contrast, in numerical simulation methods, the quantities χn and DJ are evaluated separately, and then combined to form Dn by the so-called indirect method,153,154 see e.g.ref. 155–158. The term χn can be determined in grand canonical Monte Carlo simulations by use of the fluctuation formula in eqn (37). The kinetic factor is obtained by monitoring the random walk in the lattice149
| |  | (40) |
More precisely,
eqn (40) defines the
tracer diffusion coefficient,
D*, that reflects random walks of a particle, while the jump (or kinetic) diffusion coefficient defined by
eqn (38) reflects diffusion of the centre of mass of
N particles. The difference between these two coefficients (the Haven ratio) is small, usually less than a factor of 2.
3.2 The Einstein relation
The ratio of the mobility and the diffusion coefficient is known as the Einstein relation. The application of this relation in systems with a broad energy disorder is not always transparent, therefore we discuss in the following the statement of the Einstein relation for systems in a quasi-equilibrium regime in terms of the transport coefficients that have been introduced.
We consider the motion of electrons in an organic or inorganic semiconductor material, with concentration n(x) and electric field F(x) = −∂ϕ/∂x at position x. The electrical current is given by the sum of conduction and diffusion currents
| |  | (41) |
The electrochemical potential of electrons is
ηn = −
qϕ +
μn. In equilibrium we have ∂
ηn/∂
x = 0 and consequently
| |  | (42) |
Therefore
eqn (41) gives
| |  | (43) |
Since the current in equilibrium is
jn = 0, the parenthesis in
eqn (43) is zero. This imposes a relationship (Einstein’s) between the mobility and the chemical diffusion coefficient. Such a relation can be stated in two equivalent forms.
Eqn (34) is the generalized Einstein relation,
159 and it differs from the classical Einstein relationship by the thermodynamic factor, so that for classical statistics, with
χn = 1, the traditional relationship is recovered.
Eqn (32) is the standard Einstein relation, but it includes the jump diffusion coefficient. These relations were already obtained with hindsight in the previous section, by including the mobility as the transport coefficient in the diffusion law,
eqn (28). Now
eqn (41) can be written in a similar form, as follows:
| |  | (44) |
This linear relationship between the electrical current and the gradient of the electrochemical potential,
ηn, is usually employed in electronic device modeling, and it is also used in nanostructured photoelectrochemical solar cells.
160,161
It is possible to adopt an alternative expression for the mobility that includes the factor χn.91,162 In this procedure, it is assumed that in the quasi-equilibrium situation only electrons within kBT of the Fermi level contribute significantly to the conductivity.163,164 The effective density of carriers ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) is given by164
is given by164
| |  | (45) |
In terms of the
normal mobility, the electron conductivity is
| |  | (46) |
Then one can define an effective carrier mobility
ûn =
σn/
q![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif)
,
| |  | (47) |
It is clear that
ûn expresses the chemical diffusion coefficient in units of mobility, while the standard mobility relates to the jump diffusion coefficient, as stated in
eqn (32). When discussing
experimental data, it should be born in mind that both mobilities are related as
un =
χnûn, so they can have very different values. For example in assemblies of
quantum dots the thermodynamic factor can take large values,
165,166 as discussed below.
Using eqn (34) and (35), the conductivity can be expressed in terms of chemical diffusion coefficient and chemical capacitance as
| |  | (48) |
This last expression can also be written as
| |  | (49) |
which is the standard form in studies of metal–insulator transition, for example.
167 However, it appears that
eqn (48)55 could be suitable for the analysis of electrochemistry experiments, since the three quantities appearing in
eqn (48) can be measured directly and separately by electrochemical methods. In contrast, the mobility
un, is usually obtained from the conductivity and the total carrier number,
eqn (46).
168,169 In a system with a peak-shaped DOS, there are site-saturation effects affecting the mobility. When the number of carriers
n is very large the conductivity decreases and eventually becomes null, which implies that
un→ 0, according to
eqn (46), see
Fig. 17(c). This is in fact observed in the electrochemistry of conducting
polymers due to the finite (Gaussian) DOS.
170,171
In recent years, the relevance of eqn (34) (in different formulations) has been increasingly realized in relation with disordered materials with a broad distribution of states in the energy space. For example non-ideal Einstein relation was observed in hydrogenated amorphous silicon172 and this was explained in terms of the thermodynamic factor of the exponential distribution.173 The same thermodynamic factor, which is given below in eqn (55), is observed for electron diffusion in nanoporous TiO2 in ref. 127. Several works have also discussed the Einstein relation in organic semiconductors with a Gaussian distribution of electronic or polaronic states.174–179
 |
| | Fig. 17 Representation of several quantities for electron accumulation and diffusion in a cubic array of QDs 3 nm diameter and 1 nm interdot distance. (a) Isotherm (number of electrons vs. potential). (b) Chemical capacitance and thermodynamic factor. (c) Jump (DJ) and chemical (Dn) diffusion coefficients. Parameters: T = 300 K, ν0 = 1012 s−1, a = 0.2 × 10−7 cm. | |
3.3
Transport along discrete energy levels
In this section we consider a number of models for electron transport along discrete energy levels. The models can be applied to the hopping of electrons in arrays of quantum dots, or electron transport between localized sites in a homogeneous semiconductor. The main aim of these models is to obtain the parameters of macroscopic diffusion (chemical capacitance, chemical diffusion coefficient, etc.) as a function of the Fermi level, in relation to the microscopic properties determining electron accumulation and hops. We will analyze step by step models of increasing complexity. We start with the assumption of independent carrier transport in a single energy level, then in several energy levels and thereafter discuss the effects of short-range interactions.
We first consider a simple model that introduces some important concepts related to the finite occupation of electron sites.55 It is a 3-dimensional solid composed of a cubic lattice of weakly interacting quantum dots of radius R and separation d, with a single electronic state at the energy level E0, that can be occupied at most by one carrier, as indicated in Fig. 16(a). This model neglects all interactions and also stands, with obvious modifications, for electron hopping in a single energy level in a nanostructured material. The model, with addition of mean-field interactions, is also applied for Li-ion diffusion in battery materials such as Li1−xCoO2.106
Since the electrons do not interact with each other, the random statistical distribution is valid, and the probability of occupancy is determined by Fermi statistics, eqn (6). The single electronic state is filled when the Fermi level crosses the site energy, as seen in Fig. 17(a). The chemical capacitance takes the form of eqn (9), where N = l−3 is the volume density of electronic states. The thermodynamic factor is
| | 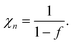 | (50) |
When
EFn≈
E0 the chemical capacitance peaks,
Fig. 17(b). Thereafter the statistics departs strongly from dilution and the thermodynamic factor increases by orders of magnitude because of the departure from ideality by the exclusion “interaction”,
Fig. 17(b): a carrier in a localized site exerts an infinite repulsion over others attempting to hop to that site.
Ref. 180 discusses the Einstein relation in this model.
The average distance travelled by an electron in one hop between dots is l = 2R + d. The mean effective jump frequency is Γ(f) = ν(1 −f), which gives the number of jumps into empty sites per unit time. The hopping rate constant ν for electron hopping between neighboring dots has the form ν = ν0exp(−2d/a), in terms of the decay length a of the wave function in the localized state, and the attempt-to-hop frequency ν0.181
In the case f≪ 1 (i.e., EFn≪E0) one obtains the diluted limit corresponding to Maxwell–Boltzmann statistics. The occupancy restriction is lifted and χn = 1. Let us define the diffusion coefficient in the dilute limit, which is a constant D0 = l2ν/6. For arbitrary f the jump diffusion coefficient can be written DJ = (1 −f)D0 in terms of the diluted value. When χn increases the jump diffusion coefficient decreases considerably due to scarcity of vacant neighbors to accept hopping electrons, Fig. 17(c). The occupancy dependencies of χn and DJ compensate exactly giving the constant chemical diffusion coefficient Dn = D0,55 see Fig. 17(c). In general this model is a good first approximation to the materials with a peak-shaped chemical capacitance. As mentioned above, it should be observed that the mobility un (proportional to DJ) decreases when the carrier number saturates at high Fermi level, producing a decrease of the conductivity. It should also be remarked that Dn and un behave in very different ways.
We now consider the effects of energy distribution in the electronic states. The simplest approach is to assume a static distribution of energy levels. The sites have different energies that are independent of occupation of neighboring sites. The probability of occupancy is determined by Fermi statistics with a common chemical potential (Fermi level) for the different levels. A two-level system is indicated in Fig. 16(b), and it describes well certain ion–intercalation systems.183–185 This is a model in which carrier transport occurs only through the shallow level, while the deep state captures and releases carriers, which affects the transient behaviour of the system.182,186 This assumption is the basis of all multiple trapping models.
Main features of the two-level model with trapping transport of Fig. 16(b) are shown in Fig. 18.182 Thermodynamic quantities in this model are composed of a combination of the features of the separate states, which were discussed in Fig. 17. First Fig. 18(a) shows the consecutive charging of the two levels as the Fermi level increases, and Fig. 18(b) shows the corresponding peaks of the chemical capacitance. The thermodynamic factor shows a peak at the intermediate values of energy between the two levels, and then increases when the two-level system approaches full occupancy. Since the transport along the shallow level is delayed by the trapping in the deep level, when the later is filled there is a strong increase of the chemical diffusion coefficient, as shown in Fig. 18(d). However, the conductivity, represented by diffusion resistance182 in Fig. 18(c), is not affected by the occupancy of the deep level. This is because the conductivity is a steady-state property, that reflects only the hopping along the transport (shallow) level.
 |
| | Fig. 18 Representation of a two state system with E1 = E0− 10kBT and sites concentration N0 = 1/3N, N2 = 2/3N. (a) Occupancy dependence on voltage. (b) Chemical capacitance and thermodynamic factor. (c) Diffusion resistance. (d) Chemical diffusion coefficient.182 | |
Let us consider the effect of interactions between particles in nearest neighbor sites (or quantum dots). A calculation of Monte Carlo simulations187 of a two-dimensional two-level lattice gas with repulsive interactions between nearest neighbors is shown in Fig. 19. J = E2−E1 is the interaction energy between carriers on nearest neighbor sites, where E1 and E2 are site energies (N1 = 1/3N, N2 = 2/3N). In this model system, the transport goes through the lines of Fig. 19(a), as suggested in the scheme of Fig. 16(c). The critical temperature of this system is given by J/kBTc = 3.064,188 and the results of Fig. 19 correspond to the temperature T = 1.2Tc, above the critical value. Therefore the separation between the two energy levels is of the order of the thermal energy, E2−E1 = 2.55kBT.
 |
| | Fig. 19 (a) Arrangement of sites in the two-level systems. The lines indicate the transport pathways. Results of Monte Carlo simulations for this system at T = 1.2Tc: (b) Fractional occupancies of the two levels and total number of particles; (c) chemical capacitance and thermodynamic factor and (d) jump diffusion coefficient, as a function of the electrochemical potential. Data courtesy of V. S. Vikhrenko, adapted from ref. 187. | |
With respect to the non-interacting two-level system discussed before in Fig. 18, in which the states are occupied sequentially when the Fermi level crosses the state energy, an entirely new feature in Fig. 19(b) is a strong decrease of the occupancy of the deep site when the Fermi level lies between the energies of the two levels, Fig. 19(b). This is reflected in a new peak of the chemical capacitance, Fig. 19(b), or equivalently, a dip in the thermodynamic factor. The inversion of the population of the deep level near c = 1/2 is due to interactions between carriers. At c = 1/3 some particles appear at the shallow sublattice, however, their interaction with particles on the deep sublattice is weak. At c = 1/2 particles on the shallow sublattice force the other particles to move on the shallow sublattice because there are many sites on this sublattice and particles do not interact with each other. It follows, that such a behavior is energetically and combinatorially preferred. This process happens without strong external influence what leads to high chemical capacitance at c = 1/2. The jump diffusion coefficient is characterized by minimum value at c = 1/3 because at this concentration almost all the deep sites are occupied. When the concentration is approaching this value and a particle jumps to a nearest shallow site it is repelled back by its neighbors on the nearest deep sites. At c > 1/3 some particles must be on the shallow sublattice and thus the mobility sharply increases due to “exclusion” mechanisms.187 A complete calculation of one-dimensional diffusion in two-level systems with interactions is given in ref. 154.
Next we consider a study of electron transport in a cubic array of quantum dots with discrete energy levels, see Fig. 16(d). The energy for addition of electrons to a quantum dot is considered in the scheme of Franceschestti and Zunger,189,190 taking into account the self-energy of the electron interacting with its image charge at the surface of the particle, a weak electrostatic interaction of electrons in a dot, due to screening by the external medium, and the exchange energy.166 The rate of transfer between energy levels in different dots consists of the Miller–Abrahams hopping rate181 considering only nearest neighbors. Disorder is incorporated in the array of quantum dotsvia a log-normal distribution of sizes with relative standard deviation σR that causes dispersion from the size dependence of the single-particle energy levels and that of the electrostatic interaction and polarization energies. The conductivity is calculated from Monte Carlo simulations of the electron flux maintaining a small difference of electrochemical potential at the contacts. The mobility is determined from eqn (46) and the chemical diffusion coefficient is obtained by determining the electron gradient with eqn (29). Then the thermodynamic factor is obtained from eqn (34).
In Fig. 20 several quantities are represented as a function of the electrochemical potential of the injected electrons, both for low and high disorder. Fig. 20(a)–(c) show the thermodynamic features corresponding to electron charging and the associated thermodynamic factor and electrochemical capacitance. It was shown166 that these features can be successfully modelled using a mean-field approximation and the equilibrium definition of the thermodynamic factor, eqn (31), with respect to the electrochemical potential. A salient characteristic of the results is the presence of strong Coulomb blockade effect for the low-disorder sample when completing the 1S0 shell at n = 2 and the 1P0 shell (n = 8) at ηn = 3.3 eV. This gives rise to a large increase in the thermodynamic factor, which increases by a factor of 1000 at n = 2 and a factor of 10 at n = 8. Additional minor peaks are obtained when the average occupation number is an integer. However, for the array with σR = 0.1 these features are almost completely smoothed. These results indicate that the apparition of Coulomb blockades necessitates both small size dispersion and a Coulomb interaction energy that is larger than kBT.
 |
| | Fig. 20 Representation of several quantities for electron accumulation and diffusion in a cubic array of QDs 3 nm mean radius and 2 nm interdot distance, parametric on size dispersion. (a) Isotherm (number of electrons vs. potential). (b) Thermodynamic factor. (c) Chemical capacitance. (d) Mobility. (e) Chemical diffusion coefficient. (f) Conductivity. Parameters: T = 300 K, ν0 = 1012 s−1, a = 0.5 × 10−7 cm. Data courtesy of J. van de Lagemaat, adapted from ref. 166. | |
A main result obtained in this study166 is the considerable difference between Fermi level dependencies of the mobility and chemical diffusion coefficient in the low-disorder array, as a result of the large thermodynamic factor. Thus while the diffusion coefficient only decreases by a factor of 10 in the 1S0 shell-filling region, the mobility shows a strong minimum with a decay of three orders of magnitude.191 It is also noteworthy that the conductivity, Fig. 20(f), when averaged over local peaks remains nearly constant during the filling of the P shell, due to compensation of the increase in carrier density with the decrease in the mobility.
3.4
Transport in a continuous density of states
Multiple trapping in a broad distribution of states.
We have already mentioned that results of electron transport in DSC have been largely interpreted in terms of the MT model in a continuous distribution of states. Let us analyze this model, represented in Fig. 16(e), in more detail. Electronic states are composed of a transport state (usually identified with the lower edge of the conduction band) at the energy level Ec, with a diffusion coefficient D0, and a density of localized states g(E) distributed in the bandgap. The total electron density is n = nc + nL, i.e. the sum of electron densities in conduction band and localized states, Fig. 9. In general for the multiple trapping model we obtain the thermodynamic factor,55| |  | (51) |
The mean effective jump frequency is obtained from the MT condition that only free electrons in transport states contribute to the diffusion process, hence the jump diffusion coefficient is | |  | (52) |
Using eqn (32) and (46), the electron conductivity can be written as | |  | (53) |
Applying eqn (52), it is found that | |  | (54) |
The only Fermi-level dependent quantity in eqn (54) is the free electron density, and this is observed experimentally in nanostructured TiO2.58 As already commented in connection with the two-level system, the steady-state conduction is not affected by the trapping process, because the traps remain in equilibrium. Alternatively, one can view conduction as the result of the displacement of the whole electron density, eqn (53), but with the jump diffusion coefficient, which is not constant.
The chemical diffusion coefficient of electrons, Dn, is given by eqn (30). The effect of trapping in the chemical diffusion coefficient is dominant when ∂nL/∂nc≫ 1. In this case the result is
| |  | (55) |
The prefactor in
eqn (55) is the relationship of free to trapped number of electrons for a small variation of the Fermi level. This prefactor describes the delay of response of the chemical diffusion coefficient, with respect to the free electrons diffusion coefficient, by the trapping and detrapping process.
136,192 Such a delay is unavoidable when measuring the chemical diffusion coefficient by any transient technique. In the quasistatic approximation
136 the effect of electron trapping kinetics is completely described in terms of electrons densities. This is related to application of the principle of detailed balance, that links the kinetic constants for trapping and detrapping to the equilibrium occupancies.
193 Using the zero temperature limit of the Fermi function, it is obtained that the reciprocal of the prefactor in
eqn (55) is given by
136| | 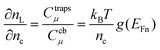 | (56) |
see
eqn (14) and (15).
Multiple trapping in exponential distribution.
Let us consider in particular the exponential distribution of localized states, with a characteristic energy kBT0, given in eqn (10). As mentioned before it is well established that nanostructured TiO2 used in DSC (anatase) shows this type of distribution of states in the bandgap,13,40,66,82,95 and even the direct monitoring of Fermi level has been realized.194,195 The main features of the MT model for this distribution55 are illustrated in simulation in Fig. 21 with realistic parameter values.82,125 We first discuss the regime of electrochemical potentials in which the Fermi level is well below the conduction band. Hence the free electron density is much lower than trapped electrons number, nc/nL≪ 1.
 |
| | Fig. 21 Representation of several quantities for charge accumulation and diffusion by multiple trapping in a nanostructured semiconductor electrode of thickness L = 10 μm with an exponential distribution of bandgap states. (a) Isotherm (total charge vs. potential). (b) Chemical capacitance and thermodynamic factor. (c) Free electrons diffusion coefficient (D0), and jump (DJ) and chemical (Dn) diffusion coefficient. Parameters: Nc = 6.8 × 1020 cm−3, NL = 2.0 × 1019 cm−3, T = 300 K, T0 = 1400 K, D0 = 10−2 cm2/s. | |
Fig. 21(a) shows the extent of electron charging, and Fig. 21(b) shows the chemical capacitance of the localized states, given in eqn (15), with a slope (kBT0)−1. The thermodynamic factor is constant55
| |  | (57) |
where
| | 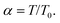 | (58) |
For the typical values of
T0,
χn≈ 5 at room temperature, as shown in
Fig. 21(b). The calculation of the jump and chemical diffusion coefficient,
eqn (30), gives, respectively
55| |  | (59) |
| |  | (60) |
Results of the diffusion coefficients are shown in Fig. 21(c).
Fig. 21 also shows the evolution of parameters when Fermi level approaches the conduction band and nc≈n. The chemical capacitance of the conduction band states is given in eqn (14) and its slope corresponds the thermal energy value (kBT)−1, reflecting the Maxwell–Boltzmann distribution of the dominant free carriers. The thermodynamic factor takes the value of 1 when approaching the conduction band from below, due to the onset of ideal statistics. In this domain MT trapping ceases to hold, because the different kinetic phenomena occur directly through the conduction band states with no interference of the traps (which are nearly full of electrons) and both DJ and Dn approach D0.
Application of multiple trapping in dye-sensitized solar cells.
The MT model just discussed has been very useful for rationalizing the experimental results on electron transport in DSC, for example the observation by IMVS of a chemical diffusion coefficient that varies with the Fermi level in the same way as shown in Fig. 21.72,134 The MT model, in combination with the quasistatic approximation136 also provides an explanation for the observed compensation between chemical diffusion coefficient and lifetime129 dependence on Fermi level, to give a nearly constant electron diffusion length as reported by L. M. Peter and other authors.6,15,72,95,135,196
Characteristic experimental results of the main parameters, obtained by EIS in several DSCs,66 are shown in Fig. 22. An exponential dependence of the total film capacitance is observed in an intermediate domain of potentials, which is interpreted as Ctrapsμ. At the more positive potentials, the metal oxide is insulating and the capacitance observed corresponds to the conducting substrate that is exposed to the solution.119 At the more negative potentials the Fermi level should approach the conduction band. As shown in Fig. 21(b) the slope of the capacitance should increase towards the thermal value (kBT)−1, but in contrast to this, the experiments in Fig. 22(a) show that the slope decreases at the more negative potentials. This is interpreted as a shift of the conduction band potential due to increasing potential drop at the Helmholtz layer, at the high electron densities considered.82 The conduction band is displaced upwards as it is approached by the Fermi level, which makes it fairly difficult to detect the extended transport states of the conduction band.55
 |
| | Fig. 22 Parameters resulting from the fit of experimental EIS spectra of three dye-sensitized solar cells at different bias potentials in the dark. The electrolyte composition in the reference cell is 0.5 M LiI, 0.05 M I2 and 0.5 M 1-methylbenzimidazole (MBI) in 3-methoxypropionitrile (3-MPN). The second cell has 0.5 M NaI instead of LiI, and the third cell has no MBI. (a) Capacitance of the cell without the contribution of the Pt capacitance. Also indicated is the estimated open-circuit voltage of the cell at 1 sun illumination (measured value is 0.58 V at 0.1 sun). (b) Chemical diffusion coefficient of electrons. (c) Transport resistance in TiO2. The lines are fits to eqn (61)–(63), and the parameters resulting from fits are indicated. T is the actual temperature of the cell, assumed 300 K, T′ is the effective temperature obtained from the slopes of the plots as indicated, and T0 is the characteristic temperature of the exponential distribution of localized states in the bandgap. Data courtesy of F. Fabregat-Santiago, adapted from ref. 66. | |
Let us make an analysis of experimental results on chemical capacitance, chemical diffusion coefficient and diffusion resistance, in order to check the predictions of the MT model with the exponential distribution of states. The potential-dependence of these elements, according to the model, are
| |  | (61) |
| |  | (62) |
| |  | (63) |
In
Fig. 22 the results of these parameters are shown for three DSCs containing different species in the electrolyte. In each case the absorption of the indicated species in the surface of TiO
2 determines the surface dipole and provokes a global shift in the potential scale (in the same way as in
Fig. 3, above). The three elements,
Ctrapsμ,
Dn and
Rdiffusion, show exponential dependencies in the potential and shift consistently in the voltage scale. We examine the reference cell, containing LiI electrolyte, in more detail. First, in the intermediate domain where the traps capacitance is observed separately, we fit the capacitance to
eqn (61) and obtain
kBT0 = 62 mV corresponding to
α = 0.42 at
T = 300 K. This implies an exponent
kBT/(1 −
α) = 44 mV for the chemical diffusion coefficient, and this in fact is the value obtained in
Fig. 22(b). The diffusion resistance is the reciprocal of the conductivity in
eqn (54), therefore the dependence on potential is given by the thermal energy
kBT = 26 mV at room temperature,
eqn (63), and this prediction is also well realized by the data in
Fig. 22(c). Recent measurements of the chemical diffusion coefficient in high efficiency
DSC at different temperatures further confirmed the predictions of MT transport,
78 and
activation energies for electron transport have been discussed as well using this model.
197
The MT model describes well the diffusion coefficient and conductivity of nanostructured TiO2 when the Fermi level lies deep in the exponential trap distribution in the bandgap. However, the free electrons diffusion coefficient D0 implicit in the MT model has not been separately identified. The Hall mobility of electrons in large single crystals of anatase-TiO2 at room temperature has the value uH = 20 cm2V−1 s−1,198 corresponding to the diffusion coefficient D0 = 0.5 cm2 s−1. But such a large value of the electron diffusion coefficient has not been approached in DSC. Measurements of electron diffusion coefficient in nanoporous TiO2electrodes, in different electrolytes and determined by different techniques, remain below the value of 10−3 cm2 s−1.78 The upper limitation to the photovoltage in DSC is given when the Fermi level meets the lower edge of the conduction band of TiO2.3,199 In Fig. 22(b) we see that the extrapolation of Dn to Voc (at 1 sun) remains lower than 10−3 cm2 s−1, which is two orders of magnitude below the value expected for bulk crystals. However, some estimates put the open circuit Fermi level at least 150 meV below the conduction band even at 1 sun. Furthermore, electron transport is normally measured under short circuit conditions where the Fermi level is almost 500 meV below the conduction band. Therefore, it is not yet clearly established whether the free electrons diffusion coefficient in DSC is consistent with the value for bulk anatase.
Hopping conduction.
The theory of hopping conduction137,138 describes the transport by carrier jumps via localized states, as indicated in Fig. 16(f). A general description of hopping conduction in disordered systems with a broad distribution of localized states is a complex problem. Given a distribution of hopping sites, the possible set of transitions are in principle known. However, averaging over all possible spatial and energy configurations in order to find the average jump rate and hopping distance that relate to the observable transport coefficients, is not feasible. The analysis is partially simplified in a system with a steep distribution of localized states, where the hopping process is well described with the concept of transport energy, originally formulated for systems with an exponential DOS.200–204 For carriers situated deep enough energetically, a particular level, called the transport energy, Et, determines each single hopping event. Therefore, when the Fermi level is well below the transport level, hopping systems behave very similar to a MT system, with the level Et playing the role of the conduction band edge in the above description. The concept of transport energy has been extended to systems with a Gaussian DOS.205–207
Another limiting case of hopping models, first suggested by Mott,208 considers the competition between hopping at different energies and at different distances, and is generally termed variable-range hopping (VRH). This approach optimizes the hopping rate of a single hop from one site to another under the constraint that at least one such hop is possible. Later, more systematic treatments were initiated that were based on percolation arguments, the so-called critical path analysis.137,138 VRH has been observed in a wide variety of systems such as Si- and Ge-based inorganic semiconductors,209 conducting polymers and assemblies of quantum dots.210
The hopping conductivity has been amply studied for bulk amorphous semiconductors137,138 and organic semiconductors with a Gaussian DOS,206,207,211–217 but these developments have not been generally applied in electrochemistry experiments. Arkhipov, Bässler and coworkers have reported some models of the electronic conductivity of electrochemically doped polymers.218,219
In an array of quantum dots with strong spatial confinement and good electronic coupling between dots, a narrow band, providing coherent transport, can be formed at each discrete energy level. However, there are several factors that lead to localization of carriers in the quantum dots,220 as discussed in the example of Fig. 20. Colloidal nanoparticles prepared by wet chemical methods fluctuate in size and chemical composition. This introduces some inherent disorder in an array of quantum dots, that produces a dispersion of the energy levels.220 The difference between energy levels in different quantum dots makes tunneling of electrons between quantum dots difficult. Moreover such dispersion leads to the random scattering of electronic waves. Thus dispersion of quantum dot sizes and fluctuation of the chemical composition contribute to localization.221 The Coulomb repulsion between two electrons (holes) sitting on the same quantum dot introduces an energy gap between occupied and empty states (Hubbard insulator). A number of characteristic phenomena for transport in disordered semiconductors have been reported in arrays of quantum dots, such as metal–insulator transitions16,222 and Mott-like conduction gaps,59,221 the VRH transport,210 and percolation thresholds depending on disorder.223
4. Conclusions and outlook
Extensive work over the last decade and a half on nanocrystalline systems and organic conductors in electrochemical configuration has brought a great deal of understanding on these systems. The knowledge initiated from a mixture of the classical concepts of electrochemistry and semiconductor physics. The main novelty came from the fact that the semiconductor Fermi level in electrolyte-surrounded nanocrystalline networks could be homogeneously moved with a potentiostat. But some general features complicate the study of these systems. First, heterogeneity at the nanoscale is always present. Second, there is no attempt at purity or ideality of materials in this field, on the contrary, materials development are driven by the need of simple preparation methods that provide effective outcomes when tested as part of complex devices. Therefore these materials usually present a great extent of disorder and variability depending on preparation methods, properties of the solution, etc. This is why the great deal of interest on nanocrystalline TiO2 for dye solar cells has been a very positive asset. A great number of laboratories and scientists focused their work on this widely accessible system, and in consequence, a large body of experimental results revealed the regularities of the physical electrochemistry (and photoelectrochemistry) of this system. As a result, a number of specific experimental methods in combination with a well-established battery of conceptual tools, which we have attempted to review here, has become available for testing the properties of similar nanocrystalline systems.
In my view, it is remarkable that the electronic properties of nanocrystalline semiconductors can now be reliably extracted and described with relatively simple concepts and one-dimensional models, taking into account the intrinsic variability, disorder and heterogeneity of these systems. These methods are now routinely applied to investigate different types of metal-oxide nanocrystalline electrodes. The techniques and concepts mentioned provide an identification of the density of electronic states, diffusion coefficient, lifetime, etc., which constitutes highly valuable information for characterizing the materials prepared and for designing new ones.
However, there are still important challenges in this field. First of all, the electronic behaviour of the nanocrystalline semiconductors consistently changes as a function of the medium (liquid or solid) filling the pores. In part this change is due to modifications of electron lifetimes, due to the variation of interfacial charge transfer properties, however the transport properties are also affected, meaning that some interaction takes place between the electronic carriers in the semiconductor and the surrounding medium. While it has been possible to control the shift of energy levels by absorption of molecular species in the surface, as discussed in the main text, additional effects of interactions are very poorly understood, and there are no swift methods to predict or analyze the behaviour of new electrolytes or organic hole conductors. Another aspect that needs more work is the high accumulation regime; the free electrons’ diffusion coefficient has not yet been clearly identified; the transport mechanism at high carrier densities is not really known, and in addition, the electrochemical effects of packing a large number of carriers in small nanoparticles have been little investigated. Finally, an important route of research is the properties of ordered nanostructures such as nanotubes, which are reaching perfection. By removing the uncertainties introduced by spatial disorder, these last systems may provide in the near future considerable information on the physical electrochemistry of nanoscale semiconductors.
Acknowledgements
The author is very grateful to Thomas Dittrich, Germà Garcia-Belmonte, Craig C. Grimes, Francisco Fabregat-Santiago, Vladimir G. Kytin, Jao van de Lagemaat, Iván Mora-Seró, Ramón Tena-Zaera, Vyacheslav S. Vikhrenko and Arie Zaban for supplying original data and figures as well as for many discussions on the topics of this paper. The work was supported by Ministerio de Educación y Ciencia of Spain under project MAT2004-05168.
References
- M. Winter and R. J. Brodd, Chem. Rev., 2004, 104, 4245 CrossRef CAS.
- B. O'Regan and M. Grätzel, Nature, 1991, 353, 737 CrossRef CAS.
- J. Bisquert, D. Cahen, S. Rühle, G. Hodes and A. Zaban, J. Phys. Chem. B, 2004, 108, 8106 CrossRef CAS.
- J. H. Burroughes, D. D. C. Bradley, A. R. Brown, R. N. Marks, K. MacKay, R. H. Friend, P. L. Burn and A. B. Holmes, Nature, 1990, 347, 539 CrossRef CAS.
- L. M. Peter, Phys. Chem. Chem. Phys., 2007, 9, 2630 RSC.
- L. M. Peter, J. Phys. Chem. C, 2007, 111, 6601 Search PubMed.
- D. Vanmaekelbergh, A. J. Houtepen and J. J. Kelly, Electrochim. Acta, 2007 DOI:10.1016/j.electacta.2007.02.045.
- J. Bisquert, F. Fabregat-Santiago, I. Mora-Seró, G. Garcia-Belmonte, E. M. Barea and E. Palomares, Inorg. Chim. Acta, 2007 DOI:10.1016/j.ica.2007.05.032.
-
J. Bisquert, in Synthesis, Properties and Applications of Oxide Nanomaterials, ed. J. A. Rodríguez and M. Fernández García, Wiley, Weinheim, 2007 Search PubMed.
- D. Vanmaekelbergh and P. Liljerorth, Chem. Soc. Rev., 2005, 34, 299 RSC.
- R. L. Willis, C. Olson, B. O'Regan, T. Lutz, J. Nelson and J. R. Durrant, J. Phys. Chem. B, 2002, 106, 7605 CrossRef CAS.
- K. Tennakone, G. K. R. Senadeera, V. P. S. Perera, I. R. M. Kottegoda and L. A. A. De Silva, Chem. Mater., 1999, 11, 2474 CrossRef CAS.
- D. Niinobe, Y. Makari, T. Kitamura, Y. Wada and S. Yanagida, J. Phys. Chem. B, 2005, 109, 17892 CrossRef CAS.
- M. Quintana, T. Edvinsson, A. Hagfeldt and G. Boschloo, J. Phys. Chem. C, 2007, 111, 1035 Search PubMed.
- Y. Fukai, Y. Kondo, S. Mori and E. Suzuki, Electrochem. Commun., 2007, 9, 1439 CrossRef CAS.
- C. P. Collier, T. Vossmeyer and J. R. Heath, Annu. Rev. Phys. Chem., 1998, 49, 371 CrossRef CAS.
- G. K. Mor, K. Shankar, M. Paulose, O. K. Varghese and C. A. Grimes, Nano Lett., 2006, 6, 215 CrossRef CAS.
- G. K. Mor, O. K. Varghese, M. Paulose, K. Shankar and C. A. Grimes, Sol. Energy Mater. Sol. Cells, 2006, 90, 2011 CrossRef CAS.
- K. Shankar, G. K. Mor, H. E. Prakasam, S. Yoriya, M. Paulose, O. K. Varghese and C. A. Grimes, Nanotechnology, 2007, 18, 065707 CrossRef.
- J. B. Baxter and E. S. Aydil, Appl. Phys. Lett., 2005, 86, 053114 CrossRef.
- W.-S. Chae, S.-W. Lee and Y.-R. Kim, Chem. Mater., 2005, 17, 3072 CrossRef CAS.
- L. E. Greene, M. Law, D. H. Tan, M. Montano, J. Goldberger, G. Somorjai and P. Yang, Nano Lett., 2005, 5, 1231 CrossRef CAS.
- M. Law, L. E. Greene, A. Radenovic, T. Kuykendall, J. Liphardt and P. Yang, J. Phys. Chem. B, 2006, 110, 22652 CrossRef CAS.
- B. Marí, M. Mollar, A. Mechkour, B. Hartiti, M. Perales and J. Cembrero, Microelectron. J., 2004, 79 Search PubMed.
- J. Cembrero, A. Elmanoumi, B. Hartiti, M. Mollar and B. Marí, Thin Solid Films, 2004, 451–452, 198 CrossRef CAS.
- J. B. Baxter and E. S. Aydil, Sol. Energy Mater. Sol. Cells, 2006, 90, 607 CrossRef CAS.
- C. Lévy-Clément, A. Katty, S. Bastide, F. Zenia, I. Mora and V. Munoz-Sanjose, Physica E, 2002, 14, 229 CrossRef CAS.
- C. Lévy-Clément, R. Tena-Zaera, M. A. Ryan, A. Katty and G. Hodes, Adv. Mater., 2005, 17, 1512 CrossRef CAS.
- R. Konenkamp, R. C. Word and M. Godinez, Nano Lett., 2005, 5, 2005 CrossRef CAS.
- X. Sun, Z. Deng and Y. Li, Mater. Chem. Phys., 2003, 80, 366 CrossRef CAS.
- G. R. R. A. Kumara, K. Tennakone, V. P. S. Perera, A. Konno, S. Kaneko and M. Okuya, J. Phys. D: Appl. Phys., 2001, 34, 868 CrossRef CAS.
- A. Zaban, S. G. Chen, S. Chappel and B. A. Gregg, Chem. Commun., 2000, 22, 2231 RSC.
- S. Chappel, S. G. Chen and A. Zaban, Langmuir, 2002, 18, 3336 CrossRef CAS.
- Y. Diamant, S. G. Chen, O. Melamed and A. Zaban, J. Phys. Chem. B, 2003, 107, 1977 CrossRef CAS.
- E. Palomares, J. N. Clifford, S. A. Haque, T. Lutz and J. R. Durrant, Chem. Commun., 2002, 1464 RSC.
- E. Palomares, J. N. Clifford, S. A. Haque, T. Lutz and J. R. Durrant, J. Am. Chem. Soc., 2003, 125, 475 CrossRef CAS.
- F. Lenzmann, M. Nanu, O. Kijatkina and A. Belaidi, Thin Solid Films, 2004, 451–452, 639 CrossRef CAS.
- F. Fabregat-Santiago, J. García-Cañadas, E. Palomares, J. N. Clifford, S. A. Haque, J. R. Durrant, G. Garcia-Belmonte and J. Bisquert, J. Appl. Phys., 2004, 96, 6903 CrossRef CAS.
- S. Ruhle, M. Greenshtein, S.-G. Chen, A. Merson, H. Pizem, C. S. Sukenik, D. Cahen and A. Zaban, J. Phys. Chem. B, 2005, 109, 18907 CrossRef.
- Z. Zhang, S. M. Zakeeruddin, B. C. O'Regan, R. Humphry-Baker and M. Grätzel, J. Phys. Chem. B, 2005, 109, 21818 CrossRef CAS.
- Z. Zhang, N. Evans, S. M. Zakeeruddin, R. Humphry-Baker and M. Grätzel, J. Phys. Chem. C, 2007, 111, 398 Search PubMed.
- A. J. Nozik, Inorg. Chem., 2005, 44, 6893 CrossRef CAS.
- A. J. Nozik, Physica E, 2002, 14, 115 CrossRef CAS.
- R. Schaller and V. Klimov, Phys. Rev. Lett., 2004, 92, 186601 CrossRef CAS.
- R. J. Ellingson, M. C. Beard, J. C. Johnson, P. Yu, O. I. Micic, A. J. Nozik, A. Shabaev and A. L. Efros, Nano Lett., 2005, 5, 865 CrossRef CAS.
- R. D. Schaller, M. Sykora, J. M. Pietryga and V. I. Klimov, Nano Lett., 2006, 6, 424 CrossRef CAS.
- T. Miyasaka and T. N. Murakami, Appl. Phys. Lett., 2004, 85, 3932 CrossRef CAS.
- A. Hauch, A. Georg, S. Baumgärtner, U. Opara-Krasovec and B. Orel, Electrochim. Acta, 2001, 46, 2131 CrossRef CAS.
- J. Bisquert, G. Garcia-Belmonte and F. Fabregat Santiago, J. Solid State Electrochem., 1999, 3, 337 CrossRef CAS.
- H. Reiss, J. Phys. Chem., 1985, 89, 3783 CrossRef CAS.
-
H. Rickert, Electrochemistry of Solids, Springer Verlag, Berlin, 1982 Search PubMed.
- I. Riess, Solid State Ionics, 1997, 95, 327 CrossRef.
- E. A. Guggenheim, J. Phys. Chem., 1929, 33, 842 CrossRef CAS.
- J. Bisquert, G. Garcia-Belmonte and J. García-Cañadas, J. Chem. Phys., 2004, 120, 6726 CrossRef CAS.
- J. Bisquert, J. Phys. Chem. B, 2004, 108, 2323 CrossRef CAS.
-
A. J. Bard and L. R. Faulkner, Electrochemical Methods, Fundamentals and Applications, John Wiley & Sons, Weinheim, 2nd edn, 2001 Search PubMed.
- A. Zaban, J. Zhang, Y. Diamant and J. Bisquert, J. Phys. Chem. B, 2003, 107, 6022 CrossRef CAS.
- I. Abayev, A. Zaban, F. Fabregat-Santiago and J. Bisquert, Phys. Status Solidi A, 2003, 196, R4 CrossRef CAS.
- A. L. Roest, J. J. Kelly and D. Vanmaekelbergh, Appl. Phys. Lett., 2003, 83, 5530 CrossRef CAS.
- J. García-Cañadas, F. Fabregat-Santiago, J. Kapla, J. Bisquert, G. Garcia-Belmonte, I. Mora-Seró and M. O. M. Edwards, Electrochim. Acta, 2004, 49, 745 CrossRef CAS.
- Q. Wang, S. M. Zakeeruddin, J. Cremer, P. Bäuerle, R. Humphry-Baker and M. Grätzel, J. Am. Chem. Soc., 2005, 127, 5706 CrossRef CAS.
- J. Bisquert, M. Grätzel, Q. Wang and F. Fabregat-Santiago, J. Phys. Chem. B, 2006, 110, 11284 CrossRef CAS.
- J. Bisquert, G. Garcia-Belmonte, F. Fabregat-Santiago, N. S. Ferriols, P. Bogdanoff and E. C. Pereira, J. Phys. Chem. B, 2000, 104, 2287 CrossRef CAS.
- J. Bisquert, J. Phys. Chem. B, 2002, 106, 325 CrossRef CAS.
- F. Fabregat-Santiago, G. Garcia-Belmonte, J. Bisquert, A. Zaban and P. Salvador, J. Phys. Chem. B, 2002, 106, 334 CrossRef CAS.
- F. Fabregat-Santiago, J. Bisquert, G. Garcia-Belmonte, G. Boschloo and A. Hagfeldt, Sol. Energy Mater. Sol. Cells, 2005, 87, 117 CrossRef CAS.
- I. Mora-Seró, J. Bisquert, F. Fabregat-Santiago, G. Garcia-Belmonte, G. Zoppi, K. Durose, Y. Proskuryakov, I. Oja, A. Belaidi, T. Dittrich, R. Tena-Zaera, A. Katty, C. Lévy-Clement, V. Barrioz and S. J. C. Irvine, Nano Lett., 2006, 6, 640 CrossRef CAS.
- P. E. de Jongh and D. Vanmaekelbergh, Phys. Rev. Lett., 1996, 77, 3427 CrossRef CAS.
- D. Vanmaekelbergh, F. Iranzo Marín and J. van de Lagemaat, Ber. Bunsen-Ges. Phys. Chem., 1996, 100, 616 CAS.
- D. Vanmaekelbergh and P. E. de Jongh, Phys. Rev. B, 2000, 61, 4699 CrossRef CAS.
- L. Dloczik, O. Ileperuma, I. Lauerman, L. M. Peter, E. A. Ponomarev, G. Redmond, N. J. Shaw and I. Uhlendorf, J. Phys. Chem. B, 1997, 101, 10281 CrossRef CAS.
- A. C. Fisher, L. M. Peter, E. A. Ponomarev, A. B. Walker and K. G. U. Wijayantha, J. Phys. Chem. B, 2000, 104, 949 CrossRef.
- G. Schlichthröl, S. Y. Huang, J. Sprague and A. J. Frank, J. Phys. Chem. B, 1997, 101, 8141 CrossRef.
- R. Kern, R. Sastrawan, J. Ferber, R. Stangl and J. Luther, Electrochim. Acta, 2002, 47, 4213 CrossRef CAS.
- Q. Wang, J.-E. Moser and M. Grätzel, J. Phys. Chem. B, 2005, 109, 14945 CrossRef CAS.
- T. Hoshikawa, R. Kikuchi and K. Eguchi, J. Electroanal. Chem., 2006, 588, 59 CrossRef CAS.
- M. Adachi, M. Sakamoto, J. Jiu, Y. Ogata and S. Isoda, J. Phys. Chem. B, 2006, 110, 13872 CrossRef CAS.
- Q. Wang, S. Ito, M. Grätzel, F. Fabregat-Santiago, I. Mora-Seró, J. Bisquert, T. Bosshoa and H. Imaic, J. Phys. Chem. B, 2006, 110, 19406 CrossRef.
- E. W. Paul, A. J. Ricco and M. S. Wrighton, J. Phys. Chem., 1985, 89, 1441 CrossRef CAS.
- E. A. Meulenkamp, J. Phys. Chem. B, 1999, 103, 7831 CrossRef CAS.
- H. G. Agrell, G. Boschloo and A. Hagfeldt, J. Phys. Chem. B, 2004, 108, 12388 CrossRef CAS.
- F. Fabregat-Santiago, I. Mora-Seró, G. Garcia-Belmonte and J. Bisquert, J. Phys. Chem. B, 2003, 107, 758 CrossRef CAS.
- J. Bisquert, G. Garcia-Belmonte and J. García-Cañadas, J. Chem. Phys., 2004, 120, 6726 CrossRef CAS.
- P. Wang, S. M. Zakeeruddin, R. Humphry-Baker and M. Grätzel, Chem. Mater., 2004, 16, 2694 CrossRef CAS.
- H. Randriamahazaka, F. Fabregat-Santiago, A. Zaban, J. García-Cañadas, G. Garcia-Belmonte and J. Bisquert, Phys. Chem. Chem. Phys., 2006, 8, 1827–1833 RSC.
- D. Kuang, C. Klein, S. Ito, J. E. Moser, R. Humphry-Baker, N. Evans, F. Duriaux, C. Grätzel, S. M. Zakeeruddin and M. Grätzel, Adv. Mater., 2007, 19, 1133 CrossRef CAS.
- J. Jamnik and J. Maier, Phys. Chem. Chem. Phys., 2001, 3, 1668 RSC.
- V. G. Kytin, J. Bisquert, I. Abayev and A. Zaban, Phys. Rev. B, 2004, 70, 193304 CrossRef.
- I. Abayev, A. Zaban, V. G. Kytin, A. A. Danilin, G. Garcia-Belmonte and J. Bisquert, J. Solid State Electrochem., 2007, 11, 647 CrossRef CAS.
- J. Bisquert, G. Garcia-Belmonte, A. Pitarch and H. Bolink, Chem. Phys. Lett., 2006, 422, 184 CrossRef CAS.
- I. N. Hulea, H. B. Brom, A. J. Houtepen, D. Vanmaekelbergh, J. J. Kelly and E. A. Meulenkamp, Phys. Rev. Lett., 2004, 93, 166601 CrossRef CAS.
- L. M. Peter, N. W. Duffy, R. L. Wang and K. G. U. Wijayantha, J. Electroanal. Chem., 2002, 524–525, 127 CrossRef CAS.
- H. Wang, J. He, G. Boschloo, H. Lindström, A. Hagfeldt and S. Lindquist, J. Phys. Chem. B, 2001, 105, 2529 CrossRef CAS.
- T. Berger, T. Lana-Villarreal, D. Monllor-Satoca and R. Gomez, J. Phys. Chem. C, 2007, 111, 9936 Search PubMed.
- M. Bailes, P. J. Cameron, K. Lobato and L. M. Peter, J. Phys. Chem. B, 2005, 109, 15429 CrossRef CAS.
- G. Boschloo and A. Hagfeldt, J. Phys. Chem. B, 2005, 109, 12093 CrossRef CAS.
- J. L. Brédas and G. B. Street, Acc. Chem. Res., 1985, 18, 309 CrossRef CAS.
- J. A. E. H. van Haare, E. E. Havinga, J. L. J. van Dongen, R. A. J. Janssen, J. Cornil and J.-L. Brédas, Chem. Eur. J., 1998, 4, 1509 CrossRef.
- A. Saxena and J. D. Gunton, Phys. Rev. B, 1987, 35, 3914 CrossRef.
- G. Paasch, P. H. Nguyen and A. J. Fischer, Chem. Phys., 1998, 227, 219 CrossRef CAS.
-
R. Kubo, Statistical Mechanics, North-Holland, Amsterdam, 1965 Search PubMed.
-
W. R. Mackinnon and R. R. Haering, in Modern Aspects of Electrochemistry, ed. R. E. White, J. O. M. Bockris and B. E. Conway, Plenum Press, New York, 1983, vol. 15, p. 235 Search PubMed.
- S. T. Coleman, W. R. McKinnon and J. R. Dahn, Phys. Rev. B, 1983, 29, 4147.
- J. R. Dahn, W. R. McKinnon and S. T. Coleman, Phys. Rev. B, 1984, 31, 484 CrossRef.
- M. Strömme, Phys. Rev. B, 1998, 58, 11015 CrossRef.
- M. D. Levi, G. Salitra, B. Markovsky, H. Teller, D. Aurbach, U. Heider and L. Heider, J. Electrochem. Soc., 1999, 146, 1279 CrossRef CAS.
- F. Lantelme, A. Mantoux, H. Groult and D. Lincot, Solid State Ionics, 2006, 177, 205 CrossRef CAS.
- T. Kudo and M. Hibino, Solid State Ionics, 1996, 84, 65 CrossRef CAS.
- G. Garcia-Belmonte, V. S. Vikhrenko, J. García-Cañadas and J. Bisquert, Solid State Ionics, 2004, 170, 123 CrossRef CAS.
- J. Garcia-Cañadas, F. Fabregat-Santiago, I. Porqueras, C. Person, J. Bisquert and G. Garcia-Belmonte, Solid State Ionics, 2004, 175, 521 CrossRef CAS.
- J. Garcia-Cañadas, G. Garcia-Belmonte, J. Bisquert, I. Porqueras and C. Person, Solid State Ionics, 2005, 176, 1701 CrossRef CAS.
- G. Garcia-Belmonte, J. García-Cañadas and J. Bisquert, J. Phys. Chem. B, 2006, 110, 4514 CrossRef CAS.
- E. V. Vakarin and J. P. Badiali, J. Phys. Chem. B, 2002, 106, 7721 CrossRef CAS.
- J. P. Badiali and E. V. Vakarin, Solid State Ionics, 2004, 171, 261 CrossRef.
- I. Mora-Seró, F. Fabregat-Santiago, B. Denier, J. Bisquert, R. Tena-Zaera, J. Elias and C. Lévy-Clement, Appl. Phys. Lett., 2006, 89, 203117 CrossRef.
- J.-J. Wu, G.-R. Chen, H.-H. Yang, C.-H. Ku and J.-Y. Lai, Appl. Phys. Lett., 2007, 90, 213109 CrossRef.
- T. Tornow and K. Schwarzburg, J. Phys. Chem. C, 2007, 111, 8692 Search PubMed.
-
R. Memming, Semiconductor Electrochemistry, Wiley-VCH, Weinheim, 2001 Search PubMed.
- F. Fabregat-Santiago, G. Garcia-Belmonte, J. Bisquert, P. Bogdanoff and A. Zaban, J. Electrochem. Soc., 2002, 150, E293.
- T. Tiedje and A. Rose, Solid State Commun., 1981, 37, 49 CrossRef CAS.
- T. Tiedje, J. M. Cebulka, D. L. Morel and B. Abeles, Phys. Rev. Lett., 1981, 46, 1425 CrossRef CAS.
- J. Orenstein and M. Kastner, Phys. Rev. Lett., 1981, 46, 1421 CrossRef CAS.
- H. Michiel, G. J. Adriaenssens and E. A. Davis, Phys. Rev. B, 1986, 34, 2486 CrossRef CAS.
- J. Nelson, Phys. Rev. B, 1999, 59, 15374 CrossRef CAS.
- A. Kambili, A. B. Walker, F. L. Qiu, A. C. Fisher, A. D. Savin and L. M. Peter, Physica E, 2002, 14, 203 CrossRef CAS.
- J. van de Lagemaat and A. J. Frank, J. Phys. Chem. B, 2000, 104, 4292 CrossRef CAS.
- J. van de Lagemaat, N. Kopidakis, N. R. Neale and A. J. Frank, Phys. Rev. B, 2005, 71, 035304 CrossRef.
- A. Zaban, M. Greenshtein and J. Bisquert, ChemPhysChem, 2003, 4, 859 CrossRef CAS.
- J. Bisquert, A. Zaban, M. Greenshtein and I. Mora-Seró, J. Am. Chem. Soc., 2004, 126, 13550 CrossRef CAS.
- F. Cao, G. Oskam, G. J. Meyer and P. C. Searson, J. Phys. Chem., 1996, 100, 17021 CrossRef.
- S. Kambe, S. Nakade, T. Kitamura, Y. Wada and S. Yanagida, J. Phys. Chem. B, 2002, 106, 2967 CrossRef CAS.
- S. Nakade, S. Kambe, M. Matsuda, Y. Saito, T. Kitamura, Y. Wada and S. Yanagida, Physica E, 2002, 14, 210 CrossRef CAS.
- S. Nakade, Y. Saito, W. Kubo, T. Kitamura, Y. Wada and S. Yanagida, Electrochem. Commun., 2003, 5, 804 CrossRef CAS.
- S. Nakade, Y. Saito, W. Kubo, T. Kitamura, Y. Wada and S. Yanagida, J. Phys. Chem. B, 2003, 107, 8607 CrossRef CAS.
- J. Krüger, R. Plass, M. Grätzel, P. J. Cameron and L. M. Peter, J. Phys. Chem. B, 2003, 107, 7536 CrossRef.
- J. Bisquert and V. S. Vikhrenko, J. Phys. Chem. B, 2004, 108, 2313 CrossRef CAS.
-
B. I. Shklovskii and A. L. Efros, Electronic Properties of Doped Semiconductors, Springer, Heidelberg, 1984 Search PubMed.
-
H. Böttger and V. V. Bryksin, Hopping Conduction in Solids, Akademie Verlag, Berlin, 1985 Search PubMed.
- J. van de Lagemaat, K. D. Benkstein and A. J. Frank, J. Phys. Chem. B, 2001, 105, 12433 CrossRef CAS.
- K. D. Benkstein, N. Kopidakis, J. Van de Lagemaat and A. J. Frank, J. Phys. Chem. B, 2003, 107, 7759 CrossRef CAS.
- T. Dittrich, A. Ofir, S. Tirosh, L. Grinis and A. Zaban, Appl. Phys. Lett., 2006, 88, 182110 CrossRef.
- L. Onsager and R. M. Fuoss, J. Phys. Chem., 1932, 36, 2689 CrossRef CAS.
- D. A. Reed and G. Ehrlich, Surf. Sci., 1981, 102, 588 CrossRef CAS.
- R. Gomer, Rep. Prog. Phys., 1990, 53, 917 CrossRef CAS.
- C. Uebing and R. Gomer, J. Chem. Phys., 1991, 95, 7626 CrossRef CAS.
- W. Weppner and R. A. Huggins, J. Electrochem. Soc., 1977, 124, 1569 CAS.
- H. Xia, L. Lu and G. Ceder, J. Power Sources, 2006, 159, 1422 CrossRef CAS.
- A. V. Myshlyatsev, A. A. Stepanov, C. Uebing and V. P. Zhdanov, Phys. Rev. B, 1995, 52, 5977 CrossRef CAS.
- L. S. Darken, Trans. Am. Inst. Min. Metall. Eng., 1948, 175, 184 Search PubMed.
-
P. T. Landsberg, Thermodynamics and Statistical Mechanics, Dover, New York, 1978 Search PubMed.
- M. D. Levi, E. Markevich and D. Aurbach, Electrochim. Acta, 2005, 51, 98 CrossRef CAS.
- C. A. Niklasson and C.-G. Granqvist, J. Mater. Chem., 2007, 17, 127 RSC.
- S. De, S. Teitel, Y. Shapir and E. H. Chimowitz, J. Chem. Phys., 2002, 116, 3012 CrossRef CAS.
- F. Bulnes, A. J. Ramirez-Pastor, J. L. Riccardo and G. Zgrablich, Surf. Sci., 2006, 600, 1917 CrossRef CAS.
- P. Argyrakis, Y. G. Groda, G. S. Bokun and V. S. Vikhrenko, Phys. Rev. E, 2001, 066108 Search PubMed.
- Y. G. Groda, P. Argyrakis, G. S. Bokun and V. S. Vikhrenko, Eur. Phys. J. B, 2003, 32, 527 CrossRef CAS.
- R. Darling and J. Newman, J. Electrochem. Soc., 1999, 146, 3765 CrossRef CAS.
- S. W. Kim and S. I. Pyun, Electrochim. Acta, 2001, 46, 987 CrossRef CAS.
- P. T. Landsberg, Eur. J. Phys., 1981, 2, 213 CrossRef CAS.
- D. Vanmaekelbergh and P. E. de Jongh, J. Phys. Chem. B, 1999, 103, 747 CrossRef CAS.
- B. A. Gregg, J. Phys. Chem. B, 2003, 107, 4688 CrossRef CAS.
- W. W. Focke and G. E. Wneck, J. Electroanal. Chem., 1988, 256, 343 CrossRef CAS.
-
N. F. Mott and E. A. Davies, Electronic Processes in Non-Crystalline Materials, Clarendon Press, Oxford, 1971 Search PubMed.
- P. N. Butcher, J. Phys. C: Solid State Phys., 1972, 5, 3164 CrossRef.
- A. L. Roest, J. J. Kelly and D. Vanmaekelbergh, Phys. Rev. Lett., 2002, 89, 036801 CrossRef CAS.
- J. van de Lagemaat, Phys. Rev. B, 2005, 72, 235319 CrossRef.
- T. G. Castner, Phys. Rev. B, 1997, 55, 4003 CrossRef.
- Y. Harima, D.-H. Kim, Y. Tsutitori, X. Jiang, R. Patil, Y. Ooyama, J. Ohshita and A. Kunai, Chem. Phys. Lett., 2006, 420, 387–390 CrossRef CAS.
- Y. Harima, F. Ogawa, R. Patil and X. Jiang, Electrochim. Acta, 2007, 52, 3615 CrossRef CAS.
- G. Zotti, S. Zecchin, B. Vercelli, A. Berlin, S. Grimoldi, M. C. Pasini and M. M. M. Raposo, Chem. Mater., 2005, 17, 6492 CrossRef CAS.
- Y. Harima, D.-H. Kim, Y. Tsutitori, X. Jiang, R. Patil, Y. Ooyama, J. Ohshita and A. Kunai, Chem. Phys. Lett., 2006, 420, 387–390 CrossRef CAS.
- Q. Gu, E. A. Schiff, S. Grebner, F. Wang and R. Schwartz, Phys. Rev. Lett., 1996, 76, 3196 CrossRef CAS.
- T. H. Nguyen and S. K. O'Leary, Appl. Phys. Lett., 2003, 83, 1998 CrossRef CAS.
- R. Richert, L. Pautmeier and H. Bässler, Phys. Rev. Lett., 1989, 63, 547 CrossRef.
- P. E. Parris, D. H. Dunlap and V. M. Kenkre, J. Polym. Sci., Polym. Phys., 1997, 35, 2803–2809 CrossRef.
- Y. Roichman and N. Tessler, Appl. Phys. Lett., 2004, 80, 1948.
- N. Tessler and Y. Roichman, Org. Electron., 2005, 6, 200–210 Search PubMed.
- Y. Q. Peng, S. Sun and C. A. Song, Mater. Sci. Semicond. Process., 2005, 8, 525 CrossRef CAS.
- A. Ohno, J.-I. Hanna, D. H. Dunlap and A. Cabral, Jpn. J. Appl. Phys., 2004, 4A, L460 CrossRef.
- S. E. Guidoni and C. M. Aldao, Eur. J. Phys., 2002, 23, 395 CrossRef.
- A. Miller and S. Abrahams, Phys. Rev., 1960, 120, 745 CrossRef CAS.
- J. Bisquert and V. S. Vikhrenko, Electrochim. Acta, 2002, 47, 3977 CrossRef CAS.
- M. D. Levi, H. Gizbar, E. Lancry, Y. Gofer, E. Levi and D. Aurbach, J. Electroanal. Chem., 2004, 569, 211 CrossRef CAS.
- M. D. Levi and D. Aurbach, J. Phys. Chem. B, 2005, 109, 2763 CrossRef CAS.
- J.-W. Lee and S.-I. Pyun, Electrochim. Acta, 2005, 50, 1777 CrossRef CAS.
- J. Bisquert, Electrochim. Acta, 2002, 47, 2435 CrossRef CAS.
- Y. G. Groda, R. N. Lasovsky and V. S. Vikhrenko, Solid State Ionics, 2005, 176, 1675 CrossRef CAS.
- A. A. Tarasenko, Z. Chvoj, L. Jastrabik, F. Nieto and C. Uebing, Phys. Rev. B, 2001, 63.
- A. Franceschetti, A. Williamson and A. Zunger, J. Phys. Chem. B, 2000, 104, 3398 CrossRef CAS.
- A. Franceschetti and A. Zunger, Appl. Phys. Lett., 2000, 76, 1731 CrossRef CAS.
- D. Yu, C. Wang and P. Guyot-Sionnest, Science, 2003, 300, 1277 CrossRef CAS.
-
A. Rose, Concepts in Photoconductivity and Allied Problems, Interscience, New York, 1963 Search PubMed.
- W. Shockley and W. T. Read, Phys. Rev., 1952, 87, 835 CrossRef.
- K. Lobato and L. M. Peter, J. Phys. Chem. B, 2006, 110, 21920 CrossRef CAS.
- K. Lobato, L. M. Peter and U. Wurfel, J. Phys. Chem. B, 2006, 110, 16201 CrossRef CAS.
- L. M. Peter and K. G. U. Wijayantha, Electrochem. Commun., 1999, 1, 576 CrossRef CAS.
- L. M. Peter, A. B. Walker, G. Boschloo and A. Hagfeldt, J. Phys. Chem. B, 2006, 110, 13694 CrossRef CAS.
- L. Forro, O. Chauvet, D. Emin, L. Zuppiroli, H. Nerger and F. Lévy, J. Appl. Phys., 1994, 75, 633 CrossRef CAS.
- D. Cahen, G. Hodes, M. Grätzel, J. F. Guillemoles and I. Riess, J. Phys. Chem. B, 2000, 104, 2053 CrossRef CAS.
- M. Grünewald and P. Thomas, Phys. Status Solidi B, 1979, 94, 125 CrossRef.
- F. R. Shapiro and D. Adler, J. Non-Cryst. Solids, 1985, 74, 189 CrossRef CAS.
- D. Monroe, Phys. Rev. Lett., 1985, 54, 146 CrossRef CAS.
- S. D. Baranovskii, P. Thomas and G. J. Andrianssens, J. Non-Cryst. Solids, 1995, 190, 283 CrossRef CAS.
- V. I. Arkhipov, E. V. Emelianova and G. J. Adriaenssens, Phys. Rev. B, 2001, 64, 125125 CrossRef.
- S. D. Baranovskii, T. Faber, F. Hensel and P. Thomas, J. Phys. C, 1997, 9, 2699 CAS.
- S. D. Baranovskii, H. Cordes, F. Hensel and G. Leising, Phys. Rev. B, 2000, 62, 7934 CrossRef CAS.
- O. Rubel, S. D. Baranovskii and P. Thomas, Phys. Rev. B, 2004, 69, 014206 CrossRef.
- N. F. Mott, J. Non-Cryst. Solids, 1968, 1, 1 CAS.
-
M. Pollak and B. Shklovskii, Hopping Transport in Solids, North Holland, Amsterdam, 1991 Search PubMed.
- D. Yu, C. Wang, B. L. Wehrenberg and P. Guyot-Sionnest, Phys. Rev. Lett., 2003, 92, 216802.
- H. Bässler, Phys. Status Solidi B, 1993, 175, 15 CrossRef.
- V. I. Arkhipov, P. Heremans, E. V. Emelianova and G. J. Adriaenssens, Appl. Phys. Lett., 2001, 79, 4154 CrossRef CAS.
- V. I. Arkhipov, E. V. Emelianova, G. J. Adriaenssens and H. Bässler, J. Non-Cryst. Solids, 2002, 299–302, 1047 CrossRef CAS.
- Arkhipov, Reynaert, Jin, Heremans, Emelianova, Adriaenssens and Bässler, Synth. Met., 2003, 138, 209 CrossRef.
- R. Coehoorn, W. F. Pasveer, P. A. Bobbert and C. J. Michels, Phys. Rev. B, 2005, 72, 155206 CrossRef.
- S. D. Baranovskii, H. Cordes, F. Hensel and G. Leising, Phys. Rev. B, 2000, 62, 7934 CrossRef CAS.
- S. D. Baranovskii, O. Rubel and P. Thomas, Thin Solid Films, 2005, 487, 2 CrossRef CAS.
- V. I. Arkhipov, P. Heremans, E. V. Emelianova, G. J. Adriaenssens and H. Bässler, Appl. Phys. Lett., 2003, 82, 3245 CrossRef CAS.
- F. Laquai, G. Wegner and H. Bässler, Philos. Trans. R. Soc. London, Ser. A, 2007, 365, 1472.
- F. Remacle, J. Phys. Chem. A, 2000, 104, 4739 CrossRef CAS.
- F. Remacle and R. D. Levine, ChemPhysChem, 2001, 2, 20 CrossRef CAS.
- H. E. Romero and M. Drndic, Phys. Rev. Lett., 2005, 95, 156801 CrossRef.
- A. A. Middleton and N. S. Wingreen, Phys. Rev. Lett., 1993, 71, 3198 CrossRef CAS.
|
| This journal is © the Owner Societies 2008 |
Click here to see how this site uses Cookies. View our privacy policy here.  Juan Bisquert
Juan Bisquert




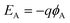







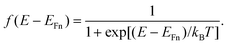


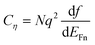






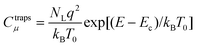





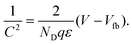


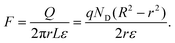
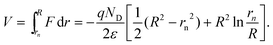













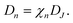





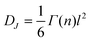





![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) is given by164
is given by164

![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) ,
,