Transient surface patterns during adhesion and coalescence of thin liquid films

Abstract

Surface deformations during the coalescence of two polymer melt films were studied by use of a surface forces apparatus (SFA). Well-ordered periodic surface ripple/finger patterns were observed during the adhesion and coalescence, which eventually disappeared, leaving smooth polymer–air interfaces. The life-times of these transient well-ordered patterns depend on the viscosity and film thickness of the polymer melts. These observations are in contrast to the conventional understanding that liquid–liquid coalescence usually occurs with the deforming surfaces remaining smoothly curved at all stages, with no esoteric shape-transitions. The results reveal a new feature associated with liquid–liquid adhesion/coalescence, which may be of key importance for a full understanding of coalescence processes. We propose an explanation for the observed phenomenon in terms of simple physical concepts, and discuss other microscopic and macroscopic (including biological) systems where similar effects are likely to occur.

---

1. Introduction

Liquid–liquid coalescence is prevalent in nature and technology, and is of great interest for many technological processes, including coating, dyeing, printing and microfluidics, and it is a key ingredient in the development of advanced polymeric materials through reactive blending processes.^1–3 The understanding of liquid–liquid coalescence has also recently become essential for the advancement of microbiological systems, such as biological cell–cell coalescence (fusion).⁴ During the last few decades much progress has been made in understanding droplet and film coalescence, both theoretically and experimentally.^1–7 However, most of the studies on liquid–liquid adhesion and coalescence have been limited to macroscopic or microscopic systems because of a lack of experimental nano-scale techniques and the complexity and rapidity of these processes. A particular issue that remains unclear is the transient surface deformations at the micro- and nano-scales associated with adhesion and coalescence of liquids.

The classic Hertz,⁸ Johnson–Kendall–Roberts (JKR),⁸ Derjaguin–Muller–Toropov (DMT),⁹ and Maugis¹⁰ theories or models of ‘contact mechanics’ describe the adhesion and deformations of two initially curved elastic or viscoelastic surfaces, but mostly in the solid state.^8,11–14 All four are static (equilibrium) models, describing the final equilibrium geometry, but not the dynamic growth of the contact immediately after adhesion or coalescence has occurred.† While there has been much work on fingering instabilities of confined liquid films under tensile loading conditions (viz.detaching or peeling surfaces, failure and crack propagation, necking and fibrillation),^15–21 and also some recent work on fingering patterns developed during crack closure (adhesion) of thin elastic solids,^22–24 the transients associated with adhesion and coalescence of either elastic solids or viscous liquids are still largely unknown, although it is generally believed that there are no abrupt changes or esoteric shape-transitions during coalescence. A detailed understanding of these transients is of fundamental interest in interface/surface science and practical importance in many industrial and biological processes.

Using a surface forces apparatus (SFA) and a combination of optical microscopy and ‘multiple beam interferometry’ employing ‘fringes of equal chromatic order’ (FECO) the separation and film thickness between two surfaces can be determined to an accuracy of ∼0.2 nm, and lateral deformations can be determined to ∼1 µm.²⁵ The SFA is therefore a good technique to study liquid film adhesion, coalescence and spreading, since it can give accurate in situ information on the neck geometry, film thickness and surface deformations at the nano-scale for the thickness, and the micro-scale for the lateral dimension.²⁵ In this study, well-ordered surface ripples/fingers were observed during the coalescence of polymer liquid films, which eventually disappeared, leaving smooth polymer–air interfaces. To our knowledge, such transient patterns and interface deformations during the initial stage of adhesion or coalescence of two viscous surfaces have not been previously reported.

2. Materials and methods

2.1 Materials

Four polymers were chosen for this study: polystyrene M_w = 800, M_w/M_n ≤1.3 (PS 800, η ≈ 2800 Pa s), was purchased from Pressure Chemical Co.; PS 590 (η ≈ 230 Pa s), M_w = 590, M_w/M_n ≤ 1.1, was purchased from Scientific Polymer Products Inc.; polydimethylsiloxane (PDMS) (η ≈ 30 Pa s) and polybutadiene (PBD) (η ≈ 6 Pa s) were purchased from Sigma-Aldrich. All polymers were used as received without further purification. The bulk shear viscosities η of the polymers used were measured using an ARES-controlled strain rheometer from Rheometrics Scientific in a cone-plate geometry with 25 mm diameter plates and a 0.1 rad cone angle at the experimental temperature of 24.0 ± 0.2 °C.

2.2 Film preparation

The polymer films were prepared by spin-coating a droplet of prefiltered (200 nm mesh size) polymer solution (PS in toluene, PBD in tetrahydrofuran, PDMS in hexane or tetrahydrofuran) on a mica substrate glued on silica disks, then very slowly drying under reduced pressure for >10 h to remove the solvent, then mounted in the SFA chamber. The film thickness T could be controlled by changing the concentration of polymer solution (1–10 wt%) and the spin-coating speed (500–5000 rpm) to obtain uniform polymer films (of PS, PBD and PDMS) in the thickness range 50–500 nm. Film thicknesses T were measured using the optical interference technique of the SFA employing fringes of equal chromatic order (FECO).²⁵

2.3 Experimental methods

The two surfaces mounted in the SFA chamber were in the ‘crossed cylinders’ geometry (each cylinder of radius R = 2 cm), which locally corresponds to a sphere of radius R on a flat surface or to two spheres of radius 2R. The polymer surfaces were brought together using a motor-controlled micrometer at various speeds from 14 to 210 nm s⁻¹. Once closer than ∼10 nm, they jumped into adhesive contact due to the attractive van der Waals force between them. The increasing contact area and local surface geometry changes during the ‘coalescence stage’ (analogous to ‘crack healing’ in materials) were then recorded for periods ranging from seconds to >10 h, after which the surfaces were separated at speeds ranging from 0.017 to 1.0 µm s⁻¹ (the ‘separation stage’, being analogous to ‘crack propagation’ or failure in materials). The polymers used in this study have high viscosities that allowed for real time visualization and VCR recording of the surface deformations using both FECO interference fringes and normal optical microscopy. The simultaneously recorded images were later analyzed. All experiments were performed at 24 °C.

3. Results and discussion

In this study, an SFA was used to study the fine details of a growing contact region immediately following the coalescence of two thin viscous polymer films on mica. A schematic of the local geometry is shown in Fig. 1, which is superficially similar to that of a Hele–Shaw cell.^15,26 A novel type of interfacial instability for this geometry, manifested by highly ordered but transient surface-ripples or fingers (Fig. 1, bottom left), was observed when a neck of high-viscosity liquid polystyrene (PS) grows and replaces the surrounding low-viscosity medium (air). In contrast, as reported before,¹⁵ during separation, viscous fingers grow inward from the PS–air interface, and cavitation bubbles also appear inside the liquid neck at separation velocities above ∼0.5 µm s⁻¹ (Fig. 1, bottom right). These fingers and cavities during separation all involved the displacement of high-viscosity fluid by low-viscosity air or vapor, as expected for a typical Saffman–Taylor fingering instability.^15,26 Similar nanoscopic and sub-microscopic effects on separation have previously been seen in different geometries and at larger (microscopic and macroscopic) length scales.^16–19 Compared with the typical Saffman–Taylor fingers on separation, the novel interfacial instability observed here during coalescence is highly ordered and appears to be contrary to the Saffman–Taylor prediction; and none of classical adhesion theories and instability models such as Rayleigh–Taylor instability,²⁷ the Richtmyer–Meshkov instability²⁸ and the Kelvin–Helmholtz instability²⁹ can directly explain the observed patterns, which are now described in more detail.

Fig. 1 Schematics (top) and normal optical microscope images (bottom) of contact geometry and transient instability regimes observed during coalescence and separation of two fluid but viscous polystyrene (PS 800) films (T = 210 nm). Left: typical highly ordered fingering patterns between r_o and r_i observed during coalescence (widths of the fingers: ∼4 µm), as also shown in Fig. 2f, the inner-most region of the deformation (r ≥ r_i) consists of air fingers protruding into the fluid. Right: more irregular Saffman–Taylor and cavitation instabilities observed during separation (width range of the fingers: 5–18 µm).

For the more viscous fluid, PS 800 (η ≈ 2800 Pa s), flat contact was observed immediately after the surfaces jumped into adhesive contact (Fig. 2a,b), i.e., the surfaces behaved transiently like elastic solids. Within about 10 s, a liquid-like meniscus could be seen to grow (Fig. 2c), with visible air fingers appearing ∼20 s later (Fig. 2d), which grew outwards with time. Surprisingly, these well-ordered fingers or surface ripples were straight and radial rather than circular around the contact area, as might be expected after a local perturbation of a liquid surface that generates circular ‘capillary waves’. Fig. 2e shows the situation after ∼5 min. For the less viscous fluid, PS 590 (η ≈ 230 Pa s), the same radius was attained within ∼5 s, and for PBD within <1 s.

Fig. 2 (a)–(k): Typical fingering patterns observed during coalescence of two PS 800 films (T = 86 nm). Widths of the fingers: 1–3 µm, distance between adjacent fingers (wavelength or periodicity) ≈ double the width. (h)–(k): Saffman–Taylor instability patterns developed during separation superimposed on those still existing from the coalescence. Width range of ST fingers (see Fig. 1): 5–10 µm, average distance between adjacent fingers: ≈ double the width. (l) Featureless appearance of surfaces after >3 h of being in contact after coalescence, as seen in a separate experiment involving no separation.

So long as the surfaces were allowed to remain in contact, the well-ordered fingers initially continued to grow (Fig. 2f,g), but for longer contact times they started to shrink and eventually disappeared, leaving one smoothly continuous surface. However, after their disappearance, the meniscus continued to grow as a smoothly rounded circular but otherwise featureless neck, as expected (Fig. 2, last panel (l)).

The life-time of the fingers (their growth and disappearance) τ decreased sharply with the viscosity of the fluid η, taking ∼10⁴ s for PS 800 (η ≈ 2800 Pa s, film thickness T = 210 nm), ∼100 s for PS 590 (η ≈ 230 Pa s, T = 101 nm), 4–5 s for polydimethylsiloxane (PDMS) (η ≈ 30 Pa s, T = 361 nm), and ∼1 s for polybutadiene (PBD) (η ≈ 6 Pa s, T = 260 nm). It therefore appears that the life-time of the transient ripples varies roughly as τ ∝ η^3/2.

On separating the surfaces, either before or after the fingers had disappeared, new types of fingers appeared that now propagated inward (Fig. 2h–k). These were much less regular, more rounded and had significantly larger widths, and appeared to be a typical Saffman–Taylor fingering instability due to the inward flow of low-viscosity air.¹⁵

The transient nature of the air fingers during coalescence is shown graphically in Fig. 3, where the inner and outer diameters, 2r_i and 2r_o, of the fingers' boundaries (defined in Fig. 1 and Fig. 2f) are plotted as a function of time for PS 800. The inner radius r_i was found to follow a function of the form r_i ∝ tⁿ, where n = 0.19 ± 0.02. The results for the lower-viscosity polymers were qualitatively similar but occurred over a much shorter time-scale; however, the exponents were almost the same: n = 0.23 ± 0.04 for PS 590, and n = 0.23 ± 0.05 for PDMS and PBD. The outer radius increased with time in a similar way to the inner radius, but r_o was less well-defined than r_i. There is a short time-period when the rate of growth of the outer radius slows down until the two boundaries merge, when the fingers totally disappear.

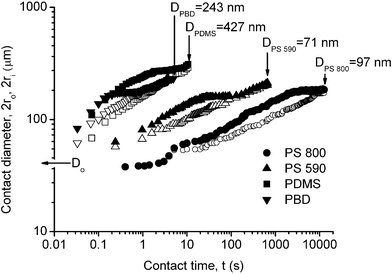Fig. 3 Outer and inner fingering diameters, as defined in Fig. 1 and shown in Fig. 2fvs. contact time t, for PS 800, T = 86 nm; PS 590, T = 101 nm; PDMS, T = 361 nm; PBD, T = 260 nm. Solid symbols for 2r_o; open symbols for 2r_i. D is the minimum gap distance between the two mica surfaces, where D_o = 2T is the initial gap distance at t = 0, defined as the instant the two surfaces first come into adhesive contact (cf.Fig. 2b). The results were independent of the initial approach velocity of the surfaces, which varied in the range 14–210 nm s⁻¹.

Overall, the average neck radius rvs. time curves, follow

r = (r_i + r_o)/2 ∝ tⁿ, (1)

with n = 0.2–0.3, and appear to be independent of whether fingers are present or not, and are therefore representative of a more general phenomenon which has been studied before for smooth circular necks. Thus, Eggers et al.³ presented a full theory based on a scaling argument that predicts the following equation for the bridge radius between two drops at the early stage of coalescence: r ∼ (tγ/πη) ln(tγ/ηR), where γ is the surface tension, R is the drop radius. Approximate solutions were also derived for liquids with very low viscosity (e.g., water η = 1 mPa s) when the inertia of the fluid becomes important: r ∼ (γR/ρ)^1/4t^1/2, where ρ is the fluid density, which was confirmed by recent experiments and other simulations.^3,6,30 Classic wetting (liquid spreading) theories^31,32 predict that in the early ‘capillary regime’ of spreading the droplet radius on a solid surface obeys r ∼ Ω^3/10(tγ_LV/η)^1/10, where Ω is the liquid volume and γ_LV is the liquid–air interfacial tension, and r ∼ (tρgΩ³/η)^1/8 in the later ‘gravitational regime’. However, in recent experiments on water-drop spreading on a glass plate, Biance et al.³³ argued that there exists an inertial regime at the beginning of spreading which confirmed Eggers, Lister and Stone's³ predictions of r ∼ t^1/2 for the droplet radius, and τ ∼ (ργR/η²)^1/8(ρR³/γ)^1/2, so τ ∼ η^−1/4, for the duration time of the inertial regime (after which the spreading follows the classical theory). For water drops of radius r ≈ 1 mm the duration time of the inertial regime is typically in the order of 1 ms.

Our systems show a similar scaling relationship r ∝ f(ρ,γ,R,η,T)tⁿ with n = 0.2–0.3, where f(ρ,γ,R,η,T) is a function of the polymer density ρ, surface tension γ, viscosity η, film thickness T, and local film radius of curvature R. The exponent n thus appears to belong somewhere in between the above two regimes (i.e., between n = 0.1 and n = 0.5). The likely reason for the observed exponents falling in between these two limiting cases may be due to our system involving the spreading of liquid films on the same material (i.e., film coalescence rather than true spreading).

One intuitive explanation for the observed transient fingering is that it is due to the impact of the liquid films on each other when the two surfaces jump into contact due to the van der Waals forces. The impact of drops on solid and liquid surfaces is of wide practical importance, and has been investigated for more than a hundred years.^34–36 Different impact patterns, such as neck distortion, radial jetting and crown formation occur depending on the impact speed, film thickness, etc.^34–36 Two further types of experiments were performed that showed that the initial impact was not the cause of the fingers in our systems: (1) Two glassy films of high MW polystyrene (T_g > experimental room temperature) were first brought into adhesive contact at room temperature; then the SFA chamber was slowly heated to a temperature above T_g. Transient fingers appeared during the heating as the contact geometry changed from that corresponding to a classical elastic solid–solid JKR contact to that of liquid–liquid coalescence; (2) Two moisture-sensitive films of glucose (another material that has a high glass transition temperature) were brought into contact in dry N₂ gas in the glassy state; then the SFA chamber was purged with humid air (relative humidity 50%). Again, transient fingers were observed as the sugar adsorbed water and softened, changing the contact geometry from solid-like to liquid-like.

The appearance of the highly ordered interfacial fingering patterns during coalescence appears to be a new type of phenomenon, not previously reported or immediately explainable by current theories. We propose that this phenomenon is a manifestation of the viscous nature of flowing or accelerating fluids confined to a complex geometry, where the driving force in our specific case is the high negative Laplace pressure generated in the fluid film, due to the highly curved concave meniscus at the rim. Thus, from the images of Fig. 2b,c, the meniscus radius r_m (Fig. 1, top left) can be estimated to be r_m ≤ 7 nm, which corresponds to a negative Laplace pressure of P = γ_PS–air/r_m = (34 × 10⁻³ J m⁻²)/(7 × 10⁻⁹ m) ≈ 5 MPa ≈ 50 atm. This tensile pressure sucks fluid into the neck region. The likely flow lines are shown in Fig. 1 (top left), showing where the polymer film thins by the small arrows at radii ≥ r_o. At these points the fluid and surfaces move (accelerate) both normally and laterally as air displaces the thinning fluid films in the region just outside the growing neck (supplying fluid to it). In this region, a low-viscosity fluid displaces a high-viscosity fluid, producing a Saffman–Taylor instability.

In the Saffman–Taylor problem, the minimum wavelength λ_c for a Hele–Shaw cell parallel-plate geometry is given by eqn (2), where b is the distance between the two parallel plates, η₁ and η₂ are the viscosities of the two fluids, V is the speed normal to the interface where the less viscous fluid 2 pushes fluid 1:^15,37

A simple geometric consideration assuming that the net volume of polymer does not change during coalescence leads to the following relationship:

V₁ ≈ r_o³V₂/Rw(2r_o − w), (3)

where, as shown in Fig. 1, V₂ ≈ dr_o/dt is the velocity of the growing neck radius, V₁ is the velocity of the air pushing the polymer surface (the rate of film thinning) at r ≥ r_o, w is the width of the film-thinning region, and R is radius of the surface. From the experiments, r_o ≫ w, so we may write

V₁ ≈ r_o²V₂/2Rw, (4)

where V₁ can be inserted into eqn (2) to estimate the expected magnitude of the wavelength in the film-thinning region. Using the following values from the experiment results: r_o ≈ 20 µm, w ≈ r_o/10 ≈ 2 µm, and V₂ ≈ dr_o/dt ≈ 5 µm s⁻¹, we obtain V₁ ≈ 25 nm s⁻¹. Thus, for γ = 33 mN m⁻¹, η₁ = 2800 Pa s and putting b ≈ T/2, where T is the thickness of the polymer film (since b must be less than T), eqn (2) yields λ_c ≈ 2 µm for T = 100 nm, implying that viscous waves with wavelength greater than 2 µm are expected. For η₁ = 230 Pa s, we obtain λ_c ≈ 7 µm. These dimensions are consistent with the wavelengths (periodicity) of the fingers observed in our systems.

If the above analysis is correct, viscous or capillary waves are to be expected in the small outer regions of width w in Fig. 1, developing into the observed ripples. With time, as the meniscus or neck volume grows, r_m increases, which lowers the Laplace pressure and fluid flow-rate. As the flow subsides, the rippled region diminishes, until the instability disappears and the fluid–air interface is again smooth. However, it should be noted that, overall, our whole system behaves more as a viscous fluid (polymer) pushing a less viscous fluid (air) as the contact region expands during the coalescence process. The Saffman–Taylor fingering arises because in some local region of this complex geometry, and for a certain time, the reverse occurs.

While this type of transient fingering instability may arise whenever there are critical viscous and velocity gradients, the driving forces may be diverse, and not necessarily due to surface tension or Laplace pressure effects. Such instabilities may therefore arise wherever coalescence, collisions and film thinning occur involving liquid–liquid, solid–liquid, and even soft solid–solid systems, which can occur in very different areas of science and engineering, such as biological cell–cell coalescence, coatings, dyeing and printing.

To put things into a broader and more quantitative perspective, from the limited data so far available on the four liquids studied with viscosities ranging from 2800 to 6 Pa s, the life-times of the transient ripples varied roughly as η^3/2. If so, then for common (low-viscosity) liquids such as water, alcohols and light oils (η = 0.001–0.01 Pa s), these transient effects would be over within 1–100 µs. These very short times could be the reason why such effects have not been previously observed. Rippled surfaces may also arise during the adhesion and coalescence or thinning of medium to high-viscosity materials such as polymer melts (∼10³ Pa s), pitch (∼10⁷ Pa s), glaciers (∼10¹¹ Pa s), glass sheets (∼10⁴⁰ Pa s), and gold films.

4. Conclusions

Well-ordered periodic surface ripple/finger patterns were observed during liquid–liquid coalescence, which eventually disappeared, leaving smooth liquid–air interfaces. The life-times τ of the transient patterns scale with the viscosity of the polymers as τ ∝ η^3/2. The contact radius r increases with time t as r ∝ f(ρ,γ,R,η,T)tⁿ, with n = 0.2–0.3. These observations are in contrast to the conventional understanding that liquid–liquid adhesion and coalescence usually occur with no abrupt changes or esoteric shape transitions. The results thus reveal a new aspect of liquid–liquid adhesion and coalescence. Finally, the highly regular natural patterns observed may be manipulated to produce equally highly ordered nano-scale structures if one can preserve the transient patterns using some method such as UV cross-linking or rapid quenching.

Acknowledgements

This work was supported by NASA grant NAG3-2115. Boxin Zhao is supported by a NSERC (Natural Sciences and Engineering Research Council of Canada) postdoctoral fellowship award. Yu Tian is supported by a Huaxin Distinguished Scientist Scholarship from Tsinghua University.

References

1. L. G. Leal, Phys. Fluids, 2004, 16, 1833–1851.
2. D. G. A. L. Aarts, M. Schmidt and H. N. W. Lekkerkerker, Science, 2004, 304, 847–850.
3. J. Eggers, J. R. Lister and H. A. Stone, J. Fluid Mech., 1999, 401, 293–310.
4. D. Cuvelier, I. Derenyi, P. Bassereau and P. Nassoy, Biophys. J., 2005, 88, 2714–2726.
5. S. L. Carnie, D. Y. C. Chan, C. Lewis, R. Manica and R. R. Dagastine, Langmuir, 2005, 21, 2912–2922.
6. D. G. A. L. Aarts, H. N. W. Lekkerkerker, H. Guo, G. H. Wegdam and D. Bonn, Phys. Rev. Lett., 2005, 95, 164503.
7. N. H. Chen, T. Kuhl, R. Tadmor, Q. Lin and J. Israelachvili, Phys. Rev. Lett., 2004, 92, 024501.
8. K. L. Johnson, Contact mechanics, Cambridge University Press, Cambridge/New York, 1985.
9. B. V. Derjaguin, V. M. Muller and Y. P. Toporov, J. Colloid Interface Sci., 1975, 53, 314–326.
10. D. Maugis, J. Colloid Interface Sci., 1992, 150, 243–269.
11. E. Barthel and G. Haiat, J. Adhesion, 2004, 80, 1–19.
12. K. L. Johnson and J. A. Greenwood, J. Colloid Interface Sci., 1997, 192, 326–333.
13. K. R. Shull, Mater. Sci. Eng., R, 2002, 36, 1–45.
14. C. Y. Hui, J. M. Baney and E. J. Kramer, Langmuir, 1998, 14, 6570–6578.
15. H. B. Zeng, N. Maeda, N. H. Chen, M. Tirrell and J. Israelachvili, Macromolecules, 2006, 39, 2350–2363.
16. A. J. Crosby, K. R. Shull, H. Lakrout and C. Creton, J. Appl. Phys., 2000, 88, 2956–2966.
17. D. Derks, A. Lindner, C. Creton and D. Bonn, J. Appl. Phys., 2003, 93, 1557–1566.
18. S. Poivet, F. Nallet, C. Gay, J. Teisseire and P. Fabre, Eur. Phys. J. E, 2004, 15, 97–116.
19. M. Tirumkudulu, W. B. Russel and T. J. Huang, Phys. Fluids, 2003, 15, 1588–1605.
20. K. R. Shull, C. M. Flanigan and A. J. Crosby, Phys. Rev. Lett., 2000, 84, 3057–3060.
21. K. R. Shull and C. Creton, J. Polym. Sci., Part B: Polym. Phys., 2004, 42, 4023–4043.
22. A. Ghatak and M. K. Chaudhury, Langmuir, 2003, 19, 2621–2631.
23. W. Monch and S. Herminghaus, Europhys. Lett., 2001, 53, 525–531.
24. A. Ghatak, M. K. Chaudhury, V. Shenoy and A. Sharma, Phys. Rev. Lett., 2000, 85, 4329–4332.
25. J. Israelachvili, J. Colloid Interface Sci., 1973, 44, 259–272.
26. P. G. Saffman and G. Taylor, Proc. R. Soc. London, Ser. A, 1958, 245, 312.
27. H. J. Kull, Phys. Rep., 1991, 206, 197–325.
28. M. Brouillette, Annu. Rev. Fluid Mech., 2002, 34, 445–468.
29. J. W. Miles, J. Fluid Mech., 1959, 6, 583–598.
30. L. Duchemin, J. Eggers and C. Josserand, J. Fluid Mech., 2003, 487, 167–178.
31. L. Leger and J. F. Joanny, Rep. Prog. Phys., 1992, 55, 431–486.
32. P. G. Degennes, Rev. Mod. Phys., 1985, 57, 827–863.
33. A. L. Biance, C. Clanet and D. Quere, Phys. Rev. E, 2004, 69, 016301.
34. D. A. Weiss and A. L. Yarin, J. Fluid Mech., 1999, 385, 229–254.
35. M. Rein, Fluid Dyn. Res., 1993, 12, 61–93.
36. W. C. Macklin and G. J. Metaxas, J. Appl. Phys., 1976, 47, 3963–3970.
37. R. L. Chuoke, P. Vanmeurs and C. Vanderpoel, Trans. Am. Inst. Mining Metallurgical Eng., 1959, 216, 188–194.

---

Footnote

† We distinguish between adhesion and coalescence based on the different time-scales of these two processes: there is an initial rapid ‘elastic-like’ deformation of the surfaces as they first come into adhesive contact. This is followed by a slow evolution of the contact region associated with molecular diffusion and bulk viscous flow. The first process often occurs at a high Deborah number (De > 1) where the liquid behaves like a solid; the second at De < 1. See ref. 21

---