A theory for heterogeneous states of polymer melts produced by single chain crystal melting
T. C. B.
McLeish
Polymers and Complex Fluids Group and Polymer IRC, Department of Physics and Astronomy, University of Leeds, Leeds, UK LS2 9JT
First published on 19th October 2006
Abstract
We consider the polymer physics of a possible molecular mechanism for disentangled melt states observed recently. We find that the route from molten, but only marginally-overlapping single crystals to the equilibrium state must pass over a free-energy barrier that becomes large at high molecular weights. The penalty arises from elastic distortions of the entanglement network as the chains diffuse. A critical molecular weight arises naturally from the competition of elastic distortion and the free-energy of confinement. We calculate the barrier and critical molecular weight at both a simple single-chain level, and at a “one-loop” level of co-operative motion, finding that many-chain effects alter the physics quantitatively, but not qualitatively. Several new experiments are suggested.
1. Introduction
The recent observations of the long-lived low-modulus melts by Spiess et al.1 pose very challenging theoretical questions. A careful annealing protocol of sufficiently high molecular weight (>300 k) polyethylene composed of single-chain crystals produced a melt state with unusual properties. An initial annealing period at 136 °C before full melting at 180 °C gave rise to the new state, whereas direct melting at 180 °C produced a normal melt. Both the modulus and viscosity of the melt were reduced by as much as an order of magnitude from their equilibrium values, depending on the annealing time, yet the terminal stress-relaxation rates were comparable to those of the normal melt. More remarkable still was the observation of extremely long annealing times of the new melt state. For very high molecular weights this could be immeasurably long, even at melt temperatures of 180 °C. Yet further deep-cycling in temperature was able to re-equilibrate the melt, ruling out any permanent chemical change to the ensemble of polymer chains. An important clue to the possible microscopic origins of this unusual behaviour came from NMR measurements of local dynamics: the new melt state displayed two populations of subchains, one with orientational relaxation at the same timescales as an equilibrated melt, and a new population with faster dynamics. This observation suggested the label “heterogeneous” for the new melt state. A second vital feature of the experimental protocol is that the temperature of the annealing period lay between two distinct melting transitions observed by DSC. Measurements of the activation energy of the two transitions and comparisons to earlier work2 suggested that at this temperature only “slow melting” from the crystal extremities dominated.Whatever the morphology and chain configurations that emerge from the preparation route, the principal difficulty is to understand how stress-relaxation is still achieved (with an unchanged or similar terminal time to that of the normal melt) without annealing at similar timescales to the normal melt state. This is because all current theories (and experiments) of polymer melt dynamics, whether for entangled or unentangled chains, predict a correlation between stress-relaxation and single-chain diffusion of polymer molecules.3 Simply, by the time a polymer chain has diffused its own radius of gyration, then the oriented internal conformations that give rise to stress have also decayed. On the other hand such long-range diffusion of chains will also erase any heterogeneous spatial structure initially imposed on the melt.
It is the goal of this work to show that no new fundamental physics beyond our current “tube” models of entanglement-dominated polymer dynamics, and the statistical mechanics of flexible chains, is required to give a quantitative account of these observations. A simple theory for a heterogeneous melt structure that (1) arises naturally from the temperature history applied and (2) accounts for the observed two dynamic populations, also predicts a strong barrier to chain diffusion, while permitting stress relaxation. In the following section we describe the model of the heterogeneous state at a scaling-level of mathematics. In Section 3 we use a simple single-chain treatment to calculate timescales for whole chain and partial chain reptation, and find a critical molecular weight. In Section 4 we attempt a first approximation to many-chain effects. We conclude by suggesting a range of new experiments that may test these ideas.
2. A model
The model is summarised in Fig. 1. On melting at 136 °C, we assume following Rastogi et al.,1 that only the extremities of the single-chain crystals melt. As they do this the melted chains will form and fill regions that compartmentalise the remaining crystals with partitions whose width grows as more chain melts away from the crystals. The dynamics of these chain ends are rapid and the melt density and structure are not expected to depart very greatly from those of a normal melt, so there is no reason to suppose that these regions would be very much less entangled than the equilibrium melt either. They would therefore deform elastically with a modulus similar to that of the “plateau modulus” of the melt, G0, independent of the chain degree of polymerisation, N. | ||
| Fig. 1 A model for the heterogeneous structure—on low-temperature melting the outer portions of the original crystals (left) form entangled normal melt regions. These partition the remaining crystal cores into “cells” (right). On further melting the inner regions of these cells contain unentangled melt. | ||
On further raising the temperature to 180 °C, the remaining central parts of the crystals melt. However, this material has been melted faster than its ability to change topological interactions with itself or other chains, in contrast with the melt occupying the partitioning regions. The result is that the cells of the partitioned melt now contain molten, but unentangled chain. These regions would have essentially zero local elastic modulus on the scale of the plateau modulus. In terms of the monomer size, b, they have a volume of Nb3. So if the volume fraction of entangled, “partitioning”, melt is ϕe, then the resulting modulus of the composite melt, given its uniform connectivity, would be
| G2 ≃ ϕeG0 |
3. Elastically-suppressed reptation
In order for such a partitioned, “cellular” form of heterogeneous melt to regain a uniform entangled state, the individual chains must expand their conformations from the radius of the single-chain cells (of size R ≃ N1/3b) to the Gaussian radius of the equilibrium Rg ≃ N1/2b. At the same time each chain increases its overlap with others from zero to a number of the order N1/2. On rapid melting, this process can be very fast as it is driven against only frictional constraints by the strong free energy of confinement.4 Such a “chain explosion” has been observed by neutron scattering.5 In the case of the heterogeneous melt, however, chains leaving and entering the original “cells” must result in strong elastic deformations of the entangled material of the cell walls. This will result in a free-energy barrier to chain motion. We show in this section that it is a property of this model that single-chain (non-co-operative) reptation may be strongly suppressed by elastic deformation of the partitioning regions.3.1 Whole chain
In terms of the monomer volume (taken here to be equal to the step length cubed) b3, the melt modulus is | (1) |
The elastic free energy change on the reptation of the whole or part of a chain from one “cell” to the next can be written in terms of the relative change ΔV in the volume V of a cell. As the chain reptates, so volume in one cell (which the chain leaves) is exchanged for volume in a neighbouring cell (which the chain enters). This must cause elastic deformation of the entangled region between the cells (since this survives the process—it is composed typically of chains from several crystals). The modulus for this deformation is just the melt plateau modulus of the entangled region, so:
 | (2) |
 | (3) |
In fact the barriers to co-operative reptation, in which the actual penalties are lower by virtue of the mutual diffusion of several chains, will still be large. This is because there is additional entropic cost to the correlation of many chain motions in this way. A more precise calculation can be made (see below in Section 4), but as we will see this will just modify the exponent of (N/Ne) within the expression for the free energy barrier. The essential point here is that the coordination number of chains in this special melt state is very low (of order 10 and comparable to that of colloidal particles in the dense fluid state), when compared to the value of N1/2 experienced in the normal polymer melt. This means that the fluctuations in local chain number density are much greater as the chains diffuse. But unlike the diffusion of soft colloidal particles, these fluctuations couple to the elastic deformation of the normal partitioning regions of the melt.
3.2 Partial chain reptation
Although we have seen that the diffusion of entire chains can be strongly suppressed by the presence of the elastic partitioning regions, fractions of chains may diffuse with far smaller penalties. Partial reptation of chains is only strongly suppressed after an amount of chain (say n monomers) has left the average region, such that the resulting elastic penalty is of the order the thermal energy. In this case we put ΔV = n/N in eqn (2), so that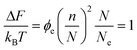 | (4) |
 . So in the case of well-entangled chains, several entanglements may be relaxed by partial reptation and/or contour length fluctuation without any free-energy barrier. Note that this is all that is required to relax stress completely, since it is only these sections of the chains in the regions of their extremities that reside in entangled regions and give rise to rheological stress, an important feature of this picture to which we return below.
. So in the case of well-entangled chains, several entanglements may be relaxed by partial reptation and/or contour length fluctuation without any free-energy barrier. Note that this is all that is required to relax stress completely, since it is only these sections of the chains in the regions of their extremities that reside in entangled regions and give rise to rheological stress, an important feature of this picture to which we return below.
Furthermore, one can argue that the entangled fraction of the chains is established against the growing elasticity of the cell walls in a self-consistent way. For as reptation begins on melting, these regions become established. As the entangled regions broaden, so the elastically entangled fraction ϕe grows, and will be to a rough approximation just equal to the fraction of chain length reptated: ϕe
≃
n/N. Putting this result in eqn (4) and keeping the approximation n
≪
N now gives
| nstable = (NeN2)1/3 |
Of course the entangled regions will still coarsen after this “stable” value is reached, but only logarithmically in time as further growth becomes activated by elastic deformation.
An important check on the self-consistency check of the model is that this non-activated degree of partial reptation carries material from one cell into typically one neighbouring cell and no further. If this is not true then the “strong fluctuation” argument for localisation fails. To do this we calculate the size of the random walk of the subchain with nstable monomers, and compare it to the cell size. The former (in units of b) is just (nstable)1/2 = N1/6eN1/3 while the latter is just N1/3 by the volume of a single chain. So they scale with N in just the same way, and are indeed of the same order of magnitude apart from the factor N1/6e. This might be a concern if Ne were very large, but for polyethylene Ne itself is of the order 10, since the Kuhn segment is best taken as the mean length of a consecutive series of trans conformational states, so that the resulting prefactor is close to unity.
3.3 Effect on relaxation modulus
There are some immediate predictions of this model which are as yet not fully tested. One is that there should be correlations between annealing time, the modulus of the heterogeneous melt, and the subsequent rate of modulus build-up. The longer the annealing time, the higher is ϕe and the greater the entangled fraction, and so the modulus of the heterogeneous melt. At the same time, the elastic penalty for whole chain reptation (and so chain diffusion) is also higher, so the rate of subsequent annealing will anti-correlate with the modulus. This was apparently seen in an unreported data set by Rastogi6 (and is visible in curves (ii) and (iii) in Fig. 4a of ref. 1).There are also some changes expected to the terminal time for stress relaxation in the heterogeneous melt with respect to the normal melt. As we saw in the last section, our picture does explain why stress-relaxation occurs without full chain diffusion. The chains are only required to reptate a fraction nstable/N ≃ (Ne/N)1/3 of the whole chain length for stress relaxation. This is because only this fraction of the chain resides in the entangled partition regions of the melt. The consequences of the partitioned morphology of Fig. 1 for the structure of entanglements along a representative chain is shown in Fig. 2. This structure was anticipated in ref. 1; we are now able to make predictions for the sizes of the entangled and unentangled regions in terms of molecular weight (N) and structure (Ne). The metallocene samples C and D reported in ref. 1 both have N/Ne ≃ 106 so we would expect to find ϕe to be about 0.1, which is indeed in line with the reduced plateau modulus. But we would also expect a rather faster terminal time in the heterogeneous state. A lower bound on the terminal time would be τdϕ2e, which would be of the order of 100 times faster than normal reptation. However, some fraction of the annealed entangled regions would have been created from slower, activated, reptation moves, so in turn requires similar activated reptation to disentangle and re-entangle them. Because of this the actual current terminal time is expected to exhibit classical “ageing”—the longest relaxation time is equal to the current “waiting” time (time since full chain melting) at the melt temperature.7 However these exponentially slow relaxations of stress would carry correspondingly low amplitude in terms of their contribution to the stress, and so give rise to a gentle tail to the rheological relaxation spectrum that would not differ greatly from that of a normal polydisperse melt. In the case of monodisperse melts however, the change in the relaxation spectrum predicted by this model ought to be measurable, and corresponds to the bulk of stress being lost at faster times than in the normal melt.
 | ||
| Fig. 2 The entanglement structure of a single chain. Only the extremities exist within entangled regions of the melt, which physically exist in the cell partitions. Reptation dynamics that disentangle these regions will only result in complete stress relaxation. | ||
3.4 Confinement entropy and a critical molecular weight
The elastic free energy from deformation of the partition regions of the heterogeneous melt is of course not the only term controlling the kinetics of relaxation to the equilibrium melt state—there is the energy of confinement itself (otherwise there would be no reason to return to equilibrium!). To confine a Gaussian chain to a region of size R costs a confinement energy8 | (5) |
In our case Rg = N1/2b and R = N1/3b so that Fconf
≃
kBTN1/3. This (negative) contribution will act to reduce the barrier we calculated above in eqn (2) and (4). The question arises of the position of the “barrier” along the highly projected reaction co-ordinate of R, but this does not change the scaling structure of Fconf. In fact, to make a simple estimate of the effect of placing the barrier, we observe that the largest elastic deformation occurs when a chain has distributed itself between two adjacent cells, which in turn just renormalises the coefficient in the expression for Fconf by  in eqn (5). Now the total free energy barrier can be estimated:
in eqn (5). Now the total free energy barrier can be estimated:
 | (6) |
This expression has the property that a barrier only arises above a critical molecular weight. For small chains the confinement free energy that drives chain “explosion” overwhelms the elastic trap.4 We note that this is just what is observed qualitatively. Samples of polyethylene with Mw < 300 k did not exhibit any of the multiple effects characteristic of the heterogeneous melt.1 At the non-co-operative level we may calculate the critical molecular weight by just setting the barrier free energy to zero to obtain
 | (7) |
We will find that this result is modified somewhat by co-operative effects (see below), but it is certainly consistent with the large value for the threshold molecular weight of the experiments.
4. Co-operative loop corrections
The treatment above lies open to the criticism that by co-operative motion, chains may avoid paying the elastic barrier penalty in large part. They might do this so that as chain A moves partly into the cell of chain B, so B moves into that of C, and so on until one member of the cycle simultaneously returns to the cell of A. In this way the volume of material within the cells is not greatly changed, yet all the chains have begun to partition themselves between more than one cell. A full calculation of the highly co-operative space of transitions that this scheme represents is daunting, but we can estimate its effect on the structure of our problem by summing over all loops, and searching for the most probable. We find that the barrier free energy remains, but is renormalised in magnitude and scaling with molecular weight. This is because there is still an effective entropy to pay for a “transition state” that requires co-operative motion around a loop. This opposes the reduction in elastic free energy.We start from the number of closed loops of m steps in d dimensions cm ≃ Azmm−dν, where ν is the Flory exponent and z is the functionality of the discrete lattice (number of choices of neighbouring sites for a step).8 The entropy associated with a closed loop of attempted steps of chains from one cell to a neighbouring one arises from the probability that a loop is chosen rather than an open ended path of m steps, of which there are Ω(m) ≃ zm. So
 | (8) |
 | (9) |
Differentiating this expression gives the dominant loop size for chain transport of m* ≃ (2ϕeN/3Ne)1/3, and a renormalised barrier height of
 | (10) |
So the co-operative dynamics between cells does provide a renormalisation of the barrier, indeed at the level of the exponent. However the barrier is still many times the thermal energy for well-entangled chains.
4.1 Critical molecular weight correction and relaxation times
The critical molecular weight is renormalised to a higher value by these co-operative motions. By combining the new result of eqn (10) with the confinement free energy just as in Section 3 above, we now find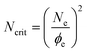 | (11) |
Now the barrier free energy including the confinement term can be expressed in a prediction for the equilibration time of the melt by the associated activated process:
 | (12) |
This is closely approximated by an exponential linear in N − Ncrit for accessible molecular weights (see Fig. 3). The value of Ncrit that now emerges is of the order of 103. For PE, the Kuhn segment is probably best represented by the mean run of trans isomers (of order 10), giving a molecular weight of a Kuhn segment of the order of 102. So we expect a value of Mcrit to be of the order of 105, in agreement with the molecular weights explored to date, but suggesting that experiments on melts with molecular weights of order 200 k would be very helpful as they should give rise to equilibration times that are much longer than the normal reptation times, but not so long as to be unmeasurable.
 | ||
| Fig. 3 Barrier (in units of the thermal energy) for chain re-entanglement in a co-operative model. The dimensionless molecular weight x is given in terms of Kuhn lengths. | ||
In such samples it should also be possible to measure the rheological (stress) relaxation spectrum. As we noted above, this should have two regimes: a set of fast relaxation modes arising from non-activated tube disengagement from the chain extremities. This should be identical to the fast reptation/fluctuation modes of linear chains.9 A second set of slower modes comes from the activated diffusion of chains relaxing parts of the partitioning regions of the melt that were themselves created by activated motions of the chains against the elastic barriers. An approximate result for the relaxation modulus G(t) in this regime can be calculated by inverting the full expression for the barrier-dominated relaxation times (eqn (12)) written in terms of the partial chain reptation co-ordinate n and observing that G(t) ≃
G2 [n(τmax) −
n(t)] for tube renewal in the partitions. Here τmax is the annealing time and sets the longest (aged) relaxation time of the heterogeneous melt. The result for the slow relaxation modes is
5 Conclusions
A mechanism for localising chains in the heterogeneous melt that simultaneously allows for stress relaxations and arises naturally from the preparation protocol has been proposed. The elastic distortions of the heterogeneous melt structure are the underlying cause of the localisation, which forces the chains either to move in a highly co-operative way or to pay strong elastic penalties to diffuse. A compromise between the two choices arises as the favoured route to relax the structure, but this still carries a high free energy barrier for highly entangled chains. Even at a level of scaling dependencies, the model gives quantitative predictions for the barrier-height (and so annealing) times as a function of molecular weight, and for the critical molecular weight below which the effect does not appear in terms of the entanglement molecular weight. Several experiments are suggested:• Monitoring the frequency-dependent modulus during the annealing should detect changes (shifts to higher frequencies for most stress-relaxation and the appearance of the low-frequency aged part of the spectrum). This should be done as a function of molecular weight using monodisperse materials if possible.
• Checks of the correlations between annealing time, heterogeneous modulus, and recovery rate should be made at a range of molecular weights.
• Measures of single chain diffusion from scattering methods are highly desirable. These should correlate with annealing kinetics to the full melt.
• Direct SANS/SAXS scattering from the heterogeneous melts should be attempted. There is every reason to expect small density differences between normal and unentangled melt regions that may show up as direct markers of the “imprint” of the former crystalline morphology on the melt state.
• Highly non-linear shear flow applied to the melt ought to disrupt the entangled regions and so provide a direct route to recovery of the normal melt.
It is hoped that a systematic exploration of the experiments suggested by this first model will clarify the underlying structures of this remarkable new material.
Acknowledgements
Extended and useful conversations are acknowledged with S. Rastogi, D. Lippits, G. Peters, D. Read, C. Bailly and A. Likhtman.References
- S. Rastogi, D. R. Lippits, G. W. M. Peters, R. Graf, Y. Yao and H. W. Spiess, Nat. Mater., 2005, 4, 635 CrossRef CAS
.
- S. Rastogi and L. Kurelec, J. Mater. Sci., 2000, 35, 5121 CrossRef CAS
.
-
M. Doi and S. F. Edwards, The Theory of Polymer Dynamics, Oxford University Press, Oxford, 1986 Search PubMed
.
- P. G. de Gennes, C. R. Acad. Sci., Ser. IIb: Mec., Phys., Chim., Astron., 1995, 321, 363 Search PubMed
.
- P. Barham and D. M. Sadler, Polymer, 1991, 32, 393 CrossRef CAS
.
-
S. Rastogi, personal communication
.
- S. M. Fielding, P. Sollich and M. E. Cates, J. Rheol., 2000, 44, 323 CrossRef CAS
.
-
P. G. de Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, Cornell, 1982 Search PubMed
.
- A. E. Likhtman and T. C. B. McLeish, Macromolecules, 2002, 35, 6332 CrossRef CAS
.
| This journal is © The Royal Society of Chemistry 2007 |

