Instabilities in liquid foams†
D.
Weaire‡
a,
M. F.
Vaz
a,
P. I. C.
Teixeira§
b and
M. A.
Fortes
a
aInstituto de Ciência e Engenharia de Materiais e Superfícies and Departamento de Engenharia de Materiais, Instituto Superior Técnico, Av. Rovisco Pais, 1049-001, Lisboa, Portugal
bFaculdade de Engenharia, Universidade Católica Portuguesa, Estrada de Talaíde, 2635-631, Rio de Mouro, Portugal
First published on 2nd November 2006
Abstract
Instabilities play a central role in the physics of foams. Some that change the topology of a dry foam are indicated by the laws promulgated by Plateau in his 1873 book. Their occurrence is less clearly predictable in wet foams. Various other instabilities are related to gravitational loading and gas compressibility. We gather up many examples as a guide to future research and identify problems that remain, including what we call pre-emptive instabilities, which occur before they are expected on the basis of Plateau's laws.
 D. WeairePermanent address—Department of Physics, Trinity College, Dublin 2, Ireland. D. WeairePermanent address—Department of Physics, Trinity College, Dublin 2, Ireland. | Denis Weaire is Erasmus Smith Professor in the School of Physics of Trinity College Dublin. His research group has combined theory, simulation and experiment in helping to establish the modern development of the physics of foams, over two decades, as described in the books The Kelvin Problem, Physics of Foams and Pursuit of Perfect Packing. |
 M. F. Vaz M. F. Vaz | M. Fatima Vaz is an assistant professor in the Department of Materials Engineering of Instituto Superior Técnico in Lisbon. Her research work includes theory, experiments and simulations of liquid foams and of solid cellular materials, such as ceramic foams. |
 P. I. C. TeixeiraPresent address—Instituto Superior de Engenharia de Lisboa, Rua Conselheiro Emídio Navarro 1, 1950-062 Lisboa, and Centro de Física Teórica e Computacional, Universidade de Lisboa, Avenida Professor Gama Pinto 2, 1649-003 Lisboa, Portugal P. I. C. TeixeiraPresent address—Instituto Superior de Engenharia de Lisboa, Rua Conselheiro Emídio Navarro 1, 1950-062 Lisboa, and Centro de Física Teórica e Computacional, Universidade de Lisboa, Avenida Professor Gama Pinto 2, 1649-003 Lisboa, Portugal | Paulo Teixeira is a lecturer in the School of Engineering of Lisbon Polytechnic. He has done (mostly theoretical, and some simulation) research on a variety of soft matter systems, including dipolar fluids, liquid crystals, elastomers, polymers and foams. |
 M. A. Fortes M. A. Fortes | Manuel A. Fortes is a full professor in the Department of Materials Engineering of Instituto Superior Técnico (IST) in Lisbon. His interest in liquid foams arose from previous work on cellular materials, particularly on cork. Research in foams includes theory, experiments and simulations of foam structure and properties. He leads a research group on cellular materials (including liquid foams) at the Instituto de Ciência e Engenharia de Materiais e Superfícies in IST. |
Introduction
The physics of foams began (and almost ended, as it became unfashionable for a time) in the work of J. A. F. Plateau, culminating in his impressive magnum opus.1 Of course, it had many antecedents, dutifully recounted by Plateau himself, but even the basic concept of surface tension/energy had remained obscure until well into the 19th century. Today it seems obvious and elementary that the (free) energy of a large enough body of liquid may be usefully expressed as| E = Ebulk + Esurface | (1) |
From the mists of such debates, there gradually emerged the simple theory that we take for granted today. Young, Monge, Laplace and others showed how it could be used to explain the various effects subsumed under “capillarity”.2–4 A key result was the Young–Laplace Law, which relates the equilibrium pressure difference across a fluid interface to its surface tension σ and curvature,
 | (2) |
 . In equilibrium, Δp and, hence, r are the same for all points on an interface, but r1 and r2 may vary. Eqn (2) acquires another factor of 2 for a soap film on account of its two liquid/gas interfaces. This assumes that the interactions between the two film surfaces make a negligible contribution to its energy.
. In equilibrium, Δp and, hence, r are the same for all points on an interface, but r1 and r2 may vary. Eqn (2) acquires another factor of 2 for a soap film on account of its two liquid/gas interfaces. This assumes that the interactions between the two film surfaces make a negligible contribution to its energy.
In arriving at this long-delayed insight, Young and Laplace used physical and mathematical (or British and French) perspectives, respectively. While the former talked directly of an isotropic surface tension with unprecedented clarity, the latter formally introduced a somewhat abstract quantity H, essentially representing the same thing. Mutual and acrimonious misunderstanding ensued.2 The subject's adherents still stretch between the two extremes, with contrasting styles.
It fell to Plateau1 to promulgate the general principle of minimisation of surface area (and hence surface energy), usually for a body of liquid considered incompressible and hence of fixed volume, or for a soap film in a frame. Hence, his name is still honoured by mathematicians in the “Plateau problem”,3 relating to existence theorems that address the mathematical solutions for such films. With the help of his wife and students he manifested some of the simpler consequences of the principle of minimisation of surface energy, and with some mathematical assistance from the geometer Lamarle5 showed that it was sufficient to explain them all. Plateau's achievement in surveying the static structure of films and foams remains unrivalled, but is inevitably surpassed in scope and sophistication today, with the aid of the computer.
From the very outset, he focused repeatedly on the instabilities that set bounds to the ranges over which particular structures can be maintained. They remain of great interest today, in relation to a number of fields. These include the study of capillary effects under microgravity (e.g. ref. 6), the description of foam flow in porous media,7 the formation of jets and droplets,8 and new developments in microfluidics, as well as the physics of foams.
We shall concentrate mainly on the core problems of foam physics, directly descended from those of the 19th century.9 We seek to bring Plateau's conclusions up to date. Most of them have stood the test of time. As the subject moves from problems of statics to those of dynamics, instabilities gain importance and often stand at the threshold of new research problems.
The topological instabilities of Plateau set outer bounds to critical points. In some cases they are pre-empted by an earlier transformation in practice. We shall argue that such pre-emptive instabilities are common in three dimensions. This does not seem to have been generally appreciated up to the present point.
As we shall see, straightforward experiments on foams identify a variety of well-defined instabilities, most of which result in rearrangements on a time-scale of less than a second, suitable for observation, for example by video.
Film rupture (and consequent collapse of foam) presents an important type of instability that will be entirely omitted here. It has its origins in the fluctuations of film thickness and the local influences of particles and immiscible droplets. Still poorly understood, it is addressed in a rich field of research, but this is of a different character to what is discussed here. While the cases that we cover may ultimately lead to consideration of microscopic properties of films, at the onset they have to do with the geometry of bubbles and the minimisation of their surface energy, within an elementary model.
Types of instability
What do we mean by instability in this context? It has the same commonplace meaning that is familiar in mechanics, but some explanation may be helpful.Except where indicated, we shall deal only with static equilibrium structures. One that is in stable equilibrium remains essentially unchanged when subjected to small displacements (consistent with any constraints, such as volume conservation). A stable configuration minimises energy with respect to all displacements. Nevertheless, the term “minimal surface” is widely used in the weaker sense that the energy is stationary.
It often happens that, as some control parameter is varied (for example, the dimensions of a frame to which a soap film configuration is attached, or the prescribed volumes of bubbles in a foam) we reach a limiting point of stability. This means that continuing beyond this point, the system either
(a) develops an asymmetry without encountering any discontinuity in the configuration, or
(b) jumps away from this initial configuration to settle in another which is not close to it.
The consequences of the former type of instability (second order, in the language of phase transitions) may often be predicted by purely static modelling. The latter is more problematic and may require a dynamic model, because the system is out of equilibrium during the transition. Such models are under scrutiny in current research: they will not be covered in any detail here.
In practice, this desideratum is often disregarded and the system is assumed to settle in the “nearest” state of stable equilibrium, or that which is reached by some algorithm which seeks out the new equilibrium in a steepest-descent search. It may be obvious that this is its correct destination, if there are no other competing choices nearby.
In some cases (in which there is no change in connectivity at the instability), an analysis of the Hessian matrix, which describes the quadratic variation of energy (surface area) with respect to all possible modes of small distortion, serves to identify those that are least stable and those that lose stability at the threshold. The relevant analysis evaluates the lowest eigenvalues of the Hessian matrix, together with their eigenvectors. See the ESI for an explanation of the Hessian matrix method and its technical details.†
The eigenvalues of the Hessian matrix are the coefficients of the quadratic variation for those modes. One eigenvalue may go to zero at a point of instability, and is identified with the unstable mode that is our object of interest. These modes are essentially the “soft modes” of the solid state physicist. They can offer indications of the nature of the instability and suggest where it will take the system.
However, the kind of instability which Plateau's classic rules1,9 entail is not quite of this character. In his idealised model for a dry foam, films are infinitesimally thin, and represented in single surfaces meeting in lines, which in turn meet in vertices. In this case, the instabilities occur as a consequence of an abrupt topological change. This occurs because Plateau's necessary conditions for equilibrium are not satisfied, for example by a vertex of more than four lines. There is no hint of the instability until this point is reached. It is necessary to resolve the vertex into a new configuration of Plateau-allowed vertices before applying a stability analysis. This may contain linear as well as quadratic terms, in which case the linear ones have primary significance.
Specific examples of instability
(a) The Rayleigh–Plateau instability for a cylindrical surface
This classic type of instability was first investigated by Plateau, while Rayleigh10 is given credit for its later elaboration.Plateau remarked that configurations in which bubbles have large aspect ratios tend to be unstable, quite generally. Indeed we shall see that a related instability is to be found in confined foams11 as in Fig. 1. Moreover, something akin to the Rayleigh–Plateau instability must be at the heart of most common processes of foam formation. Shaking a liquid/gas mixture is remarkably efficient in creating a foam of small bubbles, presumably by the elongation of larger ones to a point of instability, rather as in section (h) below. But here we consider the simplest case, that of a closed cylinder of uniform circular cross section, diameter D, and length L, which is formed, for example, by a soap film between two solid plates upon which the film is free to move. The enclosed volume is to be considered fixed. We shall frequently make such an assumption, so let us note here that a measure of the relative effect of the compressibility of the enclosed gas is the size variation between adjacent bubbles due to compressibility. For millimetre-sized bubbles, hence with film curvature radii of the order of 1 cm, eqn (2) with σ ∼ 10−1 N m−1 gives Δp ∼ 10 Pa = 10−4 atm for a typical variation of pressure between bubbles. If we now recall that the compressibility of an ideal gas is the inverse of its pressure p0 and this is typically of the order of 1 atm, then the typical bubble size variation will be ΔV ∼ Δp/p0 ∼ 10−4 which is usually negligibly small. In real foams of the usual kind, compressibility becomes important only for extremely small bubble sizes or pressures,12 and can provoke a special type of instability there. We will return to this point in section (k).
 | ||
| Fig. 1 Sequence of surfaces in the numerical simulation of the Rayleigh–Plateau instability for a cylindrical surface, e.g. a soap film, between two plates (adapted from ref. 11). | ||
If the circular ends of the film are free to move on the surface of the plate, the Hessian modes of expansion and contraction are similar to standing waves.10 The mode of largest wavelength is the first to become unstable as L is slowly increased. The critical value1 is given by
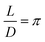 | (3) |
This instability is of the second type mentioned above and leads eventually to configurations such as that indicated in Fig. 1, consisting of one or more distinct bubbles, attached to the plates or free, depending on the liquid viscosity and other factors.
(b) Other instabilities of cylindrical surfaces
The above case is only one of a family of possibilities considered by Plateau. Another is the case of two open rings of diameter D, separated by a distance L along a common axis, as in Fig. 2. The enclosed volume is no longer conserved. | ||
| Fig. 2 A cylindrical bubble between two open rings (adapted from ref. 13). | ||
The solution for the surface which connects these rings and conforms to the Laplace–Young law (with pressure difference zero) has as its generating curve (which is to be revolved around the axis) the same catenary curve (y = cosh(x/c)) that provides the solution for a cable suspended between two points. But such a solution for the generating curve, only exists for L/D ≤ 0.6627. If the ratio is continuously increased from a small value, the surface must become unstable at or before this point is reached. For L/D < 0.6627, there are two solutions of which the one with the smaller “neck” (relative to L or D) is unstable, and the other is stable up to the critical point.
This example is susceptible to standard variational calculus (see, e.g., ref. 14 and 15). Note that the transition from the continuous differentiable to the discontinuous solution, occurs when the catenoid still has a finite radius at x = 0, i.e., the static solution never pinches off to a point.
This is an instructive example in many ways, so we include a geometrical diagram to further explain its main features (Fig. 3). In particular, this may be regarded as a pre-emptive instability, using a term adopted for the purpose of this article, with the following meaning. With fixed D, the neck diameter decreases as the two rings are pulled apart. The naïve expectation is instability when the neck vanishes and the topology must change. However, the actual instability occurs much earlier. A similar analysis shows that when the diameter D1 of one ring is fixed and the other diameter D2 is reduced, we encounter the same kind of instability at a point which depends on the separation L.
 | ||
| Fig. 3 The catenary curve y(x) provides the solution of the two-ring problem. Here we keep the neck radius R = 1 (also the radius of curvature of the profile) fixed, and explore solutions with a particular ratio D/L (ring diameter D and separation L). A straight line with slope D/L intersects the curve in two points for L/D < 0.6627. Each such point gives a solution (rescaled as necessary), for given D and L. | ||
(c) Plateau's topological instabilities in 2d and 3d
Central to Plateau's achievement is his formulation of rules for the local equilibrium of systems composed of soap films. One such rule is the Laplace–Young Law [eqn (2)], mentioned above. In general this places a condition on the subtle, doubly-curved shape of the films that make up a soap froth and the bubble pressures. But what of their intersections?Here we speak of an ideal dry foam, in the first instance. That is, it is considered to consist of films (lamellae) of infinitesimal thickness, meeting in lines. These lines meet at points (known as vertices, nodes or junctions). The energy is exclusively contributed by the films.
To begin with, consider a 2d foam, such as may be realised by trapping bubbles between two glass plates. This is idealised in terms of lines (which in this case represent films in the real system, spanning the two plates). The lines surround cells and meet at points. Only three lines can meet at such a 2d vertex (at 120 degrees). If conditions are varied in such a way that the length of one of the cell sides goes to zero, and forms a fourfold vertex, we necessarily encounter an instability and the system jumps to a different configuration that is in accord with Plateau's rules. This is the “T1 process” (Fig. 4),16 whose role in disordered 2d foams was underscored by C. S. Smith.17 It punctuates the otherwise smooth evolution of the structure under coarsening or shear.
 | ||
| Fig. 4 T1 process in two dimensions.9 | ||
The proof of the instability of the fourfold vertex in 2d is quite elementary. It is considered to be dissociated into two threefold vertices connected by an edge of infinitesimal length. For at least one of the two possible configurations of this kind, the surface tension forces are unbalanced in such a way as to increase the length of the new edge.
Although sometimes compounded in avalanches, these T1 changes are indeed the essence of 2d foam relaxation and rheology and may be displayed in very simple demonstrations. In the case of an ordered 2d (honeycomb) structure, they provide the mechanism for simple defects (dislocations consisting of adjacent 5- and 7-sided cells) to migrate. The pioneering calculations of Kraynik18 are slightly misleading in this respect, in that he assumed simultaneous T1 changes throughout the honeycomb structure, whereas actual specimens are deformed by defect migration.19 This is reminiscent of the historic misapprehension of the nature of the plasticity of metals.
Reverting to three dimensions, we see that the same argument may be used to justify Plateau's rule that allows films to meet only three at a time. They do so at 120 degrees, to conform to the equilibrium of surface tensions at the point. But the problem of how many lines (Plateau borders) can meet at a vertex is not so simple. The most elementary vertex, in 3d, has four lines and six films, and the relevant Plateau rule stipulates that no other vertex is stable; anything with more lines must dissociate, just as in two dimensions. To our knowledge there is no straightforward proof of this, treating such vertices in a general way, and that remains an open problem. Lamarle5 achieved a long proof by exhaustion of cases, and this has been refined by modern mathematicians, but without condensation to anything more compact. He explicitly described unstable deformations for all of them, except the fourfold case that remains the sole stable vertex. Again we remark that Lamarle's theorem only sets bounds on stable structures. See in particular section (e).
(d) Topological changes in frames and foams
Plateau developed his rules by the observation of soap film structures in frames, some of which are of high symmetry, such that naïve expectation would point to a symmetric configuration that is forbidden by the above rule. The most familiar case is that of the cubic frame (Fig. 5a,b), in which the actual soap film configuration breaks the symmetry of the frame in which it resides, introducing a central quadrilateral face, whose normal points in one of the three cubic directions. | ||
| Fig. 5 Plateau's frames, with attached handles: (a) cubic, with the observed film configuration, (b) the unstable symmetric configuration for the cubic frame, (c) the tetrahedral vertex, and (d) the triangular prismatic frame. (adapted from ref. 1). | ||
In a foam, forbidden multiple vertices are commonly approached in the processes of deformation or coarsening, and topological changes result. Unlike the 2d case, here there are two elementary topological processes that are the inverse of one another but of different character (Fig. 6). Respectively, they are provoked when a line or a triangular face shrinks to the point of vanishing.20 One might suggest that the notation T1 and T1′ would be appropriate, to indicate that these two processes are not the same (as they are in 2d). These changes are indeed commonly observed in foams although they often occur together in a compound topological change that results in the rotation of a quadrilateral face.9,21 We might symbolically represent this as T3,
| T3 = T1 + T1′ (rotation of quadrilateral face) | (4) |
 | ||
| Fig. 6 T1′ and T1 rearrangements in a 3d dry foam.9 | ||
Very careful observation (or calculation) is required to conclude whether any of these changes is made pre-emptively. Kraynik has noted a pre-emptive T3 change in simulations of shear for the Kelvin structure.22 In the next section, we shall argue that this pre-emptive character is rather general, taking another special case as prototype.
(e) The triangular frame and the T1′ change
Although the implications are rather general, let us examine the problem of pre-emptive instability in the context of a triangular prismatic frame (Fig. 5d), another of Plateau's classic constructions. He described what we have called the T1 and T1′ processes. What follows is based on a rather crude repetition of his experiment23,24 using a frame whose axial ratio c/a (= height/width) may be varied. The case of T1 is straightforward, with instability at the point of vanishing edge length. That of T1′ is more problematical. Indeed we undertook this experiment after being puzzled by the nature of the limiting state as the Plateau instability is approached: it entails the approach to infinity of components of local curvature. In practice, it was observed that this crisis was avoided by a pre-emptive instability, as c/a was varied slowly, so as to decrease the area of the triangular face at the centre (Fig. 5d).At a certain critical value of c/a, the triangular face collapses spontaneously, shrinking to a point, and this provokes the T1′ change to the configuration shown in Fig. 5d.
(f) Wet foams
Up to now we have been dealing with an ideal dry foam. A real foam has a finite liquid fraction. While the soap films may still be idealised as infinitesimally thin, the lines at which they meet in the dry foam are to be replaced by Plateau borders of finite cross-sectional area, which swell as further liquid is incorporated. In such a model, we may still talk of topology, but Plateau's topological rules are less and less respected as we move away from the dry limit. This gradual relaxation of rules that are strict in the dry limit is not fully worked out as yet—let us summarise some of the existing conventional wisdom.In a 2d wet foam, there are finite Plateau borders and there can be stable multiple borders with more than three sides,25,26e.g. a fourfold border (Fig. 7). The T1 process occurs in two stages: border coalescence, and border separation as is illustrated in Fig. 7.
 | ||
| Fig. 7 For a wet foam the intermediate configuration may be stable, as demonstrated here.26 A stable fourfold border is formed upon increasing the liquid fraction. | ||
There has been no general treatment by simulation of instabilities in 3d wet foam, along the lines of that of Bolton and Weaire25 for two dimensions. Qualitatively, it seems clear that the gradual relaxation of Plateau's rules should proceed in a similar way.
An interesting question (and one that occurred to Plateau himself) is as follows. How much liquid is required to stabilise the eightfold symmetric vertex in the cubic frame of Fig. 5b? Inspired by experiments in which this liquid was introduced in a continuous draining process (Fig. 8), it was suggested by in het Panhuis et al.27 that the answer might be paradoxical. It might be that any finite liquid fraction, however small, stabilises the vertex against small displacements, in the model that we have defined. (They were unaware that Plateau had performed rather better experiments with density-matched liquids, also finding a very close approach to the “dry” symmetric vertex.)
 | ||
| Fig. 8 Increasing the liquid fraction by introducing steady drainage (by liquid input) at the top can restore a stable eightfold vertex27cf. Fig. 5. | ||
However, exhaustive calculations by K. Brakke28,29 countered this notion and resulted in an estimate of the critical liquid fraction for stability of the 8-connected vertex, ϕ = 0.000278. This seems extraordinarily small, and as yet inexplicably so.
A further complication for wet foams is the observed concatenation of many elementary T1 changes, in cascades or avalanches.19,30 The wetter the foam, the larger these avalanches become.
(g) Other 3d instabilities in wet foam
An interesting case occurs wherever a face shrinks and vanishes in a 3d wet foam, upon increasing the liquid fraction. At this point two bubbles lose contact. Whether this is necessarily a point of instability is not obvious, but it would seem so from observation. The classic example is that of the Kelvin (bcc) structure (Fig. 9), in which each dry foam cell has eight hexagonal faces and six quadrilateral faces, closely related to those exhibited by Plateau's cubic frame (Fig. 5) As liquid is added, the films associated with the quadrilateral faces are reduced to a small circle and then vanish. At (or just before?) this point an instability is observed. | ||
| Fig. 9 Kelvin (bcc) structure. | ||
Observing this in the surface layers of a draining foam, Weaire et al.31 interpreted it in terms of the instability of a bcc atomic structure when second-nearest neighbour interactions are absent. While this argument makes a connection with those made in metallurgy, it would be better in this case to make an analysis in terms more closely related to surface energy and bubble interactions. This instability is also related to the problem of the interface in the three-dimension honeycomb of the bee, or the analogous foam structure.32
Bulk Kelvin structures have been produced only to a limited extent,33,34 but remarkably so, since this is not the structure of lowest energy for monodisperse dry foam.35 The question of what bulk structure would emerge from the above instability, upon producing a wet Kelvin foam, remains unanswered.
(h) 2d–3d foam transitions
A two-dimensional foam which consists (for example) of a mass of bubbles trapped between two adjacent plates, undergoes a progressive transformation to a three-dimensional foam, as the plate spacing is increased. How does this proceed? This question was answered by Cox et al.,11 using experiments, simulations and an approximate mathematical treatment.As a convenient example, a 2d “flower” cluster of cells obtained by trapping bubbles between two glass plates or between one plate and a liquid surface, was used. A central bubble is surrounded by n petals, all of the same volume. As the spacing increases by changing the height of the cluster, the foam cells become elongated. One might naïvely expect this to continue indefinitely, at least in the ideal dry foam. However, instabilities enter and convert the foam into a double layer of bubbles, as soon as the spacing is of the order of the cell diameter. It is the cells with less than six sides that are susceptible to the initial change, which is essentially the Rayleigh–Plateau instability of section (a), here dubbed the “wine bottle instability”. As confirmed by Brakke and Morgan,36 when the central bubble is small and has fewer than six sides, it becomes unstable first. When the central cell is large or has six or more sides, it drives the Rayleigh–Plateau instability of a petal.
Several final different 3d configurations may be obtained in the 2d to 3d transition, depending on the volume ratio of the petals and the central cell. Fig. 10 shows some examples from the simulations of Cox et al.11
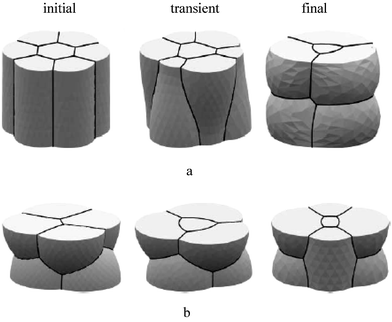 | ||
| Fig. 10 (a) 2d to 3d transition with petals suffering a wine bottle instability and (b) several possible configurations after the 2d to 3d transition (adapted from ref. 11). | ||
For cells of equal volume V, the estimated critical plate spacing dcrit for the central instability contains n, the number of cell sides
 | (5) |
(i) Ordered double layers
An ordered double layer of monodisperse bubbles presents a perfect hexagonal structure on both sides, separated by a faceted wall in the middle. For the dry foam, the cells are arranged in the manner of a slice taken from the Kelvin structure, perpendicular to the 〈110〉 direction (with some small geometrical adjustment). Upon increasing the liquid fraction, the same sort of instability as considered in section (g) is found, converting the structure into that of close packing. Upon once more decreasing the liquid fraction, there is an instability of the Plateau type everywhere as wet multiple vertices become dry and hence unstable. There is considerable hysteresis, a general property of topological instabilities that we have not emphasised up to this point.(j) Ordered cylindrical structures
Structures of monodisperse bubbles contained in cylindrical columns readily form ordered structures provided that the bubble diameter is not very much smaller than that of the tube.37,38 Originally pursued out of curiosity, these systems now excite interest in the context of microfluidics.39A remarkable sequence of structures of increasing complexity is observed as the bubble diameter is varied. For any given sample, this may be effected by either introducing a flow of liquid at the top, producing a steady state that approximates equilibrium40 or by compressing the system with a piston.41 The most impressive demonstration of foam instability is thereby produced: at certain points the structure is rearranged by an elaborate sequence of topological changes, which proceeds along the tube in a periodic manner, reminiscent of Scottish country dancing.
The most elementary example (apart from the one in the following section, which is special) is the change from the staircase structure to the bamboo structure (Fig. 11). This is clearly necessary when the area of the horizontal faces of the staircase structure approaches zero. However, once again, a pre-emptive instability is found as first noted in calculations by Reinelt et al.38 One can again associate this with a “curvature crisis”. The horizontal interior Plateau border has a curvature which would tend to infinity in the limit considered, because of the boundary conditions that require it to be normal to the cylindrical tube surface, which it meets.
 | ||
| Fig. 11 Transition from the staircase to the bamboo structure (reproduced by kind permission of the authors of ref. 38). | ||
(k) Instability of the bamboo structure upon compression
In an ideal model of a dry foam, the instability (bamboo → staircase) which is the reverse of that just considered, does not occur. The parallel flat films of the bamboo structure may be thought arbitrarily close together. In practice, the bamboo → staircase transition is clearly observed. It has to do with the interaction of the finite wall Plateau borders which are absent from the idealised model. When these touch, instability is provoked and is very similar to the T1 process in a wet 2d foam.(l) Instability due to gas compressibility
Hitherto we have considered the compressibility of both liquid and gas to be negligible, as is often the case. However, as discussed in section (a), compressibility may become significant if the pressure is low and/or the bubble size is very small. It is difficult to realise these conditions in practice. Nevertheless the consequences, as predicted by Aref and Vainchtein,12 are interesting. A foam of sufficiently compressible gas “phase separates” into regions of large and small bubbles with different gas densities. This may be attributed to the negative second derivative of surface area with respect to bubble volume, which eventually overcomes the positive energy cost due to expansion/compression of gas. How this would actually proceed in an experiment is as yet unknown.(m) 2d flower clusters
Configurations of the type shown in Fig. 12 were introduced by the Lisbon and the Dublin groups42,43 (but are to be found in the notebooks of Lord Kelvin!). We have already met these in section (h).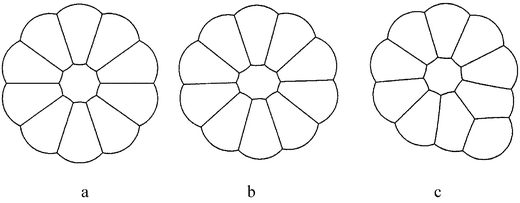 | ||
| Fig. 12 2d-Flower clusters with 10 equal petals: (a) symmetrical, (b) asymmetrical and (c) ejected configurations (adapted from ref. 44). | ||
The simplest 2d flower cluster consists of a central cell surrounded by n equal petals. Exact solutions were easily provided, as clusters have n-fold symmetry.42 Simulations with the Surface Evolver were done to investigate the uniqueness of stable configurations for given topology.43 They revealed that, for a flower cluster of more than six petals, when the area of its central cell is reduced, there is a symmetry-breaking instability at a certain point. In a flower cluster with one shell of petals, the critical area corresponds to the energy minimum and to zero eigenvalues of the Hessian matrix. Beyond this point, the cluster becomes “floppy”, that is it may be given any configuration within the bounds that maintain its topology. Asymmetrical configurations arise with lower energy than the symmetrical arrangement. Asymmetrical configurations (Fig. 12b) were never observed experimentally.
A further type of instability which is observed in experiments for n > 6 is a change in topology due to the ejection of a bubble (Fig. 12c) which was initially in contact with the central cell.44,45
No instability occurs for flower clusters with n < 6. The decrease in the central cell area, gives rise only to the vanishing of the central cell.44,45
(n) Symmetry breaking in the contact of opposed surfaces and bubbles
Firstly suppose that two convex surfaces of liquid (for simplicity, spherical), stabilised by surfactant, meet and do not coalesce.46 Now proceed to push them closer together. A point is reached at which the symmetry is broken by instability and the two bodies of liquid no longer simply meet “head-on”.When two 2d bubbles are opposed and form an intervening film (Fig. 13) the effect is much the same but simpler to describe.47,48 When deforming two bubbles between two bars as in Fig. 13, instabilities occur for critical values of bar spacing. The compression of the two bubbles leads, at a critical point, to a buckling or slant configuration, where the inter-bubble film is inclined. Further compression induces T1 and provokes a topological transition into a bamboo arrangement.
 | ||
| Fig. 13 Compression of two 2d bubbles between bars. Compression leads to a buckled or slant configuration.47 | ||
Another instability of this type is the tilting of the inter-bubble film for a compressed pair of 3d bubbles, was demonstrated by Bohn.49 In both 2d and 3d, this transition may be readily understood in terms of the “floppy” property of section (m).
(o) Gravitational instability
In all of the above, gravity has played no part. In a wet foam of large bubbles, it may be significant, not just in determining the equilibrium distribution of liquid throughout the sample, but also its local geometrical arrangement. It can even render this unstable, in principle.50In practice this has been observed in experiments of continuous drainage,27 but in foams it may be pre-empted by yet another instability, that of convection.51
(p) Instability of bamboo structure under gravity
While instabilities under gravity are in principle quite general, the special case of the bamboo structure in a vertical tube is particularly interesting on account of its simplicity, and it has been analysed by Carrier.52 It is necessary only to consider a single film in a vertical bamboo structure and determine its form as the amount of liquid in the Plateau border is increased quasistatically. Initially horizontal, the film develops a curvature, as there is a pressure difference across the film which supports the weight of the liquid. Beyond a certain point no solution is found and experiments show that the cylindrical symmetry is broken by the formation of a droplet ejected from the wall Plateau border, more or less maintaining the system in its marginally stable state.(q) 3d bubble chains
Under increasing extension (Fig. 14) the bubble chain provides another example of a pre-emptive instability (and the curvature crisis that we have associated with other cases). Bohn's exhaustive description49 of this system, identifying both stable and unstable solutions, should be a model for the general understanding of more complicated cases, including the T1 process of section (e) above. | ||
| Fig. 14 Instability of a 3d bubble chain under elongation as observed by Bohn.49 The middle configuration is transient. (Reproduced by kind permission of the author of ref. 49). | ||
We may tentatively advance the generalisation that topological instabilities which entail any infinite curvature upon their approach are generally pre-empted, but as yet have no proof of this (even for special cases).
Viscous effects
In a quasistatic description we generally consider the system to jump instantaneously to its new configuration. In practice a finite time is required. It is dictated by effects that we may vaguely characterise as “viscous”, but in most cases they have not been unambiguously identified. One experimental observation that relates to this finite time of relaxation was made on the cylindrical structures of section (j)53 in which a transition proceeds down the column with a finite velocity, related to the time of relaxation and the energy difference that is the driving force for the structural change.In the 2d case, detailed simulations54 have shown the relaxation after a T1 change, within a model in which (in addition to the usual idealisations for a dry foam) a viscous drag is exerted on moving lines (and is in reality attributed to the viscous drag exerted on the wall Plateau borders as they slide on the confining plates). In this model, the velocity of the dissociating vertices is initially infinite, varying with time as its inverse square root, and eventually decaying to zero exponentially. This “toy model” is probably quite unrealistic, and some experiments already point to that conclusion.55 The matter is best left there, in anticipation of much research in the coming years.
Conclusions
Although our subject is a classic one, famously founded a century and a half ago, both experiment and close scrutiny of theory continue to raise questions. With increasing attention being paid to the world of soft matter, these questions are of lively interest. As the subject progresses in its basic competencies from static to dynamic effects, instabilities may not appear in so clear-cut a form as in the above examples, but they will always be part of the framework of qualitative understanding and its essential vocabulary.Furthermore, the stationary properties of foam structures must be intimately related to problems of existence and uniqueness of equilibrium structures and the fashionable topic of “energy landscapes”. A foam has a rich energy landscape if alternative topological arrangements are included. But for one fixed topological structure, is the stable minimum (if it exists) unique? This is the kind of question raised by Graner et al.56 and it provoked the studies described in section (m). It was a question largely disregarded by Weaire and Kermode57 in formulating the first full simulation of an ideal 2d dry foam. They used Plateau's laws, not energy minimisation, but were sufficiently aware of the problem to repeat simulations with added random initial perturbations, to confirm that they returned to the same configuration. Indeed it seems that for practical purposes the 2d case is rather straightforward, although Graner's conjecture would appear to be false.43
But this assertion should not be carried over casually into three dimensions, where there are stronger possibilities of complicated landscapes.
Even in the case of static structures, Plateau's research programme is clearly far from exhausted.
Acknowledgements
DW acknowledges the support of the European Space Agency, SFI grant 05/RFP/PHY0016, and thanks the Gulbenkian Foundation for the award of a Gulbenkian Professorship, during the tenure of which this article was written.As ever, Ken Brakke provided helpful advice and special thanks are due to Simon Cox for advice and calculations.
References
- J. A. F. Plateau, Statique Expérimentale et Théorique des Liquides Soumis aux Seules Forces Moléculaires, Gauthier-Villard, Paris, 1873. An English translation has been made available by K. Brakke on the website: http://www.susqu.edu/brakke/evolver/evolver.html Search PubMed.
- J. S. Rowlinson, Cohesion, Cambridge University Press, Cambridge, 2002 Search PubMed.
- A. T. Fomenko, The Plateau Problem, Gordon and Breach Science Publishers, New York, 1989 Search PubMed.
- S. Hildebrandt and A. Tromba, The Parsimonious Universe: Shape and Form in the Natural World, Springer-Verlag, New York, 1996 Search PubMed.
- E. Lamarle, Mem. Acad. R. Belg, 1864–7, 35, 36 Search PubMed.
- P. Concus, R. Finn and M. Weislogel, Exp. Fluids, 2000, 28, 197–205 CrossRef.
- M. Chen, Y. Yortsos and W. R. Rossen, Coll. Surf., A, 2005, 256, 181–189 Search PubMed.
- E. F. Goedde and M. C. Yuen, J. Fluid Mech., 1970, 40, 495–511 CrossRef.
- D. Weaire and S. Hutzler, The Physics of Foams, Oxford University Press, Oxford, 1999 Search PubMed.
- Lord Rayleigh, Proc. London Math. Soc., 1878, 10, 4–13 Search PubMed; reprinted in Scientific Papers by Lord Rayleigh, I and II, 1964, Dover, vol. I, pp 361–401, vol. II, pp 103–117 Search PubMed.
- S. J. Cox, D. Weaire and M. Fátima Vaz, Eur. Phys. J. E, 2002, 7, 311 CAS.
- H. Aref and D. L. Vainchtein, Phys. Fluids, 2000, 12, 23–28 CrossRef CAS.
- C. V. Boys, Soap-bubbles and the Forces which Mould them, Society for Promoting Christian Knowledge, London, 1896 Search PubMed.
- R. Courant and H. Robbins, What is Mathematics?, 2nd edn, Oxford University Press, New York, 1979 Search PubMed.
- T. M. Apostol, Calculus, 2nd edn, John Wiley, New York, 1969, vol. II Search PubMed.
- D. Weaire and N. Rivier, Contemp. Phys., 1984, 25, 59 CrossRef.
- C. S. Smith, Metal Interfaces, American Society for Metals, Cleveland, 1952, 65–108 Search PubMed.
- A. M. Kraynik, Ann. Rev. Fluid Mech., 1988, 20, 325–357 Search PubMed.
- M. Emilia Rosa and M. A. Fortes, Philos. Mag. A, 1998, 77, 1423 CAS.
- M. A. Fortes and A. C. Ferro, Acta Metall., 1985, 33, 1697–1708 CrossRef CAS.
- A. C. Ferro and M. A. Fortes, Interface Sci., 1997, 5, 263–278 CrossRef CAS.
- A. M. Kraynik, private communication.
- S. Hutzler, D. Weaire, S. J. Cox, A. van der Net and E. Janiaud, to be published.
- M. Emília Rosa and M. A. Fortes, to be published.
- F. Bolton and D. Weaire, Philos. Mag. B, 1992, 65, 473.
- M. A. Fortes, M. Fátima Vaz and P. I. C. Teixeira, Philos. Mag., 2005, 85, 1291–1302 CrossRef CAS.
- M. in het Panhuis, S. Hutzler, D. Weaire and R. Phelan, Philos. Mag. B, 1998, 78, 1–12 CrossRef CAS.
- K. Brakke, Colloids Surf., A, 2004, 263, 4–10.
- http://www.susqu.edu/brakke/evolver/evolver.html .
- S. Hutzler, D. Weaire and F. Bolton, Philos. Mag. B, 1995, 71, 277–289 CrossRef CAS.
- D. Weaire, N. Pittet, S. Hutzler and D. Pardal, Phys. Rev. Lett., 1993, 71, 2670–2673 CrossRef CAS.
- D. Weaire and R. Phelan, Philos. Mag. Lett., 1994, 70, 345–350 CrossRef CAS.
- M. Emília Rosa, M. A. Fortes and M. Fátima Vaz, Eur. Phys. J. E, 2002, 7, 129–140 CrossRef CAS.
- A. van der Net, S. Hutzler, W. Drenckhan and D. Weaire, to be published.
- The Kelvin Problem, ed. D. Weaire, Taylor and Francis, London, 1996 Search PubMed.
- K. A. Brakke and F. Morgan, Eur. Phys. J. E, 2002, 9, 453 CrossRef CAS.
- N. Pittet, N. Rivier and D. Weaire, Forma, 1995, 10, 65 Search PubMed.
- D. Reinelt, P. Boltenhagen and N. Rivier, Eur. Phys. J. E, 2001, 4, 299 CrossRef CAS.
- W. Drenckhan and D. Weaire, to be published.
- D. Weaire, S. Hutzler and N. Pittet, Forma, 1992, 7, 259 Search PubMed.
- N. Pittet and P. Bothenhagen, private communication, unpublished.
- M. F. Vaz and M. A. Fortes, J. Phys.: Condens. Matter, 2001, 13, 1395 CrossRef CAS.
- D. Weaire, S. J. Cox and F. Graner, Eur. Phys. J. E, 2002, 7, 123 CrossRef CAS.
- S. J. Cox, M. F. Vaz and D. Weaire, Eur. Phys. J. E, 2003, 11, 29 CrossRef CAS.
- M. F. Vaz and M. A. Fortes, Eur. Phys. J. E, 2003, 11, 95 CrossRef CAS.
- G. Bradley and D. Weaire, Comput. Sci. Eng., 2001, 3, 16–21 CrossRef CAS.
- M. A. Fortes, M. E. Rosa, M. F. Vaz and P. I. C. Teixeira, Eur. Phys. J. E, 2004, 15, 395 CrossRef CAS.
- M. F. Vaz and S. J. Cox, Philos. Mag. Lett., 2005, 85, 415 CrossRef CAS.
- S. Bohn, Eur. Phys. J. E, 2003, 11, 177 CrossRef CAS.
- D. Weaire, N. Kern and G. Verbist, Philos. Mag. Lett., 2004, 84, 117–125 CrossRef CAS.
- S. Hutzler, D. Weaire and R. Crawford, Europhys. Lett., 1998, 41, 461–465 CrossRef CAS.
- V. Carrier, to be published.
- S. Hutzler, D. Weaire and R. Crawford, Philos. Mag. B, 1997, 75, 845–857 CrossRef CAS.
- N. Kern, D. Weaire, A. Martin, S. Hutzler and S. J. Cox, Phys. Rev. E, 2004, 70, 041411 Search PubMed.
- H. Stone and M. Durand, Phys. Rev. Lett., in press Search PubMed.
- F. Graner, Y. Jiang, E. Janiaud and C. Flament, Phys. Rev. E, 2001, 63, 011402 Search PubMed.
- D. Weaire and J. P. Kermode, Philos. Mag. B, 1984, 50, 379.
Footnotes |
| † Electronic supplementary information (ESI) available: The Hessian matrix and its eigenvalues. See DOI: 10.1039/b608466b |
| ‡ Permanent address—Department of Physics, Trinity College, Dublin 2, Ireland. |
| § Present address—Instituto Superior de Engenharia de Lisboa, Rua Conselheiro Emídio Navarro 1, 1950-062 Lisboa, and Centro de Física Teórica e Computacional, Universidade de Lisboa, Avenida Professor Gama Pinto 2, 1649-003 Lisboa, Portugal |
| This journal is © The Royal Society of Chemistry 2007 |
