Three dimensional visualisation of human facial exposure to solar ultraviolet

Abstract

A three dimensional computer model of the human face has been developed to represent solar ultraviolet exposures recorded by dosimeter measurements on a manikin headform under low cloud conditions and various solar zenith angles. Additionally, polysulfone dosimeters have been successfully miniaturised to provide the detailed measurements required across the face. The headform used in this research was scanned at 709 individual locations to make a wireframe mesh consisting of 18 vertical contours and 49 horizontal contours covering half the manikin's frontal facial topography. Additionally, the back of the headform and neck have also been scanned at 576 locations. Each scanned location has been used as a viable dosimeter position on the headform and represents a grid intersection point on the developed computer wireframe. A series of exposures recorded by dosimeters have been translated into three dimensional exposure ratio maps, representing ambient solar ultraviolet exposure. High dosimeter density has allowed for the development of individual topographic contour models which take into account complex variation in the face and improve upon previously employed techniques which utilise fewer dosimeters to interpolate exposure across facial contours. Exposure ratios for solar zenith angle ranges of 0°–30°, 30°–50°, and 50°–80° have been developed.

---

Introduction

The frequency and distribution of environmental ultraviolet radiation (UV) on exposed sites of the human body has been linked to the occurrence of non-melanoma skin cancers.¹ The increased risk of the development of cutaneous malignant melanoma, cataracts and premature ageing of the skin due to environmental exposures to UV is also well defined. The regular monitoring of solar UV radiation is however often related to horizontal surfaces. Additionally, the provision of the UV index is for a horizontal surface.² Models that relate exposures of a horizontal surface to the topography of the human body can be used to better define the causative role of environmental UV to skin and ocular disorders. Previously, manikin headforms employing polysulfone dosimeters have been used to develop exposure models to various sites on the human face.^3,4 These models provide biologically damaging exposures to the face based on the measurement of erythemal exposures to various sites located on the headform. While accurate at predicting environmental UV exposures to specific facial sites, these models rely on interpolation techniques to predict exposures between measurement sites.

Developing accurate models to predict environmental UV exposure across complex shapes like the human face requires the chosen dosimeter sites to be as close together as possible to reduce interpolation errors between measurement sites while simultaneously accounting for variations in orientation and shading caused by facial topography. One approach to the measurement of UV exposure over a human body has been to measure with radiometers the UV irradiances to 27 differently inclined surfaces over a period of 2 min.⁵ These measurements, interpolated in two dimensions, allow visualization of the total UV exposure received over the human body. An alternate approach to allow the visualization of UV exposure over the human facial region, involves the measurement of solar UV exposures to an extensive number of facial sites. This approach has been developed and is described in this paper. By developing a model based on actual dosimeter measurements recorded in close proximity to one another, this research extends previous research³ to visualize UV exposures under various physical environments and conditions.

Materials and methods

Modelling the headform

The previously employed method³ represented two-dimensional UV exposures calculated from graphical interpolations of 16 measurement sites layered on top of a forward facing photograph. The method reported in this paper has extended the previous method to create a three dimensional model wireframe from 709 individual measurement locations plotted across an x–y–z grid of a manikin headform. The newly developed model utilises the same manikin headform employed previously.³ The physical life-size dimensions of the headform and the miniaturised dosimeters used in this research facilitate the advantage of being able to be studied in realistic environments including under tree shade and restrictive urban areas.

Each measurement location on the newly developed model has been plotted along one of eighteen vertical contours each separated by 5 mm spanning from the centre of the headform to the ear to include the manikin's full frontal facial topography. Each vertical contour covering the vertex to the nose, the chin and upper neck is made up of 50 measurement sites. The number of measurement sites along vertical contours is reduced to 5 for sites measured along the ear. Measurement sites on each horizontal and vertical contour are spaced 5 mm apart relative to a horizontal and vertical plane. To represent the entire headform in three dimensional space each of the vertical contours have been mirrored so that the model consists of a symmetrical left and right side. The measurement sites recorded along each vertical contour were used to construct 49 horizontal contours which, when combined with the vertical contours, form the three dimensional grid. Intersections between vertical and horizontal contours represent individual measurement sites for dosimeters which have also been marked on the manikin headform. Fig. 1 compares the marked manikin headform with the 3D computer model.

Fig. 1 Comparison of the manikin headform with the computer model. The photograph indicates the position of viable dosimeter locations which correspond with model wireframe grid intersections.

The headform model was developed using MATLAB version 7 (The MathWorks, Inc. 2004) and can be viewed from any angle and varying levels of magnification. The model has been divided into two halves. UV exposure maps developed from dosimeter measurements recorded at specific sites (grid intersections) are represented on the model's left side. Fig. 1 depicts the facial exposure wireframe developed for this research. The figure shows both the exposure wireframe and dosimeter locations used to develop a facial exposure map. It should be noted that variations in surface brightness on the computer model's reference surface skin (right side) do not indicate UV exposure levels. This surface has been included for reference. As the frontal facial model incorporates up to 709 viable dosimeter locations, the accuracy of any developed exposure map can be compared to the total number of dosimeter measurements used to create it.

Dosimeter miniaturisation

Using the developed wireframe model, a series of facial UV exposures expressed as percentages relative to a horizontal plane have been developed. Environmental UV exposure sets were recorded between solar zenith angle (SZA) ranges of 0°–30°, 30°–50° and 50°–80° on an open sporting ground at least 30 m from the nearest buildings. The manikin headform was placed on a base, completing approximately two revolutions every minute (Fig. 2). Rotating platforms have been used previously to investigate the influence of solar UV on various sites of the human body and to approximate the random movements of human subjects.⁶

Fig. 2 Exposure location with manikin headform and rotating platform photographed in 60° increments showing the surrounding environment. The headform was placed in a vertical position at a height of approximately 30 cm rotating twice every minute.

Small flexible polysulfone dosimeters were utilised so that they could be attached closely together on the manikin headform. The dosimeters employed for this research were manufactured from polysulfone sheets cast at the University of Southern Queensland and fit to small flexible rectangular holders measuring approximately 10 by 15 mm with a clear aperture of 6 mm onto which the polysulfone was adhered. A technique explaining the manufacture and subsequent absolute sensitivity of the polysulfone film utilised for this research has been given previously.⁷ The newly developed dosimeters have been made smaller compared to previously employed dosimeters in order to allow for the required density of measurement points over the face. Fig. 1 shows the positions of dosimeters placed along vertical contours 1, 7, 14 and 18 located on the centre of the face, through the eye, the side of the face and ear respectively. The change in optical absorbency due to UV exposure of each individual polysulfone dosimeter was measured at 330 nm in a UV spectrophotometer (model UV1601, Shimadzu Co. Kyoto) at four specific aperture locations and averaged over each individual dosimeter to be utilised as a single UV measurement point that can be located on the model grid.

UV Exposure ratios

Levels of relative exposure for each SZA are calculated as:From eqn (1), E is the exposure ratio varying from 0 to 100 plotted on the model wireframe as a specific colour; ΔA is the recorded change in optical absorbency measured at 330 nm for any specific polysulfone dosimeter; and ΔA_Hor is the measured change in optical absorbency at 330 nm for a reference dosimeter placed on a horizontal plane. For the purpose of this research, the horizontal plane change in absorbency was averaged across three separate dosimeters placed on the manikin's rotating base. K is a constant used to represent the relative response of polysulfone to the erythemally weighted UV exposure⁸ and can be omitted when calculating exposures relative to a horizontal plane. The equation presented here eliminates the need to calibrate the erythemal response of individual dosimeters to obtain a polynomial calibration curve. The equation has been used previously to approximate erythemal exposure and exposure ratios on manikin headforms.^3,9

Contour interpolation

Fig. 3 depicts the facial exposure ratios for the respective SZA ranges produced from the measured changes in absorbency for dosimeters placed along a series of vertical contours. Environmental UV exposure ratios measured on the manikin headform ranging from 0–100 are represented on the model wireframe by specific colours. Fig. 4 depicts the individual dosimeter locations used to produce each of the exposure ratio sets of Fig. 3. Exposure ratio data were collected at the same location for each listed SZA range at the University of Southern Queensland Toowoomba campus (27.5° S 151.9° E). The location is removed from an urban environment and has consistently low aerosol concentrations. Results were collected on a grass surface and the recorded UV albedo for all SZA ranges did not exceed 5%. The respective ozone levels for each SZA range were recorded by the Total Ozone Mapping Spectrometer¹⁰ SZA 0°–30°: 264 DU; SZA 30°–50°: 284 DU; SZA 50°–80°: 260 DU. Data was collected under clear sky conditions, with the exception of SZA 0°–30° in which the cumulus cloud cover reached a maximum of 4 oktas.

Fig. 3 (a) Exposure ratio at SZA range 0°–30°, 18 February, 10:20–12:05. (b) Exposure ratio at SZA range 30°–50°, 16 September, 12:00–14:30. (c) Exposure ratio at SZA range 50°–80°, 27 May, 13:00–16:00.

Fig. 4 Dosimeter positions from left for SZA: 0°–30°; 30°–50°; 50°–80°.

The developed 3D exposure grid has two significant advantages over previous facial exposure models. Firstly, coloured exposures are indicative of actual data values. There are no blending errors created by mixing coloured data with a background image of the headform. Secondly, as the grid accommodates closer dosimeter positions, the grid intersections represent actual measured exposures at specific dosimeter locations, reducing errors due to interpolating exposure ratios between dosimeter measurement points.

Exposure ratios and assigned colour values for each contour in the wireframe are represented as linear interpolated averages within each 5 mm segment separating dosimeter grid locations. Segments of a horizontal or vertical contour between any adjoining dosimeter intersection points are coloured on the wireframe mesh depending on the interpolated recorded exposure ratios of both dosimeters in an adjacent pair. Segments between adjacent grid intersections, for both vertical and horizontal contours are divided into 5 colour levels.

Results

Fig. 5 illustrates the versatility and improvement in accuracy that can be achieved with future versions of the developed model when compared to previous models which have employed fewer dosimeters and linear interpolation techniques to represent large scale facial exposures. Fig. 5 provides example data which compare the predicted exposure along a horizontal contour connecting the ear, cheek and nose using only three measurement sites (Fig. 5(a)) compared to the same exposure contour calculated using 18 measurement sites (Fig. 5(b)). Note that the data provided for this contour comparison are intended for illustration purposes only and do not form part of the exposure data set used to produce the illustrations provided in Fig. 3. For clarity, Fig. 5 illustrates the change in colour along the contour underneath the 3D wireframe representation of the selected contour. Variations in the colour on this exposed contour clearly indicate that interpolation across varying facial topography is more accurate when a greater number of measurement locations are used. The comparison highlights the limitations of previous models which linearly interpolate exposures between widely spaced dosimeter sites.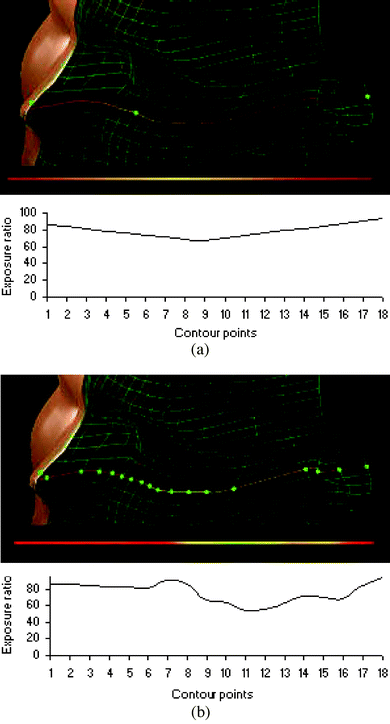

Fig. 5 (a) Linearly interpolated exposure ratio map interpolated from three dosimeter measurements at positions CN1, CN9 and CN18 for the same horizontal contour plotted in Fig. 5(b). (b) Exposure ratio map represented across 18 dosimeter sites along a single horizontal contour connecting the nose, cheek and ear.

By limiting the number of dosimeters used in creating a contour map, detail in the effective exposures along the contour can be lost if linear interpolation is used. Collection of further data along each horizontal and vertical contour used to create the entire facial wireframe is intended to be used with this model using the technique presented here to develop exposure profiles for each individual contour that match actual facial UV exposure distributions. The current computer model developed from this research allows accurate facial contour data to be collected under various conditions such that UV exposure profiles can be fitted to each contour which will allow measurement of exposures along contours that in the future utilise fewer dosimeters and simultaneously take into account variation in facial topography.

Fitting solutions to develop contour profiles

The modelled wireframe can be used to reduce the number of dosimeters required to plot an accurate facial exposure that takes into account facial topography. Fig. 6 represents a polynomial exposure profile fit to the horizontal contour extending from the ear through to the nose illustrated in Fig. 5(a). This exposure profile has been interpolated using a third order polynomial and was developed from 18 dosimeter exposures for a SZA in the range of 30° to 50° under clear sky conditions. Although a better fit to the data could be achieved with a higher order polynomial and could be used with the technique presented, a third order fit seems sufficient here for the purposes of illustration. Increasing the order of the polynomial fit to the data, while advantageous for this specific manikin headform may be unnecessary considering the detailed variation in individual facial topographies. Fig. 6 illustrates the benefit of using limited data collected at a later date within the same SZA range by fitting that data to the previously determined polynomial exposure profile, representing UV exposures based on facial topography rather than linear interpolation.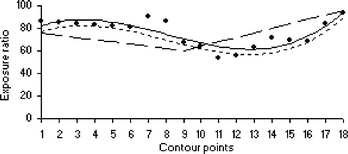

Fig. 6 Dot points—measured exposure ratios recorded along a single horizontal contour connecting the nose, cheek and ear. Solid line—third order polynomial fit exposure profile of the above data set. Small dashed line—example exposure profile developed from three dosimeter measurements utilising the previously measured exposure profile. Long dashed line—example linear interpolated exposure profile developed from the same three example dosimeter measurements.

As an example, three exposures recorded at a later date at contour points CN1, CN9 and CN18 have been averaged and compared with the same three points that form part of the original data set which was used to develop the polynomial exposure profile for the contour illustrated in Fig. 5(a). The difference between the three averaged dosimeter points of the original data set and the average of the three example dosimeter measurements determines an offset value which is used to displace the original polynomial profile, representing the predicted exposure along the entire contour. Using this technique, three dosimeter measurements can estimate the exposure along a single contour based on previously collected data. In Fig. 6, the original data set polynomial profile (solid line) includes exposure ratios of 86 recorded at intersection point CN1, 67 recorded at intersection point CN9 and 94 recorded at intersection point CN18. Continuing the example, later measurements performed using only three dosimeters record exposure ratios of 76 at CN1, 60 at CN9 and 96 at CN18 resulting in a difference of −5 when averaged across all three dosimeter locations and compared with the same exposure locations of the original contour profile data. The resulting exposure contour estimate is plotted in Fig. 6 (small dashed line), displaced by −5 exposure ratio units from the solid polynomial profile.

Table 1 compares the effectiveness of linear interpolation with the averaged polynomial fitting technique described above to represent the estimated exposure across the horizontal contour of Fig. 5(a) when utilising only three measurement points. The estimated exposures of both the linear interpolation and averaged polynomial fit were compared at each point in the original data set. The comparison shows clearly that the error expressed relative to each of the original 18 measured dosimeter locations is significantly less for the polynomial fitting technique. As is also evident in Fig. 6, more advanced curve fitting techniques could be applied to the method outlined here to further reduce the relative error of future exposure profile estimates.

Table 1 Relative error measured across the horizontal contour pictured in Fig. 5(a) comparing the third order polynomial fit and linear interpolation of three dosimeter measurements with the original data set

Measured contour exposure ratio data provided from the original data set	Polynomial fit of CN1, CN9 and CN18		Linear fit of CN1, CN9 and CN18
	Value	Relative error (%)	Value	Relative error (%)
86	81	−6	76	−12
85	80	−6	74	−13
84	79	−6	72	−14
83	78	−6	70	−16
82	77	−6	68	−17
81	76	−6	66	−19
91	86	−5	64	−30
86	81	−6	62	−28
67	62	−7	60	−10
64	59	−8	64	0
54	49	−9	68	26
56	51	−9	72	29
63	58	−8	76	21
72	67	−7	80	11
70	65	−7	84	20
68	63	−7	88	29
84	79	−6	92	10
94	89	−5	96	2

---

Exposure ratio plots

Full facial exposure ratio plots include exposure data that have been averaged across different regions of the face to complete the graphical models presented in Fig. 3. For reference, Tables 2, 3 and 4 list the x–y–z grid intersection exposure ratio percentage levels used to plot the facial exposure ratio maps for each of the SZA ranges. Data in these tables, listed from the first row to the last correspond with exposure levels located on the top of the manikin headform through to the neck. The exposure percentage level has been arranged so that corresponding horizontal contour levels can also be read across each table. Currently, data on the 709 intersection point grid is averaged using linear interpolation between both vertical and horizontal contours. Measured dosimeter exposure values calculated from eqn (1) are listed in bold font, each of the other data points, representing grid intersections, listed in the tables are interpolated data. Fig. 3(b) (SZA 30°–50°, Table 3) and Fig. 3(c) (SZA 50°–80°, Table 4), did not utilise dosimeters placed on the ear. For simplicity, vertical contours CN15, CN16, CN17 and CN18 in Table 3 and Table 4 repeat exposures recorded along the side of the head measured by vertical contour CN14. This simplification would seem to be a reasonable estimate given all vertical contours after CN14 are orientated in approximately the same facial plane. Due to measurement density, dosimeters were also positioned along every second point of each measured vertical contour used to produce the plots of Fig. 3. The plots presented in Fig. 3 therefore illustrate the estimated exposure ratio for each of the atmospheric conditions listed previously within each SZA range. Future work will extend the model to include exposure data for all contours under clear sky and higher cloud cases.

Table 2 Exposure ratio percentage for each of the vertical facial contours for the SZA range 0°–30° (bold exposures represent actual measurements)

CN1 nose	CN2	CN3	CN4	CN5	CN6	CN7 eye	CN8	CN9	CN10	CN11	CN12	CN13	CN14 side	CN15	CN16	CN17	CN18 ear
100	100	100	100	100	100
91	93	95	97	99	99	99	99
82	86	90	94	98	98	98	98	98	98
73	77	81	84	88	84	81	77	73	70	66
64	68	71	75	78	75	73	70	68	65	63	63
55	58	61	64	67	65	64	63	62	60	59	59	59
46	48	51	53	55	54	54	53	52	51	51	51	51	51
52	53	53	54	55	52	50	48	46	44	42	42	42	42
58	57	56	55	54	51	49	46	43	41	38	38	38	38	38
51	52	53	53	54	51	47	44	41	37	34	34	34	34	34
44	47	49	52	54	51	48	45	42	39	36	36	36	36	36
43	45	47	49	52	49	47	45	43	40	38	38	38	38	38	38
42	44	46	47	49	47	45	43	41	39	37	37	37	37	37	37
44	46	48	50	53	50	47	44	42	39	36	36	36	36	36	36
46	49	51	54	56	53	51	48	46	43	41	41	41	41	41	41
37	38	38	39	39	40	41	42	43	44	45	45	45	45	45	45
28	27	25	24	22	23	24	25	25	26	27	27	27	27	27	27
30	26	22	18	14	13	12	11	11	10	9	9	9	9	9	9
33	26	19	12	5	6	6	7	7	8	8	8	8	8	8	8
35	27	20	12	5	5	6	6	6	7	7	7	7	7	7	7
37	29	21	13	5	6	6	7	7	8	9	9	9	9	9	9
39	33	27	21	14	14	13	12	11	11	10	18	26	34	42	50	58
42	37	33	28	24	23	23	23	23	22	22	26	30	33	37	41	45
44	41	38	36	33	33	33	33	34	34	34	34	33	33	32	32	31	31
46	45	44	43	42	42	41	41	40	40	40	36	32	29	25	22	18	18
27	30	32	35	38	39	40	41	43	44	45	40	35	30	25	20	15	15
8	14	21	27	33	33	34	34	34	34	35	31	27	23	19	15	11	11
7	12	18	23	29	28	27	26	26	25	24	22	21	19	17	16	14	14
6	11	15	20	24	23	22	21	20	19	19	18	18	18	18	17	17
18	21	24	27	30	27	24	22	19	16	13	14	14	15	16	16	17
29	31	33	34	36	32	28	24	20	16	13	13	13	13	13	13
21	23	25	27	30	27	24	21	18	15	12	12	12	12	12	12
13	16	18	21	23	21	20	18	16	14	13	13	13	13	13	13
23	23	24	24	24	22	20	19	17	15	13	13	13	13	13
33	31	29	27	25	23	21	19	17	15	13	13	13
20	19	19	18	18	17	16	15	14	13	12	12	12
7	8	9	9	10	11	11	12	13	13	14	14	14
13	14	15	16	18	17	17	17	17	16	16	16
18	20	22	23	25	23	21	20	18	16	14	14
24	23	22	22	21	20	18	17	15	14	12	12
29	26	23	20	17	16	15	15	14	13	12	12
19	17	16	14	13	13	13	13	12	12	12	12
8	8	9	9	9	10	11	12	13	14	16	16
5	6	7	8	9	10	12	14	16	17	19	19
2	4	5	7	9	10	12	14	16	17	19	19
3	4	5	7	8	10	12	14	15	17	19	19
3	4	6	7	8	10	12	14	16	18	20	20
5	6	7	8	10	11	13	15	17	18	20	20
6	7	9	10	11	13	15	17	19	21	23	23
6	7	9	10	11	13	16	18	20	23	25	25

---

Table 3 Exposure ratio percentage for each of the vertical facial contours for the SZA range 30°–50° (bold exposures represent actual measurements)

CN1 nose	CN2	CN3	CN4	CN5	CN6	CN7 eye	CN8	CN9	CN10	CN11	CN12	CN13	CN14 side	CN15	CN16	CN17	CN18 ear
100	100	100	100	100	100
100	100	100	100	100	100	100	100
93	94	95	97	98	99	100	100	100	100
86	88	91	93	95	98	100	100	100	100	100
78	82	85	89	93	96	100	100	100	100	100	100
71	75	79	83	87	91	95	95	95	95	95	95	95
68	72	75	79	83	86	90	90	89	89	89	89	88	88
65	68	71	75	78	81	84	85	85	86	86	87	87	88
64	67	69	72	74	77	79	79	79	79	79	79	79	79	79
62	63	64	66	67	68	69	69	69	69	70	70	70	70	70
64	63	62	61	60	59	58	59	59	60	60	61	61	62	62
66	66	67	67	67	68	68	66	64	62	59	57	55	53	53	53
67	69	70	72	74	75	77	73	70	66	63	59	56	52	52	52
69	71	72	74	76	77	79	75	71	67	63	59	55	51	51	51
67	70	72	75	77	80	82	77	72	67	61	56	51	46	46	46
66	63	60	57	53	50	47	46	45	44	43	42	41	40	40	40
51	45	38	32	25	19	12	16	20	24	29	33	37	41	41	41
35	31	28	24	20	17	13	17	21	25	30	34	38	42	42	42
37	33	29	25	21	17	13	18	22	27	31	36	40	45	45	45
38	35	31	28	24	21	17	21	26	30	35	39	44	48	48	48
60	54	47	41	34	28	21	24	28	31	35	38	42	45	45	45
82	73	64	55	45	36	27	29	31	33	36	38	40	42	42	42	42
90	81	71	62	52	43	33	36	38	41	43	46	48	51	51	51	51
98	91	85	78	71	65	58	58	59	59	59	59	60	60	60	60	60	60
77	78	79	80	81	82	83	79	75	71	66	62	58	54	54	54	54	54
56	58	60	62	63	65	67	64	61	58	56	53	50	47	47	47	47	47
32	35	38	42	45	48	51	49	48	46	45	43	42	40	40	40	40	40
9	15	21	27	33	39	45	43	41	39	38	36	34	32	32	32	32	32
20	23	26	30	33	36	39	38	37	36	35	34	33	32	32	32	32
31	34	36	39	42	44	47	45	43	41	38	36	34	32	32	32	32
49	50	51	52	52	53	54	51	48	45	41	38	35	32	32	32
67	64	60	57	54	50	47	45	42	40	38	36	33	31	31	31
39	39	39	40	40	40	40	37	34	31	27	24	21	18	18	18
12	16	20	24	28	32	36	32	27	23	19	15	10	6	6
31	31	31	31	31	31	31	31	31	31	31	31	31
50	47	43	40	36	33	29	29	29	29	29	29	29
30	29	29	28	27	27	26	26	26	26	26	26	26
11	15	19	23	26	30	34	34	34	34	34	34
32	34	35	37	39	40	42	42	42	42	42	42
54	52	49	47	45	42	40	40	40	40	40	40
44	43	42	41	40	39	38	38	38	38	38	38
34	34	33	33	33	32	32	32	32	32	32	32
21	22	23	24	24	25	26	26	26	26	26	26
8	10	12	14	15	17	19	19	19	19	19	19
8	9	10	11	11	12	13	13	13	13	13	13
8	10	12	14	15	17	19	19	19	19	19	19
8	11	13	16	19	21	24	24	24	24	24	24
10	12	15	17	19	22	24	24	24	24	24	24
12	14	16	19	21	23	25	25	25	25	25	25
12	14	16	19	21	23	25	25	25	25	25	25

---

Table 4 Exposure ratio percentage for each of the vertical facial contours for the SZA range 50°–80° (bold exposures represent actual measurements)

CN1 nose	CN2	CN3	CN4	CN5	CN6	CN7 eye	CN8	CN9	CN10	CN11	CN12	CN13	CN14 side	CN15	CN16	CN17	CN18 ear
100	100	100	100	100	100
100	100	100	100	100	100	73	73
100	98	96	93	91	89	87	87	87	87
100	100	100	100	100	100	100	100	100	100	100
100	99	97	96	95	93	92	92	92	92	92	92
89	88	87	87	86	85	84	84	84	84	84	84	84
78	79	79	80	81	81	82	81	80	79	78	77	76	75
86	85	84	83	82	81	80	78	77	75	74	72	71	69
94	93	91	90	88	87	85	82	79	76	72	69	66	63	63
91	91	91	91	90	90	90	89	88	86	85	84	83	82	82
88	87	86	85	84	83	83	85	88	90	93	95	98	100	100
88	86	84	82	79	77	75	76	78	79	80	81	83	84	84	84
88	87	85	84	82	81	79	77	76	74	73	71	70	68	68	68
90	89	88	87	85	84	83	80	77	73	70	67	64	61	61	61
92	90	89	87	86	84	83	78	74	70	66	61	57	53	53	53
74	75	77	78	79	81	82	77	71	66	60	55	49	44	44	44
56	54	53	51	50	48	47	45	43	41	39	38	36	34	34	34
49	42	36	30	24	17	11	19	26	34	41	49	56	64	64	64
41	38	35	32	29	26	23	33	43	53	63	74	84	94	94	94
54	51	47	44	41	37	34	39	43	48	52	57	61	66	66	66
67	62	57	53	48	43	38	38	38	38	37	37	37	37	37	37
84	77	70	63	56	49	42	44	46	48	51	53	55	57	57	57	57
100	92	84	75	67	59	51	54	58	62	66	69	73	77	77	77	77
67	65	64	63	62	60	59	59	59	60	60	60	60	61	61	61	61	61
33	39	45	51	57	63	69	65	62	58	55	51	48	44	44	44	44	44
29	37	46	54	62	71	79	74	69	64	59	54	49	44	44	44	44	44
25	32	39	46	53	60	68	64	61	57	54	50	47	43	43	43	43	43
23	29	34	40	45	51	56	55	55	54	54	53	53	52	52	52	52	52
21	27	32	38	43	49	54	55	56	57	58	59	60	61	61	61	61
43	45	46	48	49	51	52	51	50	49	48	47	46	46	46	46	46
65	63	62	60	59	57	56	52	48	45	41	37	34	30	30	30
52	53	54	56	57	58	59	55	51	47	44	40	36	32	32	32
39	41	43	46	48	50	52	49	47	44	42	39	37	34	34	34
52	50	49	48	47	46	45	43	42	40	39	37	36	34	34
64	60	57	53	49	46	42	42	42	42	42	42	42
43	42	42	41	40	40	39	39	39	39	39	39	39
22	25	28	31	34	37	40	40	40	40	40	40	40
29	31	33	35	37	39	41	41	41	41	41	41
36	39	41	44	47	49	52	52	52	52	52	52
49	51	54	56	58	61	63	63	63	63	63	63
62	59	56	53	50	47	44	44	44	44	44	44
46	42	39	35	32	28	25	25	25	25	25	25
29	27	25	23	21	19	17	17	17	17	17	17
18	16	15	13	11	10	8	8	8	8	8	8
7	7	6	6	5	5	4	4	4	4	4	4
1	1	1	1	0	0	0	0	0	0	0	0
7	7	7	8	8	8	8	8	8	8	8	8
13	14	14	15	15	16	16	16	16	16	16	16
21	22	23	24	25	26	27	27	27	27	27	27
28	30	31	33	34	36	37	27	37	37	37	37

---

Erythemal headform exposure

Apart from the development of exposure ratio estimates and contour exposure profiles, the developed model provides a suitable framework onto which biologically effective exposures can be directly plotted. To demonstrate the versatility of the model wireframe, calibrated erythemal exposures have been plotted onto a 3D wireframe model of the entire headform, including the back of head and neck. Fig. 7 is a three dimensional visualisation of a 300 min exposure recorded at the same location used to produce the SZA exposure ratio plots of Fig. 3. The figure has been developed from 63 dosimeter exposures placed on the headform. Grid intersection points not directly measured have been linearly interpolated. For this exposure, cumulus cloud cover measured less than 2 oktas, the average surface albedo was recorded as 5% over the entire exposure interval. Stratospheric ozone concentration listed by the total ozone mapping spectrometer¹⁰ during the exposure interval was listed as 284 DU. For the figure, erythemal exposure is given in minimal erythemal dose (MED) where 1 MED corresponds to 200 J m⁻² of erythemally effective UV. The absolute change in optical absorbency of the miniaturised dosimeters measured at 330 nm was calibrated to a portable SUV meter, (model 3D, Solar Light Co. USA). The resulting calibration curve used to determine the MED of each dosimeter placed on the manikin headform is provided in Fig. 8. For comparison, the miniaturised dosimeter calibration curve is given with a calibration curve that utilises larger dosimeters. Fig. 8 indicates that the optical absorbency of the miniaturised dosimeters is slightly higher than the larger aperture dosimeters. The average increase in optical absorbency at 330 nm compared to the larger aperture dosimeters was measured as +0.014. This corresponds to a relative increase of 6% when compared to the highest change in absorbency recorded in the 300 min exposure interval.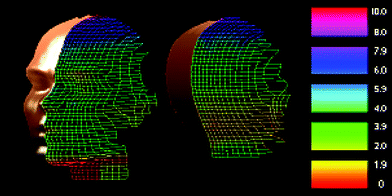

Fig. 7 Erythemal exposure (MED) recorded 7 July, 11:30–16:30.

Fig. 8 Dot points—the larger aperture dosimeter changes in optical absorbency at 330 nm. Cross points—6 mm aperture dosimeter changes in optical absorbency at 330 nm. Dashed line—erythemal exposure calibration curve fitted to 6 mm aperture dosimeter data.

Conclusions

The three dimensional UV exposure model developed from this research improves upon previous methods used to predict UV exposures using dosimeters and manikin headforms. The developed facial wireframe has reduced interpolation errors resulting from variation in facial topography. A technique for plotting UV exposures to a much higher resolution than has been achieved previously has been explained. Significantly, this research extends previous work by providing a model that takes physical topographic facial features and the resulting shading caused by those features into account.

Combinations of dosimeters can be placed in up to 709 frontal facial locations and an additional 576 rear headform locations using the model wireframe. The developed model can accommodate various biological action spectra and has demonstrated its effectiveness in producing accurate UV facial hot-spot maps. The results show a clear broadening in facial exposure with increasing SZA affecting the lower proximities of the face. Similar studies which take into account variation in the environment, surface albedo, head tilt angle and hats or eyewear worn by the manikin could be represented effectively using the developed 3D facial model. The development of biologically effective facial exposure maps using this model could be linked to the frequency and incidence of facial skin cancers. Additionally, an examination of ocular exposure utilising a higher density grid could be developed using the method described here provided dosimeter sizes can be reduced to provide the required accuracy.

As part of the method, a technique has been described for interpolating dosimeter exposures across individual contours. The technique, demonstrated for a single contour here could be applied to all contours in future versions of the model wireframe enabling accurate exposures to be determined with a much greater reduction in the total number of dosimeters required.

Acknowledgements

The authors would like to thank the technical staff at the University of Southern Queensland who have assisted with the development and maintenance of the equipment required for this research.

References

1. B. L. Diffey, Solar ultraviolet radiation effects on biological systems, Phys. Med. Biol., 1991, 36(3), 299–328.
2. WMO (World Meteorological Organization), Report of the WMO meeting of experts on UV-B measurements, data quality and standardization of UV indices, WMO/TD-NO 625, WMO, Les Diablerets, Switzerland, 25–28 July, 1994.
3. N. J. Downs, M. G. Kimlin, A. V. Parisi and J. J. McGrath, Modelling Human Facial UV Exposure, Radiat. Prot. Australas., 2001, 17(3), 103–109.
4. M. G. Kimlin, A. V. Parisi and J. C. F. Wong, The facial distribution of erythemal ultraviolet exposure in south east Queensland, Phys. Med. Biol., 1998, 43(2), 231–240.
5. P. Hoeppe, A. Oppenrieder, C. Erianto, P. Koepke, J. Reuder, M. Seefeldner and D. Nowak, Visualization of UV exposure of the human body based on data from a scanning UV-measuring system, Int. J. Biometeorol., 2004, 49, 18–25.
6. A. V. Parisi, L. R. Meldrum, J. C. F. Wong, J. Aitkin and R. A. Fleming, Lifetime erythemal ultraviolet exposure estimates for selected population groups in south east Queensland, Phys. Med. Biol., 1999, 44(12), 2947–2953.
7. A. V. Parisi, L. R. Meldrum and M. G. Kimlin, Polysulfone film thickness and its effects in ultraviolet radiation dosimetry, Protection Against the Hazards of UVR, Internet Conference, 18 Jan–5 Feb 1999.
8. CIE (International Commission on Illumination), A reference action spectrum for ultraviolet induced erythema in human skin, Comm. Int. Eclairage J., 1987, 6, 17–22.
9. D. K. Airey, J. C. F. Wong and R. A. Fleming, A comparison of human- and headform-based measurements of solar ultraviolet B dose, Photodermatol. Photoimmunol. Photomed., 1995, 11(4), 155–158.
10. Total Ozone Mapping Spectrometer, National Aeronautics and Space Administration, 2006, (viewed 5 August 2006: http://jwocky.gsfc.nasa.gov/).

---