A tautomeric equilibrium between functionalized 2-formylphenylboronic acids and corresponding 1,3-dihydro-1,3-dihydroxybenzo[c][2,1]oxaboroles

Abstract

Functionalized 2-formylphenylboronic acids undergo an unprecedented tautomeric rearrangement in solution to form corresponding 1,3-dihydro-1,3-dihydroxybenzo[c][2,1]oxaboroles. X-Ray analyses of selected examples revealed diverse solid-state molecular structures from a planar open form with a hydrogen-bonded carbonyl group (X = 3-F) through a twisted conformer showing a weak carbonyl–boron interaction (X = 3,5-Br₂) to a cyclic oxaborole derivative (X = 3-Br). Variable-temperature ¹H NMR spectroscopy was used to determine equilibrium constants as well as enthalpies and entropies of tautomerization in a mixed solvent [D₆]acetone–D₂O (95 : 5). A computational approach to the process by DFT (B3LYP) and MP2 methods has also been performed.

---

Introduction

Recently, arylboronic acids have been commonly used in organic synthesis, especially as coupling partners in synthesis of biaryls.¹ Furthermore, specific properties of the boronic group have become the basis for other applications. For instance, the formation of cyclic boronates from boronic acids and 1,2- and 1,3-diols² led to a development of various systems containing the arylboronic acid functionality which can act as fluorescent PET “on–off” monosaccharide receptors.³ Some of them have been synthesized using simple formylphenylboronic acids as precursors.^4,5 Another potentially promising but less recognized field is the use of boronic acids in supramolecular assembly due to hydrogen bonding interactions by B(OH)₂ groups.⁶ In contrast to numerous reports concerning the preparation and synthetic application of arylboronic acids their structure has been studied less extensively. Some ortho-functionalized arylboronic acids and esters tend to form boron heterocycles bearing a resemblance to naturally occurring purines.⁷ Accordingly, 1,3-dihydro-1-hydroxybenzo[c][2,1]oxaboroles can be regarded as half-esters of 2-(hydroxymethyl)phenylboronic acid or its derivatives. A few such heterocycles have been structurally characterized.⁸ Now we have found that related species can exist in tautomeric equilibrium with functionalized 2-formylphenylboronic acids. Hence, there is no need for water elimination as a driving force of a cyclization . This observation represents a new aspect of boronic acid chemistry.

Results and discussion

NMR evidence for a ring–chain tautomerism in 2-formylphenylboronic acids

Surprisingly, we have found that 3-fluoro-2-formylphenylboronic acid (1) reveals a specific behaviour in a [D₆]acetone solution as proved by the ¹H NMR analysis. D₂O (5 wt%) was added to avoid a potential competing equilibration with the corresponding anhydride. Furthermore, a peak assignment is facilitated due to the exchange of hydroxyl proton resonances. The ¹H NMR spectrum of 1 shows two sets of signals indicating the existence of two different structures (Fig. 1). The first one is the structure with separate formyl and B(OH)₂ groups as confirmed by the signal of the aldehyde proton at 10.33 ppm. The signal at 6.40 ppm of a comparable intensity points unequivocally to a quaternization of the aldehyde carbon. This can be rationalized assuming a cyclic structure of 1,3-dihydro-1,3-dihydroxy-4-fluorobenzo[c][2,1]oxaborole (1-II) to be formed to a significant extent as shown in Scheme 1. The structural difference between 1-I and 1-II is reflected by different multiplets in the aromatic region. Accordingly, co-existence of both tautomers can also be observed using ¹³C NMR spectroscopy, where a number of resonances is duplicated. Moreover, characteristic peaks at 189.6 and 96.1 ppm can be assigned to the formyl and hemiacetal carbons, respectively. We have synthesized a series of other functionalized 2-formylphenylboronic acids 2–8 to check if the observed process has a general character. In all cases ¹H NMR spectra of their solutions in [D₆]acetone exhibit resonances in the range 10.12–10.35 ppm (CHO) and 6.15–6.35 ppm (CHOH). Similarly, in ¹³C NMR spectra the existence of two tautomeric forms is manifested by two peaks in the range 190.9–195.6 ppm (CHO) and 96.4–98.8 ppm (CHOH). The acids 1–8 have also been characterized by ¹¹B NMR spectroscopy. The spectra show one signal in the range 28–32 ppm (h_1/2 = 200–250 Hz), which indicates that the formation of a cyclic tautomer has little effect on the boron chemical shift; a shoulder was observed only in the spectrum of 1. In most cases, broad boron resonances of both tautomers overlap with each other and hence cannot be observed separately.

Scheme 1 Tautomeric rearrangement of functionalized 2-formylphenylboronic acids.

Fig. 1 The ¹H NMR spectrum of 1 in [D₆]acetone–D₂O (95 : 5).

A chain–ring tautomeric equilibrium in 1–8 shows analogy with a formation of 3-hydroxyphthalide⁹ from 2-formylbenzoic acidisoelectronic with 2-formylphenylboronic acid (Scheme 2). Moreover, an ortho-CHO group greatly facilitates hydrolysis of N,N-dialkylbenzamides resulting in 3-hydroxyphthalide.¹⁰ A cyclic hemiacetal is formed from 2-(hydroxymethyl)benzaldehyde, too.¹¹ However, in both cases the equilibrium is shifted towards cyclic tautomers, whereas for a more efficient formation of an analogous boron heterocycle the presence of fluorine or other substituent in a 3-position is required.¹² It should be stressed that reactions leading to related 1,3-dihydro-1-hydroxybenzo[c][2,1]oxaboroles are intramolecular esterifications that can be assumed to be more entropy-favored due to elimination of water molecule.^13,14 Another pertinent example to be noted here is the behavior of another isoelectronic system, namely 2-nitrobenzaldehyde. This compound undergoes a facile photoisomerization to give 2-nitrosobenzoic acidvia intramolecular oxygen transfer from a nitro to a formyl group (Scheme 2).¹⁵ However, the mechanism of this reaction involving a formation of an analogous cyclic intermediate (or a transition state ) has not been proved.

Scheme 2

Solution equilibrium studies

We were interested in more precise information about a nature of tautomeric equilibrium in solution. Wet [D₆]acetone (containing 5 wt% D₂O) was used as a standard solvent. 1 has been chosen as a model compound as it shows an optimal ratio of tautomeric forms (i.e., close to 1). Initial kinetic experiments using ¹H NMR spectroscopy revealed that at room and higher temperatures equilibration 1-I ↔ 1-II is rapid on the macroscopic time scale: after a rapid (ca. 3 min) cooling from 321 to 293 K an integral ratio of hemiacetal vs. aldehyde protons (further denoted as K_obs) was equal within experimental error to the value obtained when the sample was kept for a longer time at 293 K. However, at 253 K a relaxation to the state of equilibrium is much slower and needs ca. 1 h to go to completion. Under these conditions K_obs increases to 1.8 reflecting a higher stability of 1-II at a lower temperature.

In addition, we have found that increasing total concentration of 1 decreases K_obs(293 K) values from the value of 1.09 for 0.02 M solution to 0.85 for 0.8 M solution; this effect was much weaker at higher temperature (321 K). Hence, this ratio cannot be simply taken as the thermodynamic equilibrium constant K_cycl of the tautomerization process. Supported by the results of X-ray analysis, we suggest that the dimerization of 1-I can also occur to a significant extent in solution at higher concentrations (Scheme 3). Assuming two competing equilibrium processes to proceed, estimation of the dimerization constant K_dim(293 K) yielded the value of 0.3.¹⁶ This corresponds to an association degree α of 10% for a 0.5 M solution. To eliminate concentration effects, K_cycl values have been estimated from the spectra of dilute solutions (0.02 M, D₂O : boronic acid ratio ≅150 : 1). Under these conditions, for 1α = 0.5% at 293 K, and hence K_cycl ≅ K_obs. Temperature dependence of ln K_cycl for compounds 1–3 and 5–8 is shown in Fig. 2. Further calculations show the tautomerization to be slightly exothermic with ΔH values falling in the range –8.0(3) to –17.7(4) kJ mol^–1. These results are summarized in Table 1.

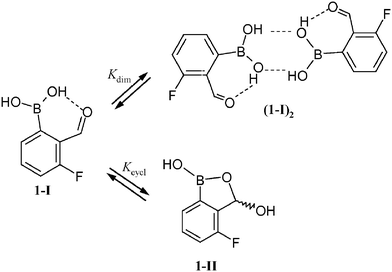Scheme 3 The competition between dimerization and cyclization of 1.

Fig. 2 Temperature dependence of the cyclization constant, K_cycl, in [D₆]acetone–D₂O (95 : 5), for functionalized 2-formylphenylboronic acids 1–3 and 5–8.

Table 1 Selected thermodynamic data for the tautomeric cyclization of functionalized 2-formylphenylboronic acids 1–8

Compd	Solvent^a	K cycl @303 K^b	ΔHcycl^c /kJ mol^–1	ΔScycl^c /J K^–1 mol^–1
a Contains 5 wt% D2O. b Measured at c = 0.02 mol dm^–3. c Assumed to be temperature-independent and estimated by least-squares method using linear van’t Hoff equation. d Measured at 298 K. e See ref. 17.
1	[D6]acetone	0.94	–10.7 ± 0.2	–36.0 ± 0.4
1	[D6]dmso	1.45^d	—	—
1	D2O	0.17	—	—
2	[D6]acetone	4.74	–12.5 ± 0.5	–28.3 ± 1.7
3	[D6]acetone	6.22	–13.7 ± 0.3	–30.0 ± 1.0
4	[D6]acetone	ca. 10^e	—	—
5	[D6]acetone	4.94	–12.0 ± 0.5	–26.4 ± 1.6
6	[D6]acetone	0.46	–8.7 ± 0.7	–35.4 ± 2.1
7	[D6]acetone	4.21	–17.7 ± 0.4	–46.5 ± 1.2
8	[D6]acetone	0.19	–8.0 ± 0.3	–40.1 ± 1.0

---

The tautomeric equilibrium in 1 was also investigated using other solvents. In [D₆]dmso–D₂O (95 : 5) a comparable behavior was observed with K_obs decreasing gradually from the value of 1.45 to 0.77 over a temperature range of 298–368 K. In contrast, with D₂O as a solvent the form 1-I is strongly preferred (K_obs = 0.19 at 293 K). This result points that the equilibrium can be significantly influenced by solvent effects. It should be noted that contrary to the behaviour in [D₆]acetone and [D₆]dmso the signals are broadened which suggests a quite rapid exchange between 1-I and 1-II on the ¹H NMR time-scale. This may suggest that water can be involved in the mechanism of the tautomerization .

As can be seen in Table 1 the equilibrium is substituent-dependent. Heavier halogen analogues 2–5 as well as 7 (X = 3-Me₃Si) show a stronger tendency to form corresponding oxaboroles in [D₆]acetone–D₂O than does 1. For the acid 4 bearing iodine in the 3-position we obtained the highest value of K_cycl = 10,¹⁷ which suggests unequivocally that a proximity of a bulky substituent plays a significant role. This view could be supported by the behavior of 4-bromo-2-formylphenylboronic acid8, which cyclizes to a lesser extent (K_cycl = 0.19 at 303 K). However, the situation observed for 5 and 6 illustrates that other changes may also be important. In the case of 5, the value of K_cycl is close to that found for the monobromo analogue 3. In the case of 6, the effect of the remote methoxy groups leads to the better stabilization of the open form (K_cycl = 0.46 at 303 K). The last example demonstrates clearly that in fact it is difficult to rationalize the equilibrium shift in terms of one predominant factor. The contribution from electronic effects is debatable as differences in thermodynamic data are small and cannot be meaningfully interpreted. We suppose that irrespective of specific steric interactions a varying (depending on substituents) stabilization by a solvent may be important for a delicate balance between both tautomeric forms.

X-Ray crystallographic study

We have undertaken X-ray diffraction analyses to check if the ring–chain tautomerism is revealed also in the solid state. In crystals of 1 obtained from acetone molecules exist in form I. The molecular structure of 1-I is shown in Fig. 3 and selected bond lengths and angles are given in Table 2.

Fig. 3 An ORTEP diagram of hydrogen bonded dimer of 1 with the atom numbering scheme. The atoms labelled with a prime (′) are at symmetry equivalent position (–x, –y, –z). Displacement ellipsoids are drawn at the 50% probability level.

Table 2 X-Ray and calculated gas-phase geometries (B3LYP/6-311+G**, in brackets selected values calculated by MP2/6-31+G* method) of open forms I of 1, 2, 5 and 2-formylphenylboronic acid (FPB)

	1-I (X-ray)	1-I (calc.)	2-I (calc.)	5-I (X-ray)	FPB (X-ray)^a	FPB (calc.)
Bond lengths (Å)
O(1)–B(1)	1.3440(19)	1.375	1.376	1.353(4)	1.351(3)	1.375
O(2)–B(1)	1.3494(19)	1.349	1.348	1.353(4)	1.358(2)	1.351
C(1)–B(1)	1.590(2)	1.599	1.604	1.598(4)	1.585(2)	1.594
O(3)–C(7)	1.2066(19)	1.221	1.221	1.208(4)	1.212(2)	1.219
C(1)–C(2)	1.4210(19)	1.429	1.432	1.401(4)	1.424(2)	1.425
X–C(3)	1.3556(17)^b	1.357^b	1.769^c	1.895(3)^d	—	—
X–C(5)	—	—	—	1.891(3)^d	—	—

---

Bond angles (°)
O(1)–B(1)–O(2)	118.62(14)	118.10	117.76	119.3(2)	118.94(18)	117.99
O(1)–B(1)–C(1)	115.86(13)	114.75	114.49	118.1(2)	116.24(14)	115.09
O(2)–B(1)–C(1)	125.50(13)	127.15	127.75	121.8(2)	124.82(13)	126.92
O(3)–C(7)–C(2)	127.51(14)	127.19	127.44	122.3(3)	128.14(15)	128.53
C(7)–C(2)–C(1)	126.25(13)	126.58	124.69	118.1(2)	126.70(15)	126.36
C(2)–C(1)–B(1)	128.03(12)	127.97	128.76	121.9(3)	128.14(15)	128.33

---

Torsion angles (°)
a Data taken from ref. 19. b X = F. c X = Cl. d X = Br.
C(2)–C(1)–B(1)–O(2)	–10.02(27)	0.06 [13.86]	–0.36 [–24.03]	83.58(2)	4.42(28)	–0.11 [–2.32]
C(1)–C(2)–C(7)–O(3)	2.84(29)	–0.14 [–16.59]	0.40 [34.09]	7.96(2)	–5.11(31)	–0.04 [4.21]

---

The entire molecule of 1-I is almost planar. The formyl group is essentially coplanar with the phenyl ring, while the B(OH)₂ group is slightly twisted (by 10.3(1)°) relative to the phenyl plane. One hydroxyl H atom [H(2)] is directed to the formyl group forming an intramolecular hydrogen bond while the other one [H(1)] is engaged in an intermolecular hydrogen bond. In consequence, adjacent monomeric moieties of 1 are connected by the pair of intermolecular O–H⋯O hydrogen bridges leading to the H-bonded centrosymmetric dimer with eight-membered ring (Fig. 3) typical of many boronic acids.¹⁸ Detailed hydrogen bonding geometries are given in Table 3. The intramolecular O–H⋯O interaction introduces some angular strain and causes significant deviation of selected endocyclic bond angles from ideal value for sp² hybridization [e.g., B(1)–C(1)–C(2) 128.03(12)°, C(1)–C(2)–C(7) 126.25(13)°]. A similar molecular structure was reported for the parent 2-formylphenylboronic acid.¹⁹ The compound 5 crystallizes as a monohydrate with centrosymmetric dimers of the form 5-I due to hydrogen-bonding interactions between dihydroxyboryl groups. The molecular structure of the dimer is shown in Fig. 4 and selected bond lengths and angles are given in Table 2.

Fig. 4 An ORTEP diagram of a hydrogen bonded dimer of 5 with the atom numbering scheme. The atoms labelled with a prime (′) are at symmetry equivalent position (–x, –y, –z). Displacement ellipsoids are drawn at the 50% probability level.

Table 3 Hydrogen bonding geometry (Å, °) for 1 and 5

	d(H⋯A)	d(D⋯A)	∠D–H⋯A
1
O(1)–H(1)⋯O(2)^#1	1.92(2)	2.7740(17)	175(3)
O(2)–H(2)⋯O(3)	1.70(3)	2.5801(18)	165(2)

---

5
a Symmetry transformations: ^#1 –x, –y, –z; ^#2 –1 + x, y, z; ^#3 1 – x, 1 – y, –z; ^#4 1 – x, 1 – y, 1 – z.
O(1)–H(1)⋯O(2)^#1	1.93	2.744(3)	175
O(2)–H(2)⋯O(4)^#2	1.85	2.652(4)	167
O(4)–(4A)⋯O(3)^#3	2.01(5)	2.865(3)	161(5)
O(4)–H(4B)⋯O(1)	2.02(6)	2.800(4)	176(5)
C(4)–H(4)⋯O(4)^#4	2.40	3.324(4)	172

---

Contrary to 1, the B(OH)₂ group is oriented almost perpendicularly to the phenyl ring and the dihedral angle between least-squares planes of both moieties is 79.37(14)°. The angle C(1)–C(2)–C(7) of 118.1(2)° is much smaller than that in 1 which supports the view that the buttressing effect²⁰ of bromine impacts destabilization of a planar structure and twisting of the B(OH)₂ group. An important feature of 5 is a weak oxygen–boron interaction as indicated both by short C=O⋯B contact [2.561(4) Å] and significant displacement of boron atom from the plane defined by C(1), O(1), O(2) atoms [0.069(3) Å] towards the carbonyl oxygen. In a related 2-acetylphenylboronic acid twisting of the B(OH)₂ group with respect to the aromatic ring (77.4°) allowed for a comparable C=O⋯B contact of 2.49 Ų¹ with simultaneous perching of boron from the basal CO₂ plane (0.078 Å). It should be noticed, that a much stronger B⋯O intramolecular coordination has been found, for instance in amide ortho-functionalized catecholborates 2-(R₂NCO)ArB(1,2-O₂C₆H₄), Ar = Ph, 3-MeC₆H₄, R = Et, iPr.²² Strikingly, such interaction was not observed in a closely related pinacol ester 2-(iPr₂NCO)PhB(1,2-O₂C₂Me₄).²³

Molecules of water interact with B(OH)₂ groups both as a hydrogen acceptor and donor. Consequently, twelve-membered H-bonded rings with an extended-chair conformation are constructed. Adjacent dimeric moieties of 5 linked together through water-bridges form infinite chains along the crystallographic a-axis (Fig. 5(a)). Chains are then cross-linked into wave-layers parallel to the (001) plane by C=O⋯H–OH bonds formed between water molecules and carbonyl O atoms. Phenyl rings are almost perpendicular to the layer. Such an arrangement allows the p-CH groups and oxygen atoms of water from adjacent layers to form weaker C–H⋯O interlayer bonds (Fig. 5(b)). Compound 5 thus adopts an interesting hydrogen-bonded 3D network structure in which water molecules serve as the tetrahedral connectors assembled with dimeric boronic acid units.

Fig. 5 (a) A view of the H-bonded layer structure of 5. The dashed lines represent O–H⋯O hydrogen bonds. (b) Side view of the layer along a axis showing interlayer C–H⋯O connections (dotted lines). Hydrogen atoms are omitted excluding those involved in H-bond formation.

A very similar compound, 3, crystallizes also as a stable monohydrate, but contrary to 5, involves cyclic forms 3-II. Nevertheless, the analysis proved difficult due to substantial disorder observed in all measured crystals. The best approximation of the structure was obtained during the solution and refinement in the Cc space group. There are four independent molecules per asymmetric unit as two pairs of S and R stereoisomers. The geometry of the molecules is almost the same. The molecular structure of one of them is presented in Fig. 6. The molecule of 3-II is comprised of two almost planar fused rings, similar to other benzoxaborole derivatives.⁸ The sum of the valence angles around the B(1) center of 360° for all molecules shows the typical sp² hybridization. The mean values of C(1)–B(1), B(1)–O(1), B(1)–O(2) and C(7)–O(2) bond lengths are equal to 1.55, 1.35, 1.37 and 1.45 Å, respectively, and fall in ranges observed for the aforementioned structures.

Fig. 6 An ORTEP diagram of the molecular structure of 3 with the atom numbering scheme. Displacement ellipsoids are drawn for oxygen and bromine atoms at the 50% probability level.

We detected that the crystal structure contains layers of molecules connected via hydrogen bonded water molecules (Fig. 7). The adjacent layers are related by a c-glide plane. All of them are parallel to the (001) plane. The symmetry of a layer can be described by the 2-periodic layer-group symmetry p2₁/b11 with the non-periodic direction being parallel to c. The new a_L and b_L basis vectors of a layer are consistent with the vectors of the reduced primitive cell (a_L = b_L = 7.185 Å, γ_L ≈ 90°). The layer symmetry is broken through the stacking of the layers (it is a possible explanation for Z′ = 4). A layer can occupy either of two different positions (related by translation by 0.5a or 0.5b vector), which are almost equivalent with respect to the nearest layer. Thus, the disorder arises through stacking faults and could be analyzed by an order–disorder theory using local symmetry operations. The final refinement converged to R₁ = 0.0593 but the resultant geometry parameters show relatively high esds, thus the further presentation of the detailed geometry analysis is not justified. Nonetheless, the topology of the double-layer is interesting. Molecules of water interact with both B(OH) and C(OH) hydroxy groups and form four-connected, almost tetrahedral nodes of a resulting H-bonded 2D-network. The O⋯O contacts vary from 2.65 to 2.77 Å and from 2.77 to 2.83 Å for BO⋯O and CO⋯O interactions, respectively. The H-bonded net consists of fused rings formed by eight hydrogen bridges and connected together through water molecules. Hence, taking into account only water molecules, the resulting 2D-net can be reduced to a simple 4-connected uninodal 4⁴6² net.

Fig. 7 (a) A view of the H-bonded double-layer structure of 3·H₂O. (b) Side view of the double-layer along the [11̄0] direction. The dashed lines represent O⋯O contacts. Hydrogen atoms are omitted for clarity.

In addition to X-ray structural studies we have employed IR spectroscopy to determine the basic structure of compounds 1–3 and 5–8 in the solid state using a characteristic band of C=O group absorption as a probe. For compounds 1, 5, 6 and 8 strong bands are observed in the range 1647–1684 cm^–1, confirming the stability of corresponding open forms I in the solid state. These values are significantly lower when compared to the standard wavenumbers of C=O group bands for simple benzaldehydes. This can be explained primarily by intra- and/or intermolecular hydrogen-bonding interactions decreasing the C=O bond order. For the remaining compounds 2, 3 and 7, IR spectra exhibit only weak bands in the range 1670–1680 cm^–1, thus providing an evidence of stability of corresponding cyclic structures of type II.

Theoretical calculations

Results of calculations of 2-formylphenylboronic acid and its halogenated analogues 1 and 2 under gas-phase conditions gain an extended insight into the nature of the observed tautomerism . We have found equilibrium geometries for open I, cyclic II and open twisted forms of the aforementioned boronic acids (Table 2, for full data set see ESI‡ ). The energies were obtained by geometry optimization at all theoretical levels, followed by the calculation of the vibrational frequencies at the same level (no imaginary frequency). This allowed correction for zero-point energies (ZPE) and conversion of the calculated energies to 298 K.

An approximately planar conformation of the open tautomeric form I with an intramolecular hydrogen bond between B(OH)₂ and CHO groups was predicted as the most stable, i.e., as a global minimum, irrespective of the calculation method (with ZPE correction included). The MP2 relative electronic energies (without ZPE correction) for compound 2-II are in the range –1.16 to 2.49 kJ (Table 4, for 6-31+G* and 6-31G* basis sets, respectively), which suggests comparable stabilities of forms I and II. In addition, in the case of 2-I, MP2 calculations point to twisting of the B(OH)₂ group, from ca. 10° (aug-cc-pVDZ basis set) to 24° (the others), and the CHO one to the phenyl ring.

Table 4 The calculated relative energies of tautomeric forms I and II

		ΔE/kJ mol^–1
Compound	Form	MP2 aug-cc-pVDZ	MP2 6-31+G*	MP2 6-31G*	B3LYP 6-311+G**
	I (planar)	0.00	0.00	0.00	0.00
	II	15.99	12.74	16.41	26.89
	I (twisted)	19.09	14.74	18.93	23.29
	I (planar)	0.00	0.00	0.00	0.00
	II	11.05	9.90	15.41	23.16
	I (twisted)	15.16	11.30	16.18	19.64
	I (planar)	0.00	0.00	0.00	0.00
	II	1.37	–1.16	2.49	12.23
	I (twisted)	8.65	7.16	9.00	13.05

---

The B3LYP calculated geometries of planar forms I are in better agreement than MP2 ones with those yielded by X-ray analyses (Table 2). A significant elongation (ca. 0.03 Å) of one of B–O bonds in the gas phase structures is due to the lack of hydrogen-bonding interactions by an adjacent O–H group; for analogy, in the case of hydrogen-bonded p-nitrophenol complexes with bases, lengthening of a C–O bond indicates a weaker hydrogen-bond.²⁴

Relative electronic energies were calculated vs. the torsion angle O(1)–B(1)–C(1)–C(2) at B3LYP/6-311+G** (Fig. 8) and MP2/6-31G* (see ESI‡ ) levels of theory: obtained curves are qualitatively almost identical. However, the MP2 curve runs below the B3LYP one, which is in accord to results found for single-bond torsional potentials in other conjugated systems.²⁵ For perpendicularly twisted conformations of the form I local minima are observed (Fig. 8) with relative electronic energies dependent on the calculation method (Table 4) in the range 15–23, 11–20 and 7–13 kJ mol^–1 for 2-formylphenylboronic acid, 1 and 2, respectively. Including ZPE correction, relative energies of I (twisted form) decrease and fall in the range 12–20, 8–16 and 3–10 kJ mol^–1, respectively. These minima could be rationalized in terms of a weak boron–carbonyl interaction being plausible for such geometry due to a partial overlap of a 2p orbital of the boron and a lone pair of the carbonyl oxygen atom. However, it should be noted that there is only a slight deviation of the boron atom from planar sp² hybridisation. Alternatively, the small energy gain could be rationalized in terms of weak electrostatic attractive forces.

Fig. 8 Dependence of calculated (B3LYP/6-311+G**) relative energy, kJ mol^–1, of open forms I on a O(1)BC(1)C(2) torsion angle in 2-formylphenylboronic acid and its analogues 1 and 2.

Calculated relative energies of cyclic forms II without and with ZPE correction fall in the range 13–27, 10–23, –1 to 12 (Table 4) and 18–31, 14–27, 3–17 kJ mol^–1 for 2-formylphenylboronic acid, 1 and 2, respectively. The stability order of I (twisted) and II forms changes when including ZPE correction: electronic energies are in favour of form II, whereas with a ZPE correction twisted form of I is predicted to be more stable. To point out some exceptions, B3LYP electronic energy results for 2-formylphenylboronic acid and 1 predict open twisted forms as more stable than cyclic tautomers whereas MP2/6-31+G* (with ZPE) calculation of 2 suggests a cyclic form II as more stable. All computational methods predict relative energies of I (twisted) and II forms to be decreased upon increasing van der Waals radius of a halogen in a 3-position of the phenyl ring.

To summarize this point, the effect of a halogen increasing the relative stability of a twisted form I and a cyclic form II and the much stronger tendency of 2 to form a cyclic tautomer has been predicted, in agreement with experimental observations. Hence, it seems that gas-phase ab initio calculations are useful for prediction of substituent effects. We suppose that an appropriate solvent plays a significant role in a stabilization of a cyclic form II. However, it is clear that for a more precise information (e.g., estimation of K_cycl) other effects (especially specific hydrogen-bonding interactions with a polar solvent ) must be rigorously taken into account.

Conclusions

It has been demonstrated that substituted 2-formylphenylboronic acids exhibit remarkable structural diversity manifested especially by a chain–ring tautomerism . Such a behavior in solution is easily monitored by ¹H and ¹³C NMR spectroscopy and predictable by theoretical calculation. This is important from the viewpoint of theoretical interest as well as in practical terms of boronic acid analysis and purity determination. Moreover, we believe that reported here and future structural investigations of arylboronic acids will result in novel applications, especially in the field of supramolecular chemistry.

Experimental

General comments

All reactions were carried out under an argon atmosphere. Solvents were stored over sodium wire before use. Butyllithium (10 M solution in hexanes), triethyl borate (99%), anhydrous trimethyl orthoformate (99.8%), anhydrous N,N-dimethylformamide (99.8%) and chlorotrimethylsilane (99%) were used as received. All bromobenzaldehydes or their acetals were prepared according to the literature procedures. ¹H and ¹³C NMR chemical shifts are given relative to TMS using residual solvent resonances. ¹¹B NMR chemical shifts are given relative to Et₂O·BF₃. Due to a varying proportions of tautomers, numbers of nuclei obtained by integration of ¹H NMR resonances in spectra of arylboronic acids (e.g., 1 H), are not given. Accordingly, for a necessary view, ¹H and ¹³C NMR spectra are provided in the ESI.‡

Syntheses

1-Bromo-3-chloro-2-(dimethoxymethyl)benzene . To a mixture of 2-bromo-6-chlorobenzaldehyde (9.6 g, 50 mmol) (prepared in 75% yield using the known procedure²⁶ from 2-bromo-6-chlorobenzene), trimethyl orthoformate (6.4 g, 60 mmol) and methanol (10 mL) a drop of conc. H₂SO₄ was added. The mixture was heated for 1 h at reflux and neutralized with sodium methoxide. Volatiles were removed under reduced pressure and the residue was distilled in vacuo to give the title compound (12.9 g, 97%), bp 95–100 °C (ca. 1 Torr) as a colorless oil (Found: C, 40.6; H, 3.8. Calc. for C₉H₁₀BrClO₂: C, 40.7; H, 3.8%); δ_H (CDCl₃; 400 MHz; Me₄Si) 7.51 (1 H, dd, J 8.0 and 1.0, Ph), 7.35 (1 H, dd, J 8.0 and 1.0, Ph), 7.09 (1 H t, J 8.0, Ph), 5.84 (1 H, s, CH(OMe)₂) and 3.48 (6 H, s, CH(OMe)₂); δ_C (CDCl₃; 100.6 MHz; Me₄Si) 134.9, 133.8, 132.5, 130.2, 130.1, 123.8, 105.5 and 55.8.

1,3-Dibromo-2-(dimethoxymethyl)benzene . A similar protection was performed with 2,6-dibromobenzaldehyde²⁶ (26.4 g, 0.10 mol), to give the title compound (30.5 g, 98%), bp 110–113 °C (ca. 1 Torr) as a colorless oil (Found: C, 34.8; H, 3.2. Calc. for C₉H₁₀Br₂O₂: C, 34.9; H, 3.25%); δ_H (CDCl₃; 400 MHz; Me₄Si) 7.56 (2 H; d, J 8.0, Ph), 7.01 (1 H, t, J 8.0, Ph), 5.83 (1 H, s, CH(OMe)₂) and 3.48 (6 H, s, CH(OMe)₂); δ_C (CDCl₃; 100.6 MHz; Me₄Si) 134.9, 133.4, 130.5, 123.8, 106.7 and 55.7.

3-Fluoro-2-formylphenylboronic acid 1 . This compound was received from Aldrich. Crystals suitable for X-ray analysis were grown from water–acetone solution by slow evaporation of the solvent, mp 127–129 °C (Found: C, 50.1; H, 3.65. Calc. for C₇H₆BFO₃: C, 50.1; H, 3.6%); ν_max(KBr)/cm^–1 3332, 3080, 1676, 1560, 1352, 1236 and 796; δ_H [(CD₃)₂CO–D₂O, 95 : 5; 400 MHz; Me₄Si] 10.33 (d, J 1.0), 7.64 (td, J 8.0 and 5.0), 7.51 (d, J 7.5), 7.43 (td, J 8.0 and 4.5), 7.39 (d, J 8.0) 7.21 (ddd, J 11.0, 8.0 and 1.0), 7.16 (ddd, J 10.0, 8.0 and 1.0), and 6.43 ppm (s); δ_B [(CD₃)₂CO–D₂O, 95 : 5; 128.3 MHz, BF₃·Et₂O] 28; δ_C [(CD₃)₂CO–D₂O, 95 : 5; 100.6 MHz; Me₄Si] 189.6 (d, J 7.5), 165.2 (d, J 256), 158.8 (d, J 251), 140.8 (d, J 13.0), 136.5 (d, J 9.0), 132.1 (d, J 6.0), 129.2 (d, J 4.0), 127.4 (d, J 6.0), 126.8 (d, J 4.0), 118.5 (d, J 20.0) and 116.6 (d, J 20.5), 96.1.

3-Chloro-2-formylphenylboronic acid 2 . A solution of 1-bromo-3-chloro-2-(dimethoxymethyl)benzene (5.31 g, 20 mmol) in diethyl ether (10 mL) was added to a solution of BuLi (20 mmol) in diethyl ether (20 mL) at –78 °C. After 15 min stirring B(OEt)₃ (3.2 g, 22 mmol) was added at –78 °C. The mixture was stirred for 30 min, then it was allowed to warm to ca. –50 °C followed by hydrolysis with 2 M aq. HCl. The organic layer was separated followed by evaporation of the solvent under reduced pressure. To an oily residue water (20 mL) and a drop of conc. aq. HCl were added. The mixture was heated shortly to ca. 70 °C to cleave the acetal moiety followed by removal of methanolin vacuo. The crude solid product was filtered off and washed with water (3 × 5 mL) and toluene (2 × 5 mL) to give 2·H₂O (3.03 g, 75%) as colorless crystals, mp 84–88 °C (Found: C, 41.9; H, 4.1. Calc. for C₇H₆BClO₃·H₂O: C, 41.55; H, 4.0%); ν_max(KBr)/cm^–1 3364, 3212, 3068, 1404, 1220 and 1080; δ_H [(CD₃)₂CO–D₂O, 95 : 5; 400 MHz; Me₄Si] 10.40 (d, J 0.5 Hz), 7.64 (dd, J 7.5 and 1.0), 7.56 (m), 7.45–7.36 (m) and 6.30 (s); δ_B [(CD₃)₂CO–D₂O, 95 : 5; 128.3 MHz; BF₃·Et₂O] 31; δ_C [(CD₃)₂CO–D₂O, 95 : 5; 100.6 MHz; Me₄Si] 190.9, 150.9, 136.4, 134.7, 134.4, 131.4, 130.5, 130.4, 129.6, 129.1, 128.5 and 96.4.

3-Bromo-2-formylphenylboronic acid 3 . This compound was obtained as described for 2 from 1,3-dibromo-2-(dimethoxymethyl)benzene (6.20 g, 20 mmol) as colorless crystals of the monohydrate 3·H₂O (4.00 g, 81%), mp 98–101 °C (Found: C, 34.2; H, 3.3. Calc. for C₇H₆BBrO₃·H₂O: C, 34.1; H, 3.3%); ν_max(KBr)/cm^–1 3348, 3208, 3076, 1400, 1216 and 1076; δ_H [(CD₃)₂CO–D₂O, 95 : 5; 400 MHz; Me₄Si] 10.29 (s), 7.67 (dd, J 7.5 and 1.0), 7.63–7.60 (m), 7.49–7.46 (m), 7.30 (t, J 7.5) and 6.21 (s); δ_B[(CD₃)₂CO–D₂O, 95 : 5; 128.3 MHz; BF₃·Et₂O] 31; δ_C [(CD₃)₂CO–D₂O, 95 : 5; 100.6 MHz; Me₄Si] 193.5, 153.4, 136.4, 135.1, 133.5, 131.5, 131.2, 129.9, 129.7, 126.2, 118.2 and 98.0 ppm.

3-Iodo-2-formylphenylboronic acid 4 . The solution of 1,3-dibromo-2-(dimethoxymethyl)benzene (6.20 g, 20 mmol) in diethyl ether (10 mL) was added to the solution of BuLi (20 mmol) in diethyl ether (20 mL) at –78 °C. After 15 min stirring the solution of B(OEt)₃ (3.2 g, 22 mmol) was added at –78 °C. The mixture was stirred for 30 min, then it was carefully hydrolyzed with 2 M aq. HCl (0 °C, pH = 6–7). The organic phase was separated and solvents were removed in vacuo. A solution of N-butyldiethanolamine (3.22 g, 20 mmol) in Et₂O (20 mL) was added to the residue and the mixture was stirred for 1 h at rt. Solvents were removed in vacuo and the residue was redissolved in THF–Et₂O (1 : 1, 30 mL) and cooled to –78 °C followed by addition of BuLi (2 M, 10 mL) and iodine (3.2 g, 22 mmol) in THF (10 mL). After hydrolysis with 2 M aq. HCl, the organic phase was concentrated. The residue was redissolved in Et₂O (30 mL) and washed with water (20 mL) and aq. Na₂S₂O₃ (10 wt%, 20 mL). Subsequent workup was performed as described for 2, to give 4 as a crystalline material (1.75 g), containing ca. 25% of 3, δ_H [(CD₃)₂CO–D₂O, 95 : 5; 400 MHz; Me₄Si] 10.05 (s), 7.95 (dd, J 8.0 and 1.0), 7.88 (dd, J 8.0 and 1.0), 7.71 (dd, J 8.0 and 1.0), 7.31 (t, J 7.5), 7.15 (t, J 7.5), 6.06 (s).

3,5-Dibromo-2-formylphenylboronic acid 5 . The formyl group of 2,4,6-tribromobenzaldehyde²⁶ (3.10 g, 9 mmol) was protected using the method described for 1-bromo-3-chloro-2-(dimethoxymethyl)benzene, to give crude 1,3,5-tribromo-2-(dimethoxymethyl)benzene (3.10 g, 8.0 mmol). This compound was consecutively treated with BuLi and B(OEt)₃ as described for 2, to give 5·H₂O as colorless crystals (1.80 g, 70%), mp 224–227 °C (Found: C, 25.9; H, 2.35. Calc. for C₇H₅BBr₂O₃·H₂O: C, 25.8; H, 2.2%). ν_max(KBr)/cm^–1 3398, 3252, 3079, 1666, 1532, 1383, 1342 and 860; δ_H [(CD₃)₂CO–D₂O, 95 : 5; 400 MHz; Me₄Si] 10.24 (s), 7.87 (d, J 1.5), 7.83 (d, J 1.5), 7.80 (d, J 1.5 Hz), 7.60 (d, J 1.5) and 6.19 (s); δ_B [(CD₃)₂CO–D₂O, 95 : 5; 128.3 MHz; BF₃·Et₂O] 31; δ_C [(CD₃)₂CO–D₂O, 95 : 5; 100.6 MHz; Me₄Si] 192.9, 152.9, 137.2, 135.8, 134.7, 132.8, 129.2, 127.0, 123.9, 119.4 and 98.1.

3-Bromo-2-formyl-5-methoxyphenylboronic acid 6 . The formyl group of 2,6-dibromo-4-methoxybenzaldehyde²⁷ (2.94 g, 10 mmol) was protected using the method described for 1-bromo-3-chloro-2-(dimethoxymethyl)benzene, to give crude 1,3-dibromo-2-(dimethoxymethyl)-5-methoxybenzene (2.95 g, 8.5 mmol). This compound was consecutively treated with BuLi and B(OEt)₃ as described for 2, to give 6·H₂O as colourless crystals (1.75 g, 78%), mp 145–148 °C (Found: C, 35.1; H, 3.6. Calc. for C₈H₈BBrO₄·H₂O: C, 34.7; H, 3.65%); ν_max(KBr)/cm^–1 3414, 3262, 3085, 2987, 1647, 1592, 1540, 1348, 1263 and 809; δ_H [(CD₃)₂CO–D₂O, 95 : 5; 400 MHz; Me₄Si] 10.12 (d, J 1.0), 7.21 (d, J 2.0), 7.16 (m), 6.97 (dd, J 2.5 and 1.0), 6.15 (s), 3.90 (s) and 3.82 (s); δ_B [(CD₃)₂CO–D₂O, 95 : 5; 128.3 MHz; BF₃·Et₂O] 30; δ_C [(CD₃)₂CO–D₂O, 95 : 5; 100.6 MHz; Me₄Si] 192.1, 164.7, 161.9, 145.9, 129.8, 128.6, 121.6, 118.6, 118.4, 117.6, 114.2, 98.1, 56.4 and 56.1.

2-Formyl-3-(trimethylsilyl)phenylboronic acid 7 . A solution of 1,3-dibromo-2-(dimethoxymethyl)benzene (6.20 g, 20 mmol) in diethyl ether (10 mL) was added to the solution of BuLi (20 mmol) in diethyl ether (20 mL) at –78 °C. After 15 min stirring the solution of TMSCl (2.40 g, 22 mmol) in THF (10 mL) was added at –78 °C. The mixture was stirred for 30 min, then it was allowed to warm to rt. Solvents were removed in vacuo. The residue was redissolved in THF–Et₂O (1 : 1, 30 mL) and cooled to –78 °C followed by addition of BuLi (2 M, 10 mL) and B(OEt)₃ (3.2 g, 22 mmol). Subsequent workup was performed as described for 2, to give 7 as colorless crystals (4.00 g, 81%), mp 72–75 °C (Found: C, 54.0; H, 6.8. Calc. for C₁₀H₁₅BSiO₃: C, 54.1; H, 6.8%); ν_max(KBr)/cm^–1 3544, 3464, 3296, 2925, 1584, 1444, 1248, 956 and 840; δ_H [(CD₃)₂CO–D₂O, 95 : 5; 400 MHz; Me₄Si] 10.35 (s), 7.68 (dd, J 7.5 and 1.0), 7.65 (d, J 7.5), 7.59 (dd, J 7.5 and 1.0), 7.52 (t, J 7.5), 7.30 (t, J 7.5), 6.32 (s), 0.33 (s) and 0.32 ppm (s); δ_B [(CD₃)₂CO–D₂O, 95 : 5; 128.3 MHz; BF₃·Et₂O] 32; δ_C [(CD₃)₂CO–D₂O, 95 : 5; 100.6 MHz; Me₄Si] 195.6, 160.7, 144.9, 142.2, 137.7, 136.1, 135.2, 134.5, 132.4, 131.5, 128.4, 98.8, 0.5 and –0.3.

4-Bromo-2-formylphenylboronic acid 8 . This compound was obtained as described for 2 from 1,4-dibromo-2-(dimethoxymethyl)benzene²⁸ (3.10 g, 10 mmol) as colorless crystals (1.85 g, 79%), mp 128–131 °C (Found: C, 36.6; H, 2.8. Calc. for C₇H₆BBrO₃: C, 36.7; H, 2.6%); ν_max(KBr)/cm^–1 3374, 3218, 3079, 1684, 1532, 1338, 1189, 1090, 1342 and 724; δ_H [(CD₃)₂CO–D₂O, 95 : 5; 400 MHz; Me₄Si] 10.26 (s), 8.03 (d, J 2.0), 7.79 (dd, J 8.0 and 2.0), 7.74 (d, t, J 8.0), 7.62 (m), 7.55 (dd, J 8.0 and 2.0) and 6.24 (s); δ_B [(CD₃)₂CO–D₂O, 95 : 5; 128.3 MHz; BF₃·Et₂O] 28; δ_C [(CD₃)₂CO–D₂O, 95 : 5; 100.6 MHz; Me₄Si] 194.3, 158.0, 142.8, 137.1, 136.4, 133.1, 132.6, 132.4, 126.8, 126.0, 124.2 and 97.8.

Solution equilibrium studies

Samples for ¹H NMR analyses were taken as dilute (0.02 M) solutions of compounds 1–3 and 5–8 in wet [D₆]acetone (5 wt% D₂O). Prior to the acquisition, samples were thermostated for a time sufficient to allow the equilibrium to be reached (ca. 10 min). Spectra were recorded at four temperatures in the range 298–321 K. Chemical shifts were determined using internal solvent resonances and given relative to TMS. ΔH and ΔS values were calculated using a linear van’t Hoff plot, ln K_cycl = f(1/T). A summary of results is presented in Table 1.

X-Ray diffraction

Details including crystal data, data collection and refinement parameters are provided in Table 5. X-ray diffraction data for single crystals of 1, 3 and 5 were collected at room temperature on a Siemens P3 diffractometer with graphite-monochromated Mo-Kα radiation. The measured intensities were processed with the Lorentz and polarization effects. Numerical absorption correction based on a well-defined crystal shape was performed for compound 5. The structures were solved by direct methods using the SHELXS-97 program,²⁹ and refined by the full-matrix least-squares method against F² (SHELXL-97).³⁰ In both cases all non-hydrogen atoms were anisotropically refined. All hydrogen atoms in 5 and water hydrogens in 1 were located from difference maps and their positional and isotropic thermal parameters were refined. The remaining hydrogen atoms in 1 were introduced at geometrically idealized coordinates with a fixed isotropic displacement parameter equal to 1.2 times the value of the equivalent isotropic displacement parameter of the parent carbon. During the final stages of refinement an extinction correction was applied for intensities collected for 1. In both cases, the final Fourier-difference maps have no significant chemical meaning.

Table 5 Crystal data, data collection and refinement parameters for compounds 1, 3 and 5

	1	3·H2O	5·H2O
a Goodness of fit S = {[w(Fo^2 – Fc^2)^2]/(n – p)}^1/2 where n is the number of reflections and p is the total number of parameters refined. b R 1 = ∑∥Fo| – |Fc∥/∑|Fc|, wR2 = {∑[w(Fo^2 – Fc^2)^2]/∑[w(Fo^2)^2]}^1/2.
Empirical formula	C7H6BFO3	C7H6BBrO3·H2O	C7H5BBr2O3·H2O
M r	167.93	246.85	325.76
Radiation (λ/Å)	Mo-Kα (0.710 73)	Mo-Kα (0.710 73)	Mo-Kα (0.710 73)
T/K	293(2) K	293(2) K	293(2) K
Crystal system	Triclinic	Monoclinic	Triclinic
Space group (no.)	P1̄ (2)	Cc (9)	P1̄ (2)
Z (Z′)	2 (1)	16 (4)	2 (1)
a/Å	7.2136(9)	11.159(3)	7.0559(16)
b/Å	7.6191(8)	11.116(2)	8.3747(18)
c/Å	8.1010(11)	29.383(7)	9.656(2)
α/°	102.960(10)	90	89.986(17)
β/°	106.797(10)	94.473(18)	99.607(18)
γ/°	111.387(9)	90	108.329(17)
V/Å^3	368.75(8)	3633.6(14)	533.2(2)
D c/Mg m^–3	1.512	1.805	2.029
µ/mm^–1	0.130	4.501	7.584
Max./min. transmission	—	0.24031/0.43515	0.5754/0.1491
θ Range/° (data collection)	2.8-25.0	2.59-25.04	2.1 to 25.0
Index ranges, hkl	0 to 8, –9 to 8, –9 to 9	0 to 13, 0 to 13, –34 to 34	–8 to 8, –9 to 9, –11 to 11
Reflections collected	1415	3296	4077
Unique reflections (Rint)	1302 (0.0116)	3296 (0.0000)	1877 (0.0169)
Data/restraints/parameters	1302/0/134	3296/278/319	1877/0/137
Goodness-of-fit on F^2^a	1.066	1.040	1.050
Reflections with I > 2σ(I)	1143	2557	1609
Final R indices (I > 2σ(I))^b	R 1 = 0.0327,wR2 = 0.0874	R 1 = 0.0593,wR2 = 0.1481	R1 = 0.0253, wR2 = 0.0622
R Indices (all data)^b	R 1 = 0.0370, wR2 = 0.0907	R 1 = 0.0809, wR2 = 0.1617	R1 = 0.0327, wR2 = 0.0652
Δρmax, min/e Å^–3	+0.180 and –0.122	+ 0.764 and –0.782	+0.367 and –0.398

---

Several attempts of collecting X-ray data for crystals of compound 3 obtained from separate batches revealed a substantial disorder in all measured crystals. After processing with the Lorentz-polarization effects and numerical absorption correction the solving (direct methods) and refinement (full-matrix least squares) procedures were applied for all data sets. The best solution and then the approximation of the structure were obtained in the Cc space group with four independent molecules of 3-II and four water molecules in the asymmetric unit. Only the heaviest atoms (Br, O) were anisotropically refined. It was determined that the molecules are arranged into layers in the (001) plane. After the analysis of the residual maxima on the Fourier maps the disorder (layer-stacking faults) was modeled as a superposition of two identical layers shifted by 0.5a (or 0.5b) vector. The positional and thermal parameters of the major layer component were refined while the minor one was introduced entirely as a rigid group (including water oxygens) with a common isotropic thermal parameter. The geometry of the rigid group was subsequently corrected according to changes of the major group on successive stages of the refinement. The final occupation factor for the minor component was refined to 0.114(3). The hydrogen atoms of 3 were introduced at geometrically idealized coordinates with a fixed isotropic displacement parameter. Water hydrogen atoms were not included in the refinement.

ORTEP drawings were made using ORTEP3 for Windows.³¹ The geometrical parameters for structural analysis were calculated using the PLATON package.³²

CCDC reference numbers 614639 (1), 614640 (5·H₂O) and 626865 (3·H₂O).

For crystallographic data in CIF or other electronic format see DOI: 10.1039/b611195e

Theoretical calculations

Becke-style 3-parameter density functional method using the Lee–Yang–Parr correlation functional³³ with 6-311+G** basis set (B3LYP/6-311+G**) and the second-order Møller–Plesset perturbation method³⁴ with 6-31G* basis set (MP2/6-31G*), 6-31+G* one (MP2/6-311+G*) and the Dunning basis set³⁵ aug-cc-pVDZ (MP2/aug-cc-pVDZ) were used to optimize the geometry of the molecules. DFT (B3LYP) calculations generate good results for an equilibrium geometry of a molecule.³⁶ All calculations were performed using the Gaussian03³⁷ series of programs. Obtained geometries were characterized as minima by calculating the vibrational frequencies (no imaginary frequencies). The rotational barriers for tautomeric forms I (Scheme 1, X = H, F, Cl, Y = H) were computed at B3LYP/6-311+G** and MP2/6-31G* levels of theory. For each fixed torsion angle O(1)–B–C(1)–C(2) all remaining internal degrees of freedom were optimized for both methods.

Acknowledgements

This work was supported by the Warsaw University of Technology. The support by Aldrich Chemical Co., Inc., Milwaukee, WI, through continuous donation of chemicals and equipment is gratefully acknowledged. The authors thank the Interdisciplinary Centre for Mathematical and Computational Modelling (Warsaw, Poland) for computational facilities.

References

1. For reviews, see: (a) N. Miyaura and A. Suzuki, Chem. Rev., 1995, 95, 2457; (b) J. Hassan, M. Sévignon, C. Gozzi, E. Schulz and M. Lemaire, Chem. Rev., 2002, 102, 1359.
2. H. G. Kuivila, A. H. Keough and E. J. Soboczenski, J. Org. Chem., 1954, 19, 780.
3. T. D. James and S. Shinkai, Top. Curr. Chem., 2002, 218, 159.
4. L. I. Bosch, M. F. Mahon and T. D. James, Tetrahedron Lett., 2004, 45, 2859.
5. S. Arimori, L. I. Bosch, C. J. Ward and T. D. James, Tetrahedron Lett., 2001, 42, 4553.
6. J. H. Fournier, T. Maris, J. D. Wuest, W. Guo and E. Galoppini, J. Am. Chem. Soc., 2003, 125, 1002.
7. M. P. Groziak, A. D. Ganguly and P. D. Robinson, J. Am. Chem. Soc., 1994, 116, 7597.
8. (a) V. L. Arcus, L. Main and B. K. Nicholson, J. Organomet. Chem., 1993, 460, 139; (b) V. V. Zhdankin, P. J. III Persichini, L. Zhang, S. Fix and P. Kiprof, Tetrahedron Lett., 1999, 40, 6705; (c) L.-Y. Tan, A. J. P. White, D. E. Widdowson, R. Wilhelm and D. J. Williams, J. Chem. Soc., Perkin Trans. 1, 2001, 3269; (d) A. Sporzyński, M. Lewandowski, P. Rogowska and M. K. Cyrański, Appl. Organomet. Chem., 2005, 19, 1202; (e) Y. Yamamoto, J. Ishii, H. Nishiyama and K. Itoh, J. Am. Chem. Soc., 2005, 127, 9625.
9. J. Kagan, J. Org. Chem., 1967, 32, 4060.
10. F. M. Hauser, P. Hewawasam and V. M. Baghdanov, J. Org. Chem., 1988, 53, 224.
11. J. Harron, R. A. McClelland, C. Thankachan and T. Tidwell, J. Org. Chem., 1981, 46, 903.
12. For 2-formylphenylboronic acid in [D₆]acetone–D₂O, only a small amount of a cyclic form (ca. 5%) was detected by a careful ¹H NMR analysis at r.t.
13. H. R. Snyder, A. J. Reedy and W. J. Lennarz, J. Am. Chem. Soc., 1958, 80, 835.
14. P. Tschampel and H. R. Snyder, J. Org. Chem., 1964, 29, 2168.
15. P. A. Leighton and F. A. Lucy, J. Chem. Phys., 1934, 2, 756.
16. K _dim and K_cycl were calculated by the least-squares method, using the following equation derived from equilibria in Scheme 2
    .
17. This compound was prepared with a substantial amount of the acid 3 impurity, and therefore it was not characterized in detail.
18. (a) S. J. Rettig and J. Trotter, Can. J. Chem., 1977, 55, 3071; (b) H. Feulner, G. Linti and H. Nöth, Chem. Ber., 1990, 123, 1841; (c) M. Pilkington, J. D. Wallis and S. Larsen, J. Chem. Soc., Chem. Commun., 1995, 1499; (d) F. R. Fronczek, St. N. N. Luce and R. M. Strongin, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2001, 57, 1423; (e) S. M. Cornet, K. B. Dillon, C. D. Entwistle, M. A. Fox, A. E. Goeta, H. P. Goodwin, T. B. Marder and A. L. Thompson, Dalton Trans., 2003, 4395; (f) S. Das, V. L. Alexeev, A. C. Sharma, S. J. Geib and S. A. Asher, Tetrahedron Lett., 2003, 44, 7719; (g) B. Zarychta, J. Zaleski, A. Sporzyński, M. Dąbrowski and J. Serwatowski, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2004, 60, o344; (h) P. Rodriguez-Cuamatzi, G. Vargas-Diaz, T. Maris, J. D. Wuest and H. Höpfl, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2004, 60, o1316; (i) J.-M. Lo, S.-M. Chen, M.-H. Chen, Y.-J. Chen, F.-L. Liao and T.-H. Lu, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2004, 60, o1851; (j) P. N. Horton, M. B. Hursthouse, M. A. Beckett and M. P. Rugen-Hankey, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2004, 60, o2204; (k) Y. Yang, J. O. Escobedo, A. Wong, C. M. Schowalter, M. C. Touchy, L. Jiao, W. E. Crowe, F. R. Fronczek and R. M. Strongin, J. Org. Chem., 2005, 70, 6907.
19. W. H. Scouten, X.-C. Liu, N. Khangin, D. F. Mullica and E. L. Sappenfield, J. Chem. Crystallogr., 1994, 24, 621.
20. R. Adams and H. C. Yuan, Chem. Rev., 1933, 12, 261.
21. A. Ganguly, C. Y. Meyers and P. D. Robinson, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2003, 59, o759.
22. X.-C. Liu, J. L. Hubbard and W. H. Scouten, J. Organomet. Chem., 1995, 493, 91.
23. S. W. Coghlan, R. L. Giles, J. A. K. Howard, L. G. F. Patrick, M. R. Probert, G. E. Smith and A. Whiting, J. Organomet. Chem., 2005, 690, 4784.
24. T. M. Krygowski, J. E. Zachara and H. Szatyłowicz, J. Phys. Org. Chem., 2005, 18, 110.
25. A. Karpfen, C. H. Choi and M. Kertesz, J. Phys. Chem. A, 1997, 101, 7426.
26. S. Luliński and J. Serwatowski, J. Org. Chem., 2003, 68, 5384.
27. M. Dąbrowski, J. Kubicka, S. Luliński and J. Serwatowski, Tetrahedron Lett., 2005, 46, 4175.
28. M. Dąbrowski, J. Kubicka, S. Luliński and J. Serwatowski, Tetrahedron, 2005, 61, 6590.
29. G. M. Sheldrick, SHELXS-97, Program for Structure Solution, Acta Crystallogr., Sect. A, 1990, 46, 467.
30. G. M. Sheldrick, SHELXL-97, Program for Crystal Structure Refinement, Universität Göttingen, Göttingen, Germany, 1997.
31. L. J. Farrugia, J. Appl. Crystallogr., 1997, 30, 565.
32. (a) A. L. Spek, PLATON, A Multipurpose Crystallographic Tool, Utrecht University, Utrecht, The Netherlands, 2002; (b) A. L. Spek, Acta Crystallogr., Sect. A, 1990, 46, C34.
33. (a) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter, 1988, 37, 785; (b) A. D. Becke, J. Phys. Chem., 1993, 98, 1372; (c) A. D. Becke, J. Chem. Phys., 1993, 98, 5648; (d) P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623.
34. (a) C. Möller and M. S. Plesset, Phys. Rev., 1934, 46, 618; (b) R. Krishnan and J. A. Pople, Int. J. Quantum Chem., 1978, 14, 91.
35. (a) T. H. Dunning, Jr, J. Chem. Phys., 1989, 89, 1007; (b) R. A. Kendall, T. H. Dunning, Jr and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796; (c) D. E. Woon and T. H. Dunning, Jr, J. Chem. Phys., 1993, 98, 1358.
36. F. De Proft and P. Geerlings, Chem. Rev., 2001, 101, 1451.
37. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. G. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, GAUSSIAN 03 (Revision C.02), Gaussian, Inc., Wallingford, CT, 2004.

---

Footnotes

† Dedicated to Professor Tadeusz M. Krygowski from the University of Warsaw on the occasion of his 70th birthday.

‡ Electronic supplementary information (ESI) available: ¹H, ¹³C NMR and IR spectra of functionalized 2-formylphenylboronic acids, selected thermodynamic and theoretical calculation data. See DOI: 10.1039/b611195e

---