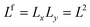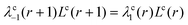On the curvature dependence of the interfacial tension in a symmetric three-component interface
Received
11th September 2006
, Accepted 8th November 2006
First published on 28th November 2006
Abstract
We consider a symmetric interface between two polymers AN and BN in a common monomeric solvent S using the mean-field Scheutjens–Fleer self-consistent field theory and focus on the curvature dependence of the interfacial tension. In multi-component systems there is not one unique scenario to curve such an interface. We elaborate on this by keeping either the chemical potential of the solvent or the bulk concentration of the solvent fixed, that is we focus on the semi-grand canonical ensemble case. Following Helfrich, we expand the surface tension as a Taylor series in the curvature parameters and find that there is a non-zero linear dependence of the interfacial tension on the mean curvature in both cases. This implies a finite Tolman length. In a thermodynamic analysis we prove that the non-zero Tolman length is related to the adsorption of solvent at the interface. Similar, but not the same, correlations between the solvent adsorption and the Tolman length are found in the two scenarios. This result indicates that one should be careful with symmetry arguments in a Helfrich analysis, in particular for systems that have a finite interfacial tension: one not only should consider the structural symmetry of the interface, but also consider the constraints that are enforced upon imposing the curvature. The volume fraction of solvent, the chain length N as well as the interaction parameter χAB in the system can be used to take the system in the direction of the critical point. The usual critical behavior is found. Both the width of the interface and the Tolman length diverge, whereas the density difference between the two phases, adsorbed amount of solvent at the interface, interfacial tension, spontaneous curvature, mean bending modulus as well as the Gaussian bending modulus vanish upon approach of the critical point.
Introduction
The properties of the boundary between two adjacent bulk phases has drawn the attention of many researchers because of its relevance for numerous applications. Interfaces are fascinatingly complex because of their inhomogeneous structure even when the two bulk phases are far from the critical point. Interfaces between polymeric phases are on first sight even more complex as the conformational degrees of freedom of the chains in the interfacial zone poses extra complications to reckon with. However, when the polymer solutions are above a threshold concentration such that the chains overlap, each polymer chain interacts with many neighbors and as a result a mean-field description becomes reasonable. This insight is applied in the field of polymer technology, e.g. for the description of polymer blends. Below, our interest is in the interface that exists in a ternary system of two types of polymer that have a solubility gap in the presence of a low molecular weight common good solvent. The mean-field theory of such a system is conceptually similar to that of a simple binary liquid discussed by van der Waals more than a century ago. We take this classical problem as the starting point of our investigations.
In a recent publication1 we briefly discussed the self-consistent field (SCF) predictions for the curvature dependence of the interfacial tension in such a polymer–polymer interface. Here we will give a more complete analysis of this problem and discuss not only the numerical SCF results, but complement this with a classical thermodynamic analysis. As usual, a homogeneously curved interface can be parameterised by the mean curvature  and Gaussian curvature
and Gaussian curvature  , where R1 and R2 are the principal radii of curvature. In the limit of small curvatures it makes sense to write the surface tension γ as a Taylor series expansion around the flat interface
, where R1 and R2 are the principal radii of curvature. In the limit of small curvatures it makes sense to write the surface tension γ as a Taylor series expansion around the flat interface
| |  | (1) |
defining the Gaussian bending modulus
![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif)
, the mean bending modulus
kc and the so-called spontaneous curvature
J0 (which is, as we will see, sometimes a misleading terminology). Alternatively, one can expand around the spontaneous curvature and find
| |  | (2) |
where

. Helfrich
2,3 used this expansion for the curvature dependence of
lipid bilayer membranes. Unsupported, freely floating bilayers have a vanishing surface tension and the flat bilayer is typically the ground state situation. Very often a symmetry argument is used to substantiate the assumption of the absence of a spontaneous curvature. The idea is that the flat bilayer can bend with equal likelihood in one or the other direction, and thus the flat state should be some optimum (in this case a minimum) of the free energy. As a result, for freely floating membranes the first two terms in
eqn (1) vanish and the mean bending modulus necessarily is positive. For the interface between two immiscible solutions the surface tension of the flat interface typically is finite. Moreover, in general the linear term in
J will not vanish either. In this case there is no guiding principle that will dictate the sign of the mean bending modulus. As a result, all terms of
eqn (1) are relevant.
It is possible, at least in theory, to design fully symmetric interfaces in the following way. We take component A forming an A-rich phase and place this next to component B forming the B-rich phase. A and B repel each other but the two coexisting phases are otherwise identical, i.e. the components have equal molar volumes, the phases are equally compressible etc. Now, when the A compound is replaced by the B one and vice versa the A-rich phase transforms into the B-rich phase and vice versa. If in the process nothing happens (no drift in compositions, the interfacial tension is the same, etc.) the interface is noted to be symmetric. In the very special case of symmetric interfaces it is believed that the linear term in eqn (1) is again absent. The key argument is that for the symmetric interface it is irrelevant whether the interface is curved in one direction or in the other, i.e., it is immaterial which phase is internalised. As a result the flat interface should have an optimum surface tension (a maximum or minimum) and it is natural to believe that an expansion around this optimum implies J0 = 0. Recently we argued, by a detailed numerical analysis, that the symmetry argument is flawed.1 Below we will go into more detail about the SCF calculations and give a rigorous thermodynamic argument that supports the numerical SCF analysis.
van der Waals interface
In 1893 van der Waals4 introduced a simple model that allowed him to predict the structure of an interface between two monomeric solvents, A and B. This result is nowadays a textbook example that can be reproduced in a simple lattice model, wherein the monomers occupy all lattice sites that interact with their neighbors only.5 In this system the mean-field approximation is applied in lattice layers (fluctuations in the local composition are ignored in the x–y plane) and volume fraction gradients in the z directions are accounted for. Lattice layers are referred to by lattice coordinates using (x, y, z) or in general by the r coordinate. The lattice coordinates can be seen as dimensionless distances. Below we will use the letter R to refer to a real distances. The lattice site length b, with a typical value of b
≈ 0.5 nm is used to convert from real distances to layer numbers, R
∼
rb. Some intricacies in this conversion are discussed below.
In this lattice model the interface is symmetric; the A-rich and B-rich phases have exactly complementary compositions (i.e. the binodal is symmetric). Below we will be interested not only in the flat interface, but also in homogeneously curved interfaces, i.e. when the interface has a cylindrical or spherical shape. The lattice layers are in this case referred to by the general coordinate r, and the mean-field approximation is applied to all lattice sites within each layer. In Appendix 1 one can find further details. Here it suffices to say that in these systems the number of lattice sites at coordinate r is a function of the geometry, i.e., L(r) = LxLy for the flat interface, L(r) ∝
Lxr for the cylindrical interface oriented in the x direction, and L(r) ∝
r2 in the spherical geometry.
In all these systems one can write the free energy
| | 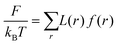 | (3) |
where
kBT the thermal energy. Here the volume of the system is given by

. The dimensionless free energy density is given by
| |  | (4) |
where
χ is the Flory–Huggins interaction parameter, and the angular brackets indicate a three-layer average
| |  | (5) |
Here the
a priori step probabilities
λr′−r(
r) give the fraction of neighbors of a site at coordinate
r with sites at
r′ =
r
− 1,
r, or
r + 1, respectively. These are chosen differently for each geometry and we again refer the reader to Appendix 1 for details. In the flat case
λ−1(
r) =
λ1(
r) =
λ1, and for a simple cubic lattice this value equals 1/6 and
λ0(
r) =
λ0 = 1 − 2
λ1. There exists a profile
φA(
r) such that the free energy of
eqn (3) is minimised. In general this solution can be found numerically,
e.g., by the Scheutjens–Fleer SCF scheme (see below). For the flat lattice (we return to the
z coordinate) an analytical solutions exist near the critical point. In this limit the (continuous) profile is given by
5,6| |  | (6) |
where
ε = 2
kBT(
χ
− 2)/
b3,
c = 16
kBT/3
b3, and

is an analytical expression for the binodal in the system which is accurate near the critical point. The interfacial width
W is given by

, where
B = 2
λ1χkBT/
b. It is convenient to define Δ
χ =
χ
− 2 (inverse of the reduced temperature). When this parameter approaches zero, the volume fraction difference between the two phases vanishes
φA(
∞) −
φA(−
∞) ∝ (Δ
χ)
1/2. In the same limit the interfacial width diverges
W
∝
b(Δ
χ)
−1/2. The interfacial tension is given by
| |  | (7) |
Within the van der Waals model it is possible to evaluate the effect of curvature of the interface and extract from this the bending moduli. Blokhuis and Bedeaux showed
7 that
| |  | (8) |
| |  | (9) |
When the mean bending modulus is negative, as is the case for this simple interface, the terminology for
J0 as the spontaneous curvature is misleading; it would be better to refer to
J0 as the worst curvature. We conform, however, to the nomenclature used in the literature for clarity. Note that the flat interface does not spontaneously start to curve in an experimental case because the surface tension is finite. In such a case the free energy is lowest when the area is minimized, and thus the surface remains flat.
We recall that this simple interface is completely symmetric. For this reason it was not a surprise that the spontaneous curvature J0 = 0. Oversteegen and Blokhuis8 have revisited this system using a lattice model using the Scheutjens–Fleer procedure. They found exact correspondence between the analytical theory and the numerical lattice approach near the critical point. Deviations between the methods appeared for Δχ > 0.5. These differences were attributed to the breakdown of the (Landau) free energy expansion needed in the analytical approach. Again it was found that J0 = 0. However, at this point yet another interesting problem presents itself. Given the fact that symmetry arguments in the Helfrich analysis are suspicious1 (we will show this in detail below), why then does the simple (symmetric) two-component system give J0 = 0? Again, our thermodynamic analysis will give a solution for this dilemma.
It is well-known that near the critical point the molecular details become of little importance.6 This means that we expect qualitatively the same results for a binary mixture of two equally long polymers AN and BN. The critical interaction parameter becomes inversely proportional to the chain length χcr = 2/N and the critical volume fraction remains φcrA = φcrB = 0.5 as found from the Flory–Huggins theory.9 Not too far from the critical point the interface again assumes the tanh profile and the similar scaling behavior for various interfacial properties is recovered (not shown), including the fact that the spontaneous curvature vanishes (shown below).
The addition of a non-selective monomeric solvent to the binary polymer system is, on first sight, rather innocent. From the Flory–Huggins theory9 it is easily shown that when χAS = χBS = 0 the critical volume fraction is found at exactly half the overall polymer volume fraction, i.e., φcrA = φcrB = (1−
φs)/2 = φ/2 where the volume fraction of polymer is given by φ. The critical interaction parameter is found at χcr = 2/(Nφ). By choice of the model, this three-component system features an interface that still is completely symmetric. The monomeric solvent distributes equally in both coexisting phases and the two phases have complementary compositions with respect to A and B. If the symmetry arguments used above apply, we should expect a vanishing spontaneous curvature. The new feature however is that we now may expect that the solvent will adsorb to some extend at the interface between the polymer A rich and the polymer B rich phases. The driving force for this accumulation of solvent is that it reduces the number of unfavorable A–B contacts at the interface. In our previous paper1 we showed that this adsorption is linked to the fact that the spontaneous curvature does not vanish despite the symmetry of the interface. As this result is not trivial it is necessary to go into full details.
In the next section we will elaborate on a lattice model in which it is possible to accurately solve for the structural as well as thermodynamical properties of a binary polymer system diluted with a common solvent. Within this approach the polymer chains are modeled as freely-jointed chains allowing the use of an efficient propagator formalism to evaluate the partition function. The curvature is imposed onto the interface and a Helfrich analysis gives accurately the mechanical properties of the interface. In the Results section it is shown that for this symmetric three-component system the spontaneous curvature does not vanish. In the Discussion and in particular in the section in which we present a thermodynamic analysis, we will elaborate on this observation and explain why it is dangerous to rely on symmetry arguments in a Helfrich analysis.
Scheutjens–Fleer self-consistent field analysis
The start of the analysis is to write the mean-field free energy for a spatially inhomogeneous system in which polymer molecules are present. Scheutjens and Fleer10–13 worked out that the partition function and the corresponding free energy can be written in the general form| |  | (10) |
where the index i refers to the molecule species A, B, and S, with chain lengths NA = NB = N and NS = 1. The free energy of eqn (10) consists of four contributions. The first one essentially equals 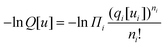 , and is thus the dimensionless free energy for given ‘external’ potential fields. The second term (first term in the summation over the layers r) in eqn (10) removes from the free energy the potential energy of these molecules, which implies a Legendre transformation such that the first two terms give the dimensionless entropy −S/kB, wherein the conformational degrees of freedom (including translation and mixing) are accounted for. The third term in eqn (10) adds back the (mean field) interaction part to the free energy as in eqn (4). Finally, the fourth term in eqn (10) essentially takes care of the incompressibility constraint. Here u′(r) is a Lagrange parameter coupled to the requirement that at each coordinate Σiφi(r) = 1.
, and is thus the dimensionless free energy for given ‘external’ potential fields. The second term (first term in the summation over the layers r) in eqn (10) removes from the free energy the potential energy of these molecules, which implies a Legendre transformation such that the first two terms give the dimensionless entropy −S/kB, wherein the conformational degrees of freedom (including translation and mixing) are accounted for. The third term in eqn (10) adds back the (mean field) interaction part to the free energy as in eqn (4). Finally, the fourth term in eqn (10) essentially takes care of the incompressibility constraint. Here u′(r) is a Lagrange parameter coupled to the requirement that at each coordinate Σiφi(r) = 1.
As in the van der Waals model we now need to find the equilibrium volume fraction profiles. For this the free energy should be extremized both with respect to the potential fields as well as to the volume fraction profiles and the volume fractions should obey the incompressibility constraint. Formally, the extremum of eqn (10) is easily specified because the Lagrange parameter u′(r) decouples the volume fractions such that they can be differentiated as if they were independent quantities. The extremization leads to the following set of equations
| |  | (11) |
| |  | (12) |
| |  | (13) |
where
eqn (11) and (12) obviously must be implemented for each molecule type
i and
χij is only non-zero if
i and
j represent the segment types A and B or
vice versa. All three equations should be obeyed for all coordinates
r. This set of equations is the core of the so-called SCF calculations.
Eqn (12) proves how the self-consistent potentials should be calculated, namely from the differentiation of the last two terms in the free energy.
10Eqn (11) shows how to compute the volume fractions, namely by differentiating (minus) the logarithm of the partition function with respect to the local segment potential. Below we will show that there is a more direct way to compute the volume fractions once the segment potentials are known. The third equation simply expresses that the potentials
u′(
r) are chosen such that the incompressibility is obeyed.
To evaluate the partition function qi (u) it is convenient to introduce Boltzmann weights Gi(r) = exp−ui(r). Note that the segment potentials as defined in eqn (12) are dimensionless, i.e., normalised by kBT. It is also convenient to use a reference for the potential ui(r) ≡
ui(r) −
ui(∞). For monomers j the partition function simply follows from the summation over all coordinates qj = ΣrL(r)Gj(r) and the volume fractions follow according to eqn (11) by
| |  | (14) |
where the number of molecules
nj = ∑
rL(
r)
φj(
r). On the r.h.s. we use the fact that the Boltzmann weights are normalised to unity in the bulk. When we insert the result from
eqn (14) back into
eqn (10) it is easily shown that for a system with two monomeric components the free energy density of
eqn (4) is recovered (the normalisation of the interactions with respect of the interactions in the bulk is inconsequential).
Scheutjens and Fleer10–13 showed that on a lattice the partition function (first put forward by Edwards14) may be evaluated using a relatively simple propagator scheme which implies a Markov approximation
| |  | (15) |
where again the angular brackets indicate a three-layer weighted average as in
eqn (5).
Eqn (15) is started by
Gi(
r, 1) =
Gi(
r). The single-chain partition function simply follows from
qi = ∑
rL(
r)
Gi(
r,
N). The volume fraction profile now follows either from differentiating to the segment potential as indicated by
eqn (11), or from the so-called composition law, in which two sub-partition functions for two complementary chain parts are combined
| |  | (16) |
where again the normalisation may be simplified
ni/
qi =
φbi/
Ni. To solve
eqn (11)–(13) is somewhat complicated because all the quantities mutually depend on each other. A so-called SCF solution is routinely found up to high precision using a numerical procedure.
13 Such a solution has the property that the potentials both follow from and generate the volume fraction profiles. In addition, the volume fractions obey the incompressibility constraint. Inserting these self-consistent volume fractions and segment potentials into
eqn (10) gives the extremized Helmholtz energy. From this we can find other parameters such as the grand potential
Ω =
kBT∑
rL(
r)
ω(
r), where
ω(
r) is the dimensionless grand potential density. This grand potential density is in general not uniquely defined because one has to make a choice regarding the bookkeeping of the pair interactions.
6,15 When the non-local binary interactions are evenly distributed over the two coordinates involved, we can write the grand potential density as
| |  | (17) |
For the flat interface the surface tension
γ = (
kBT/
b2)∑
zω(
z). The choice mentioned above has no physical consequences for the value predicted for the bending moduli or the spontaneous curvature (Tolman length).
16
Results
Our molecular model has very few parameters. First, there is the Flory–Huggins interaction parameter χ. Second, there is the chain length of the polymeric components N and third, there is the overall amount of solvent in the system. It is convenient to introduce Δχ
≡
χNφ
− 2 which is a parameter that vanishes at the critical point. We will use this parameter below to investigate the scaling behavior of various interfacial properties. In the above we have kept the parameter λ1 as a variable. Ideally one would like to use an isotropic (simple cubic lattice) value, i.e., λ1 = 1/6. However, experience has shown that calculations are more straightforward by using λ1 = 1/3. Physically this means that the lattice site in such a model is not isotropic. When the thickness of a lattice layer is given by b, the area is equal to 2b2. As a consequence we have to reduce the surface tension by a factor of two to convert the numerical data based on λ1 = 1/3 to those expected for the simple cubic lattice. As we are focusing on the scaling behavior, the choice of λ1 is inconsequential.
Let us choose to refer to the part of the system far from the interface at large values of z, or in the curved systems large values of r, to be the bulk solution. Without losing generality we can further select the phase that is more concentrated with A and dilute in B to be at low r values. This implies that the bulk is relatively rich in B and dilute in A. The position of the interface is determined by fixing the number of molecules of type A in the system. For the flat interface the number of molecules per unit area is  . In the case of the cylindrical coordinate system the number of molecules per unit length is given by
. In the case of the cylindrical coordinate system the number of molecules per unit length is given by 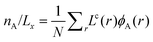 , and for the spherical case we have the number of molecules per droplet
, and for the spherical case we have the number of molecules per droplet 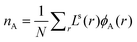 . As explained above the volume fraction of A in the bulk follows from φbA = NnA/qA. We are going to control the amount of solvent in the system by fixing the volume fraction of S in the bulk. In other words φbS is an input parameter. This means that the bulk volume fraction of the component B is given by φbB = 1 −
φbA
−
φbS. This choice corresponds in good approximation to a semi-open system, i.e. we focus on the semi-grand canonical ensemble case. By choosing to normalise the volume fraction profiles of the B component using φbB/N we automatically obey the constraint that the bulk is incompressible and the results follow accurately the Gibbs–Duhem relation that couples the chemical potentials of the three molecules.
. As explained above the volume fraction of A in the bulk follows from φbA = NnA/qA. We are going to control the amount of solvent in the system by fixing the volume fraction of S in the bulk. In other words φbS is an input parameter. This means that the bulk volume fraction of the component B is given by φbB = 1 −
φbA
−
φbS. This choice corresponds in good approximation to a semi-open system, i.e. we focus on the semi-grand canonical ensemble case. By choosing to normalise the volume fraction profiles of the B component using φbB/N we automatically obey the constraint that the bulk is incompressible and the results follow accurately the Gibbs–Duhem relation that couples the chemical potentials of the three molecules.
Flat interface
In Fig. 1a an example is shown of the volume fraction profiles across the liquid–liquid interface for the case in which N = 100 φbs = 0.8, and χ = 0.15. This combination will give a reduced interaction Δχ = 1. In this graph the volume fraction profiles of the polymers are indicated on the left ordinate and that of the solvent on the right one. We choose z = 0 exactly at the plane of symmetry; by definition of the symmetric interface we now have φA(−z) = φB(z) and φS(−z) = φS(z). The volume fraction profile of the polymer units is clearly hyperbolic-tangent-like. We would like to draw special attention to the solvent profile which is dotted. Far from the interface the solvent has the volume fraction of 0.8, but at the interface the density is somewhat higher. The accumulation of solvent is easily explained by the fact that the solvent can screen unfavorable interactions between the polymer units. The greater the amount of solvent in the interface, the fewer the unfavorable contacts. In Fig. 1b we give the corresponding grand potential density profile. Obviously, the grand potential density profile is also exactly symmetric (ω(−z) = ω(z)). Moreover the value far from the interface is identical to zero. At the interface the grand potential density goes through a maximum. The summation of ω(z) over all z is proportional to the interfacial tension, which is obviously positive. The width of the interface W may be defined in several ways. Upon inspection we may guess it to be of the order of 10 lattice units. We will not go into these details and mention that the width increases as a power law W
∝ (Δχ)−0.5 upon the approach toward the critical point.
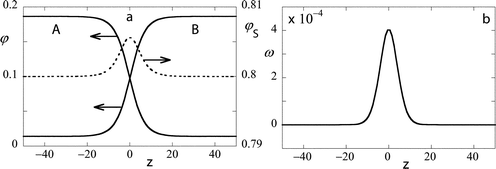 |
| | Fig. 1 (a) The volume fraction profile across a flat interface; A and B segments continuous lines (left ordinate), S dotted line (right ordinate). The z coordinate is chosen such that z = 0 is at the center of the interface. (b) The grand potential density (multiplied by 104 and in units kBT/(2b3)) profile across a flat interface. Parameters: N = 100, φbS = 0.8, and χ = 0.15. The symmetric binodal values are φ(1)A = 0.185 86, φ(2)A = 0.014 14. | |
The adsorption of solvent at the interface can be interpreted as a depletion effect of the polymers. For semi-dilute polymer solutions next to a non-adsorbing interface, the grand potential corresponding to the depletion effect can be estimated from the work needed to push the polymers against the osmotic pressure Π away from the surface by a distance proportional to the mesh (blob) size ξ. Thus γ
∝
Πξ, where the osmotic pressure is given by Π
∝ (kBT/b3)φ2 and the mesh size in semi-dilute polymer solutions is ξ
∝
bφ−0.5. As a result we expect that the depletion contribution to the surface tension will scale with the polymer concentration φ3/2. From eqn (7) we also expect that the surface tension will be proportional to √χ. This motivates us to define a reduce surface tension  and plot this quantity as a function of the reduced interaction parameter in Fig. 2. In this graph we have collected results for different N and φ, which accurately collapse onto a single ‘master curve’. This indicates that the surface tension is given by:
and plot this quantity as a function of the reduced interaction parameter in Fig. 2. In this graph we have collected results for different N and φ, which accurately collapse onto a single ‘master curve’. This indicates that the surface tension is given by:
| |  | (18) |
As expected the surface tension vanishes as a power law upon the approach of the critical conditions,
i.e.,
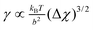
. The power law exponent is identical to that of the van der Waals model. The fitted numerical constant (40) has a reasonable value when the coefficients for the osmotic pressure, mesh size and those of
eqn (7) are implemented. The exact value should, however, follow from an analytical model.
Eqn (18) is consistent with old predictions by Hong and Noolandi.
17
 |
| | Fig. 2 (a) The normalised surface tension  in units kBT/(2b2) as a function of the reduced interaction parameter Δχ in double logarithmic coordinates. (b) The normalised adsorbed amount of the solvent at the interface in units kBT/(2b2) as a function of the reduced interaction parameter Δχ in double logarithmic coordinates. (b) The normalised adsorbed amount of the solvent at the interface  in units b−2. Results are presented for (N, φ) = (100. 0.3), (100, 0.2), (100, 0.1), (200, 0.2), (50, 0.2) and in (a) also (N, φ) = (100, 0.5), (100, 0.4). The dotted lines represent the power law behavior. in units b−2. Results are presented for (N, φ) = (100. 0.3), (100, 0.2), (100, 0.1), (200, 0.2), (50, 0.2) and in (a) also (N, φ) = (100, 0.5), (100, 0.4). The dotted lines represent the power law behavior. | |
In Fig. 2b information is given about the excess adsorbed amount of solvent (per unit area) defined by ΓS = b−2Σz(φS(z) −
φbS. It appears that when this quantity is reduced by  the curves are reasonably well collapsed onto a master curve unless the polymer concentration is too high. In all cases we found a power law decay of the adsorbed amount of solvent upon the approach toward the critical point and it does so as
the curves are reasonably well collapsed onto a master curve unless the polymer concentration is too high. In all cases we found a power law decay of the adsorbed amount of solvent upon the approach toward the critical point and it does so as  . Below we will pay attention to the adsorption of the solvent in more detail. As in the van der Waals system, the difference in volume fraction of A between the two phases vanishes upon the approach of the critical point φB(−∞) −
φB(∞) = φA(−∞) −
φA(∞) ∝ (Δχ)1/2 (not shown).
. Below we will pay attention to the adsorption of the solvent in more detail. As in the van der Waals system, the difference in volume fraction of A between the two phases vanishes upon the approach of the critical point φB(−∞) −
φB(∞) = φA(−∞) −
φA(∞) ∝ (Δχ)1/2 (not shown).
Curved interfaces
Curved interfaces frequently occur in soft condensed matter, for example in nucleation of droplets in super-saturated mixtures that have a solubility gap, emulsions, foams, etc. Much is known about the thermodynamics of curved interfaces and we will discuss the intricacies of curved interfaces as they necessarily present themselves in our system below. Let us first consider an example similar to the result given in Fig. 1 and impose a cylindrical shape onto the interface. Referring to Fig. 3, we have modeled a cylindrical system with rM = 200 lattice layers. In this system we fixed nA/Lx = 33 chains per unit length of the cylinder such that the interface is located approximately at r
≈ 50.
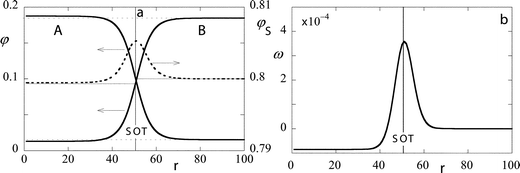 |
| | Fig. 3 (a) The volume fraction profile across a cylindrical interface; A and B segments continuous lines (left ordinate), S dotted line (right ordinate). The r coordinate is chosen such that r = 1 is the first lattice layer at the center of the cylinder. (b) The grand potential density (multiplied by 104 and in units kBT/(2b2)) profile across a cylindrical interface. Parameters: N = 100, φbS = 0.8, χ = 0.15, and nA/Lx = 33. | |
The radial volume fraction profiles of the three molecular components are presented in Fig. 3a. On first sight there are very few differences with respect to the results given for the flat interface in Fig. 1a. However, upon closer inspection it can be seen that both the composition in the internal phase as well as the composition in the external phase has changed with respect to the flat interface. In Fig. 3a we have added dotted lines to help one see this difference in the volume fractions. It can be seen that the component A has a relatively high concentration in the internal phase as well as in the external one, whereas just the opposite is the case for the component B. As for the solvent we have imposed a value of exactly 0.8 on the volume fraction φbS in the outer phase, and the suppression of the solvent volume fraction in the inside phase is easily observed. All these small changes are expected. The curved interface exists at a slightly increased chemical potential of the components. In other words the solution is somewhat super-saturated with the internal phase component (Kelvin effect).
In Fig. 3b we presented the corresponding grand potential density profile. As in the flat case ω(r) has a pronounced maximum at the interface. Unlike in the flat interface the grand potential density has a negative value in the internalised volume. Far from the interface this value assumes a constant value. There is no ambiguity in evaluating the ω(r) in the center, which is minus the (dimensionless) Laplace pressure. In this example we find ΔP = 8.5051 × 10−5kBT(2b3). Integration of the grand potential density gives the overall grand potential of the droplet per unit length. Again this quantity is unambiguously computed and in this example Ω/(Lxb) = Σr(Lc(r)/Lx)ω(r) = 0.66987kBT/b. It is well-known that
| |  | (19) |
| |  | (20) |
| |  | (21) |
For the cylindrical case we proceed with
eqn (20). Here
R is the radius of the cylindrically curved phase which is rich in component A. As we can choose this radius as we like, it is clear that the surface tension will be a function of this choice. Thus,
γ =
γ(
r). There exists a value for this radius
R for which

(the square brackets indicate that the change of the surface tension is taken as a result of the change in the
choice of the radius
R). The value of the
R chosen is called the surface of tension (SOT) and indicated by
RSOT. At the SOT we have
γSOT = Δ
PRSOT for the cylindrically curved interface and
γSOT = Δ
PRSOT/2 for the spherical case. Now,
| |  | (22) |
| |  | (23) |
Applying
eqn (23) to the result of
Fig. 3 we obtain
RSOT
≈ 50.067
b, which is very close to the value of the radius we aimed for when we generated the density profiles of
Fig. 3. We have drawn the position of the SOT in
Fig. 3, where we have realised that segments in layer
r are positioned at a distance
R = (
r
− 1/2)
b from the center. Interestingly, the SOT is positioned slightly to a lower
r coordinate than where the maximum in the
solvent profile is, or where the A and B profiles cross. This crossing point occurs at
rA=B
≈ 51.11, or equivalently at
RA=B = 50.61
b. The latter position is exactly at the maximum of the
solvent profile and also at the maximum of the grand potential density profile (
Fig. 3b).
At this stage we may also evaluate the equimolar Gibbs planes RGA. It is only possible to define such plane for the A and B component
| |  | (24) |
| |  | (25) |
| |  | (26) |
| |  | (27) |
where
eqn (24) and (25) are for the spherical shaped interface and
eqn (26) and (27) apply to the cylindrical interface.
It turns out that the Gibbs plane of B is shifted for the case in Fig. 3 by 0.43 lattice units to a larger layer number than that of A essentially independent of the imposed curvature. The SOT plane is for this curvature J not exactly at the average of the two Gibbs planes. However, in the limit of J
→ 0 and in line with symmetry considerations it is true that the SOT is at the average of the two Gibbs planes. We did not present the Gibbs planes in Fig. 3 because on the scale used in this figure it would be hard to see the difference between them.
After the SOT is determined it is possible to evaluate the surface tension at the SOT γSOT for various imposed curvatures. To make changes in the imposed curvature one actually makes changes in the number of molecules of, e.g., component A (which is internalised) in the system. In Fig. 4a a typical result is presented in which γSOT is plotted as a function of the mean curvature J = 1/RSOT for the cylindrically curved interface as well as for the spherical case for which J = 2/RSOT. It is important to mention that while imposing the curvature of the internal ‘droplet’, we have fixed the solvent volume fraction in the bulk to φbS = 0.8. In the Discussion we will elaborate on the alternative to keep the chemical potential of the solvent fixed in such analysis. In Fig. 4a we have combined the result of the cylindrical and spherical cases. The dots represent the individual calculations and the lines represent parabolic fits through the data points. The value found for γ(0) from the fit exactly coincides with the surface tension of the flat interface. The remarkable result is that a hill parabola (a convex curve) is found with a maximum that is not at J = 0. The hill parabola means that the bending modulus kc is negative; we find kc = −0.136kBT. In the cylindrically curved interface the maximum is positioned (by definition (see eqn (1)) at J = J0 and we find J0b = 0.00979. The maximum in the spherical case is given by J = kcJ0/(kc + 1/2![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ). Using the kc from the cylindrically curved interface we find a positive value for the Gaussian bending modulus
). Using the kc from the cylindrically curved interface we find a positive value for the Gaussian bending modulus ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) = 0.021 kBT. The spontaneous curvature as recovered from the fitting of the spherically curved interface is, within error, the same as that for the cylindrical interface. It should be mentioned that the definition of the sign of the curvature is still arbitrary. We could also have chosen the B-rich phase to be on the inside. For symmetry reasons we obtain exactly the same result for this case. This means that for the negative curvatures the curvature dependence is the same, implying that a negative J0 also exists. As a result the surface tension at J = 0 has two distinct derivatives (∂γ/∂J)J↓0 = −(∂γ/∂J)J↑0.
= 0.021 kBT. The spontaneous curvature as recovered from the fitting of the spherically curved interface is, within error, the same as that for the cylindrical interface. It should be mentioned that the definition of the sign of the curvature is still arbitrary. We could also have chosen the B-rich phase to be on the inside. For symmetry reasons we obtain exactly the same result for this case. This means that for the negative curvatures the curvature dependence is the same, implying that a negative J0 also exists. As a result the surface tension at J = 0 has two distinct derivatives (∂γ/∂J)J↓0 = −(∂γ/∂J)J↑0.
 |
| | Fig. 4 (a) The surface tension evaluated at the SOT in units of kBT/2b2 computed using the SOT as a function of the mean curvature in the cylindrically J = 1/RSOT and spherically J = 2/RSOT curved interface (both in units b−1). (b) The excess adsorbed amount per unit area ΓS of the solvent in units b−2, computed using the SOT plane, as a function of the curvature in the cylindrically and spherically curved interface. Upon imposing the curvature we have fixed the bulk concentration of the solvent to φbS = 0.8. Parameters: N = 100 and χ = 0.15. | |
In Fig. 4b we have presented the excess adsorbed amount of solvent as a function of the curvature both for the spherically as well as the cylindrically curved interfaces. These are evaluated using the SOT as the plane of reference:
| |  | (28) |
| |  | (29) |
for the spherical and cylindrical cases, respectively. We refer to
Fig. 3a for a graphical illustration of these equations.
ΓS counts the amount of
solvent molecules in excess of the volume faction of the horizontal line to the right of the SOT plus the amount of
solvent molecules in excess of the volume faction of the horizontal line to the left of the SOT and normalizes this by the area of the interface (measured at the SOT). Referring to
Fig. 4b we find in both geometries that the adsorbed amount is an increasing function of the (mean) curvature in the system. This result can also be fitted by a parabola and this parabola has a minimum very close to
J = 0. Note that the adsorbed amount per unit area for a given curvature does not deviate much from that of the flat interface.
The non-zero value of the spontaneous curvature is, at first sight, a surprising result. This calls for a more detailed investigation. In Fig. 5a we show the result of the mean bending modulus (left ordinate) as well as the ‘spontaneous’ curvature (right ordinate) as a function of the volume fraction of solvent in the bulk for the case in which N = 100 and χ = 0.1. In the limit that there is no solvent in the system, we return to a two-component system. Inspection of Fig. 5a shows that for the symmetric two-component system J0 = 0 and the mean bending modulus is negative. Both results are consistent with the van der Waals model. For the parameters used in Fig. 5, i.e., N = 100 and χ = 0.1, the critical volume fraction of solvent is at φbS = 0.8. This means that above this value there is a homogeneous phase only. From the van der Waals theory we know that the bending moduli vanish upon the approach toward the critical point and indeed this result is recovered in Fig. 5a, where it is found that the mean bending modulus goes smoothly and monotonically to zero. It is natural to expect (we return to this in the Discussion) that the spontaneous curvature should also vanish in this limit. Inspection of Fig. 5a shows that this is indeed the case. As a result the ‘spontaneous’ curvature goes through a maximum. This maximum is found for the present parameters to be around φbS
≈ 0.5.
 |
| | Fig. 5 (a) The mean bending modulus kc in units of kBT (left ordinate) and the ‘spontaneous’ curvature J0 in units b−1 (right ordinate) as a function of the volume fraction of solvent in the bulk φbS. (b) The excess adsorbed amount of solvent per unit area of the flat interface as a function of the volume fraction of solvent in the bulk. Parameters: N = 100, χ = 0.1. | |
In Fig. 5b we present the adsorbed amount of solvent that is present at the flat interface as a function of the volume fraction of solvent in the bulk. Again, this adsorbed amount should vanish both at φbS = 0 and at the critical condition, i.e. at φbS = 0.8. The latter must be true because in the absence of an interface there is nothing to adsorb onto. Again, it is natural to expect that the adsorbed amount ΓS goes through a maximum, and this maximum is found also at φbS = 0.5. The correlation between J0(φbS) and ΓS(φbS) is striking. It tells us that the reason for a finite spontaneous curvature in this system must be related to the adsorption of solvent onto this liquid–liquid interface.
It is possible to repeat the fitting procedure illustrated in Fig. 4a for various values of the governing parameters N, χ and φS. A selection of the results is presented in Fig. 6. In this graph we plot the bending moduli (left ordinate) and spontaneous curvature (right ordinate) as a function of the reduced interaction parameter on a double logarithmic scale. As the mean bending modulus is negative we plot, of course, the absolute value. Both the mean bending modulus as well as the Gaussian bending modulus scale accurately with the reduced interaction parameter −kc
∝
kBT(Δχ)1/2 and ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ∝
kBT(Δχ)1/2. Remarkably the numerical coefficients are very close to the ones given in eqn (9). The result for the ‘spontaneous’ curvature is somewhat more complicated as could already be expected from the non-monotonous behavior found in Fig. 5. In the limit of Δχ < 1, however, it is found that the spontaneous curvature displays power law behavior, i.e. J0b
∝ (Δχ)0.5.
∝
kBT(Δχ)1/2. Remarkably the numerical coefficients are very close to the ones given in eqn (9). The result for the ‘spontaneous’ curvature is somewhat more complicated as could already be expected from the non-monotonous behavior found in Fig. 5. In the limit of Δχ < 1, however, it is found that the spontaneous curvature displays power law behavior, i.e. J0b
∝ (Δχ)0.5.
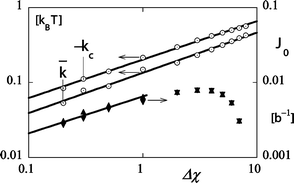 |
| | Fig. 6 Minus the mean bending modulus (open spheres) and the Gaussian bending modulus (open squares) (both in units kBT) as well as the spontaneous curvature (b−1) (right ordinate; point down triangles result from the cylindrically curved interface, point up closed triangles result from the spherically curved interface) as a function of the reduced interaction parameter for the same systems as in Fig. 5 in double logarithmic coordinates. Parameters N = 100 and χ = 0.1. | |
Discussion and classical thermodynamics
Dextran and gelatin are two polymeric species, both soluble in water, and have a miscibility gap under experimental conditions. They form water-in-water emulsions that are used in food systems. For this system there are estimates available in the literature for the mean bending modulus near the critical point as large as kc
∝ 500 kBT.18 This result is in strong contrast with the predictions given above. One may wonder if there is some hidden problem in the calculations presented thus far. Above we have already identified one possible snag: we have assumed that it is possible to fix the volume fraction of solvent in the B-rich phase while the curvature of the droplets is changed. As the concentration of solvent is a free variable, it should be possible to design an experiment in which this condition is met. However, such an experiment will not be trivial. One may wonder how sensitive the predictions are for small changes in the ‘experimental’ setup. We may design the experiment such that the chemical potential of the solvent is kept constant. In this case one imposes the curvature of the emulsion droplets, while the system is in equilibrium (e.g. through some semi-permeable membrane) with a reservoir with fixed solvent chemical potential. The chemical potential of all molecular species can be evaluated using the Flory–Huggins theory and only the bulk volume fractions of all components enter:| |  | (30) |
| |  | (31) |
| |  | (32) |
The calculation scheme in which the chemical potential of the solvent is fixed involves a more extended iteration scheme. Typically calculations for given solvent volume fractions are still performed but this solvent volume fraction is adjusted until the chemical potential of the solvent is equal to some pre-assigned value for each value of J. In Fig. 7 we present the results for the parameter settings very similar to that of Fig. 5a, i.e. N = 100 and χ = 0.1. The direct comparison of results presented in Fig. 7 with those in Fig. 5a is not possible because both graphs represent essentially different ‘experimental’ conditions. However in first order the volume fraction of solvent φbS
≈ exp(μS
−
μ#S)/kBT which enables a qualitative comparison. The correspondence between Fig. 5a and 7 proves that there are no qualitative changes. Again the mean bending modulus is negative and tends toward zero in the limit toward the critical point, which occurs when μS
−
μ#S
≈
−0.0261kBT. More importantly, the spontaneous curvature goes once again through a maximum and goes toward zero at the critical point. Also in the limit that the system approaches the two-component system, i.e. when the chemical potential of solvent is extremely negative, the spontaneous curvature goes to zero (for obvious reasons not plotted). We conclude that the non-zero spontaneous curvature, nor the negative value of the mean bending modulus is a result of some unrealistic constraint imposed on our system when we curved the interfaces.
 |
| | Fig. 7 The mean bending modulus in units kBT and the spontaneous curvature (b−1) as a function of the fixed chemical potential of the solvent in units of kBT. Other parameters as in Fig. 5. | |
It is of interest to know whether this result is due to some model features or is generic. If it is a generic result one should be able to also prove this in a thermodynamic framework. Let us concentrate on the linear dependence of the interfacial tension. The Helfrich equation eqn (1) simplifies to
| |  | (33) |
where on the right hand side we have introduced Tolman’s length
δ19| |  | (34) |
Systems with
γ (0) = 0 such as freely-floating
lipid bilayers, have an undefined Tolman length and this indicates that such systems should be treated separately. The interfacial tension of the flat interface however is finite and the Tolman length is well-defined. As in general
kc
≠ 0, we notice that a non-zero spontaneous curvature
J0
≠ 0 coincides with a non-zero Tolman length
δ
≠ 0. Referring to
Fig. 8a where the situation of a one-component fluid–vapor interface is depicted, the Tolman length is defined as the distance between the Gibbs plane, where the excess adsorption at the interface is exactly zero, and the SOT. If the adsorption is computed using the SOT as the plane of reference,
Γ
≡
Γ(SOT) and the volume fraction difference between the condensed (inner phase) and the vapor phase (outer phase) is given by Δ
φ, then the Tolman length may be computed from
δ =
b3Γ/Δ
φ. It is instructive to show this. We will see that it follows from a combination of the Gibbs adsorption equation and a pair of Gibbs–Duhem relations applicable for inner and outer phases. The Gibbs adsorption equation reads:
| |  | (35) |
where
Sσa is the excess entropy per unit area. For fixed temperature (as we will do in the remainder) this term can be disregarded. Now let us take the curvature
J as the ‘control’ variable. We have
| |  | (36) |
where we propose that in the multi-component system there is also a Tolman length
δ. At the SOT we know that
J = Δ
P/
γSOT. In the limit of
J
→ 0 we can write
| |  | (37) |
from which it follows that the Tolman length is given by
| |  | (38) |
Let us first apply this equation to the symmetric two-component system. In the limit of
J
→ 0 it must be true that
ΓA =
ΓB = 0 and the Tolman length vanishes irrespective how the chemical potentials depend on Δ
P. In passing we note that it must be expected that
∂μ/
∂P
∝
φ is finite. As there is a large difference in volume fraction of A and B in the droplet phase there must be a large difference in the response of the chemical potential upon an applied Laplace pressure (we will elaborate somewhat more on this below).
 |
| | Fig. 8 (a) Schematic radial volume fraction profile φ(r) of a condensed phase (droplet with radius R
→
∞) in a vapor solution. Indicated are: the Tolman length δ, the Gibbs dividing plane, the surface of tension (SOT), the volume fraction difference Δφ between the inner (small r coordinate) and outer phase (large r coordinate), the adsorption Γ counted with respect to the SOT (shaded area).19 (b) Schematic diagram for the definition of the adsorbed amount of solvent ΓS (top shaded area) and the negative ΓA and ΓB (bottom shaded area) with respect to the SOT in a symmetric three-component system (limit droplet radius R
→
∞. The two Gibbs planes are indicated. This graph is for illustrative purpose exaggerated with respect to the more realistic graph given in Fig. 1a. | |
We may now apply eqn (38) to the symmetric three-component system. Referring to Fig. 8b it must be true that ΓS = NΓA + NΓB, and it is trivial to see that ΓS
≠ 0. At this point it is clear why the SOT is chosen as the plane of reference to count the adsorbed amount. In the limit of J
→ 0 we have for symmetry reasons −ΓA = −ΓB = 1/2ΓS/N and we may simplify eqn (38) to
| |  | (39) |
We have checked the outcome of
eqn (39) numerically and the results for the spontaneous curvature (
δ) is identical to the direct fitting of the data to the Helfrich
eqn (1), proving the internal consistency of the analysis.
Eqn (39) confirms the main observation of this paper, namely that the spontaneous curvature J0 and the excess adsorption of the solvent ΓS are correlated (both for the systems in which the curvature was imposed at fixed φS, see Fig. 5a, as well as in those where μS was constant, see Fig. 7). Eqn (39) can now be used to argue that indeed the Tolman length in the three-component system (and directly related to this the non-zero spontaneous curvature J0) is (in general) finite. To show this we need to prove that the term within the brackets in eqn (39) is in general non-zero. Again, one should expect that this term in non-zero simply because the composition in the droplet is very different with respect to the polymer A and polymer B (and solvent).
Returning to the general case of i components we now may make use of appropriate Gibbs–Duhem relations. In the case of an imposed curvature we have an internal phase (in) and an external phase (out) and the chemical potentials accommodate the pressure difference such that for the inner phase
| | 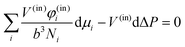 | (40) |
and for the outer phase
| |  | (41) |
where the ambient pressure is assumed to be constant. In both
eqn (40) and (41) we can divide by the volume. Of interest is the variation with respect to the value of the Laplace pressure Δ
P and as both
eqn (40) and (41) must apply we suggest taking the difference between the two as our constraint relation. Defining Δ
φ
≡
φi(in)
−
φi(out) we have
| |  | (42) |
Applying
eqn (42) to a one-component system we find that
∂μ/
∂Δ
P =
b3N/Δ
φ. Inserting this in
eqn (38) we find
δ =
b3
Γ
N/
φ. This result was already proposed by Tolman
19 (for
N = 1) and is illustrated in
Fig. 8a. Again in the symmetric two-component interface the
δ = 0 because
Γ = 0, not due to some symmetry argument.
Application to the three-component system is somewhat more involved. It is easy to see that the solvent term is small and we may as well take the conditions such that μS is fixed. In this case eqn (42) simplifies to  . To have a zero Tolman length eqn (39) implies
. To have a zero Tolman length eqn (39) implies  . As b3d(ΔP) = (Δφi/N)dμi we automatically come in conflict with eqn (42). We thus must conclude that the Tolman length is, in general, finite for a three-component system.
. As b3d(ΔP) = (Δφi/N)dμi we automatically come in conflict with eqn (42). We thus must conclude that the Tolman length is, in general, finite for a three-component system.
We may approach eqn (39) from a different perspective. Indeed, eqn (39) indicates that it is not impossible to obtain three-component systems with a zero Tolman length. For this either the adsorption of the solvent ΓS, or  should be zero. To tune the interactions such that the adsorption is zero is tedious. The second alternative in fact specifies the thermodynamic route which should be obeyed such that the symmetric interface has its optimum at J = 0. It is at least in principle feasible to consider the solvent as an effective medium and define effective chemical potentials of A and B by
should be zero. To tune the interactions such that the adsorption is zero is tedious. The second alternative in fact specifies the thermodynamic route which should be obeyed such that the symmetric interface has its optimum at J = 0. It is at least in principle feasible to consider the solvent as an effective medium and define effective chemical potentials of A and B by ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) A = μA
−
NAμS and
A = μA
−
NAμS and ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) B = μB
−
NBμS. As in our case NA = NB = N we arrive at the condition
B = μB
−
NBμS. As in our case NA = NB = N we arrive at the condition  . Thus, when the interface is curved under the conditions that
. Thus, when the interface is curved under the conditions that ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) A +
A + ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) B = constant, we should expect that the Tolman length vanishes. van Male and Blokhuis showed25 that this condition is generated approximately in an incompressible (nA = nB, V,T) ensemble, i.e., when there are equal amounts of A and B (indicated by nA = nB). When this interface is curved the solvent increases in one phase and decreases by the same amount in the other phase such that the solvent in the A-rich phase plus the solvent in the B-rich phase remains constant, i.e. φS(A) + φS(B) = constant (losses due to adsorption can be ignored in the limit of J
→ 0). When the interface is curved at a fixed bulk concentration of solvent, or at a fixed chemical potential of the solvent, one loses the ability to keep
B = constant, we should expect that the Tolman length vanishes. van Male and Blokhuis showed25 that this condition is generated approximately in an incompressible (nA = nB, V,T) ensemble, i.e., when there are equal amounts of A and B (indicated by nA = nB). When this interface is curved the solvent increases in one phase and decreases by the same amount in the other phase such that the solvent in the A-rich phase plus the solvent in the B-rich phase remains constant, i.e. φS(A) + φS(B) = constant (losses due to adsorption can be ignored in the limit of J
→ 0). When the interface is curved at a fixed bulk concentration of solvent, or at a fixed chemical potential of the solvent, one loses the ability to keep ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) A +
A + ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) B = constant. In this paper we have concentrated on semi-grand canonical ensembles basically because of two reasons. The first one is that semi-open systems are experimentally more accessible than strict canonical ones. The second reason is that calculations on canonical systems with a variable curvature of the interface are extremely laborious.
B = constant. In this paper we have concentrated on semi-grand canonical ensembles basically because of two reasons. The first one is that semi-open systems are experimentally more accessible than strict canonical ones. The second reason is that calculations on canonical systems with a variable curvature of the interface are extremely laborious.
We may now return to eqn (1) and investigate how the various terms in this expansion behave just above the critical point, i.e.
Δχ < 1. Above we mentioned that the interface width W increases upon the approach of the critical point. We can only identify emulsion droplets if the radius of the emulsion droplets exceed the width of the interface. This means that the curvature should be less than Jb < (Δχ)1/2 and Kb2 < (Δχ)1. Using these scaling relations for the curvatures, we find that all the terms in the Helfrich expansion (eqn (1)) decay similarly: γ(0,0) ∝ (kBT/b2)(Δχ)3/2, kcJ0J
∝ (kBT/b2)2(Δχ)3/2, kcJ2
∝ (kBT/b2)(Δχ)3/2 and ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) K
∝ (kBT/b2)(Δχ)3/2. To us this is one extra argument why the reported high bending moduli in the dextran–gelatin system18 should be reconsidered.
K
∝ (kBT/b2)(Δχ)3/2. To us this is one extra argument why the reported high bending moduli in the dextran–gelatin system18 should be reconsidered.
Using eqn (34) and inserting the scaling dependences for the spontaneous curvature, the mean bending modulus and the interfacial tension, we find that upon the approach toward the critical point the Tolman length diverges δ
∝
bΔχ−0.5, similarly as the width W of the interface (and as the bulk correlation length). This result is in contrast to a recent prediction of Blokhuis and Kuipers who concluded that, for the (mean field) van der Waals equation of state, the Tolman length goes to a constant at the critical point.20 However, our result is consistent with arguments given by Phillips and Mohanty.21 Several other authors report a weak divergence of the Tolman length albeit that the non-mean field scaling exponent is still uncertain.22–24
Above we argued that it is natural to expect that for a symmetric interface the flat interface represents some optimum situation. The finite value of the interfacial tension (and the fact that the interfacial tension marginally depends on the curvature of the interface) tells us that the global free energy minimum is the one with a minimal surface area. Therefore the flat state is the equilibrium one. The result of Fig. 4a confirms this expectation in another way, as the uncurved interface represents at least a local minimum. However the surface tension can not be differentiated at J = 0 because the derivative from the positive side and that of the negative side have opposite signs. This is mathematically the reason why the spontaneous curvature J0 can still be finite. Because of this peculiar behavior one should be cautious to use symmetry arguments in a Helfrich analysis. For systems with a finite tension γ(0) > 0 it is possible to have a Tolman length, and in general this length is non-zero. In symmetric two-component systems, however, it is true that the equimolar plane coincides with the SOT and the Tolman length vanishes. We saw this happen in the numerical calculations as well as in the thermodynamic analysis. However in the three-component system there is typically a finite Tolman length. More specifically, the value of the Tolman length depends on exactly how the interface is curved, i.e. for fixed μS (analogous to a fixed pressure in a two-component lattice gas), fixed bulk concentration of solvent, or at fixed ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) A +
A + ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) B.
B.
In experimental systems (such as the dextran–gelatin system) the ideal case in which the uncurved interface is symmetric will (in general) not be true. As a result there will be an intrinsic reason for the system to feature some non-zero spontaneous curvature. More interesting scenarios are possible, e.g. when there are molecules in the system that are amphiphilic and adsorb strongly onto the interface. In this case it is possible that the surface tension is significantly reduced, while simultaneously the bending moduli are expected to increase (and most likely will be positive). For such systems it is much more likely that the interface is not dominated by the surface tension, but rather by the bending moduli (including the Tolman length). Such situation occurs, e.g., in microemulsion systems. In the present system however, it is not the case and the physics of the interface is controlled by the surface tension, while the Tolman length and bending moduli are secondary. Minor curvature corrections for the interfacial tension may however be important for predicting nucleation rates.
Above we found that in general interfaces with a finite interfacial tension have a non-zero preferential curvature. This result is not only of academic interest but may have implications for applications as well. Our results are not limited to the particular example elaborated on above. A more simple system presents itself in a compressible binary mixture of two simple solvents (note that the mean-field approximation is expected to give only qualitative results in this case). Within a lattice model such a binary system maps onto an incompressible three-component system of monomers, in which the vacant lattice sites are seen as a third component. The chemical potential of these vacancies can be related to the pressure, etc. Also, in this case we expect a finite Tolman length (this system is also semi-open). Again, the result that J0 = 0 in a purely two-component system must be considered as a very special case: in general the liquid–liquid interface has J0
≠ 0.
Conclusions
We have studied the interface between two immiscible polymer solutions, both enriched in a common unselective solvent. We focused on the curvature dependence of the interfacial tension studied in a semi-grand canonical ensemble. The fully symmetric case was analysed wherein all polymers were equally long. Within a mean-field SCF model we are able to evaluate the structure of the interface and found a small accumulation of the solvent at the interface. This adsorption is attributed to the screening by the solvent of unfavorable polymer–polymer interactions. The curvature corrections to the interfacial tension, i.e. parametrised in first order by the Tolman length and in second order by the elastic moduli of the interface are for experimental systems very small especially close to the critical point. Nevertheless we were able to compute these mechanical parameters accurately. We found a small but negative mean bending modulus, an even smaller but positive Gaussian bending modulus and more surprisingly a finite preferential curvature. The latter was unexpected because the structure of the interface was fully symmetric. We argued that the adsorption of solvent onto the interface is the physical reason for the non-zero spontaneous curvature. Moreover we showed that in a semi-grand canonical ensemble it is not possible to provide pure symmetric thermodynamic constraints. The most important implication of our result is that one should be careful in using symmetry arguments in a Helfrich analysis. It definitely does not suffice to consider only the structural symmetry of the interface. One should also include the thermodynamic constraints that are imposed while bending the interface in the considerations.
1. Appendix: lattice parameters in curved systems
We distinguish the flat interface indicated by super index f, the cylindrical interface c, and the spherical one S. The geometry is implemented in the lattice model by taking the number of lattice sites per “layer” (referred to generically by the variable r) according to| | 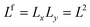 | (43) |
| |  | (44) |
| |  | (45) |
where L is typically chosen to be large enough for end-effects to be ignored and there is one direction in which volume fraction gradients occur. It is understood that in the spherical and cylindrical cases the r = 1 coordinate is the layer closest to the center of the sphere or cylinder, respectively.
The key notion is that the step-probabilities λ should be chosen according to the geometry and therefore are a function of the coordinate r. The internal balance dictates that
| | 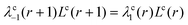 | (46) |
| |  | (47) |
Consistent with the internal balance we choose these step probabilities to depend on the common area that is crossed by going from one coordinate to a neighboring one. The dimensionless outer area of all sites at coordinate
r is given in the cylindrical coordinate system by
Ac(
r) =
L2π
r and for the spherical case
As(
r) = 4π
r2. Using these we write
| |  | (48) |
| |  | (49) |
| |  | (50) |
| |  | (51) |
| |  | (52) |
| |  | (53) |
These
a priori step probabilities are used in the local three-layer averages as given in
eqn (5). It is possible to show that the angular bracket, operating on a continuous function
X(
r), can be approximated as
| |  | (54) |
where for the spherical coordinates
a = 2 and for the cylindrical one
a = 1 and for the flat case
a = 0.
The angular brackets are found in the evaluation of the interaction energy, the self-consistent potentials as well as in the propagators. As a result the curvature corrections are implemented at all levels of computations.
Acknowledgements
We like to thank Jan van Male for useful discussions regarding the consequences of eqn (39) for curving in the canonical ensemble.
References
- F. A. M. Leermakers, P. A. Barneveld, J. Sprakel and N. A. M. Besseling, Phys. Rev. Lett., 2006, 97, 066103 CrossRef CAS.
- W. Helfrich, Z. Naturforsch., 1973, 28c, 693 Search PubMed.
-
W. Helfrich, in Elasticity and Thermal Undulations of Fluid Films of Amphiphiles Liquids at Interfaces, ed. J. Charvalin, J. F. Joanny and J. Zinn-Justin, North-Holland, Amsterdam, 1990 Search PubMed.
-
J. D. van der Waals, Thermodynamische theorie der capillariteit in de onderstelling van continue dichtheidsverandering, Verhand. Kon. Akad. v Wetensch., 1893, in Dutch Search PubMed; J. D. van der Waals, J. Stat. Phys., 1979, 20, 197 Search PubMed.
-
S. A. Safran, in Statistical Thermodynamics of Surfaces, Interfaces, and Membranes, ed. D. Pines, Addison-Wesley, New York, 1994, vol. 90 Search PubMed.
-
J. S. Rowlinson and B. Widom, Molecular Theory of Capillarity, Clarendon Press, Oxford, 1982 Search PubMed.
- E. M. Blokhuis and D. Bedeaux, Mol. Phys., 1993, 80, 705 CrossRef CAS.
- S. M. Oversteegen and E. M. Blokhuis, J. Chem. Phys., 2000, 112, 2980 CrossRef CAS.
-
P. Flory, Principles of Polymer Chemistry, Cornell University Press, Ithaca, NY, 1953 Search PubMed.
-
G. J. Fleer, M. A. Cohen Stuart, J. M. H. M. Scheutjens, T. Cosgrove and B. Vincent, Polymers at Interfaces, Chapman and Hall, London, 1993 Search PubMed.
- J. M. H. M. Scheutjens and G. J. Fleer, J. Phys. Chem., 1979, 83, 1619 CrossRef CAS.
- J. M. H. M. Scheutjens and G. J. Fleer, J. Phys. Chem., 1980, 84, 178 CrossRef CAS.
- O. A. Evers, J. M. H. M. Scheutjens and G. J. Fleer, Macromolecules, 1990, 23, 5221 CrossRef CAS.
- S. F. Edwards, Proc. Phys. Soc., 1965, 85, 613 CrossRef CAS.
- S. M. Oversteegen, P. A. Barneveld, F. A. M. Leermakers and J. Lyklema, Langmuir, 1999, 15, 8609 CrossRef CAS.
- S. M. Oversteegen, P. A. Barneveld, J. van Male, F. A. M. Leermakers and J. Lyklema, Phys. Chem. Chem. Phys., 1999, 1, 4987 RSC.
- K. M. Hong and J. Noolandi, Macromolecules, 1981, 14, 736 CrossRef CAS.
- E. Scholten, L. M. C. Sagis and E. van der Linden, J. Phys. Chem. B, 2004, 108, 12164 CrossRef CAS.
- R. C. Tolman, J. Chem. Phys., 1949, 17, 333 CrossRef CAS.
- E. M. Blokhuis and J. Kuipers, J. Chem. Phys., 2006, 124, 074701 CrossRef.
- P. Phillips and U. Mohanty, J. Chem. Phys., 1985, 83, 6392 CrossRef CAS.
- M. P. A. fisher and M. wortis, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 29, 6252 CrossRef CAS.
- S. J. Hemingway, J. R. Henderson and J. S. Rowlinson, Faraday Symp. Chem. Soc., 1981, 16, 33 RSC.
- J. S. Rowlinson, J. Phys. A: Math. Gen., 1984, 17, L–357.
-
J. van Male, E. M. Blokhuis, 2006, private communication.
|
| This journal is © the Owner Societies 2007 |
Click here to see how this site uses Cookies. View our privacy policy here.  and Gaussian curvature
and Gaussian curvature  , where R1 and R2 are the principal radii of curvature. In the limit of small curvatures it makes sense to write the surface tension γ as a Taylor series expansion around the flat interface
, where R1 and R2 are the principal radii of curvature. In the limit of small curvatures it makes sense to write the surface tension γ as a Taylor series expansion around the flat interface
![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) , the mean bending modulus kc and the so-called spontaneous curvature J0 (which is, as we will see, sometimes a misleading terminology). Alternatively, one can expand around the spontaneous curvature and find
, the mean bending modulus kc and the so-called spontaneous curvature J0 (which is, as we will see, sometimes a misleading terminology). Alternatively, one can expand around the spontaneous curvature and find
 . Helfrich2,3 used this expansion for the curvature dependence of lipid bilayer membranes. Unsupported, freely floating bilayers have a vanishing surface tension and the flat bilayer is typically the ground state situation. Very often a symmetry argument is used to substantiate the assumption of the absence of a spontaneous curvature. The idea is that the flat bilayer can bend with equal likelihood in one or the other direction, and thus the flat state should be some optimum (in this case a minimum) of the free energy. As a result, for freely floating membranes the first two terms in eqn (1) vanish and the mean bending modulus necessarily is positive. For the interface between two immiscible solutions the surface tension of the flat interface typically is finite. Moreover, in general the linear term in J will not vanish either. In this case there is no guiding principle that will dictate the sign of the mean bending modulus. As a result, all terms of eqn (1) are relevant.
. Helfrich2,3 used this expansion for the curvature dependence of lipid bilayer membranes. Unsupported, freely floating bilayers have a vanishing surface tension and the flat bilayer is typically the ground state situation. Very often a symmetry argument is used to substantiate the assumption of the absence of a spontaneous curvature. The idea is that the flat bilayer can bend with equal likelihood in one or the other direction, and thus the flat state should be some optimum (in this case a minimum) of the free energy. As a result, for freely floating membranes the first two terms in eqn (1) vanish and the mean bending modulus necessarily is positive. For the interface between two immiscible solutions the surface tension of the flat interface typically is finite. Moreover, in general the linear term in J will not vanish either. In this case there is no guiding principle that will dictate the sign of the mean bending modulus. As a result, all terms of eqn (1) are relevant.
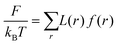
 . The dimensionless free energy density is given by
. The dimensionless free energy density is given by


 is an analytical expression for the binodal in the system which is accurate near the critical point. The interfacial width W is given by
is an analytical expression for the binodal in the system which is accurate near the critical point. The interfacial width W is given by  , where B = 2λ1χkBT/b. It is convenient to define Δχ = χ
− 2 (inverse of the reduced temperature). When this parameter approaches zero, the volume fraction difference between the two phases vanishes φA(∞) −
φA(−∞) ∝ (Δχ)1/2. In the same limit the interfacial width diverges W
∝
b(Δχ)−1/2. The interfacial tension is given by
, where B = 2λ1χkBT/b. It is convenient to define Δχ = χ
− 2 (inverse of the reduced temperature). When this parameter approaches zero, the volume fraction difference between the two phases vanishes φA(∞) −
φA(−∞) ∝ (Δχ)1/2. In the same limit the interfacial width diverges W
∝
b(Δχ)−1/2. The interfacial tension is given by



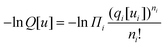 , and is thus the dimensionless free energy for given ‘external’ potential fields. The second term (first term in the summation over the layers r) in eqn (10) removes from the free energy the potential energy of these molecules, which implies a Legendre transformation such that the first two terms give the dimensionless entropy −S/kB, wherein the conformational degrees of freedom (including translation and mixing) are accounted for. The third term in eqn (10) adds back the (mean field) interaction part to the free energy as in eqn (4). Finally, the fourth term in eqn (10) essentially takes care of the incompressibility constraint. Here u′(r) is a Lagrange parameter coupled to the requirement that at each coordinate Σiφi(r) = 1.
, and is thus the dimensionless free energy for given ‘external’ potential fields. The second term (first term in the summation over the layers r) in eqn (10) removes from the free energy the potential energy of these molecules, which implies a Legendre transformation such that the first two terms give the dimensionless entropy −S/kB, wherein the conformational degrees of freedom (including translation and mixing) are accounted for. The third term in eqn (10) adds back the (mean field) interaction part to the free energy as in eqn (4). Finally, the fourth term in eqn (10) essentially takes care of the incompressibility constraint. Here u′(r) is a Lagrange parameter coupled to the requirement that at each coordinate Σiφi(r) = 1.







 . In the case of the cylindrical coordinate system the number of molecules per unit length is given by
. In the case of the cylindrical coordinate system the number of molecules per unit length is given by 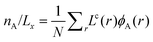 , and for the spherical case we have the number of molecules per droplet
, and for the spherical case we have the number of molecules per droplet 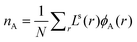 . As explained above the volume fraction of A in the bulk follows from φbA = NnA/qA. We are going to control the amount of solvent in the system by fixing the volume fraction of S in the bulk. In other words φbS is an input parameter. This means that the bulk volume fraction of the component B is given by φbB = 1 −
φbA
−
φbS. This choice corresponds in good approximation to a semi-open system, i.e. we focus on the semi-grand canonical ensemble case. By choosing to normalise the volume fraction profiles of the B component using φbB/N we automatically obey the constraint that the bulk is incompressible and the results follow accurately the Gibbs–Duhem relation that couples the chemical potentials of the three molecules.
. As explained above the volume fraction of A in the bulk follows from φbA = NnA/qA. We are going to control the amount of solvent in the system by fixing the volume fraction of S in the bulk. In other words φbS is an input parameter. This means that the bulk volume fraction of the component B is given by φbB = 1 −
φbA
−
φbS. This choice corresponds in good approximation to a semi-open system, i.e. we focus on the semi-grand canonical ensemble case. By choosing to normalise the volume fraction profiles of the B component using φbB/N we automatically obey the constraint that the bulk is incompressible and the results follow accurately the Gibbs–Duhem relation that couples the chemical potentials of the three molecules.
 and plot this quantity as a function of the reduced interaction parameter in Fig. 2. In this graph we have collected results for different N and φ, which accurately collapse onto a single ‘master curve’. This indicates that the surface tension is given by:
and plot this quantity as a function of the reduced interaction parameter in Fig. 2. In this graph we have collected results for different N and φ, which accurately collapse onto a single ‘master curve’. This indicates that the surface tension is given by:
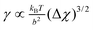 . The power law exponent is identical to that of the van der Waals model. The fitted numerical constant (40) has a reasonable value when the coefficients for the osmotic pressure, mesh size and those of eqn (7) are implemented. The exact value should, however, follow from an analytical model. Eqn (18) is consistent with old predictions by Hong and Noolandi.17
. The power law exponent is identical to that of the van der Waals model. The fitted numerical constant (40) has a reasonable value when the coefficients for the osmotic pressure, mesh size and those of eqn (7) are implemented. The exact value should, however, follow from an analytical model. Eqn (18) is consistent with old predictions by Hong and Noolandi.17

 in units kBT/(2b2) as a function of the reduced interaction parameter Δχ in double logarithmic coordinates. (b) The normalised adsorbed amount of the solvent at the interface
in units kBT/(2b2) as a function of the reduced interaction parameter Δχ in double logarithmic coordinates. (b) The normalised adsorbed amount of the solvent at the interface  in units b−2. Results are presented for (N, φ) = (100. 0.3), (100, 0.2), (100, 0.1), (200, 0.2), (50, 0.2) and in (a) also (N, φ) = (100, 0.5), (100, 0.4). The dotted lines represent the power law behavior.
in units b−2. Results are presented for (N, φ) = (100. 0.3), (100, 0.2), (100, 0.1), (200, 0.2), (50, 0.2) and in (a) also (N, φ) = (100, 0.5), (100, 0.4). The dotted lines represent the power law behavior. the curves are reasonably well collapsed onto a master curve unless the polymer concentration is too high. In all cases we found a power law decay of the adsorbed amount of solvent upon the approach toward the critical point and it does so as
the curves are reasonably well collapsed onto a master curve unless the polymer concentration is too high. In all cases we found a power law decay of the adsorbed amount of solvent upon the approach toward the critical point and it does so as  . Below we will pay attention to the adsorption of the solvent in more detail. As in the van der Waals system, the difference in volume fraction of A between the two phases vanishes upon the approach of the critical point φB(−∞) −
φB(∞) = φA(−∞) −
φA(∞) ∝ (Δχ)1/2 (not shown).
. Below we will pay attention to the adsorption of the solvent in more detail. As in the van der Waals system, the difference in volume fraction of A between the two phases vanishes upon the approach of the critical point φB(−∞) −
φB(∞) = φA(−∞) −
φA(∞) ∝ (Δχ)1/2 (not shown).



 (the square brackets indicate that the change of the surface tension is taken as a result of the change in the choice of the radius R). The value of the R chosen is called the surface of tension (SOT) and indicated by RSOT. At the SOT we have γSOT = ΔPRSOT for the cylindrically curved interface and γSOT = ΔPRSOT/2 for the spherical case. Now,
(the square brackets indicate that the change of the surface tension is taken as a result of the change in the choice of the radius R). The value of the R chosen is called the surface of tension (SOT) and indicated by RSOT. At the SOT we have γSOT = ΔPRSOT for the cylindrically curved interface and γSOT = ΔPRSOT/2 for the spherical case. Now,





![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ). Using the kc from the cylindrically curved interface we find a positive value for the Gaussian bending modulus
). Using the kc from the cylindrically curved interface we find a positive value for the Gaussian bending modulus ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) = 0.021 kBT. The spontaneous curvature as recovered from the fitting of the spherically curved interface is, within error, the same as that for the cylindrical interface. It should be mentioned that the definition of the sign of the curvature is still arbitrary. We could also have chosen the B-rich phase to be on the inside. For symmetry reasons we obtain exactly the same result for this case. This means that for the negative curvatures the curvature dependence is the same, implying that a negative J0 also exists. As a result the surface tension at J = 0 has two distinct derivatives (∂γ/∂J)J↓0 = −(∂γ/∂J)J↑0.
= 0.021 kBT. The spontaneous curvature as recovered from the fitting of the spherically curved interface is, within error, the same as that for the cylindrical interface. It should be mentioned that the definition of the sign of the curvature is still arbitrary. We could also have chosen the B-rich phase to be on the inside. For symmetry reasons we obtain exactly the same result for this case. This means that for the negative curvatures the curvature dependence is the same, implying that a negative J0 also exists. As a result the surface tension at J = 0 has two distinct derivatives (∂γ/∂J)J↓0 = −(∂γ/∂J)J↑0.



![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ∝
kBT(Δχ)1/2. Remarkably the numerical coefficients are very close to the ones given in eqn (9). The result for the ‘spontaneous’ curvature is somewhat more complicated as could already be expected from the non-monotonous behavior found in Fig. 5. In the limit of Δχ < 1, however, it is found that the spontaneous curvature displays power law behavior, i.e. J0b
∝ (Δχ)0.5.
∝
kBT(Δχ)1/2. Remarkably the numerical coefficients are very close to the ones given in eqn (9). The result for the ‘spontaneous’ curvature is somewhat more complicated as could already be expected from the non-monotonous behavior found in Fig. 5. In the limit of Δχ < 1, however, it is found that the spontaneous curvature displays power law behavior, i.e. J0b
∝ (Δχ)0.5.












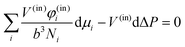


 . To have a zero Tolman length eqn (39) implies
. To have a zero Tolman length eqn (39) implies  . As b3d(ΔP) = (Δφi/N)dμi we automatically come in conflict with eqn (42). We thus must conclude that the Tolman length is, in general, finite for a three-component system.
. As b3d(ΔP) = (Δφi/N)dμi we automatically come in conflict with eqn (42). We thus must conclude that the Tolman length is, in general, finite for a three-component system. should be zero. To tune the interactions such that the adsorption is zero is tedious. The second alternative in fact specifies the thermodynamic route which should be obeyed such that the symmetric interface has its optimum at J = 0. It is at least in principle feasible to consider the solvent as an effective medium and define effective chemical potentials of A and B by
should be zero. To tune the interactions such that the adsorption is zero is tedious. The second alternative in fact specifies the thermodynamic route which should be obeyed such that the symmetric interface has its optimum at J = 0. It is at least in principle feasible to consider the solvent as an effective medium and define effective chemical potentials of A and B by ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) A = μA
−
NAμS and
A = μA
−
NAμS and ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) B = μB
−
NBμS. As in our case NA = NB = N we arrive at the condition
B = μB
−
NBμS. As in our case NA = NB = N we arrive at the condition  . Thus, when the interface is curved under the conditions that
. Thus, when the interface is curved under the conditions that ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) A +
A + ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) B = constant, we should expect that the Tolman length vanishes. van Male and Blokhuis showed25 that this condition is generated approximately in an incompressible (nA = nB, V,T) ensemble, i.e., when there are equal amounts of A and B (indicated by nA = nB). When this interface is curved the solvent increases in one phase and decreases by the same amount in the other phase such that the solvent in the A-rich phase plus the solvent in the B-rich phase remains constant, i.e. φS(A) + φS(B) = constant (losses due to adsorption can be ignored in the limit of J
→ 0). When the interface is curved at a fixed bulk concentration of solvent, or at a fixed chemical potential of the solvent, one loses the ability to keep
B = constant, we should expect that the Tolman length vanishes. van Male and Blokhuis showed25 that this condition is generated approximately in an incompressible (nA = nB, V,T) ensemble, i.e., when there are equal amounts of A and B (indicated by nA = nB). When this interface is curved the solvent increases in one phase and decreases by the same amount in the other phase such that the solvent in the A-rich phase plus the solvent in the B-rich phase remains constant, i.e. φS(A) + φS(B) = constant (losses due to adsorption can be ignored in the limit of J
→ 0). When the interface is curved at a fixed bulk concentration of solvent, or at a fixed chemical potential of the solvent, one loses the ability to keep ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) A +
A + ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) B = constant. In this paper we have concentrated on semi-grand canonical ensembles basically because of two reasons. The first one is that semi-open systems are experimentally more accessible than strict canonical ones. The second reason is that calculations on canonical systems with a variable curvature of the interface are extremely laborious.
B = constant. In this paper we have concentrated on semi-grand canonical ensembles basically because of two reasons. The first one is that semi-open systems are experimentally more accessible than strict canonical ones. The second reason is that calculations on canonical systems with a variable curvature of the interface are extremely laborious.![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) K
∝ (kBT/b2)(Δχ)3/2. To us this is one extra argument why the reported high bending moduli in the dextran–gelatin system18 should be reconsidered.
K
∝ (kBT/b2)(Δχ)3/2. To us this is one extra argument why the reported high bending moduli in the dextran–gelatin system18 should be reconsidered.![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) A +
A + ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) B.
B.