NMR measurements of scalar-coupling distributions in disordered solids

Abstract

The measurement of scalar (J) couplings by solid-state NMR is a field of great interest, since this interaction is a rich source of local structural information, complementary to dipolar and chemical shift interactions. Here, we first demonstrate that J-coupling distributions exist and can be observed in disordered solids, as illustrated with the observation of a pair-specific distribution of ²J(³¹P–N–³¹P) couplings in a bis-phosphino amine, and we investigate the potential effects of such distributions on the measurement of average J-coupling constants. Second, we show that the measurement of two-dimensional (2D) distributions of J-couplings provides a much richer probe of local structural disorder than one-dimensional distributions, and we introduce new methods that provide different (selective or non-selective) ways of measuring 2D J distributions in a wide range of disordered systems. These methods are finally applied to a slightly disordered polymorphic sample of fully ¹³C-enriched cellulose, and then to the bis-phosphino amine sample, from which 2D ²J_PP-coupling distributions are clearly identified and interpreted.

---

1. Introduction

The measurement of scalar (J) couplings by spin-echo modulation^1,2 in solid-state NMR has recently become a topic of high interest.^3–8 Indeed, J-couplings are a rich source of local structural information, as has been illustrated for a long time in liquid-state NMR, for instance through the Karplus relationships that relate ³J_HH couplings to dihedral angles between vicinal protons,^9,10 and more generally with the widespread observation of the dependence of J-couplings on dihedral and bond angles,¹¹ or on the nature of the chemical bonds.¹² In the solid state, spin-echo measurements of such a small interaction compared to the often dominant anisotropic interactions are possible because of the long rare-spin transverse dephasing times T₂′^13,14 that can be obtained under fast Magic-Angle Spinning (MAS) and efficient heteronucear decoupling techniques.^15–17 As a result, though J-couplings are often not resolved in one-dimensional (1D) spectra of solids, especially when they are disordered, J multiplets can be observed in a J-resolved dimension where the inhomogeneous broadening is refocused,^14,18 and the robustness of the resulting J-coupling modulation over a wide range of conditions has recently been demonstrated theoretically by Duma et al.⁷

So far, however, despite a few noticeable examples,^3,8 the structural interpretation of the J-coupling constants measured in solids has been limited, essentially because this interaction is sensitive to an ensemble of structural features. Dipolar couplings, which can be directly interpreted in terms of inter-nuclear distances, have thus often been found more attractive than scalar couplings in the solid-state NMR community.^19,20 However, recent advances in ab initio calculations of indirect spin–spin coupling constants provide a potentially powerful tool for the structural interpretation of J-couplings in solids.^21,22

Because disordered systems cannot be accessed in detail by conventional diffusion or diffraction methods, the characterization of structural disorder is of major interest for solid-state NMR. Indeed, NMR provides detailed molecular-level information in polymers, glasses, or heterogeneous materials lacking long-range molecular order, making it an attractive tool for materials science²³ or structural biology, where, for example, protein folding and/or degradation or polymorphism can be characterized.^24,25 Few examples of J-coupling measurements in disordered solids have been reported so far,^5,6,26,27 and they have never been used as probes of the local structural disorder . Recently, distributions of J-coupling constants have been reported from J-resolved experiments carried out on disordered solids, first in a phosphate glass, where distributed ²J_PP splittings (in the J-resolved dimension) have been observed along the ³¹P chemical shift distributions in a phosphate glass.⁵ Similarly, a site-specific ²J_SiSi-coupling distribution has been reported in a fully ²⁹Si-enriched silicate through a variable splitting (in the J-resolved dimension) due to clear variations in ²J(²⁹Si–O–²⁹Si)-coupling values along the broad chemical-shift distribution corresponding to a given type of tetrahedrally-coordinated ²⁹Si.²⁷ In both cases, however, the distribution observed was not specific to a given pair of sites, and may arise from an ensemble of J-couplings between several unresolved sites, or several potential pairs.

Here, we aim to demonstrate that disorder in solids produces a distribution of J-couplings between individual pairs of sites in the sample, and that such pair-specific distributions can be observed experimentally. First, we evaluate the effect of the presence of a J-coupling distribution on measured average J-coupling values by numerical simulations, and the existence of a pair-specific ²J_PP distribution is then demonstrated on a slightly disordered sample of bis-phosphino amine. Second, we show that the measurement of two-dimensional (2D) distributions of J-couplings provides a much richer probe of local structural disorder than 1D distributions, and we introduce new methods that provide different (selective or non-selective) ways of measuring 2D-J-distributions in a wide range of disordered systems. These methods are finally applied to a slightly disordered polymorphic fully ¹³C-enriched sample of cellulose, and then to the bis-phosphino amine sample, from which 2D ²J(³¹P–N–³¹P)-coupling distributions are clearly identified and discussed in terms of local structural deviations from a single structure.

2. Experimental

2.a. Samples

The 11% ¹³C-enriched cellulose sample was extracted from wood that was grown in a 20% ¹³C-enriched CO₂ atmosphere.²⁸ An analysis of the sample on the basis of canonical structures observed in model samples was proposed in ref. 29.

The partly crystalline, fully ¹³C-enriched sample of cellulose I_α and I_β was synthesized at the Centre d’Etudes et de Recherches sur les Macromolécules Végétales (Grenoble, France) according to the procedure described in ref. 30.

The sample of N,N-bis(diphenylphosphino)-N-((S)-α-methylbenzyl)amine (1) was synthesized at the Laboratoire d’Etudes Dynamiques et Structurales de la Sélectivité (Grenoble, France), for use as a π-acceptor bi-dentate ligand of a dicobalt complex, which has been studied as a candidate catalyst for asymmetric Pauson–Khand reactions.^31,32

2.b. NMR experiments

NMR experiments were carried out on a Bruker AVANCE 500 wide bore spectrometer and a Bruker AVANCE 700 standard bore spectrometer (as indicated in the figure captions). All experiments were recorded using a 2.5 mm double resonance probehead (providing spinning frequencies up to 35 kHz). Further details are given in the appropriate figure captions.

For consistency with the cellulose literature, ¹³C chemical shifts reported here are referenced (±0.1 ppm) with respect to the CH₂ group of adamantane (at 10 kHz, T = 293 K) at 38.48 ppm, which corresponds to 0.00 ppm for neat TMS. Such reference has commonly been used in solids since Earl and Vanderhart,³³ and was recently refined by Morcombe and Zilm.³⁴ According to the authors, this commonly-used scale is actually shifted by 0.71 ppm with respect to the IUPAC convention for liquid-state NMR, in which adamantane CH₂ has a chemical shift of 37.77 ppm with respect to 1% TMS in CDCl₃. Phosphorus-31 chemical shifts are referenced with respect to aqueous 85% H₃PO₄ (spinning at 1 kHz, T = 293 K).

2.c. Estimation of the errors on the measured J-coupling constants

Error bars on the experimental intensities of the echo modulation were systematically assumed to be equal to the largest of either the standard deviation in the noise region or twice the standard deviation of the best fit. Though it is not as precise as a statistical treatment over a large number of similar experiments, this method yields a reasonable estimation of the errors. A large number of similar fits were repeated with the addition of random noise (with a standard deviation equal to the experimental error bar) to the experimental data, and the error on the measured J-coupling was taken as the standard deviation of the series of J-coupling constants thus obtained.

3. Numerical simulations of the effects of a J distribution

3.a. Simulations of a J-coupling modulation in the presence of a J distribution

As mentioned above, J-couplings can be measured in disordered solids because the broad inhomogeneous chemical shift distributions arising from structural disorder are refocused during a spin-echo, thus leading to long transverse dephasing times T₂′ compared to the apparent dephasing time T₂*.¹⁴ However, so far, this has essentially been exploited to observe the modulation of the integrated intensity of a given site under the effects of all its J-coupled neighbors. Yet, a broad chemical shift distribution resulting from a distribution of local environments, such as slightly distorted bond angles or dihedral angles, naturally also corresponds to distributions of J-coupling constants between the observed site and the connected neighbors. Thus, the validity of the measurements reported so far in disordered solids relies on the stability of the measured J-coupling constant with respect to the presence of a distribution, and, therefore, we first analyze the potential effects of the presence of a J-coupling distribution on the measurement of average J-coupling constants through spin-echo modulation.

This was investigated by means of simple numerical simulations. We consider the simplest case of an isolated spin-pair in a disordered solid (or the case of a spin-pair in a multi-spin system that is artificially isolated by means of the z-filtered IPAP sequence³⁵). Since the J-couplings are observed through a spin-echo (τ-π-τ), the chemical shifts are refocused, and the width and shape of the chemical-shift distribution are not an issue, as long as we consider that the signal observed is obtained by integration over the whole distribution of the observed site. The effects of the J-coupling distribution are therefore simulated as the sum of an ensemble of J-coupling echo modulations having the same T₂′, and a distribution of the values of the J-coupling constants. The observed signal as a function of the τ delay is consequently given by:

where the probability P(J) is given by the shape of the J-coupling distribution.

In Fig. 1, we present the results of such numerical simulations, for a system having an average J-coupling constant of 50 Hz, and a transverse dephasing time T₂′ of 100 ms. The J-coupling distribution is taken as a Gaussian distribution with a standard deviation from the average value varied from 0 to 20 Hz. Fig. 1(a) shows the series of modulation curves obtained. The strongest effect is clearly faster apparent dephasing times as the width of the J-distribution increases. This is illustrated in Fig. 1(b), where we show the apparent T₂′ that is fitted for each curve. The J distribution does not affect the true T₂′ of the detected nuclei (which is kept the same in all curves), but it leads to an apparent increased dephasing. (Indeed, if the evolution under the J-coupling to the coupled spins were refocused by means of a semi-selective pulse that irradiates the observed site and does not irradiate the coupled spins, this apparent additional dephasing would disappear, as would the J-modulation.) This apparent increased dephasing might lead to difficulties in measuring average J-coupling constants in disordered systems, in the case of low J-coupling values and/or of fast transverse dephasing inherent to the system (due to dynamic effects, for example). Nevertheless, it is remarkable, as shown in Fig. 1(c), that the measured J-coupling constant is expected to be highly stable with respect to the width of the distribution, especially as long as the standard deviation of the J-couplings from the average value is less than 10% (±5 Hz in the simulation shown here), where the resulting overestimation of the apparent average value is less than 0.2%. As a result, though inducing a faster apparent decay, in most cases the presence of a J-coupling distribution does not prevent the accurate measurement of the average coupling constant.

Fig. 1 Numerical simulations of the spin-echo modulation curves obtained from a spin-pair having randomly distributed J-coupling values. Each modulation curve is obtained by summing an ensemble of 2048 modulation curves having the same amplitude and T₂′ (100 ms), and a J-coupling value moved around an average value of 50 Hz, according to a Gaussian distribution with a standard deviation ranging form 0 to 20 Hz. (a) Superposition of the series of modulation curves obtained by increasing the standard deviation of the J-distribution from 0 (black) to 20 Hz (light grey). Increasing apparent dephasing is observed when increasing the width of the J-distribution, as confirmed in (b) by the plot of the fitted dephasing time as a function the standard deviation. The fitted average J-coupling constant (c) increases only very slightly with the width of the distribution, indicating that the measured average value is stable with respect to the presence of a distribution.

3.b. Distributions of one-bond carbon–carbon J-couplings in disordered cellulose

We now turn our attention to the 11% ¹³C-enriched cellulose extracted from wood, whose CP-MAS spectrum is shown in Fig. 2(a), with the assignment of the six distinct types of carbon. One-bond ¹³C–¹³C coupling measurements were reported for this system,⁶ which is made up of an ensemble of known polymorphs of cellulose, as well as of disordered domains, which results in broad lines in the CP-MAS spectrum.²⁹ In ref. 6, ¹J_CC-coupling constants were obtained by fitting the evolution of the integrated signals of the resolved sites as a function of the τ delay of the spin-echo to a function being the superposition of a single exponential or “background” component, arising from the non-labeled neighbors of the detected site, and of a cosine-modulated component due to the labeled neighbors. The quality of the data and the large magnitude of the measured ¹J_CC couplings (from 37 to 45 Hz) enabled the level of enrichment on each site to be fitted as well as T₂′ for both components.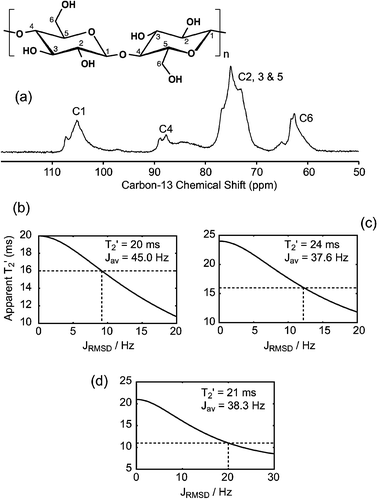

Fig. 2 (a) ¹³C CP-MAS spectrum of 11% ¹³C-enriched cellulose extracted from wood, recorded in 128 scans at 125.76 MHz (11.74 T) at the MAS frequency of 25 kHz, and using SPINAL64⁶⁶ heteronuclear decoupling at the proton nutation frequency of 140 kHz. Cross polarization from protons to carbons was achieved by an adiabatic passage through the Hartmann–Hahn condition,⁶⁷ with a contact time of 1 ms. (b, c, d) Numerical simulations reproducing the apparent dephasing behavior of the J-modulated components in disordered cellulose extracted from wood measured in ref. 6. The intrinsic T₂′ values indicated on each plot are taken identical, as measured in ref. 6 for the mono-exponential component of each site, and the J-coupling corresponds to the fitted value on the same site. The standard deviation is then increased from 0 to 20 or 30 Hz. The expected width of the underlying J-coupling distribution is finally given by the intersection between the curve describing the evolution of the apparent dephasing time as a function of the distribution width (solid line) and the dashed line indicating the apparent T₂′ measured for the J-modulated component in ref. 6. (b) For site C1, a J-distribution of standard deviation ±9 Hz could explain the apparent dephasing time of 16 ms measured for the J-modulated component, compared to 20 ms for the background component. (c) Simulation of site C4, where a standard deviation of ±12 Hz is required to explain the differences between the T₂′ of the J-modulated and background components. (d) For sites C2–C3–C5, a distribution of standard deviation ±20 Hz is postulated.

In that case, the presence of the structural disorder was considered as a challenge for the application of the method, and not as a structural issue to be addressed. In particular, as mentioned above, each resolved site corresponds to a distribution of structures, (as illustrated in ref. 14 by the broad apparent line widths Δ* compared to the refocused line widths Δ′), suggesting that the observed J-couplings actually arise from an ensemble of structures, which may potentially have different J-couplings for a given pair of sites. As a consequence, the J-coupling constants reported in ref. 6 may be average values over the ensemble of couplings within a given pair. Furthermore, as a consequence of the use of non-selective pulses, the measured J-couplings were not pair specific. Indeed, in the case of site 4, for example, the measured value arises from both ¹J(¹³C4–¹³C3) and ¹J(¹³C4–¹³C5) (both being, in addition, potentially distributed), which significantly contribute to the dispersion of J-coupling constants. Here, in view of the analysis proposed in Section 3.a, we aim to show that the systematic differences observed previously⁶ between the T₂′ of the background and the J-modulated components could be due to the presence of a J-distribution.

In Fig. 2(b,c,d), we show the results of similar simulations as in Fig. 1, where the parameters were chosen to reproduce the measurements reported in ref. 6, the intrinsic T₂′ being the one extracted from the single-exponential component of the considered site, and the average J-constant being the coupling measured for this site. The intersection of the simulated apparent dephasing time (solid line) and the dashed line, corresponding to the T₂′ of the cosine-modulated component, yields the standard deviation of the J-distribution that would potentially be responsible for the difference in T₂′ observed between the J-modulated and background components. Thus, a J-distribution of standard deviation ∼9 Hz on ¹J_C1–C2, for an average value of ¹J_C1–C2 = 45 Hz, could explain the apparent value of T₂′ = 16 ms for the J-modulated component of site 1 compared to T₂′ = 21 ms for the single exponential background (Fig. 2(b)). In the same way, a distribution of 37 ± 12 Hz can be postulated for site 4 (mixture of ¹J_C3–C4 and ¹J_C4–C5), as shown in Fig. 2(c), and a distribution of 38 ± 20 Hz for non-resolved sites 2, 3 and 5 (mixture of ¹J_C1–C2, ¹J_C2–C3, ¹J_C3–C4, ¹J_C4–C5, and ¹J_C5–C6), as shown in Fig. 2(d). Here, the presence of several distinct pairs clearly (and not surprisingly) further increases the apparent dephasing, since it will naturally lead to a broader J-coupling distribution than variations within a single pair. Moreover, the fact that no J-coupling constant could be observed in ref. 6 for site C5–C6 could also be attributed to the presence of quite a broad J-coupling distribution.

The standard deviations predicted from this analysis seem, however, somewhat large, and there could be other effects (such as those suggested in ref. 6) that contribute to the differences between the intrinsic T₂′ for the background parts and the apparent T₂′ for the J-modulated components, though J-coupling distributions are probably the major source of these differences.

This example (in combination with previous observations^5,27) indicates that J-coupling distributions exist in disordered solids, and can be roughly estimated from the apparent T₂′ value, provided the true T₂′ of the spins is known. However, this approach suffers from some degree of uncertainty, and will tend to overestimate the coupling distribution in most cases, since the T₂′ of an isolated spin is expected to be systematically longer than the T₂′ of a labelled spin-pair. In the following, new methods to observe directly these distributions will be introduced.

4. Measurements of 1D J-coupling distributions

4.a. Measurement of the ²J(³¹P–N–³¹P)-coupling distribution in a bis-phosphino amine

As mentioned above, since disordered solids have inhomogeneously broadened peaks, 1D spectra already allow a certain degree of resolution among the ensemble of structures that compose a disordered solid sample. As a result, J-coupling distributions can potentially be observed along the one-dimensional chemical shift distributions, as very recently demonstrated by Massiot and co-workers.^5,27 Here, we report the observation of a ²J(³¹P–N–³¹P)-coupling distribution obtained on (1), whose formula is shown in Fig. 3(a). Phosphorus–phosphorus indirect couplings have been routinely measured for years by solid-state NMR due to the high magnetogyric ratio of ³¹P and to its nearly-100% natural abundance.^1,2

Fig. 3 (a) Planar formula of N,N-bis(diphenylphosphino)-N-((S)-α-methylbenzyl)amine (1). (b) First row of the ³¹P pseudo-2D z-filtered spin-echo experiment on (1), at 202.47 MHz (11.74 T), obtained for τ = 0 ms. The numbering corresponds to the residues in the X-ray structure, and the assignment was obtained from first principles calculations (reported elsewhere³⁶). (c) Pulse sequence of the z-filtered spin-echo experiment for measuring 1D J-distributions. The role of the z-filters is discussed in detail in the text. (d)J-distribution (solid line) measured for site 4b, with the error bars being indicated by the dashed lines. The J-coupling variations observed along the chemical shift distribution of site 4b are clearly significant with respect to the calculated errors. (e) One modulation curve (for the signal at 48.0 ppm) among the ensemble of modulation fits that generate the J-distribution of Fig. 3(d) over the chemical shift distribution of site 4b. The pseudo-2D z-filtered spin-echo experiment was recorded at the spinning frequency of 30 kHz. SPINAL64⁶⁶ heteronuclear decoupling was applied at a proton nutation frequency of 140 kHz, and a 2 ms contact time was used for CP from protons to phosphorus. A total of 25 rotor-synchronized τ-delay increments of 1 ms with 32 scans each were used to observe the J-modulation, with a recycle delay of 6 s, and z-filters of 5 ms and 10 ms were used after CP and before detection, respectively. The sample temperature was 310 ± 2 K.

Fig. 3(b) shows the CP-MAS spectrum of (1), together with the assignment to the 4 molecules in the asymmetric unit of the X-ray structure. The “a” and “b” letters refer to the two ³¹P nuclei in each residue, respectively, at high and low frequency. The details of the assignment will be described elsewhere on the basis of first principles chemical shift calculations.³⁶ Each resonance is roughly 200 Hz broad. In addition, refocused INADEQUATE¹⁴ spectra have been recorded and discussed in detail,^29,37 since they provide narrow elongated cross peaks corresponding to highly correlated inhomogeneous broadening, which was postulated to be due to slight structural disorder within the crystalline environment described by the X-ray structure.

J-coupling distributions were measured for (1) using the z-filtered spin-echo modulation sequence shown in Fig. 3(c). The analysis was limited only to sites 3a and 4b, which are the only fully resolved sites in the spectrum, so as to avoid any averaging over two different molecules in the asymmetric unit, thus providing exclusively pair-specific J-coupling measurements. A fit of the echo modulation was carried out for each point along the 1D chemical shift distribution. The result obtained for site 4b is shown in Fig. 3(d), and clearly shows a variation in the J-coupling constants as the chemical shift varies for one given molecule in the asymmetric unit.

An example of the spin-echo modulation for those residues 4 that have a site 4b that resonates at 48.0 ppm is shown in Fig. 3(e), together with the corresponding fit, which is in excellent agreement with the experimental data. It is noteworthy that, although the modulation from each frequency inside a given line is very well described by a single value of J, the variation of the J-coupling constant within a given site is larger than the errors and thus clearly significant (for site 4b, J varies from 22.3 to 21.8 Hz between 47.1 and 48.3 ppm). Moreover, site 3a also yields a (smaller) J-coupling distribution of ±0.1 Hz around 25.4 Hz (data not shown). However, given the small variations in the J values, some experimental aspects of this experiment deserve attention for the existence of the distribution to be confirmed.

First, the role of the z-filter subsequent to CP is to circumvent the effects of undesired evolution under the J-couplings, which can occur during simultaneous irradiation of coupled ³¹P during the cross polarization from ¹H to ³¹P. Indeed, it has been shown that undesired double-quantum coherences are generated during simultaneous inversion of J-coupled spins using long soft-pulses.³⁸ Similarly, Miao and Freeman have shown that the τ delay corresponding to the maximum intensity of the anti-phase sine-modulated components during the spin-echo is shifted (backward in time) by approximately half the duration of the pulse when two coupled spins are simultaneously refocused using long soft-pulses, again because of evolution occurring during the pulse.³⁹ As a result, since the coupled spins are simultaneously irradiated for a long time during the CP, the z-filter subsequent to CP is essential for the accurate measurement of the J-coupling modulation. This effect is further discussed elsewhere.³⁵

Second, anti-phase terms are generated during the spin-echo through the action of the J-coupling interaction and are at their maximum intensity at the position of the root of the in-phase cosine-modulated components, and may cause distortions of the observed modulation if the intensity is not integrated over the whole peak (in which case, anti-phase contributions would cancel out due to their anti-symmetric nature). As a consequence, the z-filter that follows the spin-echo (Fig. 3(c)) plays a crucial role. The phase of the 90° pulse subsequent to the spin-echo is set orthogonal to the phase of the cosine-modulated components, so that the cosine-modulated contributions are sent back to the z-axis, while the anti-phase contributions are kept in the transverse plane for dephasing, which is enhanced by switching off the heteronuclear decoupling during the z-filter. Complete dephasing of the undesired contributions is expected for z-filter lengths significantly longer than the T₂* in the absence heteronuclear decoupling. In the case of the results shown in Fig. 3, the z-filter length was set to 10 ms, and the observation of the Free Induction Decay (FID) in the absence of heteronuclear decoupling (spinning at 30 kHz) shows that the signal detected at t₂ = 10 ms is approximately 1% of the signal at the beginning of the detection period. This ensures that the distribution of J-couplings observed in Fig. 3(d) does not arise from distortions of the modulation due to anti-phase contributions along the chemical shift distribution. However, spin diffusion might occur during the z-filters, and we therefore show in the ESI† a spin-diffusion experiment obtained on (1), under similar conditions as the experiment for measuring J-distributions. No cross peaks are observed using a mixing time of 10 ms in this experiment, indicating that no magnetization transfer through spin-diffusion occurs during a z-filter of comparable length.

The discussion above thus validates the quality of the experimental data, and, in combination with the analysis of the robustness of the spin-echo modulations in solids by Duma et al.,⁷ allows us to demonstrate that pair-specific J-coupling distributions can be observed by solid-state NMR, even for small variations in J.

4.b. Limitations of 1D J-coupling distributions

The primary limitation of the z-filtered spin-echo modulation for measuring J-coupling distributions arises from site overlap. The way to overcome this limitation is fairly evident: rather than measuring a J-coupling constant for each point in the 1D chemical shift distribution, J-distributions should be measured for each point in a 2D chemical shift correlation spectrum.

The second limitation is illustrated in Fig. 4, which shows the comparison of two 2D correlation cross peaks obtained from two fundamentally different types of solids having some level of structural disorder . Fig. 4(a) shows a cross peak between the two J-coupled sites 3a and 3b of (1), obtained from a refocused INADEQUATE¹⁴ spectrum (not shown). This cross peak has a remarkably linear elongated shape, in which each frequency in the horizontal (direct) dimension correlates with a narrower distribution of frequencies in the vertical (indirect) dimension. On the contrary, a similar Single Quantum–Single Quantum (SQ–SQ) cross peak between two J-coupled sites (C1–C2) from 11% ¹³C enriched cellulose extracted from wood (Fig. 4(b)) exhibits a substantially more complicated shape, in which one chemical shift in the direct dimension corresponds to a broad set of distinct frequencies (with several maxima) in the indirect dimension. This is a clear indication that the frequency considered here in the direct dimension corresponds to an ensemble of structures that yield accidentally-degenerated frequencies of one site. As a result, each frequency in the direct dimension may contain a distribution of J-couplings. This would lead to the averaging effect discussed above and illustrated in Fig. 1, which generally results in an underestimated width of the resulting J-distribution. In the next section, we therefore introduce two variants of a new experiment that provide different ways of encoding J-coupling distributions on the basis of such 2D chemical shift correlation peaks.

Fig. 4 Comparison of two Single Quantum-Single Quantum (SQ-SQ) cross peaks obtained from different disordered solids, (1) in (a), and the disordered cellulose extracted from wood in (b) (C1–C2 correlation). As outlined by the solid lines, one chemical shift of one site may correspond to an ensemble of different structures, thus potentially yielding distinct J-coupling values. Both cross peaks were obtained from refocused INADEQUATE spectra shown in ref. 29, recorded on a 11.74 T spectrometer, and sheared from Double Quantum-Single Quantum (DQ-SQ) to SQ-SQ.

5. Two-dimensional J-coupling distributions

5.a. Pulse sequences for measuring two-dimensional J-coupling distributions

As mentioned above, the measurement of 2D distributions of scalar couplings requires the recording of an additional chemical shift dimension. The more sensitive the two individual chemical shift distributions are to the variations of the local environments that are responsible for the J-distribution, the better the final resolution of the distribution will be. As a consequence, it is natural to measure the distribution of J_AB on the basis of a direct A-B cross peak. Since A and B are J-coupled by definition, the most suitable pulse sequences use through-bond correlation (though through-space methods could, in principle, be used as well). Much effort has recently been provided for developing robust homonuclear through-bond correlation techniques in solid-state NMR,^14,40–46 and though most of these methods could have been used in the present study, we employed the refocused INADEQUATE experiment, whose robustness for both ordered and disordered solids has been repeatedly demonstrated,^{14,17,47–54} and in which the t₁ (indirect) and the t₂ (direct) dimensions provide Double Quantum-Single Quantum (DQ-SQ) through-bond correlation spectra. An additional spin-echo τ-π-τ was appended in order to observe J-coupling modulations by incrementing the τ delay in a pseudo-3D fashion. (The term “pseudo 3D” here indicates that no Fourier transformation is required in the spin-echo (τ) dimension, though it could be envisaged to provide a J-resolved dimension.^1,2) The principle of such experiments was already proposed, although not implemented, in ref. 6.

The first sequence (Fig. 5(a)) starts with the conventional refocused INADEQUATE experiment, during which the magnetization is transferred between J-coupled neighbors to create DQ coherences that evolve in the indirect dimension (other coherences being filtered out). These DQ coherences are converted back to anti-phase SQ coherences after t₁, and then to in-phase coherences through the second spin-echo. At this point, the magnetization is sent back to the z-axis during a z-filter, which removes undesired remaining anti-phase terms. The subsequent 90° pulse defines the origin of the following spin-echo modulation for measuring J-couplings. Finally, another z-filter is applied before acquisition to remove the anti-phase contributions created during the spin-echo (see discussion in Section 4.a). This experiment is repeated for a given number of incremented rotor-synchronized τ values, which yield a series of 2D DQ-SQ spectra in which the intensity of every point in a cross peak is modulated, as a function of τ, under the J-couplings between the two correlated sites. This pulse sequence is particularly well adapted for the observation of the modulation between isolated spin-pairs, as passive couplings can produce artifacts that may affect the measurement of the J-couplings. A second variant is introduced, which enables time saving in the measurement of J-coupling distributions, by limiting the spectral width in the indirect dimension through selective excitation.

Fig. 5 Pulse sequences for the measurement of 2D J-coupling distributions in disordered solids. Both contain a refocused INADEQUATE block that provides a 2D spectrum on the basis of through-bond magnetization transfer, and a spin-echo for measuring J-coupling modulation in a third dimension. (a) Non-selective method, which provides a J-modulation in the case of isolated spin-pairs (see Section 5.c for application to (1)). (b) Selective method, which provides series of 2D spectra of small spectral width in the indirect DQ dimension if an extremity of a linear spin system is chosen as the excited spin, thus reducing the experimental time (see Section 5.b for an application to the C5–C6 pair of cellulose).

The pulse sequence shown in Fig. 5(b) is similar to that of Fig. 5(a), with the only difference being an additional z-filter after CP, followed by a selective excitation pulse that enables one to transfer the magnetization from only one selected resolved site in the sample. Given a linear A-B-C spin system, the semi-selective pulse can be applied either to A or C, in order to selectively create DQ coherences, respectively, between A and B or between B and C. During the final spin-echo, the cross peak whose frequency in the direct SQ dimension corresponds to the excited site will exhibit a J-modulation under the coupling to site B, as a function of τ. The main advantage of this method is that the spectral width in the indirect dimension can be dramatically reduced, since only one pair of cross peaks will appear in the 2D spectra, at the same DQ frequency. The DQ-dimension is thus acquired with a limited number of points in t₁, providing a considerable time saving,^55,56 of crucial importance for such pseudo-3D experiment. We note, moreover, that both methods can be applied to partially as well as fully isotopically-enriched systems, since the refocused INADEQUATE block systematically eliminates background contributions due to non-labeled neighbors.

5.b. Application to cellulose I

In this section, we present the results obtained using the pulse sequence of Fig. 5(b) on a fully ¹³C-enriched sample made up of a mixture of celluloses I_α and I_β, whose CP-MAS spectrum is shown in Fig. 6(a). The following analysis will focus on pair C5–C6, for which a large distribution of ¹J_CC-couplings was hypothesized in the sample of 11% ¹³C-enriched cellulose extracted from wood. Since C5 is J-coupled to both sites C4 and C6, C6 (which is only coupled to C5) must be the selectively excited site S (Fig. 5(b)), on which the ¹J_C5–C6-modulation will be observed. Fig. 6(b) shows the semi-selective 2D spectrum obtained for τ = 0 ms. In Fig. 6(c), we show the evolution of the row at 138.1 ppm in the indirect dimension (dotted line in Fig. 6(b)) as a function of the τ delay, and see that the intensity of the C6 signal is modulated by the J_C5–C6-coupling, whereas no clear modulation is observed on site C5, which is also coupled to C4, and consequently experiences a double modulation. Fig. 6(d) shows the resulting 2D J-coupling map, obtained by first shearing all of the DQ-SQ spectra of the series to convert them into SQ-SQ spectra.^29,57 For all the points in the region of the C6 cross peak, the evolution of the intensity as a function of τ is fitted, and the measured ¹J_C5–C6-coupling constant is then reported in Fig. 6(d) (colored map), with the SQ-SQ cross peak (τ = 0) superimposed (solid lines). The two intense signals at (71.5 ppm, 65.6 ppm) and (73.0 ppm, 65.4 ppm) correspond to the C5–C6 signal of the two non-equivalent residues, with the forms I_α and I_β being unresolved in this particular case,⁴⁹ and the small signals at (75.5 ppm, 62.5 ppm) and (74.3 ppm, 61.7 ppm) correspond to amorphous domains of cellulose. The experimental reliability of the values in the J-coupling map is probed through the corresponding error map, Fig. 6(e), as a contour plot of the errors on the J-value along the 2D cross peak, and which was calculated according to the procedure described in Section 2.c, using 128 random fluctuations around the experimental values.

Fig. 6 Experiment for the measurement of the 2D distribution of J-couplings for the C5–C6 pair of fully ¹³C-enriched cellulose I_α and I_β. (a) Semi-developed formula of cellulose. The two rings are non-equivalent, which gives rise to 12 distinct sites for each form of cellulose. The 176.06 MHz (16.44 Tesla) CP-MAS spectrum was recorded in 8 scans at 24 kHz MAS, using SPINAL64 ¹H decoupling at 125 kHz, and cross polarization from protons to carbons was achieved using an adiabatic passage through the Hartmann and Hahn condition,⁶⁷ with a contact time of 1 ms. (b) First 2D spectrum of the pseudo-3D experiment for measuring 2D J-coupling distributions, the excited site being C6. The scale in the indirect dimension contains the whole spectral width (7.1 ppm, or 1250 Hz). (c) Modulation of the extracted row at 138.1 ppm (dashed line in (b)) as a function of half the spin-echo duration τ. A pure modulation is observed for site C6, which is only coupled to C5, whereas C5 shows a more complex behavior due to its additional coupling to C4. (d) 2D J-coupling distribution map, which shows small variations in the measured ¹J_CC-coupling constant, with the contour plot of the 2D SQ-SQ spectrum superimposed in black. (e) Map of error bars that are calculated for each point in the 2D map, according to the procedure described in Section 2.c, using 128 random fluctuations. The experiment for measuring 2D J-distributions was recorded using Cosine Modulated (CM) heteronuclear decoupling⁶⁸ at a proton nutation frequency of 125 kHz, with phase parameters being optimized using the principles of the Transverse Dephasing OPtimization approach (TDOP).^16,17 The duration of the z-filters was set to 2, 2 and 3 ms, respectively, after CP, before the J-modulation spin-echo, and before acquisition. An E-BURP⁶⁹ pulse of 4.5 ms was used for the semi-selective excitation of site C6. Each 2D spectrum was acquired within 256 transients, and 20 t₁ increments, with a spectral width of 1250 Hz in the indirect dimension, and a recycle delay of 3 s. The experiment was repeated for 9 rotor-synchronized values of τ ranging from 0 to 8 ms, for a total duration of 40 h.

Though small variations of the ¹J(¹³C5–¹³C6)-coupling are observed in the map of Fig. 6(d), they are at the limit of the error bars. One-bond couplings are essentially sensitive to substitution of surrounding nuclei,¹² or to the nature of the chemical bond.⁵⁸ The structure of celluloses I_α and I_β has recently been reported from X-ray and neutron diffraction studies on samples made of either pure cellulose I_α or pure cellulose I_β,^59–61 allowing a close comparison of these two forms, which generally coexist, even within the same microfibril, in native cellulose. One major difference between the I_α and I_β forms is that cellulose I_α is made up of equivalent chains sheared with respect to each other along the fibril axis, the repeating unit being the two adjacent glucosyl residues, of different conformations, labeled u and d. On the other hand, the adjacent residues are conformationally equivalent in cellulose I_β, and the unit cell involves two distinct parallel chains: the origin and center chains. As a consequence of these differences the two forms belong to two distinct space groups: I_α having a monoclinic P2₁unit cell , while cellulose I_β belongs to a triclinic P1 space group.

One of the main sources of variations of the ¹J(¹³C5–¹³C6)-coupling is expected to be the χ and χ′ angles, which correspond to the O5–C5–C6–O6 and C4–C5–C6–O6 dihedral angles, respectively. These angles are identical between the two conformationally-equivalent residues of cellulose I^(u)_α and I^(d)_α,⁶⁰ and similar values have been found between the (χ, χ′) angles in forms I^(d)_α and I^origin_β. Yet a small difference of about 10° in (χ, χ′) has been observed from I^(u)_α and I^centre_β, which is responsible for a very small splitting (about 0.5 ppm in the direct F₂ dimension) in the region around (73.0 ppm, 65.4 ppm) in a refocused INADEQUATE spectrum obtained in TDOP conditions (not shown). However, in the spectrum (for τ = 0 ms) shown in Fig. 6b, this splitting is not visible as a line broadening of 60 Hz was applied in both dimensions to reduce the experimental noise. As a consequence, in this particular case, potential differences in the ¹J_C5–C6 due to the orientation of the hydroxymethyl group are averaged out because of the overlap of the C5–C6 cross-peak signals arising from I^(u)_α and I^centre_β.

Finally, another potential source of variation of the ¹J_C5–C6-coupling may be the orientation of the hydrogen of the primary alcohol function, and thus of the lone electron pairs of O6, in α position with respect to C6, as this effect is known to influence ¹J_CC-couplings.¹¹ The orientation of this hydrogen is highly related to the hydrogen-bonding network of cellulose. In the neutron diffraction studies, several possible positions have been observed⁶⁰ due to the strongly labile character of this proton, which thus probably also results in an averaging of the ¹J_C5–C6-coupling, preventing the observation of strong variations in Fig. 6(d).

Thus, the weak variations observed along the 2D J-coupling distribution are probably due to continuous small deviations of the χ and χ′ angles, the C5–C6 distance and the hydrogen bonding network within the microfibrils. In particular, we note that a smaller ¹J_C5–C6-coupling value of 44 ± 2 Hz is measured for the amorphous components at (75.5 ppm, 62.5 ppm) and (74.3 ppm, 61.7 ppm), assigned to the surface of the microfibrils,^62–64 compared to the crystalline components (46 ± 1 Hz). In addition, we can also postulate that extension at the bottom of the region containing the crystalline forms, around (75 ppm, 65.5 ppm) might arise from defaults in the microfibrils, though this has to be confirmed, and also yield substantially smaller C5–C6 coupling than the crystalline components.

This suggests that, if a larger ¹J_C5–C6-coupling distribution exists in the disordered sample of cellulose extracted from wood, as postulated in Section 3.b (though we recall that the method used there will tend to overestimate the size of the distribution), it probably arises from significant differences between cellulose I and cellulose II, for example to the anti-parallel arrangement of the origin and center chains in cellulose II, and most probably to differences between ¹J_C5–C6-values for the crystalline components and the abundant amorphous phase present in the sample extracted from wood.^6,29 Unfortunately, though similar experiments were carried out on the disordered sample (not shown), the low level of enrichment led to low overall sensitivity, and so far prevented the observation of significant differences in the ¹J_C5–C6-coupling, because of large errors on the measured J-values.

5.c. Application to the bis-phosphino amine: observation of a 2D ²J_PP distribution

In Section 4.a, we have already shown that small 1D J-coupling distributions can be observed for two of the four distinct ³¹P–³¹P pairs in (1). In this section, we apply the pulse sequence of Fig. 5(a) in order to measure J-couplings from the unresolved peaks in the spectrum. Indeed, we already know that all the peaks are fully resolved in the INADEQUATE spectrum,^29,37 and a single J-modulation is thus expected for all of the peaks in the third dimension. Furthermore, the 2D distributions potentially provide a richer source of information compared to the 1D distributions, as discussed in Section 4.b.

Fig. 7(a) shows the first 2D spectrum of the series, obtained for τ = 2.5 ms, and sheared from DQ-SQ to SQ-SQ.²⁹ The 2D J-coupling distribution obtained for pair 1a-1b is shown in Fig. 7(b, left), together with the corresponding map of error bars (Fig. 7(b, right)). A clear distribution is observed, with ²J(³¹P–N–³¹P)-coupling constants ranging from 26 to 30 Hz, the error bars being below ±0.8 Hz for the most part of the cross peak. Not surprisingly, the error map has a similar shape to the cross-peak intensity, and is strongly different from the J-distribution profile, indicating that the major source of error here is the random noise, and not systematic errors. Fig. 7(c) shows the J-coupling distribution corresponding to the pair of cross-peaks 2a–2b, which are also overlapped with other sites in the 1D spectrum, so that no distribution could be measured from the 1D experiment. Again, distributed J-coupling constants from 24 to 28 Hz are observed, with perfectly symmetric profiles of the two cross peaks with respect to the diagonal, which is an additional indication of the validity of this result. Similarly, the symmetry within each pair of J-distributions was observed for all the cross peaks in the sample, which suggests in particular that the non-intuitive distribution of J-coupling values perpendicularly to the main direction of the cross peaks is not an artifact and has a structural origin. Such effects cannot be seen from the experiment of Fig. 3, where the J-coupling values along a direction perpendicular to the main axis of the cross peaks are averaged out. This also explains why the range of variation observed in Fig. 3(d) is small (±0.2 Hz) compared to Fig. 8(b) and (c). Such a strong variation of J-couplings for a given site is a clear indication that ²J_PP-couplings are sensitive to only slight deviations from a given structure (the distortions that are responsible for this distribution being small enough for there to be a X-ray structure⁶⁵).

Fig. 7 Results obtained through the application of the pulse sequence of Fig. 5(a) to (1). (a). Sheared (from DQ-SQ to SQ-SQ) 2D spectrum (for τ = 2.5 ms) from the pseudo-3D experiment for measuring 2D J-coupling distributions. A 2D distribution was observed for each cross peak in this spectrum. (b, left) J-coupling map for the cross peak between 1a and 1b, outlined in Fig. 7(a), arising from the modulation under ²J(³¹P_1a–N–³¹P_1b) as a function of τ, together with the corresponding error estimates (b, right), which notably follow the intensity of the cross peak rather than the J-coupling distribution. (c, left) J-couplings obtained from both cross peaks between 2a and 2b, and corresponding errors. The symmetry of the J-coupling distributions for both peaks with respect to the diagonal is an indication of the validity of the observed distribution. This experiment was recorded using the pulse sequence shown in Fig. 5(a), at the ³¹P frequency 283.42 MHz (16.44 Telsa), and a MAS frequency of 32 kHz. Polarization transfer from ¹H to ³¹P was achieved with a contact time of 2 ms through an adiabatic shape on the proton channel.⁶⁷ The SPINAL64⁶⁶ scheme at a proton nutation frequency of 125 kHz was used for heteronuclear decoupling. The z-filters were set to 10 ms each (during which negligible spin-diffusion occurs, as confirmed by spin-diffusion experiments), and the τ₀ delay was experimentally optimized to 8 ms for best efficiency. For each value of the final spin-echo delay 2τ, ranging from 2.5 to 22. 5 ms, a 2D experiment was obtained with 112 rotor-synchronized t₁ increments, using 32 transients, and a recycling delay of 6 s, corresponding to an experimental time of 6 h for each value of τ, and 55 h in total.

Fig. 8 Plot of the average ²J_PP-coupling values for the 4 residues in the asymmetric unit of (1), as a function of the corresponding (average) P–N–P bond angles (a) and distances (b) extracted from the X-ray structure.⁶⁵ A clear dependence of the ²J(P–N–P)-couplings as a function of these local structural parameters is observed. Rough trends are indicated by dotted lines.

Furthermore, the average J-coupling constants for all the residues in the asymmetric unit are also obtained from this experiment by fitting the evolution of the integrated signal over the entire cross peaks as a function of τ, and are summarized in Table 1. According to Fig. 1(c) and the related discussion in Section 3, the average J-coupling value should not be overestimated by more than 1% given the standard deviations in the observed distributions (below 10%), and the reported values should thus be highly reliable. The variations observed in the average ²J_PP-coupling constants from one residue to another again indicate that such interactions are strongly sensitive to structural variations. Fig. 8 illustrates this point with the plots of the different average ²J_PP-couplings as functions of the P–N–P bond angles and P–P distances extracted from the crystal structure. A fairly clear dependence on these local parameters is observed, with high J-coupling constants corresponding to large bond angles and distances.

Table 1 Average ²J_PP-coupling constants in N,N-bis(diphenylphosphino)-N-((S)-α-methylbenzyl)amine (1)

Pair	Detected	Measured ^2JPP/Hz	Retained ^2JPP/Hz
a Obtained using the z-filtered spin-echo experiment (Section 4.a).
3a–3b	3a	26.0 ± 0.2	25.9 ± 0.2
	3b	26.1 ± 0.2
	3a^a	25.8 ± 0.1
2a–2b	2a and 2b	26.4 ± 0.3	26.4 ± 0.3
1a–1b	1a	27.9 ± 0.3	27.8 ± 0.3
	1b	27.7 ± 0.1
4a–4b	4a	24.2 ± 0.5	22.7 ± 0.3
	4b	22.9 ± 0.2
	4b^a	22.6 ± 0.1

---

Crudely modeling the variation of the J-couplings as functions of the P–N–P bond angle and P–P distance by a linear trend, as indicated by the dotted lines in Fig. 8(a) and (b), we can analyze the structural distortions that would be associated with the variations in J observed for the correlation peaks. In particular, an interpretation can be proposed for the a priori unexpectedly broad distribution of the ²J_1a–1b-coupling constants along the indirect dimension in Fig. 7(b), which vary from 26 Hz to 30 Hz. In this case, we can roughly estimate that increasing the ²J_1a–1b by about 4 Hz may correspond to a structural variation involving increasing the P_1a–N–P_1b bond angle by about 1.5°, and P_1a–P_2a distance by about 0.01 Å, while decreasing the chemical shift of ³¹P-site 1b by 1 ppm and keeping the chemical shift of site 1a constant.

This example clearly illustrates the rich potential of such 2D J-coupling distributions as a source of structural information for the characterization of the local structural disorder . A more quantitative approach can also be considered through ab initio calculations of J-couplings and of chemical shifts. This is currently under investigation, and shall be reported elsewhere.³⁶

Conclusions

The existence of J-coupling distributions, and their effects on the measurement of average J-coupling values, have been analyzed and discussed. The presence of a distribution of J-coupling constants should not lead to significantly modified measured average values, though it will induce a faster dephasing. The presence of ¹J_CC distributions is then shown to be potentially responsible for the differences reported in the literature⁶ between the apparent T₂′ values of J-coupled moieties and isolated background moieties in partially ¹³C-enriched disordered cellulose. Using a z-filtered spin-echo experiment, we have demonstrated the existence of a pair-specific distribution of ²J(³¹P–N–³¹P)-coupling constants in a slightly disordered bis-phosphino amine sample. However, the poor resolution provided by 1D spectra is found to be strongly limiting for the measurement and interpretation of J-coupling distributions, and we therefore introduced pseudo-3D NMR methods that provide 2D J-coupling distributions on the basis of refocused INADEQUATE spectra. A selective method, which allows a reduced indirect spectral width and thus reasonable experimental time, was applied to a fully ¹³C-enriched sample of slightly disordered cellulose I_α and I_β, where only low amplitude variations were observed for the C5–C6 pair. This was attributed to the poor sensitivity of ¹J_CC couplings to structural variations, and to the highly similar local structure of the considered fragment between the two residues of cellulose I_α and I_β. Nevertheless, significant differences in ¹J_C5–C6 were observed between the amorphous and the crystalline components of cellulose I. Finally, significant 2D distributions of ²J(³¹P–N–³¹P) couplings were obtained by using a non-selective version of the method on the bis-phosphino amine sample, demonstrating the ability of the method to provide 2D J-coupling distributions, and showing the sensitivity of two-bond coupling distributions to local structural variations. The distributions thus provide a powerful probe for characterizing local structural disorder , as illustrated by a semi-quantitative analysis of the J-coupling variations in terms of small changes in the P–N–P bond angle, of the order of about 1.5°, and in the P–P distance, of about 0.01 Å, within a single cross peak of a given residue.

Acknowledgements

We are grateful to Y. Gimbert and M. Bardet (Grenoble) for providing us with the samples of disordered cellulose and of bis-phosphino amine, and to Steven P. Brown (Warwick) for stimulating discussions. NMR spectra were recorded at the Rhône-Alpes Large Scale Facility for NMR (www.ralf-nmr.fr).

References

1. A. Kubo and C. A. McDowell, J. Chem. Phys., 1990, 92, 7156–7170.
2. G. Wu and R. E. Wasylishen, Inorg. Chem., 1992, 31, 145–148.
3. S. P. Brown, M. Perez-Torralba, D. Sanz, R. M. Claramunt and L. Emsley, Chem. Commun., 2002, 1852–1853.
4. A. Lesage, L. Emsley, M. Chabanas, C. Coperet and J. M. Basset, Angew. Chem., Int. Ed., 2002, 41, 4535.
5. F. Fayon, I. J. King, R. K. Harris, J. S. O. Evans and D. Massiot, C. R. Chim., 2004, 7, 351–361.
6. S. P. Brown and L. Emsley, J. Magn. Reson., 2004, 171, 43–47.
7. L. Duma, W. C. Lai, M. Carravetta, L. Emsley, S. P. Brown and M. H. Levitt, ChemPhysChem, 2004, 5, 815–833.
8. W. C. Lai, N. McLean, A. Gansmüller, M. A. Verhoeven, G. C. Antonioli, M. Carravetta, L. Duma, P. H. M. Bovee-Geurts, O. G. Johannessen, H. J. M. de Groot, J. Lugtenburg, L. Emsley, S. P. Brown, R. C. D. Brown, W. J. DeGrip and M. H. Levitt, J. Am. Chem. Soc., 2006, 128, 3878–3879.
9. M. Karplus, J. Chem. Phys., 1959, 30, 11–15.
10. M. Karplus, J. Am. Chem. Soc., 1963, 85, 2870–2871.
11. R. H. Contreras and J. E. Peralta, Prog. Nucl. Magn. Reson. Spectrosc., 2000, 37, 321–425.
12. R. H. Contreras, J. E. Peralta, C. G. Giribet, M. C. De Azua and J. C. Facelli, in Annu. Rep. Nucl. Magn. Reson. Spectrosc., 2000, vol. 41, pp. 55–184.
13. B. A. Cowans and J. B. Grutzner, J. Magn. Reson., Ser. A, 1993, 105, 10–18.
14. A. Lesage, M. Bardet and L. Emsley, J. Am. Chem. Soc., 1999, 121, 10987–10993.
15. G. De Paepe, A. Lesage and L. Emsley, J. Chem. Phys., 2003, 119, 4833–4841.
16. G. De Paepe, N. Giraud, A. Lesage, P. Hodgkinson, A. Bockmann and L. Emsley, J. Am. Chem. Soc., 2003, 125, 13938–13939.
17. G. De Paepe, A. Lesage, S. Steuernagel and L. Emsley, ChemPhysChem, 2004, 5, 869–875.
18. D. L. Vanderhart, W. L. Earl and A. N. Garroway, J. Magn. Reson., 1981, 44, 361–401.
19. D. D. Laws, H. M. L. Bitter and A. Jerschow, Angew. Chem., Int. Ed., 2002, 41, 3096–3129.
20. I. Schnell, Prog. Nucl. Magn. Reson. Spectrosc., 2004, 45, 145–207.
21. T. Helgaker, M. Jaszunski and K. Ruud, Chem. Rev., 1999, 99, 293–352.
22. J. Vaara, J. Jokisaari, R. E. Wasylishen and D. L. Bryce, Prog. Nucl. Magn. Reson. Spectrosc., 2002, 41, 233–304.
23. K. Schmidt-Rohr and H. W. Spiess, Multi-dimensional solid-state NMR and polymers, Academic Press, San Diego, 1994.
24. R. H. Havlin and R. Tycko, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 3284–3289.
25. A. Lange, K. Giller, S. Hornig, M. F. Martin-Eauclaire, O. Pongs, S. Becker and M. Baldus, Nature, 2006, 440, 959–962.
26. H. Lock, J. C. Xiong, Y. C. Wen, B. A. Parkinson and G. E. Maciel, Solid State Nucl. Magn. Reson., 2001, 20, 118–129.
27. D. Massiot, F. Fayon, V. Montouillout, D. Iuga, C. Morais and Z. Gan, 4th Alpine Conference on Solid-State NMR, Chamonix, 2005.
28. M. Bardet, D. Gagnaire, R. Nardin, D. Robert and M. Vincendon, Holzforschung, 1986, 40, 17–24.
29. S. Cadars, A. Lesage and L. Emsley, J. Am. Chem. Soc., 2005, 127, 4466–4476.
30. D. Gagnaire and F. R. Taravel, Eur. J. Biochem., 1980, 103, 133–143.
31. Y. Gimbert, F. Robert, A. Durif, M. T. Averbuch, N. Kann and A. E. Greene, J. Org. Chem., 1999, 64, 3492–3497.
32. D. Konya, F. Robert, Y. Gimbert and A. E. Greene, Tetrahedron Lett., 2004, 45, 6975–6978.
33. W. L. Earl and D. L. Vanderhart, J. Magn. Reson., 1982, 48, 35–54.
34. C. R. Morcombe and K. W. Zilm, J. Magn. Reson., 2003, 162, 479–486.
35. S. Cadars, A. Lesage, N. Hedin, B. F. Chmelka and L. Emsley, J. Chem. Phys. B, 2006, 110, 16982–16991.
36. S. Cadars, A. Lesage, P. Sautet, C. J. Pickard and L. Emsley, manuscript in preparation.
37. D. Sakellariou, S. P. Brown, A. Lesage, S. Hediger, M. Bardet, C. A. Meriles, A. Pines and L. Emsley, J. Am. Chem. Soc., 2003, 125, 4376–4380.
38. L. Emsley, I. Burghardt and G. Bodenhausen, J. Magn. Reson., 1990, 90, 214–220.
39. X. J. Miao and R. Freeman, J. Magn. Reson., Ser. A, 1996, 119, 90–100.
40. M. Baldus and B. H. Meier, J. Magn. Reson., Ser. A, 1996, 121, 65–69.
41. A. Lesage, C. Auger, S. Caldarelli and L. Emsley, J. Am. Chem. Soc., 1997, 119, 7867–7868.
42. R. Verel, J. D. van Beek and B. H. Meier, J. Magn. Reson., 1999, 140, 300–303.
43. A. S. D. Heindrichs, H. Geen, C. Giordani and J. J. Titman, Chem. Phys. Lett., 2001, 335, 89–96.
44. L. J. Mueller, D. W. Elliott, K. C. Kim, C. A. Reed and P. D. W. Boyd, J. Am. Chem. Soc., 2002, 124, 9360–9361.
45. E. H. Hardy, A. Detken and B. H. Meier, J. Magn. Reson., 2003, 165, 208–218.
46. L. J. Mueller, D. W. Elliott, G. M. Leskowitz, J. Struppe, R. A. Olsen, K. C. Kim and C. A. Reed, J. Magn. Reson., 2004, 168, 327–335.
47. G. Grasso, T. M. de Swiet and J. J. Titman, J. Phys. Chem. B, 2002, 106, 8676–8680.
48. S. P. Brown, M. Perez-Torralba, D. Sanz, R. M. Claramunt and L. Emsley, J. Am. Chem. Soc., 2002, 124, 1152–1153.
49. H. Kono, T. Erata and M. Takai, Macromolecules, 2003, 36, 5131–5138.
50. H. Kono, Y. Numata, T. Erata and M. Takai, Macromolecules, 2004, 37, 5310–5316.
51. H. Kono, Y. Numata, T. Erata and M. Takai, Polymer, 2004, 45, 2843–2852.
52. T. N. Pham, S. Masiero, G. Gottarello and S. P. Brown, J. Am. Chem. Soc., 2005, 127, 16018–16019.
53. J. Emery, N. Dacheux and N. Clavier, Solid State Nucl. Magn. Reson., 2006, 29, 294–304.
54. R. K. Harris, S. A. Joyce, C. J. Pickard, S. Cadars and L. Emsley, Phys. Chem. Chem. Phys., 2006, 8, 137–143.
55. L. Emsley, in Nuclear Magnetic Resonance Pt C, 1994, vol. 239, pp. 207–246.
56. L. Emsley, in Encyclopaedia of NMR, ed. D. M. Grant and R. K. Harris, Wiley, Chichester, 1996, pp. 4228–4236.
57. R. R. Ernst, G. Bodenhausen and A. Wokaun, Principles of Nuclear Magnetic Resonance in One and Two Dimensions, Oxford Science Publications, New York, 1987.
58. D. Cremer, E. Kraka, A. A. Wu and W. Luttke, ChemPhysChem, 2004, 5, 349–366.
59. Y. Nishiyama, P. Langan and H. Chanzy, J. Am. Chem. Soc., 2002, 124, 9074–9082.
60. Y. Nishiyama, J. Sugiyama, H. Chanzy and P. Langan, J. Am. Chem. Soc., 2003, 125, 14300–14306.
61. P. Langan, N. Sukumar, Y. Nishiyama and H. Chanzy, Cellulose, 2005, 12, 551–562.
62. R. H. Newman, Solid State Nucl. Magn. Reson., 1999, 15, 21–29.
63. L. Heux, E. Dinand and M. R. Vignon, Carbohydr. Polym., 1999, 40, 115–124.
64. S. Montanari, M. Rountani, L. Heux and M. R. Vignon, Macromolecules, 2005, 38, 1665–1671.
65. F. Robert, Y. Gimbert, M. T. Averbuch-Pouchot and A. E. Greene, Z. Krist.-New Cryst. Struct., 2000, 215, 233–236.
66. B. M. Fung, A. K. Khitrin and K. Ermolaev, J. Magn. Reson., 2000, 142, 97–101.
67. M. Baldus, D. G. Geurts, S. Hediger and B. H. Meier, J. Magn. Reson., Ser. A, 1996, 118, 140–144.
68. G. De Paepe, B. Elena and L. Emsley, J. Chem. Phys., 2004, 121, 3165–3180.
69. H. Geen and R. Freeman, J. Magn. Reson., 1991, 93, 93–141.

---

Footnote

† Electronic supplementary information (ESI) available: Phosphorus-31 spin-diffusion experiment on (1). See DOI: 10.1039/b611096g

---