New software for searching the Cambridge Structural Database for solvated and unsolvated crystal structures applied to hydrates

Abstract

In this paper we describe several new pieces of software that allow the Cambridge Structural Database (CSD) to be searched for solvated and unsolvated crystal structures. One program finds all pairs of solvated and unsolvated crystal structures of the same chemical compound for a given solvent; another program finds all crystal structures that were grown from a particular solvent. In addition, an algorithm was implemented to determine the stereochemistry of a crystal structure from its 3-D atomic coordinates. Results for water as the solvent molecule are presented. It is found that about 25% of all crystal structures grown from water form hydrates. If a chemical compound is soluble in water, it seems almost impossible to predict if it will form a hydrate or not, although presence of both donors and acceptors in the host compound appears to be required. Chiral molecules produce significantly more hydrates, presumably including water to achieve close packing in spite of the lack of inversion centres.

---

1. Introduction

When growing crystals from solution, the solvent used sometimes plays a role in determining the crystal structure that is obtained. This role can range from influencing the polymorph that is grown to being built in into the crystal structure itself to form a solvate. Quantifying the role solvents play in organic crystal structures is the first step towards understanding and influencing this role. The Cambridge Structural Database (CSD,¹ version 5.27, November 2005) contains virtually all published small-molecule crystal structures, which makes the CSD the data source par excellence for such studies.

In previous studies, Görbitz and Hersleth quantified the number of solvent-containing CSD entries.² Unsurprisingly, water was found to be the most abundant solvent in organic crystal structures, water being incorporated 8 times more often than the second most abundant solvent, methanol. Nangia and Desiraju³ took this one step further and attempted to include the frequencies with which the solvents had been used for crystal growth. The amount of work involved necessarily limited the number of publications from which these frequencies were derived; water was not considered in their study. Gillon et al.⁴ and Infantes and Motherwell^5–7 used the CSD to study the environment of water molecules in hydrates. As early as 1991, Desiraju⁸ attempted to rationalise hydrate formation in terms of the presence of hydrogen bonding groups. Desiraju concluded, based on a random sample of hydrates from the CSD, that hydrate formation occurs when the number of hydrogen-bond acceptors outnumbers the number of donors, i.e. when the donor/acceptor ratio is small. This rationale is based on the Etter hydrogen bonding rule⁹ that “all good proton donors and acceptors are used in hydrogen bonding”. When a molecule shows an imbalance of strong donors and acceptors there may be some unsatisfied donors and acceptors, and the addition of water to the crystal structure reduces the imbalance. Unfortunately, a comparison against a control sample of anhydrated structures was not included. Infantes et al.¹⁰ used a QSAR-type approach to predict hydrate formation based on an analysis of the CSD.

Although the CSD is complete as far as coverage of the published literature is concerned, the type of data that can be extracted from the CSD is limited by the options available in the interface of the search program provided (ConQuest¹¹). In the current paper, we will describe several in-house pieces of software that can be used to search the CSD for solvated and unsolvated crystal structures in novel ways.

A computer program was developed to find those chemical compounds for which both a solvated and an unsolvated forms exist, allowing us to investigate the role the solvent molecules are playing by analysing the differences between the solvated and the unsolvated crystal structures.

An unbiased way of analysing unsolvated crystal structures is to only include those crystal structures that were grown in the presence of the solvent of interest. A program was written for this purpose.

The CSD does not store information on the stereochemistry of the entries, and an algorithm was implemented to derive this information from the 3-D atomic coordinates.

All this software can be used with any solvent molecule, but the special case of water as solvent molecule is presented here because of its wide ranging importance in industry and in particular in pharmaceutical industries; furthermore, its abundance allows for better statistics. A more comprehensive survey including 51 solvents (including water) has been conducted for which the manuscript is in preparation.

2.1 Methodology

An in-house computer program called Solvates was written to search the CSD for solvated versus unsolvated pairs of crystal structures of the same chemical compound (Fig. 1). The program accepts a 2-D connectivity of a molecule sketched in ConQuest,¹¹ and as far as the program is concerned, this molecule is the target “solvent molecule”. Obviously, the program accepts any molecule, whether generally regarded to be a solvent or not. The program only accepts one solvent at a time, and if multiple solvents are deemed to be of interest, they must be processed in separate runs of the program.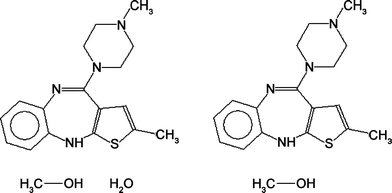

Fig. 1 An example of a hydrate versus anhydrate pair, the 2-D connectivities of CSD entries ELEVOG and UNOGOT are shown. There must be a 1-to-1 match between all molecules (other than the water molecule); in this case, the methanol was required to be present in both structures.

The program first locates all CSD entries that contain the solvent molecule. In the second step, the solvent molecule is removed from each of these entries, and the CSD is searched for the chemical compound that remains. There are no restrictions on the complexity of the chemical compound that is left: counter ions, co-crystals and any remaining solvent molecules are all included in the comparison (see Fig. 1). The number of pair-wise comparisons in this second step is potentially huge: for water, the most abundant solvent in the CSD, this number is 11 billion for the November 2005 release. Carrying out this many comparisons of 2-D connectivities would be prohibitively slow, while generating a successful hit for only a small fraction of these comparisons. Therefore, an intermediate screening step that is much faster but less reliable is used to reduce the number of comparisons. During the screening step, a 2-D connectivity is represented by its topological index: a close to unique single number that attempts to encapsulate the full 2-D connectivity.^12,13 Comparison of full 2-D connectivities is only necessary for those pairs that matched during the screening step; for water, this reduces the number of comparisons from 11 billion to four thousand.

The 2-D connectivities in the CSD do not store stereochemical information, and pairs of diastereomers would be included in the list, as would enantiomerically pure compounds versus their racemates. This is undesirable, as stereochemically different compounds are chemically different species, and the Solvates program therefore contains an algorithm to check the stereochemical consistency of the hits based on the 3-D atomic coordinates and space group stored in the CSD. The algorithm is restricted to stereocentres with four neighbours, but space-group symmetry and the presence of enantiomers in the asymmetric unit are taken into account. In practice, this means that the algorithm performs poorly for organometallic coordination compounds, but is satisfactory for most organic compounds.

CSD entries containing different amounts of the same solvent, e.g.paracetamol monohydrate (CSD refcode HUMJEE) and paracetamol dihydrate (WAFNAT), are both included as hydrates of paracetamol anhydrate (HXACAN), but the dihydrate is not considered to be a hydrated form of the monohydrate.

The result is a list of CSD refcodes of hydrate–anhydrate pairs (Fig. 2), an example of the 3-D structure of a pair is given in Fig. 3. The sample of molecules covered shows a very great range of chemical diversity; some examples are metal complexes such as (adeninato-N9)-methyl-mercury(II) (ADMEHH/CUYCUU), pharmaceutical organic molecules e.g.Olanzapine (AQOMAU/UNOGIN), salts of organic molecules e.g.L-arginine hydrochloride (ARGHCL10/LARGIN02), very small molecules e.g.Ammonium hydrogen oxalate (AHOXLH/MOYHAJ), and very large e.g. Enniatin B (BICMEF/DESYIJ). We note also that the chemical diversity covers a wide range of hydrogen bonding ability, which is studied in detail below. A final point to note is that it is quite common for there to be incomplete sets of hydrogen coordinates, particularly for water.

Fig. 2 Start of the list of CSD structures as pairs of reference codes for water as the solvent molecule. The first column identifies the compound with water present, the second is the corresponding unsolvated compound.

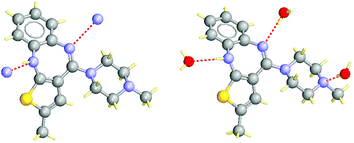Fig. 3 Example of a structural pair, CSD refcode UNOGIN (left) is the anhydrous crystal, AQOMAU (right) is a dihydrate. Hydrogen bonds are shown as dotted lines. There are three unsatisfied acceptors in the anhydrate, two in the hydrate.

The Solvates program also writes out those solvated entries for which no corresponding unsolvated crystal structure could be found in the CSD, i.e. a list of “solvates-only” structures.

This suggests the preparation of a third list: a list of unsolvated structures for which no solvate exists. In order to ensure that the absence of water in the crystal is not due to water not having been available during the crystal growth process, the CSD was searched for all entries for which it was explicitly recorded that the crystal was grown in the presence of water. Information on the solvent from which the crystal was grown is available for about 80 000 CSD entries, and an in-house computer program was written to find those CSD entries where the solvent description field included at least one of the words “water”, “H2O”, “deuteriumoxide”, “aqueous” or “dilute” (as in “dilute hydrochloric acid”). Extensive manual examination of the results indicates that these search terms, though leaving some room for false hits and missed hits, give a fairly accurate list of (published) crystal structures grown in the presence of water.

Readers interested in the functionality that the Solvates program provides should contact the Cambridge Crystallographic Data Centre.

2.2 Preprocessing

The CSD tries to objectively and exhaustively cover all small-molecule crystal structures published to date. As a result, crystal structures that some crystallographers might consider to be of questionable quality are also included, as are duplicates of previously published structures. Both types of structure are undesirable for the type of statistical survey presented in this paper; therefore, rather than using the whole CSD, only a carefully selected subset was used. This subset was prepared by first filtering the contents of the CSD based on 14 quality criteria, followed by clustering of the remaining entries into sets of redeterminations of unique polymorphs. Among the redeterminations, one entry was selected as the best representative of that polymorph. The details are described elsewhere.¹⁴ Because we are interested in the hydrogen bonding in the crystal structures, we chose the best representative based on the presence of hydrogens.

Organometallic compounds are difficult to process for water because it is often not clear if the water is a free solvent or a metal-coordinating ligand; the six-coordinated metal centres also present problems for the stereochemistry-comparison code. CSD entries containing a metal were therefore removed from the set.

Fig. 4 shows the effect of the preprocessing step on the list from Fig. 2: the number of pairs of structures was reduced from 2602 to 374. In Fig. 4, JAYPUU and JAYPUU01 are polymorphs. AQOMAUand AQOMAU01 are two polymorphs of the dihydrate of UNOGIN, whereas AQOMEY is the trihydrate of UNOGIN.

Fig. 4 As Fig. 2, after preprocessing to eliminate questionable structures, redeterminations and organometallics.

2.3 Statistical analysis

We processed these entries using the RPluto program in the same manner as an earlier study on the average number of contacts of hydrogen bonding groups.⁶ A set of 110 chemical groups (ESI† ) were pre-coded in table form for the analysis, including all likely hydrogen bond donor or acceptor groups involving atoms of element types O, N, S, F, Cl, Br and I. For each entry we calculated all inter- and intramolecular non-bonded contacts between atoms A⋯B even when hydrogen atom coordinates were not present. We allocated contact radii to atoms as follows: O 1.57, N 1.61, S 1.85, F 1.52, Cl 1.80, Br 1.90 and I 2.03 Å. A contact is defined as a distance less than or equal to the sum of these radii—intramolecular contacts require hydrogen coordinates to be present and the angle B–H⋯A to be greater than 100°. Note that these contacts will also include some that are not hydrogen bonds such as C=O⋯O=C and C–Cl⋯Cl–C.

We use the concept of the number of possible donors, NPD, and the number of possible acceptors, NPA, per structure. The NPD is simply defined as the number of hydrogen atoms on a group, C–NH₂ is counted as NPD = 2, for instance. Each O, N, S, F, Cl, Br and I atom is counted as a possible acceptor, NPA = 1, irrespective of their chemical context. The only exceptions occur for (positively) charged N, planar N with three connections and halogens covalently bonded to carbon, which never accept and have NPA = 0. Thus, a water molecule, H₂O, has NPD = 2, NPA = 1, COOH has NPD = 1, NPA = 2, and C–NH₃⁺ has NPD = 3, NPA = 0. This pays no attention to the observed frequency of hydrogen-bond donor or acceptor bonds: it is a measure of the possibility for a donor or acceptor bond.

CSD reference code lists, the defined functional groups, and the RPluto command script are given in the ESI.†

These files were analysed with a program CONTAN, written for this study, to calculate various statistics for each CSD data sample. This program creates statistics on the counts of each group, and the average number of contacts for each group. This takes into account that some groups such as SO₄^2– and COOH consist of more than one atom. There are also facilities to select entries to form statistics for sub-sets, selected on groups with specified occurrence per compound, e.g. exactly 2 H₂O, or 1 NHR₃⁺, 1 Cl^– and 1 to 10 water molecules. One is also able to select structures for simple group contact environments, e.g. OH₂⋯Cl^–⋯H₂O, or H₂O with 3 contacts to H₂O, CONH and CONH.

2.4 The influence of hydration on close packing

The crystal structure of pure H₂O, i.e. ice, is not close packed due to the many hydrogen bonds that are formed. A similar effect is therefore expected to be observed in at least some of the hydrate versus anhydrate pairs. It is not straightforward to quantify how close-packed a crystal structure is. For ice, the effect is usually exemplified by comparing the densities of liquid water to that of ice, both near 0 °C. Unfortunately, this simple approach is not valid in our samples for two reasons.

First, density depends on the atomic weights of the atoms in the unit cell , and adding a light molecule such as water to, say, a bromine-containing compound always reduces the density of that crystal structure, even if the water allows the molecules to pack more closely. Therefore, rather than working with densities, we must use molecular volumes, and in order to isolate the contribution of the main molecule in the hydrated structure, the contribution of the water molecules must be subtracted.

Second, our pairs of crystal structures were not necessarily determined at the same temperature, which has to be corrected for.

The volume of a water molecule in the solid state at room temperature, V^mol_est (water, 298 K), can be calculated to be 21.55 ų using the average atomic volumes derived from CSD data by Hofmann.¹⁵ Beaucamp et al.¹⁶ derived a volume of 22.951 ų for a molecule of H₂O from CSD data, but this slightly bigger volume already implicitly incorporates the hydrogen-bonding effect that we are trying to measure and we therefore prefer to use Hofmann's unbiased values. Hofmann's atomic volumes were derived such that their sum equals the unit-cell volume, i.e. the empty space present when packing spheres has been absorbed into the atomic volumes. Hofmann also determined the temperature dependence of the volumes, which allows us to correct for temperature differences. We can now quantify the close-packing of the main molecule, corrected for temperature and for the presence of waters, as follows:

V^mol_est (compound, 298 K) = (V^cell_obs (T)_exp (1.0 – (0.95 × 10^–4 K^–1(T_exp – 298 K))) – V^mol_est (water, 298 K) N_water)/Z (1)

where V^cell_obs (T_exp) is the observed unit-cell volume at the temperature of the experiment, N_water is the number of water molecules in the unit cell and Z is the number of molecules in the unit cell . The result is V^mol_est (compound, 298 K), the volume per molecule at room temperature corrected for the contribution of the waters. Comparing different compounds is easier if the relative volume change per water molecule is calculated:

Before preprocessing, some of the changes in the molecular volume between the hydrate and the anhydrate were rather large, and some of these outliers were examined manually. For several of these pairs, the unit-cell volumes of the hydrate and the anhydrate were virtually identical, as were the crystal structures except for the presence of the water molecules. In several of these cases the R-factor of the “anhydrate” was >10%, and the R-factor was always higher than for the corresponding hydrate structure. We therefore suspect that most of these “anhydrates” are in fact hydrates, and that the water was missed when the structure was determined. The preprocessing described above removes most of these outliers.

2.5 The influence of molecular flexibility

We attempted to quantify the impact of molecular flexibility by examining the distributions of the number of torsion angles for the three data sets. A flexible torsion angle is defined as any torsion angle involving four contiguous atoms where the bond between the two central atoms is a single bond that is not part of a ring system, and where the two central atoms are bonded to each other and to at least one other non-hydrogen atom (so as to avoid counting a methyl group as flexible).

2.6 The influence of chirality

Kitaigorodskii¹⁷ stated that the presence of inversion centres in a crystal structure generally allows for an optimal close packing. Enantiopure compounds cannot crystallise with inversion centres, and can therefore be expected, on the whole, to have more problems achieving close packing. Add to this the assumption that water can be incorporated into a crystal structure as a space filler to improve the close packing, and one might expect enantiopure compounds to exhibit a higher proportion of hydrates (or solvates in general) than average. To test this assumption, the set of 100 864 crystal structures was subdivided into three sets of crystal structures of enantiopure, racemic and achiral (including meso) compounds; for each of the three sets the percentage of hydrates was calculated.

Chiral molecules can be expected to be biased towards biologically relevant compounds, i.e. those compounds that either were obtained from a natural source or show biological activity. Because biologically relevant molecules tend to contain higher than average numbers of oxygen and nitrogen and tend to be water soluble, they would bias the sample. These biologically relevant compounds are flagged as such in the CSD, and a simple ConQuest search sufficed to remove these compounds from the sample.

3. Results and discussion

In this analysis we refer to the five samples as per Table 1, which lists the numbers of analysed crystal structures:

Table 1 The subsets of CSD entries used

Sample	Number of entries left after preprocessing	Number of entries used for analysis with RPluto
Anhydrates whole CSD	93 440	5146
Anhydrates from water	1123	1093
Hydrates-of-anhydrate	374	364
Anhydrates-of-hydrate	374	372
Hydrates-only	5267	5232

---

Out of all 100 864 organic-only entries in the preprocessed subset of the CSD, 5972 are hydrates, which is 5.9%. There were 40 000 entries grown from water in the CSD; filtering out disordered or suspicious structures, duplicates and organometallics left 1440 structures. 1123 of these were anhydrates, 317 were hydrates; thus, when growing a crystal from water, there appears to be a 22% chance of forming a hydrate. This figure is probably a slight underestimate, because disordered structures are eliminated in the preprocessing step and solvated structures are more often disordered; the real figure is therefore probably closer to 25%.

Surprisingly, for 11 of the anhydrates grown from water the corresponding hydrate was present in the CSD. All 11 structures were closely examined, but all 11 appeared to be genuine anhydrates and no indication was found that the water molecules had simply been missed. Their CSD refcodes are BERYAZ, BISMEV04, EVODUO, GLUCIT02, HXACAN12, IYAWAG, IYAXAH, IZAJUO, KAMPIY, LARGIN02 and LSERIN20. For most of these, the solvent was a mixture of water and, say, ethanol. In these cases, for the water to remain mixed with the ethanol is entropically favoured over getting trapped in a crystal structure. This suggests that it is possible to find an ethanol/water ratio where both the hydrate and the anhydrate can grow concomitantly.

We are fully aware that these samples only reflect the reported experimental literature, and that there is the possibility that the hydrate list could have non-hydrate pairs as a result of future experiments. Similarly, the fact that there is no hydrate reported in the CSD does not mean that it cannot easily be made.

3.1 Number of water molecules per structure

It is notable that the average number of waters per hydrate structure is greater than 1, namely 1.6 (Hydrates-only) and 1.4 (Hydrates-of-anhydrate) showing the importance of di- and tri-hydrates in the sample (Fig. 5). The distributions of the hydration number for the Hydrates-only sample is shown in Fig. 6, where we see a definite tendency for higher molecular weight molecules to have a higher hydrate water count. The possible donor and acceptor atoms per structure also increase with higher water count (though beyond six waters the number of observations—12 or less—becomes rather low for statistical purposes). A very similar histogram is seen for the Hydrates-of-anhydrate structures.

Fig. 5 Frequency of number of included water molecules per asymmetric unit for the Hydrates-only sample.

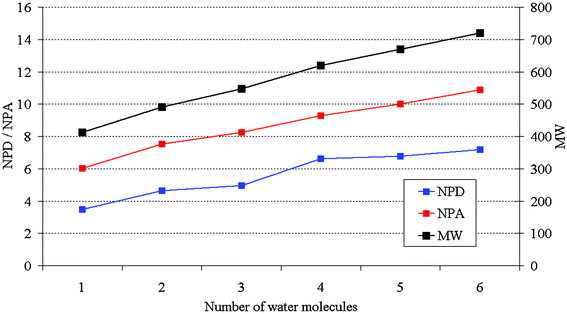Fig. 6 Average molecular weight (MW), number of possible donors (NPD) and number of possible acceptors (NPA) as a function of the number of waters per asymmetric unit in the crystal structures. These data are for the Hydrates-only sample.

3.2 Average number of functional groups

The main postulated rationale for the incorporation of water being the additional hydrogen bonds formed, it is to be expected that the average number of hydrogen-bonding functional groups increases when comparing the set of anhydrous crystal structures to the set of hydrated crystal structures. In order to test this hypothesis, we calculated the average number of each of the 110 functional groups available in RPluto for the Anhydrates grown from water sample and for the Hydrates-only sample. Groups that occurred less than 50 times were omitted as not statistically significant; 62 groups remained. In order to aid the visualisation of the results, the ratios of the average numbers of functional groups in the two samples is plotted in Fig. 7.

Fig. 7 Ratios of the average numbers of functional groups in the Hydrates-only sample and the Anhydrates grown from water sample. (a) Functional groups that occur more often in hydrates than in anhydrates (grown from water); SO₄²⁻ through X-I have a value of infinity, i.e. never occur as an anhydrate; (b) (note the change of scale): functional groups that occur equally often in both samples (NH₄⁺ through X-Br) or that occur more often in anhydrates (grown from water) than in hydrates.

When a group occurs more frequently in the Hydrates-only set than the anhydrate set (ratio >1.0) there is a higher presence of polar groups. Further study of these distributions is beyond the scope of this paper, and has been discussed elsewhere under the concept of “hydrate affinity”.⁵ However, it is noteworthy that there are certain groups which are populated much more frequently in Hydrates-only than in Anhydrates-only samples, such as R₂PO₂^–, Cl^– and C–NH₃⁺. The converse applies to hydrophobic groups such as CF₃, C–Cl, and, interestingly, –O–CO–NH. Note that the preference for hydrates of the OH group strongly depends on the chemical context of the group: HO–CR₃ > HO–CR₂ > HO–CHR₂ > HO–CH₂R.

3.3 Average number of contacts per functional group

The main postulated rationale for the incorporation of water being the additional hydrogen bonds formed, it is to be expected that the number of contacts when going from an anhydrous to a hydrated crystal structure increases. This is the type of question that would be very hard to get meaningful data for without the Solvates program, which for the first time allows us to investigate the anhydrous and the hydrated crystal structures of the same chemical compound side by side.

Because the sample size is so small, the further subdivision into the 110 functional groups leaves many groups with less than 20 occurrences; these were discarded as not statistically significant. For groups with 20 or more instances, the average number of contacts in the hydrates and the anhydrates is shown in Fig. 8.

Fig. 8 Average number of contacts per functional group for the anhydrous (red) and the hydrated (blue) crystal structures, for functional groups with count >20.

These results show that in almost every case the average number of contacts per group increases when we move from the anhydrous to the hydrated crystal structure. This is not surprising, as generally there must be more hydrogen bonds in the hydrated structure, but it is interesting that increases are not only seen for polar groups, but several of the non-polar groups also show an increase in contacts. It must be remembered that the contacts are not entirely hydrogen bonds, and include other short contacts such as NO₂⋯NO₂.

We see the most significant increase in contacts for the Cl^– group, which moves towards its preferred number of contacts as 3. Other groups showing notable increases are CONH, COO^–, NH₃R⁺, NR₂, C=O and C–Br.

3.4 What is the water doing?

The study of average contacts of H-bonding groups¹⁰ shows that most groups have a “preferred” number of contacts, e.g. Cl^– prefers 3. Rationalisation of hydrate formation is easier if we consider a driving force towards attainment of such preferred values, rather than the rather simplistic counting of donor and acceptor atoms. We find support for this explanation when we examine the list of anhydrate/hydrate pairs, which we illustrate with the two examples shown in Fig. 9 and 10.

Fig. 9 The hydrogen-bonding pattern of the anhydrous form of 4-dimethylaminopyridinium chloride (top, CSD refcode JUBKAS), and the hydrogen-bonding pattern of the corresponding dihydrate (bottom, CSD refcode DMAPYC, Z′ = 2). The anhydrous salt has Cl^– atoms rather below their preferred level of hydrogen bonding (3 contacts). The addition of water allows Cl^– to form 3 contacts, and the water comfortably hydrogen bonded with at least two strong donor bonds to the Cl^–.

Fig. 10 CSD refcodes AMEPOX and AMEQAK. Packing problems of the anhydrous form causes three unsatisfied donors and acceptors—water forms two donor and two acceptor bonds, and now all donors and all acceptors but one are satisfied.

3.5 Counts of donor and acceptor atoms

Table 2 shows the average number of possible hydrogen-bond donors and acceptors for the data sets. The values for the hydrate/anhydrate pairs were derived from only about 370 entries and are the least accurate; the remaining figures were derived from at least 1000 CSD entries each. It is clear that a low donor/acceptor ratio is not the rationale behind hydrate formation, contradicting Desiraju's hypothesis. Although there is a clear trend that the probability of obtaining a hydrate increases when the absolute number of hydrogen-bond donors and acceptors increases, the numbers vary little for the sets ranging from Anhydrates from water to Hydrates-only: if a compound is soluble in water, it is impossible to predict whether or not it will form a hydrate based on the average number of donors or acceptors or their ratio.

Table 2 The average number of possible hydrogen-bond donors and acceptors

Sample	Size	Donors	Acceptors	D/A^a
a D/A = Donor/Acceptor ratio
Anhydrates (whole CSD)	5146	1.2	4.3	0.28
Anhydrates (from H2O)	1093	3.2	5.5	0.58
Anhydrate/hydrate pairs	372/364	3.2	4.9	0.65
Hydrates-only	5232	4.0	6.4	0.63

---

3.6 Counts of unsatisfied donor and acceptor atoms

Here we define an unsatisfied donor or acceptor atom as one having no hydrogen bonded contacts. Table 3 shows the average number of unsatisfied hydrogen-bond donors and acceptors in the crystal structures as determined from the 3-D atomic coordinates before and after removing the contributions from the water molecules. There are about five times more unsatisfied acceptors than there are donors. Due to the way this has been counted, this is an underestimate: the assumption that every hydrogen atom corresponds to a single donor is reasonable, but a species like Cl^– is counted as a single acceptor, whereas in practice it needs to form about three hydrogen bonds to be satisfied.

Table 3 The average number of unsatisfied hydrogen-bond donors and acceptors in the crystal structures

	Including water		Excluding water
	Donors	Acceptors	Donors	Acceptors
Anhydrates (whole CSD)	0.2	2.8	—	—
Anhydrates (from H2O)	0.3	2.2	—	—
Anhydrate/hydrate pairs	0.4	1.7	—	—
Anhydrate/hydrate pairs	0.4	1.1	1.2	2.6
Hydrates-only	0.3	1.8	1.1	3.3

---

Examination of the average counts of unsatisfied donor and acceptor atoms, including water molecules if present, shows that anhydrates in the CSD have a low unsatisfied donor count of 0.2, but a relatively high unsatisfied acceptor count of 2.8. This reflects the fact that many of the anhydrate entries have few donors, or even zero donors. However, the Hydrates-only sample shows an unsatisfied donor average that is slightly higher, 0.3, but an unsatisfied acceptor average that is considerably lower, 1.8. This suggests that a primary role for water is to reduce the number of unsatisfied acceptors. This is in accord with the observations of Gillon et al.,⁴ and Infantes et al.,¹⁰ that the average hydrogen-bond count for water is 1.9 donor bonds and 1.0 acceptor bonds. Thus addition of water to a crystal structure has an average effect of reducing the number of unsatisfied acceptors.

If we subtract the contacts to water molecules in the Hydrates-only sample structures we can count the resulting unsatisfied donor and acceptor atoms. This has the effect of increasing the number of unsatisfied acceptors from 1.8 to 3.3 (difference +1.5) and unsatisfied donors from 0.3 to 1.1 (difference +0.8), indicating that the water molecules frequently contribute two donor H-bonds, and one acceptor bond. (We should not pretend, of course, that such an artificial removal of water molecules from hydrate structures will represent real stable crystal structures, as there are other rearrangements of hydrogen bonds often possible to lower the lattice energy.)

This leaves the question whether it is the number of unsatisfied donors or the number of unsatisfied acceptors that determines if a hydrate will form. The figures in Tables 2 and 3 lend support to either interpretation, and we can only draw a tentative conclusion. A striking feature of the anhydrate crystal structures taken randomly from the CSD, is that they contain relatively high numbers of possible hydrogen-bond acceptors, and relatively high numbers of unsatisfied hydrogen-bond acceptors. This suggests that crystal structures can cope with relatively high levels of unsatisfied hydrogen-bond acceptors. This is in stark contrast to the hydrogen-bond donors: there are significantly less possible donors present in the anhydrates, and in none of the samples does the average number of unsatisfied donors ever exceed 0.4; but when the water is removed, the number of unsatisfied donors increases to three times this value. These observations strongly suggest that unsatisfied hydrogen-bond donors are highly unfavourable for crystal structures, and satisfying these unsatisfied donors appears to be the main driving force for incorporating water. However, this cannot be the complete picture: every water molecule comes with its own two donors, which in turn need to be satisfied. That this is indeed the case is clearly demonstrated by the fact that removing the water from the hydrated structures on average leaves 1.5 acceptors unsatisfied. We seem to have the apparent contradiction then, that water is incorporated to satisfy an unsatisfied donor of the host molecule, but in doing so creates two new unsatisfied donors… which are satisfied by the host molecule.

However, this is not necessarily a contradiction. Spatial packing restrictions can prevent donors and acceptors from achieving geometric conditions for the hydrogen bond: the water molecule being freely mobile, with six degrees of freedom, can act to resolve such spatial conflicts by forming bridges between such unsatisfied donors and acceptors. Furthermore, hydrogen bonds mediated viawater are by definition cooperative in nature, and are therefore stronger than the direct hydrogen bonds between two groups from the host would have been.

3.7 The influence of hydration on close packing

Fig. 11 shows the distribution of the volume changes. One third (35%) of the volume changes is negative, two thirds (65%) is positive. The average volume change is +1.2%, i.e. on average a molecule occupies more volume when water molecules are introduced into the crystal structure. By analogy with ice, positive volume changes are presumably due to the hydrogen-bonded networks that are formed. Indeed, the greatest positive volume change is observed for a very small molecule, tert-butanol, incorporating no less than seven water molecules (Fig. 12). Negative volume changes, on the other hand, are most likely due to the small water molecules acting as space-filler, a role that one would expect to become more predominant as the size of the molecule (as measured by its volume in the solid state) increases. This is indeed the trend that is suggested in Fig. 13.

Fig. 11 The distribution of ΔV^mol_{anhydrate → hydrate} (see eqn (2) for definition). 0% is indicated by a red line; it can be seen that on average, the hydrate forms pack less closely than the anhydrate forms.

Fig. 12 The crystal structure of tert-butanol heptahydrate (refcode LEBKEI). The molecular volume of the anhydrate (described as “very hygroscopic”) is increased by 20% with the uptake of seven water molecules. Hydrogen bonds are shown as dotted red lines.

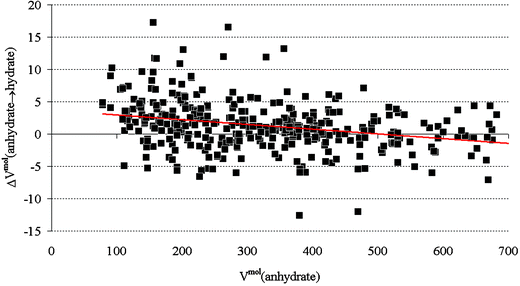Fig. 13 Scatter plot of ΔV^mol_{anhydrate → hydrate} (see eqn (2) for definition) as a function of the molecular volume of the anhydrate (in ų). The least-squares fit through the points is included as a red line. The plot suggests that the role of the water as space-filler is more noticeable when the molecular volume of the anhydrate is greater.

3.8 The influence of molecular flexibility

No difference between the distributions was observed, and all distributions agree with the distribution of flexible torsion angles observed for the whole CSD.

3.9 The influence of chirality

The raw data are shown in Table 4. Of the 100 864 crystal structures in the sample, 24 874 (25%) were enantiopure, 18 244 (18%) were racemic and 57 746 (57%) were achiral. 20% of the chiral compounds (5085 out of 24 874 entries) were flagged as biologically relevant, versus 6% of the racemic and achiral compounds. 11% of the biologically relevant compounds occur as a hydrate in the CSD. After subtracting the biologically relevant compounds from the sample, the percentage of hydrates for the chiral, racemic and achiral compounds is 8.1, 2.7 and 5.2% respectively. I.e., even when corrected for the biological origin of many chiral compounds, chiral compounds are substantially more likely to form hydrates as compared to achiral compounds, whereas hydrate formation is relatively rare for racemic compounds.

Table 4 Numbers of chiral, racemic and achiral compounds for the whole subset, for all hydrates in the subset, for all the non-biologically relevant compounds in the subset and for the hydrates of the non-biologically relevant compounds

	All	Hydrates	Non-bio	Non-bio hydrates	% Non-bio hydrates
Chiral	24 874	2247	19 789	1594	8.1%
Racemic	18 244	546	17 127	455	2.7%
Achiral	57 746	3179	54 490	2842	5.2%
Total	100 864	5972	91 406	4891	5.4%

---

4. Conclusions

The main conclusion must be that statistical surveys into the behaviour of hydrates are difficult due to the severe bias that is introduced at many levels. We hope that including several previously inaccessible subsets of anhydrates—those grown from water and those for which a hydrate exists—as well as the inclusion of stereochemistry information and a random control group from the CSD allows for more reliable studies in the future.

25% of crystals grown from water are hydrates. The group of chemical compounds that can be dissolved in water in the first place can be expected to be highly biased with respect to the presence of hydrogen-bond donors and acceptors, so this high number is perhaps hardly surprising.

We tentatively conclude that unsatisfied hydrogen-bond donors appear to be the main driving force behind hydrate formation. However, at the same time, hydrates tend not to form if no acceptors are present.

If a chemical compound crystallises as a hydrate, the number of water molecules incorporated per structure increases with the number of possible hydrogen-bond donors and acceptors, and with the molecular weight of the compound.

The relative volume change associated with hydration shows a vague trend suggesting that on average larger molecules use water more often as space filler than smaller molecules, whereas the smaller molecules use the hydrogen-bonding capabilities of the water. However, the trend is vague and lacks predictive power.

Molecular flexibility does not seem to affect hydrate formation, at least not for the definition of molecular flexibility that we have chosen.

There is a strong tendency for chiral compounds to form hydrates. This inclusion of water molecules by chiral compounds presumably serves the purpose of improving the close packing of these compounds in the absence of inversion centres.

Acknowledgements

Dr Greg Shields is gratefully acknowledged for substantial extensions to the initial version of the stereochemistry perception code.

References

1. F. H. Allen, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 380.
2. C. H. Görbitz and H.-P. Hersleth, Acta Crystallogr., Sect. B: Struct. Sci., 2000, 56, 526.
3. A. Nangia and G. R. Desiraju, Chem. Commun., 1999, 605.
4. A. L. Gillon, N. Feeder, R. J. Davey and R. Storey, Cryst. Growth Des., 2003, 3, 663.
5. L. Infantes, J. Chisholm and S. Motherwell, CrystEngComm, 2003, 5, 480.
6. L. Infantes and W. D. S. Motherwell, Chem. Commun., 2004, 1166.
7. L. Infantes and W. D. S. Motherwell, Z. Kristallogr., 2005, 220, 333.
8. G. R. Desiraju, J. Chem. Soc., Chem. Commun., 1991, 426.
9. M. C. Etter, Acc. Chem. Res., 1990, 23, 120.
10. L. Infantes, L. Fabian and W. D. S. Motherwell, CrystEngComm, 2006, 8 , submitted.
11. I. J. Bruno, J. C. Cole, P. R. Edgington, M. Kessler, C. F. Macrae, P. McCabe, J. Pearson and R. Taylor, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 389.
12. L. A. Evans, M. F. Lynch and P. Willett, J. Chem. Inf. Comput. Sci., 1978, 18, 146.
13. D. Bawden, J. T. Catlow, T. K. Devon, J. M. Dalton, M. F. Lynch and P. Willett, J. Chem. Inf. Comput. Sci., 1981, 21, 83.
14. J. Van de Streek, Acta Crystallogr., Sect. B: Struct. Sci., 2006, 62, 567.
15. D. W. M. Hofmann, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 489.
16. S. Beaucamp, N. Marchet, D. Mathieu and V. Agafonov, Acta Crystallogr., Sect. B: Struct. Sci., 2003, 59, 498.
17. A. I. Kitaigorodskii, Organic Chemical Crystallography. 1961, New York: Consultants Bureau.

---

Footnote

† Electronic supplementary information (ESI) available: Table of chemical groups used by RPluto for processing of H-bond contacts and CSD refcode lists of hydrate/anhydrate structures, structures grown from water and hydrates-only structures. See DOI: 10.1039/b613332k

---