X-Ray microanalytical techniques based on synchrotron radiation

Abstract

The development of 3rd generation synchrotron radiation sources like European Synchrotron Radiation Facility (ESRF) in parallel with recent advances in the technology of X-ray microfocusing elements like Kirkpatrick–Baez (KB) mirrors, diffractive (Fresnel zone plates, FZP) and refractive (compound refractive lenses, CRL) optics, makes it possible to use X-ray microscopy techniques with high energy X-rays (energy superior to 4 keV). Spectroscopy, imaging, tomography and diffraction studies of samples with hard X-rays at micrometre and sub-micrometre spatial resolutions are now possible. The concept of combining these techniques as a high-energy microscopy has been proposed and successfully realized at the ESRF beamlines. Therefore a short summary of X-ray microscopy techniques is presented first. The main emphasis will be put on those methods which aim to produce sub-micron and nanometre resolution. These methods fall into three broad categories: reflective, refractive and diffractive optics. The basic principles and recent achievements will be discussed for all optical devices. Recent applications of synchrotron based microanalytical techniques to characterise radioactive fuel particles (UO₂) released from the Chernobyl reactor are reported.

---

Irina Snigireva

Irina Snigireva was born in Russia, in 1957. She received her PhD in solid state physics from the Russian Academy of Sciences in Chernogolovka in 1988 in the area of electron microscopy. Between 1988 and 1993 she was a scientist in the Institute of Microelectronics Technology of the Russian Academy of Sciences. Since 1993 she has been responsible for the Microimaging Laboratory at the European Synchrotron Radiation Facility in Grenoble, France. Her current research interests are: development of X-ray optics, high energy X-ray microscopy and coherent imaging techniques.

Introduction

X-Ray microscopy offers important and desirable visualization and characterization capabilities of great importance to a large variety of scientific topics, in particular to biological, medical and environmental sciences. The resolution of X-ray microscopy is intermediate between visible light microscope on the one hand and the electron microscope on the other. Instruments available today deliver about five times better resolution then visible light microscopes on a routine basis and the best achievable resolution today is 15–30 nm.¹ The ultimate resolution of X-ray microscopy is limited in principle only by the wavelength. X-rays are more penetrating than electrons; furthermore X-ray penetrating power varies much more strongly with photon energy and chemical composition. As a consequence, X-ray microscopes can image samples without sectioning in the natural state and in atmospheric-pressure air. X-ray absorption edges (jumps in the absorption cross section curve which occur when the X-ray passes the threshold energy for removing an inner-shell electron) and near-edge resonance’s enable to map both chemical elements and their chemical binding states.

During recent years, considerable progress has been made in X-ray microscopy in the hard X-ray regime (E > 4 keV), that was pushed by the simultaneous development of high brilliance, high energy X-ray sources coupled with advances in manufacturing technologies of focusing optics. One of the key strength of hard X-ray microscopy is the large penetration depth of hard X-rays in matter (around 1 mm), allowing one to probe the inner structure of an object without the need for destructive sample preparation. Resolution in the order of 100 nm was reached with photon energies up to 30 keV. High energy X-rays give access to K-edges of medium light elements and L-M-edges of heavy materials for microspectroscopy, chemical or trace element mapping. Fluorescence yield is significantly greater then for soft X-rays. Short wavelength is very favorable for diffraction studies. For hard X-rays, optical elements have generally larger focal lengths and depth of field that are advantageous for the use of specific sample environment like pressure cells or controlled temperature. Normally experiments do not need vacuum, therefore samples can be investigated in the air: biological and environmental systems can be studied in the natural state.

In this paper we will provide a short summary of X-ray microscopy techniques. The main emphasis will be put on those methods which aim to produce sub-micron and nanometre resolution. These methods fall into three broad categories: reflective, refractive and diffractive optics. The basic principles and recent achievements will be discussed for all optical devices. Recent applications of synchrotron based microanalytical techniques to characterise radioactive fuel particles (UO₂) released from the Chernobyl reactor will be reported.

X-Ray microscopy

X-Ray microscopy can be divided into two classes: full field microscopy and scanning microscopy. There are two versions of full field X-ray imaging and microscopy. The first is in-line lens-less imaging with parallel and conical beams.^2–4 The second version is full field transmission X-ray microscope, which uses the same optical arrangement as conventional light and transmission electron microscopes.^5–7 Such type of microscopes uses optical elements like Fresnel zone plates or refractive optics as objective lenses for high-resolution imaging. Scanning microscopes usually use a focusing optics to form a finely focused spots or microprobe through which the specimen is rastered.^8–10 The microscope of choice is generally determined by the specimen and observation to be made on it. The main advantage of scanning transmission microscopes over other types of microscopes is the ability to record high quality images from samples of widely varying sizes and to complement these images with high resolution spectroscopy measurements. Table 1 summarizes different types of X-ray microscopes available nowadays.

Table 1 Comparison of the features of different types of X-ray microscopy

Type of microscopy	Source	Energy	Mode of contrast	Optics	Resolution/nm
SR, synchrotron radiation sources; Lab, laboratory based sources; XANES, X-ray absorption near edge spectroscopy; EXAFS, extended X-ray absorption fine spectroscopy.
Full-field	In-line imaging	SR	>1 keV	Absorption/phase XANES/EXAFS	—	500–1000
	Soft X-ray microscopy	SR, Lab	<4 keV	Amplitude/phase XANES	FZP	20–50
	Hard X-ray microscopy	SR, Lab	>4 keV	Amplitude/phase XANES/EXAFS possible	FZP, CRL	100–500
Scanning	Soft X-ray scanning microscopy	SR	<4 keV	Absorption, fluorescence, XANES/EXAFS, photoemission	FZP	20–50
	Hard X-ray microprobe	SR, Lab	>4 keV	Absorption, fluorescence, XANES/EXAFS, diffraction	FZP, CRL, KB	100–1000

---

In-line imaging/microradiography

X-Ray imaging at high energies such as contact radiography and projection microscopy and tomography has been used for many years to nondestructively discern the features of the internal structure of the objects in material science, biology and medicine. In so doing the main contrast formation is an absorption that makes some limitation in imaging of the light density materials. For imaging at micrometre and sub-micrometre resolution there is no way to overcome these limits except phase contrast imaging. At high X-ray energies phase shift term can be up to 1000 times greater the absorption. Imaging in phase contrast was strongly pushed with the advent of the undulator sources at 3rd generation SR sources like ESRF.^2,3 In the simple in-line geometry (Fig. 1) an object is illuminated by a distant small X-ray source, which generates an almost parallel beam. A typical source-sample distance L₁ is 30–50 m. The X-rays emerging from the sample at their various angles will propagate through the free space until they reach the detector. With the detector immediately behind the sample (L₂ = 0), one will get a conventional absorption image. If the detector is placed at some distance behind the sample, we will observe interference pattern as different components of the beam, having been diffracted by the sample, interfere with each other on further propagation through the space. The optimum positioning of the detector for best enhancement effects varies from sample to sample, depending on the X-ray wavelength, and the size of the features of interest. This in-line phase sensitive imaging was first explored at the ESRF and now routinely used for imaging various kinds of samples. Since the beam is almost parallel, the resolution of this type of microscopy is determined by the detector resolution. Normally a resolution is below a 1 μm. However, it has the advantage of being simple since it needs no optics. When 2D projection microscopy is combined with tomography a 3D-structure determination can be achieved. For that purpose the sample has to be rotated in small steps around an axis perpendicular to the X-ray beam and for each step a micrograph is taken. Sophisticated tomography algorithms are available which allow the reconstruction of the 3-dimensional geometric structure of the sample.^11–14

Fig. 1 Setup for X-ray in-line imaging.

Transmission X-ray microscope (TXRM)

The full field transmission microscope (TXRM), illustrated schematically in Fig. 2, uses the same optical arrangement as conventional light and transmission electron microscopes. The basic approach is to use a high quality imaging optics as a microscope objective to create a magnified image of the object.^5–7 When the object is placed slightly outside the focal distance (L₁ is slightly larger than F) then a strongly magnified image is generated at a distance L₂ = L₁F/(L₁ − F) with magnification L₂/L₁ = F/(L₁ − F). This technique offers the possibility of dynamic imaging and adapted for phase contrast imaging.

Fig. 2 Optical schematic of transmission X-ray microscope.

Concerning hard X-rays there are two types of optics available today with sufficient quality to be used in the development of full field imaging: Fresnel zone plates (FZPs) and compound refractive lenses (CRLs). Both have in common that their focal length for X-rays with photon energies around 10 keV and higher is of order of metres and that their apertures are limited to several hundred micrometres. The length of the setup will increase as M increasingly differs from unity. The length of the entire microscope can be in the order of 10–25 metres.^15–23 Another implication of long focal length is a very small numerical aperture, which limits the resolution of the imaging setup. The resolution of about 100–300 nm is achievable.^15–17

Scanning X-ray microscope

Finally, we consider X-ray microscopy in the scanning mode, illustrated in Fig. 3. The basic idea in scanning microscopy is to form a microprobe across which the specimen is mechanically scanned. A proportional counter detects the transmitted X-rays and the image is built up pixel by pixel.^8–10 The focused X-ray probe can also be used to excite other process such as photoelectrons, fluorescent X-rays. The spatial resolution is limited by the focusing optics.

Fig. 3 Schematic of scanning transmission X-ray microscope.

In the case of hard X-rays the microfocus is generated KB mirrors, FZ plate or parabolic CRL. The high-energy microfocusing optics benefit from longer focal lengths and larger depth of field up to a few millimetres, that is advantageous for the use of specific sample environment like furnace or high-pressure cells. A shorter wavelength is favourable for diffraction studies including wide and small angle scattering. In the microprobe, the strategy is to scan the beam over the sample and to measure a signal in diffraction, fluorescence or absorption (XANES, EXAFS) for each beam position.^{15,16,24–34} When combining scanning microscopy with tomographic techniques the inner structure of a sample can be reconstructed, including the distribution of different atomic species and even of the valence of atoms.^35–39

X-Ray optics

Ever since the discovery of X-rays the possibility of using them to image the microscopic structure of biological and non-biological materials has been discussed. However, the practical implementation of an X-ray microscope was hampered until recently by the lack of intense sources giving radiation of the required wavelength and by the severe difficulties in the manufacturing of suitable optical components. All available microfocusing devices for hard X-rays are presented in the Table 2. The resolution for the all presented optical systems overcomes the 100 nm limit and spot size about 0.5 micron sizes becoming routinely used. From their principles of operation these optical systems are subdivided into three broad groups: reflective, refractive and diffractive optics.

Table 2 Microfocusing optics for hard X-rays

	Reflective				Diffractive	Refractive
	Kirkpatrick–Baez systems		Capillaries	Waveguides	Fresnel zone plates	Refractive lenses
ΔE/E is energy bandwidth, Δ is the best available resolution in nanometres, wb is white beam.
	Mirrors, Kirkpatrick & Baez, 1948^40	Multilayers, Underwood et al., 1986^42	Kreger, 1948^50	Feng et al., 1993^54	Baez, 1952^60	Snigirev et al., 1996^65
E	<30 keV	<80 keV	<20 keV	<20 keV	<30 keV (80)	<1 MeV
ΔE/E	Wb	10^−2	Wb	10^−3	10^−3	10^−2
Δ	40 nm, Mimura et al., 2005^45	86 nm, Hignette et al., 2005^49	50 nm, Bilderback et al., 1994^53	40 × 25 nm^2, Salditt et al., 2005^59	60 nm Kagoshima et al., 2003^16	50 nm Schroer et al., 2005^73

---

Reflective optics: mirrors and multilayers

Conventional mirrors, used for visible wavelength, cannot be used, because the reflectivity at normal incidence is too low, typically less then one hundred thousand X-ray photons will be reflected. High reflectivity can be obtained at grazing incidence angles below critical angle. The critical angle θ_c, is equal to (2δ)^1/2, where δ is the refractive index decrement of the material at the energy of X-ray photon. For hard X-rays the typical values are 0.1 to 10 mrad. To reduce the astigmatism Kirkpatrick and Baez proposed to use two spherical or cylindrical mirrors in a crossed configuration.⁴⁰Fig. 4 shows a geometrical arrangement of a so-called Kirkpatrick–Baez system (KB mirrors). To enhance the reflectivity the multilayer mirrors, where the refractive index varies periodically with depth, can be used.^41,42 To build such mirrors, alternative layers are evaporated or spattered onto a blank with a thickness λ/4 and relatively high refractive index and relatively low refractive index, respectively. The weak radiation reflected at the interfaces of the multiplayer is superimposed coherently and in phase and can give a considerably increased reflectivity. The reflecting focusing systems can be either static,^43–47 with mirrors polished according to the proper figure optimized for a given incidence angle and focus. Or it can be dynamic, with actuators bending flat mirrors into the elliptic shapes required by the experiment.^48,49 Today, as a result of improved techniques for developing highly finished and perfect surfaces, ellipsoidal and paraboloidal mirrors can be manufactured to a high degree of perfection and focusing down to 100 nm spot size is achievable with KB systems.^45,49

Fig. 4 Two-mirror Kirkpatrick–Baez system. θ is the mirror incidence angle.

The reflecting mirrors are able to focus X-rays over large energy range, whereas Bragg reflecting mirrors only focus a small fraction of the radiation continuum. As, within a given energy interval, the optical properties for total reflecting optics are independent of the X-ray wavelength, the focal spot is retained while tuning the energy. Therefore, experiments requiring energy tuning, like spectroscopy, can be performed without any readjustment of the optics. However the disadvantage of grazing incidence optics is low acceptance and it is mostly used for scanning microscopes.

Capillaries

Monocapillary optics relies on total external reflection of the X-rays from the internal surface of the tube to transport X-rays (Fig. 5). Similar to reflective mirrors to keep the X-rays from being absorbed in the wall of the capillary, the angle of incidence must be kept below the critical angle. Typical glass materials that have been used to fabricate capillary optics are borosilicate; lead based and silica glasses. For hard X-rays the typical values for critical angles are 0.1 to 10 mrad.

Fig. 5 Schematic of condensing capillary optics. θ is the incidence angle and α is the angle of capillary linear taper.

The simplest form of a capillary is straight (cylindrical) glass tube; have first been used in the 1950s to guide X-rays from the source point to a distant sample. This leads to an effective reduction of the source sample distance and thus to an increase in flux on the sample. The next step was to use tapered capillaries not only to guide but moreover to squeeze the X-rays to a very small spot.^50–53 The first experiments were performed with conventional X-ray tubes. In the late 80s conical tapered capillaries were tested at synchrotron facilities.^51–53 The optical properties of conical capillaries have been found to be fairly bad compared to parabolic or ellipsoid shaped. Thus in the recent years the manufacturing of ellipsoid capillaries has been forced. Current topics of the development are reproducibility, surface quality and material choice. Many groups worldwide are involved in the capillary technique.

The condensing capillaries have the potential to produce very small beams (∼50 nm), because the beam size is defined by the exit hole diameter of the glass.⁵³ Similar to mirrors, the advantage of these grazing incidence devices over many other competing microbeam optics (zone plates, etc.) is that they work over a wide energy range without changing the position to which the beam focuses. A potential drawback of capillaries for submicron beams is that the sample has to be placed near the tip, generally within 20 to 100 times the exit tip inside diameter.

Waveguides

An X-ray planar waveguide is a thin film resonator in which a low absorbing material is enclosed between two metal layers with smaller refractive index.⁵⁴ For particular grazing incidence angles, a resonator effect takes place inside the resonator film. The beam is compressed in one direction and the trapped wave emerges from the end of the waveguide with enhanced intensity. In the direction of beam compression, the beam leaves the waveguide with the vertical size limited by the resonator layer thickness, which can be as small as 100 nm.^55–57 The cover layer and under layer can also be constituted of the same material. A schematic representation of thin film waveguide is shown in Fig. 6. To date, X-ray waveguide optics have been exclusively one-dimensional, whereas most nanobeam applications require two-dimensional point beams. It was reported recently in ref. 58,59 the first proof of principle that resonant beam coupling can be realized in two dimensions. Also, the reported hard X-ray beam with a cross section of 25 × 47 nm² (FWHM) is impressive; many technological improvements will be required before this device can be used as an efficient X-ray point source.

Fig. 6 Schematic design of the waveguide structure. θ is the incidence angle on the waveguide surface; the incidence angle α on the interior metal surface of the waveguide differs from the θ due to the refraction on the film.

Fresnel zone plates

The focusing properties of zone plates were first discussed in the latter part of the 19th century and Baez originally suggested their use as X-ray optical elements in 1952.⁶⁰ In their most common form, this is circular diffraction grating that works as a lens for monochromatic light. Fresnel zone plate consists of a series of concentric rings of radius r²_n = nλF and the rings become narrower at larger radii until the last, finest zone of width Δr_n is reached (Fig. 7). Linear, square, elliptical zone plates have also been considered, but only circular and, to a lesser extent, linear and elliptical forms have generally been used. The focusing capability is based on constructive interference of the wavefront modified by passage through the zone plate. The wavefront modification is obtained through the introduction of a relative change in amplitude or phase in the beams emerging from two neighboring zones. A zone plate is called an amplitude zone plate if the focusing results from different absorption between two neighboring zones. It is called a phase zone plate if the phase change upon transmission through a zone is the mechanism for focusing.

Fig. 7 Fresnel zone plate.

Just as the Rayleigh resolution of a light microscope lens is determined by its numerical aperture, A_n, the Rayleigh resolution of a zone plate is determined by its maximum diffraction angle A_n = λ/(2Δr_n), so that the Rayleigh resolution is 1.22Δr_n. Using state-of-the-art lithographic technologies, zone plates with last or outermost ring width of less than 20 nm can currently be fabricated.¹ If illuminated with X-ray beam whose spatial coherence length is equal to or greater than the diameter of the zone plate, a diffraction-limited focus can be obtained. The efficiency of a binary FZP reaches its maximum value when the structure height is chosen to introduce a phase shift of π. In the soft X-ray region, zone plate efficiency is limited to about 15% due to photoelectric absorption. For X-ray energies greater than 3 keV, it is in principle possible to produce phase zone plates with focusing efficiencies close to 40%. As a phase shift generally decreases with increasing photon energy, high and higher structures are required to provide useful efficiency values for harder X-rays. For example, appropriate zone thickness for 10 keV X-rays is estimated to be about 2 μm even for high density material like gold or tantalum. The resulting extreme aspect ratios (height/width of finest zone), are the reason why FZPs for hard X-rays cannot be made with zone width as small as the ones for soft X-rays. To improve the focusing efficiency of a zone, plates with a blazed zone profile were manufactured and 55% efficiency for the nickel circular zone plate at 7 keV was measured.^61,62

Recently proposed sputtered–sliced Fresnel zone plates have an exceptionally high aspect ratio suitable for focusing 100 keV X-rays,^15,63 but the small aperture strongly limits applicability of these FZPs. We propose to use silicon-based FZPs made by Si microfabrication technology which provides high accuracy and reproducibility (Fig. 8). To overcome limits on the thickness of the phase-shifting material, one can attempt a multiple zone plate setup. Two identical Si chips were used for stacking in order to focus 50 keV X-rays.⁶⁴ The use of single 30 μm thick zone plate at 50 keV would result in 15% efficiency, whereas the doubled system with 60 μm zone height will have efficiency 35%. Thus, there is a significant improvement in going from one to two and three such elements. It should be noted that such systems would provide a focus beam with more than 20% efficiency in the energy range from 40 to 130 keV.

Fig. 8 Image in scanning electron microscope (SEM) of the Si based Fresnel zone plate. The structure is 60 μm high and Δr_n is 0.4 μm.

Refractive lenses

Refractive lenses made of glass are among the most widely used optical components for visible light, with the wide spectrum of applications in focusing and imaging. Refractive lenses for X-rays were considered unfeasible for a long time due to the weak refraction and strong absorption. However, in 1996 it was shown that focusing by X-ray lenses is possible.^65,66 Since the (1 − δ) in the index of refraction is smaller than 1, lenses must have a concave shape (Fig. 9a). In order to obtain a focal length F in the range of one metre many single lenses have to be stacked behind each other to form a compound refractive lens (CRL) as shown in Fig. 9b. Fabricating the lenses from low-Z materials like Li, Be, B, C and Al minimizes the problems associated with absorption. The focal length of such CRL with parabolic profile s² = 2Rw and N individual biconcave lenses is F = R/2Nδ, where R is the radius of curvature at the apex of parabola. A lens with thickness 2w₀ + d has an aperture .

Fig. 9 Parabolic compound refractive lens (CRL). The individual lenses (a) and stacked behind one another to form a CRL (b).

Refractive lenses act as a normal conventional lens and we can apply the Gauss lens formula, which relates the source distance L₁, the image distance L₂ and the focal distance FviaL₂ = FL₁(L₁ − F). The diffraction-limited resolution of the lens Δ is defined by an effective aperture: Δ = 0.75λ/2A_n, where the numerical aperture is A_n = A_eff/2L₂. A_eff is the effective aperture of the lens, reduced by photon absorption and scattering, compared with the geometrical aperture 2R₀. Nowadays the parabolic refractive lenses, made of aluminum and beryllium, are available and widely used for hard X-ray microscopy applications (Fig. 10). Parabolic refractive lenses can be used to focus hard X-ray in the range from 5 keV to 150 keV. They can be used like glass lenses are used for visible light providing the resolution in the order of 300–500 nm, the main difference being that numerical aperture is much smaller than 1.^18–22,67 They focus in both directions, free of spherical aberrations and other distortions. They are compact, robust and easy to align and to operate. Their main applications are in micro- and nanofocusing, in imaging by absorption and phase contrast.^{21,22,30–33} In combination with tomography they allow 3D imaging of opaque media with sub-micrometre resolution.^35–39

Fig. 10 Cross section of individual parabolic CRL (a) and photograph of aluminum CRL assembly (b).

Recently, microelectronics planar fabrication technology has been applied to obtain silicon-based devices.^68,69 It is possible to make a composite lens consisting of a set of parallel parabolas with different focal distances. To change the focal distance or the desirable working energy, one can switch from one array to another by moving the composite lens.⁷⁰ Using the same approach of the Si planar technology, nanofocusing lenses were developed.^71,72 They have a focal distance in the range of a few millimetres at hard X-ray energies. In a crossed geometry, two lenses were used to generate a nanobeam with a lateral size of 50 nm by 50 nm with 1.6 × 10⁸ photons s⁻¹at 21 keV.⁷³ The planar lens technology is being transferred to materials like diamond that has low X-ray absorption, low thermal expansion and high heat conductivity.^74,75

Applications

X-Ray microscopy has developed into a powerful, versatile tool that has been implemented at various beamlines and is being applied to a large variety of scientific topics. Among the 40 beamlines in operation at the ESRF, seven beamlines are dedicated to X-ray microscopy techniques. The field of modern X-ray microscopy has now reached a state where a combination of imaging/tomography, spectroscopy and diffraction can be used over wide range of energies. In the harder X-ray region, in addition, it is possible to combine high resolution imaging and tomography with X-ray induced fluorescence for many applications. A number of applications such as the study of the environmental impact of fly ash particles, mapping of trace metal distribution in fluid inclusion and others illustrate the power of combining techniques.^{32,33,76–79} In this paper we present high energy microscopy for characterization of micrometre sized radioactive fuel particles.^30,31

3D microscopy of hot uranium particles

Following nuclear events such as nuclear weapons tests, nuclear accidents or discharges from nuclear installations, a major fraction of radionuclides released to the environment is associated with radioactive particles. After deposition, particle weathering occurs and the trapped radionuclides may become mobile. During the Chernobyl accident about 6–8 tonnes of uranium fuel were released into the atmosphere. Large fuel particles varying in size and radionuclide composition were deposited within 30 km around the reactor, whereas small-sized particles were found up to 2000 km from the site. During the initial explosion mechanical destruction of fuel rods occurred at high temperature and pressure and fuel particles were deposited to the west of the reactor. During the subsequent reactor core fire U fuel particles were released under high temperature and oxidizing conditions and transported by the wind to the north and northeast from the plant. Thus, the particles deposited after the Chernobyl accident, although originating from the same reactor core, were released under different temperature, pressure and redox conditions. To assess the long term consequences, information on particle characteristics, such as the morphological structure and the oxidation state of matrix elements, is needed since they influence the weathering rates and the subsequent mobilization of radionuclides.

For the first time different SR-based X-ray microscopic techniques have been combined and utilised to characterise individual micrometre sized radioactive particles. Chernobyl radioactive particles were characterized by micro-tomography, micro-X-ray absorption near edge spectroscopy (μ-XANES) and micro-diffraction (μ-XRD) techniques explored at the ESRF ID22 beamline. Combination of these microanalytical techniques allows one to obtain the volume distribution of U, to identify crystallographic structures and to obtain information on the distribution of oxidation states for U. The ID 22 experimental set-up is shown in Fig. 11. X-Ray radiation from the undulator passes through a Si monochromator, providing an X-ray beam with selected energy. The fixed exit double crystal monochromator allows tuning the energy across absorbing edges, keeping the beam position on the sample. The monochromatic beam is focused down to micrometre dimensions by a FZP or CRL. At 17 keV, FZP-generated beam size was 0.5 × 5 μm² while the flux at the sample was 10⁹−10¹⁰ ph s⁻¹. Optical microscope and high resolution CCD camera were used to position the sample in the focused beam. To calibrate the results obtained, well defined standards with respect to crystallographic structures and oxidation states were applied (U_met, UO₂, U₃O₈ and UO₂Ac₂*2H₂O, etc.). The absorption spectra were recorded with pindiodes, while fluorescence spectra were recorded using a Si(Li) energy dispersive detector having an area of 12 mm mounted at 90 degrees to the incident beam and 15 mm from the sample.

Fig. 11 Experimental setup used for: (a) microtomography and (b) micro-X-ray absorption near edge spectroscopy (μ-XANES) and micro-diffraction (μ-XRD) techniques.

Computed microtomography in projection geometry was done on different hot particles, mounted on the tip of a glass capillary, which was placed on a microtomography stage with eight degrees of freedom for alignment and rotation. The sample was rotated around a horizontal axis to obtain the highest resolution in the plane of reconstruction. During the rotation, images were recorded with 18 keV photons using a high resolution, cooled CCD-based X-ray detector with a resolution of 0.6 microns. The tomograms of a “west” and a “north” particle are presented in Fig. 12. The tomogram of the “west” particle shows a homogeneous distribution of uranium within the particle and the presence of channels or cavities, probably due to the formation of volatile fission products in the fuel during operation. On the other hand, the “north” particle has an inhomogeneous uranium distribution and is very loosely packed. The porosity can be attributed partly to the fact that U had been oxidized during the release.

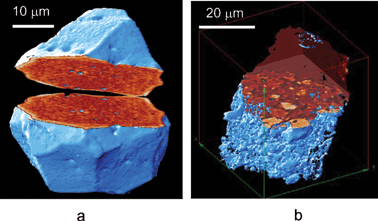Fig. 12 Three-dimensional visualisation of the west (a) and north (b) particles, by cutting the data block the inner particle structure is visualised.

To establish the crystallographic structure of the particles μ-XRD analysis was applied using powder diffraction patterns to obtain the occurrence of uranium-oxide phases according to the U–O-phase diagram. In μ-diffraction, particles were exposed for 3–5 s at different energies between 17 keV and 25 keV. Large area fibre coupled CCD camera placed 15 mm from the sample provided information on the Debye–Scherrer-ring diameters. μ-XRD of the fuel particles collected from within and to the north of the reactor demonstrated that U was present as U₂O₅/U₃O₈, i.e. U in the UO₂ fuel particles have been oxidised. However, uranium in particles collected to the west of the reactor is not oxidised and weak signals of UO₂ and possibly UO and UC₂ were obtained.

Additional information on U oxidation state can be obtained by μ-XANES. The μ-XANES spectra were obtained at 0.8 eV increment over a 160 eV energy range extending from about 40 eV below and 120 eV above the U L_III absorption edge at 17.163 keV. Differences in U-oxidation states were determined by shifts in pre-edge and bound-state edge features in μ-XANES spectra due to increase in the binding energy of the core electron levels. By determining the inflection point energy as a function of photon energy for the standards, a correlation between the inflection point energy and oxidation state was obtained. The μ-XANES spectra of standards reflected a shift of the inflection point energy (central location of the edge position) with oxidation state, a near-linear relationship, having a slope of about 1 eV/oxidation state unit.

μ-XANES spectra of particles collected to the north of the reactor overlapped with U₃O₈ standard spectra and the inflection point energies corresponded to oxidation state 5.0 ± 0.5, in agreement with the U₂O₅/U₃O₈ results from μ-XAD. Similar results were obtained for particles collected from within the reactor and for particles annealed under air (UO₂ standard, UO₂ fuel, particles from inside the reactor). Thus, oxidation of UO₂ to U₂O₅/U₃O₈ was evident for particles released during the reactor fire and oxidation cannot be attributed to post-accident weathering in natural ecosystems only as oxidised U-particles also were found inside the reactor. Surprisingly, μ-XANES spectra of particles collected to the west of the reactor, did not overlap with any of the standards, but occurred as an intermediate between metallic U (oxidation state 0) and UO₂ (oxidation state 4) with inflection point energies corresponding to the oxidation state 2.5 ± 0.5. Thus, results from μ-XANES demonstrated that U in UO₂ fuel particles were reduced during the immediate explosion. Considering the high temperature and pressure conditions during the initial accident, interaction with graphite from the damaged graphite moderator seems plausible. Although μ-XAD diffraction pattern indicated presence of UC₂, further analysis is needed to establish phases containing reduced U.

By performing a μ-XANES line scan, i.e. positioning the X-ray microbeam at various locations along a line thorough the particle and determining the first inflection point of the local XANES profile, the distribution of the oxidation state across the particle was attained. It turned out that for west particles (released during the explosion of the reactor) an outer layer with reduced U (2.5 ± 0.5) with an inner UO₂ core was identified (Fig. 13). The distribution of oxidation states of U within the particle was determined from a series of absorption images covering the particle. In each pixel the oxidation state was determined from the location of first inflection point. The μ-XANES images of the west and north particles are presented in Fig. 14. As can be seen, the north particle has a core of UO₂ surrounded by an oxidized U₂O₃/U₃O₅ surface layer, whereas the west particle is not oxidized and in some areas close to the surface, U is reduced.

Fig. 13 SEM image of the west particle (a) and horizontal line scan of U-oxidation state across this particle (b). Scan path is indicated as a dashed line.

Fig. 14 Micro-XANES images of the west (a) and north (b) particles. Each pixel of the image represents the U-oxidation state.

The present results demonstrate that the oxidation state of uranium in fuel particles vary according to the release scenario. During the initial explosion, reduced U (2.5 ± 0.5) fuel particles with reminiscence of the UO₂ core were released and deposited west of the reactor. These particles are relatively inert i.e. less susceptible to weathering. The weathering rate is relatively slow and the subsequent mobilisation of associated radionuclides is delayed. During the fire, however, oxidised U₂O₅/U₃O₈ fuel particles with UO₂ cores were released and deposited to the north and probably also to the east and south of the reactor. These particles are more susceptible to weathering. Thus, the hypothesis that particle characteristics like composition, distribution, crystallographic structure and oxidation states, are source-related and release scenario dependent is fully supported.

Being key factors determining particle weathering rates, subsequent mobilisation and ecosystem transfer of associated radionuclides, these findings demonstrate that particle characteristics are essential input parameters in ecosystem transfer models for areas significantly contaminated with radioactive particles (nuclear test sites, accidental or waste sites). Unless particle characteristics and the impact of particles are taken into account, assessment model predictions suffer from large uncertainties. The present work also demonstrates that the combination of synchrotron-based hard X-ray microscopic techniques is an extremely powerful tool for providing information on key particle characteristics needed in impact assessment studies.

References

1. W. Chao, B. Harteneck, J. A. Liddle, E. Anderson and D. T. Attwood, Nature (London), 2005, 435, 1210.
2. A. Snigirev, I. Snigireva, V. Kohn, S. Kuznetsov and I. Schelokov, Rev. Sci. Instrum., 1995, 66, 5486.
3. P. Cloetens, R. Barrett, J. Baruchel, J. P. Guigay and M. Schlenker, J. Phys. D: Appl. Phys., 1996, 29, 133.
4. S. W. Wilkins, T. E. Gureyev, D. Gao, A. Pogany and A. W. Stevenson, Nature (London), 1996, 384, 335.
5. B. Niemann, D. Rudolph and G. Schmahl, Opt. Commun., 1974, 12, 160.
6. B. Niemann, G. Schneider, P. Guttmann, D. Rudolph and G. Schmahl, in X-ray Microscopy IV, ed. V. V. Aristov and A. I. Erko, Bogorodski Pechatnik, Cherngolovka, Moscow region, 1994, p. 66.
7. D. Rudolph, G. Schmahl and B. Niemann, in Modern Microscopes, ed. P. J. Duke and A. G. Michette, Plenum, New York, 1990, pp. 59–67.
8. H. Rarback, J. M. Kenney, J. Kirz, M. R. Howells, P. Chang, P. J. Coane, R. Feder, P. J. Houzego, D. P. Kern, D. Sayre, Springer Series in Optical Sciences, Springer Verlag, Berlin, 1984, vol. 43, p. 203.
9. C. Jakobsen, M. R. Howells, J. Kirz and S. Rohman, J. Opt. Soc. Am., 1990, A7, 1847.
10. M. R. Howells, C. J. Jakobsen and S. Lindaas, in X-ray Microscopy IV, ed. V. V. Aristov and A. I. Erko, Bogorodski Pechatnik, Cherngolovka, Moscow region, 1994, p. 414.
11. A. C. Kak and M. Slaney, Principles of Computerized Tomographic imaging, Institute of Electrical and Electronics Engineers, New York, 1988.
12. C. Raven, A. Snigirev, I. Snigireva, P. Spanne, A. Souvorov and V. Kohn, Appl. Phys. Lett., 1996, 69, 1826.
13. P. Cloetens, W. Ludwig, J. Baruchel, D. Van Dyck, J. Van Landuyt, J. P. Guigay and M. Schlenker, Appl. Phys. Lett., 1999, 75, 2912.
14. G. T. Herman, Image Reconstruction from Projection, Academic Press, New York, 1980.
15. Y. Suzuki, M. Awaji, A. Takeuchi, H. Takano, K. Uesugi, Y. Komura, N. Kamijo, M. Yasumoto and S. Tamura, J. Phys. IV, 2003, 104, 35.
16. Y. Kagoshima, Y. Yokoyama, T. Niimi, T. Koyama, Y. Tsusaka, J. Matsui and K. Takai, J. Phys. IV, 2003, 104, 49.
17. W. Leitenberger, T. Weitkamp, M. Drakopoulos, I. Snigireva and A. Snigirev, Opt. Commun., 2000, 180, 233.
18. B. Lengeler, C. G. Schroer, M. Richwin, J. Tummler, M. Drakopoulos, A. Snigirev and I. Snigireva, Appl. Phys. Lett., 1999, 74, 3924.
19. B. Lengeler, C. Schroer, J. Tummler, B. Benner, M. Richwin, A. Snigirev, I. Snigireva and M. Drakopoulos, J. Synchrotron Radiat., 1999, 6, 1153.
20. B. Lengeler, C. Schroer, B. Benner, F. Gunsler, M. Kuhlmann, J. Tummler, A. Simionovici, M. Drakopoulos, A. Snigirev and I. Snigireva, Nucl. Instrum. Methods, 2001, A467–468, 944.
21. C. Schroer, F. Gunsler, B. Benner, M. Kuhlmann, J. Tummler, B. Lengeler, C. Rau, T. Weitkamp, A. Snigirev and I. Snigireva, Nucl. Instrum. Methods, 2001, A467–468, 966.
22. C. G. Schroer, B. Benner, T. F. Günzler, M. Kuhlmann, B. Lengeler, C. Rau, T. Weitkamp, A. Snigirev and I. Snigireva, Proc. SPIE-Int. Soc. Opt. Eng., 2002, 4503, 23.
23. Y. Kohmura, K. Okada, M. Awaji, Y. Suzuki, T. Ishikawa, Yu. I. Dudchik, N. N. Kolchevsky and F. F. Komarov, AIP Conf. Proc., 2000, CP507, 566.
24. Y. Kagoshima, T. Koyama, I. Wada, T. Niimi, Y. Tsusaka, J. Matsui, S. Kimura, M. Kotera and K. Takai, AIP Conf. Proc., 2004, CP705, 1263.
25. W. Yun, S. T. Pratt, R. M. Miller, Z. Cai, D. B. Hunter, A. G. Jarstfer, K. M. Kemner, B. Lai, H.-R. Lee, D. G. Legnini, W. Rodrigues and C. I. Smith, J. Synchrotron Radiat., 1998, 5, 1390.
26. Z. Cai, B. Lai, Y. Xiao and S. Xu, J. Phys. IV, 2003, 104, 17.
27. K. M. Kemner, S. D. Kelly, B. Lai, J. Maser, E. J. O'Loughlin, D. Sholto-Douglas, Z. Cai, M. A. Schneegurt, C. F. Kulpa Jr. and K. H. Nealson, Science, 2004, 306, 686.
28. T. Buonassisi, A. A. Istratov, M. Heuer, M. A. Marcus, R. Jonczyk, J. Isenberg, B. Lai, Z. Cai, S. Heald, W. Warta, R. Schindler, G. Willeke and E. R. Weber, J. Appl. Phys., 2005, 97, 074901.
29. Y. Xiao, Z. Cai, Z. L. Wang, B. Lai and Y. S. Chu, J. Synchrotron Radiat., 2005, 12(2), 124.
30. B. Salbu, T. Krekling, O. C. Lind, D. H. Oughton, M. Drakopoulos, A. Simionovici, I. Snigireva, A. Snigirev, T. Weitkamp, F. Adams, K. Janssens and V. A. Kashparov, Nucl. Instrum. Methods, 2001, A467–468, 1249.
31. B. Salbu, K. Janssens, O. C. Lind, A. Simionovici, T. Krekling, M. Drakopoulos, I. Snigireva and A. Snigirev, Proceedings of Actinide-XAS-2000, Nuclear Energy Agency (NEA), Organisation for Economic Co-operation and Development (OECD), Paris, France, 2002, p. 119.
32. P. Phillipot, B. Menez, A. Simionovici, A. Chabiron, M. Cuney, A. Snigirev and I. Snigireva, Terra Nova, 2000, 12, 84.
33. P. Phillipot, B. Menez, M. Drakopoulos, A. Simionovici, A. Snigirev and I. Snigireva, Chem. Geol., 2001, 173(1–3), 151.
34. A. Otten, S. Köster, B. Struth, A. Snigirev and T. Pfohl, J. Synchrotron Radiat., 2005, 12, 745.
35. C. G. Schroer, J. Tummler, F. Gunzler, B. Lengeler, W. H. Schroder, A. J. Kuhn, A. Simionovici, A. Snigirev and I. Snigireva, Proc. SPIE-Int. Soc. Opt. Eng., 2000, 4142, 287.
36. C. G. Schroer, B. Benner, T. F. Günzler, M. Kuhlmann, B. Lengeler, W. H. Schröder, A. J. Kuhn, A. S. Simionovici, A. Snigirev and I. Snigireva, Proc. SPIE-Int. Soc. Opt. Eng., 2002, 4503, 230.
37. C. G. Schroer, J. Meyer, M. Kuhlmann, B. Benner, T. F. Gunsler, B. Lengeler, C. Rau, T. Weitkamp, A. Snigirev and I. Snigireva, Appl. Phys. Lett., 2002, 81, 1527.
38. C. G. Schroer, T. F. Günzler, M. Kuhlmann, O. Kurapova, S. Feste, M. Schweitzer, B. Lengeler, W. H. Schröder, A. Somogyi, A. S. Simionovici, A. Snigirev and I. Snigireva, Proc. SPIE-Int. Soc. Opt. Eng., 2004, 5535, 162.
39. C. G. Schroer, B. Benner, T. F. Günzler, M. Kuhlmann, J. Patommel, B. Lengeler, A. Somogyi, T. Weitkamp, C. Rau, A. Snigirev and I. Snigireva, Proc. SPIE-Int. Soc. Opt. Eng., 2004, 5535, 701.
40. P. Kirkpatrick and A. Baez, J. Opt. Soc. Am., 1948, 38, 766.
41. J. H. Underwood and T. W. Barbee, J. Appl. Opt., 1981, 20, 3027.
42. J. Underwood, T. Barbee and C. Frieder, J. Appl. Opt., 1986, 25(11), 1730.
43. Y. Mori, K. Yamauchi, H. Mimura, Y. Sano, A. Saito, K. Ueno, K. Endo, A. Souvorov, M. Yabashi, K. Tamasaku and T. Ishikawa, Proc. SPIE-Int. Soc. Opt. Eng., 2002, 4782, 58.
44. K. Yamamura, K. Yamauchi, H. Mimura, Y. Sano, A. Saito, K. Endo, A. Souvorov, M. Yabashi, K. Tamasaku, T. Ishikawa and Y. Mori, Rev. Sci. Instrum., 2003, 74, 4549.
45. H. Mimura, S. Matsuyama, H. Yumoto, H. Hara, K. Yamamura, Y. Sano, M. Shibahara, K. Endo, Y. Mori, Y. Nishino, K. Tamasku, M. Yabashi, T. Ishikawa and K. Yamauchi, Jpn. J. Appl. Phys., 2005, 44, L539.
46. G. E. Ice, J.-S. Chung, J. Tischler, A. Lunt and L. Assoufid, Rev. Sci. Instrum., 2000, 71, 2635.
47. C. Liu, L. Assoufid, R. Conley, A. T. Macrander, G. E. Ice and J. Z. Tischler, Opt. Eng., 2003, 42, 3622–3628.
48. Y. Dabin, G. Rostaing, O. Hignette, A. Rommeveaux and A. Freund, Proc. SPIE-Int. Soc. Opt. Eng., 2002, 4782, 235.
49. O. Hignette, P. Cloetens, G. Rostaing, P. Bernard and C. Morawe, Rev. Sci. Instrum., 2005, 76, 063709.
50. D. R. Kreger, Recl. Trav. Bot. Neerl., 1948, 41, 603.
51. E. A. Stern, Z. Kalman, A. Lewis and K. Lieberman, Appl. Opt., 1988, 27, 5135.
52. P. Engstrøm, S. Larrson, Å. Rindby, A. Buttkewitz, S. Garbe, G. Gaul, A. Knöchel and F. Lechtenberg, Nucl. Instrum. Methods, 1991, A302, 547.
53. D. H. Bilderback, S. A. Hoffman and D. J. Thiel, Science, 1994, 263, 201.
54. Y. P. Feng, S. K. Sinha, H. W. Deckman, J. B. Hastings and D. P. Siddons, Phys. Rev. Lett., 1993, 71, 537.
55. S. Di Fonzo, W. Jark, S. Lagomarsino, C. Giannini, L. De Caro, A. Cedola and M. Muller, Nature (London), 2000, 403, 638.
56. W. Jark, A. Cedola, S. Di Fonzo, M. Fiordelisi, S. Lagomarsino, N. P. Konovalenko and V. A. Chernov, Appl. Phys. Lett., 2001, 78, 1192.
57. A. Cedola and S. Lagomarsino, Synchrotron Radiat. News, 2004, 17, 30.
58. F. Pfeiffer, C. David, M. Burghammer, C. Riekel and T. Salditt, Science, 2002, 12, 297.
59. A. Jarre, C. Fuhse, C. Ollinger, J. Seeger, R. Tucoulou and T. Salditt, Phys. Rev. Lett., 2005, 94, 074801.
60. A. V. Baez, J. Opt. Soc. Am., 1961, 51, 405.
61. W. Yun, B. Lai, A. A. Krasnoperova, E. Di Fabrizio, Z. Cao, F. Cerina, Z. Chen, M. Gentili and E. Gluskin, Rev. Sci. Instrum., 1999, 70, 3537.
62. E. Di Fabrizio, F. Romanato, M. Gentili, S. Cabrini, B. Kaulich, J. Susini and R. Barrett, Nature (London), 1999, 401, 895.
63. N. Kamijo, Y. Syuzuki, H. Takano, S. Tamura, M. Yasumoto, A. Takeuchi and M. Awaji, Rev. Sci. Instrum., 2003, 74(12), 5101.
64. I. Snigireva, A. Snigirev, V. Kohn, V. Yunkin, C. Mocuta and G. Vaughan, to be published.
65. A. Snigirev, V. Kohn, I. Snigireva and B. Lengeler, Nature (London), 1996, 384, 49.
66. A. Snigirev, V. Kohn, I. Snigireva, A. Souvorov and B. Lengeler, Appl. Opt., 1998, 37, 653.
67. C. G. Schroer, M. Kuhlmann, B. Lengeler, T. F. Gunsler, O. Kurapova, B. Benner, C. Rau, A. S. Simionovici, A. Snigirev and I. Snigireva, Proc. SPIE-Int. Soc. Opt. Eng., 2002, 4783, 10.
68. V. Aristov, M. Grigoriev, S. Kuznetsov, L. Shabelnikov, V. Yunkin, T. Weitkamp, C. Rau, I. Snigireva, A. Snigirev, M. Hoffmann and E. Voges, Appl. Phys. Lett., 2000, 77, 4058.
69. I. Snigireva, A. Snigirev, C. Rau, T. Weitkamp, V. Aristov, M. Grigoriev, S. Kuznetsov, L. Shabelnikov, V. Yunkin, M. Hoffmann and E. Voges, Nucl. Instrum. Methods, 2001, A467–468, 982.
70. I. Snigireva, A. Snigirev, V. Yunkin, M. Drakopoulos, M. Grigoriev, S. Kuznetsov, M. Chukalina, M. Hoffmann, D. Nuesse and E. Voges, Proceedings of the 6th International Conference on X-ray Microscopy, ed. W. Mayer-Ilse, T. Warwick and D. Attwood, AIP Conference Proceedings, Melville, NY, 2004, vol. 705, p. 708.
71. C. G. Schroer, M. Kuhlmann, U. T. Hunger, T. F. Gunsler, O. Kurapova, S. Feste, F. Frehse, B. Lengeler, M. Drakopoulos, A. Somogyi, A. S. Simionovici, A. Snigirev, I. Snigireva, C. Schug and W. H. Schroder, Appl. Phys. Lett., 2003, 82, 1485.
72. C. G. Schroer, T. F. Günzler, M. Kuhlmann, O. Kurapova, S. Feste, M. Schweitzer, B. Lengeler, W. H. Schröder, A. Somogyi, A. S. Simionovici, A. Snigirev and I. Snigireva, Proc. SPIE-Int. Soc. Opt. Eng., 2004, 5535, 162.
73. C. G. Schroer, O. Kurapova, J. Patommel, P. Boye, J. Feldkamp, B. Lengeler, M. Burghammer, C. Riekel, L. Vincze, A. Van der Hart and M. Kuchler, Appl. Phys. Lett., 2005, 87, 124103.
74. A. Snigirev, V. Yunkin, I. Snigireva, M. Di Michiel, M. Drakopoulos, S. Kouznetsov, L. Shabelnikov, M. Grigoriev, V. Ralchenko, I. Sychov, M. Hoffmann and E. Voges, Proc. SPIE-Int. Soc. Opt. Eng., 2002, 4783, 1.
75. B. Nohammer, J. Hoszowska, A. K. Freund and C. David, J. Synchrotron Radiat., 2003, 10, 168.
76. M. C. Camerani, A. Somogyi, M. Drakopoulos and B.-M. Steenari, Spectrochim. Acta, Part B, 2001, 56, 1355.
77. M. C. Camerani-Pinazani, A. Somogyi, A. Simionovici, S. Ansell, B.-M. Steenari and O. Lindqvist, Environ. Sci. Technol., 2002, 36, 3165.
78. M. C. Camerani, B. Golosio, A. Somogyi, A. Simionovici, B.-M. Steenari and I. Panas, Anal. Chem., 2004, 76, 1586.
79. M. C. Camerani-Pinzani, S. Ansell, A. Somogyi, B.-M. Steenari and O. Lindqvist, Anal. Chem., 2004, 76, 1596.

---

Footnote

† Presented at the Fifth International Symposium on Modern Principles of Air Monitoring & Biomonitoring, June 12–16 2005, Norway.

---