Assigning carbon-13 NMR spectra to crystal structures by the INADEQUATE pulse sequence and first principles computation: a case study of two forms of testosterone

Abstract

A ¹³C CPMAS NMR experiment at high field (11.7 T) has produced significantly improved dispersion for the α form of testosterone, allowing revisions and extensions to be made to the assignments. Correlations shown by an INADEQUATE two-dimensional spectrum, recorded at 16.5 T, have allowed the components of most of the doublet signals to be grouped into two sets (for the two crystallographically independent molecules). First-principles computations, employing a fully solid-state approach, have been used to obtain values for the crystallographic splittings, which are discussed in relation to the experimental values. This procedure enables assignments to the two groups to be suggested for all but one of the remaining doublet signals. It also allows the two sets of signals to be identified specifically to the two independent molecules in the crystal structure. Computations were also carried out for the β form of testosterone (a dihydrate). The shift differences between the α and β forms were compared with the experimental data, with encouraging results. Comparisons were also made between computed and experimental shielding anisotropies and asymmetries for three of the carbons of the α form. The methodology has a high potential for future applications, though more examples need to be evaluated before general conclusions can be drawn.

---

Introduction

Now that high-resolution ¹³C spectra of organic solids can be obtained relatively easily, it has become important to improve the methods of spectral assignment and to understand the factors affecting chemical shifts. In particular, it is of interest to understand to what extent carbon-13 chemical shifts can be used to help determine crystal structures in powdered crystalline solids.^1–3 First principles computation offers the hope of being able to predict or explain chemical shifts, and recently NMR calculations have been incorporated into the Castep program^4–6 which makes use of the translational symmetry inherent in crystal structures. Such methods rely on density functional theory (DFT) and use plane waves and pseudopotentials.⁷ They have already had some success.^8–12 However, correctly reproducing shieldings relative to some reference, in order to match computation and experiment, is still fraught with many problems.

Two areas where chemical shift calculations could provide particular interest are shift differences (i) between polymorphs or solvates, and (ii) between different independent molecules in a given crystal, in cases where there is more than one molecule in the asymmetric unit. Both of these situations depend on the local crystallographic environment of molecules and (often small) variations in molecular geometry. Not only are these cases of great interest in themselves, notably for pharmaceutical applications, but also it is clear that many of the difficulties inherent in the computational method itself could be overcome if comparisons are made between shifts for the same carbon in the same molecule but in different circumstances, as is true in both the above circumstances.

A third situation where comparisons can be made for the same carbon in the same molecule is where shielding anisotropies and asymmetries are concerned.

Assignments are particularly problematic in the case of crystallographically inequivalent molecules in the unit cell since one-dimensional spectra offer no enlightenment as to which lines in a spectrum belong to a particular independent molecule. Of course, two-dimensional dipolar recoupling experiments such as RFDR can link neighbouring atoms via dipolar couplings and the INADEQUATE sequence and its derivatives give data on connectivities viaJ-couplings. Both of these types of pulse sequence provide the appropriate links in principle. However, they usually require either global ¹³C isotopic enrichment or very long spectrometer times. To our knowledge such work has only been reported for three organic systems with more than one molecule in the asymmetric unit, once with enrichment¹³ and twice without.^2,14

In this article we provide an example of the determination of the two molecules in the asymmetric unit cell for the α form of 17β-hydroxyandrost-4-en-3-one, testosterone (I), in comparison to the β form, to evaluate these ideas and to compare computation with experiment. The results serve to simultaneously test the applicability of the computations and to aid spectral assignment. Notably, we obtain reasonable agreement between experiment and calculation, and by using both the experimental INADEQUATE connectivities and the calculated chemical shifts we are able to completely assign the resonances to the two individual molecules in the unit cell. This allows us to evaluate the accuracy of the calculated chemical shift splittings between the two molecules and the shift differences between the two forms.

Testosterone has a number of forms and we discuss herein the α and β cases, both of which have known crystal structures^15,16 (Cambridge Crystallographic Database codes TESTON10 and TESTOM01, respectively), though the determinations are over 30 years old. The α form is anhydrous and has two molecules in the asymmetric unit. It contains these molecules linked alternately in a chain by hydrogen bonding between the hydroxyl group at C-17 and the carbonyl group at C-3. The β form, on the other hand, is a monohydrate, with a single independent formula unit. It contains relatively isolated testosterone molecules, each hydrogen-bonded to three water molecules (two at the carbonyl end and one at the hydroxyl end). The ¹³C CP/MAS spectra have been reported and largely assigned.¹⁷ These show crystallographic splittings in the resonance frequencies for corresponding carbons in the two independent molecules for the α form of up to 2.3 ppm and differences in shifts between average α values and those for the β form of up to 3.1 ppm. The small magnitude of these differences should provide a stringent test of the computational methods and, to some degree, provide an estimate of the upper bound on the current accuracy of first principles techniques.

For the present work we have re-run the ¹³C CPMAS spectrum of the α form (obtained originally from the Glaxo company) at high magnetic field (16.5 T) in order to obtain more accurate values of the crystallographic splittings, and we have obtained INADEQUATE spectra at 11.7 T so that correlations could be made between signals for the individual independent molecules as far as possible.

First principles computations of the shifts for both α and β forms were then carried out and the results compared with the experimental data.

Experimental

(a) NMR spectroscopy

The CPMAS spectrum shown in Fig. 2 was obtained on a narrow-bore Bruker Avance spectrometer operating at ¹H and ¹³C frequencies of 700 and 176 MHz, respectively and referenced by replacement to the exact centre of the proton-coupled ¹³C quadruplet for tetramethylsilane (obtained at 5 kHz MAS and 293 K). A 4 mm double-resonance probe providing magic-angle spinning frequencies up to 15 kHz was used. The MAS rate was set to 10 kHz and the SPINAL64 sequence¹⁸ at a proton nutation frequency of 90 kHz was used for decoupling the protons. The spectrum was acquired with 128 transients and a recycle delay of 3 s. The cross polarisation contact time for transferring the magnetization from protons to carbons was set to 2 ms. A long acquisition time of 50 ms was required because of the high degree of crystallinity of the testosterone sample. A moderately low temperature of 273 K (bearing gas) was used for the sample in order to avoid degradation because of the heating caused by the spinning.

Fig. 1 Structures of the α (top) and β (bottom) forms of testosterone. The hydrogens have been omitted for clarity, but the hydrogen bonds are indicated. The U and V molecules for α testosterone are separately identified.

Fig. 2 The 176 MHz ¹³C spectrum for the α form of testosterone: (a) High-frequency region; (b) low-frequency region.

The refocused INADEQUATE spectrum¹⁹ of natural abundance testosterone was acquired on a wide-bore Bruker Avance spectrometer operating at ¹H and ¹³C frequencies of 500.1 and 125.8 MHz, respectively, using a 4 mm double-resonance probe. The sequence was slightly improved by using 58°(0°)–140°(180°)–344°(0°)–140°(180°)–54°(0°) composite pulses.^20,21 A z-filter (of 3 ms duration) was also added at the end of the sequence. The MAS frequency was 10 kHz and proton decoupling was achieved using SPINAL64 at a proton nutation frequency of 100 kHz. Adjusting the decoupling sequence to obtain long transverse dephasing times^22,23 has been shown to be essential to record natural abundance INADEQUATE experiments in a reasonable time. 160 t₁ increments were used with 512 transients for each value and the recycle delay was set to 3 s, so that the total experimental time was about 3 days. The TPPI procedure was used for quadrature detection in the indirect dimension.^24–26 The contact time for cross polarization was 4 ms, the acquisition time was set to 20 ms and the τ delays of both echoes of the refocused INADEQUATE experiment were experimentally optimized for best efficiency and found to be 3 ms. The pulse sequence and phase cycle are available at the web site http//www.ens-lyon.fr/CHIMIE. The temperature was set to 273 K. During the processing, line broadenings of 20 and 80 Hz were used in the direct and indirect dimensions, respectively.

(b) Computations

The crystal structures for the α and β forms of testosterone were obtained from the Cambridge Crystallographic Database. The positions of the hydrogen atoms were adjusted in a constrained geometry optimisation using Castep, which is a DFT-based code. The difference between this method and quantum chemical techniques is that the charge density and wavefunctions are described using a planewave basis set and so the translational symmetry of the system is implicit. The interaction of the valence electrons with the nucleus and the core electrons is represented by a pseudopotential, the use of which greatly enhances the computational efficiency of the approach. In all of our calculations the electron correlation effects are modelled using the generalised gradient approximation of Perdew, Burke and Ernzerhof.²⁷ For the geometry optimisation we employ “ultrasoft” pseudopotentials,²⁸ a planewave cut-off energy of 400 eV and a 1 × 1 × 2 Monkhorst–Pack²⁹ grid to sample the Brillouin zone. The NMR calculations were performed using the gauge including projector augmented wave approach (GIPAW)⁵ at the larger cut-off of 440 eV, also using Castep. This method allows for a fully solid-state treatment of the system under investigation. The calculations are performed on the full unit cell as obtained from the Cambridge Crystallographic Database. The lattice volume is fixed to the experimental value, so the intermolecular interactions are effectively taken into account. Hydrogen bonds are well-described within DFT, although weak Van der Waals interactions less so.

The positions of only the hydrogen atoms were allowed to relax since location of heavy atoms by diffraction methods is significantly more accurate than those for hydrogens. Of course the computations are carried out for essentially static atomic positions and therefore do not take account of molecular-level mobility except insofar as it determines the crystal structure.

The output of a first principles NMR calculation is the absolute shielding tensor. The conventions used for shielding parameters are as follows;

Isotropic shielding, σ_iso = (σ_XX + σ_YY + σ_ZZ)/3

Anisotropy, ζ = σ_ZZ − σ_iso

Asymmetry, η = (σ_YY − σ_XX)/ζ

The isotropic chemical shift, δ_iso is given by δ_iso = −(σ_iso − σ_ref), where σ_ref is the nuclear shielding of the reference system.

To compare directly with experiment, the absolute shielding must be converted to the chemical shift using an appropriate reference shielding. In the case of ¹³C, a full simulation of liquid tetramethylsilane would be time-consuming and might potentially introduce unnecessary errors. As an alternative to this, the calculated shielding is plotted against the experimental shifts and a linear regression is performed, imposing a slope of unity. The shielding is then converted using the reference obtained from the regression. A fit of the α data against the newly obtained experimental values yielded an intercept of 169.82 ppm and an RMS error of 3.53 ppm. The regression of the β data, which was fitted to the previously published data but adjusted by a value of 0.45 ppm (see the Results section), had an intercept of 168.50 ppm, with an RMS error of 4.38 ppm. A combined fit of α and β data gave a value of 169.17 ppm for the reference shielding and had an RMS of 3.97 ppm. When the correlation for the α form was carried out without the restriction on the slope (the fitted value of which became 1.06), the RMS error fell to 2.25, but of course the intercept (shielding of the reference) also changed, to 172.56 ppm. In keeping with the expression given above for relating the shift to the shielding, obtaining the reference shift by constraining the slope to unity is the preferred approach.

Results and discussion

The 176 MHz ¹³C CPMAS one-dimensional spectrum of the α form of solid testosterone is shown in Fig. 2, with the low-frequency region displayed at a greater scale expansion than the high-frequency part. The resolution is significantly better than spectra recorded at lower fields and there appears to be only one accidental degeneracy, at 33.76 ppm. The crystallographic splittings are clearly visible for most carbons, but initially there were some ambiguities in the assignments of lines in the region between δ = 28 and δ = 39 ppm.

A two-dimensional CPMAS refocused INADEQUATE spectrum of the α form is shown in Fig. 3 and 4. The low-frequency part is displayed in Fig. 3, with expansions shown in Fig. 4. This experiment notably allowed us to assign the signals in the ambiguous region, revealing some necessary re-assignments from those published previously¹⁷. Ref. 17 also contains the solution-state chemical shifts for comparison. The new chemical shifts and assignments are displayed in Table 1. Crucially, the cross-peaks enabled us to assign the resonances to the two independent molecules in most cases (see also below).

Fig. 3 Low-frequency region of the INADEQUATE spectrum of the α form of testosterone, obtained using the 11.7 T spectrometer. The 1-D traces are from the 176 MHz spectrum. The assignments of the two independent molecules are given in different colours.

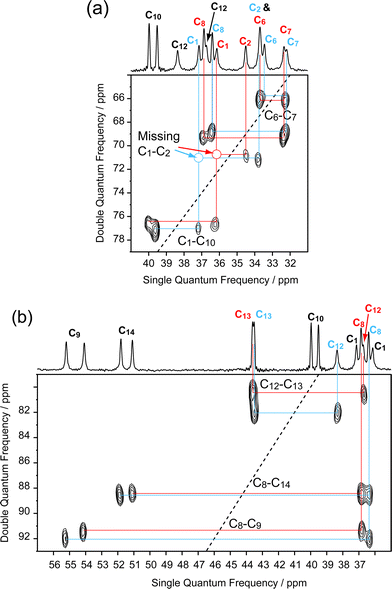Fig. 4 Expansions of the INADEQUATE spectrum, revealing specific correlations for the crowded region of the 1-D spectrum.

Table 1 Carbon-13 chemical shifts for molecules U and V of the α form of testosterone, as obtained experimentally at 176 MHz and computed using the GIPAW approach (with only hydrogen positions relaxed)

	Molecule U		Molecule V
Carbon number	Experimental shift	Computed shift	Experimental shift	Computed shift
a In these cases the assignment to U and V molecules is not available experimentally and has therefore been made tentatively from the computations. b The assignment to U and V molecules is not certain on the simple basis of the experimental data, although suggested. Of course, changing the sign of these entries would affect other pairs, including C17. c These two shifts may be interchanged.
3^a	201.22	204.37	202.72	204.70
5	170.64	182.56	172.09	182.72
4^a	125.67	128.73	125.17	127.04
17	80.35	83.42	82.69	86.82
9	54.14	55.24	55.26	55.37
14	51.14	51.35	51.86	51.35
13^b	43.67	41.52	43.57	41.71
10	40.03	40.60	39.57	39.49
12	36.78	36.91	38.41	37.40
1	36.19	35.53	37.20	35.63
8	36.92	35.77	36.44	34.18
2	34.55	32.68	33.76	30.94
6	33.76	35.08	33.50	33.85
7^b	32.40	32.85	32.25	32.35
16^b	30.19	26.55	29.86	26.38
15	24.33^c	22.99	24.23^c	22.49
11	22.99	19.68	22.02	20.91
19	18.56	14.93	17.92	14.20
18	11.67	7.94	12.21	7.80

---

Table 1 also contains the results of the computations. There is clearly a moderately good general correlation between the experimental and theoretical data. However, there are some discrepancies, the most remarkable of which is for C5, where the difference in the computed and measured shifts is approximately 11 ppm. We have no firm explanation for this anomaly. However, there are, in general, at least two possible sources of error influencing the computed data which may account for such an effect: the quality of the original crystal structure and the level of theory used for the computations. It is well known^3,30 that reported uncertainties in atomic positions from diffraction measurements can propagate to significant computed chemical shift variations. The crystal structure is rather old and therefore it is quite likely that the resolution is not as accurate as this level of calculation would require. The forces on the constrained atoms after the partial geometry optimisation was performed were still moderately large (∼1.2 eV Å⁻¹), which indicates that further optimisation of this structure would yield significant changes from that obtained experimentally. Additional calculations proved that this was indeed the case. However, the merit of this type of approach is unclear given that the simulation (which calculates what the structure would be at 0 K without zero-point vibrations) and experimental determination are performed under very different circumstances. It is also feasible that errors in the computed shifts might be attributable to a limitation of the density functional in adequately describing electron correlation in the region of this particular carbon. It would be interesting to investigate this possibility further, although the size of the system would make this an expensive calculation for higher levels of theory. It may be noted that the C5 shift does not appear to be so anomalous if the slope of the correlation is not constrained to be unity.

Computations have also been carried out for the β form (see the electronic supplementary information (ESI)), and Fig. 5 is a plot of the combined data for the two forms. The computed shielding constants were converted to chemical shifts by the procedure mentioned in the experimental section.

Fig. 5 Combined plot of computed and experimental chemical shifts for the α and β forms of testosterone. In the case of the α form, average values for the two independent molecules have been used. The shieldings were converted to chemical shifts using a reference value of 169.17 ppm obtained from a constrained linear regression of both α and β values. The RMS error for all of the shifts was found to be 3.97.

Note that the 2-D experiment also enabled us to correlate most, though not all, the signals for a given independent molecule of the α form (see Table 1 and Fig. 2 and 3) but that we cannot from the NMR experiment alone determine which molecule is which. The experimental crystallographic splittings are given in Table 2, with the relative signs where these could be deduced. The computed splittings are also listed including their signs (which are those obtained by subtracting the shifts of the “V” molecule from those of the “U” molecule—see Fig. 1(a)).

Table 2 Computed and experimental crystallographic splittings for α-testosterone^a

	Splitting/ppm			Splitting/ppm
Carbon no.	Comp.	Expt.	Carbon no.	Comp.	Expt.
a Signs given as U − V. b Signs not accessed experimentally. c The splitting sign is not certain on the simple basis of the experimental data, although suggested. Of course, changing the sign of these entries would affect other pairs, including C17.
1	−0.10	−1.01	11	−1.23	+0.97
2	1.74	+0.79	12	−0.50	−1.63
3	−0.33	±1.50^b	13	−0.19	+ 0.10^c
4	1.69	±0.50^b	14	−0.00	−0.72
5	−0.16	−1.45	15	0.50	±0.10^b
6	1.22	+0.26	16	0.17	+0.33^c
7	0.50	+0.15^c	17	−3.40	−2.34
8	1.59	+0.48	18	0.14	−0.54
9	−0.13	−1.12	19	0.73	+0.64
10	1.11	+0.46

---

Whilst the agreement of the magnitudes of the computed crystallographic splittings with those determined by the INADEQUATE experiments is not close, it is noteworthy that the computed sign is correct in each of the four cases where the experimental splitting is more than 1 ppm and its sign is known. The correct sign is also found for nearly all the remaining cases of known experimental sign. In addition, the opposite relative signs for C16 and C17 are correctly computed. The only really anomalous (“incorrect”) result is for C11. Our overall view is that the results are encouraging, and we are moderately sure that the sign of the biggest splitting (for C17) is negative as computed. We also suggest the signs for C3 and C4 are probably as computed.

Most importantly, we can use the computations to assign the shifts to the U and V molecules, thereby establishing the crystallographic assignment of the doublet lines, and, where experimental signs are still unknown, the computations allow prediction of crystallographic assignments. The result is that we are able using this combined INADEQUATE/computation approach to assign all the resonances in the spectrum except three at the most to identified carbon atoms in the crystal structure.

The computations also allow comparisons to be made between theoretical and experimental results for the differences between β shifts and average α shifts for the same carbons. These data are given in Table 3, in the compilation of which the experimental values for the β form from the literature have been adjusted by 0.50 ppm, since this seems to be a consistent difference between the literature data and our 176 MHz shifts for the α form (probably arising from referencing issues). It is encouraging to note that the correct sign of the difference is obtained for 10 out of the 13 cases where experimentally it is greater than 0.5 ppm. Intriguingly, the three values that do not have their signs correctly predicted are all associated with the five-membered ring. Generally, the computations seem to overestimate the magnitude of the differences, possibly because the computations take no account of any molecular mobility. However, the fact that the method does systematically reproduce most of the features of the polymorph differences despite the limitations of DFT and the use of a static molecular model is impressive.

Table 3 Computed and experimental^a shift differences between the α and β forms of testosterone, given as α − β

	Shift/ppm			Shift/ppm
Carbon number	Computed	Experimental	Carbon number	Computed	Experimental
a The published experimental shifts for the β form have been increased by 0.50 ppm to account for a systematic difference between the new and old values for the α form.
1	3.02	1.4	11	1.72	1.5
2	−1.12	−1.2	12	2.80	2.3
3	1.16	1.8	13	−0.04	0.0
4	0.70	0.7	14	0.13	−0.1
5	−5.21	−2.4	15	1.81	0.3
6	1.29	0.1	16	−0.04	1.2
7	−1.46	−1.2	17	−1.11	0.8
8	1.84	1.4	18	0.76	−0.7
9	−0.69	0.0	19	2.35	1.3
10	−0.20	0.4

---

The final comparison that can be made is with shielding anisotropies and asymmetries. These are automatically produced by the computations but they are not easy to determine experimentally because the spectra are relatively crowded. However, values are in the literature³¹ for C3, C4 and C5 for the α form. These are compared to the computed data in Table 4. The values for the two independent molecules are very similar, so only averages have been used. Once more, the results are encouraging. The computed anisotropies are of the correct sign and are in the right order. The asymmetries are reasonably well fitted, especially given the known difficulty of measuring values of less than 0.2.

Table 4 Comparison of computed and experimental shielding anisotropies, Δσ, and asymmetries, η, for the α form of testosterone (averages for the two independent molecules)

	Anisotropy/ppm		Asymmetry
Carbon number	Experiment	Computation	Experiment	Computation
3	159	198	0.00	0.12
4	−102	−119	0.73	0.68
5	171	234	0.66	0.54

---

Conclusions

Using a combined INADEQUATE NMR and Castep computational approach, we have been able to assign all the resonances in the crystalline α form of testosterone to individual atoms in the two molecules in the asymmetric unit cell. The computational results discussed herein, obtained using the GIPAW approach, are at current state-of the-art level. They show promise of being of considerable value for understanding chemical shifts in solids and for assignment of resonances, though of course the potential will need to be further evaluated before general conclusions can be drawn. As demonstrated here, it should be particularly valuable to link shifts for independent molecules in cases where the asymmetric unit contains more than one molecule, and thence to assign the shifts to specific crystallographic sites. Continued refinement in the use of calculations to make NMR assignments, through the thorough understanding of factors influencing subtle changes in chemical shifts in cases like testosterone, could eventually reduce or obviate the need for lengthy INADEQUATE experiments.

Acknowledgements

One of us (RKH) thanks the Leverhulme Trust for the award of an Emeritus Fellowship. The computational resources were provided by the Cambridge–Cranfield High Performance Computing Facility. CJP is supported by an EPSRC advanced research fellowship. SAJ is also supported by EPSRC, under Grant No. S61263/01. NMR spectra were recorded at the Center for High-field NMR in Lyon.

References

1. R. K. Harris, Solid State Sci., 2004, 6, 1025.
2. R. A. Olsen, J. Struppe, D. W. Elliott, R. J. Thomas and L. J. Mueller, J. Am. Chem. Soc., 2003, 125, 11784.
3. J. C. Facelli and D. M. Grant, Nature, 1993, 365, 325.
4. M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip and M. C. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717.
5. C. J. Pickard and F. Mauri, Phys. Rev. B, 2001, 63 , 245101.
6. R. K. Harris, P. Y. Ghi, H. Puschmann, D. C. Apperley, U. J. Griesser, R. B. Hammond, C. Ma, K. J. Roberts, G. J. Pearce, J. R. Yates and C. J. Pickard, Org. Process Res. Dev., 2005 DOI:10.1021/op0500990.
7. M. C. Payne, M. P. Teter, D. C. Allen, T. A. Arias and J. D. Joannopoulos, Rev. Mod. Phys., 1992, 64, 1045.
8. J. R. Yates, S. E. Dobbins, C. J. Pickard, F. Mauri, P. Y. Ghi and R. K. Harris, Phys. Chem. Chem. Phys., 2005, 7, 1402.
9. J. R. Yates, T. N. Pham, C. J. Pickard, F. Mauri, A. M. Amado, A. M. Gil and S. P. Brown, J. Am. Chem. Soc., 2005, 127, 10216.
10. J. R. Yates, C. J. Pickard, M. C. Payne, R. Dupree, M. Profeta and F. Mauri, J. Phys. Chem. A, 2004, 108, 6032.
11. C. Gervais, M. Profeta, V. Lafond, C. Bonhomme, T. Azais, M. Mutin, C. J. Pickard, F. Mauri and F. Babonneau, Magn. Reson. Chem., 2004, 42, 445.
12. C. Gervais, R. Dupree, K. J. Pike, C. Bonhomme, M. Profeta, C. J. Pickard and F. Mauri, J. Phys. Chem., 2005 , in press.
13. M. T. Zell, B. E. Padden, D. J. W. Grant, M.-C. Chapeau, I. Prakash and E. J. Munson, J. Am. Chem. Soc., 1999, 121, 1372.
14. G. De Paepe, A. Lesage, S. Steuernagel and L. Emsley, ChemPhysChem, 2004, 5, 869.
15. P. J. Roberts, R. C. Petterson, G. M. Sheldrick, N. W. Isaacs and O. Kennard, J. Chem. Soc., Perkin Trans. 2, 1973, 1978.
16. G. Precigoux, M. Hospital and G. Vanden Bosche, Cryst. Struct. Commun., 1973, 3, 435.
17. R. A. Fletton, R. K. Harris, A. M. Kenwright, R. W. Lancaster, K. J. Packer and N. Sheppard, Spectrochim. Acta, Part A, 1987, 43, 1111.
18. B. M. Fung, A. K. Khitrin and K. Ermolaev, J. Magn. Reson., 2000, 142, 97.
19. A. Lesage, M. Bardet and L. Emsley, J. Am. Chem. Soc., 1999, 121, 10987.
20. M. H. Levitt, in Encyclopedia of NMR, eds-in-chief D. M. Grant and R. K. Harris, Wiley, Chichester, 1996, vol. 2, p. 1396.
21. A. J. Shaka and A. Pines, J. Magn. Reson., 1987, 71, 495.
22. G. De Paepe, N. Giraud, A. Lesage, P. Hodgkinson, A. Beckmann and L. Emsley, J. Am. Chem. Soc., 2003, 125, 13938.
23. G. De Paepe, A. Lesage and L. Emsley, J. Chem. Phys., 2003, 119, 4833.
24. G. Drobny, A. Pines, S. Sinton, D. P. Weitekamp and D. Wemmer, Faraday Symp. Chem. Soc., 1978, 13, 49.
25. G. Bodenhausen, R. L. Vold and R. R. Vold, J. Magn. Reson., 1980, 37, 93.
26. D. Marion and K. Wuthrich, Biochem. Biophys. Res. Commun., 1983, 113, 967.
27. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
28. D. Vanderbilt, Phys. Rev. B, 1990, 41, 7892.
29. H. J. Monkhorst and J. D. Pack, Phys. Rev. B, 1976, 13, 5188.
30. R. J. Iuliucci, J. C. Facelli, D. W. Alderman and D. M. Grant, J. Am. Chem. Soc., 1995, 117, 2336.
31. E. A. Christopher, R. K. Harris and R. A. Fletton, Solid State NMR, 1992, 1, 93.

---

Footnote

† Electronic supplementary information (ESI) available: Chemical shifts for β-testosterone, shielding tensor parameters for α- and β-testosterone. See DOI: 10.1039/b513392k

---