The effect of surface attachment on ligand binding: studying the association of Mg2+, Ca2+ and Sr2+ by 1-thioglycerol and 1,4-dithiothreitol monolayers
Doron
Burshtain
and
Daniel
Mandler
*
Department of Inorganic and Analytical chemistry, The Hebrew University of Jerusalem, Jerusalem 91904, Israel. E-mail: mandler@vms.huji.ac.il; Fax: +972 2 658 5319; Tel: +972 2 658 5831
First published on 1st November 2005
Abstract
The difference in the heterogeneous binding of Mg2+, Ca2+ and Sr2+ ions by 1-thioglycerol (TG) and 1,4-dithiothreitol (DTT) spontaneously adsorbed monolayers on Au has been studied following the changes in the double layer capacity. A mathematical treatment, based on calculating the electrochemical potential difference at the monolayer–electrolyte interface, has followed our recent work1 which dealt with the acid–base equilibrium at the interface as a means of calculating the pK of ionizable SAMs and their binding with Cd2+. Experimentally, spontaneously adsorbed monolayers of TG and DTT were assembled on Au surfaces and studied by impedance spectroscopy and alternating current voltammetry (ACV). The capacity was measured for each of the modified surfaces at increasing concentrations of the divalent metal ions separately. The goal of this study has been to examine the effect of metal ion binding by similar ligands that are differently attached onto the surface. TG and DTT monolayers differ in their flexibility, which is a result of their attachment to the surface through one and two arms, respectively. The general trend of the apparent heterogeneous association constants of the divalent metal ions, which were calculated from the capacity measurements, was substantially different from the classical Irving–Williams series2–4 that is applicable to homogeneous systems. This difference could be nicely explained by the reduction of the degree of freedom and flexibility of the attached ligands.
Introduction
The significance of metal ions in biological and artificial systems is evident. The catalytic activity of many enzymes as well as organometallic compounds depends first and foremost on the metal ion.5,6 Complexation between metal ions and ligands is an acid–base reaction that is driven primarily by electrostatic interactions. In spite of the fact that binding depends on the nature of the atom donor, e.g., oxygen, nitrogen and sulfur, many of the ligands obey the Irving–Williams series, which predicts2–4 that the association binding constants for the first row divalent metals are in the following order: Ba2+ < Sr2+ < Ca2+ < Mg2+ < Mn2+ < Fe2+ < Co2+ < Ni2+<Cu2+ < Zn2+. In general, this series projects, mostly, electrostatic effects, and to a lower extent stereo-mechanical properties of the ligand. The sharp increase in the stability constant of Ni(II), Co(II), Fe(II) and Cu(II) complexes is explained by the ligand field theory.7ω-Functionalized SAMs have been used quite intensively for selectively interacting and extracting metal ions.8–26 We have shown that the functional groups at the monolayer/electrolyte interface can introduce the selectivity element required in electrochemical sensing.27–32 Thus, for example, Cr(VI) was selectively extracted and determined using a pyridinium based SAM31 whereas Cd(II) was preferentially determined by an ω-mercaptoalkanoic acid SAM.28,32
While the homogeneous association constants of metal ions by a wide range of organic ligands have continuously been studied using numerous methods, and comprehensive data are available for many metal ions, ligands and solvent systems;33–35 compiled data involving heterogeneous binding by surface bound ligands do not exist. Only a few methods have been developed and applied for studying and determining the heterogeneous stability constants of metal ions by organic ligands.1,36–47 Echegoyen et al. reported on the interaction between crown ether based SAMs and alkali metal39 studied by impedance spectroscopy. Grätzel also studied similar systems.40 Yet, previous to our work,1 the only system involving the association of cations by SAMs, which has been treated mathematically as a means of evaluating the heterogeneous association constant, was the deprotonation of ω-mercaptoalkanoic acid monolayers.1,36–38,41–47
Due to the fact that in many cases, e.g., heterogeneous catalysis, metal ions strongly interact with different functional groups at the liquid/solid and liquid/liquid interfaces, it is evident that determining the association of metal ionic species with surface bound ligands is of interest and significance to many fields. Recently, we have extended a thermodynamic approach based on measuring the differential capacity of the solid/electrolyte interface for determining the association constant of metal ions by a self-assembled monolayer.1 SAMs represent, in many cases, a well-organized array of ligands that are anticipated to behave homogeneously towards metal ions.
This study is a continuation of our previous work1 where we developed the thermodynamic model and applied it to monodentate ligands, i.e., mercaptoalkanoic acid monolayers. In our present investigation we have extended this treatment and studied the heterogeneous binding of 1-thioglycerol (TG) and 1,4-dithiothreitol (DTT) spontaneously adsorbed monolayers on gold by divalent metal ions of the second row, i.e., Mg2+, Ca2+ and Sr2+. The decision to study these particular systems stems from the importance of understanding the effect of ligand attachment through one and two anchoring sites onto a surface on their binding of a series of metal ions of the same row. In essence, we find that the binding of metal ions in heterogeneous systems strongly depends on the degree of freedom of the bound ligand. Namely, TG binds the selected metal ions with the same strength, while DTT binds each of the metal ions differently exhibiting stronger association towards Sr2+ ions. The explanation for this difference can be found in the (O–C–C–O) torsional angle which is fixed for bound-DTT whilst variable for TG on the Au surface.
Experimental
Instrumentation
Capacity and impedance were measured using an EcoChemie potentiostat (PGstat30) equipped with a frequency analyzer (FRA). Details of the frequency and potential applied are given below. pH was measured continuously during the capacity measurements using a Ciba Corning Check-Mate 90 pH meter. A BAS 100B/W electrochemical analyzer was used for carrying out cyclic voltammetry experiments.Materials
1-Thioglycerol (TG) ≥98% (Merck) and threo-1,4-dithiothreitol (DTT) ≥99% (Merck) were used as received. All other reagents were of the purest commercially available grade and were used without any further pretreatment, namely, sodium nitrate 99.995% (Aldrich), strontium nitrate 99.995% (Aldrich), magnesium nitrate 99.995% (Aldrich) and calcium nitrate hydrate 99.997% (Aldrich). H2SO4 solutions were prepared from H2SO4 96% in H2O w/w Suprapur® (Merck). Highly pure water (18 MΩ cm−1) was obtained from a Barnstead Easypure UV system. The working electrode was made of a gold rod, 99.99%, 3.0 mm diam. (Aldrich), embedded in a Teflon sheath. The electrode was polished gradually down to 0.05 μm using micropolish II (Buehler). Then it was electrochemically cycled (25 cycles between −0.5 V–1.8 V vs. Ag/AgCl KCl satd.) in 0.1 M H2SO4 solution and rinsed with pure water. The electrode was further modified as described below. The reference electrode for all measurements was an Ag/AgCl (KCl satd.) electrode while an Au wire was used as the auxiliary electrode.Procedures
Monolayers of 1-thioglycerol, (TG), or threo-1,4-dithiothreitol, (DTT), were formed by immersing the Au working electrode into 1 mM of the thiol solution dissolved in ethanol for 12–24 h. Then the electrode was carefully rinsed with ethanol and water and placed in a three electrode cell. The geometric area of the Au electrode in contact with the aqueous solution in the cell was 0.0707 cm2. The pH was recorded in the cell throughout the experiment. Exactly 10 mL of an aqueous solution of 0.4 M NaNO3 was added to the cell and bubbled with Ar for 10 min. The capacity, which was measured as a function of time upon immersing the electrode into this solution, showed negligible change. An AC voltage of 7 mV peak-to-peak and 320 Hz was superimposed on the DC potential. The Au potential at which the capacity was recorded was set to 0.0 V vs. Ag/AgCl unless otherwise noted. All measurements were performed at 23 ± 2 °C. The concentration of the metal ions was increased gradually.Impedance measurements at a fixed potential (−0.4 V) were performed at frequencies between 0.1–65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Hz and an AC amplitude of 10 mV. The experiments were conducted in solutions containing 0.1 M NaNO3 and various concentrations of metal ion, which were added from a concentrated solution.
000 Hz and an AC amplitude of 10 mV. The experiments were conducted in solutions containing 0.1 M NaNO3 and various concentrations of metal ion, which were added from a concentrated solution.
The excess of surface coverage of the thiol was determined from the reductive desorption waves measured by cyclic voltammetry in a thiol-free solution of NaOH 10−5 M (pH 9.0) and 5 mM K2SO4.
Mathematical treatment
Following along our treatment1 based on the approach developed initially by White et al.,36,37 which formulated the equilibrium between an ionizable monolayer and the electrolyte in terms of the electrochemical potential, we can describe the equilibrium at the interface for a metal ion that is bound to either TG or DTT on the surface:R(OH)2(surf) + Mn+(aq)
![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) R(OH)2 Mn+(surf) R(OH)2 Mn+(surf) | (1) |
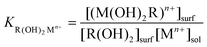 | (2) |
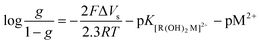 | (3) |
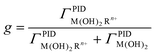 | (4) |
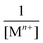 for g = 0.5 (half of the layers is occupied) corrected by
for g = 0.5 (half of the layers is occupied) corrected by 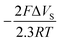 . Therefore, ΔVS needs to be determined, which can be estimated from the following relation:
. Therefore, ΔVS needs to be determined, which can be estimated from the following relation:| Eapplied − EPZC = ΔVF + ΔVS | (5) |
| ΔVF = ϕMetal − ϕPID | (6) |
| ΔVS = ϕPID − ϕS | (7) |
| Eapplied − E′PZC = ΔVS | (8) |
As the interfacial capacity is sensitive to the change of charge that is associated with ions binding by the interface, it can readily provide the fraction of the monolayer that binds cations. Fig. 1 shows schematically the different capacitive components in such a system. The capacity of the diffuse layer, CS, is in series with the two capacitors summing the capacity of the monolayer–electrolyte interface. The total capacity of each part depends on the respective fraction of the monolayer that is either free, 1 − g, or associated, g, with metal ions. Finally, another capacitor was added for the alkyl part of the monolayer, Cchain, which evidently depends reciprocally on the length of the chains. The total capacity of the interface is therefore:
 | (9) |
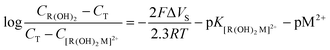 | (10) |
2R(OH)2(surf) + Mn+(aq)
![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) [R(OH)2]2 Mn+(surf) [R(OH)2]2 Mn+(surf) | (11) |
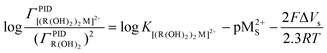 | (12) |
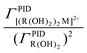 and obtain K[(R((OH)2)2M2+].
and obtain K[(R((OH)2)2M2+].
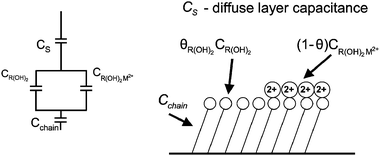 | ||
| Fig. 1 Schematic of the monolayer and the capacitive components involved: CS—capacity of the diffuse layer, CR(OH)2—capacity of the monolayer, CR(OH)2M2+—capacity of the metal bound monolayer, CChain—capacity of the alkyl chain. Each of the capacitive components of the monolayer functional group is multiplied by the fraction of the monolayer θ, that is associated with it. | ||
Results and discussion
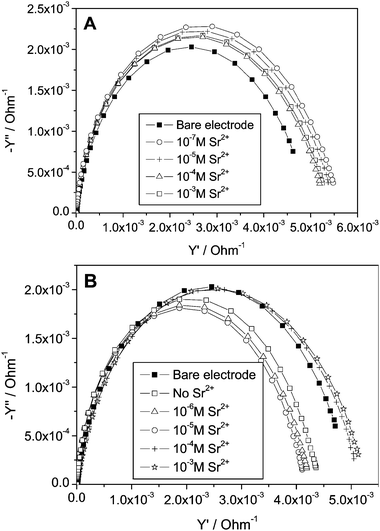
Fig. 2 shows Nyquist plots of Au electrodes covered with monolayers of 1-thioglycerol (TG) and threo-1,4-dithiothreitol (DTT) in a solution containing different concentrations of Sr2+ ions. The response of a bare electrode, which was not affected by the concentration of Sr2+, is also shown. The potential in which the impedance was measured (−0.4 V) does not drive any Faradaic process. Impedance spectroscopy has widely been used to characterize self-assembled monolayers.39,50–61 Basically, in the absence of a redox couple it is expected that a self-assembled monolayer covered electrode will behave similarly to a capacitor and a resistor in series, representing the interfacial capacity and the resistance of the solution, respectively. This should give a Nyquist plot, a straight line parallel to the y-axis. Obtaining a semi-circle such as that shown in Fig. 2 indicates that the capacitive element is not ideal, or in other words, it is highly permeable to ions. Hence, it is evident from both plots that the TG and DTT monolayers are not blocking layers and presumably are not highly ordered. This means that both monolayers will hardly contribute any resistance to the electrochemical cell, however, as described in Fig. 1, they are likely to play a role as an additional capacitive element though not an ideal Helmholtz capacitor since they are not ionic insulators.62 It can already be seen that at least for the DTT monolayer, the impedance spectrum is affected by the addition of Sr2+. The impedance response of such permeable monolayers and even of a bare polycrystalline Au electrode in an electrolyte solution is known to deviate from that of an ideal capacitor due to inhomogeneities, surface roughness, etc. The equivalent circuit can be best described by replacing the pure capacitor by a constant phase element (CPE).63,64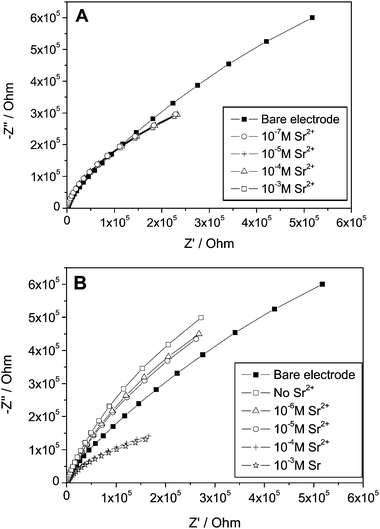 | ||
| Fig. 2 Nyquist plots obtained with an Au polycrystalline electrode at −0.40 V vs. Hg/HgSO4 in electrolyte solution containing 0.1 M NaNO3, and various concentrations of Sr(NO3)2. (A) Au coated with 1-thioglycerol (TG); (B) Au electrode coated with 1,4-dithiothreitol (DTT). | ||
For a series combination of capacitors, as we have in our system (Fig. 1), it is convenient to plot the admittance (Y = Z−1) rather than the impedance (Z). The appearance of a semicircle in the admittance plane plot allows tracking of small changes, in particular, at low frequencies as compared with the impedance plots. Fig. 3 shows the admittance plots for TG (Fig. 3A) and DTT (Fig. 3B) monolayer Au electrodes in different Sr2+ concentrations. The semicircle spectrum can be attributed to a mass transfer-controlled system rather than a kinetically-control process.65 This means that we can represent our electrochemical cell system as an equivalent electrical circuit containing a capacitor (CT in eqn (10)) in a series with a resistor (R), denoting the solution resistance. As can be seen the semicircles are not perfect even for a bare Au electrode. This compression in the imaginary axis can be corrected, as stated above, by replacing the capacitor by a CPE. Since the initial electrolyte concentration in our system is high, the solution resistance, R, can be considered as a constant element in our system. Moreover, there are no specific interactions, e.g., adsorption or under potential deposition, of the metal ions used in this study and the gold surface that need to be taken into account. This suggests that any change in the double layer capacity as a result of adding the metal ions must be due to the binding of the metal ions by the monolayer. Indeed, in both Fig. 3A and 3B a gradual change of the admittance plot upon the addition of metal ions can be seen. This can be attributed to the change of the capacitive properties of the plane of ion dissociation (PID) where the monolayer head-groups become charged, increasing the capacity of the PID and at the same time also affecting ion transfer to the surface. This is in accordance with previous studies such as by Schweiss66 who showed that the total interfacial capacitance changed as a result of charging the head groups of a monolayer.
The changes in the admittance, which were detected upon increasing the concentration of Sr2+, could primarily be assigned to the capacity changes of the PID. This made it possible to follow these change by measuring the capacity at a single frequency. Hence the system was equilibrated and measured at a frequency 320 Hz where the changes upon adding metal ions were most noticeable. This treatment is allowed also due to the fact that our system (as we can see from Fig. 2 and 3) is mass-transfer and not kinetically-controlled.65 In the course of our study we noticed that relatively high concentrations of metal ions (of the order of 10−2 M) were required in order to obtain noticeable changes in the capacity. The ionic strength was also increased (0.4 M NaNO3) as we found that this signified the changes in capacity. Single frequency capacity measurements allow measuring double layer capacity in high electrolyte concentration, however, prevent full comparison with capacity calculated from impedance measurements, which were carried out under lower electrolyte concentrations.
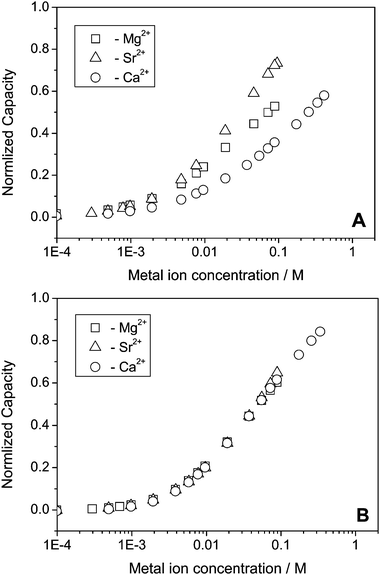
Fig. 4 shows the normalized capacity as a function of Ca2+, Mg2+ and Sr2+ concentration for a polycrystalline Au disk electrode modified with DTT and TG monolayers. Notice that a logarithmic scale is used for the concentration axis. Since we wanted to follow after the capacity changes rather than comparing the absolute values, we plotted the fraction of the capacity (eqn (13))
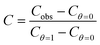 | (13) |
 | ||
| Fig. 4 Normalized capacity of Au coated electrodes, (A) DTT, (B) TG as a function of metal ion concentration. | ||
Table 1 summarizes the calculated heterogeneous stability constants of Sr2+, Ca2+ and Mg2+ to DTT and TG based on eqn (3), and (12) and the experimental results (Fig. 4) where g = 0.5. Comparing both systems shows that the titration curves of the three metal ions overlap in the case of the TG monolayer while there is a significant difference (taking into account the logarithmic scale) between the curves of Mg2+, Sr2+ and Ca2+. This means that TG does not differentiate between the three metal ions and binds them equally. On the other hand, a DTT monolayer binds the metal ions in the following order Sr2+ > Mg2+ > Ca2+. The difference between TG and DTT is presumably due to the degree of freedom of the head group. TG binds to the Au surface through only one thiol group, leaving a higher level of freedom to the head group to move around the intermediate C–C bond. This provides the head group the flexibility to adjust to each metal ion according to its size, and therefore eventually, binds them equally.
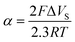 where (1 : 1) stands for a complex comprising one metal ion per ligand, while (1 : 2) stands for a complex of one metal ion per two ligands (the standard deviation for both pK was calculated (n = 15) and is ca. ±0.006)
where (1 : 1) stands for a complex comprising one metal ion per ligand, while (1 : 2) stands for a complex of one metal ion per two ligands (the standard deviation for both pK was calculated (n = 15) and is ca. ±0.006)
| Monolayer | α | Metal ion | p[M2+] at g = 0.5 | pK[R(OH)2M]2+ (1 : 1) | pK[R(OH)2)2M]2+ (1 : 2) |
|---|---|---|---|---|---|
| DTT | 15.682 | Mg2+ | 1.16178 | −16.844 | −18.006 |
| Ca2+ | 0.62452 | −16.307 | −16.931 | ||
| Sr2+ | 1.53783 | −17.220 | −18.758 | ||
| TG | 21.137 | Mg2+ | 1.29907 | −22.436 | −23.735 |
| Ca2+ | 1.30519 | −22.442 | −23.747 | ||
| Sr2+ | 1.33326 | −22.470 | −23.804 |
The difference in binding of the metal ions by bound DTT deserves a more careful discussion, in particular taking into account that the order of the heterogeneous binding is almost opposite to the homogeneous binding (the Irving–Williams series). Recently, MacDairmid et al.67 investigated the structure of DTT monolayers on Au(111) and concluded that a compact but primarily disordered layer was formed and that the symmetry observed suggested that much of the DTT bound to the surface via both thiols. Furthermore, previous ellipsometry and contact angle measurements are also consistent with DTT adsorption via two Au–S bonds.68–70 The structure of DTT on Au(111) suggested by MacDairmid is 2√3 × √3, which means that the distance between the sulfur atoms is ca. 5.0 Å. This limits the conformation of the molecule on the surface, forcing the torsional angle of the O–C–C–O to vary between 58°–61° (Fig. 5, based on conventional software). Concomitantly, it reduces significantly the degree of freedom around the intermediate C–C bond, and therefore a constant distance between the two hydroxyl groups is attained, which leaves a constant space for the different metal ions. As a result, the metal ions of the same row in the Periodic Table, which are isoelectronic, however, differing in their ionic radii will bind differently to the monolayer.
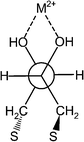 | ||
| Fig. 5 Newman projection of threo-DTT, which is bound onto a surface and binds a metal ion. | ||
Furthermore, we determined the excess of surface concentration DTT by cyclic voltammetry (not shown). Integration of the cathodic desorption voltammetry of TG and DTT suggests that there is a notable difference between their surface concentrations. While the excess of surface concentration of TG on an Au polycrystalline electrode is 4.6 × 10−10 ± 0.2 × 10−10 mol cm−2, that of DTT is 1.9 × 10−10 ± 0.2 × 10−10 mol cm−2 (a two-electron process, due to two binding sites per molecule, was assumed for the reductive desorption of DTT). The lower surface concentration of DTT is reasonable taking into account that binding of TG to Au through one thiol group allows a more perpendicular and therefore, condensed orientation than that of DTT. This suggests that DTT indeed binds to the Au surface through both thiol groups, where the torsional angle between the two OH groups is approximately 58°–61°.
Fixing the distance between the two oxygen atoms is likely to affect the binding of ions with different radii. While binding of ions of the second row by DTT in homogeneous solutions will cause the C–C to rotate until the optimal distance between the metal ion and the OH groups is attained, a surface-bound DTT will be almost unable to change its conformation.
Hence, it is interesting to compare the binding of such surface bound DTT with crystallographic data of systems, possessing an ethylene glycol moiety. Such crystallographic data indicates the optimal torsional angle of oxygens in the case of different ions. Searching the Cambridge Structural Database (CSD) revealed interesting information about the complexation of Mg2+, Ca2+ and Sr2+ by molecules bearing an ethylene glycol moiety. There is a clear correlation between the O–C–C–O torsional angle, the angle formed between the metal ion and the oxygen atoms, O–M–O, and the metal–oxygen bond length (Table 2). It is not surprising that as the radius of the ion increases the torsional angle as well as the M–O bond increase whereas the O–M–O angle decreases (Fig. 5).
| Metal ion | Ion radii/Å | O–C–C–O Angle/° | O–M–O Angle/° | M–O Bond length/Å |
|---|---|---|---|---|
| Mg2+ | 0.78 | 47–50 | 69–74 | 2.1–2.2 |
| Ca2+ | 1.06 | 51–57 | 64–68 | 2.4–2.5 |
| Sr2+ | 1.27 | 57–60 | 59–63 | 2.6–2.7 |
There are a few systems where crystallographic data exist for the same ligand associated with different metal ions. For example, Smith71 studied the complexes formed between some of the second row metals and 12-crown-4. He found that while the O–Sr2+–O angle in the crown ether complex was 62.6°, that of O–Ca2+–O was 65.8°. This explains nicely the greater affinity of surface bound DTT to Sr2+. The surface lattice dictates a O–C–C–O torsional angle (between 58°–61°), which better fits the largest ion, i.e., Sr2+.
Previous studies72 carried out in homogeneous solutions indicated that the strength of Mg2+vs. Ca2+ binding depended on the system. Basically, electrostatic considerations would suggest that the smallest ion would bind more strongly. This is correct as long as the bidentate ligand can adjust the torsional angle. Reduction of the degree of freedom, as can be found in our heterogeneous system, dictates a different binding order. The fact that Mg2+ binds more strongly to the bound DTT than Ca2+ is presumably due to the competition between the electrostatic contribution and the size of the cavity.
To summarize, we have found that on DTT spontaneously adsorbed monolayers the binding strength is Sr2+ > Mg2+ > Ca2+, where on TG monolayer, Sr2+ ≅ Ca2+ ≅ Mg2+. In general we observed that TG binds divalent metal ions of the second row better than DTT. This is in contrast with the Irving–Williams series which generally predicts the binding order to be Mg2+ > Ca2+ > Sr2+.
Conclusions
We have extended our method for determining heterogeneous association constants by capacity measurements to a surface bound bidentate ligand. Studying the binding of a series of alkaline-earth metals by two similar molecules that differ by the mode of attachment to the surface reveals very interesting findings. Not only that the order of heterogeneous binding is different than homogeneous binding but reducing the flexibility of the bound ligands strongly affects their binding. This means that it is basically possible to predict the heterogeneous binding if the orientation and configuration of the bound ligand are known. Moreover, it offers an interesting approach for controlling the binding affinities of metal ions by surfaces, such as required in chromatography and sensing devices, by carefully structuring the solid–liquid interface at the molecular level.Acknowledgements
This study was supported by the American Israeli Binational Science Foundation (BSF, Grant No 97/00198) and by the Israel Science Foundation (grant No. 200/02).References
- D. Burshtain and D. Mandler, ChemPhysChem, 2004, 5, 1532 CrossRef CAS
.
- H. Irving and R. J. P. Williams, Nature, 1948, 162, 746 CrossRef CAS
.
- H. Irving and R. J. P. Williams, J. Chem. Soc., 1953, 3192 RSC
.
-
L. E. Orgel, An introduction to Transition-Metal Chemistry: Ligand-Field Theory, Methuen and Co., Ltd., London, 1961 Search PubMed
.
- B. L. Martin, B. T. Li, C. X. Liao and D. J. Rhode, Arch. Biochem. Biophys., 2000, 280, 71 CrossRef
.
- M. R. Thorne, P. J. Greasley and M. G. Gore, Biochem. J., 1996, 315, 989 CAS
.
- F. A. Cotton, J. Chem. Educ., 1964, 41, 466 CrossRef CAS
.
- K. F. Cheng, C. M. Drain and K. Grohmann, Inorg. Chem., 2003, 42, 2075 CrossRef CAS
.
- G. Ambrosi, P. Dapporto, M. Formica, V. Fusi, L. Giorgi, A. Guerri, M. Micheloni, P. Paoli, R. Pontellini and P. Rossi, Chem. Eur. J., 2003, 9, 800 CrossRef CAS
.
- H. Xu, X. H. Xu, R. Dabestani, G. M. Brown, L. Fan, S. Patton and H. F. Ji, J. Chem. Soc., Perkin Trans. 2, 2002, 2, 636 RSC
.
- K. Rurack, Spectrochim. Acta, Part A, 2001, 57, 2161 CrossRef CAS
.
- D. C. Schwartz and M. Hochstrasser, Trends Biochem. Sci., 2003, 28, 321 CrossRef CAS
.
- C. H. Huang and A. T. Stone, Environ. Sci. Technol., 2000, 34, 4117 CrossRef CAS
.
- S. Yasuike, Yakugaku Zasshi, 2003, 123, 577 CrossRef CAS
.
- J. Hickman, D. Ofer, P. E. Laibinis, G. M. Whitesides and M. S. Wrighton, Science, 1991, 252, 688 CrossRef CAS
.
- J. Wang, H. Wu and L. Angnes, Anal. Chem., 1993, 65, 193 CrossRef CAS
.
- I. Willner and A. Riklin, Anal. Chem., 1994, 66, 1535 CrossRef CAS
.
- C. Duan and M. E. Mayerhoff, Anal. Chem., 1994, 66, 1369 CrossRef CAS
.
- M. Collinson, E. Bowden and M. Tarlov, Langmuir, 1992, 8, 1247 CrossRef CAS
.
- L. Haussling, H. Ringsdorf, F. J. Scmitt and W. Knoll, Langmuir, 1991, 7, 1837 CrossRef
.
- M. Niwa, T. Mori, E. Nishio, H. Nishimura and N. Higashi, J. Chem. Soc., Chem. Commun., 1992, 547 RSC
.
- F. Malem and D. Mandler, Anal. Chem., 1993, 65, 37 CrossRef CAS
.
- C. D. Bain, E. B. Troughton, Y. T. Tao, J. Evall and G. M. Whitesides, J. Am. Chem. Soc., 1989, 111, 321 CrossRef CAS
.
- R. W. Murry, Acc. Chem. Res., 1980, 13, 135 CrossRef CAS
.
- A. Merz, Top. Curr. Chem., 1990, 49, 152
.
-
R. W. Murray, in Electroanal. Chem., ed. A. J. Bard, Marcel Dekker, New York, 1984, vol. 13, p. 191 Search PubMed
.
- I. Turyan and D. Mandler, Anal. Chem., 1993, 65, 2089 CrossRef CAS
.
- I. Turyan and D. Mandler, Fresenius’ J. Anal. Chem., 1994, 349, 491 CAS
.
- I. Turyan and D. Mandler, Nature, 1993, 362, 703 CrossRef CAS
.
- I. Turyan and D. Mandler, Electroanalysis, 1994, 6, 775
.
- I. Turyan and D. Mandler, Anal. Chem., 1997, 69, 894 CrossRef CAS
.
- I. Turyan and D. Mandler, Anal. Chem., 1994, 66, 58 CrossRef CAS
.
-
J. J. Christensen and R. M. Izatt, Handbook of Metal Ligand Heats and Related Thermodynamic Quantities, Marcel Dekker, Inc., New-York, 1970 Search PubMed
.
-
L. G. Sillen, A. E. Martell, D. D. Perrin and E. Hoegfeld, Stability Constants of Metal-Ion Complexes, Chemical Society special publication, 1982 Search PubMed
.
-
M. T. Beck, Chemistry of Complex Equilibria, Van Nostrand Reinhold Company, London, 1970 Search PubMed
.
- C. P. Smith and H. S. White, Langmuir, 1993, 9, 1 CrossRef CAS
.
- H. S. White, J. D. Peterson, Q. Cui and K. J. Stevenson, J. Phys. Chem. B, 1998, 102, 2930 CrossRef CAS
.
- T. Kakiuchi, M. Iida, S. Imabayashi and K. Niki, Langmuir, 2000, 16, 5397 CrossRef CAS
.
- M. A. Herranz, B. Colonna and L. Echegoyen, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 5040 CrossRef CAS
.
- R. Kashyap and K. Grätzl, Anal. Chem., 1999, 71, 2814 CrossRef CAS
.
- M. C. Leopold, J. A. Black and F. E. Bowden, Langmuir, 2002, 18, 978 CrossRef CAS
.
- C. D. Bain and G. M. Whitesides, Langmuir, 1989, 5, 1370 CrossRef CAS
.
- S. E. Creager and J. Clarke, Langmuir, 1994, 10, 3675 CrossRef CAS
.
- T. R. Lee, R. L. Carey, H. A. Bieuyck and G. M. Whitesides, Langmuir, 1994, 10, 741 CrossRef CAS
.
- R. C. Chatelier, C. J. Drummond, D. Y. C. Chan, Z. R. Vasic, T. R. Gengenbah and H. J. Griesser, Langmuir, 1995, 11, 4122 CrossRef CAS
.
- J. Wang, L. M. Frostman and M. D. Ward, J. Phys. Chem., 1992, 96, 5224 CrossRef CAS
.
- K. Shimazu, T. Teranishi, K. Sugihara and K. Uosaki, Chem. Lett., 1998, 669 CrossRef CAS
.
-
P. Delahay, in Double Layer and Electrode Kinetics Advances: In Electrochemistry and Electrochemical Engineering, ed. P. Delahay and C. W. Tobias, Wiley Interscience, New-York, 1965 Search PubMed
.
- A. N. Becka and C. J. Miller, J. Phys. Chem., 1993, 97, 6233 CrossRef CAS
.
- Z. H. Jin, D. V. Vezenov, Y. W. Lee, J. E. Zull, C. N. Sukenik and R. F. Savinell, Langmuir, 1994, 10, 2662 CrossRef CAS
.
- V. Molonero and E. J. Calvo, J. Electroanal. Chem., 1998, 445, 17 CrossRef CAS
.
- G. K. Jenning, J. C. Munro, T. H. Yong and P. E. Laibinis, Langmuir, 1998, 14, 6130 CrossRef
.
- Y. Ousten, S. Mejdi, A. Fenech, J. Y. Deletage, L. Bechou, M. G. Perichaud and Y. Danto, Microelectron. Reliab., 1998, 38, 1539 CrossRef
.
- K. Nakano, H. Taira, M. Maeda and M. Takagi, Bunseki Kagaku, 1998, 47, 929 CAS
.
- T. Morita, S. Kimura, S. Kobayashi and Y. Imanishi, J. Am. Chem. Soc., 2000, 122, 2850 CrossRef CAS
.
- E. Boubour and R. B. Lennox, Langmuir, 2000, 16, 4222 CrossRef CAS
.
- Z. Quam, X. Wu, S. Chen, S. Zhao and H. Ma, Corrosion, 2001, 57, 195 Search PubMed
.
- L. V. Protsailo and W. R. Fawcett, Langmuir, 2002, 18, 8933 CrossRef CAS
.
- H. A. Chao, D. H. Zavitz and M. Ovadia, Biosens. Bioelectron., 2003, 18, 11 CrossRef
.
- R. Naumann, S. M. Schiller, F. Giess, B. Grohe, K. B. Hartman, I. Karcher, I. Koper, J. Lubben, K. Vasiler and W. Knoll, Langmuir, 2003, 19, 5435 CrossRef CAS
.
- D. Yanm, J. A. Saunders and G. K. Jennings, Langmuir, 2003, 19, 9290 CrossRef
.
- E. Boubour and B. Lennox, Langmuir, 2000, 16, 4222 CrossRef CAS
.
- T. Pajkossy, J. Electroanal. Chem., 1994, 364, 111 CrossRef CAS
.
- K. Bandyopadhyay, L. Shu, H. Liu and L. Echegoyen, Langmuir, 2000, 16, 2706 CrossRef CAS
.
-
A. J. Bard and L. R. Faulkner, Electrochemical methods: fundamentals and applications, John Wiley & Sons, 2nd edn, 2001, pp. 386–387 Search PubMed
.
- R. Schweiss, C. Werner and W. Knoll, J. Electroanal. Chem., 2003, 540, 145 CrossRef CAS
.
- A. R. MacDairmid, M. C. Gallagher and T. J. Banks, J. Phys. Chem. B, 2003, 107, 9789 CrossRef CAS
.
- J. T. Banks, T. T. Yu and H. Z. Yu, J. Phys. Chem. B, 2002, 106, 3538 CrossRef CAS
.
- R. G. Nuzzo and D. L. Allara, J. Am. Chem. Soc., 1983, 105, 4481 CrossRef CAS
.
- R. G. Nuzzo, F. A. Fusco and D. L. Allara, J. Am. Chem. Soc., 1987, 109, 2358 CrossRef CAS
.
- P. C. Junk, L. M. Louis and M. K. Smith, Z. Anorg. Allg. Chem., 2002, 628, 1196 CrossRef CAS
.
-
F. A. Cotton, G. Wilkinson, C. A. Murillo and M. Bochmann, Advanced Inorganic Chemistry, John Wiley & Sons Inc., 6th edn, 1999 Search PubMed
.
| This journal is © the Owner Societies 2006 |