Combined kinetics and iterative target transformation factor analysis for spectroscopic monitoring of reactions
Antonio R.
Carvalho
,
Jirut
Wattoom
,
Lifeng
Zhu
and
Richard G.
Brereton
*
School of Chemistry, University of Bristol, Cantock's Close, Bristol, UK BS8 1TS
First published on 18th November 2005
Abstract
Obtaining rate constants and concentration profiles from spectroscopy is important in reaction monitoring. In this paper, we combined kinetic equations and Iterative Target Transformation Factor Analysis (ITTFA) to resolve spectroscopic data acquired during the course of a reaction. This approach is based on the fact that ITTFA needs a first guess (test vectors) of the parameters that will be estimated (target vectors). Three methods are compared. In the first, originally proposed by Furusjö and Danielsson, kinetic modelling is only used to provide the initial test vectors for ITTFA. In the second the rate constant used to provide the test vectors is optimised until a best fit is reached. In the third, a guess of the rate constant is used to provide the test vectors to ITTFA. The outcome of ITTFA is then used to fit the kinetic model and obtain a new guess of the rate constant. With this constant new concentration profiles are generated and provided to the ITTFA algorithm as new test vectors, in an iterative manner, minimising the residuals of the predicted dataset, until convergence. The second and third methods are new implementations of ITTFA and are compared to the first, established, method. First order (both one and two step) and second order reactions were simulated and instrumental noise was introduced. An experimental second order reaction was also employed to test the methods.
1. Introduction
ITTFA (Iterative Target Transform Factor Analysis) has been available as a tool to the chemometrician for two decades.1,2 Some of the original applications were in hyphenated chromatography, the aim being to determine the profiles and spectra in an unresolved cluster. A key step in ITTFA involves first obtaining a guess of the characteristics of each component in a mixture. There are many strategies for obtaining these first guesses, often trying to identify the purest point in a mixture. In chromatography this could correspond to the point that is most characteristic of each component.3Over the past few years, ITTFA has been applied to reaction monitoring.3–5 Often the starting point of the algorithm is to find the point in a reaction most characteristic of each component, for example for a reaction U → V → W, the first point is most characteristic of U, the last of W (although it may not correspond to pure W unless the reaction goes to completion) and an intermediate point corresponds to a high concentration of V. These test vectors are then refined by the algorithm, based on certain properties such as non-negativity, in an iterative way.
Traditional approaches to ITTFA, however, take no account of kinetics, and in some circumstances can provide quite poor models. In this paper we combine ITTFA with kinetic modelling, investigating three possible approaches. The first, based on work by Furusjö and Danielsson, uses a guess of the rate constants to provide estimated profiles for each component as the starting vectors. In addition, two new modifications of ITTFA are described, which employ an iterative method that uses these guesses and then refines them repeating ITTFA several times using new guesses each time. The performance of these three methods are compared to each other and also to ITTFA using a non-kinetic method for obtaining test vectors. These approaches have in common the combination of what is often called hard (kinetic) and soft (multivariate) modelling, and are an effective alternative to the traditional implementation that we find is more effective in reaction monitoring.
In this paper we look at three simulated reactions of different orders and a reaction known to be second order6 and compare the performance of the methods to the traditional implementation of ITTFA.
2. Theory
2.1. Kinetics
In this paper, different types of reactions are simulated, with different orders and different numbers of reactants.7–9 Dataset 1 is a first order reaction where one starting material gives a single product when the reaction is catalysed. We have, in this case, the following scheme,| U → W |
Dataset 2 consists of a second order reaction of the form,
| U + V → W |
| U → V |
| V → W |
Using kinetic equations it is possible to estimate concentration profiles for each type of reaction studied, as long as we know the initial concentrations and have an estimate of the rate constant(s).10–13 For brevity we do not describe the kinetic equations in full in this paper, as they are available in standard texts.
2.2. Iterative target transformation factor analysis
Iterative target transformation factor analysis (ITTFA) is a soft modelling curve resolution technique that can be used to resolve reaction systems.2,14,15 In its original form, it does not force any specific kinetic behaviour on the data.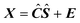 | (1) |
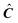 is an I
×
N matrix with its columns representing the concentration profiles of the N components, and
is an I
×
N matrix with its columns representing the concentration profiles of the N components, and 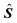 is an N
×
J matrix with the pure absorption spectra of the N components represented by its rows. The matrix E represents the error and has the same dimensions as X.3 ITTFA along with most methods for factor analysis attempts to determine
is an N
×
J matrix with the pure absorption spectra of the N components represented by its rows. The matrix E represents the error and has the same dimensions as X.3 ITTFA along with most methods for factor analysis attempts to determine  and
and  as described below.
as described below.
Principal Component Analysis (PCA) can be used to decompose the matrix X and calculate the Scores T and Loadings P. These vectors have no physical meaning, needing a non-orthogonal matrix R to relate to real concentration profiles defined in eqn (1), so that:
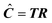 | (2) |
 | (3) |
The optimum rotation matrix that best relates the abstract solution to a real meaningful quantity has to be determined.3,4,16 Target testing is performed with test vectors that are good approximations of suspected real factors.
Evolving PCA (EPCA), which some authors consider to be the first step of Evolving Factor Analysis (EFA), is one common method for providing test vectors and is adopted in this paper;17 the idea behind the method is time-dependent rank analysis.
The changes in the eigenvalues with time are used to obtain initial test vectors since they reflect the changes in the spectra of the absorbing compounds. The EPCA profiles obtained are refined to give initial estimates of the concentration profiles. To this purpose, the minimum difference between the forward and reverse EPCA profiles is chosen to produce the first guess of the concentration profiles, for each of the components. Each profile is then normalised to a maximum value of 1, and is used as the test vector. In this paper, we use this approach for the initial determination of test vectors by a non-kinetic method. There are several other methods available that do not take kinetic information into account, but we find that most result in fairly similar results, and the aim is to compare a non-kinetic method to kinetic methods.
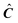 to the target-testing algorithm would return the same matrix. Therefore
to the target-testing algorithm would return the same matrix. Therefore 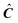 has to be modified to force the target-testing to converge to a better solution (if any).16 To refine a vector all the data beyond the boundaries marked by the first negative regions encountered as one moves to higher or lower times from the maxima in the test vector are truncated and set to 0. The new refined vector is used to produce a new predicted vector in an iterative fashion, each time having fewer negative regions. This procedure is repeated until convergence.
has to be modified to force the target-testing to converge to a better solution (if any).16 To refine a vector all the data beyond the boundaries marked by the first negative regions encountered as one moves to higher or lower times from the maxima in the test vector are truncated and set to 0. The new refined vector is used to produce a new predicted vector in an iterative fashion, each time having fewer negative regions. This procedure is repeated until convergence.
There are other possible ways to refine test vectors. A good approach was suggested by Bro and de Jong using non-negative least-squares. The method is based on the standard algorithm NNLS by Lawson and Hanson,18 but modified to take advantage of the special characteristics of algorithms involving repeated use of non-negativity constraints.19 Recently Gemperline and Cash proposed the use of soft constraints in soft modelling resolution problems, where small constraints are permitted.20
 . In this study the iteration process is ended on the first occurrence of any of the following:
. In this study the iteration process is ended on the first occurrence of any of the following:
• when the adaptation of the target is no longer possible,
• when the relative root mean square difference between the new and old solutions is below a given tolerance, as chosen by the user (e.g., 1 × 10−7 M in this application), commonly regarded as convergence, or
• the allowed number of iterations has been reached (e.g., 100 in this application).
An alternative criterion that could be used is the theory of error in target testing developed by Malinowski.17
2.3. Combined kinetic modelling with ITTFA
A possible alternative approach to section 2.2.2 is to use an external method to provide the target vector. If we are confident about the kinetics of the reaction under study, this should be a good approach for obtaining an estimate of the real concentration profiles. In this case, we do not need a guess of the test vector but of one or more of the rate constants. This is quite a common situation for example when it is required to optimise reaction conditions or monitor reactions for determining process stability or to study the temperature effects on a reaction. Under such circumstances the basic kinetics is unchanged, and it is primarily the aim to measure the rate constant. The spectra of all the components may be unknown, however, for example the spectrum of an intermediate, and may change with temperature or reaction conditions, so it is not always possible to obtain pure spectroscopic information on every reactant.Using kinetic equations in target testing has been reported previously in the literature. Furusjö and Danielsson21–24 adopted a trial value of the rate constant to create concentration profiles Ctrial, employing a least-squares fit, where:
| R = T+Ctrial | (4) |
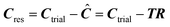 | (5) |
Below are presented three possibilities of combining kinetics with ITTFA.
1) Make an initial guess of the rate constant(s).
2) Use the current value of the rate constant(s) and the known initial concentrations to calculate the concentration profiles of the all the reaction components kCtrial.
3) Use the concentration profiles obtained in step 2 as the first guess of the test vectors in the ITTFA algorithm.
4) Proceed as described in sections 2.2.3 and 2.2.4 until a solution  is obtained.
is obtained.
The results obtained in step 4 are the final output of the method, although kinetic profiles can be fitted to the profiles obtained to achieve an estimate of the rate constant.
1) Make an initial guess of the rate constant(s).
2) Use the current value of the rate constant(s) and the known initial concentrations to calculate the concentration profiles of the all the reaction components kCtrial.
3) Use kCtrial as the first guess of the test vectors in ITTFA.
4) Proceed as described in sections 2.2.3 and 2.2.4 and a solution  is obtained.
is obtained.
5) Calculate the residuals Cres according to 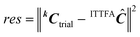 .
.
6) Update the estimate of k and return to step (2) until the residuals are minimised.
In this method, different values of kCtrial are tested as a first guess of the concentration profiles. kCtrial is obtained using kinetic equations, and the method converges to the approximation of the ITTFA profile to the kinetic profile. The final estimate(s) of k are the best guess rate constant(s).
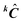 . This matrix is used to estimate
. This matrix is used to estimate 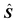 , which together with
, which together with  returns
returns 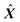 . A comparison between
. A comparison between  and X will reveal if the current estimate of k is adequate. Problems arise when
and X will reveal if the current estimate of k is adequate. Problems arise when  is rank deficient. However, since we are only interested in estimates of the concentration profiles and not in those of the pure spectra, the alternating least squares approach can be used.28 The basis is that the kinetics including the number of reactants and the starting concentrations are fixed. If, for example, the change in reactant concentrations is Δ moles at time t, then for a second order reaction the concentration of the three components will be [U]0
−
Δ, [V]0
−
Δ and [W]0 + Δ respectively. Only a single rate constant is required to predict Δ, even though the matrix may be rank deficient. Without knowledge of the starting concentrations, of course, the problem would not be soluble using this approach.
is rank deficient. However, since we are only interested in estimates of the concentration profiles and not in those of the pure spectra, the alternating least squares approach can be used.28 The basis is that the kinetics including the number of reactants and the starting concentrations are fixed. If, for example, the change in reactant concentrations is Δ moles at time t, then for a second order reaction the concentration of the three components will be [U]0
−
Δ, [V]0
−
Δ and [W]0 + Δ respectively. Only a single rate constant is required to predict Δ, even though the matrix may be rank deficient. Without knowledge of the starting concentrations, of course, the problem would not be soluble using this approach.
The algorithm for this method is shown below.
1) Make an initial guess of the rate constant(s).
2) Use the current value of the rate constant(s) and the known initial concentrations to calculate the concentration profiles of the all the reaction components kCtrial.
3) Use kCtrial as the first guess of the test vectors in the ITTFA algorithm.
5) Proceed as described in sections 2.2.3 and 2.2.4 until a solution  is obtained.
is obtained.
6) Fit kinetic concentration profiles to the ITTFA profiles, calculating the sum of squares residuals  , and obtaining the fitted rate constant(s).
, and obtaining the fitted rate constant(s).
7) Use the fitted rate constant(s) to generate kinetic concentration profiles  .
.
8) Calculate 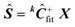 , where “+” refers to a pseudoinverse.
, where “+” refers to a pseudoinverse.
9) Determine the predicted dataset according to 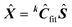 .
.
10) Calculate the sum of squares residuals,  .
.
11) Update the estimate of the rate constant(s) and return to step (2) until res2 is minimised.
3. Datasets
The methods described previously were used and tested in several reaction datasets, from different types of reactions. The datasets used are described below and a summary and their reference (number) is presented in Table 1.29| Dataset # | Reaction | Type |
|---|---|---|
| 1 | U → V | Simulated |
| 2 | U + V → W | Simulated |
| 3 | U → V → W | Simulated |
| 4 | U + V → W | Real |
3.1. Simulated datasets
The pure spectrum of each of the components of the reaction was simulated to appear similar to those typically seen in UV/Vis spectroscopy. Care was taken that some overlap was observed between the spectra of the compounds, in order to represent a realistic and challenging problem.
For dataset 1, k was set to 0.06 min−1, with [U]0 = 0.33 M. For the dataset 2, k was set to 0.06 M−1 min−1, [U]0 = 0.33 M and [V]0 = 0.66 M. For dataset 3, k1 was set to 0.06 min−1 and k2 to 0.12 min−1 with [U]0 = 0.33 M. The values chosen for the initial concentrations were based on their similarity with the initial concentrations used in the real reaction acquired with the UV/Vis probe (dataset 4). An example of the concentration profiles and pure spectra of the compounds obtained with the simulation is presented in Fig. 1.
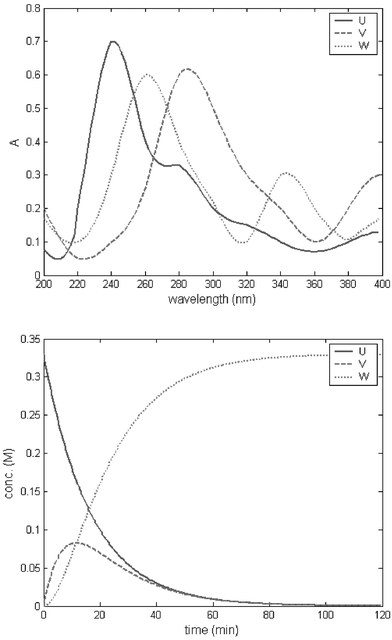 | ||
| Fig. 1 Simulated pure spectra of the components U, V and W (top) and simulated concentration profiles (bottom) for dataset 3. | ||
Error free response matrices were subsequently created by multiplying C and S, where C is matrix of the concentration profiles and S the matrix of the pure spectra.
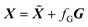 | (6) |
 represents the noise free data matrix. This type of noise is more commonly known as white noise. The percentage of noise introduced in the original data matrix can be defined as the ratio of fG to the maximum absorbance in the noise free data matrix.
represents the noise free data matrix. This type of noise is more commonly known as white noise. The percentage of noise introduced in the original data matrix can be defined as the ratio of fG to the maximum absorbance in the noise free data matrix.
In this particular case, the percentage of white noise introduced into the simulated data matrix was 0.5%. This is actually a value higher than usually observed when working with a UV/Vis probe. A graphical example of the error introduced is shown in Fig. 2.
 | ||
| Fig. 2 Example of the comparison between the raw simulated dataset 2 (left) and the same dataset with the introduction of 0.5% white noise (right). | ||
After the introduction of noise, the simulated datasets were used to test the methods cited previously. An example of this simulated data is shown in Fig. 3.
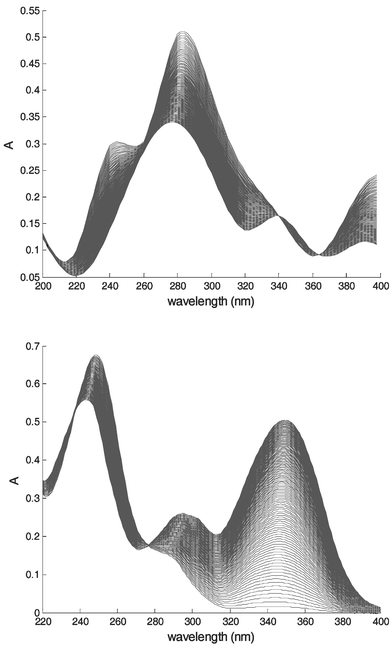 | ||
| Fig. 3 Spectra of dataset 2 (upper) and of the real dataset acquired with the UV/Vis probe (lower). | ||
3.2. Experimental dataset
The methods presented previously were also applied to a real reaction. For this purpose, the second order reaction between benzophenone (Fluka, 99%, Switzerland) and phenylhydrazine (Lancaster, 97%, UK) to give benzophenone phenylhydrazone was studied. This reaction was started by addition of glacial acetic acid (Fisher Scientific, Laboratory Reagent grade, UK) and is run at 25 °C. The reaction was followed using an attenuated total reflection (ATR) UV/Vis spectroscopic probe (Hellma, Müllheim, Germany) connected by fibre-optic cables to a MCS500UV-Vis spectrometer (Zeiss, Jena, Germany). A spectrum was taken every minute over a period of 124 min, making a total of 125 spectra, including the first one. The spectra acquired are illustrated in Fig. 3. The reaction has been shown to follow second order kinetics,2,29 providing the acid concentration is well in excess of the reactants (as is the case in this application) and it is not the purpose of this paper to compare models based on different reaction orders, but to describe a new approach of combining kinetics and ITTFA models.3.3. Testing procedure
Using the datasets described above, the methods presented in Section 2 were applied. By testing methods with different datasets, with diverse specificities gives an idea of the robustness of the method and its applicability.For the methods described in Section 2.3, the initial guess of the concentration profiles influences the results significantly. Therefore, in order to test different levels of error in the input, several concentration profiles were simulated, with different levels of error in the rate constant relative to the original simulated concentration profiles. The error was introduced in various levels, up to a maximum of 1000% error. A 1000% error in k implies that the initial guess of the rate constant is 10 times the true rate constant, to check what happens if a very poor initial estimate of k is employed. The error levels are presented in Table 2. −99.99% was used instead of −100% to avoid running the methods with an initial guess of k of zero. In the case of dataset 4, k was used that would generate kinetic profiles that would result in a reaction that was close to completion at the end of the kinetic run.
| Error level in k | Dataset 1 | Dataset 2 | Dataset 3 | |
|---|---|---|---|---|
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) 1/min−1
1/min−1 |
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) 1/M−1 min−1
1/M−1 min−1 |
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) 1/min−1
1/min−1 |
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) 2/min−1
2/min−1 |
|
| −99.99% | 6.0 × 10−6 | 6.0 × 10−6 | 6.0 × 10−6 | 1.2 × 10−5 |
| −10% | 0.054 | 0.054 | 0.054 | 0.108 |
| +10% | 0.066 | 0.066 | 0.066 | 0.132 |
| +100% | 0.12 | 0.12 | 0.12 | 0.24 |
| +1000% | 0.66 | 0.66 | 0.66 | 1.32 |
The methods and calculations presented above were coded in Matlab® R13, using a Pentium 4 2.0 GHz with 384 Mb of RAM.
4. Results and discussion
In view of the fact that in ITTFA, no information is provided to the model about the initial concentration of the reagents, both ITTFA and the kinetic profiles had to be normalised to allow comparison. In datasets 1, 2 and 4, the concentration profile of the product was used to estimate k. In dataset 3, the profile of the intermediate was preferred. This was because, as expected, the fit was better due to the more characteristic profile of the intermediate, that is strongly influenced by the values of both kinetic constants. It would also be possible to do the fit to all reactants, but in some circumstances, if one species has consistently higher concentration throughout (for example a starting material in excess), it will dominate, whereas the profiles that change most such as those of intermediates will be poorly represented. The kinetic information is often most easily obtained from profiles of intermediates and products.Using EPCA to provide the test vectors yields reasonable results for the simulated datasets (Table 3), in particular for the single step reactions. The concentration profiles obtained for dataset 2 are shown in Fig. 4. This figure is presented to show the influence of the changes established by the methods introduced above (particularly here by method A). As one can see in the profiles for traditional implementations of ITTFA, they are heavily influenced by rotational ambiguity because we are dealing with a rank deficient dataset. Fig. 4 shows the improvements obtained with the introduction of kinetic constraints as far as this rotational ambiguity is concerned. This feature will also be observed with methods B and C below. For the two-step reaction, the error increases considerably, but the method is still capable of detecting that the second step of the reaction is faster than the first one. For the experimental dataset, the concentration profiles obtained were quite poor, as can be observed in Fig. 5.
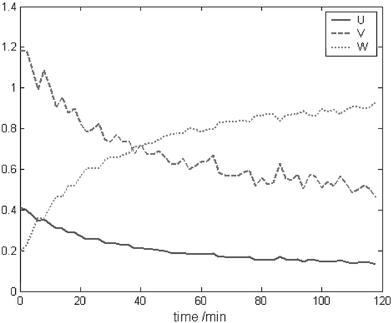 | ||
| Fig. 4 Concentration profiles obtained with ITTFA using EPCA for the selection of the test vectors, for dataset 2. | ||
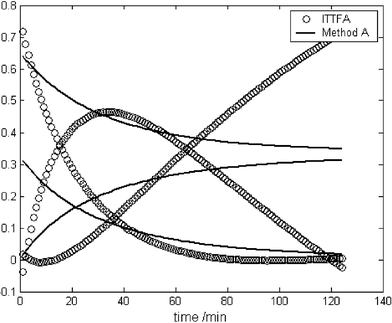 | ||
| Fig. 5 Comparison of the profiles obtained using traditional ITTFA (○) and method A (—) for the real dataset. | ||
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) 1
1
|
% Error |
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) 2
2
|
% Error | |
|---|---|---|---|---|
| Dataset 1 | 0.0594 | −1.00 | — | — |
| Dataset 2 | 0.0542 | −9.67 | — | — |
| Dataset 3 | 0.0187 | −68.83 | 0.2623 | +118.58 |
For method A the influence of the test vector in the prediction is presented in Table 4. When compared to the results from ITTFA, the rate constants obtained are quite similar for dataset 1, but improve significantly for dataset 2. In this case, similar results to ITTFA are obtained only when the test vectors are in 1000% error. This partly explains the better fit for the experimental dataset, where the concentration profiles are what would be expected from a second order reaction (Fig. 5). Employing kinetic profiles forced an improved behaviour in the ITTFA algorithm. For dataset 3, the results obtained were not particularly good, especially when the error in the initial guess of k is very high. In some cases, the predicted rate constants have a higher error than the one introduced in the test vector. This is a consequence of rotational ambiguities, where the high degree of error in the test vector generates an erroneous rotation matrix, with the kinetic vectors leading the algorithm to a wrong estimate.
| Error level in k | Pred. k | Dataset 1 | Dataset 2 | Dataset 3 | |
|---|---|---|---|---|---|
| Calc. err. |
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) 1/min−1
1/min−1 |
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) 1/M−1 min−1
1/M−1 min−1 |
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) 1/min−1
1/min−1 |
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) 2/min−1
2/min−1 |
|
| −99.99% | k | 0.0594 | 0.0532 | 0.0000 | 0.0860 |
| % Err. | −1.00 | −11.33 | −100.00 | −28.33 | |
| −10% | k | 0.0594 | 0.0571 | 0.0356 | 0.1857 |
| % Err. | −1.00 | −4.83 | −40.67 | +54.75 | |
| +10% | k | 0.0593 | 0.0573 | 0.0521 | 0.1508 |
| % Err. | −1.17 | −4.50 | −13.17 | +25.67 | |
| +100% | k | 0.0591 | 0.0577 | 0.0388 | 1.7438 |
| % Err. | −1.50 | −3.83 | −35.33 | +1353.17 | |
| +1000% | k | 0.0569 | 0.0545 | 4.7002 | 0.1787 |
| % Err. | −5.17 | −9.17 | +7733.67 | +48.92 | |
In method B there is an important improvement from method A, with the dependence on the initial guess of k significantly reduced. The results are presented in Table 5. The improvement is significant particularly with dataset 3, where the predictions are generally quite accurate. Method B only returns poor results when the error is considerably high, with the method converging to an incorrect minimum. In these situations one can use an alternative way to refine the test vectors, as suggested by Bro and de Jong.19Table 5 indicates that it is preferable to overestimate than to underestimate k.
| Error level in k | Pred. k | Dataset 1 | Dataset 2 | Dataset 3 | |
|---|---|---|---|---|---|
| Calc. err. |
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) 1/min−1
1/min−1 |
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) 1/M−1 min−1
1/M−1 min−1 |
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) 1/min−1
1/min−1 |
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) 2/min−1
2/min−1 |
|
| −99.99% | k | 4.443 × 10−5 | 3.820 × 10−4 | 9.031 × 10−5 | 0.20831 |
| % Err. | −99.93 | −99.36 | −99.85 | 73.59 | |
| −10% | k | 0.0591 | 0.0578 | 0.0575 | 0.1267 |
| % Err. | −0.86 | −3.67 | −4.19 | +5.54 | |
| +10% | k | 0.00595 | 0.0578 | 0.0575 | 0.1266 |
| % Err. | −0.74 | −3.66 | −4.18 | +5.50 | |
| +100% | k | 0.0595 | 0.0578 | 0.0574 | 0.1267 |
| % Err. | −0.78 | −3.59 | −4.22 | +5.59 | |
| +1000% | k | 0.0596 | 0.0578 | 0.16865 | 2.1581 |
| % Err. | −0.63 | 3.64 | +181.08 | +1698.42 | |
In method C each iteration slowly forces the profiles to obey a given kinetic model. This is clearly illustrated in Fig. 6. In this case, a one-step reaction model was forced while modelling dataset 3. This means that the second order reaction profiles were used to provide the test vectors for the method when investigating dataset 3. In the first iteration, it is clear that the method picked up a two-step reaction pattern. With the progress of the iterations, a second order model is forced, and eventually U + V → W profiles are observed. As in general hard modelling, the information provided to the model becomes quite important and inaccurate information yields poor estimates.
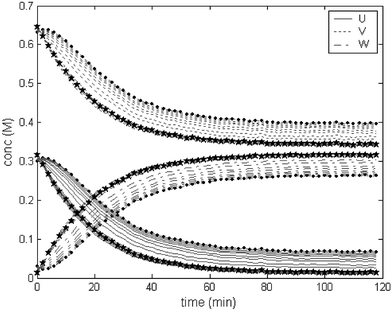 | ||
| Fig. 6 Evolution of the iterations with method C. In this case, a model of the type U + V → W was fitted to dataset 3 (U → V → W). The lines with points (•) represent the first iteration and the lines with stars (★) represent the last iteration. It is possible to observe that the initial iterations show a non-ideal behaviour for a second order reaction, suggesting that the kinetic model chosen is perhaps not appropriate. | ||
The results obtained with method C are very satisfactory, usually around 1% error and below, independently of the initial guess of the rate constant(s) (see Table 6). There is a significant improvement over method B when a high level of error in the initial value of k is present.
| Error level in k | Pred. k | Dataset 1 | Dataset 2 | Dataset 3 | |
|---|---|---|---|---|---|
| Calc. err. |
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) 1/min−1
1/min−1 |
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) 1/M−1 min−1
1/M−1 min−1 |
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) 1/min−1
1/min−1 |
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) 2/min−1
2/min−1 |
|
| −99.99% | k | 0.0531 | 0.0599 | 0.0592 | 0.1221 |
| % Err. | −11.50 | −0.167 | −1.33 | +1.75 | |
| −10% | k | 0.0596 | 0.0598 | 0.0593 | 0.1213 |
| % Err. | −0.667 | −0.33 | −1.17 | +1.08 | |
| +10% | k | 0.0595 | 0.0599 | 0.0593 | 0.1213 |
| % Err. | −0.833 | −0.167 | −1.17 | +1.08 | |
| +100% | k | 0.0596 | 0.0599 | 0.0593 | 0.1214 |
| % Err. | −0.667 | −0.167 | −1.17 | +1.17 | |
| +1000% | k | 0.0596 | 0.0599 | 0.0593 | 0.1213 |
| % Err. | −0.667 | −0.167 | −1.17 | +1.08 | |
From previous studies and for comparison purposes, the rate constant of the reaction between benzophenone and phenylhydrazine, under the same conditions, was found to be 0.026 M−1 min−1 using a PLS model with calibration29 and an average value of 0.026 M−1 min−1 using the method proposed by Thurston et al. that has been previously applied to this reaction.6 Examining Table 7 one can see that the results obtained with both ITTFA and method A are quite significantly in error, although they are significantly better with method A, since the concentration profiles match what would be expected from a second order reaction. Nevertheless, the value of the rate constant is still quite dependent on the initial guess of k, as discussed previously. The high error in the concentration profiles obtained with ITTFA are related to the poor initial guess provided by EPCA for the experimental dataset.
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) 1/M−1 min−1
1/M−1 min−1 |
|
|---|---|
| ITTFA | 0.0053 |
| Method A | 0.0515 |
| Method B | 0.0275 |
| Method C | 0.0252 |
For dataset 4, the performance of methods B and C is again quite satisfactory, with the predicted k value quite similar to the value calculated previously. This is expected since dataset 4 is quite similar to dataset 2, where good results had been obtained. In addition, the reaction under study is a clean second order reaction, so the test vectors used are quite good approximations of the concentration profiles expected, and it has a quite low signal to noise ratio, even smaller than the one present in dataset 2.
5. Conclusion
Methods B and C for curve resolution described in this paper are new modifications of ITTFA that incorporate kinetics information. Method A is an implementation of the traditional ITTFA with the simple difference that kinetics are employed for the estimation of the initial test vector. The methods are compared to an implementation of ITTFA which does not incorporate any kinetic information, using model-free approaches for the estimation of initial test vectors. All that is required for the modifications is a knowledge of the kinetics and an initial estimate of the rate constant, which allows values in a broad range and still achieves effective results.By applying kinetic information to the multivariate model, some problems with ITTFA can be overcome, leading the algorithm to converge in the right direction. This is a clear advantage of the methods presented. A possible problem is when inappropriate kinetic models are employed. As in all science the greater the knowledge of the system the more reliably it can be modelled, and if there is knowledge of the order of the reaction as well as multivariate spectroscopic information it is appropriate that both types of knowledge are combined.
In the case of method A, there was an improvement relative to the results obtained with ITTFA, but it was found that this method is quite dependent on the initial estimations of the rate constant. The method gave quite poor results for the two-step reaction, even when a good guess of k was used. The performance with the real dataset, even though still with a significant error, improved significantly on the ITTFA result.
Methods B and C worked quite well with all the reactions studied, including the two step reaction and the real dataset. Method C usually outperforms method B but has the disadvantage of involving more steps and being less straightforward. The investigation of the results may provide the detection of a wrong mode, which would not be feasible using only hard (kinetic) modelling. In soft modelling (ITTFA), no assumption is made about the kinetics, so the results take whatever form best fits the data, according to the test vectors provided. In kinetic modelling the results are now completely dependent on the kinetic model chosen. It is quite difficult in that case to assess the quality of the model selected since different models can recreate the original dataset almost perfectly. This demonstrates the applicability and relevance of the methods presented, in particular methods B and C, as discussed above. Whilst a certain kinetic model is forced on the data, it is still possible to assess the model chosen upon investigation of the iterations of the method and therefore methods B and C are successful combinations of some of the good features of both soft and hard modelling.
Acknowledgements
A. R. Carvalho would like to thank Glaxo Smith Kline and the University of Bristol for financial support.References
- E. R. Malinowski, Factor Analysis in Chemistry, Wiley, New York, 3rd edn, 2002, p. 158 Search PubMed.
- P. J. Gemperline, J. Chem. Inf. Comput. Sci., 1984, 24, 206 CrossRef CAS.
- Z. L. Zhu, W. Z. Cheng and Y. Zhao, Chemom. Intell. Lab. Syst., 2002, 64, 157 CrossRef CAS.
- J. H. Jiang, Y. Liang and Y. Ozaki, Chemom. Intell. Lab. Syst., 2004, 71, 1 CrossRef CAS.
- M. Esteban, C. Ariño, J. M. Díaz-Cruz and R. Tauler, Trends Anal. Chem., 2000, 19, 49 CrossRef CAS.
- T. J. Thurston, R. G. Brereton, D. J. Foord and R. E. A. Escott, J. Chemom., 2003, 17, 313 CrossRef CAS.
- J. H. Espenson, Chemical Kinetics and Reaction Mechanisms, McGraw-Hill, New York, 2nd edn, 1995, p. 72 Search PubMed.
- R. L. Liboff, Introduction to the Theory of Kinetic Equations, Wiley, New York, 1969, p. 123 Search PubMed.
- F. Wilkinson, Chemical Kinetics and Reaction Mechanisms, Van Nostrand Reinhold Co., New York, 1980, p. 12 Search PubMed.
- A. R. Carvalho, R. G. Brereton, T. J. Thurston and R. E. A. Escott, Chemom. Intell. Lab. Syst., 2004, 71, 47 CrossRef CAS.
- S. Wold, N. Kettaneh, H. Fridén and A. Holmberg, Chemom. Intell. Lab. Syst., 1998, 44, 331 CrossRef CAS.
- R. G. Brereton, Chemometrics: Data Analysis for the Laboratory and Chemical Plant, Wiley, Chichester, 2003, p. 339 Search PubMed.
- T. J. Thurston and R. G. Brereton, Analyst, 2002, 127, 659 RSC.
- M. Esteban, C. Ariño, J. M. Díaz-Cruz, M. S. Díaz-Cruz and R. Tauler, Trends Anal. Chem., 2000, 19, 49 CrossRef CAS.
- P. J. Gemperline and J. C. Hamilton, J. Chemom., 1989, 3, 455 CAS.
- B. G. M. Vandeginste, W. Derks and G. Kateman, Anal. Chim. Acta, 1985, 173, 253 CrossRef CAS.
- E. R. Malinowski, Anal. Chim. Acta, 1978, 103, 339 CrossRef CAS.
- C. L. Lawson and R. J. Hanson, Solving Least Squares Problems, Prentice-Hall, Englewood Cliffs, NJ, 1974 Search PubMed.
- R. Bro and S. de Jong, J. Chemom., 1997, 11, 393 CrossRef CAS.
- P. J. Gemperline and E. Cash, Anal. Chem., 2003, 75, 4236 CrossRef CAS.
- E. Furusjö and L. G. Danielsson, Anal. Chim. Acta, 1998, 373, 83 CrossRef CAS.
- E. Furusjö and L. G. Danielsson, J. Chemom., 2000, 14, 483 CrossRef CAS.
- E. Furusjö and L. G. Danielsson, Chemom. Intell. Lab. Syst., 2000, 50, 63 CrossRef CAS.
- E. Furusjö, O. Svensson and L. G. Danielsson, Chemom. Intell. Lab. Syst., 2003, 66, 1 CrossRef CAS.
- H. Haario and V. M. Taavitsainen, Chemom. Intell. Lab. Syst., 1998, 44, 77 CrossRef CAS.
- P. Jandanklang, M. Maeder and A. Whitson, J. Chemom., 2001, 15, 511 CrossRef CAS.
- A. de Juan, M. Maeder, M. Martinez and R. Tauler, Anal. Chim. Acta, 2001, 442, 337 CrossRef CAS.
- M. Amrhein, B. Srinivasan, D. Bonvin and M. M. Schumacher, Chemom. Intell. Lab. Syst., 1996, 33, 17 CrossRef CAS.
- A. R. Carvalho, M. N. Sanchez, J. Wattoom and R. G. Brereton, Talanta, DOI:10.1016/j.talanta.2005.07.053.
| This journal is © The Royal Society of Chemistry 2006 |
