Light-induced electron transfer in porphyrin–calixarene conjugates

Abstract

The fluorescence from a set of porphyrin–calixarene complexes is quenched upon addition of benzo-1,4-quinone (BQ) in fluid solution. In N,N-dimethylformamide solution, fluorescence quenching involves both static and dynamic interactions but there are no obvious differences between porphyrins with or without the appended calixarene. Under such conditions, the static quenching behaviour is attributed to π-complexation between the reactants and it is concluded that the calixarene cavity does not bind BQ. An additional static component is apparent in dichloromethane solution. This latter effect involves partial fluorescence quenching, for which the intramolecular rate constant can be obtained by time-resolved fluorescence spectroscopy. The derived rate constants depend on molecular structure in a manner consistent with fluorescence quenching being due to electron transfer. In all cases, however, the dominant quenching step involves diffusional contact between the porphyrin nucleus and a non-bound molecule of BQ.

---

Introduction

The availability of a well-defined solid-state structure of the bacterial photosynthetic reaction centre complex^1–6 offers an exceptional opportunity to test and refine theories related to long-range electron transfer and energy storage, with specific applications in biological and artificial systems. The three-dimensional structure of the reaction centre complex shows a highly organized atomic coordination between the various redox-active components and the surrounding protein matrix. Electron transfer in the reaction centre complex starts from a pair of non-covalent bacteriochlorophyll molecules, which are porphyrin derivatives, and finishes by the one-electron reduction of a plastoquinone molecule.^7–11 This long-range process (e.g., 80 Å distance) is fast, irreversible and essentially temperature independent.

Understanding the key factors that govern energy and electron transfer in natural photosynthetic systems is a prerequisite for the design and manufacture of different types of artificial systems, such as solar energy conversion devices. Towards this direction, a great number of photophysical and photochemical experiments have been carried out with small molecular entities intended to function as mimics for the natural process. Many of these artificial models are based on porphyrin, metalloporphyrin and/or quinone moieties.^12–15 Also, different supramolecular model systems have been made in order to obtain improved insight into the mechanisms of charge separation and electron transfer.^16–23

In order to exploit, or duplicate, the natural system we need to develop a genuine understanding of the reaction centre complex and, in particular, to understand the structural factors. It is clear that Nature has taken great trouble to arrange the various cofactors in exact positions, without using covalent bonding. Structural factors that affect the rate of electron transfer in the natural process have been extensively studied in covalently linked donor–acceptor molecules. Research on these model compounds has been extremely informative and has shown, for example, how parameters such as the distance and orientation of the donor and acceptor subunits, the electronic nature of the bridging spacer unit, temperature and solvent polarity, dynamics and viscosity affect the rate of charge separation. Also, more sophisticated models comprising donor–acceptor assemblies that do not depend on covalent bonding have been studied. These latter systems allow us to learn more about the role of the protein framework in promoting long-range electron transfer.

Here, we consider the role of supramolecular systems whereby a quinone is held at a remote site by way of non-covalent interactions. The idea behind this system is to enquire if it is possible to set up a long-range electron transfer from a porphyrin-based electron donor to the bound quinone. Light-induced electron transfer can take place through the intervening space, without the need to follow a sigma-bonded framework. Some related model systems have been reported earlier that involve porphyrin–quinone^24,25 or porphyrin–calixarene molecular dyads.^26–29 Calixarenes are interesting candidates for use in such model systems because they possess a central cavity able to bind a quinone.^30–35 These compounds are readily available in a pure state with conformations known from X-ray data and CPK models. Numerous applications have been reported for the binding of ions and organic molecules with calix[n]arenes.³⁰ For instance, the effect of molecular dimension on the binding properties of different calix[n]arenes towards a series of quinone derivatives has been investigated.³⁶ The results indicate high stability constants in certain cases. It seems that hydrogen bonding interactions between the two phenolic OH groups on the calixarene and the carboxyl groups of the quinone are responsible for most of the binding energy. This is not a particularly strong type of binding and might allow the reduced quinone to escape from the binding pocket.

Six new supramolecular assemblies are used in order to examine the effect of orientation and distance on the quenching process. It is very well known that quinones are excellent quenchers for the fluorescence of porphyrin derivatives, including chlorophyll, and that quenching is due to electron transfer. In these compounds, a calix[4]arene subunit is linked at the ortho, meta or para position of a meso-phenyl ring from a tetratolyl porphyrin. The porphyrin is available both as the free-base derivative or as the corresponding zinc(II) complex. The generic structures of these isomers are presented in Fig. 1. Free-base meso-tetratolyl porphyrin (H₂TTP) is used as a reference for each of the free-base compounds whilst zinc(II) meso-tetratolyl porphyrin (ZnTTP) acts as a control molecule for the metallated derivatives.

Fig. 1 Structural representation of the porphyrin–calixarene conjugates used in this work.

Experimental

Synthesis of the various porphyrin–calixarene conjugates will be reported elsewhere. The compounds were fully characterised by ¹H and ¹³C NMR, mass spectrometry and elemental analysis. Reference compounds were prepared by standard methods and purified by extensive column chromatography on silica. Solvents were spectroscopic grade (Aldrich) and were used as received. Benzo-1,4-quinone was vacuum sublimed and stored in the dark. All solutions were freshly prepared and protected against exposure to room light.

Absorption spectra were recorded with a Hitachi U3310 spectrophotometer and fluorescence studies were made with a Hitachi F4500 spectrofluorimeter. All solutions were optically dilute and purged with N₂ as required. Time-resolved fluorescence measurements were made by the time-correlated, single-photon counting method. Excitation at 590 nm was made with a frequency-doubled, mode-locked Nd-YAG laser pumped cavity-dumped Rhodamine 6G dye laser. Emission was detected at 90° to excitation and isolated with a high radiance monochromator. A microchannel plate detector was used to monitor the signal. The time resolution of this set-up, after deconvolution of the instrument response function, was about 50 ps.

Spectroscopic titrations were made by adding fixed aliquots of a stock solution of benzo-1,4-quinone to a solution of the porphyrin in freshly distilled DMF or CH₂Cl₂. At least 30 different concentrations of quinone were added. The solution was allowed to equilibrate for 10 min in the dark. Absorption and fluorescence spectra were recorded after each addition and the data were transferred to a PC for analysis. Absorption spectral changes were analysed with SPECFIT while the results of the fluorescence titrations were analysed with purpose-written software. All titrations were repeated at least three times.

Results and discussion

Molecular modelling

The compounds investigated here are intended to bind a molecule of benzo-1,4-quinone (BQ) inside the cavity provided by the calixarene receptor. However, it is well known that porphyrins undergo diffusional electron-transfer quenching with BQ in fluid solution and, under certain conditions, form a π-complex with BQ. The latter species is a ground-state complex that quenches porphyrin fluorescence by the so-called static effect. In order to establish if BQ can enter the cavity, a set of molecular docking studies was made.

A simple docking procedure, of the type normally used to model ligand-receptor interactions in biological systems, is used here to investigate the more favourable interactions between the various subunits. It is recognised that the Global Range Molecular Matching software (GRAMM)³⁷ can help identify binding sites and geometries. The calculations start by finding an optimised structure; an operation that can be performed in most quantum mechanical software packages. We used MOPAC with the PM3 method to calculate the minimised structures of calixarene, benzoquinone and ZnTTP subunits. The structures are saved as ‘.ent’ files, which form the main input for the GRAMM software. We used all of the defaults of the programme as the parameters file, except the 3D information of the ligand and the receptor. The calculations were performed in two separate runs, once for calixarene with BQ and secondly for ZnTTP with BQ. The results are depicted in Fig. 2.

Fig. 2 Computed structures for the two complexation sites available to the porphyrin–calixarene conjugates. The upper panel shows BQ binding to the calixarene cavity while the lower panel shows π-stacking between the porphyrin and BQ.

These figures show only the most favourable interactions; however, there are lots of other interactions that are energetically less favourable. In the case of interaction between calixarene and BQ, most of the complexes are very similar to that shown in Fig. 2. This finding confirms that the calixarene cavity has the appropriate dimensions to bind a BQ molecule. Likewise, the computer modelling studies confirm that BQ forms a π-complex with the porphyrin nucleus. This is a charge-transfer complex. The binding energies for the two complexes are comparable such that it is unlikely π-complexation can be eliminated in favour of encapsulation even in a good solvent.

Binding in DMF

The absorption spectral properties of the free-base porphyrins (H₂TTP and its ortho, meta and para calixarene conjugates) in N,N-dimethylformamide (DMF) include an intense Soret band, and four Q-bands. Since there are no obvious differences between the reference compound and its conjugates we conclude that the calixarene unit makes no significant contribution to the overall spectrum, at least over the visible spectral range. Likewise, there were only minor variations in the fluorescence quantum yields (Φ_F) and fluorescence lifetimes (τ_S) measured in deoxygenated DMF (Table 1). Addition of increasing concentration of BQ had no effect on the absorption spectrum but quenched fluorescence from the porphyrin subunit. An example of the decrease in fluorescence intensity upon successive addition of BQ is depicted in Fig. 3.

Table 1 Fluorescence quenching data collected in DMF

Compound	Φ F	τ S / ns	K / M^−1	k q / 10^9 M^−1 s^−1
H2TTP	0.12	10.5	13	3.5
H2P-ortho	0.11	9.4	9	3.2
H2P-meta	0.11	10.5	13	3.6
H2P-para	0.12	10.3	14	3.2
ZnTTP	0.044	2.1	24	6.5
ZnP-ortho	0.042	1.9	21	6.0
ZnP-meta	0.041	2.0	26	6.6
ZnP-para	0.044	2.0	25	6.2

---

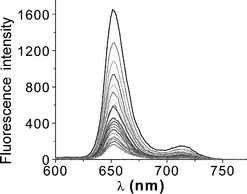Fig. 3 Effect of added BQ (0–0.12 M) on the fluorescence observed for the para isomer of the free-base porphyrin–calixarene conjugate in DMF.

Similar behaviour was found in each case. Stern–Volmer plots constructed from the fluorescence quenching data deviate upwards from linearity. Two suggested mechanisms for this observation are (i) static quenching due to the formation of ground-state complexes between the porphyrin and quencher,³⁸ as reported earlier for H₂TTP and ZnTTP systems,^14,39 or (ii) a transient effect in the diffusion-controlled reaction. This latter effect influences both the fluorescence intensity and the decay lifetime.⁴⁰ There is no obvious difference between the quenching curves for the different isomers and for the control. This behaviour suggests that the calixarene cavity does not bind BQ in DMF solution.

A series of time-resolved fluorescence experiments confirmed the above situation. Thus, emission from the ortho-substituted porphyrin–calixarene dyad decays via first-order kinetics in DMF at room temperature. The derived fluorescence lifetime was 9.4 ns. Upon stepwise addition of BQ, the fluorescence decay rate increased progressively but remained strictly mono-exponential (Fig. 4). Even at high concentrations of BQ, there was no indication for a fast component in the observed decay profile. This finding indicates that the so-called transient effect is not operative under these conditions since a characteristic feature of such behaviour is the introduction of a very short-lived component into the decay records. The time resolution used in this study was around 50 ps, which should easily be sufficient to observe the onset of the transient effect. The time-resolved fluorescence profiles also show that the π-stacked complex does not fluoresce in DMF since its lifetime could not be measured. In agreement with the earlier work,^14,39 this π-complex is believed to be very short lived and to undergo extremely fast internal conversion to restore the ground-state complex. This complex causes the static quenching.

Fig. 4 Time-resolved fluorescence decay profiles recorded for the ortho isomer of the free-base porphyrin–calixarene conjugate in DMF on successive addition of BQ (see Fig. 5 for details).

The derived fluorescence lifetimes recorded in the presence of predetermined quantities of BQ permit calculation of the bimolecular quenching rate constant k_q as 3.5 × 10⁹ M⁻¹ s⁻¹ in DMF (Fig. 5). As expected, this is close to the diffusion-controlled rate limit at room temperature.⁴¹ The site of attachment has little influence on the diffusional quenching properties. There does seem, however, to be small differences in the static component among the various isomers. In particular, the ortho-isomer shows the least amount of static quenching. This might be due to partial blocking of the face of the porphyrin by the appended calixarene. The corresponding ZnTTP-based conjugates showed very similar behaviour (Table 1).

Fig. 5 Stern–Volmer plots constructed for the dynamic quenching of porphyrin fluorescence by BQ in DMF solution: free-base porphyrin (open circles) and zinc porphyrin (filled).

On the assumption that BQ associates with the porphyrin nucleus in the form of a π-stacked complex (Fig. 2), an attempt was made to measure the stability constant (K). This was done by extracting the static quenching component from the overall fluorescence yield determined at each concentration of BQ.⁴⁰ In each case, the dynamic component was calculated from the measured diffusional rate constant and the molar concentration of BQ. The residual fluorescence at each [BQ] was considered in terms of a 1 ∶ 1 complex with the stipulation that the complex did not fluoresce.⁴² Reasonable plots were obtained in each case (Fig. 6). From the non-linear, least-squares fits it was concluded that the average stability constants for formation of the π-complex in DMF are 12 ± 3 and 24 ± 4 M⁻¹, respectively, for the H₂TTP and ZnTTP derived systems (Table 1). Thus, π-complexation is fairly weak. The higher binding affinity shown by the metallated porphyrins arises because they are better electron donors.

Fig. 6 Relative fluorescence quenching contribution to a 1 ∶ 1 binding model. The solid line drawn through the data points corresponds to the stability constant given in Table 1.

Fluorescence quenching of the free-base porphyrin conjugates in CH₂Cl₂

Similar behaviour was found in CH₂Cl₂ solution. Thus, addition of BQ had no obvious effect on the absorption spectrum but quenched fluorescence from the porphyrin subunit. The change of fluorescence intensity upon titration with BQ was used to compile Stern–Volmer plots for each system. In all cases, upwards deviation from linearity was found, indicating the formation of complexes in addition to dynamic quenching. It is now clear, however, that the substituted compounds display more pronounced static quenching than does the reference compound. This is unlike the situation found in DMF and suggests that the calixarene cavity might be involved in binding a second molecule of BQ.

The important questions to ask at this stage are: How many channels are involved in the static quenching process, π-stack, the calixarene cavity or both? What are the relevant stability constants for each type of complexation process? In order to address these issues we first studied the fluorescence quenching caused by addition of BQ to a solution of H₂TTP in CH₂Cl₂, knowing that this system lacks the calixarene cavity. A set of time-resolved fluorescence studies was made with laser excitation at 590 nm. In the absence of added BQ the fluorescence decay profile is mono-exonential and corresponds to an excited-singlet state lifetime of 7.1 ns (Fig. 7). This value is slightly shorter than that found in DMF because the solvent exerts a small external heavy-atom effect that leads to enhanced intersystem crossing to the triplet manifold. The decay profiles remain mono-exponential in the presence of BQ but the derived lifetime decreases progressively with increasing concentration of added BQ (Fig. 7). There is no indication for the so-called transient effect.⁴⁰

Fig. 7 Time-resolved fluorescence decay profiles recorded upon successive addition of BQ to H₂TTP in CH₂Cl₂ (see Fig. 8 for details).

The lifetimes can be used to construct a Stern–Volmer plot that corresponds exclusively to the dynamic quenching component (Fig. 8). This allows calculation of the diffusional quenching rate constant (k_q) as being 9.1 × 10⁹ M⁻¹ s⁻¹, under these conditions. Using these values for the lifetime and bimolecular quenching rate constant, it becomes possible to isolate the static component from the quenching data. Expressing this value in terms of a 1 ∶ 1 binding process gives rise to a stability constant of 15.5 M⁻¹. This process is attributed to π-complexation. The derived K is slightly higher than that found in DMF, probably because the less polar solvent will favour tighter binding in a charge-transfer complex. It might be noted that fitting the static component to successive formation of 1 ∶ 1 and 1 ∶ 2 complexes did not improve the quality of the fit. In principle, it is possible for H₂TTP to bind two molecules of BQ, one on each face, but this behaviour is not favoured under our conditions. It is not possible to use particularly high concentrations of BQ in these experiments because of the strong dynamic quenching.

Fig. 8 Stern–Volmer plot constructed for the dynamical quenching effect of BQ on fluorescence from H₂TTP in CH₂Cl₂.

Similar experiments were made with the calixarene-derived samples and again it should be stressed that only the H₂TTP chromophore absorbs at 590 nm. Each dyad was found to give a single-exponential fluorescence decay profile following laser excitation in CH₂Cl₂. The derived lifetimes are given in Table 2 and show a slight variation among the isomers. In each case, the fluorescence lifetime of the dyad was somewhat shorter than that of the control compound but this effect is attributed to subtle changes in the geometry around the porphyrin ring. In the presence of low concentrations of BQ, the fluorescence decay profile became non-exponential (Fig. 9). For each concentration of added BQ, the decay record could be fitted satisfactorily to the sum of two exponentials. The shorter-lived component (τ₁) was found to be independent of [BQ] but highly sensitive to the nature of the dyad. Although the lifetime of this species remained independent of the concentration of added BQ its fractional amplitude (A₁) increased with increasing [BQ]. The lifetime of the longer-lived component (τ₂) was found to decrease progressively with increasing [BQ] and its fractional amplitude (A₂) decreased as the concentration of quencher was increased. This latter lifetime gave rise to a linear Stern–Volmer plot and can be attributed to the dynamic (or diffusional) quenching component (Fig. 10). The shorter-lived species, which is clearly a case of static quenching, is assigned to quenching by a BQ molecule housed within the cavity provided by the calixarene. As such, the rate constant (k_ET) for intracavity electron transfer can be obtained by comparison to the lifetime measured in the absence of BQ. The derived values are collected in Table 3.

Table 2 Fluorescence quenching data collected in CH₂Cl₂

Compound	Φ F	τ S / ns	K / M^−1	k q / 10^9 M^−1 s^−1
H2TTP	0.11	7.1	15	9.1
H2P-ortho	0.080	6.1	—	7.4
H2P-meta	0.078	5.7	—	7.0
H2P-para	0.085	6.0	—	6.8
ZnTTP	0.033	1.9	12	12.0
ZnP-ortho	0.028	1.6	—	8.5
ZnP-meta	0.030	1.7	—	9.0
ZnP-para	0.029	1.6	—	9.4

---

Table 3 Derived parameters for intracavity electron transfer in CH₂Cl₂

Cmpd	K C / M^−1	τ 1 / ps	k ET / 10^9 s^−1
H2P-ortho	32	250	4.0
H2P-meta	57	710	1.4
H2P-para	65	770	1.3
ZnP-ortho	47	87	11.5
ZnP-meta	70	455	2.2
ZnP-para	90	115	8.6

---

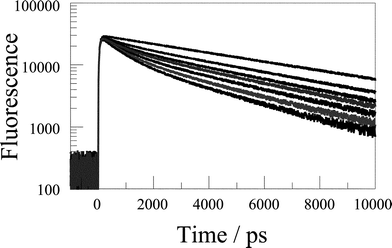Fig. 9 Time-resolved fluorescence decay profiles recorded for the para isomer of the free-base porphyrin–calixarene conjugate in CH₂Cl₂ on successive addition of BQ (see Fig. 10 for details).

Fig. 10 Stern–Volmer plot constructed for the dynamical quenching contribution made for the para isomer of the free-base porphyrin–calixarene conjugate on addition of BQ in CH₂Cl₂.

Furthermore, the stability constant (K_C) for association of BQ with the calixarene cavity is given by:

This allows calculation of K_C from the time-resolved fluorescence profiles (Fig. 11). For this analysis to work properly, it is necessary that τ₁ < τ₂ and that there is little or no diffusional quenching of τ₁. These conditions are met for the free-base dyads over a limited [BQ] range.

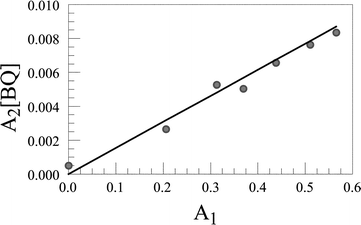Fig. 11 Fitting the static fluorescence quenching component to a 1 ∶ 1 binding model. The solid line drawn through the data points corresponds to the equilibrium constant given in Table 3 and the data refer to the para isomer of the free-base porphyrin–calixarene conjugate in CH₂Cl₂.

Fluorescence quenching of the zinc porphyrin conjugates in CH₂Cl₂

As described above for the free-base analogue in CH₂Cl₂, the steady-state fluorescence results indicate a combination of static and dynamic quenching. For ZnTTP, the time-resolved fluorescence decay profile remained mono-exponential at all concentrations of added BQ. In the absence of quencher the fluorescence lifetime (τ₀) was found to be 1.9 ns. This value is much shorter than that found for the free-base porphyrin because of the internal heavy-atom effect. Fluorescence lifetimes measured for the ZnTTP-based dyads were quite similar to that of the control (Table 2). The fluorescence lifetime measured for ZnTTP became progressively shorter as the concentration of added BQ was increased. This gave rise to a linear Stern–Volmer plot corresponding to a diffusional quenching rate constant (k_q) of 1.2 × 10¹⁰ M⁻¹ s⁻¹. After allowing for the dynamic quenching contribution, the stability constant (K) for formation of the π-complex with BQ was found to be 12 ± 3 M⁻¹ (Table 2). There was no suggestion of a significant transient effect and no obvious short-lived component in the decay profiles. The value of K is comparable to that found for the free-base analogue and similar to values found in DMF. Overall, this behaviour is remarkably similar to that found for H₂TTP except for the increased bimolecular quenching rate constant.

As found for the H₂TTP-derived dyads in CH₂Cl₂, the time-resolved fluorescence decay profiles for the ZnTTP-based dyads showed dual-exponential behaviour (Fig. 12). The shorter-lived component, again attributed to intracavity electron transfer, remains independent of [BQ] but is markedly affected by the structure of the dyad. The shortest lifetime is given by the ortho isomer whilst the meta isomer gives the longest lifetime. The lifetime of the second component seen in the decay records decreases progressively with increasing [BQ] and can be assigned to the dynamic quenching component. Using the latter values collected at different concentrations of BQ, we can calculate the diffusional quenching rate constants (Fig. 13). These values are somewhat lower than the value found for ZnTTP due to the higher diffusion coefficient of the dyads. The derived data are collected in Table 3. It is seen that the general behaviour remains as found for the free-base porphyrin derivatives but k_ET is faster. As explained for the diffusional quenching there is a higher thermodynamic driving force for light-induced electron transfer from porphyrin to quinone for ZnTTP because of its lower ionisation potential.

Fig. 12 Time-resolved fluorescence decay profiles recorded for the ortho isomer of the zinc porphyrin–calixarene conjugate in CH₂Cl₂ on successive addition of BQ.

Fig. 13 Stern–Volmer plot for the diffusional quenching contribution and the static component for BQ quenching of the fluorescence from the ortho isomer of the ZnTTP-based dyad in CH₂Cl₂ as derived from time-resolved fluorescence spectroscopy.

It is instructive to consider what affects the magnitude of k_ET, other than the thermodynamic driving force. The most important factors that mediate the rate of electron transfer are the separation distance and mutual orientation of the reactants. Most likely, electron transfer in the dyads occurs via through-space interactions and it is difficult to assess if the intervening medium differs between the various isomers. It is reasonable to suppose, however, that both the separation distance and the orientation are controlled by the position of attachment. The ortho isomer looks to provide for a shorter separation and a more coplanar arrangement. Both factors would increase the rate of electron transfer. The para isomer will hold the reactants further apart but there is increased flexibility that will favour adoption of many different orientations. This situation will serve to decrease k_ET. The meta isomer, which gives a surprisingly low k_ET for the ZnTTP-derived dyad, might be expected to show intermediate behaviour.

Conclusion

Fluorescence quenching results observed for the investigated dyads with BQ display upwards curvature from the usual Stern–Volmer behaviour. This effect is attributed to static quenching in which a BQ molecule forms a complex with either the porphyrin nucleus or the calixarene cavity. In all cases, fluorescence quenching is due to light-induced electron transfer.^14,39 After allowing for the diffusional contribution in the fluorescence quenching, it became possible to derive stability constants for the complexation steps. On the basis of steady-state and time-resolved fluorescence studies it is concluded that the control systems, ZnTTP and H₂TTP, form π-complexes with added BQ. In contrast, the dyads show preferential formation of the calixarene-bound complex in CH₂Cl₂ but π-stacking in DMF. The rate of diffusional quenching is very high in all the systems investigated and this makes for difficult data analysis. However, we have been able to extract the rates of intracavity electron transfer and these are seen to be rather high. We cannot resolve whether such electron transfer is through space or through bond but the rate constant is sensitive to the geometry of the dyad.

It is interesting to compare our results with those obtained earlier with somewhat related structures;⁴³ in all cases, the motivation for studying such systems is to mimic the reaction centre complex of the photosynthetic organism. Several systems have looked at the photophysics of a zinc porphyrin attached to BQ by way of Watson–Crick base pairing. In the case of flexible structures, electron transfer occurs by diffusional encounter between partners in the hydrogen-bonded complex.¹⁹ Whereas in the system with a rigid spacer, electron transfer most likely occurs via a through-bond process, involving the hydrogen-bonded network.²²

A different system with a zinc porphyrin attached to two calixarene units in the cone shape was reported as an efficient system for electron transfer to the BQ in the calixarene cavity. Fluorescence quenching was observed in a 1 ∶ 19 mixture of H₂O/THF, where Stern–Volmer constants of 3600 ± 800 M⁻¹ and 1100 ± 400 M⁻¹ were derived. The first value was assigned to the enhanced quenching due to complexation of BQ in the calixarene cavity. The second value, which is closer to the value of K_SV in the control molecule (250 ± 50 M⁻¹), is believed to represent the diffusional contribution by free BQ.

A further system consists of a calix[4]arene connected to the porphyrin via a benzene ring at the meso position. This system is believed to display rapid through-space electron transfer.^44,45 Analysis of the NMR spectral data for the OH group of the calixarene upon titration with BQ confirmed a 1 ∶ 1 binding model associated with a stability constant of 70 ± 1 M⁻¹. The non-linear Stern–Volmer plot obtained for this system was ascribed to both static and dynamic processes although the experimental results were not analysed in detail.

Acknowledgements

We thank the EPSRC (GR/R92615/01) and the University of Newcastle for financial support.

References

1. J. Deisenhofer, O. Epp, K. Miki, R. Huber and H. Michel, X-Ray structure analysis of a membrane-protein complex–electron density map at 3 Å resolution and a model of the photosynthetic reaction center from rhodopseudomonas-viridis, J. Mol. Biol., 1984, 180, 385–398.
2. J. Deisenhofer, O. Epp, K. Miki, R. Huber and H. Michel, Structure of the protein subunits in the photosynthetic reaction center of rhodopseudomonas-viridis at 3 Å resolution, Nature, 1985, 318, 618–624.
3. H. Michel, O. Epp and J. Deisenhofer, Pigment–protein interactions in the photosynthetic reaction center complex from rhodopseudomonas-viridis, EMBO J., 1986, 5, 2445–2451.
4. J. P. Allen, G. Feher, T. O. Yeates, H. Komiya and D. C. Rees, Structure of the reaction center from rhodobacter-sphaeroides R-26—the protein subunits, Proc. Natl. Acad. Sci. USA, 1987, 84, 6162–6166.
5. J. P. Allen, G. Feher, T. O. Yeates, H. Komiya and D. C. Rees, Structure of the reaction center from rhodobacter-sphaeroides R-26—the cofactors 1, Proc. Natl. Acad. Sci. USA, 1987, 84, 5730–5734.
6. H. Michel, 3-Dimensional crystals of a membrane-protein complex—the photosynthetic reaction center from rhodopseudomonas-viridis, J. Mol. Biol., 1982, 158, 567–572.
7. N. W. Woodbury, M. Becker, D. Middendorf and W. W. Parson, Picosecond kinetics of the initial photochemical electron-transfer reaction in bacterial photosynthetic reaction centers, Biochemistry, 1985, 24, 7516–7521.
8. J. L. Martin, J. Breton, A. J. Hoff, A. Migus and A. Antonetti, Femtosecond spectroscopy of electron transfer in the reaction center of the photosynthetic bacterium rhodopseudomonas-viridis R-26—Direct electron transfer from the dimeric bacteriochlorophyll primary donor to the bacteriopheophytin acceptor with a time constant of 2.8 ± 0.2 ps, Proc. Natl. Acad. Sci. USA, 1986, 83, 957–961.
9. J. Breton, J. L. Martin, A. Migus, A. Antonetti and A. Orszag, Femtosecond spectroscopy of excitation energy transfer and initial charge separation in the reaction center of the photosynthetic bacterium rhodopseudomonas-viridis, Proc. Natl. Acad. Sci. USA, 1986, 83, 5121–5125.
10. C. Kirmaier and D. Holten, Subpicosecond characterization of the optical properties of the primary electron donor and the mechanism of the initial electron transfer in rhodobacter-capsulatus reaction centers, FEBS Lett., 1988, 239, 211–218.
11. J. Breton, J. L. Martin, G. R. Fleming and J. C. Lambry, Low temperature femtosecond spectroscopy of the initial step of electron transfer in reaction centers of photosynthetic purple bacteria, Biochemistry, 1988, 27, 8276–8284.
12. R. S. Becker and J. B Allison, Effect of metal atom perturbations on the luminescent spectra of porphyrins, J. Chem. Phys., 1960, 32, 1410–1417.
13. R. S. Becker and J. B. Allison, Metalloporphyrins: Electronic spectra and nature of perturbations, I. Transition metal ion derivatives, J. Phys. Chem., 1963, 67, 2662–2669.
14. A. Harriman, G. Porter and N. Searle, Reversible photooxidation of zinc tetraphenylporphyrin by benzo-1,4-quinone, J. Chem. Soc., Faraday Trans. 2, 1979, 75, 1515–1521.
15. A. Harriman, Luminescence of porphyrins and metalloporphyrins. Part 1. Zinc(II), nickel(II), and manganese(II) porphyrins, J. Chem. Soc., Faraday Trans. 1, 1980, 76, 1978–1982.
16. J. Davila, A. Harriman and L. R. Milgrom, A light-harvesting array of synthetic porphyrins, Chem. Phys. Lett., 1987, 136, 427–430.
17. A. Harriman, D. Magda and J. L. Sessler, Energy transfer across a hydrogen-bonded cytosine-derived, zinc–free-base porphyrin conjugate, J. Chem. Soc., Chem. Commun., 1991, 345–348.
18. A. Harriman, D. Magda and J. L. Sessler, Photon antennae assembled by nucleic acid base pairing, J. Phys. Chem., 1991, 95, 1530–1532.
19. A. Harriman, Y. Kubo and J. L. Sessler, Molecular recognition via base pairing: Photoinduced electron transfer in hydrogen-bonded zinc porphyrin–benzoquinone conjugates, J. Am. Chem. Soc., 1992, 114, 388–390.
20. M. Brun, S. J. Atherton, A. Harriman, V. Heitz and J. P. Sauvage, Photophysics of entwined porphyrin conjugates. Competitive exciton annihilation, energy-transfer, electron-transfer, and superexchange processes, J. Am. Chem. Soc., 1992, 114, 4632–4639.
21. A. Harriman, V. L. Capuano and J. L. Sessler, Electronic energy migration in quinone-substituted, phenyl-linked dimeric and trimeric porphyrins, J. Am. Chem. Soc., 1993, 115, 4618–4628.
22. J. L. Sessler, B. Wang and A. Harriman, Long-range photoinduced electron transfer in an associated but non-covalently linked photosynthetic model system, J. Am. Chem. Soc., 1993, 115, 10 418-10419.
23. J. P. Collin, A. Harriman, V. Heitz, F. Odobel and J. P. Sauvage, Photoinduced electron- and energy-transfer processes occurring within porphyrin–metal bisterpyridyl conjugates, J. Am. Chem. Soc., 1994, 116, 5679–5690.
24. Y. Aoyama, M. Asakawa, Y. Matsui and H. Ogoshi, Molecular recognition. 16. Molecular recognition of quinones—2-point hydrogen bonding strategy for the construction of face-to-face porphyrin quinone architectures, J. Am. Chem. Soc., 1991, 113, 6233–6240.
25. T. Hayashi, T. Miyahara, N. Hashizume and H. Ogoshi, Specific molecular recognition via multipoint hydrogen bonding: Ubiquinone analogs of porphyrins having 4 convergent hydroxyl groups pairing, J. Am. Chem. Soc., 1993, 115, 2049–2051.
26. T. Nagasaki, H. Fujishima and S. Shinkai, Calix[4]arene-capped tetraphenylporphyrin—synthetic approach to a chiral capped porphyrin with regular C-4 symmetry, Chem. Lett., 1994, 35, 989–992.
27. D. M. Rudkevich, W. Verboom and D. N. Reinhoudt, Biscalix[4]arene-Zn-tetraarylporphyrins, Tetrahedron Lett., 1994, 35, 7131–7134.
28. D. Gosztola, H. Yamada and M. R. Wasielewski, Electric field effects of photogenerated ion-pairs on nearby molecules—a model for the carotenoid band shift in photosynthesis, J. Am. Chem. Soc., 1995, 117, 2041–2048.
29. R. Milbradt and J. Weiss, Efficient combination of calix[4]arenes and meso-diphenylporphyrins, Tetrahedron Lett., 1995, 36, 2999–3002.
30. C. D. Gutsche, Calixarenes: Monographs in Supramolecular Chemistry, ed. J. F. Stoddart, The Royal Society of Chemistry, London, 1989, vol. 1.
31. J. Vicens, Calixarenes: A Versatile Class of Macrocyclic Compounds, ed. V. Bhomer and J. Vicens, Kluwer Academic Publisher, Hingham, MA, 1991.
32. S. Shinkai, Calixarenes—the 3rd generation of supramolecules, Tetrahedron, 1993, 49, 8933–8968.
33. V. Böhmer, Calixarenes, macrocycles with (almost) unlimited possibilities, Angew. Chem., Int. Ed. Engl., 1995, 34, 713–745.
34. Pochini and R. Ungaro, Comprehensive Supramolecular Chemistry, ed. F. Vögtle, Elsevier Science Ltd., Oxford, 1996, vol. II, p. 103.
35. P. Lhoták and S. Shinkai, Calix[n]arenes—powerful building blocks of supramolecular chemistry, J. Synth. Org. Chem. Jpn., 1995, 53, 963–974.
36. H. M. Chawla, K. Srivinas and S. Meena, Calix[n]arene–quinone interactions—molecular recognition of 2,6-naphthoquinone by 37,38,39,40,41,42-hexahydroxycalix[6]arene, Tetrahedron, 1995, 51, 2709–2718.
37. E. Katchalski-Katzir, I. Shariv, M. Eisenstein, A. A. Friesem, C. Aflalo and I. Vakser, Molecular-surface recognition–determination of geometric fit between proteins and their ligands by correlation techniques, Proc. Natl. Acad. Sci. USA, 1992, 89, 2195–2199.
38. R. Livingston and C. Ke, Quenching of the fluorescence of chlorophyll-a solutions, J. Am. Chem. Soc., 1950, 72, 909–915.
39. S. Yamada, T. Sato, K. Kano and T. Ogawa, Fluorescence quenching of 5,10,15,20-tetra(para-tolyl)porphine and its zinc complex by quinones—charge-transfer interaction and transient effect, Photochem. Photobiol., 1983, 37, 257–262.
40. T. L. Nemzek and W. R. Ware, Kinetics of diffusion-controlled reactions: Transient effects in fluorescence quenching, J. Chem. Phys., 1975, 62, 477–489.
41. (a) R. M. Noyes, Kinetics of competitive processes when reactive fragments are produced in pairs, J. Am. Chem. Soc., 1955, 77, 2042–2045; (b) R. M Noyes, More rigorous kinetic expressions for competitive processes in solution, J. Phys. Chem., 1961, 65, 763–765.
42. (a) W. R. Ware and J. S. Novros, Kinetics of diffusion-controlled reactions. An experimental test of the theory as applied to fluorescence quenching, J. Phys. Chem., 1966, 70, 3246–3253; (b) W. R. Ware, L. J. Doemeny and T. L. Nemzek, Deconvolution of fluorescence and phosphorescence decay curves. Least-squares method, J. Phys. Chem., 1973, 77, 2038–2048.
43. C.A. Hunter, Meldola Lecture—the role of aromatic interactions in molecular recognition, Chem. Soc. Rev., 1994, 23, 101–109.
44. T. Arimura, T. Nishioka, S. Ide, Y. Suga, M. Sugihara, S. Murata and M. Tachiya, Intracomplex electron transfer in a hydrogen-bonded calixarene-porphyrin conjugate: Tweezers for a quinone, J. Photochem. Photobiol. A: Chem., 2001, 145, 123–128.
45. T. Arimura, S. Ide, H. Sugihara, S. Murata and J. L. Sessler, A non-covalent assembly for electron transfer based on a calixarene-porphyrin conjugate: Tweezers for a quinone, New J. Chem., 1999, 23, 977–979.

---

Footnotes

† Dedicated to Professor Hiroshi Masuhara on the occasion of his 60th birthday.

‡ Deceased 21st March 2004.

---