Metal ion promoted transesterifications of carboxylate esters. A structure/activity study of the efficacy of Zn2+ and La3+ to catalyze the methanolysis of some aryl and aliphatic esters
Alexei A.
Neverov
,
N. E.
Sunderland
and
R. Stan
Brown
*
Department of Chemistry, Queen's University, Kingston, Ontario, Canada K7L 3N6. E-mail: rsbrown@chem.queensu.ca; Fax: 613-533-6669; Tel: 613-533-2400
First published on 10th November 2004
Abstract
The methanolysis of various aryl and aliphatic carboxylate esters promoted by methoxide, 1,5,9-triazacyclododecane : Zn2+(−OCH3) and La3+(−OCH3), were studied and the derived rate constants (kOCH3, kcat3:Zn(OCH3) and kcatLa(OCH3)) correlated in various ways. The metal ion catalyzed reactions are very much faster than the background reactions in some cases reaching up to 7 × 106-fold acceleration when present at concentrations of 5 mmol dm−3. The data for both metals exhibit non-linear Brønsted correlations with the pKa of the leaving group which are analyzed in terms of a change in rate limiting step from formation to breakdown of a metal-coordinated tetrahedral intermediate as the pKa increases above values of ∼14.7. Plots of the log kOCH3 reaction vs. the log kcat values for each metal ion indicate low sensitivity for aryl esters and a higher sensitivity for the aliphatic esters. A mechanistic rationale for the observations is presented.
Introduction
Considering their importance to industrial processes and synthetic chemistry it is not surprising that considerable attention has been devoted to the synthesis of carboxylate esters via acid and base promoted pathways.1 Limited information is available concerning the mechanisms of action of catalysts developed to promote transesterification,2 although several examples of metal catalyzed transesterification have been reported3 and some important industrial applications are compiled in Parshall and Ittel's authoritative treatise.4In earlier studies we demonstrated that La3+![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 5a and Eu3+,5b introduced into methanol solution as their triflate or perchlorate salts along with one equivalent of NaOCH3, greatly accelerated the transesterification of both activated and non-activated esters. These metal ions have greatest activity as their monomethoxides, Ln3+(−OCH3)1, and general mechanisms were proposed consistent with the fact that the La3+ system reacts through dimeric forms (La3+2(−OCH3)2,3,4), while the Eu3+ system apparently reacts as a monomer (Eu3+(−OCH3)). One important general aspect of these reactions is revealed through comparison of the second order rate constants for Ln3+-catalyzed methanolysis with those for methoxide attack on a given ester (kcatester/kOMe−ester) which shows that the less activated esters are more susceptible to Ln3+ catalysis than the activated esters. For example, for the La3+-methoxide system the kcatester/kOMe−ester ratios for phenyl acetate, phenyl benzoate and ethyl acetate are 21, 8.9 and 2.5 respectively, while that ratio for 2,4-dinitrophenyl acetate is 0.07.5a In the case of Eu3+, the ratio is 4.3 for phenyl acetate, and 0.2 for p-nitrophenyl acetate.5b A second general aspect of the Ln3+-catalyzed systems is the rather spectacular rate enhancements seen for the methanolysis of esters in general, where the catalysis is 1–100million-fold relative to the background reaction in the presence of as little as 5 × 10−3 mol dm−3 of metal ion at near neutral sspH6 and ambient temperature. This belies the situation in water where intermolecular metal ion catalysis of hydrolysis of esters, particularly non-activated ones, is generally poor or non-existent, as opposed to intramolecular hydrolysis where the metal ion is held through binding to some group, close to the scissile C
5a and Eu3+,5b introduced into methanol solution as their triflate or perchlorate salts along with one equivalent of NaOCH3, greatly accelerated the transesterification of both activated and non-activated esters. These metal ions have greatest activity as their monomethoxides, Ln3+(−OCH3)1, and general mechanisms were proposed consistent with the fact that the La3+ system reacts through dimeric forms (La3+2(−OCH3)2,3,4), while the Eu3+ system apparently reacts as a monomer (Eu3+(−OCH3)). One important general aspect of these reactions is revealed through comparison of the second order rate constants for Ln3+-catalyzed methanolysis with those for methoxide attack on a given ester (kcatester/kOMe−ester) which shows that the less activated esters are more susceptible to Ln3+ catalysis than the activated esters. For example, for the La3+-methoxide system the kcatester/kOMe−ester ratios for phenyl acetate, phenyl benzoate and ethyl acetate are 21, 8.9 and 2.5 respectively, while that ratio for 2,4-dinitrophenyl acetate is 0.07.5a In the case of Eu3+, the ratio is 4.3 for phenyl acetate, and 0.2 for p-nitrophenyl acetate.5b A second general aspect of the Ln3+-catalyzed systems is the rather spectacular rate enhancements seen for the methanolysis of esters in general, where the catalysis is 1–100million-fold relative to the background reaction in the presence of as little as 5 × 10−3 mol dm−3 of metal ion at near neutral sspH6 and ambient temperature. This belies the situation in water where intermolecular metal ion catalysis of hydrolysis of esters, particularly non-activated ones, is generally poor or non-existent, as opposed to intramolecular hydrolysis where the metal ion is held through binding to some group, close to the scissile C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond. The origins of the rate enhancements we see in methanol are uncertain but could include stronger pre-equilibrium binding of the ester to the metal ion in the reduced polarity medium and greater nucleophilicity of the metal-coordinated methoxide to attack the transiently associated C
O bond. The origins of the rate enhancements we see in methanol are uncertain but could include stronger pre-equilibrium binding of the ester to the metal ion in the reduced polarity medium and greater nucleophilicity of the metal-coordinated methoxide to attack the transiently associated C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O unit. Clearly more work is needed to understand the origins, scope and limitations of Mx+-catalysis of transesterification.
O unit. Clearly more work is needed to understand the origins, scope and limitations of Mx+-catalysis of transesterification.
The metal catalyzed phosphoryl and acyl transfer reactions are not limited to lanthanides since we have shown that Zn2+ and Cu2+, either alone or preferably as complexes with various ligands, can promote both methanolysis of phosphate and carboxylate esters.7,8 In a recent study8 we investigated the methanolysis of some phosphate triesters such as paraoxon (1a) and fenitrothion (1b) promoted by Zn2+(−OCH3) and three of its complexes formed by association with phenanthroline (2a), 2,9-dimethylphenanthroline (2b, DMP) and 1,5,9-triazacyclododecane (3). Each of these complexes is capable also of accelerating the methanolysis of p-nitrophenyl acetate (PNPA) although the phenanthroline complexes form equilibrium distributions of inactive dimers (Phen : Zn2+ : −OCH3)2 which reduce the overall catalytic efficacy relative to the most active catalyst 3 : Zn2+ : −OCH3. A subsequent report9 has noted the problematic dimerization and suggested that Cu2+, complexed to 2,9-dimethylphenanthroline (DMP) which sterically suppresses the dimerization, is also capable of modestly promoting the methanolysis of some carboxylate esters. The Cu2+/DMP combination appears to be an unfortunate choice for metal promoted methanolysis given the known preference of that ligand for Cu+ and destabilization of the square-planar Cu2+.10 DMP does favour binding to the tetrahedral Zn2+ and gives good catalysis as the monomethoxide, but dimerization is still a problem.8 Building on our previous work on the methanolysis of phosphate esters promoted by transition metal ions7,8 we have chosen 3 : Zn2+(−OCH3)11 as a superior catalyst for the methanolysis of a series of carboxylate esters (4–15) having alcohol portions of varying leaving group ability. Herein we report the kinetic studies with the zinc complex 3 : Zn2+(−OCH3) and for comparison purposes those with (La3+(−OCH3))2.
Experimental
a. Materials
4-Chlorophenol (99+%), 3-nitrophenol (99%), 4-methoxyphenol (99%), 2,3,5-trimethylphenol, pentafluorophenol (99+%), 2,4-dimethylphenol (98%) and 2,6-dimethylphenol, 4-nitrophenol and 2,4-dinitrophenol were all acquired from Aldrich and used as received for syntheses of the corresponding esters. Acetic anhydride (98%) from Aldrich and NaOH pellets (98.8%, Fisher Scientific) were also used as received for the syntheses. Trifluoroethyl acetate, 97% (Lancaster), phenyl acetate (Aldrich) and isopropyl acetate, 99% (Aldrich) were used as received as substrates. Syntheses of the aryl esters followed the general procedure detailed in the literature,12 and in all cases gave products having 1H NMR and mass spectra consistent with the structures. Sodium methoxide, 0.5 mol dm−3 (Aldrich), as well as HCl, 0.02 mol dm−3 solution (standardized, Fisher Scientific), 1,5,9-triazacyclododecane, 97% (Aldrich) (12-3N), zinc triflate (Zn(OTf)2, 98%, Strem Chemicals) and La(OTf)3, 99.999% (Aldrich) were used as supplied.b. General UV/vis kinetics
Stock solutions (5 mmol dm−3) of each of the aryl esters were prepared in 99.8% anhydrous acetonitrile (Aldrich). For the Zn2+-catalyzed reactions, stock solutions of Zn(OTf)2 and ligand 3 were made in anhydrous methanol to 0.05 mol dm−3 and tetrabutylammonium hydroxide was diluted from 1.0 mol dm−3 (as supplied) to 0.05 mol dm−3 with dry MeOH. For each kinetic run, the catalyst was formulated in situ by adding known aliquots of Zn(OTf)2, ligand 3 and NBu4(OH), to methanol solvent such that the final volume was 2.5 ml. Since the final ratios of ligand, Zn2+ and −OCH3 were 1 : 1 : 0.5 the solution is self buffered at sspH = 9.1 corresponding to the sspKa of 3 : Zn2+(HOCH3).7,13 The kinetics were followed by monitoring the change in absorbance of 2 to 10 × 10−5 mol dm−3 of esters 4–11 at 276.9, 309, 330, 310, 283, 291, 274.6, 280 and 275.9 nm respectively. The Abs. vs. time data were fit to a standard first order exponential equation to obtain the pseudo-first order rate constants, kobs. The rates of the reaction were monitored at four to six different catalyst concentrations in duplicate ranging from 2.5 × 10−4 to 5.0 × 10−3 mol dm−3, and the gradients of the plots of kobsvs. [3 : Zn2+(−OCH3)] were taken as the second order rate constants (k2obs) for the catalyzed reaction, these rate constants being given in Table 1.| Ester | pKa of ArOH in MeOH | k OCH3/dm3 mol−1 s−1 | k cat 3:Zn(OCH3)/dm3 mol−1 s−1h | k cat La(OCH3)/dm3 mol−1 s−1i |
|---|---|---|---|---|
| a Determined as the sspH at half neutralization, this work. b From refs. 15,16,14. pKa for 12 calculated according to the method provided in ref. 14; pKaMeOH = 1.12pKaH2O + 3.56. c R. L. Schowen and K. S. Lathan, J. Am. Chem. Soc., 1967, 89, 4677. d Computed from pKaMeOH = 0.748pKaH2O + 6.53, see text. e From ref. 9. f From C. G. Milton, M. Gresser and R. L. Schowen, J. Am. Chem. Soc., 1969, 91, 2047. g Data from ref. 5a for methoxide and lanthanum reactions; lanthanum reactions determined at sspH = 8.86 for 7 and 10; values are computed from the gradient of the plot of kobsvs. [La3+]t. h Computed from the gradient of kobsvs. [3 : Zn2+(−OCH3)] plots at sspH 9.1 under self buffered conditions. i Computed from the gradient of kobsvs. [La3+] plots at sspH 8.74 under buffered conditions. | ||||
| 4 | 7.83b | 484.8 | 43.6 | 31 |
| 5 | 8.84a | 73.3 | 23.8 | 14.6 |
| 6 | 12.41b | 49.7 | 39.8 | 21.9 |
| 7 | 11.30b | 190e | 19.2 | 38.6g |
| 8 | 13.59b | 7.04 | 16.7 | 27.7 |
| 9 | 14.7c | 1.58 | 8.6 | 18.0 |
| 10 | 14.33b | 2.01(2.66)f | 13.9 | 29.33g |
| 11 | 15.04b | 0.63 | 4.28 | — |
| 12 | 15.36b | 0.49 | 4.30 | 4.33 |
| 13 | 15.78d | 12.64 | 3.00 | 10.0 |
| 14 | 18.42d | 0.057g | 0.042 | 0.071g |
| 15 | 19.79d | 0.007g | 0.006 | 0.004g |
| Methyl acetate | 18.13 | 0.17e | ||
The La3+-catalyzed reactions were monitored by UV/vis spectrophotometry under buffered (N-ethylmorpholine, 12 mmol dm−3) conditions at sspH 8.74 in the presence of 0.2 to 2.0 × 10−3 mol dm−3 La(OTf)3 as described in our earlier publications.5 The rates of methanolysis of 2 to 10 × 10−5 mol dm−3 solutions of esters 5, 6, 8, and 9 were monitored at 274.9, 335, 283 and 294 nm respectively to obtain the kobs pseudo-first order rate constants at each [La3+], and the gradients for the kobsvs. [La3+] plots were calculated to give the overall k2obs for La3+-catalyzed methanolysis which are given in Table 1. Also included in Table 1 are the reported rate constants for methanolysis of esters 4, 7 and 10 computed from kobsvs. [La3+] total data given in our previous paper.5a
The rates of methanolysis of 20 mmol dm−3 solutions of esters 13 and 14 in CD3OD were monitored at 25 °C by 1H NMR in the presence of 3 : Zn2+(−OCH3) (for ester 13) or La3+ plus one equivalent of NaOCH3 (for esters 13 and 14). The rates were determined though observation of both the rate of disappearance of the starting materials and rate of appearance of products, the pseudo-first order rate constant being evaluated from the exponential fits. The second order rate constants for catalysis were calculated as kobs/[catalyst] and are given in Table 1.
The rates of methanolysis promoted by −OCH3 in the absence of any metal ion were determined by UV/vis or 1H NMR as appropriate for a given ester: for the aryl esters the pseudo-first order rate constant for methanolysis were determined in duplicate at four different [−OCH3] ranging from 2.5 × 10−4 to 3.0 × 10−2 mol dm−3, lower [−OCH3] being used for the more reactive esters and higher [−OCH3] being used for the less reactive esters. The second order rate constants for these (kOCH3) were computed as the gradients of the kobsvs. [−OCH3] plots and are given in Table 1.
Results
Given in Table 1 are the second order rate constants for the transesterification reactions of esters 4–15 promoted by methoxide, 3 : Zn2+(−OCH3) and La3+(−OCH3). In all cases these were determined from the gradients of the plots of the pseudo-first order rate constants for methanolysis as a function of [methoxide] or [metal containing catalyst]. In the case of catalysis by 3 : Zn2+(−OCH3) the solutions were self-buffered at sspH 9.1 by adding half as much methoxide as the total added [3 : Zn2+], converting half of the latter to the active species. The La3+(−OCH3) reactions were buffered with 12 mmol dm−3N-ethyl morpholine at sspH 8.74. Also included in Table 1 are the sspKa values for the phenols from the literature or from measurements of the sspH at half neutralization. While sspKa values for most of the phenols are available14,15 or can be calculated from the methods given in references 14 and 16, the sspKa values for the aliphatic alcohols corresponding to esters 13–15 are not available, to our knowledge. We may calculate the values based on a linear regression approach similar to that used by Bosch et al. for correlating the acidities of carboxylic acids, phenols and ammonium ions in water and methanol.14 From the autoprotolysis constant of methanol (10−16.77 (mol dm−3)2)14,16 its sspKa can be computed as 18.13 on the mol dm−3 scale. As far as we know, the only other aliphatic alcohol for which a sspKa in methanol is available is hexafluoroisopropanol (sspKa = 13.4917vs. pKaH2O = 9.318), so that a linear regression (admittedly only on two data points) gives sspKa (MeOH) = 0.75pKa(H2O) + 6.53. The sspKa values for the aliphatic alcohols corresponding to 13–15 were computed from this regression line.In order to aid in visualizing trends in the data, Brønsted plots of the sspKa of phenols in methanol vs. the log second order rate constants for the methoxide, 3 : Zn2+(−OCH3) and La3+(−OCH3) catalyzed methanolysis of the esters are shown in Figs. 1, 2 and 3 respectively.
 | ||
| Fig. 1 Brønsted plots of pKa for phenol in methanol vs. log kOCH3 for the methoxide promoted methanolysis of aryl and aliphatic acetates, T = 25 °C. Dashed line of slope β = −0.656 ± 0.021 encompasses esters 6–12, while excluded data points (from the left) correspond to esters 4 and 5 respectively. Dotted line of slope β = −0.821 ± 0.044 corresponds to the three aliphatic esters 13–15 and methyl acetate. | ||
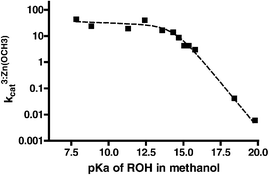 | ||
| Fig. 2 A Brønsted plot of log pKa phenol in methanol vs. log kcat3:Zn(OCH3) for methanolysis of aryl acetates promoted by 3 : Zn2+(OCH3), T = 25 °C. Dashed line corresponds to NLLSQ fit of data to eqn. (3) encompassing all esters with β1 = −0.023 ± 0.03 and β2 = −0.690 ± 0.005 with a breakpoint of pKaROH = 14.8 (see text). | ||
 | ||
| Fig. 3 A Brønsted plot of log pKa phenol in methanol vs. log kcatLa(OCH3) for methanolysis of aryl acetates promoted by La3+(−OCH3), T = 25 °C. Dashed line corresponds to NLLSQ fit of data to eqn. (3) encompasses all esters with values of β1 = 0.03 ± 0.005 and β2 = −0.715 ± 0.005 with a breakpoint of pKa = 14.7 (see text). | ||
The center part of the methoxide plot in Fig. 1 comprises seven phenols with sspKa values ranging from 11.17 to 15.04 providing a very good linear correlation with β = −0.656 ± 0.021, while the two left points for the pentafluoro and 2,4-dinitrophenyl acetates deviate markedly. The data for the aliphatic esters including methyl acetate for which the kOCH3 is reported elsewhere,9 appear to define a different line, the gradient of which is βaliphatic = −0.821 ± 0.044. Admittedly this correlation is somewhat contrived since it is based on sspKa values calculated from a linear regression of only two experimental data points. Nevertheless, it is consistent with the observation that the Brønsted plot for alkaline hydrolysis for aryl acetates vs. other acetate esters fits a similar two-line profile.19 The plots of the metal catalyzed reactions shown in Figs. 2 and 3 show definite evidence of a break where the rate constants are quite sensitive to phenols or alcohols with high sspKa values, but far less sensitive to the nature of the ROH groups with low sspKa values. In these cases there is no obvious discrepancy between aliphatic and aryl esters, so all esters are used for the subsequent treatment.
To compute the Brønsted dependences we assume that the overall metal-catalyzed processes follow eqns. (1) and (2) describing a fast pre-equilibrium binding followed by reversible creation of an intermediate, the formation and breakdown of which can be rate limiting depending on the nature of the leaving group. Steady state treatment gives the general relationship in eqn. (3) where the exponent pKa refers to the sspKa of the ROH or ArOH leaving group in methanol and the β terms correspond to the various binding and kinetic steps. Eqns. (4) and (5) correspond to limiting cases where formation and breakdown of the tetrahedral addition intermediate (CH3O-To- : Mx+) is rate limiting.
 | (1) |
 | (2) |
| kobs2 = Kbk1k2/(k−1 + k2) = CbC1C210(βb + β1 + β2)pKa/(C−110β − 1pKa + C210β2pKa) | (3) |
| kobs2 = Kbk1 = CbC110(βb + β1)pKa | (4) |
| kobs2 = Kbk1k2/k−1 = (CbC1C2/C−1)10(βb + β1 − β−1 + β2)pKa | (5) |
The dashed lines in Figs. 2 and 3 are computed from the NLLSQ fits of all the data to eqn. (3): in Fig. 2, (βb + β1) = −0.023 and (βb + β1 − β−1 + β2) = −0.710 with a breakpoint at sspKa = 14.8; in Fig. 3 (βb + β1) = −0.02 and (βb + β1 − β−1 + β2) = −0.710 with a breakpoint at pKa = 14.7.
Alternative presentations of the kinetic data are given in Figs. 4 and 5 which comprise two plots of log kOCH3vs. log kcat3:Zn(OCH3) and log kcatLa(OCH3) respectively. Following Kirsch and Jencks19 we assume that the mechanism of methoxide promoted methanolysis is similar enough for all the esters that the rate constant, kOCH3, can be used as an empirical measure of the composite effects of structural changes that incorporate both electronic and steric effects rather than using Hammett parameters or pKa values. This allows us to make a more common comparison of the effects of structural changes on the rates of methoxide and metal-promoted methoxide attack. For Zn2+, the Fig. 4 plot comprising all data fits a rather poor linear dependence (not shown) with slope = 0.73 ± 0.13 (r2 = 0.7865). Better linear relationships are drawn through the data representing the subset of aliphatic esters and aryl esters, and although there are only three aliphatic esters (13–15), the line for these is steeper than for the aryl esters (0.82 vs. 0.31). The La3+(−OCH3) vs. methoxide plot shown in Fig. 5 has a general appearance similar to that of the 3 : Zn2+(−OCH3) vs. methoxide data in Fig. 4, with an overall slope of 0.706 ± 0.117 (r2 = 0.820). While the overall correlation is not good, breaking the data into the aliphatic (esters 13–15) and aryl (esters 4–12) subsets gives two lines of quite different slopes, the aliphatic slope being greater than the aryl one by a factor of ∼5–6.
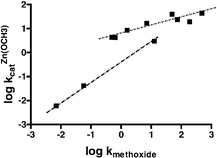 | ||
| Fig. 4 Plot of log kOCH3vs. log kcat3:Zn(OCH3) for the methoxide and 3 : Zn2+(−OCH3) catalyzed methanolysis of all acetyl esters, T = 25 °C. Lower dotted line comprises the aliphatic esters 13–15 with slope = 0.821 ± 0.030 (r2 = 0.9987), and upper dotted line comprises aryl esters 4–12, slope = 0.314 ± 0.055 (r2 = 0.8447). | ||
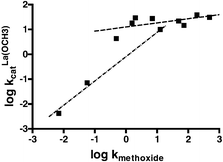 | ||
| Fig. 5 Plot of log kOCH3vs. log kcatLa(OCH3) for the methanolysis of all esters promoted by methoxide and La3+(−OCH3). Lower dashed line comprises aliphatic esters 13–15, slope = 0.914 ± 0.125 (r2 = 0.9817), while upper dotted line comprises aryl esters 4–12, slope = 0.16 ± 0.09 (r2 = 0.3607). | ||
Discussion
The various rate constants are presented in Table 1 along with their alcohol sspKa values in methanol where these are available or can be computed by literature methods from correlations with the aqueous pKa values.14 For the lanthanum methoxide promoted methanolysis the second order rate constant is determined as Δkobs/Δ[La3+] under buffered conditions at sspH 8.74 and is thus presented per La3+ ion, even though we have determined that the actual catalytic species are dimers (La3+)2(−OCH3)2,3,4 the relative importance of which depend on the sspH and the [dimer].20 The data in Table 1 reveal some interesting trends in the reactivities of the metal methoxides relative to methoxide itself. Within the aryl or aliphatic series the most activated esters toward methoxide attack, as expected, contain leaving groups with the lowest sspKa values for their corresponding alcohols, and in these cases (esters 4–7 of the aryl series and 13 of the aliphatic series) the kcat3:Zn(OCH3)/kOCH3 and kcatLa(OCH3)/kOCH3 ratios are generally less than 1. However, for the less activated esters one sees that the kcat3:Zn(OCH3)/kOCH3 and kcatLa(OCH3)/kOCH3 ratios are generally greater than unity. Although one normally anticipates that simple Brønsted considerations would make a metal-coordinated methoxide less nucleophilic than methoxide itself, in analogous hydrolyses catalyzed by metal ions this is generally interpreted to arise from a dual role for the metal ion in providing Lewis acid catalysis and delivering the Mx+-coordinated OH or OR nucleophile.21a. Uncatalyzed attack of methoxide
The plot of the log kOCH3 for methoxide-promoted methanolysis of the esters vs. the sspKa values shown in Fig. 1 provides a good linear correlation for the aryl esters except for the strongly electron withdrawing 2,4-dinitrophenyl and pentafluorophenyl derivatives which are less reactive than predicted on the basis of the sspKa data. Non-linear Hammett and Brønsted behaviours have been observed for the hydroxide-catalyzed hydrolysis of substituted aryl benzoates22 and acetates.23 Schowen24 has observed that the “ΔG‡ for methoxide promoted methanolysis of aryl acetates and carbonates in methanol are not linearly related to the ΔG° values for ionization of the corresponding phenols,” noting that “the rate process becomes less sensitive to the substituent as the electron-withdrawing power of the substituent increases”. The fall-off in the rate results from a greater importance of the resonance interaction in the equilibrium ionization processes (on which the Hammett and sspKa values are based) than in the kinetic processes where decidedly less charge development may have occurred in the rate-limiting TS.22–25 In the present study linear Brønsted behaviour (β = −0.66 ± 0.02)26 is observed for aryl esters with corresponding phenol sspKa values between 11 and 15 and for these it is probable that if the reaction is a two step one, the rate limiting step involves methoxide attack since expulsion of the leaving aryloxyl group from the anionic tetrahedral intermediate should be favoured over expulsion of the methoxide. Utilizing the ‘effective charge treatment’ described by Jencks et al.27 and Thea and Williams,28 the Brønsted β value suggests the process shown in Scheme 1 where the rate-limiting transition state has a nearly neutral aryloxy oxygen. The data are also consistent with a concerted mechanism with little cleavage of the OAr bond in the transition state, such as has been shown by Ba-Saif et al.29 for the displacement of the p-nitrophenoxy group from ester 7 by phenoxy nucleophiles.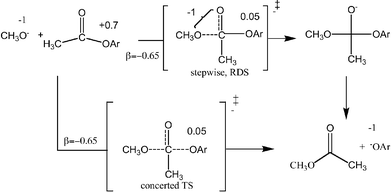 | ||
| Scheme 1 | ||
In the case of the aliphatic esters the Brønsted plot (including the literature rate constant for the kOCH3 of methyl acetate7) forms a reasonably straight line (slope = −0.821 ± 0.044) apparently separate from that for the aryl esters. Since there is only one experimental sspKa value available for a member of these four esters (methanol), we estimate the sspKa values from a linear regression relating pKa(MeOH) and pKa(H2O) which is based on the only two experimental aliphatic alcohol sspKa values in methanol of which we are aware. The sspKa values presented in Table 1 are based on this calculation and must be viewed only as estimates. Although the slope of the Brønsted line for the aliphatic esters is within experimental error of that for the aryl esters, it lies an order of magnitude higher suggesting a steric19 and perhaps electronic retardation for the aryl esters.
Methoxide attack on the aliphatic esters must go through anionic tetrahedral addition intermediates which, with equally good or poorer leaving groups than methoxide, must revert to starting materials in competition with breakdown to product, the relative amounts of which are controlled by the sspKa values of the ROH and the Brønsted β value for the k−1 and k2 steps. The Brønsted line for the four aliphatic esters shown in Fig. 1 appears to be a straight line with a slightly greater gradient than for the aryl esters, which might arise from that fact that the series encompasses cases where the rate limiting steps is k1 (13), a symmetrical case (methyl acetate) where the kobs is k1/2, and the case of isopropyl acetate where kobs = k1k2/(k−1 + k2) which, in addition to any steric hindrance to the attack of methoxide on 15, also might steepen the best fit line.
b. Catalysis by 3 : Zn2+(−OCH3) and La3+(−OCH3)
Shown in Figs. 2 and 3 are the log kcat3:Zn(OCH3) and log kcatLa(OCH3)vs.sspKa data for the methanolysis of the esters promoted by the two metal-methoxide complexes. Overall the leaving group acidity covers a range of >1011-fold while the kinetic data span a range of ∼5000-fold and 9000-fold respectively for the two metal ions. Each plot exhibits a pronounced break suggestive of at least a two-step process where formation and breakdown of some intermediate is rate-limiting. In both the cases, the descending and plateau β values are experimentally the same at −0.71 and ∼0 respectively with the breakpoint occurring at ∼sspKa = 14.7 such that he plateau region covers roughly 106-fold change in acidity of the leaving group with virtually no change in catalyzed rate constant.The Fig. 2 and 3 data are analyzed according to the processes given in eqns. (1) and (2) which give rise to the steady state expression in eqn. (3) which contains both the Mx+ + ester equilibrium binding constant (Kb) and the various rate constants for intramolecular formation and breakdown of the tetrahedral intermediate. Unlike the case where simple methoxide addition to the esters forms a highly unstable, and perhaps kinetically unstable (in the case of aryl esters)29 anionic intermediate (16), the Mx+–−OCH3 catalyzed process forms a Mx+-stabilized tetrahedral intermediate with a significant lifetime (17-To-Mx+) which can partition to starting materials and products depending on the relative transition state energies corresponding to k−1and k2 (Scheme 2).
 | ||
| Scheme 2 | ||
Since addition of methoxide to the ester is metal-ion assisted, microscopic reversibility considerations require that the departure of poor leaving groups (with high sspKa values for the corresponding alcohols) such as ethoxy or isopropoxy must also be metal ion assisted suggesting that the k2 step must be partially or entirely rate-limiting and eqn. (5) applies. As the sspKa decreases, eventually the leaving group is sufficiently good that it departs without metal-ion assistance and the rate-limiting step for the reaction must change from breakdown to formation of the intermediate, in both these cases when the sspKa is about 14.7.
It is curious that in the plateau region, where the leaving groups are good and formation of the intermediate is rate-limiting, that the computed Brønsted β is ∼0, signifying little or no dependence on the nature of the leaving group. We rationalize this observation within the framework of the limiting case of eqn. (4) where formation of the intermediate depends on the counterbalancing effects of changes in the leaving group on both the Kb and k1 steps, i.e.
(βb
+
β1)
→ 0. This situation is strongly reminiscent of the known insensitivity of the rates of acid-catalyzed hydrolysis of esters to changes in the nature of the leaving group (ρ
= 0) which Taft30 interpreted as resulting from a counterbalancing of the alkoxy/aryloxy substituent's electronic effect on protonation equilibrium and subsequent nucleophilic step of attack of water on the protonated C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O.
O.
The descending wings of Figs. 2 and 3 have strong dependence on the nature of the leaving group β = −0.71 which, when analyzed within the framework of eqn. (5), is consistent with a significant cleavage of the C–OR bond in the TS. Since the net effect of the substituent ion Kb and k1 steps cancel, this leads to the conclusion that the sum of (−β−1 + β2) is significantly negative.
c. Comparision of kOCH3 and kcat3:Zn(OCH3) or kcatLa(OCH3)
Presentation of the rate constant data as in Figs. 4 and 5 has some advantages over the customary Brønsted or Hammett plots since the latter rely on substituent induced changes to equilibrium pKa processes which may not be appropriate for how a substituent influences a particular reaction where the rate-limiting step(s) have little charge development on the departing OR. Comparison of log kOCH3vs. log kcat3:Zn(OCH3) or log kOCH3vs. log kcatLa(OCH3) allows one to assess how the rates for two reactions depend both on steric and electronic influences of the substituents and a break in such a plot requires that the substituents influence the two reactions in different ways. An additional benefit is that this treatment does not rely on experimental or estimated sspKa values for a given substituent which, if in error, may influence the conclusions based on the slopes of Brønsted plots.The plots in Figs. 4 and 5 are visually similar suggesting that both La and Zn catalysis respond to structural variations in a similar way relative to the methoxide reaction. Both plots show a break surrounded by an ascending domain encompassing the aliphatic alcohols 14 and 15, followed by a less sensitive domain encompassing the aryl esters. While one could analyze the entire series within a common relationship, another approach is to consider that there are two families encompassing the aryl and aliphatic esters. The dashed lines drawn on the figures are linear fits for the two classes and for both metal ions indicate that the aliphatic esters have a greater sensitivity for the metal-methoxide reactions than do the aryl esters, probably because the aliphatic line includes two members with poor leaving groups. The methoxide and metal-methoxide reactions are related mechanistically in that esters containing poor leaving groups such as methoxide, ethoxide and isopropoxide must go through two step processes in each case with reversibly-formed tetrahedral intermediates (To-) as shown in eqns. (6) and (1), (2) respectively.
 | (6) |
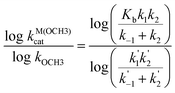 | (7) |
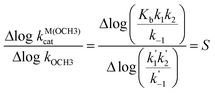 | (8) |
 | (9) |
A third way of correlating the data is presented in Fig. 6 as a plot of log kcat3:Zn(OCH3)vs. log kcatLa(OCH3). In this case, the data form a straight line with a slope of nearly unity (0.997 ± 0.071; r2 = 0.9529). The unit slope, with no break, indicates that the substituents influence both metal-methoxide reactions in the same way.
 | ||
| Fig. 6 A plot of the log kcat3:Zn(OCH3)vs. log kcatLa(OCH3) values for methanolysis of all esters promoted by 3 : Zn2+(−OCH3) and La3+(−OCH3), T = 25 °C. Dashed line represents linear regression for all data, slope = 0.997 ± 0.071 (r2 = 0.9529). | ||
Conclusions
The above study shows that the methanolysis of both aryl and aliphatic esters is greatly accelerated by the two catalytic systems described above. In the case of La3+, we have found that the catalytic entities are dimers with 2, 3 or 4 associated methoxides which are spontaneously formed in solution at the concentrations employed without the requirement of added ligands. However, transition metal ions such as Zn2+ or Cu2+ require added ligands to prevent the deleterious formation of dimers and oligomers, the latter being inactive relative to the monomeric forms. Our studies show that 1,5,9-triazacyclododecane is an optimal ligand for use with Zn2+ although phenanthroline and 2,9-dimethyl phenanthroline (DMP) can also provide catalytically active complexes despite the partial formation of dimers under these conditions.7 As little as 5 mmol dm−3 added La3+ with equimolar methoxide accelerates the methanolysis of phenyl acetate (10) by 7.8 × 106-fold relative to the background methoxide reaction at the near neutral of 8.7. The 3 : Zn2+(−OCH3) catalyst, when present at 5 mmol dm−3, accelerates the methanolysis of phenyl acetate by 1.6 × 106-fold relative to the background methoxide reaction at sspH 9.1. We observe that the best accelerations relative to the background reactions occur with less activated esters, and in many of these cases, the kcat3:Zn(OCH3)/kOCH3 or kcatLa(OCH3)/kOCH3 ratios are greater than unity.It is important to compare the efficacy of our catalytic systems to those of the Cu2+ : DMP methanolysis system9 and the 3 : Zn2+(−OH) hydrolytic system.13 The relevant data are presented in Table 2 in which it is seen that the rate constants exhibited by the lanthanum and zinc systems for the methanolysis of phenyl acetate (10) and p-nitrophenyl acetate (7) are between 660 and1400-fold larger than for the Cu2+ : DMP system and that their catalysis of ethyl acetate methanolysis is at least 100-fold larger (bearing in mind that for the latter the available comparison data are for reaction with a more reactive methyl acetate while the La3+ and Zn2+ catalysts refer to the methanolysis of ethyl acetate). A second point of note is that the La3+ and Zn2+ catalysts have second order rate constants comparable to the rate constant of methoxide attack in methanol, while the Cu2+ : DMP and 3 : Zn2+(−OH) systems are at least 100-fold (and several thousand-fold in the case of methanolysis of p-nitrophenyl acetate) less reactive than methoxide or hydroxide respectively for a given ester. Interestingly, where a comparison can be made between the second order rate constants for hydrolysis and methanolysis promoted by 3 : Zn2+(−OH) or 3 : Zn2+(−OCH3) respectively, the methanolysis reactions are about 1000-fold faster than the hydrolysis reactions with the aryl esters, and somewhat less for the aliphatic esters, again bearing in mind that the hydrolysis data are with methyl acetate and the methanolysis is with ethyl acetate.
| Substrate | |||
|---|---|---|---|
| Phenyl acetate | p-Nitrophenyl acetate | ROC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) OCH3 OCH3 |
|
| Catalyst | k2/dm3 mol−1 s−1 | k 2/dm3 mol−1 s−1 | k 2/dm3 mol−1 s−1 |
| a This work. b Ref. 9. c Computed from data given in ref. 11. d Computed from data given in Ref. 13 for reaction at pH 8.1. e From ref. 19. | |||
| La3+(−OCH3)a | 29.3 | 38.6 | 7.1 × 10−2 (R = Et) |
| 3 : Zn2+(−OCH3)a | 13.9 | 19.2 | 4.2 × 10−2 (R = Et) |
| −OCH3 (in methanol)a | 2.01 | 190b | 5.7 × 10−2 (R = Et) |
| Cu2+ : DMPb | 1.6 × 10−2 | 2.9 × 10−2 | 4.2 × 10−4 (R = Me) |
| 3 : Zn2+(−OH) (in water) | 1.5 × 10−2c | 4.9 × 10−2d | ∼4 × 10−4 (R = Me) |
| −OH (in water) | 1.26e | 9.5e | 1.1 × 10−1 (R = Et)e |
The fact that La3+ and Zn2+ systems react with many of the esters faster than does methoxide gives some clue to the mechanism of reaction. The available data are consistent with a mechanism of catalysis that involves a pre-equilibrium binding of the metal-methoxide complex with the ester followed by an internal delivery of the methoxide via a five-coordinate transition state to form an anionic tetrahedral addition intermediate stabilized by a four coordinate Zn2+. This is analogous to the general mechanism that is widely proposed for metal-ion catalyzed hydrolyses, but is kinetically equivalent to a process where an external nucleophilic hydroxide or methoxide attacks the Mx+-coordinated ester.32 It is particularly interesting that, where direct comparison can be made with the 3 : Zn2+(−OH) system in promoting the hydrolysis of these esters in water, the corresponding methanolysis promoted by 3 : Zn2+(−OCH3) is at least two to three orders of magnitude larger. The likely origins of the rate enhancements are an increased pre-equilibrium binding of the substrate, and a less solvated nucleophile attacking the Zn2+-coordinated C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O unit.
O unit.
Acknowledgements
The authors gratefully acknowledge the financial assistance of the Natural Sciences and Engineering Research Council of Canada, Queen's University and the United States Department of the Army, Army Research Office, Grant No. W911NF-04-1-0057.33 N. E. S. thanks NSERC for the award of a Summer Student Research Award. Finally, the authors thank Prof. Andrew Williams and Prof. Elisabeth Bosch for very helpful discussions concerning various aspects of this work.Notes and references
- (a) J. Koskikallio, in The Chemistry of Carboxylic Acids and Esters, ed. S. Patai, John Wiley and Sons, New York, 1969, pp. 103–136 Search PubMed; (b) M. A. Ogliaruso and J. A. Wolfe, Synthesis of Carboxylic Acids, Esters and Their Derivatives, ed. S. Patai and Z. Rappoport, John Wiley and Sons, Chichester, 1991, pp. 465–476 Search PubMed.
- (a) J. March, Advanced Organic Chemistry: Reactions, Mechanisms and Structure, 4th edn., John Wiley and Sons, New York, 1992, pp. 397–398 and references therein Search PubMed; (b) M. G. Stanton, C. B. Allen, R. M. Kissling, A. L. Linclon and M. R. Gagné, J. Am. Chem. Soc., 1998, 120, 5981 CrossRef CAS and references therein; (c) R. M. Kissling and M. R. Gagné, J. Org. Chem., 2001, 66, 9005 CrossRef CAS.
- (a) T. Okano, K. Miyamoto and J. Kiji, Chem. Lett., 1995, 246 Search PubMed; (b) P. Dutta, A. Sarkar and B. C. Ranu, J. Org. Chem., 1998, 63, 6027 CrossRef CAS; (c) L. Baldini, C. Bracchini, R. Cacciapaglia, A. Casnati, L. Mandolini and R. Ungaro, Chem. Eur. J., 2000, 6, 1322 CrossRef CAS; (d) R. Cacciapaglia, S. Di Stephano, E. Kelderman and L. Mandolini, Angew. Chem., Int. Ed., 1999, 38, 349 CrossRef; (e) W. M. Stevels, M. J. K. Ankoné, P. J. Dijkstra and J. Feijen, Macromolecules, 1996, 29, 8296 CrossRef CAS; (f) N. J. Hinde and C. D. Hall, J. Chem. Soc., Perkin Trans. 2, 1998, 1249 RSC and references therein; (g) J. Otton, S. Ratton, V. A. Vasnev, G. D. Markova, K. M. Nametov, V. I. Bakhmutov, L. I. Komarova, S. V. Vinogradova and V. V. Korshak, J. Polym. Sci. Part A Polym. Chem., 1998, 26, 2199 CrossRef; (h) R. Cacciapaglia, S. Di Stephano and L. Mandolini, J. Org. Chem., 2001, 66, 5926 CrossRef CAS.
- G. W. Parshall and S. D. Ittel, Homogeneous Catalysis. The Applications and Chemistry of Catalysis by Soluble Transition Metal Complexes, 2nd edn., Wiley-Interscience, New York, 1992, pp. 269–296 Search PubMed.
- (a) A. A. Neverov, T. McDonald, G. Gibson and R. S. Brown, Can. J. Chem., 2001, 79, 1704 CrossRef CAS; (b) A. A. Neverov, G. Gibson and R. S. Brown, Inorg. Chem., 2003, 42, 228 CrossRef CAS.
- For the designation of pH in non-aqueous solvents we use the recommendations of the IUPAC Compendium of Analytical Nomenclature. Definitive Rules 1997, 3rd edn., Blackwell, Oxford, UK, 1998 Search PubMed. If one calibrates the measuring electrode with aqueous buffers and then measures the pH of an aqueous buffer solution, the term wwpH is used; if the electrode is calibrated in water and the ‘pH’ of the neat buffered methanol solution then measured, the term swpH is used, and if the electrode is calibrated in the same solvent and the ‘pH’ reading is made, then the term sspH is used.
- W. Desloges, A. A. Neverov and R. S. Brown, Inorg. Chem., 2004, 43, 6752 CrossRef CAS.
- A. A. Neverov and R. S. Brown, Org. Biomol. Chem., 2004, 2, 2245 RSC.
- R. Cacciapaglia, S. Di Stephano, F. Fahrenkrug, U. Lüning and L. Mandolini, J. Phys. Org. Chem., 2004, 17, 350 CrossRef CAS.
- (a) S. Kitagawa, M. Munakata and A. Higashie, Inorg. Chim. Acta, 1884, 84, 79 Search PubMed; (b) A. Paulovicova, U. El-Ayanan and Y. Fukuda, Inorg. Chim. Acta, 2001, 321, 56 CrossRef CAS; (c) electrospray MS measurements on methanolic solutions containing equimolar amounts of CuCl2 and dimethylphenanthroline (DMP) indicate the presence of monovalent copper as Cu+ : DMP whereas the electrospray MS of CuCl2 in the presence of the less sterically encumbered phenanthroline parent shows only divalent copper complexes, consistent with the well-known destabilizing effects of DMP on square planar, square pyramidal and octahedral coordinate complexes and a stabilizing effect on tetrahedral or pseudo tetrahedral coordination geometries10a,b.
- The corresponding 3 : Zn2+ : −OH species, which was first reported as a model for carbonic anhydrase,13 has been investigated as to its ability to catalyze the hydrolysis of aryl esters; J. Suh, S. J. Son and M. P. Suh, Inorg. Chem., 1998, 37, 4872 Search PubMed.
- R. A. Joshi, M. K. Gurjar, N. K. Tripathy and M. S. Chorghade, Org. Process Res. Dev., 2001, 5, 176 Search PubMed.
- E. Kimura, T. Shiota, T. Kooike, M. M. Shiro and M. Kodama, J. Am. Chem. Soc., 1990, 112, 5805 CrossRef CAS report that the pKa for the aquo form of 4 : Zn2+(H2O) is 8.4.
- F. Rived, M. Rosés and E. Bosch, Anal. Chim. Acta, 1998, 374, 309 CrossRef CAS.
- (a) V. A. Palm, Tables of Rate and Equilibrium Constants of Heterocyclic Reactions, Vol. 1 (1), Proizbodstvenno-Izdatelckii Kombinat Biniti, Moscow, 1975 Search PubMed; (b) V. A. Palm, Tables of Rate and Equilibrium Constants of Heterocyclic Reactions, Suppl. Vol. 1, issue 3, Tartuskii gosudarsvennii Universitet, Tartu, 1985 Search PubMed.
- E. Bosch, F. Rived, M. Rosés and J. Sales, J. Chem. Soc., Perkin Trans. 2, 1999, 1953 RSC.
- J. Lu, Ph. D. Dissertation, The University of Western Ontario: London, Ontario, Canada, 1994, p. 228.
- B. Blesniewski, Z. Przybyszewski and Z. Paulak, J. Chem. Soc., Faraday Trans. 1, 1984, 80, 1769 RSC.
- J. F. Kirsch and W. P. Jencks, J. Am. Chem. Soc., 1964, 86, 837 CrossRef CAS.
- (a) G. T. T. Gibson, A. A. Neverov and R. S. Brown, Can. J. Chem., 2003, 81, 495 CrossRef CAS; (b) J. S. Tsang, A. A. Neverov and R. S. Brown, J. Am. Chem. Soc., 2003, 125, 7602 CrossRef CAS; (c) J. S. W. Tsang, A. A. Neverov and R. S. Brown, Org. Biomol. Chem., 2004 10.1039/b412132e; (d) we have determined that the maximal activity for the La3+ catalyzed methanolysis of esters and phosphates lies in the sspH region between 8.7–9.1, where 95% of the activity is attributed to La3+2(−OCH3)2. Thus, the conditional observed k2La(OCH3) rate constant reported in Table 1 is ∼1/2 of the k2 of the La3+2(−OCH3)2 active form.
- The rationale for this is presented in ref. 8 above, and references 3 and 4 of that publication.
- (a) Z. S. Chaw, A. Fischer and D. A. R. Happer, J. Chem. Soc. (B), 1971, 1818 RSC; (b) J. Kirsch, A. Clewell and A. Simon, J. Org. Chem., 1968, 33, 127 CrossRef CAS; (c) A. A. Humffray and J. J. Ryan, J. Chem. Soc. (B), 1967, 468 RSC.
- (a) J. J. Ryan and A. A. Humffray, J. Chem. Soc. (B), 1966, 842 RSC; (b) T. C. Bruice and M. Mayahi, J. Am. Chem. Soc., 1960, 82, 3067 CrossRef CAS; (c) J. F. Kirsch and W. P. Jencks, J. Am. Chem. Soc., 1964, 86, 837 CrossRef CAS.
- C. G. Mitton, R. L. Schowen, M. Gresser and J. Shapley, J. Am. Chem. Soc., 1969, 91, 2036 CrossRef CAS.
- We thank Professor Andrew Williams for helpful discussions on this point.
- Using the available data23 for the −OH-catalyzed hydrolysis of aryl, the Brønsted β is computed to be ∼−0.6 for aryl groups which do not contain strongly withdrawing resonators.
- (a) W. P. Jencks and M. Gilchrist, J. Am. Chem. Soc., 1968, 90, 2622 CrossRef CAS; (b) D. J. Hupe and W. P. Jencks, J. Am. Chem. Soc., 1977, 99, 451 CrossRef CAS; (c) J. M. Sayer and W. P. Jencks, J. Am. Chem. Soc., 1977, 99, 464 CrossRef CAS; (d) M. J. Gresser and W. P. Jencks, J. Am. Chem. Soc., 1977, 99, 6963 CrossRef CAS.
- (a) S. Thea and A. Williams, Chem. Soc. Rev., 1986, 15, 125 RSC; (b) A. Williams, Acc. Chem. Res., 1984, 17, 425 CrossRef CAS.
- S. Ba-Saif, A. K. Luthra and A. Williams, J. Am. Chem. Soc., 1987, 109, 6362 CrossRef CAS.
- (a) R. W. Taft, Jr., J. Am. Chem. Soc., 1952, 74, 2729 CrossRef CAS , 3120; (b) R. W. Taft, Jr., J. Am. Chem. Soc., 1053, 75, 4231 Search PubMed.
- Given that the rate-limiting step for the methoxide reaction throughout most, if not all of the series of esters is k1 we can probably replace the denominator in eqn. (8) with Δlog(k′1). In this case the difference in the slopes derived by application of eqn. (8) and (9) stems from the substituent on the k2/k1 partitioning constant in the metal catalyzed reactions.
- Suh et al.11 have proposed the 3 : Zn2+ complex promotes the hydrolysis of aryl esters via C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O corordination followed by external attack of methoxide, while Kimura et al.13 have proposed that the active species is really 3 : Zn2+(−OH). In the present cases, although we favour the internal delivery mechanism, the available pseudo-first order rate constants for the primary kinetic data, along with consideration of reasonable estimates of the pre-equilibrium binding constant and a diffusion limited rate constant for eternal methoxide attack of 1010 dm3 mol−1 s−1 do not allow us to rule out external methoxide attack.
O corordination followed by external attack of methoxide, while Kimura et al.13 have proposed that the active species is really 3 : Zn2+(−OH). In the present cases, although we favour the internal delivery mechanism, the available pseudo-first order rate constants for the primary kinetic data, along with consideration of reasonable estimates of the pre-equilibrium binding constant and a diffusion limited rate constant for eternal methoxide attack of 1010 dm3 mol−1 s−1 do not allow us to rule out external methoxide attack. - The content of the information does not necessarily reflect the position or the policy of the federal government, and no official endorsement should be inferred.
| This journal is © The Royal Society of Chemistry 2005 |



