View PDF VersionPrevious ArticleNext Article
 
DOI: 10.1039/B412294A (Paper) Org. Biomol. Chem., 2005, 3, 39-47

Conformational analysis of oleandomycin and its 8-methylene-9-oxime derivative by NMR and molecular modelling†

Predrag Novak *a, Zrinka Banić Tomišić *a, Predrag Tepeš a, Gorjana Lazarevski a, Janez Plavec b and Gordana Turkalj a
aPLIVA–RESEARCH INSTITUTE Ltd., Prilaz baruna Filipovića 29, HR-10000, Zagreb, Croatia. E-mail: predrag.novak@pliva.hr; zrinka.banic-tomisic@pliva.hr
bNational Institute of Chemistry, Hajdrihova 19, SI-1115, Ljubljana, Slovenia

Received 10th August 2004 , Accepted 12th October 2004

First published on 15th November 2004

Abstract

Conformations of the 14-membered macrolide antibiotic oleandomycin and its 8-methylene-9-oxime derivative were determined in various solvents. The experimental NMR data—coupling constants and NOE contacts—were compared with the results of molecular modelling—molecular mechanics calculations and molecular dynamics simulations. The conformational changes, on the right-hand side of the 14-membered ring, affected mostly the 3JH2,H3 values and NOE crosspeaks H3 or H4 to H11. Oleandomycin was found to be present predominantly in the C3–C5 folded-in conformations in DMSO-d6 solution, whereas in buffered D2O, acetone-d6 and CDCl3, there was a mixture of folded-in and folded-out conformational families. The predominant conformation of the 8-methylene-oleandomycin-9-oxime derivative in solution was a folded-out one although different amounts of folded-in conformation were also present depending on the solvent. Oleandrose and desosamine sugar moieties adopted the usual and expected chair conformation. The conformation around the glycosidic bonds, governing the relative orientation of sugars vs. the lactone ring, showed a certain flexibility within two conformationally close families. We believe that by combining the experimental NMR data and the molecular modelling techniques, as reported in this paper, we have made significant progress in understanding the conformational behaviour and properties of macrolides. Our belief is based on our own current studies on oleandomycins as well as on the previously reported results and best practices concerning other macrolides. A rational for macrolide conformational studies and advances in methodology has been suggested accordingly.

Introduction

Oleandomycin11 (Scheme 1) is a macrolide antibiotic composed of a polyfunctionalized 14-membered ring with oleandrose and desosamine sugar units. The exocyclic epoxide at C8 of 1 is taken to be a unique feature, without equal in any other known polyoxo macrolide. Reductive deoxygenation of C8 epoxide generated 8-methylene oleandomycin which, after treatment with hydroxylamine, gave an 8-methylene-9-oxime derivative22 (Scheme 1). A literature search has shown a lack of information concerning the conformational characteristics of oleandomycin and oleandomycin-like compounds except for four X-ray structures,3–6 three of which (1a,326 and 3,5Scheme 1) are available through the Cambridge Structural Database7 (CSD). The conformational behaviour of the related macrolide antibiotics such as erythromycin A, roxithromycin, clarithromycin, and azithromycin has been studied intensively8–15 by NMR and molecular modelling methods and by single-crystal X-ray analysis. Recently, data on the 3D structure of macrolide–ribosome complexes16–17 have once again demonstrated the importance of conformation and shape of the molecule with respect to its biological activity. Conformational analysis therefore plays an important role in the rational design of molecules with an improved biological profile.
Studied compounds.
Scheme 1 Studied compounds.

Conformational studies on other macrolides8–15 have demonstrated the existence of two major conformational families: folded-out and folded-in, referring to the outward and inward folding of the ring fragment C3–C5 (Scheme 1). The folded-out conformers have larger homonuclear 3JH2,H3 values (∼10 Hz), larger torsion angles between atoms H2 and H3 (∼±180 °) and exhibit a close space approach of protons H4 and H11, giving rise to nuclear Overhauser enhancement (NOE) crosspeaks. Much lower 3JH2,H3 values (∼2–3 Hz), lower torsion angles (∼100°) and a close space approach of atoms H3 and H11 with the corresponding NOE crosspeaks are characteristic of the folded-in conformers.8,11,14

To assess the conformational properties of oleandomycin-like compounds in solution we carried out a detailed NMR study of oleandomycin 1 (Scheme 1) and its derivative 8-methylene-oleandomycin-9-oxime 2 (Scheme 1).

Complete unambiguous assignment of 1H and 13C NMR spectra was necessary before performing conformational analysis.2,18. The information about the torsion angles, defining the conformation, was obtained from the vicinal spin–spin coupling constant data and the information about proton–proton spatial proximity was derived from the NOE data. Variable solvent and temperature experiments were performed to check the conformational flexibility and stability of the investigated molecules. Crystal structure conformations3,5,6 being unable to account for all the NMR data of 1 and 2, molecular mechanics calculations and unconstrained molecular dynamics simulations were applied for modelling the solution state conformations. The calculated molecular dynamics trajectories were searched for the conformers consistent with the experimental NMR data. The modelled solution state conformations were compared to the solid-state conformations retrieved from the Cambridge Structural Database7 and to the conformations of related macrolides in corresponding solvents.

Results and discussion

Assignments

The complete 1H and 13C atom reassignments were made on the basis of the combined use of several one- (1H and APT sequences) and two-dimensional homo- and heteronuclear experiments (COSY, HSQC and HMBC sequences). The 1H and 13C chemical shift values in CDCl3 were in general agreement with those reported previously.2,18 The values for other solvents (DMSO-d6, acetone-d6, D2O buffer) were in accordance with those obtained in CDCl3 (data deposited as electronic supplementary information†).

Vicinal coupling constants

To assess the conformational behaviour of the 14-membered macrocycle and two sugar units, oleandrose and desosamine, in compounds 1 and 2, we measured vicinal proton–proton 3JH,H coupling constants in various solvents as well as carbon–proton 3JC,H coupling constants around the glycosidic bonds. Some homonuclear coupling constants could not be determined even at high temperatures due to severe peak overlapping.

Change of solvent caused major alterations only in 3JH2,H3 values (Table 1). Unlike azithromycin,14 the two compounds failed to demonstrate a recognizable trend in the change of 3JH2,H3 coupling constant with the change of solvent polarity. According to 3JH2,H3 values (Table 1) the folded-out conformation seems to be predominant for compound 2 in all four solvents. Compound 1 tends to adopt predominantly the folded-out conformation in D2O buffer, acetone-d6 and CDCl3 and the folded-in conformation in DMSO-d6.

Table 1 Experimental vicinal proton–proton coupling constants 3JH,H/Hz for the macrocycle of compounds 1 and 2 in different solvents
  1 2
Protons D2O DMSO-d6 Acetone-d6 CDCl3 D2O DMSO-d6 Acetone-d6 CDCl3
a Unresolved. b Signal overlap.
H2,H3 7.3 3.9 6.5 8.4 9.4 8.0 7.0 7.9
H3,H4 1.5 1.5 1.4 a 1.3 1.0 1.6 1.0
H4,H5 7.4 b 7.1 7.2 10.2 10.3 9.8 10.7
H5,H6 1.7 a 1.9 2.1 a a 1.2 a
H6,H7a a a a a a a a a
H6,H7b b b 10.1 9.6 9.8 9.8 b 10.3
H10,H11 1.5 2.1 2.0 1.5 1.5 1.5 1.6 1.5
H11,H12 9.8 9.5 8.8 10.5 10.3 b b 10.1
H12,H13 1.4 2.0 1.8 1.3 1.1 1.0 1.3 1.2
H1′,H2′ 7.0 7.3 7.2 7.2 7.0 7.2 7.2 7.1
H2′,H3′ b 10.1 10.2 10.2 10.2 10.2 10.1 10.3
H3′,H4a 4.1 b 3.9 3.8 4.1 3.8 4.0 3.8
H3′,H4b b b b b b b b 9.8
H4′a,H5′ 1.9 1.8 1.9 b 1.9 2.0 2.1 1.9
H4′b,H5′ b 10.7 10.9 b 9.3 10.8 b 10.9
H1″,H2″a 1.2 1.2 1.4 1.4 1.5 1.4 1.4 1.3
H1″,H2″b 3.1 b 3.7 3.3 3.4 3.9 3.9 3.8
H2″a,H3″ 4.9 4.7 4.7 4.5 4.7 4.5 4.7 4.4
H2″b,H3″ b 11.7 11.6 11.6 b b 11.6 12.7
H3″,H4″ 9.5 9.3 9.0 9.0 9.3 9.0 9.1 9.1
H4″,H5″ 9.4 9.3 9.3 9.0 9.4 9.2 9.2 9.3

With a mixture of conformers present in solution, a temperature dependence of their relative populations and, accordingly, of the coupling constant values, can be assumed. In both compounds increasing the temperature in DMSO-d6 and buffered D2O up to 100 °C had an effect only on the value of 3JH2,H3 coupling. The coupling constant moderately decreased (Table 2) in buffered D2O and DMSO-d6 solution for 2 suggesting an increased abundance of the folded-in conformer in the mixture. For compound 1 the 3JH2,H3 value did not follow the change in temperature in buffered D2O (Table 2). This may have been due to the existence of a third stable conformer (3JH2,H3 ∼ 7 Hz) or to a temperature independent equilibrium between the two conformers. In DMSO-d6, the 3JH2,H3 value for 1 was temperature dependent and it increased with increasing temperature (Table 2) suggesting a change of conformation from the folded-in to the folded-out.

Table 2 Temperature effects on 3JH2,H3/Hz in buffered D2O and DMSO-d6 for compounds 1 and 2
  1 2
Temperature/°C DMSO-d6 D2O DMSO-d6 D2O
27 3.8 7.3 8.0 9.4
40 4.0 7.3 overlap 9.2
50 4.0 7.3 7.3 9.1
60 4.2 7.4 7.1 8.9
80 4.5 7.3 6.8 8.3
100 4.7 — 6.5 —

Heteronuclear 3JC,H coupling constants over the glycosidic bonds in 1 and 2 were obtained from multi-site selective one-dimensional experiments using Hadamard formalism19,20 (Fig. 1). The sensitivity was improved by performing four simultaneous experiments coded according to the Hadamard matrix and later separated by reference to the same matrix. The selective excitation of the macrocycle carbons C3 and C5 and sugar carbons C1′ and C1″ led to the determination of the 3JC,H values listed in Table 3. These are important for identifying the positions and mobility of the sugar moieties with respect to the lactone ring. The values of 3JC,H couplings over the glycosidic bonds in 1 and 2 are within the range of those measured for erythromycin,21 roxythromycin,21 clarithromycin21 and our recently measured data for azithromycin (Table 3), the differences, however, suggest the general conformational flexibility over both glycosidic bonds.


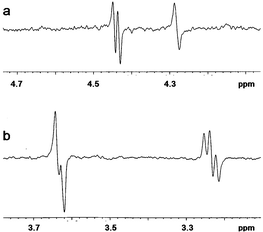Proton spectra of 1 after selective excitation of (a) C5 and (b) C1′ carbons involved in glycosidic linkage according to the Hadamard formalism.
Fig. 1 Proton spectra of 1 after selective excitation of (a) C5 and (b) C1′ carbons involved in glycosidic linkage according to the Hadamard formalism.
Table 3 Comparison of the vicinal carbon–proton coupling constants (3JC,H/Hz) over the glycosidic bond obtained from the NMR experiment for compounds 1, 2 and related macrolides21 and the ones calculated from the X-ray (CSD7) torsion angles (Φ/°) for compounds 1a, 2 and 3 (solution vs. solid state conformation)
Protons NMR X-Ray (CSD7)
1 2 Erithromycin21 Roxithromycin21 Clarithromycin21 Azithromycina 1a 3 2 6 3 5
3 J C,H measured DMSO-d6/CDCl3 3 J C,H measured CDCl3 3 J C,H measured CDCl3 3 J C,H measured CDCl3 3 J C,H measured CDCl3 3 J C,H measured CDCl3 Φ 3 J C,H calc. Φ 3 J C,H calc. Φ 3 J C,H calc.
a Unpublished data.
H3,C1″ 2.9/5.0 5.1 4.3 5.6 5.9 2.2 28.9 3.8 19.0 4.4 17.7 4.4
C3,H1″ 5.6/5.5 3.3 3.6 2.0 3.5 4.1 30.5 3.7 30.5 3.7 44.0 2.6
H5,C1′ 6.3/6.0 4.8 5.6 5.2 6.0 6.7 12.7 4.6 −25.5 3.6 0.1 4.7
C5,H1′ 3.7/3.8 3.3 2.6 5.0 3.1 3.5 51.7 2.0 34.3 3.4 41.5 2.8

The large diaxial proton–proton coupling constants in the sugar rings are in accordance with the chair conformation of sugar residues.

Nuclear Overhauser enhancement

Awan et al.11 suggested caution in the use of 3JH2,H3 as a sole indicator of the folded-out to folded-in ratio. Further conformational information can be obtained by using the NOE or ROE data. The folded-out and folded-in conformational families are characterized also by a close approach of atoms H3 and H4 to H11 which respectively give rise to H3–H11 NOE peaks in the folded-in and to H4–H11 NOE peaks in the folded-out conformers. The two types of conformer are also reported to be characterized by several other proton–proton spatial proximities such as H5–H18(6Me) for the folded-out and H4–H18(6Me) and H16(2Me)–H17(4Me) for the folded-in conformations.11

Therefore, the TPPI NOESY and States-TPPI ROESY spectra for 1 and 2 were recorded and analysed. The NOESY spectra were recorded in CDCl3 solution and the ROESY spectra in DMSO-d6, acetone-d6 and in buffered D2O (Table 4) because NOEs were close to zero in these solvents at 500 MHz, while ROEs were positive. Features of the NOESY and ROESY spectra of our utmost interest were spatial proton–proton contacts between H3 or H4 on the one side of the ring and H11 on its other side—illustrating the conformation of the macrocycle. Other interesting features were inter-sugar contacts and contacts between sugars and the lactone ring—demostrating the position of the sugar moieties.

Table 4 Qualitative nuclear Overhauser enhancement (NOE) data for compounds 1 and 2 in various solvents
  1 2
Proton D2O DMSO-d6 Acetone-d6 CDCl3 D2O DMSO-d6 Acetone-d6 CDCl3
2 4,4Me 4,4Me 4,4Me 4,4Me 4Me 4,4Me 4,4Me 4,4Me
3 6,5 2Me,6,5,11 2Me,7a,5 2Me,4,5,6 2Me,4,6 2 or 4Me,6,5 2Me,4Me,4,11,5 2Me,4,6,11
4   7b            
5 6Me 6Me 6Me 6Me,4Me,4 6Me,4 6Me,4Me 6Me,4 6Me,4Me,4,6
6   7b 7b     4    
7a   4,6,12Me 4,6,12Me 4,6,12Me   4,6 6 6
7b   6Me 6Me 6Me   6Me,6 6Me 6Me
8   7b,6Me,10Me 10Me,6Me,7b 6Me,7b,6,10Me 6Me,6 6Me,6,7b,10Me 6Me,7a,6,10Me 6Me,6,7b,10Me
10 12Me 12Me,7a,12,8a 12Me,12,7a 12Me,12,7a 12Me,7b 12Me,7a,12 12Me,12,7a,7b 12Me,7b
11 12Me,10,12,4,7a 12Me,7a,10,12,4 10Me,12Me,12,4,11 12Me,4,7a,10 4,12,10,7a 4,10,7a 12Me,12,4,7a,10 12Me,10Me,12,4,7a,10
12 13Me 13Me 13Me 10Me,13Me   10Me,13Me 10Me,13Me 10Me,13Me
13 12,11 12,11   12,11 12,11 12,11 12,11 12,11
13Me     12Me          
1′ 4Me,3′,5″ 4Me,3′,5,5′,5″ 4Me,3′,5,5′,5″ 4Me,3′,5″5,5′ 4Me,3′,5′,5″ 4Me,3′,5″,5,5′ 4Me,3′,5,5′,5″ 4Me,4′b,5′Me,3,5,5′,5″
2′   4′a,4′b,3′NMe2 4′a,4′b,3′NMe2 4′b,3′NMe2   4′b,3′NMe2 4′b,3′NMe2 4′b,3′NMe2
3′   4′a,3′NMe2 4′a,4′b,3′NMe2 4′a,3′NMe2 4′a,4′b 4′a,3′NMe2 4′a,4′b,3′NMe2 5′Me,4′a
3′NMe2   4′a,4′b 4′a 4′a,4′b   4′a,4′b 4′a,4′b 4′a,4′b
4′a   5′Me 5′Me          
5′ 4′a,4′b,3′ 4′a,4′b,3′ 4′a,4′b,3′,2′ 4′a,4′b,3′ 4′a,4′b 4′a,4′b,3′ 4′a,4′b,3′ 4′a,4′b
1″ 2Me,2″a,2″b,3 4Me,2″a,2″b,3″,3 2Me,2″a,2″b,3″,3 2Me,2″a,2″b,3 2Me,2″a,2″b,3″,5″ 2Me,2″a,2″b,3,3″,5″ 2Me,2″a,2″b,3 2Me,2″a,2″b,3
2″a 2Me 4Me 4Me 2Me   4Me 2Me 4Me
2″b                
3″ 2″a,2″b,4″ 2″a,4″ 2″a,2″b,4″ 2″a,2″b 2″a,2″b 2″a,5″Me 5″Me,4″,2″a,2″b 5″Me,4″,2″a,2″b
3″OMe   2″a 2″a 2″a,4″ 2″a 2″b 2″a 2″a
4″ 5″Me,2″b 5″Me,2″b 5″Me,2″b 5″Me,2″b 5″Me,2″b 5″Me,2″b,2″a 5″Me,2″a,2″b 5″Me,2″b
5″ 4″ 4″ 3″ 4″,3″ 4″,3″ 4″,3″ 4″ 4″,3″

A large crosspeak that appeared in the spectrum of 1 between protons H4 and H11 suggested the existence of the folded-out conformer as the predominant one in CDCl3. The peak became weaker in the buffered D2O solution and in acetone-d6. This effect could be accounted for by an inward folding of the C3–C5 region giving rise to a slight increase in the folded-in conformation. The appearance of a ROE crosspeak H3–H11 in DMSO-d6 supported the existence of the folded-in conformation. These findings were consistent with the results of our analysis of the coupling constants. The appearance of the crosspeak H5–H18(6Me) in the ROESY spectra of 1 in all solvents demonstrated that a close approach of H5 and H18(6Me) protons did not characterize only the folded-out conformations as stated previously11 but the folded-in ones as well. This is in accordance with the available crystal structures of BBOLEA3 and ZATPAL6 representing the folded-in and the folded-out conformations of oleandomycin-like compounds, respectively, where H5–H18(6Me) contact was found to be within 2.6 Å for both conformations. Thus we now believe that the H5–H18 contact can not be taken as evidence for the folded-out conformation since it has been observed for both folded-in and folded-out conformers of oleandomycin and azithromycin.

In the spectra of compound 2, the H4–H11 ROE crosspeak was relatively strong in D2O buffer and DMSO-d6 (Fig. 2) and somewhat weaker in CDCl3 and acetone-d6 where a weak H3–H11 peak also appeared (Table 3). This, along with our data concerning the coupling constants, provided support for the conclusion that compound 2 existed predominantly in the folded-out conformation in solution with some contribution of the folded-in conformer especially in acetone and CDCl3.


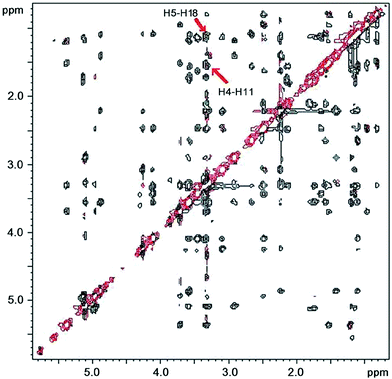States-TPPI ROESY NMR spectrum of 2 in DMSO-d6 solution at 27 °C. The key NOE crosspeaks are marked.
Fig. 2 States-TPPI ROESY NMR spectrum of 2 in DMSO-d6 solution at 27 °C. The key NOE crosspeaks are marked.

The NOE and ROE data for 1 and 2 show the expected crosspeaks for sugars in the Everett–Tyler8 chair conformation except for D2O where, owing to the poor quality of spectra, some contacts could not be identified. This conformation was characterized by H1′–H3′, H1′–H5′, H3′–H5′ and H2′–H4′(a,b) NOE crosspeaks for the chair conformation of the desosamine unit and by H2″(a,b)–H4″ and H4″–H6″(5″Me) for the chair of oleandrose sugar.

Two contacts between the macrocycle and desosamine were observed in 1 and 2: H5–H1′ and H17(4Me)–H1′. They corresponded to the perpendicular orientation of desosamine with respect to the lactone ring and agreed with the data reported for the related macrolides.8–15 Contacts between the macrocycle and oleandrose such as H3–H1″ and inter-sugar contact H1′–H5′ indicated an oleandrose position similar to that of cladinose in clarithromycin.13 For both compounds a characteristic macrocycle–oleandrose contact H16(2Me)–H1″ ROE was found in all solvents. The only exception was the DMSO solution of 1 where the H17(4Me)–H1″ crosspeak was observed instead, as a consequence of a larger proportion of the folded-in conformer. Namely, in the folded-in conformation the H17(4Me) group was closer to cladinose/oleandrose giving rise to a H17(4Me)–H1″ ROE contact.

Molecular modelling

Incorporation of the experimental NMR constraints into modelling simulations did not seem to be the right approach as it could yield an average conformation that never actually existed. Therefore, independent unconstrained molecular dynamics simulations were performed and molecular modelling focused on the 3D structural interpretation of the NMR experimental findings. In the molecular regions not covered by the NMR data i.e. C8–C9–O9/N9–OH and O14–C1–O1 modelling results were indispensable for deducing conformation. Solvents for simulations were chosen according to the changes of interest in the NMR data that we wanted to account for conformationally.

The NMR coupling constants and torsion angles obtained by modelling were compared by means of the Karplus-type equation (see Experimental). Due caution was exercized considering the parameterization of the equation and tolerance of agreement between the couplings and torsions.

The NMR NOE data were the second check point for simulation results—sampled conformations were checked for the existence of NOEs found by NMR.

Conformation of the macrocycle. After the molecular mechanics energy minimization of compound 1 (Scheme 1), performed using the Consistence Valence Force Field (cvff) in Discover,22 the initial folded-in conformation (Tables 5 and 6, conformation IN for 1a X-ray) was retained (Tables 5 and 6, conformation IN2 for 1 Modelling). Molecular dynamics (MD) simulations were performed in DMSO using the cvff in Discover.22 Two protocols were employed, one at the constant temperature of 300 K and the other at 300 K with temperature jumps to 500 K. During simulations changes in the C–C–C–C and corresponding H–C–C–H torsion angle values on the right-hand side of the macrocycle became apparent and approximately two groups of different values, corresponding to two different conformational families, could be distinguished (Tables 5 and 6). The torsions on the left-hand side of the macrocycle were more or less unchanged. The folded-in conformational family (torsion angle H2–C2–C3–H3 ∼ 100°) was the more densely populated one during simulations, but the folded-out conformers (torsion angle H2–C2–C3–H3 ∼ ±180°) could also be seen (Fig. 3a). The folded-out conformers were more abundant in the simulation with temperature jumps. The change in torsion angle values was accompanied by a change in characteristic inter-proton contacts (Fig. 3b). The difference in energy between the folded-in and folded-out conformational families was within 1.5 kcal mol−1.
Table 5 Selected torsion angles H–C–C–H (Φ/°) calculated from NMR 3JH,H data (Table 1) and the ones obtained by modelling calculations for selected folded-in and folded-out conformers of 1 and 2 in comparison with the solid state X-ray conformers of oleandomycin derivatives3,5,6 retrieved from CSD7
  1 2 1a 3 2 6 3 5
  NMR Modelling NMR Modelling X-Ray (CSD7)
  D2O DMSO Acetone CDCl3 DMSO D2O DMSO Acetone CDCl3 CDCl3 Solid state
Torsion angle OUT + IN IN OUT + IN OUT + IN IN1 IN2 OUT1 OUT2 OUT + IN OUT + IN OUT + IN OUT + IN OUTIns. OUTSyb. INIns. INSyb. IN OUT “OUT”
H2–C2–C3–H3 136.1 117.1 131.6 142.6 88.4 95.0 165.0 172.6 149.2 140.1 134.4 139.5 172.2 151.4 109.0 101.9 115.3 169.8 −179.4
H3–C3–C4–H4 −62.9 −62.9 −63.9 — −63.5 −66.1 −72.7 −75.9 −65.0 −68.7 −61.9 −68.7 −73.8 −75.6 −65.4 −61.8 −65.4 −74.6 −82.8
H4–C4–C5–H5 137.3 — 135.5 136.1 176.9 164.7 152.9 129.9 157.8 159.0 153.9 164.6 160.5 158.7 174.0 179.2 162.1 155.6 154.3
H5–C5–C6–H6 −61.9 — −60.0 −58.2 −63.5 −64.1 −85.5 −74.3 — — −95.7 — −93.4 −77.1 −67.2 −64.1 −74.0 −98.5 −72.9
H6–C6–C7–H7a — — — — −67.3 −65.8 −72.0 −71.6 — — — — −73.3 −64.7 −70.8 −61.3 −54.1 −62.5 −67.0
H6–C6–C7–H7b — — −150.8 −137.6 179.4 −179.3 175.6 175.6 150.7 150.7 — 153.5 176.4 −179.4 177.4 −176.2 −174.1 177.5 175.3
H10–C10–C11–H11 65.1 58.5 59.5 65.1 65.5 64.4 71.4 69.8 71.2 65.1 63.9 65.1 65.1 72.0 62.4 71.4 68.1 66.7 60.7
H11–C11–C12–H12 167.1 164.5 159.2 174.8 178.8 176.2 179.6 178.9 172.2 — — 170.0 176.5 174.8 175.2 164.0 173.3 176.2 172.0
H12–C12–C13–H13 −64.4 −58.6 −60.4 −65.6 −59.8 −61.6 −64.4 −66.7 −68.1 −69.6 −65.6 −66.8 −65.9 −63.7 −73.5 −63.9 −57.9 −66.2 −84.6

Table 6 Selected torsion angles C/O–C–C–C/O/N (Φ/°) for folded-in and folded-out conformers of 1 and 2 obtained by modelling calculations in comparison with the torsion angles of the solid state X-ray conformers of oleandomycin derivatives3,5,6 retrieved from CSD7
  1 2 1a 3 2 6 3 3
  Modelling (MD, DMSO) Modelling (MD, CDCl3) X-Ray (CSD7)
Torsion angle IN1 IN2 OUT1 OUT2 OUTIns. OUTSyb. INIns. INSyb. IN OUT “OUT”
O14–C1–C2–C3 107.6 97.0 110.3 119.3 106.4 117.4 125.6 81.5 83.8 109.4 122.0
C1–C2–C3–C4 −142.9 −135.9 −72.7 −66.3 −65.5 −86.5 −121.4 −130.5 −119.3 −67.0 −60.2
C2–C3–C4–C5 169.9 169.0 162.7 158.0 160.7 162.9 170.4 177.4 175.2 162.2 153.3
C3–C4–C5–C6 −59.3 −70.8 −82.9 −102.8 −75.6 −79.6 −63.2 −61.4 −75.9 −83.7 −83.3
C4–C5–C6–C7 −64.8 −65.7 −87.5 −76.2 −96.1 −78.7 −71.2 −64.3 −72.4 −90.0 −73.1
C5–C6–C7–C8 173.4 174.3 169.7 169.0 170.9 179.3 174.2 −178.0 −171.8 177.7 171.5
C6–C7–C8–C9 −57.6 −52.1 −67.9 −63.2 −95.7 −74.2 −97.2 −78.0 −65.4 −77.9 −163.2
C7–C8–C9–C10 −85.5 −83.0 −63.2 −68.7 −23.7 −63.3 −37.1 −68.9 −69.9 −49.9 43.4
C8–C9–C10–C11 100.1 98.2 106.3 105.7 92.8 105.6 104.0 106.6 107.3 103.8 49.6
C9–C10–C11–C12 −169.2 −170.8 −163.1 −164.9 −172.6 −166.3 −176.4 −167.0 −171.3 −170.2 −171.5
C10–C11–C12–C13 −178.1 179.6 −177.3 −177.9 −179.0 180.0 179.3 170.0 176.0 −178.2 168.7
C11–C12–C13–O14 −63.7 −64.5 −69.7 −72.3 −73.3 −68.4 −81.1 −65.7 −72.4 −68.4 −88.7
C12–C13–O14–C1 117.8 134.3 96.7 97.5 96.7 100.4 97.2 145.4 154.2 98.4 104.9
C13–O14–C1–C2 −160.4 −161.3 179.6 180.0 −179.4 177.7 −151.7 −173.1 −174.4 173.2 173.3
C13–O14–C1–O1 17.2 16.5 −0.9 −0.5 −1.0 −1.7 27.0 5.8 5.0 −6.7 −5.8
C3–C2–C1–O1 −70.1 −80.8 -69.3 −60.3 −72.0 −63.3 −53.1 97.4 −95.6 −70.6 −58.9
C7–C8–C9–O9/N9 92.6 94.8 115.2 109.5 156.4 116.6 145 110.8 123.1 131.7 −134.0
C11–C10–C9–O9/N9 −77.9 −79.5 −72.0 −72.4 −87.3 −74.3 −77.9 −73.1 −85.4 −77.6 −132.7
C8–C9–N9–O91 — — — — −19.8 −1.4 −16.1 −0.2 — −3.5 2.0
C10–C9–N9–O91 — — — — 160.3 178.5 165.8 179.6 — 178.1 −175.6
C9–N9–O91–H91 — — — — 177.8 −179.6 178.1 −179.8 — 175.7 161.1
C2–C3–O3–C1″ −109.2 −75.1 −99.3 −129.4 −105.5 −100.9 −82.5 −81.5 −90.4 −103.4 −101.8
C4–C3–O3–C1″ 120.3 156.0 134.1 104.3 148.9 137.0 151.3 154.7 148.8 135.0 137.3
C3–O3–C1″–C2″ 133.8 −175.4 149.2 103.2 148.9 146.8 155.8 158.3 151.9 150.5 164.6
C3–O3–C1″–O5″ −104.9 −52.1 −87.6 −135.3 −87.8 −89.9 −80.3 −77.7 −89.8 -85.6 −73.5
C4–C5–O5–C1′ −109.5 −106.0 −111.6 −100.0 −120.5 −113.8 −109.0 −110.6 109.9 −144.5 −117.8
C6–C5–O5–C1′ 122.1 124.9 121.9 132.7 114.7 122.6 122.9 124.1 130.5 92.8 118.9
C5–O5–C1′–C2′ 167.9 179.0 163.5 174.4 165.5 166.9 172.4 173.4 171.1 154.3 161.6
C5–O5–C1′–O5′ −71.6 −60.2 −76.2 −65.2 −74.0 −73.0 −66.6 −66.4 −66.6 −86.4 −77.7


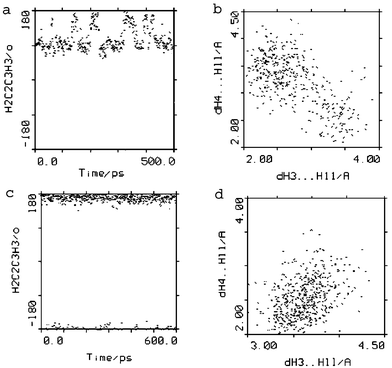Trajectory of H2–C2–C3–H3 torsion angle and H3–H11 vs. H4–H11 distances from MD simulation in DMSO at 300 K for 1 (a, b) and from MD simulation in H2O at 300 K with jumps to 500 K for 2 (c, d). Changes from predominantly folded-in (torsion angle H2–C2–C3–H3 ∼ 90°, contact H3⋯H11) to folded-out conformation (torsion angle H2–C2–C3–H3 ∼ 170°, contact H4⋯H11) can be seen for 1. No conformational changes are observed for 2; the folded-out conformation was maintained throughout simulation.
Fig. 3 Trajectory of H2–C2–C3–H3 torsion angle and H3–H11 vs. H4–H11 distances from MD simulation in DMSO at 300 K for 1 (a, b) and from MD simulation in H2O at 300 K with jumps to 500 K for 2 (c, d). Changes from predominantly folded-in (torsion angle H2–C2–C3–H3 ∼ 90°, contact H3⋯H11) to folded-out conformation (torsion angle H2–C2–C3–H3 ∼ 170°, contact H4⋯H11) can be seen for 1. No conformational changes are observed for 2; the folded-out conformation was maintained throughout simulation.

During the molecular dynamics simulations in H2O for 1 (data not shown) the folded-in conformation was no longer the more densely populated one; the folded-in and folded-out conformers of the 14-membered macrocycle were found to co-exist in a mixture.

A superposition diagram of the folded-in and folded-out conformers from MD simulations in DMSO for 1 and of the folded-in solid-state conformer for 1a3 is shown in Fig. 4.


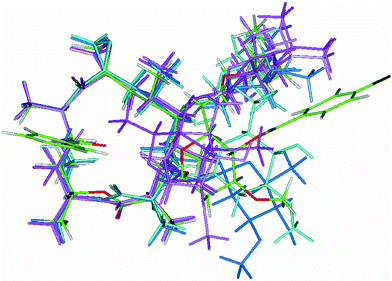Superposition diagram of the folded-in (light and dark pink; Table 6 conformations IN1 and IN2) and folded-out (light and dark turquoise; Table 6 conformations OUT1 and OUT2) conformers of 1 modelled by Insight II22 and folded-in X-ray3 conformer of 1a (coloured by atom; Table 6 conformation IN). Atoms of the macrocycle were used for superposition.
Fig. 4 Superposition diagram of the folded-in (light and dark pink; Table 6 conformations IN1 and IN2) and folded-out (light and dark turquoise; Table 6 conformations OUT1 and OUT2) conformers of 1 modelled by Insight II22 and folded-in X-ray3 conformer of 1a (coloured by atom; Table 6 conformation IN). Atoms of the macrocycle were used for superposition.

After the molecular mechanics energy minimization for compound 2, performed using cvff in Discover,22 the initial folded-out conformation (Tables 5 and 6, conformation OUT for 2 X-ray) was retained (Tables 5 and 6, conformation OUTIns. for 2 Modelling). In molecular dynamics trajectories in CDCl3 and H2O at 300 K the conformations positioned mainly around the starting folded-out molecular mechanics energy minimum were observed again (Fig. 3c and d). That meant that the average simulation value of 3JH2,H3 was larger than its experimental NMR value. The folded-in conformation, with small 3JH2,H3 coupling which would lower the average trajectory value, although expected, failed to appear during simulation even after temperature jumps to 500 K. Likewise, molecular dynamics simulations at higher temperature (500 K) failed to confirm the existence of such a conformation, although other conformations appeared but were abandoned not being in accordance with the NMR data.

In the attempt to assess the folded-in conformer of 2 a change of force field seemed appropriate. Molecular mechanics energy minimization performed on 2 in Sybyl23 using the MMFF94 force field revealed a change in conformation from the initial folded-out (Tables 5 and 6, conformation OUT for 2 X-ray) to the folded-in (Tables 5 and 6, conformation INSyb. for 2 Modelling). The folded-in conformer so obtained was reoptimized again in Discover22 using cvff (Tables 5 and 6, conformer INIns. for 2 Modelling) and had an energy exceeding that of a previous folded-out conformer by ∼ 5 kcal mol−1. In Sybyl23 the situation was different: energetically, the folded-in conformer was the more favoured one. The reoptimized folded-in conformer from Discover22 was then used as a starting point for new molecular dynamics simulation in Discover22 in CDCl3. To start from different conformations in order to better sample the conformational space seemed more advantageous than to run a very long molecular dynamics at low sampling efficiency. The folded-in conformation, however, changed almost immediately to the folded-out conformation.

During the molecular dynamics simulation in Discover22 the E ↔ Z isomerization of the oxime chain occurred for the double bond C8–C9[double bond, length as m-dash]N9–OH. This isomerization was probably due to a weak force constant for the C8–C9[double bond, length as m-dash]N9–OH torsion angle calculated by automatic parameter assignment. According to synthesis2 and X-ray data,6 only the conformers with the C8–C9[double bond, length as m-dash]N9–O torsion angle of ∼0° were considered, isomerization in the solution being highly improbable.

Fig. 5 shows a superposition diagram of the folded-out and folded-in conformers of 2 from MD simulations in CDCl3 in Discover22 and Sybyl23 as well as the folded-out solid-state conformer.6


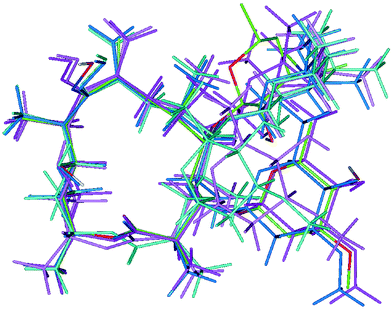Superposition diagram of the different conformers of 2: folded-out (dark pink; Table 6 conformation OUTIns.) and folded-in (light pink; Table 6 conformation INIns.) conformers from modelling in Insight II,22 folded-out (dark turquoise; Table 6 conformation OUTSyb.) and folded-in (light turquoise; Table 6 conformation INSyb.) conformers from modelling in Sybyl23 and folded-out X-ray6 conformer (coloured by atom; Table 6 conformation OUT). Formation of the hydrogen bond O11–H⋯OC1 in folded-out conformers can be observed. Atoms of the macrocycle were used for superposition.
Fig. 5 Superposition diagram of the different conformers of 2: folded-out (dark pink; Table 6 conformation OUTIns.) and folded-in (light pink; Table 6 conformation INIns.) conformers from modelling in Insight II,22 folded-out (dark turquoise; Table 6 conformation OUTSyb.) and folded-in (light turquoise; Table 6 conformation INSyb.) conformers from modelling in Sybyl23 and folded-out X-ray6 conformer (coloured by atom; Table 6 conformation OUT). Formation of the hydrogen bond O11–H⋯O[double bond, length as m-dash]C1 in folded-out conformers can be observed. Atoms of the macrocycle were used for superposition.

On the whole, conformational changes had influenced three groups of torsions at the right-hand side of the macrocycle: (a) C1–C2–C3–C4 and H2–C2–C3–H3 angles, (b) C3–C4–C5–C6 and H4–C4–C5–H5 angles, and (c) C4–C5–C6–C7 and H5–C5–C6–H6 angles (Tables 5 and 6; Fig. 4 and 5). The change (a) in torsion angles could be clearly observed from the NMR data (change in 3JH2,H3) while the other two torsion angle changes [(b) and (c)], due to their lesser extent, could not be easily recognized in the NMR data. The torsion angles at the left-hand side of the macrocycle were more or less unaffected.

The changes in torsion angles were accompanied by changes of intra-macrocycle proton to proton distances: H3,H4–H11 but also H6–H10,H11 and H7–H10,H11—the larger values being characteristic of the folded-in and the smaller ones of the folded-out conformers. All distances were within 5 Å.

Further conformational flexibility, independent of the folded-in ↔ folded-out transformation, was noticed in the regions C7–C8–C9(O9/N9–OH)–C10 and C12–C13–O14–C1[double bond, length as m-dash]O1 where different types of conformation were recognized (Table 6, Fig. 4 and 5). Comparable conformational changes were reported for clarithromycin by Steinmetz et al.12 (flexibility of the lactone region) and for roxithromycin by Gharbi-Benarous et al.24 who attributed them to hydrogen bonding. We also noticed different types of intramolecular hydrogen bonding (O11—H⋯O1[double bond, length as m-dash]C1, O11–H⋯N9/O9[double bond, length as m-dash]C9, O11–H⋯O91–N9[double bond, length as m-dash]C9 and C9[double bond, length as m-dash]N9–O91–H⋯O11) during the MD simulations but did not find their link with the conformation to be conclusive. In the solid-state folded-out conformer of 2 the presence of the hydrogen bond O11–H⋯O1[double bond, length as m-dash]C1 was registered while in the solid-state folded-in conformer of 1a there was no possibility of hydrogen bonding as the hydroxyl group at C11 was benzylated.

Conformation of the sugar rings and conformation around the glycosidic bond. During all MD simulations the oleandrose and desosamine sugar moieties kept the usual and expected chair conformation in both compounds—β-4C1 for desosamine and α-1C4 for oleandrose. The conformational behaviour of the glycosidic bond was comparable for the two compounds (1 and 2; Fig. 6). The conformational family around the X-ray conformer was the most densely populated one; the formation of another family conformationally close to the X-ray conformer could be noticed especially for compound 2 (Fig. 6c and d). With the latter compound the second conformational family seemed to be populated independently of the simulation temperature whereas in the case of 1 its population density was much lower even in simulations with temperature jumps. After the molecular mechanics energy minimization of the selected MD conformers, the conformation around the glycosidic bond of the desosamine sugar residue usually adopted conformations close to the solid-state conformer both for 1 and 2 while a few different conformations around the glycosidic bond of oleandrose proved to be stable (Table 6). In all conformers the oleandrose sugar moiety held a coplanar position towards the macrocycle and the desosamine sugar moiety a perpendicular one (Fig. 4 and 5). As molecular dynamics data revealed a certain conformational flexibility and did not support a single conformational model around the glycosidic bond, it was concluded that only conformational averaging could yield good agreement between theoretical modelling and experimental NMR results. Thus, NMR parameters were found to reflect an average conformation and to suggest that solution conformation was a mixture of different conformations which could not be adequately described solely by the crystal structure conformation.
Conformation around the glycosidic bond defined by torsion angles H5–C5–O5–C1′ and C5–O5–C1′–H1′ for the desosamine sugar moiety and by H3–C3–O3–C1″ and C3–O3–C1″–H1″ for oleandrose during the MD simulation in DMSO at 300 K for 1 (a, b) and in H2O at 300 K with jumps to 500 K for 2 (c, d).
Fig. 6 Conformation around the glycosidic bond defined by torsion angles H5–C5–O5–C1′ and C5–O5–C1′–H1′ for the desosamine sugar moiety and by H3–C3–O3–C1″ and C3–O3–C1″–H1″ for oleandrose during the MD simulation in DMSO at 300 K for 1 (a, b) and in H2O at 300 K with jumps to 500 K for 2 (c, d).

Conclusions

A combined use of NMR spectroscopy and molecular modelling has provided insight into the conformational properties of oleandomycin 1 and its 8-methylene-9-oxime derivative 2.

Oleandomycin 1 adopts predominantly the folded-in conformation in DMSO. A small amount of the folded-out conformation present increases upon heating (3JH2,H3 rises and the abundance of folded-out conformer in molecular dynamics trajectory grows with the temperature). A mixture of the folded-in and folded-out conformers exists in buffered D2O, acetone-d6 and CDCl3.

Conformational analysis for compound 2 shows the folded-out conformation to be the preferred one in all solvents (although some amounts of the folded-in conformer can also be present depending on the solvent and the temperature) and in the solid state.6

For both compounds molecular modelling has also revealed conformational flexibility in the regions around C1 and C9, which are not covered by the NMR data. It is assumed that intramolecular hydrogen bonding can have some influence on the conformation of the macrocycle, particularly on the conformation in those regions, but the evidence has not been conclusive.

The large diaxial coupling constants and characteristic NOE crosspeaks in the sugar rings as well as modelling results have provided evidence that both sugars tend to adopt the usual chair conformation characteristic also of the solid state, oleandrose being coplanar and desosamine perpendicular to the lactone ring. Both glycosidic bonds exhibit a certain conformational flexibility around the X-ray conformer.

Our results have demonstrated that the measured NMR parameters tend to reflect an average, virtual conformation and that the X-ray structures do not adequately describe solution state conformations. Compounds 1 and 2 exhibited conformational flexibility not only in the erythronolide part but also in the position of sugar rings. Bearing in mind the knowledge gained from this study, once different conformations have been modelled, in further conformational studies of the oleandomycin-type compounds the coupling constants 3JH2,H3, especially their temperature dependence, and the NOE proton–proton distances H3–H11 and H4–H11 can serve as good indicators of the aglycone ring folding.

Experimental

NMR Spectroscopy

One and two-dimensional NMR spectra were recorded on a Bruker Avance DRX500 spectrometer equipped with a 5 mm diameter inverse detection probe and z-gradient accessory working at 500.13 MHz for 1H. In 1H NMR experiments the spectral width was 5000 Hz, the number of data points 65K and the number of scans 8–64. TMS was used as the internal standard. The sample concentration was 10 mg mL−1 in CDCl3, acetone-d6 and DMSO-d6 solutions and 2 mg mL−1 in 50 mM D2O phosphate buffer (pH = 7.6) solution. Pulse scheme WATERGATE (3–9–19) was used for the water signal suppression. The digital resolution was 0.1 Hz per point.

Two-dimensional gsCOSY, ROESY and NOESYspectra were recorded under the following conditions: spectral width was 6000 Hz in both dimensions, 2K data points were applied in time domain and 512 increments were collected for each data set with linear prediction to 1K and zero filling to 2K. Scans 4–32 were applied for each increment. The relaxation delay was 1.5 s. States-TPPI ROESY spectra were obtained with the mixing time of 250 ms (400 ms for NOESY) and processed with a sine squared function shifted by π/2 in both domains, while gsCOSY spectra were processed with an unshifted sine function. The digital resolution was 2.7 and 10.7 Hz per point in f2 and f1 domains, respectively.

The HSQC and HMBC spectra were recorded with a relaxation delay of 1.5 s and 32 scans per increment. The spectral width was 31000 Hz in acquisition domain f2 and 6000 Hz in time domain f1. Data were collected into a 2048 × 256 acquisition matrix and processed using a 2K × 1K transformed matrix with zero filling in the f1 domain. Sine multiplication was performed before Fourier transformations. In HMBC spectra the delay for long-range couplings was set to 60 ms.

Measurements of long-range 13C–1H couplings were performed using the multiple 13C site selective excitation experiment19,20 on a Varian Unity Inova 600 spectrometer operating at 600.07 MHz for protons with an inverse detection gradient probe. Half-Gaussian shaped pulse truncated at the leading edge at 5% maximum intensity was used for selective 13C excitation with a duration of 25–50 ms. The relative sign of each selective pulse was set according to the Hadamard matrix. Spectral widths of 4000–5000 Hz were sampled with 32768 data points using 5000 scans for each Hadamard excitation. A BIRD module was used for a better selection of long-range couplings. The two gradients were applied before and after the last pair of 90° pulses for coherence selection and suppression of artefacts.

Molecular modelling

The coordinates from X-ray analysis, taken from the Cambridge Structural Database7 (CSD), were used as a starting point for calculations. For compound 1 the coordinates from 1a3 (Scheme 1) were taken. The p-bromobenzoyl substituents were replaced by hydroxyl groups in the Builder module of the Insight II program22 (Accelrys). Hydrogen atoms were added according to the stereochemistry in the Builder module of the Insight II program.22 For compound 2 the starting coordinates were also taken from CSD7 (Scheme 1); the coordinates for the hydroxyl hydrogens of 2 were provided by the author6 and others were generated on the basis of stereochemistry again in the Builder module of the Insight II program.22

The molecular mechanics energy minimizations were performed using cvff in the Discover module of the Insight II program.22 The atomic potentials and charges were assigned in cvff. For comparison some calculations were performed using Merck Molecular Force Field (MMFF94) and MMFF94 charges in the Sybyl package23 (Tripos).

Molecular dynamics simulations were carried out with cvff in the Discover module of the Insight II program.22 As the input for simulations, sterically relaxed X-ray structures were taken. The molecules were placed in a cubic box, which was subsequently filled with solvent molecules. Explicit solvent molecules (non-continuum solvation model) were used in order to take into account solvation effects, which is not possible in a homogeneous dielectric environment. Simulations were performed using periodic boundary conditions (PBC) with the minimum image model. Before they started, an energy minimization was performed on the whole system. Simulations were carried out in H2O for both compounds, in DMSO25 for 1 and in CDCl3 for 2. The solvents for simulations were chosen according to the effects of interest in the NMR data. For the simulations in CDCl3 and DMSO it was first necessary to adjust the density to an appropriate value for each solvent, using pNT conditions. The molecular dynamics simulations were then performed at constant volume and at 300 K, by coupling to a thermal bath, during 500 ps with the step of 1 fs preceded by an equilibration period of 50 ps. In some simulations brief temperature jumps to 500 K were performed in order to prevent staying in the same local energy gap and to help jumping over possible higher energy barriers by increasing the kinetic energy and enabling, in that way, a change of conformation. These simulations lasted for 600 ps. For compound 2, in the attempt to provoke conformational changes, MD simulations at 500 K were also performed. No constraints were applied. The coordinates were sampled every 100 steps.

The NMR coupling constants 3JH,H were transformed to torsion angle values, and vice versa, using the Karplus-type equation by Hasnoot et al.26 modified according to the electronegativity and orientation of the substituents by an in-house program based on graphic interpolation. For 3JC,H couplings over the glycosidic bond the equation by Tvaroška and Gajdoš27 was used.

All calculations were performed using PLIVA's Indigo2 SGI workstation and the Octane SGI workstation of the Ruđer Bošković Institute, Zagreb, Croatia.

Acknowledgements

Thanks from Zrinka Banić Tomišić are due to Dr. Biserka Kojić Prodić, Head, Laboratory for Chemical and Biological Crystallography, Ruđer Bošković Institute, Zagreb, Croatia for the use of hardware and software facilities.

References

  1. F. A. Hochstein, H. Els, W. D. Celmer, B. L. Shapiro and R. B. Woodward, J. Am. Chem. Soc., 1960, 82, 3225 CrossRef CAS.
  2. G. Lazarevski, G. Kobrehel, S. Đokić, L. Kolačny-Babić, B. Kojić-Prodić, D. Janković and V. Puntarec, J. Antibiot., 1994, 47, 349 CAS.
  3. H. Ogura, K. Furuhata, Y. Harada and Y. Iitaka, J. Am. Chem. Soc., 1978, 100, 6733 CrossRef CAS ; CSD refcode: BBOLEA.
  4. G. M. Bright, A. R. English, A. A. Nagel, J. A. Retsema and F. C. Sciavolino, Antimicrob. Agents Chemother., 1984, 25, 113 CAS.
  5. G. Lazarevski, G. Kobrehel, S. Đokić and L. Kolačny-Babić, J. Antibiot., 1994, 47, 349 CAS ; CSD refcode: LIDBIJ.
  6. B. Kamenar, N. Košutić Hulita, I. Vicković and G. Lazarevski, Z. Kristallogr., 1995, 210, 516 CAS ; CSD refcode: ZATPAL.
  7. F. H. Allen and O. Kennard, Chem. Des. Automat. News, 1993, 8, 31 Search PubMed.
  8. J. R. Everett and J. W. Tyler, J. Chem. Soc., Perkin Trans. 2, 1987, 1659 RSC.
  9. J. Gharbi-Benarous, P. Ladam, M. Delaforge and J.-P. Girault, J. Chem. Soc., Perkin Trans. 2, 1993, 2303 RSC.
  10. A. Awan, R. J. Brennan, A. C. Regan and J. Barber, J. Chem. Soc., Chem. Commun., 1995, 1653 RSC.
  11. A. Awan, R. J. Brennan, A. C. Regan and J. Barber, J. Chem. Soc., Perkin Trans. 2, 2000, 1645 RSC.
  12. W. E. Steinmetz, R. Bersch, J. Towson and D. Pesiri, J. Med. Chem., 1992, 35, 4842 CrossRef CAS.
  13. W. E. Steinmetz, J. D. Sadowsky, J. S. Rice, J. J. Roberts and Y. K. Bui, , Magn. Reson. Chem., 2001, 39, 163 CrossRef CAS.
  14. G. Lazarevski, M. Vinković, G. Kobrehel, S. Đokić, B. Metelko and D. Vikić-Topić, Tetrahedron, 1993, 49, 721 CrossRef CAS.
  15. N. Košutić-Hulita, D. Matak-Vinković, M. Vinkovic, P. Novak, G. Kobrehel and G. Lazarevski, Croat. Chem. Acta, 2001, 74, 327 CAS.
  16. F. Schlünzen, R. Zarivach, J. Harm, A. Bashan, A. Tocilj, R. Albrecht, A. Yonath and F. Franceschi, Nature, 2001, 413, 814 CrossRef CAS.
  17. J. L. Hansen, J. A. Ippolito, N. Ban, P. Nissen, P. B. Moore and T. A. Steitz, Mol. Cell, 2002, 10, 117 CrossRef CAS.
  18. A. A. Nagel, W. D. Celmer, M. T. Jefferson, L. A. Vincent, E. B. Whipple and G. Schutle, J. Org. Chem., 1986, 51, 5397 CrossRef CAS.
  19. E. Kupče and R. Freeman, J. Magn. Reson., Ser. A, 1993, 105, 310 CrossRef CAS.
  20. V. Blechta, F. Rio-Portillas and R. Freeman, Magn. Reson. Chem., 1994, 32, 134 CAS.
  21. G. Bertho, P. Ladam, J. Gharbi-Benarous, M. Delaforge and J-P. Girault, Int. J. Biol. Macromol., 1998, 22, 103 CrossRef CAS.
  22. Insight II release v. 2000 (modules: Builder, Discover v. 2.98, Analysis), 2002, Accelrys Inc., Paris, France.
  23. Sybyl v. 6.8, 2002, Tripos Inc., München, Germany.
  24. J. Gharbi-Benarous, P. Ladan, M. Delaforge and J. P. Girault, J. Chem. Soc., Perkin Trans. 2, 1992, 1989 RSC.
  25. D. F. Mierke and H. Kessler, J. Am. Chem. Soc., 1991, 113, 9466 CrossRef CAS.
  26. C. A. G. Haasnot, F. A. A. M. de Leeuw and C. Altona, Tetrahedron, 1980, 36, 2783 CrossRef CAS.
  27. I. Tvaroška and J. Gajdoš, Carbohydr. Res., 1995, 271, 151 CrossRef CAS.

Footnote

† Electronic supplementary information (ESI) available: 1H and 13C NMR data (DMSO-d6, acetone-d6, D2O buffer). See http://www.rsc.org/suppdata/ob/b4/b412294a/
This journal is © The Royal Society of Chemistry 2005