New light on the mechanism of the solid state [2 + 2] cycloaddition of alkenes: a database analysis

Abstract

The mechanism of the solid state [2 + 2] cycloaddition of alkenes has been investigated using the structure correlation method based on geometrical data calculated from single crystal X-ray diffraction studies retrieved from the Cambridge Structural Database (CSD). Searches were carried out for non-bonded alkene⋯alkene reactant interactions, within a limiting C⋯C separation of the sum of van der Waals radii plus 20%, and for bonded cyclobutane product fragments. The results were visualised and interpreted using principal component analysis and symmetry deformation coordinates. The reaction pathway for [2 + 2] cycloaddition was established and it was shown that (a) the alkene moieties are not required to be parallel for the reaction to occur and (b) a large twist angle of the reacting alkene fragments is permissible to form a puckered cyclobutane reaction product, as long as similar intra-annular valence angles are maintained around the four-membered ring.

---

Introduction

[2 + 2] Cycloaddition is one of the most fundamental classes of reactions in organic chemistry.¹ In the solid state, the cycloaddition of alkenes to form cyclobutane species can be activated either thermally or photochemically.^1–3 Most of these reactions occur topochemically, maintaining the symmetry of the monomer crystal lattice but with small changes in cell dimensions.^4,5 Experimentally, a number of these reactions involve single-crystal to single-crystal transformations and these can be monitored successfully using X-ray diffraction techniques. For the single-crystal to single-crystal conversion to occur a number of topochemical factors need to be favourable. In their pioneering work Schmidt and co-workers⁶ postulated that “a reaction in the solid state occurs with a minimum amount of atomic or molecular movement”. Thus, solid state reactions are strongly dependent on the distance between the reacting units and their mutual orientation and there is a maximum distance between the potentially reacting species beyond which the solid state reaction will not occur. Further, the orientation of the reactant molecules in the crystal will be related to the molecular structure in the product. It is also reasonable to assume that in bimolecular solid state reactions these molecules will be nearest neighbours.⁶ The reaction pathways available for solid state reactions are, therefore, likely to be highly constrained by comparison with [2 + 2] cycloadditions in solution or the gas phase, where much greater movement of the reacting molecules is possible.⁷ Hence, the reaction mechanism in the solid state may differ significantly from the mechanism that operates in other phases.

Since the interest in solid state reactions continues to grow, particularly due to the potential applications of the resultant products in the pharmaceutical and electronics industries, it is timely to further investigate their mechanisms. Here we present an analysis of the solid state [2 + 2] cycloaddition reaction of alkenes using structural information available in the Cambridge Structural Database (CSD)⁸ and the knowledge mining techniques that are now available. Fundamental to the methodology used is the structure correlation principle of Bürgi and Dunitz⁹ which views each specific observation of a chemical substructure in a specific crystal structure as a structural ‘snapshot’ which is determined by the chemical environment and energetics of the compound. If large numbers of these snapshots are plotted together, they can trace out energetically accessible sections of the pathway followed during a chemical reaction (Scheme 1).^9,10 A key question in applying the structure correlation principle concerns the structural parameters, or combination of parameters, that should be plotted so as to best visualise the reaction pathway, interpreted as a low energy valley in the relevant potential energy hypersurface. In the present study, we use principal component analysis to visualise the structural data and to detect interconversion pathways, which are then interpreted using symmetry deformation coordinates.

Scheme 1

Experimental

Database searches: general criteria

All searches were carried out using CSD version 5.25 (November 2003, 298 097 structures)⁸ using the program Quest3D.¹¹ Overall ‘non-bonded’ (reactant) and ‘bonded’ (product) datasets were generated, including both organic and metal–organic structures, together with separate organic and metal–organic structure datasets in each case. Secondary search criteria were applied to all retrieved datasets, so as to eliminate structures having: (a) a crystallographic R factor > 10%, (b) residual errors after CSD validation checks, (c) crystallographic disorder and (d) polymeric (catena) bonds. Data analyses were carried out using the CSD system program Vista¹² extended by one of us (GPS) to handle up to 199 999 substructural fragments.

Non-bonded reactant searches: specific criteria

These searches (Fig. 1) comprised two alkene units having their C⋯C contact distances, B2 and B4, constrained to be less than 4.078 Å, i.e. less than 2.4V_C—the sum of the van der Waals radii plus 20%. This is consistent with the proposal of Schmidt⁶ that for a solid state [2 + 2] cycloaddition reaction to occur the reacting carbons should be separated by less than 4.2 Å. Further, fragments were only accepted if the sum of the cross distances (D1 + D2 in Fig. 1) was greater than the sum of the non-bonded C⋯C distances (B2 + B4). If both alkene groups located by this process existed in the same molecule, then they were only accepted as potential reacting groups if the alkene carbons were separated by more than 4 covalent bonds within the molecule. Fragments in which one or more of the alkene carbon atoms was attached to any other atom via a double bond, as well as fullerenes, were also excluded as these structures are unlikely to undergo a [2 + 2] cycloaddition reaction.

Fig. 1 Non-bonded reactant search fragment with geometrical parameters defined.

Bonded product searches: specific criteria

The product searches were carried out using a cyclobutane fragment (Fig. 2). Structures having exocyclic double bonds were rejected as they are unlikely to have been the result of a [2 + 2] cycloaddition reaction. In addition, structures were rejected that contained (a) a bicyclobutane fragment, i.e. having a C1–C3 or C2–C4 bond, or (b) a bicyclo(1.1.0)pentane fragment, since neither species would have been formed from intramolecular alkenes separated by only three covalent bonds.

Fig. 2 Bonded cyclobutane product search fragment with geometrical parameters defined.

Geometrical descriptors and topological symmetry

For each CSD fragment that satisfied the search criteria, the Quest3D program generated the geometrical parameters whose mnemonics are shown in Fig. 1 and 2. We have also calculated the puckering angle θ for each four-membered ring as defined in Fig. 3, where θ is the complement of the dihedral angle formed about the ring diagonal by the planes C₁, C₂, C₃ and C₁, C₃, C₄ in Fig. 1 and 2.

Fig. 3 Definition of the cyclobutane ring-puckering angle θ.

In order to account for the D_2h topological symmetry of the non-bonded fragment (Fig. 1) the resultant geometrical dataset was symmetry expanded in accordance with the permutational operators listed in Table 1(a) using an external program written by one of us (GPS), since the automated PERMUTE function built into Quest3D does not operate on datasets arising from non-bonded searches. For the bonded searches, the topological symmetry of the fragment is D_4h and the PERMUTE function in Quest3D generated the symmetry-expanded dataset according to the permutational operators listed in Table 1(b).

Table 1 (a) Permutational operators applied to the geometrical parameters for fragments located by the non-bonded searches (Fig. 1, topological symmetry D_2h). (b) Permutational operators applied to the geometrical parameters for fragments located by the bonded searches (Fig. 2, topological symmetry D_4h)

Data analysis: principal component analysis and symmetry deformation parameters

Principal component analysis (PCA)¹³ is a numerical technique which carries out an eigen-analysis of the variance in an n-dimensional dataset. PCA re-expresses the original data with respect to a set of m mutually orthogonal axes, the principal components (PCs), which together account for a large percentage (say >99%) of the original variance. The PCs are generated in decreasing order of the percentage variance accounted for by each component. If the number of PCs (m) is lower than the dimensionality of the original dataset (n), then the dimensionality of the overall problem is reduced, and coordinates of the data points in PC space (termed the PC scores) may be plotted with respect to the mutually orthogonal PC axes to provide simplified visualisations of the original data.

Two factors are relevant to the application of PCA to datasets of geometrical parameters derived from crystal structure data: (a) PCA should only be applied to sets of data of similar type, e.g. distances, angles or torsion angles, and (b) when PCA is applied to datasets that have been expanded according to the highest topological symmetry of the search fragment (i.e. the dataset includes all permutational isomers), then the PCs are directly correlated to the symmetry deformation coordinates (SDCs) generated using group theory.

In the present work we have carried out separate PCAs on the 4D symmetry-expanded datasets of the distances (B1–B4), angles (A1–A4) and torsions (T1–T4), for both the non-bonded and bonded fragments depicted in Fig. 1 and 2. We have also derived the SDCs for both types of search fragments, and these are given in Table 2(a) and (b). We have then used the PC results to identify the SDCs which show the most variation in each dataset (non-bonded and bonded), and these SDCs were then used to construct scatterplots to identify any systematic geometrical trends that might indicate a reaction coordinate for [2 + 2] cycloaddition.

Table 2 (a) Symmetry deformation coordinates and principal component analysis results for the non-bonded alkene reactant search fragment having D_2h reference geometry. (b) Symmetry deformation coordinates and principal component analysis results for the bonded cyclobutane product search fragment having D_4h reference geometry

SDC label	Symmetry deformation coordinate (SDC)	Symmetry operator	Eigen value	Variance
SA1	1/2 × (A1 + A2 + A3 + A4)	Ag	0.075	1.886
SA2	1/2 × (A1 − A2 + A3 − A4)	B1g	3.773	94.330
SA3	1/2 × (A1 + A2 − A3 − A4)	B2u	0.001	0.037
SA4	1/2 × (A1 − A2 − A3 + A4)	B3u	0.150	3.747
ST1	1/2 × (T1 + T2 + T3 + T4)	Au (a)	0.016	0.401
ST2	1/2 × (T1 − T2 − T3 + T4)	Au (b)	3.977	99.415
ST3	1/√2 × (T1 − T4)	B2g	0.002	0.057
ST4	1/√2 × (T3 − T2)	B3g	0.005	0.127
SB1	1/2 × (B1 + B2 + B3 + B4)	Ag (a)	1.475	36.876
SB2	1/2 × (B1 − B2 + B3 − B4)	Ag (b)	1.872	46.807
SB3	1/√2 × (B1 − B3)	B2u	0.299	7.479
SB4	1/√2 × (B2 − B4)	B3u	0.354	8.839

---

SDC label	Symmetry deformation coordinate (SDC)	Symmetry operator	Eigen value	Variance
SA1	1/2 × (A1 + A2 + A3 + A4)	A1g	2.119	52.982
SA2	1/2 × (A1 − A2 + A3 − A4)	B2g	1.183	29.575
SA3	1/√2 × (A1 − A3)	Eu (a)	0.349	8.722
SA4	1/√2 × (A4 − A2)	Eu (b)	0.349	8.722
ST1	1/2 × (T1 + T2 + T3 + T4)	A1u	0.000	0.007
ST2	1/2 × (T1 − T2 − T3 + T4)	B1u	3.999	99.980
ST3	1/√2 × (T1 − T4)	Eg (a)	0.000	0.006
ST4	1/√2 × (T3 − T2)	Eg (b)	0.000	0.006
SB1	1/2 × (B1 + B2 + B3 + B4)	A1g	1.298	32.438
SB2	1/2 × (B1 − B2 + B3 − B4)	B1g	0.931	23.272
SB3	1/√2 × (B1 − B3)	Eu (a)	0.886	22.145
SB4	1/√2 × (B4 − B2)	Eu (b)	0.886	22.145

---

In discussing the conformational variations exhibited by the developing (Fig. 1) and actual (Fig. 2) four-membered rings, we have used the puckering angle θ (Fig. 3) throughout, since this is the well-understood single conformational parameter. We note however that ST2 in Table 2(a) and (b), which maps this conformational variation in terms of the intra-annular torsion angles in both symmetries, is linearly related to θ,¹⁴ hence plots involving ST2 or θ convey equivalent information.

Results and discussion

Non-bonded reactant searches—D_2h reference geometry

The CSD search produced 10 808 entries (22 558 substructural fragments) that satisfied all search criteria, yielding a symmetry-expanded dataset of 90 232 fragments for analysis. The PCA results (Table 2) show that the SDCs of most importance for this dataset are SA2, ST2, SB1 and SB2, and the six independent scatterplots were generated and examined for distortions that may indicate a reaction coordinate. The most significant plots are shown in Fig. 4.

Fig. 4 (a) Plot of SB1 vs. SB2. (b) Plot of SA2 vs. SB2. (c) Plot of the ring-puckering angle θ for non-bonded dataset.

Fig. 4(a) (SB1 vs. SB2) indicates that as the sum of the distances (SB1) decreases so does SB2, i.e. the difference between (B1 + B3) (the sum of the bonded alkene distances) and (B2 + B4) (the sum of the non-bonded C⋯C contact distances). The major proportion of this decrease in SB2 arises from a significant decrease in the non-bonded C⋯C distances (B2 and B4) as the transition state is approached, since there is only a relatively small increase in the bonded distances (B1and B3) as the alkene bond loses double bond character.

Similarly, Fig. 4(b) (SA2 vs. SB2) indicates that as the non-bonded distance between the two alkene groups decreases so does the difference between (A1 + A3) and (A2 + A4) (see Fig. 1). This suggests that as the non-bonded distances decrease all of the angles within the putative cyclic reaction product tend towards similar values; however, these values are not necessarily 90°. This observation is supported by the wide range of puckering angles θ (Fig. 3) that are observed for the developing cyclobutane ring. It is well known^9,14,15 that changing the intra-annular valence angles in cyclobutane by just 2° induces quite significant ring puckering, yielding a θ-value of 30°. Taken together, Fig. 4(b) and (c) provide evidence that the cyclobutane product is being generated in puckered as well as planar forms.

Using the same search criteria as described previously for the non-bonded reactant searches, separate datasets for intra- and intermolecular alkenes were created. SDC plots analogous to those in Fig. 4(a) and (b) showed similar characteristics to those for the composite dataset and indicate that intra- and intermolecular alkenes follow the same reaction pathway. However, the intramolecular dataset does exhibit a somewhat different θ-range, as illustrated in Fig. 5(a) and (b). We also examined scatterplots derived from the separate ‘organic’ and ‘metal–organic’ searches and observed that both of these datasets exhibit the same trends as those observed in the composite dataset.

Fig. 5 (a) Plot of the ring-puckering angle θ for intermolecular alkenes. (b) Plot of the ring-puckering angle θ for intramolecular alkenes.

Bonded product searches—D_4h reference geometry

The CSD search generated 1717 entries (containing 3074 cyclobutane fragments) which matched the search criteria, giving a D_4h-expanded dataset of 24 592 fragments for analysis. The D_4h symmetry was used to derive the SDCs, which are listed in Table 2(b) together with the PCA results. Again, it was found that the organic and metal–organic species show the same trends as those displayed in the composite dataset and these separate datasets were not examined further.

The SDCs that map on to the PCs that account for almost all of the variance within the dataset are SA1, SA2, ST2, SB1, SB2, SB3 and SB4. Pairwise scatterplots were examined for trends within the dataset and these reveal only small variations in bond lengths and valence angles around the ring. However examination of Fig. 6, the histogram of the puckering angle (θ, equivalent to ST2 as noted above), shows that the cyclobutane product forms across the well known range of planar and puckered forms.^6,14,15 Further analysis of the bonded dataset shows that intramolecular [2 + 2] cycloadditions would have resulted in the formation of all of the structures where the puckering angle, θ, exceeds 45°. This may well result from the mutual orientation of the reactant alkene groups being imposed by the rest of the molecule and by the constraints imposed by the solid state reaction conditions.

Fig. 6 Plot of the ring-puckering angle (θ) for cyclobutane products.

The reaction pathway

Fig. 7(a) and (b) show two of the scatterplots (SB1 vs. SB2 and SA2 vs. SB2, respectively) in which data points for the ‘reactant’ and ‘product’ searches are superimposed and displayed on the same axes. Both plots clearly show that all data points fall on a continuous pathway, but that the cluster of points that arise from the non-bonded reactant searches (black points in Fig. 7(a) and (b)) and the cluster that arises from the bonded product searches (grey points in Fig. 7(a) and (b)) are separated by a region which corresponds to the high-energy transition state for which, of course, no structural characterisations exist in the CSD.

A proposed mechanism⁷ for the [2 + 2] cycloaddition reaction in the gas phase suggests that one of the non-bonded distances, say B2 in Fig. 1, shortens first, and this is followed by a twisting of the alkene component before the other non-bonded distance, B4, shortens to form the cyclobutane product. Clearly, the large amount of atomic movement involved here would be impossible in a solid state reaction, and this is borne out by Fig. 7(a) and (b). Thus, Fig. 7(a) shows that as the alkenes approach each other the non-bonded distances (B2 and B4) tend towards similar values, as do the bonded distances (B1 and B3). This suggests that, in the solid state at least, there is a concerted shortening of both B2 and B4, and a concerted elongation of B1 and B3, as the reaction proceeds. Once formed, the cyclobutane product has closely similar bond lengths and valence angles, as illustrated by the compact nature of the (grey) product cluster.

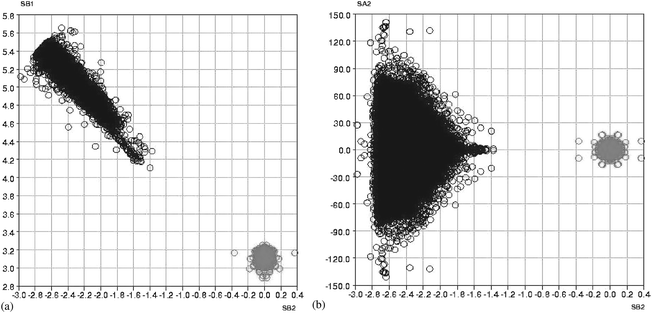Fig. 7 (a) The reaction pathway—superimposed plot of SB1 vs. SB2 for the reactants and products (black—alkene reactants, grey—cyclobutane products). (b) The reaction pathway—superimposed plot of SA2 vs. SB2 for the reactants and products (black—alkene reactants, grey—cyclobutane products).

Fig. 7(b) shows that as the non-bonded distances decrease the angles A1–A4 tend towards the same value although this is not necessarily the 90° required to form a planar cyclobutane product. The wide range of ST2 [the difference between the values of (T1 + T4) and (T2 + T3)] and of the cyclobutane puckering angle (θ) indicate that the cyclobutane fragment can form in either the planar or puckered form^6,14,15 and this is possibly dependant on the steric requirements of the groups directly attached to the alkene carbons that form the ring.

Conclusions

Crystallographic evidence shows that the formation of a cyclobutane product from two reacting alkenes via solid state [2 + 2] cycloaddition occurs through a concerted decrease in B2 and B4 (the non-bonded C⋯C distances) and a concomitant increase in B1 and B3 (the C=C double bonded distances in the reactant molecules). This is accompanied by a decreased variation in the angles around the developing four-membered ring. However, the reaction is not dependent on parallelism of the alkenes and significant twisting can be accommodated, which leads to the formation of puckered cyclobutanes, provided that similar intra-annular angles are maintained.

Our mapping of the reaction pathway, derived from many thousands of crystallographic observations, is strongly supported by the available crystallographic observations of individual solid state [2 + 2] cycloaddition reaction products. Thus, we have searched the CSD for examples of cyclobutane reaction products by restricting the substructural search query of Fig. 2 to those CSD entries containing the text string ‘irrad’ (to locate the phrases ‘irradiation product’ or ‘irradiated product’. This combined search yielded 22 CSD entries which, after the permutational symmetry had been accounted for, contained 264 cyclobutane fragments for which the puckering angle (θ) was calculated in each case. The resulting histogram (Fig. 8) shows that 80 (30%) of these examples have planar rings, while 184 (70%) have θ-values between 6° and 45°, reinforcing the conclusion from the more general analysis that solid state [2 + 2] cycloadditions of alkenes can result in both planar and puckered cyclobutane products.

Fig. 8 Histogram of the ring-puckering angle (θ) for cyclobutane fragments that have been generated by solid state photochemical reactions.

Acknowledgements

HAS acknowledges financial assistance from the EPSRC (UK) and the CCDC.

References

1. V. Ramamurthy and K. Venkatesan, Chem. Rev., 1987, 87, 433.
2. S. Ohba, H. Hosomi and Y. Ito, J. Am. Chem. Soc., 2001, 123, 6349.
3. D. B. Varshney, G. S. Papaefstathiou and L. R. MacGillivray, Chem. Commun., 2002, 1964.
4. T. Suzuki, T. Fukushima, Y. Yamashita and T. Miyashi, J. Am. Chem. Soc., 1994, 116, 2793.
5. V. Enkelmann, G. Wenger, K. Novak and G. Wagener, J. Am. Chem. Soc., 1993, 115, 10390.
6. M. D. Cohen and G. M. J. Schmidt, J. Chem. Soc., 1964, 1996; M. D. Cohen and G. M. J. Schmidt, J. Chem. Soc., 1964, 2000; M. D. Cohen and G. M. J. Schmidt, J. Chem. Soc., 1964, 2014.
7. F. Bernardi, A. Bottoni, M. Olivucci, A. Venturini and M. A. Robb, J. Chem. Soc., Faraday Trans., 1994, 90, 1617.
8. F. H. Allen, Acta Crystallogr., Sect. B: Struct. Sci., 2002, B58, 380.
9. H. B. Bürgi and J. D. Dunitz, in Structure Correlation, ed. H. B. Bürgi and J. D. Dunitz, VCH Publishers Inc., New York, 1994, vol. 1, p. 163.
10. T. P. E. Auf de Heyde and H.-B. Bürgi, Inorg. Chem., 1989, 28, 3960.
11. F. H. Allen and O. Kennard, Chem. Des. Autom. News, 1993, 8(1), 31.
12. Vista – a program for the analysis and display of crystal structure data derived from the CSD, Cambridge Crystallographic Data Centre, 12 Union Road, Cambridge, UK CB2 1EZ, 1996.
13. C. Chatfield and A. J. Collins, An Introduction to Multivariate Analysis, Chapman and Hall, London, 1980.
14. J. D. Dunitz, X-ray Analysis and the Structure of Organic Molecules, Cornell University Press, Ithaca, USA, 1979, pp. 423–424.
15. F. H. Allen, Acta Crystallogr., Sect. B: Struct. Sci., 1984, B40, 64.

---