Estimation of melting points of pyridinium bromide ionic liquids with decision trees and neural networks

Abstract

Regression trees were built with an initial pool of 1085 molecular descriptors calculated by DRAGON software for 126 pyridinium bromides, to predict the melting point. A single tree was derived with 9 nodes distributed over 5 levels in less than 2 min showing very good correlation between the estimated and experimental values (R² = 0.933, RMS = 12.61 °C). A number n of new trees were grown sequentially, without the descriptors selected by previous trees, and combination of predictions from the n trees (ensemble of trees) resulted in higher accuracy. A 3-fold cross-validation with the optimum number of trees (n = 4) yielded an R² value of 0.822. A counterpropagation neural network was trained with the variables selected by the first tree, and reasonable results were achieved (R² = 0.748). In a test set of 9 new pyridinium bromides, all the low melting point cases were successfully identified.

---

Introduction

Ionic liquids (IL) have gained an enormous importance in recent years due to their green and tuneable properties. The negligible vapour pressures allow for their potential use as green substitutes for organic volatile solvents.¹ Judicious choice of anion and cation permits production of IL's with physical and chemical properties fitted to a specific problem.² Solubility, polarity, viscosity and melting points are thus of utmost importance, and their estimation from the chemical structure is highly desired to focus synthetic efforts on IL's with the best chances of exhibiting the required characteristics.

Traditionally, chemists have relied on chemical intuition to predict such properties. But in some cases, very subtle features have a tremendous impact on the property. Fig. 1 illustrates such behaviour related to the melting point.

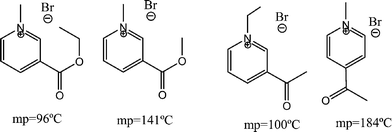Fig. 1 Examples of similar chemical structures of pyridinium bromides with highly diverse melting points.

In cases like that, computational tools can analyse experimental data to ferret out hidden relationships between aspects of the chemical structure and the melting point, and propose a predictive model.

Chemical structures can be numerically encoded by molecular descriptors. Thousands of molecular descriptors have been proposed covering features from constitution to geometry to electronic properties, and they can be easily calculated with available software. Then, relationships between molecular descriptors and the property being predicted can be obtained computationally. Models like neural networks (NN),³ decision trees,⁴ ensembles of trees,⁵ partial least squares (PLS)⁶ and multiple linear regressions (MLR) are among the most popular. Some linear relationships between molecular descriptors and melting points of ionic liquids were reported in the past.^7,8

Usually the most important features concerning models obtained from computational tools are the flexibility to model multiple mechanisms of action, the capability to deal with high dimensional data, and the level of predictive accuracy.

Neural networks and decision trees are highly flexible and are able to account for multiple mechanisms of action, while linear methods are more rigid. On the other hand NNs are not so efficient dealing with large sets of variables. Time-consuming genetic algorithms^9,10 are often used to obtain more compact and efficient sets of variables for MLR and neural networks. Decision trees are fast and efficient for high dimensional data, but usually show relatively low prediction accuracy. Accuracy can be significantly improved with ensembles of trees (forests).¹¹ Classification and regression trees (CART) have recently gained much interest in chemoinformatics, particularly for QSAR studies based on large pools of available molecular descriptors.^5,11–13

In this paper we report our studies using decision trees and ensembles of decision trees (forests) to model the melting points of a series of 126 pyridinium bromides, as a fast, flexible alternative to linear regressions. Additionally, the potential of the molecular descriptors chosen by the trees to train counterpropagation neural networks (CPG NNs) was investigated.

Methodology

Data set

In order to validate the approach, we used the same data set of 126 pyridinium bromides as Katritzky et al.⁷ with objects organized from the lowest to the highest melting point, comprising a range of melting points between 30–200 °C. The cross-validation was performed according to the Katritzky et al.⁷ work, with three subsets (set A = 1st, 4th …124th; set B = 2nd, 5th …125th; and set C = 3rd, 6th …126th).

Molecular descriptors

3D models for the 126 pyridinium cations were obtained using the CORINA 3.0 program,^14–16 and these were submitted to DRAGON 3.0 to calculate the molecular descriptors¹⁷—1045 molecular descriptors were obtained, after excluding constant or nearly constant descriptors. An additional 40 descriptors were defined to include properties such as Gasteiger charges, and were calculated with PETRA¹⁸ software version 3.1. 3D models generated by CORINA seemed particularly suitable for this study since the software is based on rules derived from a database of crystallographic structures. Descriptors calculated by DRAGON include a) 3D type descriptors, which account for the 3D geometry of the molecule (WHIM,¹⁹ geometrical, RDF,²⁰ GETAWAY,²¹ Randic molecular descriptors, charge indices and aromaticity descriptors); b) 2D type descriptors, related to the connectivity between the atoms of the molecule (including topological descriptors, molecular walk counts, BCUT, Galvez and 2D-autocorrelation descriptors); c) 1D descriptors, which encode structural information like counts of specific functional groups, and atom-centred fragments; and d) 0D descriptors which represent global characteristics of the molecule such as the atomic weight. A list of all descriptors is available in the Supplementary Information.†

Decision trees

A tree is sequentially constructed, partitioning objects from a parent node into two child nodes. Each node is produced by a logical rule, usually defined for a single variable, where objects below a certain variable's value fall into one of the two child nodes, and objects above fall into the other child node (a graphical representation of a decision tree is presented below in the Results section). The prediction for an object reaching a given terminal node is obtained as the average of the mp of the objects (in the training set) reaching the same terminal node. The entire procedure comprises three main steps. First an entire tree is constructed by data splitting into smaller nodes, each produced split is evaluated by an impurity function⁴ which decreases as long as the new split permits the child node's content to be more homogeneous than the parent node. Second, a set of smaller, nested trees is obtained by obliteration (pruning) of certain nodes of the tree obtained in the first step. The selection of the weakest branches is based on a cost-complexity⁴ measure that decides which sub-tree, from a set of sub-trees with the same number of terminal nodes, has the lowest (within node) error. Finally, from the set of all nested sub-trees, the tree giving the lowest value of error in cross-validation (where the set of objects used to grow the tree is different from the prediction set) is selected as the optimal tree.

In this study, regression trees were grown with the R program version 1.9.0 using the RPART library with the default parameters.²² A tree was obtained by submitting the 126 molecules to RPART, each molecule represented by 1085 molecular descriptors. The variables chosen for building the tree (global tree) were further evaluated in an additional 3-fold cross-validation procedure. This step employed exactly the same 3 subsets A, B, and C as in the Katritzky et al. study.⁷ The cross-validation trees were allowed to grow using a) only the variables selected for the global tree, and b) only the objects pertaining to 2 subsets. At the end, predictions were obtained for the third subset (not used for growing the tree).

Ensemble of trees (forest)

The above described methodology was followed to grow regression trees, but now n trees were sequentially grown, instead of only one. The predictions were then obtained by averaging the individual n predictions. The n trees were grown in the following sequence. The first tree was obtained starting from the entire pool of 1085 descriptors, then the descriptors selected for the first tree were erased from the input file, and this is again submitted to the R program, to construct the second tree. The sequence was repeated until n trees were obtained. A 3-fold cross-validation procedure was performed as before, for each of the n trees, and the n predictions were averaged to obtain cross-validation predictions. Results were obtained for n varying between 2 and 10.

Counterpropagation neural networks

A CPG NN consists of a 2D grid of neurons organized into an input layer and an output layer—Fig. 2 left.³ Each input neuron has as many elements (weights) as there are input parameters, and each output neuron contains as many weights as there are types of outputs. In our case we only have one type of output, the melting point. The network learns by adjusting the weights during a training phase, in which the objects from the training set are repeatedly submitted to the network.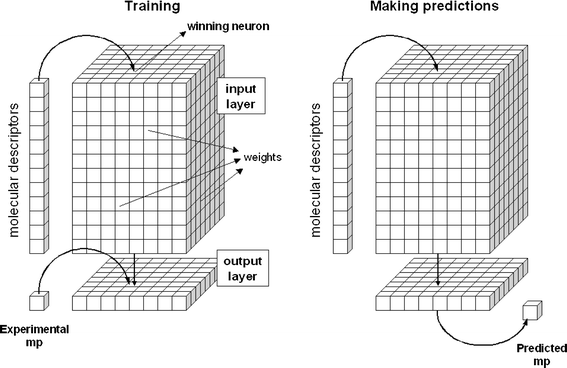

Fig. 2 Training and prediction procedures in a CPG NN that learns relationships between molecular descriptors and melting points.

Before the training, the weights are randomly generated. During the training, each object activates the neuron with the most similar input weights to the molecular descriptors of that object—this is the winning neuron. The weights of the winning neuron are adjusted to become even closer to the input vector (molecular descriptors) and the neighbouring neurons are also corrected to approach the input object, with the correction depending on the distance to the winning neuron. The corresponding output weight is also changed to become closer to the experimental value of the property being predicted. The network is trained with all the objects from the training set several times until a predefined number of cycles is reached. Afterward, the network is able to make predictions for new compounds—Fig. 2 right. When a new object (molecule) is submitted, the network activates the winning neuron, and uses the corresponding output weight as the predicted value, in our case the predicted melting point.

In this investigation, CPG NNs were trained using the descriptors selected for the first decision tree. Training and cross-validation were performed with the same subsets as for the decision trees. The molecular descriptors were linearly scaled between 0 and 1. For some experiments (see Results) each descriptor i was multiplied by a factor L − l_i, where L is the number of levels in the first tree, and l_i is the distance of the node defined by descriptor i to the root node. CPG NNs were implemented with in-house developed software based on JATOON Java applets.^23,24 The networks (with 12 × 12 neurons for the training set A + B + C and 10 × 10 neurons for the cross-validation experiments) were trained over 100 cycles, using an initial learning span of 5 neurons.

Results

Prediction of melting points by a decision tree

From the entire pool of 1085 descriptors for the 126 pyridinium bromides, a regression tree was derived with 9 nodes distributed over 5 levels—Fig. 3 and Table 1. The calculations took less than 2 min using a PC with a Pentium™ IV 2.66 GHz CPU. A good correlation (R² = 0.933, RMS = 12.61 °C) was obtained between the estimated and experimental values. The results are shown in Fig. 4 and Table 2 and evaluated according to different measures of error. In this application, accurate ranking is probably the most important feature of a predictive model to be used in establishing priorities for laboratory work. The Spearman correlation coefficient was thus included, as it measures the ability to rank objects according to a property.

Fig. 3 Regression tree model obtained for the estimation of melting points. Terminal nodes are represented with rectangles while intermediate nodes are represented with ovals. The number of objects reaching a node, as well as the average of their melting points is displayed inside each node. The rules are displayed near the corresponding nodes using names for the descriptors as defined in Table 1.

Fig. 4 Predicted values vs. experimental melting points (mp) for the set of 126 pyridinium bromides. Predictions were obtained by a regression tree grown with 126 objects described by 1085 variables.

Table 1 Molecular descriptors selected to build a regression tree

Descriptor	Description
G2	Geometrical, G2 is the gravitational index (bond restricted).
	G2 = , where the summation goes over all pairs of bonded atoms, mi is the atomic mass of atom i, and rij is the distance between atoms i and j.
RDF105u	RDF, ^20 accounts for the abundance of pairs of atoms at a distance of 10.5 Å.
HATSe	GETAWAY descriptor, ^21 accounts for the influence of individual atoms in the total shape of the molecule combined with electronegativities. HATSe is the leverage-weighted total index weighted by atomic Sanderson electronegativities.
R6P	GETAWAY descriptor, ^21 R6P is the R autocorrelation of lag 6 weighted by atomic polarizabilities.
De	WHIM descriptor, ^19 geometrical descriptor calculated on the projections of the atoms along principal axes. De is total accessibility index weighted by atomic Sanderson electronegativities.
piPCO7	Topological descriptor, 2D descriptor, independent of the conformation. piPCO7 is the molecular multiple path count of order 7.
GATS2v	2D Geary autocorrelation, 2D descriptor, independent of the conformation, obtained by the summation of all products of the terminal atoms of all the paths of path length (lag) 2 weighted by van der Waals volumes.
HATS7v	GETAWAY descriptor, ^21 accounts for the influence of individual atoms in the total shape of the molecule combined with van der Waals volume. HATS7v is the leverage-weighted autocorrelation of lag 7 weighted by atomic van der Waals volume.
H0p	GETAWAY descriptor, ^21 accounts for the influence of individual atoms in the total shape of the molecule combined with atomic polarizabilities. H0p is the H autocorrelation of lag 0 weighted by atomic polarizabilities.

---

Table 2 Predictions^a obtained by trees, CPG NNs and linear methods for the training set (entire set) and in cross-validation (CV) tests⁷

		A + B + C (training set)	A (CV)	B (CV)	C (CV)
a RMS is the root mean square of errors; R^2 is the goodness of fit correlation coefficient; R^2* is the square of the Pearson correlation coefficient; ē is the mean error, and SP is the Spearman correlation coefficient.
Decision tree	RMS	12.61	22.13	28.27	26.07
	R ^2	0.933	0.794	0.662	0.711
	R ^2*	0.933	0.795	0.708	0.714
	ē	10.07	15.95	21.76	18.61
	SP	0.940	0.871	0.798	0.818
CPG NN (trained with weighted descriptors)	RMS	24.41	29.21	23.97	31.50
	R ^2	0.748	0.640	0.757	0.578
	R ^2*	0.762	0.661	0.783	0.592
	ē	19.67	24.29	19.38	26.80
	SP	0.871	0.789	0.901	0.754
Ensemble of 3 trees	RMS	11.41	18.79	22.06	25.42
	R ^2	0.945	0.851	0.794	0.725
	R ^2*	0.946	0.855	0.809	0.737
	ē	9.420	15.33	16.82	20.06
	SP	0.937	0.925	0.873	0.858
Ensemble of 4 trees	RMS	10.82	17.11	20.32	23.67
	R ^2	0.950	0.877	0.825	0.772
	R ^2*	0.951	0.882	0.836	0.762
	ē	8.727	13.73	15.22	18.64
	SP	0.954	0.942	0.886	0.861
Ensemble of 8 trees	RMS	9.910	18.17	18.70	21.96
	R ^2	0.958	0.861	0.852	0.795
	R ^2*	0.960	0.870	0.880	0.812
	ē	8.140	14.55	14.88	17.65
	SP	0.962	0.934	0.913	0.910
Multiple linear regression (MLR)^7	RMS	23.41	27.10	25.53	24.05
	R ^2	0.788	0.769	0.779	0.757
	R ^2*	0.768	n.a.	n.a.	n.a.
	ē	18.07	n.a.	n.a.	n.a
	SP	0.871	n.a.	n.a.	n.a.

---

Prediction of melting points by ensembles of trees (forests)

Combination of the predictions from an ensemble of regression trees improved the correlation between the predicted and the experimental melting points—Figs. 5 and 6. However, increasing the number of trees (n) in the forest further than n = 4 yielded no significant advantage. A 3-fold cross-validation with the ensemble of 4 trees yielded a reasonable match between the predicted and experimental values—R² = 0.822, Fig. 7. Regression tree models for the 10 grown trees are available in the Supplementary Information.†

Fig. 5 Influence of the size of the forest on the quality of mp predictions, growing the trees with the whole data set, or in a 3-fold cross-validation procedure.

Fig. 6 Predicted vs. experimental melting points (mp) for the set of 126 pyridinium bromides. Predictions were obtained by averaging predictions from 4 regression trees grown using the 126 objects.

Fig. 7 Predicted vs. experimental melting points (mp) for the set of 126 pyridinium bromides with a 3-fold cross-validation procedure on an ensemble of 4 regression trees.

Prediction of melting points by CPG neural networks

The 9 variables selected by the first tree were investigated for their ability to train CPG NNs. We use the decision trees as a tool for a fast detection of relevant variables in order to train CPG NNs. Variables corresponding to nodes near the top of the tree are responsible for large partitions of the data set, while variables far from the root node are responsible for detail partitions. Having this in mind, we performed additional experiments multiplying the descriptors by factors according to the level they occupy in the tree—a factor of 5 for the upper level, 4 for the second level, and so on until the bottom level which gets a factor of 1. The results are shown in Table 3.

Table 3 Prediction of melting points by CPG NNs trained with unweighted and weighted descriptors selected by the trees

	Tree descriptors R^2	Tree descriptors (weighted) R^2
Prediction for the training set (A + B + C)	0.653	0.748
CV—prediction for test set A	0.475	0.640
CV—prediction for test set B	0.627	0.757
CV—prediction for test set C	0.406	0.578

---

Prediction of melting points for a new set of pyridinium bromides

A new set of 9 objects was obtained from the literature and predictions were made using the previously developed models. The predictions obtained by a single tree and by the ensemble of 4 trees are displayed in Table 4.

Table 4 Predictions for the new set of objects using a single tree and the ensemble of 4 trees

Pyridinium bromide	Experimental mp/°C	Decision tree	Ensemble of 4 trees
1-(2-Oxo-butyl)-pyridinium	180 ref. 29	138	122
1-(3-Methyl-2-oxo-butyl)-pyridinium	149 ref. 29	138	139
1-Isobutoxycarbonylmethyl-pyridinium	87 ref. 29	85	84
1-(2-Dodecanoyloxy-ethyl)-pyridinium	80.5 ref. 30	44	44
1-(2-Hexadecanoyloxy-ethyl)-pyridinium	80 ref. 30	44	44
1-(2-Icosanoyloxy-ethyl)-pyridinium	81 ref. 30	44	44
3,4-Dihydroxy-2-(1-hydroxy-ethyl)-1-methyl-pyridinium	142 ref. 31	125	108
1-Benzyl-3-(2-oxo-oxazolidine-3-carbonyl)-pyridinium	109 ref. 32	85	84
1-Benzyl-3-dimethylcarbamoyl-pyridinium	158.5 ref. 32	85	84

---

Fig. 8 shows the output layer of the CPG NN trained with the weighted descriptors for the 126 objects. The neurons were coloured according to their output values, and the 9 new objects were mapped onto the surface. The activated neurons are identified by the experimental mp of the mapped objects.

Fig. 8 Mapping of the 9 new objects onto the output layer of a CPG NN (see text). The labels shown in the map correspond to experimental mp values of the nine objects. Low mp objects were correctly identified by exciting neurons in the blue region.

Discussion

The first obtained regression tree is based on 9 molecular descriptors, and exhibits high predictive power. The root node is defined by the G2 descriptor (a gravitational index), which can be related to the size of the molecule—G2 is larger for large molecules. The first node assigns low melting points to compounds with high G2 index. This descriptor was not selected by Katritzky et al.'s approach⁷ although it was certainly available in the initial pool of descriptors—the lack of a linear relationship between the gravitational index and the mp probably prevents a linear approach to using it. Interestingly, the G2 descriptor was found to be highly correlated with boiling points in a set of 298 organic compounds, although in the opposite direction.²⁵ Further partition of the left node (low melting points) is based on the RDF descriptor at 10.5 Å, which is clearly related to long chains—detection of pairs of atoms with an interatomic distance of 10.5 Å.²⁰ In this data set, the presence of alkyl chains longer than C8 are indeed associated with melting points at the lower end of the range (<60 °C).²⁶

The descriptors involved in the right main branch of the tree are more difficult to interpret. Most of the selected descriptors are 3D descriptors, particularly GETAWAY descriptors, which are calculated from a single molecular conformation. This reinforces our initial proposal that 3D structures generated by CORINA are useful, and that working with a single conformation is realistic since the melting point can be viewed as a property of a solid. GETAWAY descriptors account for the influence of individual atoms on the shape of the molecule, and are often combined with atomic properties such as electronegativities, polarizabilities or van der Waals volumes.²¹ GETAWAY descriptors have been successful for the prediction of melting points of polycyclic aromatic hydrocarbons and polychlorinated biphenyls.²⁷ The other 3D descriptor is a WHIM descriptor, namely the total accessibility index weighted by atomic Sanderson electronegativities. WHIM descriptors were designed to capture 3D information regarding molecular size, shape, and symmetry and atom distribution with respect to the molecule as a whole.¹⁹ The De descriptor is a compactness descriptor, which encodes information about the distribution of electronegativities along the three axes of the molecule. Another size directional WHIM index was selected in a QSPR model to predict melting points of polychlorinated biphenyls.²⁸

The piPCO7 descriptor isolates a group of 12 compounds with relatively low melting point (average = 83 °C). This descriptor counts paths of order 7 and at the same time is influenced by multiple bonds. In fact, most of the isolated 12 compounds have no multiple bonds outside the pyridinium ring, and most of the 25 compounds in the right child node have a functional group with a multiple bond.

The accuracy of the predictions was significantly improved by combining several trees in an ensemble—Fig. 5 and Table 2. We chose the ensemble with 4 trees as the optimum, since after that point no significant improvement in predictive ability can be observed. This forest model accurately fits the experimental data (R² = 0.950, RMS = 10.82 °C), and performs well in cross-validation tests (R² = 0.877, 0.825, 0.772, respectively for sets A, B, and C). Interpretation of these results should take into account the difficulty of modelling melting points of organic salts, and the fuzziness associated with such data—differences of 10–15 °C in the reported mp for the same compound from different authors are not uncommon in the literature. An R² value of 0.950 compares to the value of 0.788 obtained by Katritzky et al.⁷ and the value of 0.790 obtained by Eike et al.⁸ This better fitting of the entire set (after the entire set was used to develop the model) may be due to the higher flexibility of the decision trees and the larger number of descriptors employed. A more significant comparison can be obtained with cross-validation tests using the same subsets as Katritzky et al. (Table 2)—the ensembles of trees yielded slightly better correlations than the linear methods. However, it must be emphasized that it is not possible to rigorously compare the two methods without an external set, even if the procedures here described for variable selection and cross-validation were designed to follow as much as possible those described in the previous studies. Essentially the quality of predictions by trees and MLR are not very different.

Although the ensemble of 4 trees employs 35 descriptors (9 descriptors in the first tree, 9 in the second tree, 8 in the third tree, and 9 in the fourth tree), this number overstates the real amount of information encoded by the set of descriptors. In fact, the architectures of the 4 trees overlap to a large extent, and the 4 trees use descriptors which are in most cases highly correlated, i.e. the descriptors do not change much from tree to tree, even if they are not exactly the same. The left main branch of the trees (leading to low mp predictions) is particularly similar in all the 4 trees, with almost the same content in the terminal nodes (it is constructed by descriptors related to molecular size). This explains why the ensemble predicts the same value for all the low melting point compounds—all of them get the same prediction in all trees.

Interestingly, the second tree exhibits two nodes under the right main branch defined by information content of order 1 descriptors (¹CIC and ¹IC). These two descriptors describe the connectivity of one molecule in terms of symmetry. Information content descriptors were selected both in the Katritzky et al. and Eike et al. works, and an inverse relationship between the melting points and the information content descriptors was also observed. This fact can be interpreted as low-symmetry molecules, which have low coordination ability, having low melting points.⁷

An additional experiment has shown that exclusion of highly intercorrelated descriptors from the initial pool (with Pearson correlation coefficient above 0.8) does not lead to improved predictions.

Tree construction can also be seen as a very fast method for selecting relevant variables. However, descriptors that are successfully employed by trees are not necessarily successful for CPG NNs, because the two methods use the descriptors in radically different ways. In trees, descriptors are used sequentially, some to make decisions involving all the objects, others only in small branches for a few objects. In opposition, CPG NNs always use all the descriptors simultaneously for all the objects.

CPG NNs were trained with the 9 descriptors selected by the first tree, and reasonable results could be achieved, particularly if the descriptors were weighted according to the level where they are used in the tree. The predictions were not as accurate as with the trees, but comparable to the MLR models in terms of some criteria.

Beyond predictive accuracy, CPG NNs are interesting because they provide information regarding the topology of the data. Mapping an object into a CPG NN also allows for retrieval of other objects that were mapped onto the same region, and that can to some extent explain and support the prediction. Visualisation of the output weights (Fig. 8) reveals several regions on the surface corresponding to different ranges of melting points. It is a representation of the combined relationship between the selected descriptors and the melting point of pyridinium bromides. When applied to the test set of 9 new compounds, the network mapped those with lower melting points onto dark blue neurons, and one salt with low melting point (87 °C) onto a light blue neuron. This means the network would correctly identify the salts with highest potential as ionic liquids.

The decision tree and the ensemble also recognized the low melting point objects in the test set (Table 4). The accuracy of other predictions varied. The wrong assignment of a low melting point (80–85 °C) to a salt with mp = 158 °C is the worst prediction in the set. However, for this application, a false positive (false prediction of an ionic liquid) is certainly preferable to a false negative (missing a compound with ionic liquid properties).

Conclusion

Regression trees were able to build good predictive models for the melting points of pyridinium bromides from the molecular structure. The quality of the predictions could be improved by using an ensemble of trees (forest) instead of a single tree, and the results compared well to linear regressions previously reported in the literature for the same data set. Regression trees are alternative methods, which are flexible, extremely fast to develop, and can easily screen large numbers of descriptors. Trees also showed some success as a fast method for selection of variables for neural networks. Reasonable qualitative results were obtained for a new 9 compound set, with all the low melting point objects being recognized by the decision tree, the ensemble of trees and the CPG neural networks. The described methods make use of widely available software tools and are of general applicability.

Acknowledgements

The authors thank Fundação para a Ciência e Tecnologia (Lisbon, Portugal) and FEDER fund for financial support.

References

1. J. S. Wilkes, Green Chem., 2002, 4, 73.
2. R. Sheldon, Chem. Commun., 2001, 2399.
3. J. Zupan and J. Gasteiger, Neural Networks in Chemistry and Drug Design, Wiley-VCH, Weinheim, 2nd edn., 1999.
4. L. Breiman, J. H. Friedman, R. A. Olshen and C. J. Stone, Classification and Regression Trees, Chapman & Hall/CRC, Boca Raton, FL, 2000.
5. W. Tong, H. Hong, H. Fang, Q. Xie and R. Perkins, J. Chem. Inf. Comput. Sci., 2003, 43, 525.
6. L. Erikson, H. Antti, E. Holmes, E. Johansson, T. Lundstedt, J. Shockor and S. Wold, Partial Least Squares (PLS) in Cheminformatics in Handbook of Chemoinformatics, ed. J. Gasteiger and J. Engel, Wiley-VCH, New York, 2003, vol. 3, p. 1134.
7. A. R. Katritzky, A. Lomaka, R. Petrukhin, R. Jain, M. Karelson, A. E. Visser and R. D. Rogers, J. Chem. Inf. Comput. Sci., 2002, 42, 71.
8. D. M. Eike, J. F. Brennecke and E. J. Maginn, Green Chem., 2003, 5, 323.
9. E. S. Goll and P. C. Jurs, J. Chem. Inf. Comput. Sci., 1999, 39, 974.
10. S. J. Cho and M. A. Hermsmeier, J. Chem. Inf. Comput. Sci., 2002, 42, 927 and references cited therein.
11. V. Svetnik, A. Liaw, C. Tong, J. C. Culberson, R. P. Sheridan and B. P. Feuston, J. Chem. Inf. Comput. Sci., 2003, 43, 1947.
12. M. Wagener and V. J. van Geerestein, J. Chem. Inf. Comput. Sci., 2000, 40, 280.
13. M. Daszykowski, B. Walczak, Q.-S. Xu, F. Daeyaert, M. R. de Jonge, J. Heeres, L. M. H. Koymans, P. J. Lewi, H. M. Vinkers, P. A. Janssen and D. L. Massart, J. Chem. Inf. Comput. Sci., 2004, 44, 716.
14. J. Sadowski and J. Gasteiger, Chem. Rev., 1993, 93, 2567.
15. J. Gasteiger, C. Rudolph and J. Sadowski, Tetrahedron Comput. Methodol., 1992, 3, 537.
16. J. Sadowski, J. Gasteiger and G. Klebe, J. Chem. Inf. Comput. Sci., 1994, 34, 1000.
17. DRAGON can be tested on the website http://www.disat.unimib.it/chm/dragon.htm.
18. PETRA can be tested on the website http://www2.chemie.uni-erlangen.de and is available from Molecular Networks GmbH, http://www.mol-net.de.
19. R. Todeschini and V. Consonni, Descriptors from Molecular Geometry in Handbook of Chemoinformatics, ed. J. Gasteiger and J. Engel, Wiley-VCH, New York, 2003, vol. 3, p. 1004.
20. M. C. Hemmer, V. Steinhauer and J. Gasteiger, Vib. Spectrosc., 1999, 19, 151.
21. V. Consonni, R. Todeschini and M. Pavan, J. Chem. Inf. Comput. Sci., 2002, 42, 682.
22. R program and RPART library are freely available from http://www.r-project.org/.
23. J. Aires-de-Sousa, Chemom. Intell. Lab. Syst., 2002, 61, 167.
24. The JATOON applets are available at http://www.dq.fct.unl.pt/staff/jas/jatoon..
25. A. R. Katritzky, L. Mu, V. S. Lobanov and M. Karelson, J. Phys. Chem., 1996, 100, 10400.
26. For this set of compounds, the mp slightly increases with alkyl chain length after C11. More significant variations were reported for imidazolium salts: J. D. Holbrey and K. R. Seddon, J. Chem. Soc., Dalton Trans., 1999, 2133.
27. V. Consonni, R. Todeschini, M. Pavan and P. Gramatica, J. Chem. Inf. Comput. Sci., 2002, 42, 693.
28. P. Gramatica, N. Navas and R. Todeschini, Chemom. Intell. Lab. Syst., 1998, 40, 53.
29. P. N. P. Rao, M. Amini, H. Li, A. G. Abeeb and E. E. Knaus, J. Med. Chem., 2003, 46, 4872.
30. T. Thorsteinsson, M. Másson, K. G. Kristinsson, M. A. Hjálmarsdóttir, H. Hilmarsson and T. Loftsson, J. Med. Chem., 2003, 46, 4173.
31. S. Piyamongkol, Z. D. Liu and R. C. Hider, Tetrahedron, 2001, 57, 3479.
32. S. Yamada, T. Misono, M. Ichikawa and C. Morita, Tetrahedron, 2001, 57, 8939.

---

Footnote

† Electronic supplementary information (ESI) available: ensemble of trees grown and list of initial descriptors. See http://www.rsc.org/suppdata/gc/b4/b408967g/

---