Photofragmentation of C60 in the extreme ultraviolet: statistical analysis on the appearance energies of C60−2nz+
(n
≥ 1, z
= 1–3)
Received
27th October 2004
, Accepted 8th November 2004
First published on 24th November 2004
Abstract
The ion yield curves for C60−2nz+
(n
= 1–5, z
= 1–3) produced by photoionization of C60 are measured in the photon energy (hν) range of 25–150 eV. The appearance hν values are higher by 30–33 eV than the thermochemical thresholds for dissociative ionization of C60 leading to C60−2nz+. Evaluation is made on the upper limits of the internal energies of the primary C60z+ above which C60−2n+2z+ fragments (n
≥ 1) cannot escape from further dissociating into C60−2nz+
+ C2. These upper limits agree well with the theoretical internal energies of C60z+ corresponding to the threshold for the formation of C60−2nz+. The photofragmentation of C60z+ is considered to be governed by the mechanism of internal conversion of the electronically excited states of C60z+, statistical redistribution of the excess energy among a number of vibrational modes, and sequential ejection of the C2 units.
Introduction
The C60 molecule with a compact structure of a truncated icosahedron exhibits an exceptionally high stability. However, mass spectrometric studies of C60 have revealed that appreciable fragmentation occurs when the system gains energy in excitation and ionization processes. Fragmentation mechanisms have been studied by laser multiphoton ionization,1–3 heavy-ion excitation,4,5 or electron impact ionization.6–8 Decomposition of C60z+
(z
≥ 1) primarily formed is known to lead to fragment ions with even numbered carbon atoms (C60−2nz+, n
= 1, 2,…)
via sequential loss of C2 units from C60z+ ions in high-vibrational states. In contrast, experimental studies of single photon excitation are very limited.9–13 Recent results on the relative cross section of the fullerene fragments from C60 in the region of valence electron excitation show that the appearance photon energies of C60−2n+ and C60−2n2+ are higher by 30–40 eV than the thermochemical thresholds for dissociative photoionization of C60.12 In a limited case of C60
+
hν
→ C58+
+ C2
+ e− Yoo et al.9 have discussed this large kinetic shift in terms of unimolecular decay modelled by quasiequilibrium theory. However, they could not determine the theoretical appearance energy with a good accuracy, since a reliable value for the binding energy of C60+ was not available at that time. Until then there has been no effort to apply quasiequilibrium theory to dissociative photoionization of C60 and to clarify the fragmentation mechanism of the fullerene ions in which large excess energy is initially deposited.14 In this paper we perform systematic measurements of the yield curves of the fragment ions, C60−2n+, C60−2n2+ and C60−2n3+, in a wide photon energy range of hν
= 25–150 eV. Tunable synchrotron radiation that we have utilized was found to be very powerful for determining the appearance energies of respective fragment ions and the critical internal energies of C60z+ required for the formation of C60−2nz+. These critical internal energies are then compared with the appearance internal energies of C60−2nz+ predicted by theoretical calculations based on the RRKM theory. This allows us to discuss the detailed mechanisms of unimolecular reactions induced by equilibration of the excess energy among enormous density of states of the fullerene system.
Experimental
All the measurements have been carried out at the bending magnet beamline BL2B equipped with an 18 m spherical grating monochromator of Dragon type constructed in the UVSOR synchrotron radiation facility in Okazaki.15,16 The Experimental set-up for photoionization mass spectrometry of C60 has been described in details elsewhere.17–19 Briefly a molecular beam of C60 was produced by heating the sample powder to approximately 680 K. Monochromatized synchrotron radiation was focused onto the C60 beam. The produced photoions were extracted by a pulsed electric field, mass-separated by a time-of-flight (TOF) mass spectrometer, and detected with a microchannel plate electron multiplier. In order to normalize the ion counts the fluxes of the molecular and light beams were monitored throughout the measurement by a silicon photodiode and a crystal-oscillator surface thickness monitor, respectively.
Results
Fig. 1 shows TOF mass spectra of the parent C60z+ and fragment C60−2nz+
(n
≥ 1, z
= 1–3) ions produced from C60. Taking mass spectra with scanning the monochromator we could measure the yield curves for C60−2nz+ as a function of hν. Figs. 2 and 3 illustrates the curves for C60−2n2+ with n
= 1–5 and C60−2n3+ with n
= 1 and 2, respectively. The results of C60−2n3+ can be reported for the first time. To our knowledge the curves of C60−2nz+
(z
= 1 and 2) above 100 eV have not been published. The yield curves for C60−2nz+ are considered to provide fractional abundances of C60−2nz+ within ∼25 μs after ionization, at least around the onset region for each ion. With decreasing the size of 60–2n the appearance photon energies AE(n,z) for a given z shift to higher hν positions and the curves rise more gently towards a peak. After reaching the peak all the curves decline steadily. Table 1 summarizes AE(n,z) for C60−2nz+ with n
= 1–5 and z
= 1–3. We determined AE(n,z) by reading the photon energy at which the ion yield reaches 5% of the peak height after subtracting an appropriate background. Values of AE(n,z) are found to be higher by 30–33 eV than the thermochemical thresholds6,8 for dissociative photoionization of C60 leading to C60−2nz+. Reinköster et al. have found similar large kinetic shifts12 but their appearance hν positions for z
= 1 and 2 are higher by 2–8 eV than those in Table 1, probably due to their insufficient statistics. Contrarily, the appearance energies measured in electron impact ionization7 show good agreement with our values.
Table 1 Appearance photon energies AE(n,z) for the formation of the C60−2nz+ ions from C60. All energies are in eV
|
n
|
C60−2nz+ |
z
= 1 |
z
= 2 |
z
= 3 |
|
C60−2nz+ fragment ions are not detectable.
|
| 1 |
C58z+ |
44 ± 1 |
55 ± 1 |
73 ± 1 |
| 2 |
C56z+ |
49 ± 1 |
60 ± 1 |
82 ± 1 |
| 3 |
C54z+ |
56 ± 1 |
66 ± 1 |
—a |
| 4 |
C52z+ |
—a |
74 ± 1 |
—a |
| 5 |
C50z+ |
—a |
80 ± 1 |
—a |
When C60 is photoionized at hν
= AE(n,z), we are able to write the maximum internal energy Emax(n,z) initially transmitted to C60z+ as
| | | Emax(n,z)
= AE(n,z)
+
Ev
– IP(z) | (1) |
by assuming the kinetic energy of the emitted photoelectron to be zero. Here,
Ev denotes the vibrational energy of C
60 at the sample temperature of 680 K, and IP(
z) is the ionization potential of C
60 for the formation of C
60z+
(see
Fig. 4). In this study,
Ev
= 3.3 eV is assumed and IP(
z) taken from the literature
7,20,21 are 7.6, 19.0 and 35.6 eV for
z
= 1, 2 and 3, respectively. We have evaluated
Emax(
n,
z) from
eqn. (1) using
Ev and IP(
z) and listed the resultant values in
Table 2 for C
60−2nz+ with
n
= 1–5 and
z
= 1–3. It is expected that
Emax(
n,
z) is nearly equal to the upper limit of the internal energies of the primary C
60z+ above which C
60−2n+2z+ fragments cannot escape from further dissociating into C
60−2nz+
+ C
2.
Table 2 reveals two trends in the dependences of
Emax(
n,
z) on
n and
z of the fragments. First, the difference
Emax(
n
+ 1,
z)
−
Emax(
n,
z) depends weakly on
n, varying from 5 to 9 eV. This may reflect a weak
n-dependence
6,8 of the binding energies for the unimolecular reaction
| | | C60−2n+2z+
(n
≥ 1)
→ C60−2nz+
+ C2 | (2) |
Second,
Emax(
n,
z) for a given
n is almost unchanged irrespective of
z. This remarkable finding, together with the prominent kinetic shifts, implies that internal conversion of the electronically excited states of C
60z+ results in redistribution of the excess energy among the vibrational degrees of freedom followed by successive ejection of the C
2 units, as illustrated schematically in
Fig. 4.
 |
| | Fig. 4 Scheme of the energetics of the C2 loss in dissociative photoionization of C60. The photofragmentation of C60z+ is considered to be governed by the mechanism of internal conversion of the electronically excited states of C60z+, statistical redistribution of the excess energy among a number of vibrational modes, and successive ejection of the C2 units. | |
Table 2 Upper limit Emax(n,z) of the internal energies (in eV) of the primary C60z+ ions above which C60−2n+2z+ fragments cannot escape from further dissociating into C60−2nz+
+ C2 (n
≥ 1)
| |
|
|
Observed,aEmax(n,z) |
Calculated,bERRKM(n) |
|
n
|
C60−2n+2z+ |
C60−2nz+ |
z
= 1 |
z
= 2 |
z
= 3 |
TS-1c |
TS-3d |
|
Obtained by using eqn. (1) from the appearance photon energies for the formation of C60−2nz+ from C60 in Table 1.
Appearance internal energies of C60z+ corresponding to Kn
= 0.03Knmax at 25 μs after photoionization of C60. The RRKM theory is employed to derive the rate constant for reaction (2) from which the Kn curves can be calculated.
E
RRKM(n) determined from Fig. 5. A set of the binding energies for the TS-1 model was employed.
E
RRKM(n) determined from Fig. 6. A set of the binding energies for the TS-3 model was employed.
C60−2nz+ fragment ions are not detectable.
|
| 1 |
C60z+ |
C58z+ |
39.7 ± 1 |
39.3 ± 1 |
40.7 ± 1 |
40.1 |
40.9 |
| 2 |
C58z+ |
C56z+ |
44.7 ± 1 |
44.3 ± 1 |
49.7 ± 1 |
47.1 |
47.0 |
| 3 |
C56z+ |
C54z+ |
51.7 ± 1 |
50.3 ± 1 |
—e |
52.9 |
52.8 |
| 4 |
C54z+ |
C52z+ |
—e |
58.3 ± 1 |
—e |
58.9 |
59.1 |
| 5 |
C52z+ |
C50z+ |
—e |
64.3 ± 1 |
—e |
65.1 |
65.3 |
Theoretical calculations
We employed the RRKM theory to derive the curves of fractional abundance (breakdown graphs) for C60z+ and C60−2nz+ ions (n
= 1–5) as a function of the internal energy of the primary C60z+. The microcanonical rate constant kn(ε) for reaction (2) of C60−2n+2z+ having internal excitation energy ε can be given by6,8,9,22| |  | (3) |
Here, α is the reaction path degeneracy, E0n is the critical activation energy for reaction (2), G*(ε
−
E0n) is the number of states for the transition state (activated complex), N(ε) is the density of states of C60−2n+2z+, and h is the Planck’s constant. For n
≥ 2 the ε value of C60−2n+2z+ is computed under the assumption that the energy available after dissociation of C60−2n+4z+
→ C60−2n+2z+
+ C2 is statistically partitioned between C60−2n+2z+ and C2. The detail of the calculation for reaction (2) is the same as those described in refs. 6, 8 and 9. We have used Haarhoff’s approximation22 to calculate G*(ε
−
E0n) and N(ε), assuming vibrational frequencies of C60−2n+2z+ to be replaced by those of a neutral C60 reported by Schettino et al.23
The critical activation energies E0n in eqn. (3) are taken from the binding energies of C60−2n+2z+
(n
= 1–5) for reaction (2) proposed in the papers6,8 dealing with electron impact ionization of C60. Foltin et al.6 invoked the model with a relatively loose transition state whose reaction coordinate has a frequency of ca. 1500 cm−1. This model was referred to in ref. 8 as TS-1. Later Laskin et al.3 and Matt et al.24 have revised the binding energies of C60−2n+2+
(n
= 1–5) by assuming a totally loose transition state in which the C60−2n+ and C2 fragments tumble freely. This transition state, named TS-3 in ref. 8, was consistent with a large frequency factor in the Arrhenius relation which has been expected by a very large rotational partition function of C2.25 Moreover, Laskin et al.3 found that using a thermochemical cycle for n
= 1 leads to a value of 10.0 eV for the binding energy of neutral C60, in excellent agreement with the result26 of ab initio calculations. In the present study, we adopted the two sets of the binding energies of C60−2n+2z+ recommended within RRKM theory, i.e. the sets for the TS-1 and TS-3 models. The binding energies of C60+, for example, are 7.06 eV and 9.2 eV for TS-1 and TS-3, respectively.
Every time n is increased by 1 we removed the frequencies of six vibrational modes that were judged no longer remaining in C60−2n+2z+ of reaction (2). One of these six frequencies is the frequency of the reaction coordinate in the transition state. For TS-1 model we set this frequency to 931.1 cm−1, the average value of the 174 frequencies of C60+, whereas for TS-3 this frequency was set to 1574 cm−1, the highest frequency (8Hg mode) of C60+.23 Another of the six frequencies belongs to the high-frequency 7Hg mode (1421 cm−1), corresponding to the C2 stretching vibration. The others of the six frequencies were associated with the four rotational modes of C2
(including two pseudo-translational modes): 1Hg
(266 cm−1), 2Hg
(431 cm−1), 3Hg
(709 cm−1) and 1Hu
(403 cm−1) modes of C60+ were chosen. In the transition state we assumed that these four frequencies decrease to 50 cm−1 for the TS-3 model, following the description in ref. 8.
Discussion
Figs. 5 and 6 show the fractional abundance Kn for C60−2nz+ ions (n
= 1–5) as a function of the internal energy of the primary C60z+ at 25 μs after photoionization of C60. Here, the TS-1 and TS-3 models are employed in Figs. 5 and 6, respectively. Every curve reaches a peak of Kn
=
Knmax at 7–10 eV above its onset. We defined the appearance internal energy ERRKM(n) for the formation of C60−2nz+ as the internal energy of C60z+ corresponding to Kn
= 0.03Knmax. The values of ERRKM(n) determined from Figs. 5 and 6 are listed in the seventh and eighth columns of Table 2. For the formation of C58z+, C56z+ and C54z+ERRKM(n) from Fig. 6 are 40.9, 47.0, and 52.8 eV, respectively, in excellent agreement with the observed maximum internal energies Emax(1,z), Emax(2,z) and Emax(3,z), respectively. These results are the manifestation of the validity of the present statistical treatment: large amounts of the internal energy of C60z+ is equilibrated among the vibrational degrees of freedom, and subsequent photofragmentation proceeds through reaction (2)
via a transition state with the activation energy of E0n.
 |
| | Fig. 5 Fractional abundance curves of C60z+ and C60−2nz+ ions (n
= 1–5) at 25 μs after photoionization of C60 obtained by using the RRKM theory to calculate the rate constant for reaction (2). TS-1 model (ref. 8) is adopted for the transition state, but the frequency of the reaction coordinate is modified to 931.1 cm−1. | |
 |
| | Fig. 6 Fractional abundance curves of C60z+ and C60−2nz+ ions (n
= 1–5) at 25 μs after photoionization of C60 obtained by using the RRKM theory to calculate the rate constant for reaction (2). TS-3 model (ref. 8) is adopted for the transition state. | |
The fractional abundance in Fig. 5 or 6 allows us to simulate the yield curve for C60−2nz+
(n
≥ 1) as a function of hν, if the partial photoionization cross section σ(hν,E) at hν for the initial formation of C60z+ with the internal energy E is known. The ion yield Yn,z(hν) for the C60−2nz+ fragment can be expressed as
| |  | (4) |
For
photon energies close to the threshold for fragmentation into C
60−2nz+
+
nC
2 the partial cross section
σ(
hν,
E) is assumed to be independent of
hν, because
Kn(
E) takes nonzero values only in a narrow
E range above the threshold for fragmentation (see
Figs. 5 and 6). As a consequence, the derivative of
Yn,z(
hν) with respect to
hν may satisfy the relation
| |  | (5) |
where
E′
=
hν
+
Ev
− IP(
z). The dependence of
σ(
E′) on the internal energy is much weaker than that of
Kn(
E′). It is then likely from
eqn. (5) that the derivative of the ion yield curve for C
60−2nz+
(
n
≥ 1) is proportional to the
Kn curve of C
60−2nz+ shifted by IP(
z)
−
Ev.
Fig. 7 shows the curves of the derivative of
Yn,2(
hν) which are calculated by using the yield curves of
Fig. 2 at
photon energies close to the threshold for fragmentation. The peak positions of the derivative curves for
n
= 1–4 appear to be in fair agreement with those of the fractional abundance curves in
Figs. 5 and 6.
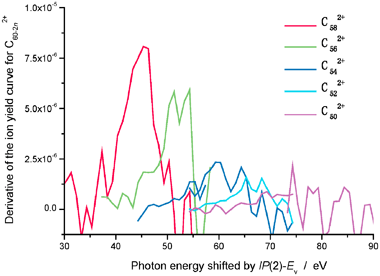 |
| | Fig. 7 Derivative of the ion yield curves of C60−2n2+ ions (n
= 1–5) with respect to hν. The observed curves in Fig. 2 are used and the energy scale of the abscissa is shifted by IP(2)
−
Ev
= 15.7 eV. | |
The ion yield of the parent C60z+ can be represented by the same expression as eqn. (4) by using the fractional abundance of C60z+ in Figs. 5 or 6. This fractional abundance is found to be more than 97% below E
∼ 40 eV, so that the C60z+ yield is strongly affected by the partial cross section σ(hν,E) in a wide range of from E
= 0 to ∼40 eV. Therefore, the C60z+ yield becomes markedly higher than the yields of C60−2nz+
(n
≥ 1). This statement is confirmed by the observed TOF spectra in Fig. 1. It is also worth noting that eqn. (5) is no longer valid for the parent ion owing to a strong dependence of σ(hν,E) on hν.
Acknowledgements
We are greatful to Mr Haruyama for sample preparation and purification. This work has been supported by a Grant-in-Aid for Scientific Research (Grant No. 14340188) from the Ministry of Education, Science, Sports and Culture, Japan, and by a grant for scientific research from Research Foundation for Opto-Science and Technology.
References
- P. Wurz and K. R. Lykke, J. Phys. Chem., 1992, 96, 10129–10139 CrossRef CAS.
- D. Ding, R. N. Compton, R. E. Haufler and C. E. Klots, J. Phys. Chem., 1993, 97, 2500–2504 CrossRef CAS.
- J. Laskin, B. Hadas, T. D. Märk and C. Lifshitz, Int. J. Mass Spectrom., 1998, 177, L9–L13 CrossRef CAS.
- B. Walch, C. L. Cocke, R. Voelpel and E. Salzborn, Phys. Rev. Lett., 1994, 72, 1439–1442 CrossRef CAS.
- T. LeBrun, H. G. Berry, S. Cheng, R. W. Dunford, H. Esbensen, D. S. Gemmell, E. P. Kanter and W. Bauer, Phys. Rev. Lett., 1994, 72, 3965–3968 CrossRef CAS.
- M. Foltin, M. Lezius, P. Scheier and T. D. Märk, J. Chem. Phys., 1993, 98, 9624–9634 CrossRef CAS.
- P. Scheier, B. Dünser, R. Wörgötter, M. Lezius, R. Robl and T. D. Märk, Int. J. Mass Spectrom. Ion Proc., 1994, 138, 77–93 CrossRef CAS.
- R. Wörgötter, B. Dünser, P. Scheier, T. D. Märk, M. Foltin, C. E. Klots, J. Laskin and C. Lifshitz, J. Chem. Phys., 1996, 104, 1225–1231 CrossRef.
- R. K. Yoo, B. Ruscic and J. Berkowitz, J. Chem. Phys., 1992, 96, 911–918 CrossRef CAS.
- T. Drewello, W. Krätschmer, M. Fieber-Erdmann and A. Ding, Int. J. Mass Spectrom. Ion Process., 1993, 124, R1–R6 CrossRef.
- M. Fieber-Erdmann, W. Krätschmer and A. Ding, Z. Phys. D, 1993, 26, S308–310.
- A. Reinköster, S. Korica, G. Prümper, J. Viefhaus, K. Godehusen, O. Schwarzkopf, M. Mast and U. Becker, J. Phys. B, 2004, 37, 2135 CrossRef.
- S. Aksela, E. Nõmmiste, J. Jauhiainen, E. Kukk, J. Karvonen, H. G. Berry, S. L. Sorensen and H. Aksela, Phys. Rev. Lett., 1995, 75, 2112–2115 CrossRef CAS.
- J. Berkowitz, J. Chem. Phys., 1999, 111, 1446–1453 CrossRef CAS.
- H. Yoshida and K. Mitsuke, J. Synchrotron Rad., 1998, 5, 774–776 CrossRef CAS.
- M. Ono, H. Yoshida, H. Hattori and K. Mitsuke, Nucl. Instrum. Methods Phys. Res. A, 2001, 467–468, 577–580 CrossRef CAS.
- J. Kou, T. Mori, M. Ono, Y. Haruyama, Y. Kubozono and K. Mitsuke, Chem. Phys. Lett., 2003, 374, 1–6 CrossRef CAS.
- T. Mori, J. Kou, M. Ono, Y. Haruyama, Y. Kubozono and K. Mitsuke, Rev. Sci. Instrum., 2003, 74, 3769–3773 CrossRef CAS.
- J. Kou, T. Mori, S. V. K. Kumar, Y. Haruyama, Y. Kubozono and K. Mitsuke, J. Chem. Phys., 2004, 120, 6005–6009 CrossRef CAS.
- J. de Vries, H. Steger, B. Kamke, C. Menzel, B. Weisser, W. Kamke and I. V. Hertel, Chem. Phys. Lett., 1992, 188, 159–162 CrossRef CAS.
- H. Steger, J. de Vries, B. Kamke, W. Kamke and T. Drewello, Chem. Phys. Lett., 1992, 194, 452–456 CrossRef CAS.
-
W. Forst, Theory of Unimolecular Reactions, Academic, New York, 1973, ch. 6 Search PubMed.
- V. Schettino, P. R. Salvi, R. Bini and G. Cardini, J. Chem. Phys., 1994, 101, 11079–11081 CrossRef CAS.
- S. Matt, O. Echt, P. Scheier and T. D. Märk, Chem. Phys. Lett., 2001, 348, 194–202 CrossRef CAS.
- K. Hansen, Philos. Mag. B, 1999, 79, 1413–1425 CrossRef CAS.
- A. D. Boese and G. E. Scuseria, Chem. Phys. Lett., 1998, 294, 233–236 CrossRef.
|
| This journal is © the Owner Societies 2005 |
Click here to see how this site uses Cookies. View our privacy policy here. 









