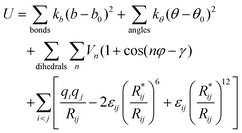Cation extraction by 18-crown-6 to a room-temperature ionic liquid: The effect of solvent humidity investigated by molecular dynamics simulations

Abstract

We report a molecular dynamics study of the solvation of 18-crown-6 (“18C6”) and of its K⁺, Cs⁺ and Sr²⁺ complexes in a room-temperature ionic liquid (IL) based on 1-butyl-3-methyl-imidazolium⁺, PF₆⁻. “Dry” [BMI][PF₆] versus “humid” [BMI][PF₆][H₂O] models of the IL are compared, demonstrating the importance of solvent humidity on the solvation properties. Upon “dissolution” of a piece of crystal, 18C6 is found to undergo a conformational change from C_i to D_3d, mainly due to enhanced interactions with the BMI⁺ solvent cations and H₂O molecules, when present. The complexes were first studied with dissociated counterions. In the dry IL, the complexed K⁺ and Sr²⁺ cations are locked at the center of the crown by 1 + 1 (K⁺), 1 + 2 or 1 + 3 (Sr²⁺) PF₆⁻ anions in facial positions, respectively. The Cs⁺ cation is perched over the crown, solvated by 3 PF₆⁻ anions. In the humid IL, the complexed K⁺ also binds to 1 + 1 PF₆⁻ facial anions only (no water), whereas Sr²⁺ is asymmetrically coordinated to at least 3 H₂O molecules. When co-complexed with Cl⁻ or NO₃⁻ counterions, Sr²⁺ is shielded from the dry IL, but coordinates up to 3 additional H₂O molecules in the humid IL, while K⁺ is not hydrated. The solvation of the “naked” K⁺, Cs⁺ and Sr²⁺ ions also markedly depends on the solvent humidity. K⁺ is coordinated to 4 PF₆⁻ anions in the dry IL and by 2 PF₆⁻ plus 3–5 H₂O in the humid IL. The most spectacular difference concerns Sr²⁺, whose first shell is purely anionic (5 PF₆⁻) in the dry IL, but all neutral (8 H₂O) in the humid IL. According to an energy component analysis, the 18C6 crown, the cations and their complexes are better solvated by the humid than by the dry IL. Finally, we report simulations of 18C6 and on its Sr ⊂ 18C6(NO₃)₂ complex at the aqueous interface with the ionic liquid, showing enhanced solvent mixing, compared to the interface with classical organic liquids. The microscopic views obtained by these simulations show the active role of the ionic and aqueous components of the liquid on the solvation of the free crown, the free cations and their complexes.

---

Introduction

Room temperature ionic liquids (hereafter noted “IL”s) are generally composed of an organic cation (e.g. ammonium, pyridinium or alkyl-imidazolium derivatives) and an X⁻ anion that can be used to primarily control the water miscibility.¹ ILs with PF₆⁻ or (CF₃SO₂)₂N⁻ as anionic components are water immiscible and can be used for liquid–liquid extraction purposes. Recent examples involve the efficient extraction of alkali and alkaline earth cations from water by crown ethers,^2–4 the Hg²⁺ or Cd²⁺ extraction by “task-specific” liquids with binding groups appended to the imidazolium cations,⁵ or the extraction of f-elements (e.g. lanthanides, uranyl cations) in the context on nuclear waste partitioning.^6–9 The low volatility and non-flammability of the ILs makes them promising alternatives over traditional ion separation techniques, provided that they are chemically stable enough.¹⁰ Little is known about the microscopic structure of these ILs and on their solvation properties which are presumably determined by the active role of the solvent ions, by solvent impurities and by the water content of the solvent. Important insights can be obtained by computer simulations.¹¹ Examples involve molecular dynamics (MD) or Monte Carlo studies on pure Ils^12–15 as well as on IL solutions with small neutral molecules,^16,17 with strontium and uranyl salts¹⁸ and trivalent lanthanide ions.¹⁹ A simulation study of water/dimethylimidazolium ionic liquid mixtures has recently been published.^16,20 Accurate description of selected components of the system can be obtained by quantum mechanical calculations “in the gas phase”,^21–25 but the latter are not sufficient to depict the complexity and dynamics of solvation.

In this paper we report a molecular dynamics study of the solvation of 18-crown-6 (“18C6”) and its Mⁿ⁺ ⊂ 18C6 complexes (the inclusion symbol “⊂” means that the complex is of inclusive type) in an IL (hereafter noted [BMI][PF₆]) based on 1-butyl-3-methyl-imidazolium⁺, PF₆⁻. Several experimental studies have been conducted on alkali and alkaline earth cation extraction by crown ethers to this solvent and related ones. Dai et al. showed that the strontium nitrate extraction by dicyclohexyl-18C6 (DC18C6) to imidazolium based ILs with PF₆⁻ or (CF₃SO₂)₂N⁻ anions is several orders of magnitude more efficient than the extraction with classical organic solvents.² Only a small amount of Cl⁻, NO₃⁻ or SO₄²⁻ anions were co-extracted from water, supporting a cation exchange mechanism. A similar conclusion has been obtained when Sr²⁺ is extracted by DC18C6 from acidic nitrate media to a series of 1-alkyl-3-methylimidazolium (CF₃SO₂)₂N⁻ based ILs.⁴ Chun et al. observed that alkali cations can be efficiently extracted by DC18C6 to ILs based on 1-alkyl-3-methylimidazolium PF₆⁻, in conditions where extraction to chloroform, nitrobenzene and octanol was undetectable.²⁶ Visser, Rogers and collaborators examined the effect of 18C6 lipophilic substitution (18C6 vs. DC18C6 vs. di(tert-butylcyclohexano)18C6 on the Na⁺, Cs⁺ and Sr²⁺ extraction in 1-alkyl-3-methylimidazolium PF₆⁻ based ILs with different compositions of the aqueous phase, also concluding on the exceptional behavior of ILs, involving in some cases complicated partition mechanism, “which necessitates a thorough understanding of ILs as solvents”.³

This led us to investigate by MD simulations the solvation of important species involved in the liquid–liquid extraction of Sr²⁺, K⁺ and Cs⁺ cations by 18C6: 18C6 uncomplexed, different types of complexes, and the free ions. We want first to gain insights into the conformation and solvation of the free crown. The complexes are then considered with Cl⁻ or NO₃⁻ as counterions, either fully dissociated or as intimate ion pairs. Those with dissociated counterions may represent the species formed by liquid–liquid extraction, while intimate ion pairs may correspond to complexes that have been directly dissolved in the IL. The di-hydrated Sr²⁺ ⊂ 18C6(H₂O)₂ complex will also be investigated. Indeed, according to EXAFS spectroscopy studies,^27,28 the strontium coordination to the nitrates is retained upon dissolution of the Sr ⊂ 18C6(NO₃)₂ complex in the IL, but is likely to be lost when the complex is extracted from water, presumably because the cation coordinates to water molecules. An important facet of our paper concerns the comparison of the “dry” [BMI][PF₆] versus “humid” [BMI][PF₆][H₂O] forms of the liquid (Fig. 1). The former may be considered as an “ideal” liquid, while the latter may depict the IL which has been contacted with water as in liquid–liquid extraction. In spite of the formation of macroscopically well separated IL/aqueous phases, the IL is hygroscopic and contains water, whose content decreases with the temperature and with the lipophilicity of the alkyl substituents attached to the imidazolium skeleton.^29–33 Our humid model contains one H₂O molecule per BMI⁺ PF₆⁻ ion pair, which is somewhat more than the experimental water solubility in the pure IL, (2.3% in weight, i.e. 0.26 in mole fraction) at 25 °C.³⁰ Due to the water-dragging effect,^34,35 and the presence of hydrophilic ions (e.g. Cl⁻, NO₃⁻, K⁺, Sr²⁺) the water content is however likely to be larger than in the pure IL, and it is important to study at the microscopic level the effect of IL humidity on the solvation of the 18C6 molecule, and of the free and complexed ions.³ Finally, we report MD simulations on 18C6 and its strontium complexes at the aqueous interface with the [BMI][PF₆] IL, in order to investigate “what happens at the interface”.³⁶

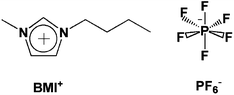Fig. 1 Ionic components of simulated IL.

Methods

The systems were simulated by classical molecular dynamics “MD” using the AMBER 7.0 software³⁷ in which the potential energy U is described by a sum of bond, angle and dihedral deformation energies and pair wise additive 1–6–12 (electrostatic and van der Waals) interactions between non-bonded atoms.
Cross terms in van der Waals interactions were constructed using the Lorentz–Berthelot rules. The parameters used for the IL’s have been tested on the pure liquid properties: those of BMI⁺ ions are taken from Stassen et al.¹³ while those of PF₆⁻ stem from the OPLS force field³⁸ and have been used by Berne et al. to simulate ILs.³⁹ The corresponding force field parameters have been tested for liquid simulations.⁴⁰ Water was described by the Jorgensen's TIP3P model.⁴¹ We note that the AMBER interaction energy between the BMI⁺ and PF₆⁻ ions (−76 kcal mol⁻¹) is identical to the BSSE corrected quantum mechanical result (HF level with a 6-31G** basis set) and both structures of the BMI⁺ PF₆⁻ dimer are similar.⁴² Similarly, the AMBER interaction energies between one H₂O molecule and one PF₆⁻ (−10.4 kcal mol⁻¹) or one BMI⁺ ion (−9.2 kcal mol⁻¹) are in good agreement with the quantum mechanically calculated energies (−9.1 and −9.7 kcal mol⁻¹, respectively at the HF/6-31+G* level, and −9.5 and −9.5 kcal mol⁻¹, respectively, at the DFT-B3LYP/6-31+G* level). The parameters for K⁺, Cs⁺, Sr²⁺⁴³ and NO₃⁻⁴⁴ were fitted on free energies of hydration. The corresponding AMBER atom types and atomic charges are given in Fig. S1 of ESI†. The 1–4 electrostatic and van der Waals interactions were scaled down by a factor of 1.2 and 2.0, respectively, as recommended by Cornell et al.⁴⁵ The systems were simulated with 3D-periodic boundary conditions. Non-bonded interactions were calculated with a 12 Å atom based cut-off, calculating the long-range electrostatics via the Ewald summation method (PME approximation).^11,46

The MD simulations were performed at 300 K or 400 K starting with random velocities. The temperature was monitored by coupling the system to a thermal bath using the Berendsen algorithm with a relaxation time of 0.2 ps. All C–H bonds were constrained with SHAKE, using the Verlet leapfrog algorithm with a time step of 2 fs to integrate the equations of motion.

The solvent boxes were of ≈48 Å length and contained 294 BMI⁺ PF₆⁻ ions (dry liquid), plus 294 H₂O molecules (humid liquid). The simulated dry liquid¹⁸ has an average density of 1.32 kg dm⁻³, close to the reported experimental values of 1.36⁴⁷ and 1.37 kg dm⁻³.⁴⁸ The humid liquid was similarly prepared from mixing-demixing MD simulations and equilibrated. Its final density, 1.30 kg dm⁻³, is close to the density of the dry IL, in agreement with the small excess volume of mixing calculated on analogous system.²⁰

The complexes were immersed in the solution, either as Mⁿ⁺ ⊂ 18C6 complexes (no explicit counterion), or as Mⁿ⁺ ⊂ 18C6, nX⁻ with dissociated X⁻ anions (at ≈15–20 Å from Mⁿ⁺) or as M ⊂ 18C6(X)_n complexes with inner sphere X⁻ anions (X⁻ = Cl⁻ or NO₃⁻). A schematic representation with the definition of the notations is given in Fig. 2 for the strontium complexes. The solutions of the free Mⁿ⁺ cations and of the Sr²⁺ ⊂ 18C6(H₂O)₂ and Sr²⁺ ⊂ 18C6(PF₆⁻)₄ complexes were similarly prepared. The neutrality of the solutions with free or complexed Mⁿ⁺ cations “without counterions” was obtained by removing 1 or 2 solvent ions. Equilibration started with 1000 steps of steepest descent energy minimization, followed by 50 ps of MD with fixed solutes (“BELLY” option of AMBER) at constant volume and by 25 ps at constant volume without constraints, followed by 25 ps at constant pressure of 1 atm. The subsequent MD trajectories calculated for 1.2 to 10.5 ns (see ESI†, Table S1) were saved every 0.5 ps and analyzed with the MDS and DRAW software.⁴⁹ Insights into energy component were obtained by group analysis, using a 17 Å cutoff distance and a reaction field correction for the electrostatics.⁵⁰ The solute/IL interaction energies were dissected into the contributions of the BMI⁺, PF₆⁻ and H₂O molecules, and into their Coulombic and van der Waals components. The average structure of the solvent was characterized by the radial distribution functions (RDFs) of the P_PF6, F_PF6, N_butyl(BMI), O_H2O or H_H2O solvent atoms around the center of the 18C6 crown or the Mⁿ⁺ cation during the last 0.2 ns. The RDFs are plotted as a function of the distances (in abscissa, expressed in Å). Integration of the first peak of the RDFs led to the average coordination number “CN”.

Fig. 2 Simulated strontium complexes. (i) Left: with coordinated X⁻ (Cl⁻ or NO₃⁻) counterions (noted Sr ⊂ 18C6(X)₂). (ii) Right: with dissociated X⁻ counterions (noted Sr²⁺ ⊂ 18C6, 2X⁻), at 15–20 Å from Sr²⁺. (iii) The Sr²⁺ ⊂ 18C6 complex (not shown) was simulated without Cl⁻ or NO₃⁻ counterion.

The IL/water interface has been built from adjacent “cubic” boxes of the [BMI][PF₆] and water, as in refs. 51, 52. The boxes were ≈45 Å in length, and contained 260 BMI⁺ PF₆⁻ ions and 2900 H₂O molecules, respectively. The solutes (36 18C6 molecules or four strontium complexes) were immersed initially at the interface, equally shared between the two liquids, and removing solvent molecules that were at less than 2 Å. The equilibration protocol was similar as in the pure ILs, and the (NVT) dynamics was performed at 300 K for 4 to 5 ns. In order to prevent the dissociation of the complexes, their Sr⋯O_crown and Sr⋯O_NO3 distances were constrained to their equilibrium values (2.83 Å) with a force constant of 30 kcal mol⁻¹ Å⁻².

Results

We first describe the conformation and solvation of the free 18C6 molecule in diluted and concentrated solutions (section 1). This is followed by the K⁺, Cs⁺ and Sr²⁺ complexes of 18C6 with dissociated counterions (section 2), and with nitrate or chloride coordinated counterions (section 3). Section 4 deals with the “free” K⁺, Cs⁺, Sr²⁺ and Cl⁻ ions. Each system is first described in the “dry” [BMI][PF₆] liquid, followed by the “humid” [BMI][PF₆][H₂O] liquid. Most simulations have been performed at 300 and 400 K, generally yielding similar results. The most noticeable effect of increased temperature concerns the dissociation of the K⁺ and Cs⁺ complexes in most cases, and the somewhat reduced cation hydration in the humid IL. In the other cases, the complexes remain inclusive, with K⁺ or Sr²⁺ close to the center of the crown and Cs⁺ perched over the crown as in solid state⁵³ and simulated structures.⁵⁴ Unless otherwise specified, the results are given at 300 K. Finally (section 5), we report the results on 18C6 and on its strontium complexes at the IL/water interface.

As concerns the comparison of the two forms of the IL, we note that diffusion is faster in the humid than in the dry IL, as indicated by the diffusion coefficients D, calculated from the Einstein equation, valid at long times:¹¹ 6Dt = 〈[r_i(t) − r_i(0)]²〉 in the humid versus dry neat liquids. The D values (in 10⁶ cm² s⁻¹), averaged over 2 ns are: 0.26 versus 0.04 for P(PF₆), 0.29 versus 0.04 for N(BMI). The water diffusion in the humid IL is still faster (5.2 × 10⁻⁶ cm² s⁻¹), following experimental trends.⁵⁵

1 Conformation and solvation of 18C6 uncomplexed in solution

1.1 The dry solution.
The 18C6 monomer: comparison of C_i vs. D_3d forms. We first simulated the 18C6 monomer (one molecule in the solvent box), starting from the C_ivs.D_3d forms. While the latter retained its conformation until the end of the dynamics (2 ns), the former became D_3d in about 0.13 ns, indicating that the D_3d form is preferred. In order to check that the sampling is sufficient, we decided to “remix” and randomize the solutions with a C_iversusD_3d crown,⁵⁶ followed by 1.2 ns of MD at 300 K. Both simulations finally led to a D_3d type form of 18C6. Typical RDFs from the center of the crown and snapshots can be seen in Fig. 3.

Fig. 3 Typical solvation patterns of 18C6 at 300 K (final snapshot with orthogonal views and RDFs). Top: C_i (frozen monomer) in the dry IL. Middle: D_3d monomer in the dry IL. Bottom: 2/12 D_3d crowns (from the dissolution of a piece of “crystal” with 12 C_i crowns) in the humid IL. The hydration patterns of the 12 crowns diluted in the dry IL and of 10/12 of the crowns in the humid IL are similar to those of the D_3d monomer in the dry IL (Middle). Other RDFs are given in Fig. S3 (See ESI†).

In all cases, the final solvent environment of the D_3d crown was similar. The RDFs display a first peak between 4 and 6 Å corresponding to the 2.0 BMI⁺ cations on the average, i.e. one at each face of the crown. The P_PF6 peak is more remote (at ≈7 Å). For a purpose of comparison, it is instructive to analyze the solvation of the C_i form, obtained from a simulation of 1.6 ns with the frozen crown (BELLY option of AMBER). The RDFs look similar, with one BMI⁺ cation tangential to each face on the crown, on the average. However, the D_3d cavity tends to be visited by the alkyl(BMI) substituents, while the C_i form has no cavity. According to an energy component analysis, the C_i and D_3d forms of the crown display attractive interactions with the solvent (−50 and −69 ± 4 kcal mol⁻¹, respectively; see Table 1), and these are stronger for the D_3d form. It is important to note that the D_3d stabilization by solvation (≈20 kcal mol⁻¹) is much larger than its intrinsically preferred stability (0.9 kcal mol⁻¹, according to an energy minimization in the gas phase). The BMI⁺ cations interact more than the PF₆⁻ anions do with the two forms of 18C6 (by ≈10 kcal mol⁻¹), which is consistent with the proximity of the cations from the electron rich core of the crown. Furthermore, the interaction with the BMI⁺ cations is mainly of van der Waals origin (83% for the D_3d form and 100% for the C_i form), while for the PF₆⁻ anions the van der Waals and Coulombic contributions are similar (See ESI†, Table S2).

Table 1 18C6 uncomplexed. Average interaction energies (kcal mol⁻¹) between one 18C6 crown and the solvent components

	Temp./K	BMI^+	PF6^–	H2O	Solvent ^c
a The crown(s), initially in the Ci conformation, became D3d during the dynamics. b Simulations performed with frozen Ci solute(s). c Fluctuations are ≈±3 kcal mol^−1 in all cases, excepted in the case of ^b, where they are ±8 kcal mol^−1.
Dry IL
1 18C6 Ci → D3d^a	300	−35	−25	—	−60
1 18C6 D3d → D3d	300	−41	−28	—	−69
1 18C6 Ci → Ci^b	300	−31	−19	—	−50
12 18C6 diluted ^a	300	−33	−25	—	−58
Humid IL
12 18C6 diluted Ci → D3d^a	300	−36	−22	−5	−64
12 18C6 diluted Ci → D3d^a	400	−30	−21	−2	−53
12 18C6 diluted Ci → Ci^b	300	30	−15	−3	−48
12 18C6 diluted Ci → Ci^b	400	−28	−15	−2	−45

---

Concentrated solutions of 18C6 molecules. A second series of simulations dealt with a more concentrated solution, with twelve 18C6 molecules in the solvent box, all initially being in the C_i conformation. Two initial distributions of the crowns were considered (see ESI†, Fig. S2). In the first one, the 18C6 molecules are “diluted” in the box, and have therefore different individual local solvent environments at the beginning of the dynamics. In less than 0.2 ns, they reorganized from C_i to D_3d and were finally (1.5 ns) all D_3d (Fig. 4). Their average RDF (Figs. 3 and S3, see ESI†) is similar to the RDF of the D_3d monomer, showing a marked peak, corresponding to 1.6 BMI⁺ cations, on the average, within 6 Å from the center of 18C6. This is somewhat less than for the 18C6 monomer, due to a reduced solvent accessibility. The peak splits into two components (at ≈4 and 5 Å) which correspond to the methyl or butyl groups of BMI⁺, respectively, pointing towards the cavity. The energy component analysis confirms that one crown interacts better with the BMI⁺ than with the PF₆⁻ ions (by ≈8 kcal mol⁻¹, on the average), thus following the same trends as the monomer (see Tables 1 and S2, see ESI†).

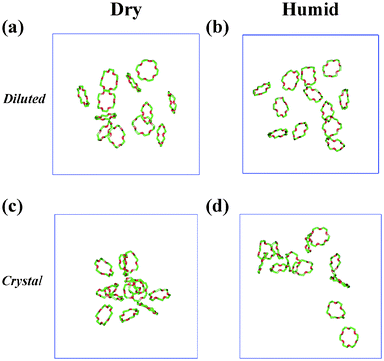Fig. 4 12 18C6 molecules in dry IL (a) and (c) versus humid (b) and (d) IL solutions. The simulations started with 12 C_i crowns “diluted” in the box (a) and (b) or from a piece of “crystal” (c) and (d). A full version is given in Fig. S2 (see ESI†).

The second arrangement consisted of a piece of the 18C6 crystal (from ref. 57) in which the C_i crowns are packed in 4 × 3 stacks. After 0.7 ns at 300 K, some of those which were at the periphery started to diffuse to the solvent and became D_3d. As diffusion was very slow, the simulation was pursued up to 3 ns, followed by 7.5 ns at 400 K, after which all 18C6 molecules were D_3d. However, even after a total of 10.5 ns of dynamics, dilution is still limited. The average final solvent RDFs (see ESI†, Fig. S3) look very similar to the RDFs of the “diluted” system, thus confirming the importance of solvation by BMI⁺ solvent cations on the C_i to D_3d conversions. Some anions are inserted into the first shell BMI⁺ cations, but the P_PF6 peak is clearly more remote (≈8 Å) from the center of the crown, corresponding to “facial”, as well as “in plane” solvation of the crown.

1.2 The humid solution. Only the “concentrated” systems with twelve 18C6 molecules of C_i symmetry were simulated in the humid IL. The diluted arrangement was studied at 300 K and 400 K, also leading to C_i → D_3d conformational changes. Dissolution of the piece of crystal (as above) was simulated at 400 K only and turned out to be more rapid than in the dry solvent. This is why the simulation was stopped at 3.7 ns, after which dilution was much more effective than in the dry IL after 10.5 ns. Typical snapshots and RDFs can be seen in Fig. 3.

At 300 K, about 75% of the crown are facially surrounded by 1 + 1 BMI⁺ cations, while 25% bind 1 H₂O at one face plus one BMI⁺ cation at the other face. One crown is doubly hydrated, with 1 H₂O at each face. The facial H₂O molecules display bridging hydrogen bonding interactions with two ether oxygens, as observed in solid state structures⁵⁸ as well as from theoretical simulations,^59,60 thus also stabilizing the D_3d form, relative to the C_i one. At 400 K, water is much more labile and does not make persistent hydrogen bonds with 18C6.

According to an energy component analysis on the “diluted system”, one D_3d crown displays somewhat stronger interactions with the humid than with the dry IL (see Tables 1 and S2, see ESI†). The difference amounts to ≈6 kcal mol⁻¹ at 300 K or 400 K. As in the dry IL, the contribution of BMI⁺ cations is dominant and decreases at higher temperature. The water contribution is small, but somewhat larger at 300 K (−5 kcal mol⁻¹ per 18C6) than at 400 K (≈−2 kcal mol⁻¹), which is consistent with the (weak) occurrence of 18C6⋯H₂O adducts at 300 K only.

2 The K⁺, Cs⁺ and Sr²⁺ ⊂ 18C6 complexes (dissociated counterions) in solution

2.1 The dry solution. During the MD simulations at 300 K in the dry IL, the three studied cations remained complexed by the crown with different arrangements, though. At least two independent simulations were performed for each complex: one without added counterion(s), and one with added X⁻ counterion(s) (X⁻ = Cl⁻ or NO₃⁻), remote enough to not interfere with the solvation of the 18C6 complex. We denote the two kinds of complexes as Mⁿ⁺ ⊂ 18C6 and Mⁿ⁺ ⊂ 18C6, nX⁻, respectively. The resulting Mⁿ⁺⋯solvent RDFs and typical snapshots at the end of the dynamics are shown in Fig. 5.

Fig. 5 18C6 complexes simulated at 300 K without counterions, or with dissociated counterions in the dry versus humid solution: final snapshots and radial distribution functions around the Sr²⁺, K⁺, or Cs⁺ atom. The characteristics of the RDFs are summarized in Table S3 (see ESI†). The RDFs at 400 K are given in Fig. S4 (see ESI†).

The two simulations of the K⁺ complex at 300 K yield similar solvation patterns. The K⁺ cation sits at the center of the crown and coordinates 1 + 1 bidentate PF₆⁻ anions, one on each face of the crown. The “first shell” BMI⁺ ions are more remote, at more than 6 Å from K⁺. Another simulation of the K⁺ ⊂ 18C6 complex for 2 ns at 400 K led to the same solvation patterns. We note the similarity between this simulated K⁺ ⊂ 18C6, 2PF₆⁻ moiety in the IL solution and the X-ray structure of the K⁺ ⊂ dibenzo-18C6, PF₆⁻ complex.⁶¹

The Cs⁺ cation remains perched over the crown and coordinates 3 PF₆⁻ anions which are more loosely bound and mobile than around the K⁺ complex. They rotate around their central phosphorus atom and, on the average, one of them achieves a monodentate binding to Cs⁺ and the two others are bidentate. On the opposite side of 18C6, one finds one BMI⁺ cation which points its butyl or methyl chains to the center of the crown, as found to the free crown. This shows that the crown solvation is mainly determined by its own interactions with the solvent rather than by repulsion with the facially complexed Cs⁺ cation.

For the Sr²⁺ complex we performed three independent simulations: one without counterions (at 300 K and 400 K) and one with dissociated Cl⁻ counterions at 300 K, generally leading to 3–4 PF₆⁻ anions coordinated to Sr²⁺. At 300 K, the Sr²⁺ ⊂ 18C6 complex (without counterion) displays a 1 + 3 coordination, i.e. one monodentate PF₆⁻ on one face, plus three bidentate PF₆⁻ on the other face that somewhat pull the cation off the center of the crown. When simulated at 400 K for 4.2 ns,⁶² this complex coordinated 1 + 2 PF₆⁻ anions. In the Sr²⁺ ⊂ 18C6, 2Cl⁻ complex (with dissociated Cl⁻ anions) the coordination is similar: 3.8 PF₆⁻ on the average, form a 1 + 3 type arrangement, as above. The single PF₆⁻ is fixed at one face of the crown in a monodentate coordination to Sr²⁺, while the 3 anions at the other face are more mobile and exchange between mono- and polydentate coordination.

We also tested the stability of a more symmetrically solvated complex with 2 PF₆⁻ anions at each face of the crown (noted Sr²⁺ ⊂ 18C6(PF₆⁻)₄) which was first model-built and optimized in the gas phase and subsequently immersed in the solution. However, after 0.3 ns of dynamics at 300 K, one PF₆⁻ anion dissociated, leading to a 1 + 2 coordination.⁶³ The Sr²⁺ cation is slightly off-centered, pulled by the two bidentate PF₆⁻, while the singly coordinated PF₆⁻ is monodentate. There is thus likely an equilibrium between the 1 + 2 and 1 + 3 solvated forms of the strontium complex in the dry IL.

2.2 The humid solution. In the humid IL, the K⁺, Cs⁺ and Sr²⁺ complexes were simulated with dissociated Cl⁻ counterions at 300 K and 400 K. At 400 K, K⁺ and Cs⁺ decomplexed (at 1.2 and 1.6 ns, respectively). K⁺ became solvated by 4 bidentate PF₆⁻ anions plus 2.6 H₂O molecules on the average, while Cs⁺ cation was hydrated by 1.9 H₂O. The Cs⁺ complex also dissociated at 300 K. This is why for the humid systems we mainly focus on Sr²⁺ and K⁺ complexes at 300 K.

Two simulations were performed on the Sr²⁺ complex, which differed by its local environment. They both reveal the importance of water coordination to the cation, at the detriment of PF₆⁻ solvent anions. In the first simulation, the complex was placed “randomly” in the solvent box and, after 2.2 ns, Sr²⁺ coordinates three H₂O molecules on one face, plus one PF₆⁻ anion on the other face of the crown at 300 K and 400 K, and this coordination was retained when the dynamics was pushed up to 5 ns at 300 K. The energy component analysis shows that Sr²⁺ ⊂ 18C6 displays stronger interactions with the humid than with the dry IL (see Tables S4 and S5), mostly due to the Sr²⁺ contribution. The “solvation energy” ranges from −370 to −390 kcal mol⁻¹ in the humid IL, and from −310 to −350 kcal mol⁻¹ in the dry IL. The reduced interactions with the solvent anions are thus compensated by the cation hydration forces and reduced repulsions with the BMI⁺ cations.

In another simulation, the complexed Sr²⁺ cation was forced to be initially coordinated by 2 + 2 PF₆⁻ anions, in order to prevent as much as possible its hydration. After 50 ps of MD with the constrained Sr²⁺ ⊂ 18C6(PF₆⁻)₄ moiety, 3 ns of free MD were performed at 300 and 400 K. Three to four PF₆⁻ anions dissociated from the complex and were replaced by water, with some differences, depending on the temperature. At 400 K, Sr²⁺ finally coordinates to 1 PF₆⁻ + 3 H₂O molecules as seen above, while at 300 K all PF₆⁻ anions moved to the second shell or to the bulk, while Sr²⁺ captured 1 + 4 H₂O molecules hydrogen bonded to PF₆⁻ anions (Fig. 5). Similar patterns are found for the “naked” Sr²⁺ cation in the humid IL (see section 4.2).

According to an energy component analysis, the 1 PF₆⁻ + 3 H₂O (300 K) and the 1 + 4 H₂O solvated Sr²⁺ ⊂ 18C6 (300 K) complexes display similar interaction energies with the IL (−390 and −370 ± 10 kcal mol⁻¹, respectively), and it is important to note that these are more negative than the interaction of Sr²⁺ ⊂ 18C6 with the “dry” IL (−330 kcal mol⁻¹ for the 1 + 2 PF₆⁻ solvated complex).

For the K⁺ complex, the effect of solvent humidity is less visible, as at 300 K the cation coordinated 1 + 1 PF₆⁻ anions (one at each face) as in the dry IL, but no water (see Fig. 5). As a result, it displays similar interactions (≈−110 kcal mol⁻¹) with the humid as with the dry IL. The same energy is found at 400 K when the K⁺ complex is constrained to remain inclusive, indicating that the sampling is sufficient. As expected, the unconstrained K⁺ “complex” that dissociated at 400 K, also interacts better with the humid than with the dry IL, by about 50 kcal mol⁻¹ (Tables S4 and S5).

3 The K⁺, Cs⁺ and Sr²⁺ complexes with coordinated Cl⁻/NO₃⁻ counterions or H₂O molecules in solution

The simulations of the M ⊂ 18C6(X)_n complexes started with the cation coordinated to the crown and to the neutralizing NO₃⁻ or Cl⁻ counterion(s), as in the X-ray structure of the Sr ⊂ 18C6(NO₃)₂ complex.⁶⁴ See also Fig. 2. At the two temperatures and in the two forms of the liquid, the Sr²⁺ cation remained complexed by 18C6 and by one or two counterions, while K⁺ and Cs⁺ decomplexed at 400 K. Cs⁺ also decomplexed at 300 K in the humid liquid. This is why we again mostly focus on the Sr²⁺ and K⁺ complexes at 300 K. Final snapshots and typical Mⁿ⁺⋯solvent RDFs are shown in Figs. 6a (dry), 6b (humid), S4 and S5 (See ESI†). The results of energy component analysis are given in Tables S4 (dry) and S5 (humid IL) (See ESI†).

Fig. 6 (a) M ⊂ 18C6(X)_n complexes simulated at 300 K with coordinated counterions X⁻ or H₂O molecules in the dry IL (left hand side, a) and the humid IL (right hand side, b). Snapshots of the first solvation shell and radial distribution functions around the Sr²⁺, K⁺, Cs⁺ ions. The characteristics of the RDFs are summarized in Table S3 (See ESI†). The results at 400 K are given in Fig. S5 (see ESI†).

3.1 The dry solution. At 300 K, the K⁺ complex remains inclusive, but its cation is somewhat pulled off the center of the crown by the NO₃⁻ or Cl⁻ counterion at one side, and is coordinated at the other side of the crown by one PF₆⁻ anion. The P_PF6 peak at ≈4 Å in the RDF is followed by a BMI⁺ peak at 6.7 Å, corresponding to BMI⁺ cations that cap the NO₃⁻ or Cl⁻ anion.

A different structure is observed at 300 K with the Cs⁺ cation which is attracted by its NO₃⁻ or Cl⁻ counterion. With Cl⁻ as counterion, Cs⁺ sits at ≈3.5 Å from the center of 18C6, solvated by 3 PF₆⁻ anions, and is therefore quasi-decomplexed. With NO₃⁻ as counterion, Cs⁺ sits closer (≈1Å) to the center of 18C6.⁶⁵

In the case of the Sr²⁺ complex, the two facial Cl⁻ or NO₃⁻ anions lock the cation at the center of the crown and shield it from the dry solvent. According to the RDFs, shielding is more pronounced with the more bulky Cl⁻ anions than with the NO₃⁻ anions. The first solvent peak around the Sr ⊂ 18C6(Cl)₂ complex starts at ≈6 Å and corresponds to the BMI⁺ cations that solvate the two chlorides. At this distance, one also finds a small Sr⋯P peak corresponding to PF₆⁻ anions attracted by Sr²⁺, but shielded by the Cl⁻ anions. In the nitrato complex, Sr²⁺ also coordinates to one PF₆⁻ solvent anion, thus moving somewhat off-centered.

The Sr²⁺ ⊂ 18C6(H₂O)₂ complex, simulated at 300 K with one water molecule at each side of the crown, remained bound but was unsymmetrical. Sr²⁺ somewhat moved off the cavity to coordinate two monodentate PF₆⁻ anions at one face (see Fig. 6a), thus somewhat pushing the water molecule away from the symmetry axis of the crown, while on the opposite face the other water molecule remained “axial”. At 400 K, Sr²⁺ ⊂ 18C6(H₂O)₂ completely decomplexed.

3.2 The humid solution. In the humid IL, the Sr ⊂ 18C6(NO₃)₂ complex retained a 1 + 1 coordination of the nitrates to Sr²⁺ during the whole dynamics (2.2 ns) at 300 K and 400 K. The nitrates however moved from bidentate to monodentate, allowing for the partial hydration of the metal, by 2.7 H₂O (300 K) or 2.1 H₂O (400 K), on the average. The Sr ⊂ 18C6(Cl)₂ complex with chloride counterions was similarly simulated for 2.2 ns. At 300 K, the two chlorides remained bound to Sr²⁺ which additionally coordinated to 2.0 H₂O molecules, but no F_PF6 atom (the shortest Sr⋯F “contact” being at more than 5 Å). At 400 K, only one Cl⁻ anion remained coordinated to Sr²⁺, while the second Cl⁻ moved to the second shell, hydrogen bonded to first shell H₂O molecules (Fig. 6b). Thus, when compared to the nitrate counterions, the chlorides display somewhat weaker pairing with Sr²⁺, but the two types of complexes clearly display a strong affinity for the water component of the IL.

Because of computer time limitations, we did not simulate all systems in the same conditions, which prevents strict energy comparison. Generally, a given system is less solvated and therefore interacts less with the IL at 400 K than at 300 K (by 50 kcal mol⁻¹ for the Sr ⊂ 18C6(NO₃)₂ complex in the humid IL). Furthermore, at a given temperature, the complex displays stronger interaction energies with the humid than with the dry IL (−224 versus −107 ± 15 kcal mol⁻¹ at 300 K for Sr ⊂ 18C6(NO₃)₂ and −146 versus −94 ± 15 kcal mol⁻¹ at 300 K for the Sr ⊂ 18C6(Cl)₂ complex). We note that the effect of humidity is much larger with nitrate than with chloride counterions due the change of binding mode of the nitrates (i.e. from bidentate to monodentate), while the two chlorides remain coordinated at 300 K.

The K ⊂ 18C6(NO₃) complex remained inclusive at 300 K, with the monodentate nitrate at one side, and one PF₆⁻ anion at the other side of the crown, without water coordinated to K⁺.⁶⁶ In spite of the lack of cation hydration, K ⊂ 18C6(NO₃) interacts somewhat better with the humid than with the dry IL (by 6 kcal mol⁻¹). At 400 K, the cation decomplexed as in the absence of counterions.

The Sr²⁺ ⊂ 18C6(H₂O)₂ complex dissociated at 300 K and 400 K, in 1.3 and 0.3 ns, respectively. Decomplexation resulted from repulsions of Sr²⁺ by BMI⁺ cations on one side of the crown, and accumulation of water on the other side, which captured the Sr²⁺ cation.⁶⁷

4 Solvation of the uncomplexed K⁺, Cs⁺, Sr²⁺ and Cl⁻ “free” ions

Typical snapshots and ion⋯solvent RDFs are shown in Fig. 7 and the RDF characteristics are summarized in Table S6 (See ESI†).

Fig. 7 Uncomplexed Sr²⁺, K⁺, Cs⁺ and Cl⁻ ions in the dry versus humid IL at 300 K. Left: Snapshot of the first solvation shells, with the contribution of the PF₆⁻ (dry IL) and H₂O (humid IL) molecules shown separately. Right hand side: Solvent RDFs around the ions in the dry versus humid IL at 300 K. The characteristics of the RDFs are summarized in Table S6 (see ESI†).

4.1 The dry solutions. The dry solutions of the “free” K⁺, Cs⁺ and Sr²⁺ and Cl⁻ ions were simulated at 300 K and 400 K for 1 to 1.5 ns. Quasi-identical results are obtained at the two temperatures and, as expected, the first solvation shell of the Mⁿ⁺ cations comprises PF₆⁻ anions only: exactly 4.0 for K⁺ and Cs⁺ and 5.0 for Sr²⁺, as seen from the single sharp peak in the M⋯P RDFs. The first peak of the M⋯F RDFs corresponds to 12.2, 11.3 and 10.1 F atoms, respectively. The PF₆⁻ coordination mode to the monovalent cations is mostly tridentate, while with Sr²⁺ it is bidentate. We notice that increasing the cation size from K⁺ and Cs⁺ does not lead to increased coordination numbers, in contrast to what is observed, e.g. in water or organic solvents. This likely stems from a compromise between the cation/PF₆⁻ attractions and the repulsions between the coordinated PF₆⁻ anions. Visual inspection of the trajectories reveals “voids” in the first solvent shell of Cs⁺ that are sometimes occupied by BMI⁺ atoms, thus also somewhat compensating for the anion-anion repulsions. This can also be seen in the BMI RDF which starts more sharply around Cs⁺ than around K⁺. The first anionic shell of the K⁺, Cs⁺ and Sr²⁺ cations is surrounded by a shell of about 4, 5 and 5 BMI⁺ solvent ions, respectively.

Each cation is strongly attracted by the liquid, in the order Cs⁺ < K⁺ ≪ Sr²⁺ (−103, −125 and −430 kcal mol⁻¹, respectively at 300 K), due to dominant attractions with the PF₆⁻ anions (see Table 2) and these energies are similar at the two studied temperatures.

Table 2 Sr²⁺, K⁺, Cs⁺ and Cl⁻ “free” ions in dry versus humid IL solution. Average interaction energies with the solvent and its components (kcal mol⁻¹)

	BMI^+	PF6^–	H2O	Solvent^a
a Fluctuations are about ±10 kcal mol^−1.
Dry IL
Sr^2+	990	−1419	—	−429
K^+	529	−654	—	−125
Cs^+	485	−588	—	−103
Cl^–	−572	464	—	−108
Humid IL
Sr^2+	852	−1086	−339	−573
K^+	470	−565	−49	−144
Cs^+	465	−552	−24	−111
Cl^–	−480	403	−94	−124

---

The Cl⁻ anion is surrounded by 4–5 BMI⁺ cations which adopt different orientations, but generally make closer contacts with Cl⁻via their C–H imidazolium protons than via their alkyl chains, as found in the chloride imidazolium ILs.^12,25,68,69

4.2 The humid solution. In the humid IL, the K⁺, Cs⁺ Sr²⁺ free cations were simulated at 300 K and 400 K, leading to different hydrated species. Sr²⁺ rapidly captured H₂O molecules to form, in less than 1 ns mainly Sr(H₂O)₈²⁺ aquo-complexes, surrounded by PF₆⁻ anions. This is why the simulation was stopped after 1.9 ns. A same hydration number (8.3 O_water, on the average) is found at the two temperatures. The first shell H₂O molecules are either hydrogen bonded to second shell H₂O molecules, or to second shell PF₆⁻ anions (7.0 at 300 K and 5.2 at 400 K, on the average). See the snapshot and RDFs in Fig. 7.

The case of K⁺ differs, as after 2.8 ns its first shell comprises a mixture of 3 to 5 H₂O molecules (3.4 at 300 K and 3.9 at 400 K, on the average), plus 2 loosely bound PF₆⁻ anions. The less hydrophilic Cs⁺ cation binds at most 2 H₂O molecules (2.0 at 300 K and 1.8 at 400 K, on the average), completed by 3 to 4 PF₆⁻ anions. Around the Sr²⁺, K⁺ and Cs⁺ cations, one finds 1 to 3 BMI⁺ cations inserted in the first shell of PF₆⁻ anions.

It is instructive to look at the solute–solvent interactions (Table 2) which are quite attractive and much stronger for Sr²⁺ than with K⁺ or Cs⁺ (about −570, −145 and −110 kcal mol⁻¹, respectively). Furthermore, each cation interacts better with the humid than with the dry liquid (by ≈140, 20 and 8 kcal mol⁻¹, respectively). This is because the reduced attractions of Mⁿ⁺ with the PF₆⁻ anions are compensated by interactions with water and reduced repulsions with the BMI⁺ cations.

In the humid IL, the Cl⁻ anion is surrounded by 3.2 BMI⁺ cations on the average (generally pointing their CH protons towards the anion), plus 4 H₂O molecules which form a relay with second shell water or PF₆⁻ molecules. As found for the other species, Cl⁻ also interacts better (by ≈15 kcal mol⁻¹) with the humid than with the dry IL.

5 18C6 and the Sr ⊂ 18C6(NO₃)₂ complexes at the ionic-liquid/water interface

The liquid–liquid interface presumably plays a key role in solvent extraction,³⁶ and it is thus important to gain microscopic insights into its nature⁷⁰ and into the distribution of partners involved in the extraction process. In the case of classical extraction, we found that the extractants and their complexes, as well as lipophilic ions are surface active,^71,72 which has deep implications in terms of complexation and extraction mechanism. Strong analogies were found between classical interfaces and those involved in supercritical-CO₂ extraction.^73,74 This is why we decided to similarly simulate the interface between the [BMI][PF₆] ionic liquid and water where 36 18C6 molecules or 4 strontium complexes were placed initially, in order to test whether they migrate to the IL phase. Final snapshots are shown in Figs. 8 and 9. For the two systems, and in contrast to what was observed at the aqueous interface with chloroform,⁷⁵ or with SC-CO₂,⁷⁶ there is important solvent mixing, leading to an ill-defined interfacial domain. There are about 30 PF₆⁻ and BMI⁺ ions in the water phase and about 70 H₂O molecules in the IL. After 5 ns of dynamics, the majority of the 18C6 molecules remained “adsorbed” at the interface, and reorganized from the C_i to the D_3d conformation.

Fig. 8 The [BMI][PF₆]/water interface with 36 18C6 free molecules (top) or with 4 strontium complexes (bottom) after 4 ns of dynamics. The solvents are shown side by side, instead of superposed, for clarity.

Fig. 9 Typical solvation patterns of the strontium complex at the [BMI][PF₆]/water interface (orthogonal views).

Another simulation was performed for 4 ns with two Sr ⊂ 18C6(NO₃)₂ plus two Sr²⁺ ⊂ 18C6 complexes initially at the interface. Again, one finds important solvent mixing with a broad interfacial region where three of the complexes are located. Interestingly, they have different types of surrounding (Figs. 8 and 9), reminiscent of what we found in the humid IL. In the Sr ⊂ 18C6(NO₃)₂ complexes where the nitrates were constrained to be bidentate, the cation further binds one H₂O molecule, while of the two Sr²⁺ ⊂ 18C6 complexes, one coordinates 3 H₂O + 1 H₂O molecules, and the other one coordinates 3 H₂O + 1 PF₆⁻ anion. As a result of their affinity for water, the complexes do not sit in the ionic liquid, but on the aqueous side of the interface or in “bulk” water.

Discussion and conclusion

We present a MD simulation study on the 18C6 and its alkali and alkaline earth complexes in a room temperature ionic liquid, including the effect of coordinated counterions or water molecules. The studied liquid has been used to conduct liquid–liquid extraction experiments and forms a biphasic system with water, but may contain a larger amount of water. This is why we modeled dry versus humid forms of the liquid. The simulations of the dry solutions may correspond to the direct dissolution of 18C6 or its complexes in a dry IL, while the humid liquid may represent the receiving phase in a liquid–liquid extraction experiment, or an IL with less hydrophobic imidazolium derivatives, or containing, e.g. hydrophilic Cl⁻ or NO₃⁻ anions.

The ionic liquid solution and ion pairing

The simulations in the dry IL point to the specific interactions of the IL components with the solute. For instance, BMI⁺ cations markedly contribute to the stabilization of the D_3d form of 18C6 uncomplexed, and the calculations predict that upon dissolution of a piece of crystal, the crown should undergo a conformational change from C_i to D_3d, as in an aqueous environment.^59,60 As concerns the cation complexes, the calculations alone are not sufficient to predict the status of their X⁻ counterions, when present. In principle, potential of mean force calculations could give insights into the cation-anion relationship,^11,77 but the task is more challenging than, e.g. in aqueous solution, due to the sampling issues and the much longer relaxation time of the IL components, compared to water. On the experimental side, the status of counterions depends on the preparation protocol, solvent humidity and solvent anions with which they compete. For instance, NO₃⁻ is co-extracted with Sr²⁺ ⊂ DC18C6 to the hydrophobic C₁₀Mim⁺ Tf₂N⁻ IL (based on 1-n-decyl-3-methylimidazolium⁺ bis[(trifluoromethyl)sulfonyl]amide⁻) without forming inner-sphere complexes,²⁸ while extraction to the less hydrophobic ILs proceeds with a cation exchange mechanism, thus with limited, or without extraction of the nitrates. On the other hand, dissolution of the Sr ⊂ DC18C6(NO₃)₂ crystal in dry or water saturated C₅Mim⁺ Tf₂N⁻ IL, the nitrate counterions remain coordinated to the strontium.²⁷ In the case of alkali cation extraction by DC18C6 to C₈Mim⁺ PF₆⁻, it also been shown that variation of the aqueous phase anion (Cl⁻/NO₃⁻/SO₄²⁻) does not effect the efficiencies and selectivities, which suggests that these anions are not co-extracted. This is why we separately considered the “naked” Mⁿ⁺ ⊂ 18C6 complexes and their analogues paired with neutralizing Cl⁻ or NO₃⁻ anions. For the Mⁿ⁺ ⊂ 18C6 complexes, the models with remote X⁻ counterions or without added X⁻ counterions yield similar solvation patterns, showing the importance of PF₆⁻ solvent anions to further coordinate the complexed Mⁿ⁺ cation in dry conditions. For instance, Sr²⁺ ⊂ 18C6 asymmetrically coordinates 1 + 3 or 1 + 2, rather than 2 + 2 PF₆⁻ anions, while K⁺ or Cs⁺ complexes further bind one PF₆⁻ anion. We have seen that, depending on the Mⁿ⁺ cation and on the “steric constraints”, PF₆⁻ may bind monodentate or bidentate to the complexed cation.

The effect of solvent humidity

According to our simulations, the solvent “humidity” has a huge effect on the solvation of the “naked” strontium complex. For instance, Sr²⁺ ⊂ 18C6 binds to about 1 + 3 H₂O molecules, at the detriment of solvent PF₆⁻ anions which sit in the second shell of strontium, hydrogen bonded to the H₂O molecules. In the case of the K⁺ ⊂ 18C6 complex, the effect of solvent is less clear, as K⁺ prefers PF₆⁻ anions to H₂O molecules in its first solvation shell. When X⁻ counterions are co-complexed, the Sr²⁺ cation still displays some affinity for water. For instance, in the Sr ⊂ 18C6(NO₃)₂ complex, Sr²⁺ is hydrated by 2–3 H₂O molecules, leading to a total coordination number of 10 oxygens, i.e. six from the crown, two from the monodentate nitrates and two from water. When the nitrates were forced to be bidentate, Sr²⁺ was hydrated by 1 H₂O only, leading to a total of 11 oxygens, i.e. one more than suggested by the EXAFS study of the extracted complex.^27,28 The case of the Sr ⊂ 18C6(Cl)₂ complex is intermediate between Sr²⁺ ⊂ 18C6 and Sr ⊂ 18C6(NO₃)₂ as, in the humid IL one Cl⁻ anion only remains bound to Sr²⁺, while the other moves to the second shell, forming Sr²⁺⋯OH₂⋯Cl⁻ interactions. We have found analogous patterns (Sr²⁺⋯OH₂⋯PF₆⁻) after simulation of the modelbuilt Sr²⁺ ⊂ 18C6(PF₆⁻)₄ complex in the humid IL. In the case of the Cs⁺ complex, Cs⁺ is loosely bound in a perching position over the crown in the dry IL, but decomplexes in the humid IL. Humidity has a spectacular effect on the solvation of the uncomplexed ions, especially Sr²⁺, which is hydrated by ≈8 H₂O molecules in the humid IL, instead of 5 PF₆⁻ anions in the dry IL. For the monovalent K⁺ and Cs⁺ ions, a mixed solvation (H₂O + PF₆⁻ ions) is observed in the humid IL.

In addition to these structural features, the energy components analysis reveals stronger interactions of the solutes with the humid, than with the dry IL. This is first found for the uncomplexed 18C6 crown, for the Mⁿ⁺ ⊂ 18C6 complexes (no counterions), as well as the Mⁿ⁺ ⊂ 18C6(NO₃⁻)_n complexes with paired nitrates. A similar conclusion holds for the uncomplexed K⁺, Cs⁺ and Sr²⁺ and NO₃⁻ ions. Although solubility not only results from solute-solvent, but also from solvent–solvent interactions, including enthalpic and entropic thermodynamic components, it can be surmised that the solubility of the studied species should be higher in the humid than in the dry IL. This is also consistent with our simulated dissolution of a piece of 18C6 crystal, which proceeds faster in the humid than in the dry liquid. Concerning the cations, the effect of humidity increases with the cation charge and an interesting analogy with lanthanide(III) triflate complexes can be noted. They display a poor solubility in dry acetonitrile solution, but their solubility increases in the presence of small quantities of water.⁷⁸ Conversely, dehydration is necessary to crystallize lanthanide triflate or perchlorate complexes, where the anions coordinate to the metal.^79–81

The formation of two distinct phases between the simulated [BMI][PF₆] liquid and water, exploited for liquid–liquid extraction purposes, might hint for some analogies between the IL and classical organic ones, also used in liquid–liquid extraction. This is not the case, due to specific interactions with the solute, which depend on the nature of the solvent anion X⁻, and on the water content. The precise concentration of water is thus an important feature which can be monitored, e.g. by changing the imidazolium alkyl substituents, or X⁻. According to recent extraction results by N-alkyl aza-18-crown-6 to the C_nmim⁺ Tf₂N⁻ ionic liquids,⁸² the cation extraction selectivity is Sr²⁺ ≫ K⁺ for C₂mim⁺ and C₄mim⁺ but K⁺ > Sr²⁺ for C₆mim⁺ and C₆mim⁺, thus showing a strong dependence of selectivity on the hydrophobicity, and thus on the water content of the IL. Our simulations in dry versus humid IL likely bracket the corresponding situations and hint at the importance of humidity on the solvation patterns and stability of the complex.

The ionic liquid/water interface

The simulations at the interface are exploratory and qualitative in nature. They however show marked differences with “classical” interfaces, involving important inter-solvents mixing. It seems that the mixing is somewhat exaggerated,⁸³ but is qualitatively consistent with the possibility of cation exchange mechanism with ILs based on BMI⁺ or analogues, which contrasts with an anion co-extraction mechanism with more hydrophobic ILs. If Mⁿ⁺ formally exchanges with n BMI⁺ solvent ions, no transfer of accompanying X⁻ anions is required, which suggests that the Mⁿ⁺ complex is well solvated by the IL, as analyzed in our study. Experimentally, the Sr²⁺ extraction by a crown ether is higher with an IL based on Tf₂N⁻, rather then PF₆⁻ anions.² This may due to stronger “effective” interactions of the strontium complex with Tf₂N⁻ than with PF₆⁻ anions, due to the higher hydrophobicity of Tf₂N⁻ and smaller water content of the Tf₂N⁻ containing liquid.² We note that, among the four strontium complexes that were initially at the interface, three moved to water and one remained “adsorbed”. It is likely not a coincidence that the latter corresponds to Sr²⁺ ⊂ 18C6 (no nitrate counterion), solvated by 1 PF₆⁻ + 3 H₂O molecules, which is more consistent with a cation exchange than with an anion co-extraction mechanism. On the other, the free crowns concentrate at the interface, as found, e.g. at the chloroform/water interface,⁷⁵ which suggests than the cation capture also takes place near the interface.

Experimentally, some cation (e.g. Sr²⁺) partitioning to the IL proceeds experimentally in the absence of crown ether,³ showing little dependence on the solvent anion A⁻ of the IL.² We note that this result is consistent with the extraction of an hydrated cation like Sr(H₂O)₈²⁺,⁸⁴ whose interactions with the IL are less dependent on the nature of the nature of A⁻ than in dry conditions. We also note that the solvation patterns of the Sr(H₂O)₈²⁺ complex that spontaneously formed in the humid liquid display marked analogies with solid state structures of Sr(H₂O)₈ with soft counterions such as dicarbollides⁸⁵ or trimercaptotriazines⁸⁶ and reminiscent of the hydration scheme of, e.g. trivalent lanthanide salts of poorly coordinating anions (e.g. triflate, or perchlorate).⁸⁷

Computational issues

These simulations are based on pair wise additive 1–6–12 potentials, thus assuming that the interactions in ionic liquids are mainly steric + electrostatic in nature. This has been discussed in our previous papers,^{18,19,42,52,88} and further validated by QM results reported in the method section of this paper, as well as by computations reported by others on ILs. As seen by our many tests at two temperatures and with different starting configurations, the sampling issues should not be overlooked. There is thus room for further theoretical an experimental investigations. Based on our experience on the prototypal 18C6 system⁵⁴ and accumulated data, we believe that the present simulations however reasonably depict the solvation of the free crown ethers, cations and their complexes. As in the early days of supramolecular chemistry,⁸⁹ the interplay between “theory” and experiment plays an important role and should cross-fertilize both fields.

Acknowledgements

The authors are grateful to IDRIS, CINES, Université Louis Pasteur, and PRACTIS for computer resources, and Etienne Engler for assistance. PV thanks the French ministry of research for a grant.

References

1. R. Hagiwara and Y. Ito, Fluorine Chem., 2000, 105, 221.
2. S. Dai, Y. H. Ju and C. E. Barnes, J. Chem. Soc. Dalton Trans., 1999, 1201.
3. A. E. Visser, R. P. Swatloski, W. M. Reichert, S. T. Griffin and R. D. Rogers, Ind. Eng. Chem. Res., 2000, 39, 3596.
4. M. L. Dietz and J. A. Dzielawa, Chem. Commun., 2001, 2124.
5. A. E. Visser, R. P. Swatlosli, W. M. Reichert, R. Mayton, S. Sheff, A. Wierzbicki, J. Davies and R. D. Rogers, Environ. Sci. Technol., 2002, 36, 2523.
6. A. E. Visser and R. D. Rogers, J. Solid State Chem., 2003, 171, 106.
7. A. E. Visser, R. P. Swatloski, S. T. Griffin, D. H. Hartman and R. D. Rogers, Separ. Sci. Technol., 2001, 36, 785.
8. S. Dai, Y. S. Shin, L. M. Toth and C. E. Barnes, Inorg. Chem., 1997, 36, 4900.
9. C. E. Barnes, Y. Shin, S. Saengkerdsub and S. Dai, Inorg. Chem., 2000, 39, 862.
10. R. P. Swatloski, J. D. Holbrey and R. D. Rogers, Green Chem., 2003, 5, 361.
11. M. P. Allen and D. J. Tildesley, in Computer Simulation of Liquids, ed. W. F. van Gunsteren and P. K. Weiner, Clarendon Press, Oxford, 1987.
12. C. G. Hanke, S. L. Price and R. M. Lynden-Bell, Mol. Phys., 2001, 99, 801.
13. J. de Andrade, E. S. Böes and H. Stassen, J. Phys. Chem. B, 2002, 106, 13344.
14. J. K. Shah, J. F. Brennecke and E. J. Maginn, Green Chem., 2002, 4, 112.
15. T. I. Morrow and E. J. Maginn, J. Phys. Chem. B, 2002, 106, 12807.
16. C. G. Hanke, N. A. Atamas and R. M. Lynden-Bell, Green Chem., 2002, 4, 107.
17. C. G. Hanke, A. Johansson, J. B. Harper and R. M. Lynden-Bell, Chem. Phys. Lett., 2003, 374, 85.
18. A. Chaumont, E. Engler and G. Wipff, Inorg. Chem., 2003, 42, 5348.
19. A. Chaumont and G. Wipff, Phys. Chem. Chem. Phys., 2003, 5, 3481.
20. C. G. Hanke and R. M. Lynden-Bell, J. Phys. Chem. B, 2003, 107, 10873.
21. C. J. J. Dymek and J. J. P. Stewart, Inorg. Chem., 1989, 28, 1472.
22. S. Takahashi, K. Suzuya, S. Kohara, N. Koura, L. A. Curtiss and M. L. Saboungi, Z. Phys. Chem., 1999, 209, 209.
23. M. S. Sitze, E. R. Schreiter, E. V. Patterson and R. G. Freeman, Inorg. Chem., 2001, 40, 2298.
24. Z. Meng, A. Dolle and W. R. Carper, J. Mol. Struct. (THEOCHEM), 2002, 585, 119.
25. E. A. Turner, C. C. Pye and R. D. Singer, J. Phys. Chem. A, 2003, 107, 2277.
26. S. Chun, S. V. Dzyuba and R. A. Bartsch, Anal. Chem., 2001, 73, 3737.
27. M. P. Jensen, J. A. Dzielawa, P. Rickert and M. L. Dietz, J. Am. Chem. Soc., 2002, 124, 10664.
28. M. L. Dietz, J. A. Dzielawa, I. Laszak, B. A. Young and M. P. Jensen, Green Chem., 2003, 5, 682.
29. K. R. Seddon, A. Stark and M. J. Torres, Pure Appl. Chem., 2000, 72, 2275.
30. J. L. Anthony, E. J. Maginn and J. F. Brennecke, J. Phys. Chem. B, 2001, 105, 10942.
31. D. S. H. Wong, J. P. Chen, J. M. Chang and C. H. Chou, Fluid Phase Equilib., 2002, 194–197, 1089.
32. J. G. Huddleston, A. E. Visser, W. M. Reichert, H. D. Willauer, G. A. Broker and R. D. Rogers, Green Chem., 2001, 3, 156.
33. K. E. Gutowski, G. A. Broker, H. D. Willauer, J. G. Huddleston, R. P. Swatloski, J. D. Holbrey and R. D. Rogers, J. Am. Chem. Soc., 2003, 125, 6632.
34. W. Fan, R.-S. Tsai, N. El Tayar, P.-A. Carrupt and B. Testa, J. Phys. Chem., 1994, 98, 329.
35. B. A. Moyer, in Molecular Recognition: Receptors for Cationic Guests, ed. J. L. Atwood, J. E. D. Davies, D. D. McNicol, F. Vögtle and J.-M. Lehn, Pergamon, New York, 1996, p. p. 325.
36. H. Watarai, Trends Anal. Chem., 1993, 12, 313.
37. D. A. Case, D. A. Pearlman, J. W. Caldwell, T. E. Cheatham III, J. Wang, W. S. Ross, C. L. Simmerling, T. A. Darden, K. M. Merz, R. V. Stanton, A. L. Cheng, J. J. Vincent, M. Crowley, V. Tsui, H. Gohlke, R. J. Radmer, Y. Duan, J. Pitera, I. Massova, G. L. Seibel, U. C. Singh, P. K. Weiner and P. A. Kollman, AMBER7, University of California, San Francisco, 2002.
38. G. A. Kaminski and W. L. Jorgensen, J. Chem. Soc. Perkin Trans. 2, 1999, 2, 2365.
39. C. J. Margulis, H. A. Stern and B. J. Berne, J. Phys. Chem. B, 2002, 106, 12017.
40. C. A. Gough, S. E. DeBolt and P. A. Kollman, J. Comput. Chem., 1992, 13, 963.
41. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926.
42. A. Chaumont and G. Wipff, J. Phys. Chem. A, 2004, 108, 3311.
43. J. Åqvist, J. Phys. Chem., 1990, 94, 8021.
44. F. C. J. M. van Veggel and D. Reinhoudt, Chem. – Eur. J., 1999, 5, 90.
45. W. D. Cornell, P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, J. Am. Chem. Soc., 1995, 117, 5179.
46. T. A. Darden, D. M. York and L. G. Pedersen, J. Chem. Phys., 1993, 98, 100899.
47. Z. Gu and J. F. Brennecke, J. Chem. Eng. Data, 2002, 47, 339.
48. P. A. Z. Suarez, S. Einloft, J. E. L. Dullius, R. F. de Souza and J. Dupont, J. Chim. Phys. Phys. Chem. Biol., 1998, 95, 1626.
49. E. Engler and G. Wipff, unpublished.
50. I. G. Tironi, R. Sperb, P. E. Smith and W. F. van Gunsteren, J. Chem. Phys., 1995, 102, 5451.
51. G. Wipff and M. Lauterbach, Supramol. Chem., 1995, 6, 187.
52. A. Chaumont and G. Wipff, Inorg. Chem., 2004, 43, 5891–5901.
53. M. Dobler, in Ionophores and their Structures, Wiley Interscience, New York, 1981.
54. G. Wipff, P. Weiner and P. A. Kollman, J. Am. Chem. Soc., 1982, 104, 3249; E. D. Glendening, D. Feller and M. A. Thompson, J. Am. Chem. Soc., 1994, 116, 10657.
55. U. Schröder, D. Wadhawan, R. G. Compton, F. Marken, P. A. Z. Suarez, C. S. Consorti, R. F. d. Souza and J. Dupont, J. Chem. Phys., 2000, 24, 1009.
56. This was achieved by about 0.5 ns of dynamics with electrostatics scaled down by a factor of 100. Then equilibration started with 50 ps of dynamics at 300 K with the frozen solute and reset electrostatics, followed by 25 ps in the (NVT) and 25 ps in the (NpT) thermodynamic ensembles.
57. P. Maverick, P. Seiler, B. Schweitzer and J. D. Dunitz, Acta Crystallogr., Sect. B, 1980, 36, 615.
58. D. Mootz, A. Albert, S. Schaefgen and D. Stäben, J. Am. Chem. Soc., 1994, 116, 12045.
59. G. Ranghino, S. Romano, J. M. Lehn and G. Wipff, J. Am. Chem. Soc., 1985, 107, 7873.
60. R. Schurhammer, P. Vayssière and G. Wipff, J. Phys. Chem. A, 2003, 11128.
61. P. Dapporto, P. Paoli, I. Matijasic and L. Tusek-Bozic, Inorg. Chim. Acta, 1996, 252, 383.
62. In order to let the solvent relax before the dynamics and to prevent asymmetrical solvation to some extent, the Sr²⁺ cation was constrained at the center of the cavity during the minimization process.
63. According to an energy component analysis, the Sr²⁺ ⊂ 18C6 moiety interacts better with the dry solvent when it binds to 1 + 3, rather then 1 + 2 PF₆⁻ anions (ΔE ≈ 20 to 50 kcal mol⁻¹, depending on the simulation).
64. P. C. Junk and J. W. Steed, J. Chem. Soc. Dalton Trans., 1999, 407.
65. The difference seems to be related to different solvation patterns of the “free face” of 18C6, which is occupied by one PF₆⁻ molecules in the nitrato salt and by one BMI⁺ cation in the chloro salt, thus attracting Cs⁺ in the former case, and repulsing Cs⁺ in the latter one.
66. This K⁺ complex was forced initially to “bind” one BMI⁺ on the free face of 18C6, opposite to the NO₃⁻ side. During the dynamics, this BMI⁺ cation was displaced by one PF₆⁻ anion, as found in the other simulations.
67. We note that this decomplexation may seem inconsistent with the spontaneous hydration of the Sr²⁺ ⊂ 18C6 complex found in the humid IL simulations. This is due to the slower relaxation time and diffusion of the solvent ions, compared to the Sr(H₂O)₂²⁺ moiety, which points to the importance of the equilibration protocol in simulations of ILs, as compared to classical liquids like water.
68. C. Hardacre, J. D. Holbrey, S. E. J. McMath, D. T. Browron and A. K. Soper, J. Chem. Phys., 2003, 118, 273.
69. S. M. Urahata and M. C. C. Ribeiro, J. Chem. Phys., 2004, 120, 1855.
70. R. M. Lynden-Bell, J. Kohanoff and M. G. Del Popolo, RSC, Farad. Discuss., 2005, 129, 1.
71. F. Berny, N. Muzet, L. Troxler and G. Wipff, in Supramolecular Science: where it is and where it is going, ed. R. Ungaro and E. Dalcanale, Kluwer Academic Publishers, Dordrecht, 1999, p. p. 95.
72. F. Berny, R. Schurhammer and G. Wipff, Inorg. Chim. Acta, 2000, 300–302, 384.
73. R. Schurhammer, F. Berny and G. Wipff, Phys. Chem. Chem. Phys., 2001, 3, 647.
74. M. Baaden, R. Schurhammer and G. Wipff, J. Phys. Chem. B, 2002, 106, 434.
75. L. Troxler and G. Wipff, Anal. Sci., 1998, 14, 43.
76. P. Vayssière and G. Wipff, Phys. Chem. Chem. Phys., 2003, 5, 127.
77. W. L. Jorgensen, Acc. Chem. Res., 1989, 22, 184.
78. P. Di Bernardo, G. R. Choppin, R. Portanova and P. Zanonato, Inorg. Chim. Acta, 1993, 12, 85.
79. K. Boumizane, M. H. Herzog-Cance, D. J. Jones, J. L. Pascal, J. Potier and J. Roziere, Polyhedron, 1991, 10, 2757.
80. J. L. Pascal, F. Favier, F. Cunin, A. Fitch and G. Vaughan, J. Solid State Chem., 1998, 139, 259.
81. M. el M. Hamidi and J.-L. Pascal, Polyhedron, 1994, 13, 1787.
82. H. Luo and P. V. Bonnesen, Anal. Chem., 2004, 76, 2773.
83. We found that scaling down the atomic charges of BMI⁺ and PF₆⁻ by 0.9 reduces the intersolvent mixing at the interface. These scaled charges lead to an interaction energy of −8.9 kcal mol⁻¹ between water and the ionic components of the simulated neat [BMI][PF₆][H₂O] ionic liquid, which is less than calculated with “standard” charges (−10.6 kcal mol⁻¹) and closer to the experimental enthalpy of water absorbing in [BMI][PF₆] (−7.2 ± 1 kcal mol⁻¹). See ref. 30.
84. We also simulated an hydrated Sr(H₂O)₉²⁺ ion in the dry IL (starting with a 8 + 1 water coordination), in order to model a “nearly dry” IL. After 2 ns, seven H₂O molecules remained in the inner-sphere of the cation which additionally coordinated one loosely bound monodentate PF₆⁻ anion, and the other two H₂O molecules moved to the second sphere, thus confirming the importance of ion hydration. Note that the 8 and 7 hydration numbers of Sr²⁺ found in the humid and “dry” IL bracket its calculated and experimental values in diluted aqueous solution. See D. J. Harris, J. P. Brodholt and D. M. Sherman, J. Phys. Chem. B, 2003, 107, 9056 and references cited therein.
85. M. J. Hardie, C. L. Raston and A. Salinas, Chem. Commun., 2001, 1850.
86. K. Henke and D. A. Atwood, Inorg. Chem., 1998, 37, 224.
87. D. L. Faithfull, J. M. Harrowfield, M. I. Ogden, B. W. Skelton, K. Third and A. H. White, Aust. J. Chem., 1992, 45, 583.
88. A. Chaumont and G. Wipff, Chem. Eur. J., 2004, 10, 3919.
89. J. M. Lehn, Struct. Bonding, 1973, 161, 1.

---

Footnote

† Electronic supplementary information (ESI) available: Figures: Snapshots and RDFs of 18C6 and its complexes in the dry and humid ionic liquid. Tables: Characteristics of the RDFs and energy component analysis. See http://www.rsc.org/suppdata/cp/b4/b412794c/

---