Correlated ionic hopping processes in crystalline and glassy electrolytes resulting in MIGRATION-type and nearly-constant-loss-type conductivities
K.
Funke
*,
R. D.
Banhatti
and
C.
Cramer
University of Münster, Institute of Physical Chemistry and Sonderforschungsbereich 458, Corrensstrasse 30, D-48149, Münster, Germany. E-mail: K.Funke@uni-muenster.de
First published on 30th November 2004
Abstract
Solid electrolytes with disordered structures may be crystalline or glassy. Their complex ionic conductivity displays a characteristic frequency dependence. Modelling the dynamics of the mobile ions, we have developed the MIGRATION concept, the acronym standing for MIsmatch Generated Relaxation for the Accommodation and Transport of IONs. With the help of the MIGRATION concept it is possible to reproduce frequency-dependent experimental conductivities and permittivities including their scaling behaviour. Scaling is a property typically observed in and below the radio frequency regime. At sufficiently high frequencies and low temperatures, however, conductivity spectra of crystals and glasses are often found to contain a second component which displays the so-called nearly-constant-loss (NCL) behaviour. Suitably modifying the MIGRATION concept, we are able to explain this feature and to show that it is caused by a displacive or hopping ionic motion that stays completely localised. Here, as in the unmodified MIGRATION concept, interactions between the ions play an essential role. Experimentally, interesting differences are detected between the NCL-type dynamics in a crystalline and in a glassy ion conductor. In crystalline γ-RbAg4I5 we find the same elementary rates for the MIGRATION-type and NCL-type hopping movements of the ions, suggesting identical barrier heights for the respective processes. On the other hand, the two rates are found to differ markedly from each other in glassy AgI-AgPO3, not only with regard to their absolute value but also in their temperature dependence. We suggest that the NCL effect in the glass results from dynamic localised displacements involving both the silver ions and negatively charged entities such as iodide ions and/or non-bridging oxygen ions.
1. Introduction
In solid electrolytes, structural and dynamic disorder is the key factor for ionic motion. The evolving scheme of Fig. 1 may serve to highlight the implications of disorder with regard to the movements of the ions. In this scheme, perfectly ordered crystals are placed at level one. At this level, no ionic transport can occur. Historically, the decisive step forward was made when site disorder was discovered and point-defect thermodynamics were developed. At this stage, level two, isolated point defects are supposed to move randomly from site to site. In fact, modern materials science and technology largely build on the concept of level two. | ||
| Fig. 1 An evolving scheme of materials science, see main text. | ||
Remarkable changes are encountered as we move on to materials with disordered structures, i.e., from level two to level three. Ionic transport can no longer be described in terms of individual defects performing random walks in a static energy landscape. Instead, we are facing a challengingly complicated many-particle problem, with the mobile ions interacting with each other and with their surrounding matrix. As indicated in Fig. 1, level-three materials may be crystalline (with one sublattice being structurally disordered), glassy or polymeric. Strictly speaking, however, only crystalline and glassy ion conductors should be termed solid electrolytes.
The transition from level two to level three is accompanied by prominent changes in the shapes of experimentally accessible functions. One of them is the frequency-dependent ionic conductivity, σ(ν).1 Let us first consider a level-two material such as silver bromide. In AgBr, at 200 °C, σ(ν) is constant up to millimetre-wave frequencies, as sketched in Fig. 2.2 According to linear response theory,3 this corresponds to a velocity correlation function of the mobile charged defects (interstitialcies in the case of AgBr) which consists only of a sharp maximum around t = 0 and is otherwise exactly zero, cf. Fig. 2. Indeed, such a maximum is the fingerprint of random walkers and, therefore, of a level-two material.
 | ||
| Fig. 2 Velocity correlation function and frequency-dependent ionic conductivity for level-two materials, with defects performing a random hopping motion, schematic. | ||
On the other hand, level-three materials are found to display the characteristic behaviour sketched in Fig. 3. Examples will be given in the following section. From a conductivity spectrum as shown in Fig. 3 we obtain, via Fourier transformation, a velocity correlation function as also shown in Fig. 3, featuring a decaying negative component in addition to the peak at t = 0. There is only one explanation for this result.4 Many, normally even most, hops are followed by correlated backward hops, thus contributing a negative component to the velocity correlation function. In the conductivity spectrum, the low-frequency plateau is caused by those hops which are not nullified by correlated backward hops and thus eventually prove “successful”. On the other hand, each individual hop is seen in the limit of the high-frequency plateau, when the sign of the electric field varies so fast that a correlated backward hop would not fit into the time window of about half a period.
 | ||
| Fig. 3 Velocity correlation function and frequency-dependent ionic conductivity for level-three materials, with ions performing a correlated hopping motion, schematic. | ||
A similar effect was predicted in 1928 by Debye and Falkenhagen for dilute strong liquid electrolytes.5,6 They considered an ion that is displaced within its ion cloud. The neighbouring ions in the cloud are then supposed to rearrange according to the new situation, but this requires time, depending on temperature. During this period of time, cf. the upper panel of Fig. 4, a backward driving force is acting on the displaced ion. Therefore, the ion may move backwards, thus restoring local equilibrium. The effect causes a slight increase of the ionic conductivity with increasing frequency.5,6
 | ||
| Fig. 4 Displacement of a “central” ion in an ionic environment. Schematic comparison of situations encountered (a) in a dilute strong liquid electrolyte and (b) in a solid electrolyte with structural disorder. | ||
In much denser ionic systems, for instance in ionic melts or in structurally disordered solid electrolytes, the specific assumptions made in Debye–Hückel theory are no longer valid. Nevertheless, after a displacement of an ion (the “central” ion) out of a local-equilibrium situation, cf. the lower panel of Fig. 4, we still envisage a competition between two distinct modes of relaxation, one along the many-particle route, with the neighbours rearranging, and one along the single-particle route, with the ion moving backwards.4,7 The central ion is now expected to experience an effective potential similar to the one shown in the figure, with an absolute minimum at its local-equilibrium position and with relative minima at vacant neighbouring sites. After a hop, the ion may, in a certain fraction of cases, eventually be accommodated at its newly occupied site. This requires a new absolute minimum to be formed there, and this is only possible, if the neighbours rearrange. However, the rearrangement of the neighbours is usually not to be considered instantaneous, but requires some time. During this time the ion has a considerable chance for hopping backwards, thus giving rise to an increase of conductivity with frequency.
In level-three materials, we expect to see an effect of correlated forward-backward motion which is much larger than in dilute liquid electrolytes, for the following reasons:
(i) the number density of the mobile ions is larger by several orders of magnitude,
(ii) the movement of the ions is well defined, via spatially separated sites, and
(iii) solid electrolytes can be studied at comparatively low temperatures, well below 0 °C.
One more point should be noted. The shape of the effective potential in Fig. 4 is due to interaction as well as local structure. This implies the possibility of heterogeneity, different sites providing different effective potentials for mobile ions. Chances for a hop to prove successful will thus depend on the local surroundings, in many cases being quite low a priori. This feature is averaged out in our treatment of the MIGRATION concept, cf. Section 2.
In view of the above, it is not surprising that in many level-three materials forward–backward correlation is so pronounced that it causes a dispersion of σ(ν) extending over many decades on both the conductivity and frequency scales.
In this paper, we discuss dispersive conductivities of solid electrolytes. The paper is organised as follows. In Section 2 we present our refined model concept which builds on the previous CMR (concept of mismatch and relaxation) model.7 We show that the characteristic features of frequency-dependent conductivities and permittivities of disordered solid electrolytes are, indeed, well reproduced. Section 3 deals with the frequency dependence of the ionic conductivity of crystalline rubidium silver iodide in its low-temperature γ-phase. Here we see that strictly localised correlated hops of ions contribute an extra high-frequency component to the conductivity. This component displays the famous NCL (nearly constant loss) behaviour8–10 while also featuring a high-frequency plateau. A straightforward model treatment shows in particular that the elementary hops finally leading to translational diffusion and those causing the NCL behaviour have the same rates, implying identical potential barriers. In Section 4, we study the corresponding effect in a silver-ion conducting glass. In this case, the elementary rates for diffusive and strictly localised ionic motion turn out to be quite different from each other, signifying the coexistence of different dynamic processes. A brief conclusion is given in Section 5.
2. The MIGRATION concept
During the past two decades, the ideas sketched in Section 1 have provided a basis for a series of models including the “jump relaxation model”,4 the “concept of mismatch and relaxation”7 and the recently formulated, more refined “MIGRATION concept”.11,12 The meaning of the acronym is MIsmatch Generated Relaxation for the Accommodation and Transport of IONs. In the physical picture conveyed by the acronym, we emphasise the mismatch introduced by the initial hop of an ion, the resulting relaxation (rearrangement) of the neighbourhood and, as a consequence of the relaxation, the accommodation (stabilisation) of the ion at its new position. Once accommodation at the new site has been achieved, an elementary step of macroscopic transport has been completed by the ion.The MIGRATION concept provides a means for reproducing experimental conductivity spectra via velocity autocorrelation functions, 〈v(0)·v(t)〉. The latter are available from a set of rules for the hopping dynamics of the mobile ions, see below. In our model treatment, we do not attempt to formulate expressions for the cross terms in the velocity correlation function. Rather, we neglect the cross terms; this amounts to assuming that the Haven ratio is always equal to one.
It is useful to introduce the time-dependent correlation factor, W(t), which is the probability for the ion to be (still or again) at its new position at time t after its “initial forward” hop. W(t) is the normalised integral of 〈v(0)·v(t)〉. While W(0) is unity by definition, the limiting value of W(t) at long times, W(∞), is the ratio of low-frequency to high-frequency conductivity, W(∞) = σ(0)/σ(∞). Utilising W(t), we find from linear response theory:3
 | (1) |
Here, ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/char_e111.gif) (ω) is the complex conductivity caused by the hopping motion of the ions. Differentiation with respect to time is denoted by a dot. Note that in log-log plots the functions W(t) and σ(ω)/σ(∞) are almost exact mirror images of each other. Of course, the same holds true when scaled functions are introduced by WS(t)
=
W(t)/W(∞) and σS(ω)
=
σ(ω)/σ(0), see Fig. 5.
(ω) is the complex conductivity caused by the hopping motion of the ions. Differentiation with respect to time is denoted by a dot. Note that in log-log plots the functions W(t) and σ(ω)/σ(∞) are almost exact mirror images of each other. Of course, the same holds true when scaled functions are introduced by WS(t)
=
W(t)/W(∞) and σS(ω)
=
σ(ω)/σ(0), see Fig. 5.
 | ||
| Fig. 5 Scaled conductivity spectrum due to ionic hopping, σS(ω) = σ(ω)/σ(0), and corresponding scaled time-dependent correlation factor, WS(t) = W(t)/W(∞), schematic. | ||
In order to find the proper shape of W(t), we apply the set of rules that constitute the MIGRATION concept.11,12 These are:
 | (2) |
 | (3) |
| N(t) = N(∞) + (Bg(t))λ. | (4) |
In eqn. (3) we formulate the rate of decay of g(t), which is −ġ(t). Besides being proportional to the driving force, g(t), it is also proportional to the time-dependent elementary hopping rate, denoted by Γ0. Thirdly, −ġ(t) is proportional to W(t), since the mobile neighbours perform correlated forward–backward jumps in the same fashion as the central ion does. Finally, the hopping motion of the neighbours causes an increasing degree of shielding of the central dipole. We, therefore, write −ġ(t) ∝ N(t), where N(t) is an effective number of mobile neighbours which still notice the dipole at time t.
For the decay of N(t), see eqn. (4), we have chosen an empirical function that yields excellent agreement with the experimental spectra.12 In most cases best results are obtained with λ = 1, while in others we need to choose somewhat larger values.7 In eqn. (4), the decaying function is not N(t) itself, but N(t) − N(∞) where N(∞) is an effective number of nearest neighbours, i.e., of those ions that never get shielded. Indeed, a non-zero value of N(∞) turns out to be essential for obtaining finite values of the low-frequency permittivity.12
Eqns. (2) to (4) yield the following rate equation for the scaled time-dependent correlation factor, WS(t) = W(t)/W(∞),
| −ẆS = ω0WS2ln WS((ln WS)λ+ N(∞)). | (5) |
| ω0 = Γ0W(∞) = Γ0exp(−B). | (6) |
The influence of the term N(∞) in eqn. (5) is restricted to angular frequencies below about ω0/10, where it affects ε(ω) significantly.12 On the other hand, N(∞) does not noticeably influence σ(ω) at any frequency. Therefore, if only σ(ω) is concerned, eqn. (5) may be replaced with the simpler equation
| −ẆS = ω0WS2(ln WS)K, | (7) |
| K = 1 + λ. | (8) |
| ωS = ω/ω0 and tS = tω0. | (9) |
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) S(ωS)
=
S(ωS)
=
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (ωS)/σ(0), is expected to be independent of temperature as long as
(ωS)/σ(0), is expected to be independent of temperature as long as
(i) the conduction mechanism does not change and
(ii) the frequency is well below the high-frequency plateau.
The second condition is usually fulfilled if the measured conductivities are restricted to the so-called impedance frequency regime, below a few megahertz. For examples, see below.
In Figs. 6–9 experimental data and model spectra obtained from the MIGRATION concept are compared with each other. The conductivity spectrum presented in Fig. 6 has been taken from a crystalline electrolyte, Na-β″-alumina.19 It extends beyond 1 THz and comprises not only the conductivity component caused by the hopping motion of the mobile ions, σhop(ν), but also the one caused by the excitation of vibrations, σvib(ν). The solid line results from eqn. (1), with WS(t) − and hence W(t) − from eqn. (7).
 | ||
| Fig. 6 Frequency-dependent conductivity, σ(ν), of crystalline Na-β″-alumina at 473 K. The solid line results from the MIGRATION concept. | ||
In glassy electrolytes, the vibrational contribution to the conductivity normally extends to rather low frequencies. This is easily explained by the absence of Brillouin zones and of the corresponding selection rules. Therefore, the high-frequency plateau of σhop(ν) is usually swamped by the low-frequency flank of σvib(ν). In Fig. 7, we present a conductivity isotherm of glassy Ag2S·GeS2 including both σhop(ν) and σvib(ν).20 In this example, the low-frequency flank of σvib(ν) varies exactly as frequency squared, and we have attempted to remove it from the total conductivity spectrum. Although the resulting component, σhop(ν), shows considerable scatter in the microwave regime, there is a clear indication of a high-frequency plateau, and the spectrum σhop(ν) as a whole is nicely reproduced by the MIGRATION concept.7
 | ||
| Fig. 7 Frequency-dependent conductivity, σ(ν), of glassy Ag2S·GeS2 at 273 K (+). Removing the vibrational contribution (cf. main text) results in a non-vibrational component (○) which is well reproduced by the MIGRATION concept. | ||
By contrast to Figs. 6 and 7, the data shown in Figs. 8 and 9 have been measured exclusively in the impedance regime, at frequencies not exceeding 10 MHz. The figures are scaled representations of the conductivity and permittivity, i.e., of σS(ωS) and εS(ωS), respectively. The scaled conductivity spectrum of Fig. 8 has been obtained by superimposing several conductivity isotherms of one particular glass, viz. 0.3 Na2O·0.7 B2O3. Most remarkably, however, the shape of this experimental “master curve” is characteristic of many glassy and crystalline electrolytes.7 For comparison, a solid line has been included in Fig. 8. This line is our model master curve as derived from eqns. (1) and (7), with λ = 1, corresponding to K = 2.
 | ||
| Fig. 8 Experimental frequency-dependent conductivities of glassy 0.3 Na2O·0.7 B2O3 in a scaled representation. The shape of the dispersion is found to be the same in many crystalline and glassy ion conductors (“master curve”). The solid line results from the MIGRATION concept, with K = 2, i.e., λ = 1. | ||
 | ||
| Fig. 9 Scaled permittivity of 0.2 Na2O·0.8 GeO2 glass. The solid curve has been obtained from the MIGRATION concept, with λ = 1 and N(∞) = 0.075. | ||
In Fig. 9, we present scaled permittivities of glassy 0.2 Na2O·0.8 GeO2.12 Since
 | (10) |
 | (11) |
In eqns. (10) and (11), ε(∞) denotes the high-frequency permittivity, which is not caused by ionic hopping, but by faster processes. In Fig. 9, different experimental permittivity isotherms are found to collapse onto one single curve. Note that the slight increase of the data observed at low frequencies is an experimental artefact caused by electrode polarisation, which can never be totally avoided. The solid line results from the MIGRATION concept, with WS derived from eqn. (5). The value used for λ is 1. Note that the value of N(∞), which contains structural information, is also temperature-independent.12
3. The NCL effect in rubidium silver iodide
The MIGRATION concept has proved very successful in reproducing frequency-dependent conductivities and permittivities such as those discussed in Section 2. This includes the phases α and β of crystalline rubidium silver iodide, RbAg4I5, which is a prominent member of the class of optimised silver ion conductors with structurally disordered silver sublattices. A comparison of experimental and model spectra of α and β rubidium silver iodide was given in ref. 7.At low temperatures and high frequencies, however, a new effect comes into play. This is clearly visible in the spectrum shown in Fig. 10, which is a non-vibrational conductivity isotherm of rubidium silver iodide in its γ-phase at 113 K. It has been obtained from the corresponding experimental spectrum by carefully removing the low-frequency flank of the slow vibrational contribution.21,11 Remarkably, the isotherm of Fig. 10 can no longer be reproduced in terms of the MIGRATION concept alone. Rather, a second component appears to be superimposed at frequencies above 10 MHz. Varying roughly linearly with frequency, this component bears the distinguishing mark of the NCL (nearly constant loss) effect.8–10
 | ||
| Fig. 10 Non-vibrational conductivity spectrum of γ-RbAg4I5 at 113 K, along with a model spectrum (solid line). The spectrum is decomposed into its MIGRATION-type and NCL-type components. Arrows indicate the positions of the onset and end frequencies of the regime where the NCL-type component varies linearly with frequency. Note the identity ν1 = Γ0/(2π), cf. main text. The value of λ used is 1.6. | ||
In Fig. 10, the non-vibrational frequency-dependent conductivity is compared with a model spectrum, represented by the solid line. This model spectrum consists of two components, one of them being MIGRATION-type, the other NCL-type:11
| σhop(ν) = σMIG(ν) + σNCL(ν) | (12) |
The plateau regime of the dielectric loss cannot be explained in terms of an assembly of individual non-interacting ions, each of them placed within a double-well potential of a given shape. Such a model would result in a Debye-type correlation factor, WDebye(t), with
| WDebye(t) = exp(−t/τ), | (13) |
 | (14) |
This correlation factor yields a Lorentzian loss function, not featuring the plateau we need to explain.
Of course, a broadening of the loss function can be achieved by introducing a distribution of relaxation times, τ, possibly resulting from a distribution of shapes of static local potentials. This procedure, first suggested by Pollak and Pike, has come to be called the asymmetric double well potential (ADWP) model.22
In our treatment, however, we only consider the mutual interactions between the ions in the assembly and do not introduce different shapes of static potentials. This is equivalent to considering an assembly of interacting fluctuating dipoles. In fact, such an assembly has been studied by Dieterich and coworkers in a Monte Carlo simulation.23 Their results and ours, see below, are indeed completely consistent with each other.
In his papers on the nearly constant loss, Jain has coined the term “jellyfish movement” in order to emphasise the many-particle correlations causing the effect.24,25 At the same time, he has been using the ADWP model to describe the spectra. For a justification, one may employ an ergodic mapping argument in which the distribution of shapes introduced in the ADWP model is regarded as a series of snapshots taken of the time-dependent potential that one obtains by considering the interactions.
To introduce the interaction, we replace eqn. (14) with
 | (15) |
Trying to fit the experimental data of Fig. 10 with eqn. (12), we find that best results are obtained, if the elementary hopping rates of the localised motion and of the MIGRATION-type component, 1/τ and Γ0, respectively, are assumed to be identical.11 Likewise, the same proportionality constant, B, is chosen for the two processes. For describing the NCL effect, eqn. (2) is thus simply replaced with
 | (16) |
 | (17) |
Inserting σNCL(ν) into eqn. (12), we obtain the complete model spectrum shown in Fig. 10 along with the experimental data.
To keep the equations simple, it is useful to introduce an approximation for WNCL(t). The approximation is based on the observation that the NCL-type process alone makes g(t) decrease by only one or two per cent. In eqns. (3) and (4) we, therefore, put g(t) = 1. Inserting the expression for the rate of decay of g(t) into eqn. (16) and separating the variables, we find for WNCL(t) after integrating:
 | (18) |
| 2πν1 = ω1 = Γ0 and 2πν2 = ω2 = Γ0BK. | (19) |
If, on the other hand, the interaction between the mobile ions is considered, and if ν1 is much smaller than ν2, then a linear frequency dependence of σNCL(ν) will occur in the frequency range between ν1 and ν2. In Fig. 10, the positions of ν1 and ν2 have been marked on the frequency scale. The width of the linear regime increases with decreasing temperature, since increasing values of B imply increasing ratios of ν2/ν1.
In our modelling for rubidium silver iodide, Γ0 and 1/τ are identical. This implies that the elementary hopping rates are the same for potentially successful and strictly localised hops of the mobile ions. The difference between the two kinds of hop is, therefore, not in the height of the barrier to be surmounted, but rather in the connectivity of the respective target site which may or may not provide access to unblocked passageways. A structural refinement of γ-RbAg4I5, which is currently underway, will provide possibilities to correlate the structural and dynamic aspects of ionic motion in this phase.
Recently, Leon, Ngai and coworkers analysed temperature- and frequency-dependent conductivities of a crystalline and a glassy lithium ion conductor, measured in the impedance frequency regime.26 At each temperature, they determined the onset angular frequency of the NCL behaviour and identified it with the elementary hopping rate of the lithium ions.26 This is in perfect agreement with our present results for rubidium silver iodide.
4. The NCL effect in a silver iodide–silver metaphosphate glass
In recent years, we have been able to show that frequency-dependent conductivities of glassy electrolytes, taken in the impedance frequency regime below a few megahertz, are generally well reproduced by our model concept. In the particular case of glassy Ag2S·GeS2, cf. Fig. 7, we could even show that total conductivity spectra taken at different temperatures are well described by superposition of a MIGRATION-type contribution and a vibrational component.On the other hand, we have also encountered a number of glassy electrolytes where high-frequency conductivities are found to deviate substantially from our model expectations, see, e.g., ref. 27. One example is the highly ion-conducting silver iodide – silver metaphosphate glass with composition AgI·AgPO3. Its 293 K conductivity isotherm is presented in Fig. 11.
 | ||
| Fig. 11 Frequency-dependent conductivity of glassy AgI·AgPO3 at 293 K. Note that the “master curve” of Fig. 8 does not fit the data in and beyond the microwave regime. | ||
Evidently, the master curve of Fig. 8 no longer fits the data in and beyond the microwave regime. In previous publications, we have considered this deviation, i.e., the difference between the total conductivity and the “master-curve” contribution. Interestingly, this difference appears to vary with frequency according to a power law with an exponent of about 1.4, see Fig. 12.27 However, possible dynamic origins of such a power law are still a matter in dispute. In the following, a quite different treatment of the data is presented, which is at the same time simpler and more physical.
 | ||
| Fig. 12 For glassy AgI·AgPO3 at 293 K, circles represent a “reduced” conductivity, σred(ν), which is the difference between the conductivity spectrum of Fig. 11 and the “master curve” of Fig. 8. Boxes are conductivities measured at 103 K. Within the limits of error, these are indistinguishable from the corresponding reduced conductivities. | ||
In fact, the deviation in Fig. 11 is most easily explained in terms of a nearly constant loss component. To detect this component, the decisive step is to remove the vibrational conductivity from the total spectrum. This is possible, since at sufficiently low temperature, see the 103 K isotherm in Fig. 12, the low-frequency part of σvib(ν) is found to vary with frequency in the usual way, i.e., as frequency squared. The same frequency dependence was encountered earlier in glassy Ag2S·GeS2 and in crystalline RbAg4I5. We, therefore, conclude that the far-infrared spectrum measured at 103 K no longer contains contributions due to the activated hopping motion of mobile ions. The vibrational component is now removed from total experimental spectra taken at higher temperatures, in order to obtain frequency-dependent conductivities that are only due to displacive or hopping processes of the ions.
The non-vibrational conductivity isotherm, σnon-vib(ν), thus obtained from the 293 K spectrum is shown in Fig. 13. Remarkably, its overall shape strongly resembles the 113 K isotherm of rubidium silver iodide, cf. Fig. 10, featuring a similar NCL-type section as well as a similar saturation of the conductivity in the limit of high frequencies. These characteristics are preserved as the temperature is increased to 363 K, which is just above the glass transition temperature, see Fig. 14. The existence of a (slightly) thermally activated high frequency plateau of σnon-vib(ν) is an unexpected and important result. In view of the shape of the non-vibrational spectra of Figs. 13 and 14, we have employed the superposition introduced in eqn. (12) for a further analysis of the frequency dependence.
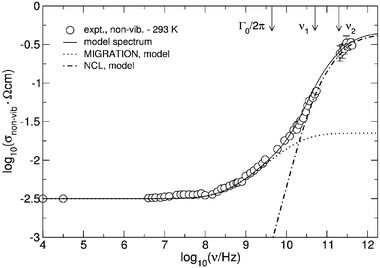 | ||
| Fig. 13 Non-vibrational conductivity spectrum of glassy AgI·AgPO3 at 293 K, along with a model spectrum (solid line). As in Fig. 10, the spectrum is decomposed into its MIGRATION-type and NCL-type components. Note that the elementary hopping rate of the mobile silver ions, Γ0, and the elementary rate of the localised displacements, 1/τ = 2πν1, are not identical. | ||
 | ||
| Fig. 14 Non-vibrational conductivity spectrum of glassy AgI·AgPO3 at 363 K, along with a model spectrum (solid line). Note that ν1 is much less temperature-dependent than Γ0. | ||
By contrast with the case of rubidium silver iodide, best results are now obtained, if the elementary rates for potentially translational hops and for localised displacements are assumed not to be identical, the localised movements exhibiting clearly higher rates and a much lower activation energy than the potentially translational ones. Therefore, our equations pertaining to the NCL effect have to be reformulated, resubstituting a temperature-dependent rate of localised elementary hops, 1/τ, for Γ0. This applies in particular to the definition of the frequencies ν1 and ν2, see eqn. (19), which are required for expressing WNCL(t) according to eqn. (18). This function, WNCL(t), is then again used to determine σNCL(ν) viaeqn. (17).
The weight of the NCL component in its high-frequency limit must be proportional to the elementary rate, ν1. Therefore, it can be used for a rough estimate of the activation energy of ν1 = 1/(2πτ), which turns out to be no larger than about 0.05 eV. Extrapolation shows that, in the impedance regime, the NCL effect will still be measurable at 30 K. At 10 K, however, σNCL(∞) as well as the upper crossover frequency, ν2, will be too small to detect.
For comparison with the localised motion, we note that the activation energy for the translational motion of the mobile silver ions, i.e. for σ(0)T, is about 0.30 eV, while that of Γ0 is between 0.15 eV and 0.20 eV.
There are two important consequences of our present observations.
(i) We envisage a more complex dynamic situation in the glass than in the crystalline material discussed in Section 3. For their strictly localised displacements, the ions in the glass need to surmount only very small energy barriers. At 293 K, these displacements are by a factor of ten more frequent than the elementary hops of the translationally mobile silver ions. This factor rapidly increases as the temperature is further reduced. At the same time, we find quite similar ratios, σMIG(∞)/Γ0 and σNCL(∞)/ν1, for the two effects. This implies that the respective products, n(qx0)2, must be of the same order of magnitude. Here, n, q and x0 denote number densities, charges and displacements, respectively. Therefore, the rapid localised movement has to be considered ubiquitous in the glass, with a large value of n. Also, qx0, which plays the role of a dipole moment, must be reasonably large. This is possible, if the cations and their negatively charged neighbours move locally and cooperatively in opposite directions. We thus arrive at a view of the non-vibrational local dynamics which is well in line with the idea of a “jellyfish movement” introduced by Jain.25 For AgI·AgPO3, this view implies that not only the silver ions, but also the non-bridging oxygen ions and/or the iodide ions play an essential role in the NCL-type motion. This would explain why a corresponding effect has not been found in Ag2S·GeS2 glass, cf. Fig. 7. To learn more about the anionic species involved, it would be interesting to investigate the relative intensity of the NCL effect as a function of AgI content. Measuring complete conductivity spectra for various compositions is, of course, very time consuming and has not yet been done.
(ii) In the last few years, the NCL phenomenon has been reported for many disordered ionic materials, with measurements done almost exclusively in the impedance frequency range. Notably, NCL behaviour has still been observed at liquid-helium temperatures.10 In view of our present high-frequency results, the following conclusion can be drawn. Although the correlated localised displacements detected in glassy AgI·AgPO3 are already characterised by an unusually small activation energy, there must be others, present in many materials, that are still less activated. This is required to make such processes visible at temperatures as low as a few Kelvin, since otherwise σNCL(∞) will become so small that the linear part of σNCL(ν), where the conductivity is even smaller, will shift outside (to lower frequencies than) the conventional impedance regime. A prediction is now attempted concerning the development of the NCL effect in glassy AgI·AgPO3 with decreasing temperature. We envisage a whole range of possible dynamic displacements requiring different thermal activation. With decreasing temperature, there will be a continuous transition towards less and less activated displacive processes playing the major role in the NCL-type conductivity, even if the structure provides restricted probabilities for them to occur. As a result, impedance-frequency conductivity measurements may well show the NCL effect even at liquid-helium temperatures.
5. Conclusion
Ionic transport in materials with disordered structures involves complex many-particle correlations. Time-resolved information on the relevant processes is available from ionic conductivity spectra spanning wide frequency ranges. We have shown that the essential features of such spectra may be understood in terms of the MIGRATION concept, its equations modelling the ion dynamics. In particular, our model perfectly reproduces the long-time, low-frequency properties of the spectra including their scaling behaviour. Moreover, examples have been given, cf. Figs. 6 and 7, for which the entire non-vibrational conductivity, from low frequencies up to the far infrared, is well explained in terms of the MIGRATION concept.In other ion-conducting materials, we have encountered substantial differences between the experimental data and the expectations according to our model. These differences are due to extra contributions to the conductivity which occur at high frequencies and low temperatures and bear the signature of the NCL effect. Here, we have reported on such NCL components in the low-temperature γ-phase of crystalline rubidium silver iodide and in glassy silver iodide–silver metaphosphate. The NCL-type conductivities have been traced back to highly cooperative, strictly localised ionic hops or displacements. In γ-RbAg4I5, these are “regular” hops of silver ions which remain localised because of lacking structural connectivity of the available sites. In the silver-ion conducting AgI·AgPO3 glass, however, the NCL behaviour has to be attributed to cooperative local processes which are much less activated. We suggest that these involve silver ions as well as negatively charged entities such as iodide ions and/or non-bridging oxygen ions.
A structural refinement of γ-RbAg4I5 is presently under way. At the same time, we try to extend our model to include different degrees of availability of suitable vacant cation sites. Such an extension will be particularly useful for studying the ionic motion in structures that are characterised by a general shortage of suitable cation sites, such as many glasses as well as γ-RbAg4I5. It is possible that the procedure then yields conductivity spectra featuring a gradual transition from an apparently purely MIGRATION-type to an apparently purely NCL-type behaviour. In a further step, such a treatment may help understand the very pronounced changes in the ion dynamics and especially in the DC conductivity occurring when the amount of mobile ions is varied in a glass or when a second mobile species is introduced (mixed alkali effect). It will be interesting to see, if in these cases structure and dynamics can be related to each other via a varying availability of suitable cation sites.
Notations
| t | Time |
| T | Temperature |
| ν | Frequency |
| ω | Angular frequency |
| i | Imaginary unit |
| v | Velocity (vectorial) |
| ⁁ | Symbol denoting a complex quantity |
| 〈v(0)·v(t)〉 | Velocity autocorrelation function |
| ε 0 | Permittivity of a vacuum |
| Γ 0 | Elementary hopping rate |
| σ | Electrical conductivity |
| σ hop | Conductivity due to hopping motion of the ions |
| σ vib | Conductivity due to vibrational motion |
| σ non-vib | Difference, σ − σvib |
| σ MIG | Conductivity as described by the MIGRATION concept |
| σ red | Difference, σ − σMIG |
| σ NCL | Conductivity caused by strictly localised displacements of interacting ions |
| σ(0) | DC conductivity |
| σ(∞) | High-frequency value of σhop |
| ε | Relative permittivity |
| ε(∞) | Value of ε(ν) at frequencies just below the dispersion of ε caused by vibrations |
| ε″ | Imaginary part of relative complex permittivity |
| W(t) | Time-dependent correlation factor, i.e., normalised integral of 〈v(0)·〈v(t)〉, with W(0) = 1 |
| W(∞) | Long-time limiting value of W(t) |
| W S(t) | Scaled time-dependent correlation factor, i.e., W(t)/W(∞) |
| B | Model parameter, which is −ln W(∞) |
| σ S(ν) | Scaled frequency-dependent conductivity due to hops, i.e., σhop(ν)/σ(0) |
| ω 0 | Rate of successful hops, i.e., Γ0W(∞) |
| ω S | Scaled angular frequency, i.e., ω/ω0 |
| t S | Scaled time, i.e., tω0 |
| ε S | Scaled permittivity, i.e., (l/ωS)Im ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) S S |
| g(t) | Normalised mismatch function, with g(0) = 1 and g(∞) = 0 |
| N(t) | Effective number of mobile neighbours which still notice the local dipole at time t |
| λ | Empirical parameter in eqn. (4) |
| K | λ + 1 |
| τ | Relaxation time |
| W Debye (t) | exp (−t/τ) |
| W NCL(t) | Time-dependent correlation factor due to strictly localised displacive movements of interacting ions |
| ν 1 | Onset frequency of linear regime of σNCL |
| ν 2 | End frequency of linear regime of σNCL |
| n | Number density |
| q | Charge |
| x 0 | Elementary displacement |
Acknowledgements
It is a pleasure to thank M. D. Ingram, H. Jain and A. S. Nowick for many fruitful discussions. We are indebted to S. Brunklaus, J. Gockel, E. Grüter-Höge, R. Holtwick and D. Zurwellen for their experimental data on glassy AgI·AgPO3. We also would like to thank D. Wilmer for his help in the data analysis and A. Krüssel for technical help. Financial support from Fonds der Chemischen Industrie is gratefully acknowledged.References
- K. Funke and C. Cramer, in Encyclopedia of Materials: Science and Technology, eds. K. H. J. Buschow, R. W. Cahn, M. C. Flemings, B. Ilschner, E. J. Kramer and S. Mahajan, Elsevier, Oxford, 2001, Vol. 1, 189 Search PubMed.
- K. Funke, D. Wilmer, T. Lauxtermann, R. Holzgreve and S. M. Bennington, Solid State Ionics, 1996, 86–88, 141 CrossRef.
- R. Kubo, J. Phys. Soc. Jpn., 1957, 12, 570.
- K. Funke, Prog. Solid State Chem., 1993, 22, 111 CrossRef CAS.
- P. Debye and H. Falkenhagen, Phys. Z., 1928, 29, 121 Search PubMed.
- P. Debye and H. Falkenhagen, Phys. Z., 1928, 29, 401 Search PubMed.
- K. Funke, R. D. Banhatti, S. Brückner, C. Cramer, C. Krieger, A. Mandanici, C. Martini and I. Ross, Phys. Chem. Chem. Phys., 2002, 4, 3155 RSC.
- W. K. Lee, J. F. Liu and A. S. Nowick, Phys. Rev. Lett., 1991, 67, 1559 CrossRef CAS.
- X. Lu and H. Jain, Phys. Chem. Solids, 1994, 55, 1433 Search PubMed.
- A. S. Nowick, A. V. Vaysleyb and W. Liu, Solid State Ionics, 1998, 105, 121 CrossRef CAS.
- K. Funke, R. D. Banhatti, I. Ross and D. Wilmer, Z. Phys. Chem., 2003, 217, 1245 Search PubMed.
- (a) K. Funke and R. D. Banhatti, Solid State Ionics, 2004, 169, 1 CrossRef CAS; (b) K. Funke and R. D. Banhatti, Mater. Res. Soc. Symp. Proc., 2003, 756, 3 CAS.
- S. Summerfield, Philos. Mag. B, 1985, 52, 9.
- H. E. Taylor, Trans. Faraday Soc., 1956, 52, 873 RSC.
- J. O. Isard, J. Non-Cryst. Solids, 1970, 4, 357 CrossRef CAS.
- J. R. Dyre, J. Appl. Phys., 1988, 64, 2456 CrossRef.
- H. Kahnt, Ber. Bunsen-Ges. Phys. Chem., 1991, 95, 1021 CAS.
- B. Roling, K. Funke, A. Happe and M. D. Ingram, Phys. Rev. Lett., 1997, 78, 2160 CrossRef CAS.
- R. Hoppe, T. Kloidt and K. Funke, Ber. Bunsen-Ges. Phys. Chem., 1991, 95, 1025 CAS.
- C. Cramer, S. Brückner, Y. Gao, K. Funke, R. Belin, G. Taillades and A. Pradel, J. Non-Cryst. Solids, 2002, 307–310, 905 CrossRef CAS.
- I. Ross, PhD Thesis, Department of Chemistry, Münster, 2003.
- M. Pollak and G. E. Pike, Phys. Rev. Lett., 1972, 28, 1449 CrossRef CAS.
- B. Rinn, W. Dieterich and P. Maass, Philos. Mag. B, 1998, 77, 1283 CrossRef CAS.
- H. Jain, Met. Mater. Process., 1999, 11, 317 Search PubMed.
- H. Jain, S. Krishnaswami and O. Kanert, J. Non-Cryst. Solids, 2002, 307–310, 1017 CrossRef CAS.
- C. Leon, A. Rivera, A. Varez, J. Sanz, J. Santamaria and K. L. Ngai, Phys. Rev. Lett., 2001, 86, 1279 CrossRef CAS.
- C. Cramer, S. Brunklaus, Y. Gao and K. Funke, J. Phys.: Condens. Matter, 2003, 15, S2309 CrossRef CAS.
| This journal is © the Owner Societies 2005 |
