Headgroup organization and hydration of methylated phosphatidylethanolamines in Langmuir monolayers

Abstract

Subtle differences in the molecular conformation of fully hydrated phospholipids, and in their interaction with the water reservoir, were assessed as functions of headgroup methylation with surface-sensitive X-ray scattering. To achieve such a structural and functional comparison, diacylphosphatidylethanolamines (PEs) and their mono-, di- and trimethylated (diacylphosphatidylcholine, PC) derivatives in surface monolayers on water have been studied. While the molecular structures of these lipids are quite similar, their subtle distinctions lead to surprisingly large differences in their overall organization. Independent of the surface pressure, π, the amine function in PE extends 1–2 Å further into the subphase than those of the methylated headgroups. Not only is the exposure of the amine moiety to water in PE thus larger than that of the other lipids, but also the phosphate and lipid backbone of PE are more hydrated than that of PC. Overall, the PE headgroup hydration is ≈25% larger than that of PE-N-Me, PE-N-Me₂ or PC. The main reason for these differences resides in their distinct capabilities to donate hydrogen bonds, but differences in the hydrophobicities of the amine functions on the lipid headgroups may also play a role. While the impact of amine methylation on the headgroup interaction with the water subphase appears rather straightforward, there are also differences in lipid backbone organization and acyl chain packing. The results presented here provide a deeper understanding of lipid conformation as the hydrophobicity of the terminal headgroup fragment is systematically altered and may also impact on our understanding of the molecular details of membrane fusion.

---

1. Introduction

Biological membranes are intrinsically disordered systems that play an eminently important role as a supramolecular constituent of living organisms by forming the structural basis of compartmentalization within the cell. Because they are disordered, both in-plane and out-of-plane, their molecular detail is difficult to assess, as high-resolution crystallography cannot be applied. Yet it has been argued that the structural and chemical heterogeneity of, particularly, membrane surfaces¹ is key to many important biological processes, such as cell-cell communication, membrane protein folding and insertion, or the control of complex biochemical syntheses. A successful approach to solve structural and functional questions in membrane biophysics has been the investigation of well-defined model systems, be it in the form of vesicles, “black” lipid membranes, bilayers on solid support, or simple lipid monolayers on aqueous surfaces, so-called Langmuir monolayers.^2–5

Monolayers have been intensively studied for their unique properties as quasi-2D systems, their complex phase behavior, as well as the ease by which their molecular properties may be controlled. From the perspective of membrane biochemistry, many physiologically important interactions take place at the interface between the membrane and the aqueous compartment – i.e. at the location of the lipid headgroups. This is because the headgroups are chemically promiscuous¹ in the sense that they may act as a reaction partner in many different weak chemical interactions, such as salt bridges, dipolar interactions, hydrogen bonds, hydrophobic interaction sites, etc. Extensive X-ray and neutron diffraction studies of dehydrated multibilayer stacks⁶ have established that the interfacial region of a bilayer has about the same combined thickness, ≈30 Å, as the hydrophobic interior of the membrane. Moreover, this interfacial region defines also the steepest gradient in the dielectric constant as one approaches the hydrophobic interior of the membrane (ε ≈ 2) from the aqueous bulk (ε ≈ 80).¹ Surface-sensitive X-ray scattering investigations^7–9 have been extensively used to determine the structure of Langmuir films in great detail. Grazing incidence X-ray diffraction (GIXD) is capable of assessing the atomic level details of lipid acyl chain packing if the molecules possess at least hexatic order.^10,11 Specular X-ray or neutron reflectometry determines the scattering length density (SLD) distribution normal to the interface^12–15 regardless of whether the molecules are ordered or disordered. The latter technique is thus capable of answering structural questions on membrane models that are close to their physiologically significant, fluid state.

Hydration properties of biomembrane models¹⁶ have been intensively studied in recent years with various techniques.^17–21 Typically, these approaches determine thermodynamic or structural parameters as a function of water activity in partially dehydrated systems, e.g. membrane “swelling” as a function of water content. However, studies of fully hydrated systems are rare. In fact, we are not aware of a direct, high-resolution structural characterization of fully hydrated lipid surfaces as a function of molecular architecture. To fill this void, we take an entirely different, novel approach in this work and demonstrate that the surface-sensitive scattering of X-rays from a surface monolayer, which resides on a semi-infinite reservoir of water and is thus fully hydrated, can be employed to obtain such information. We determine how the substitution of methyl groups for hydrogens on the phospholipid ethanolamine moiety influences headgroup conformation and chain packing within the monolayer and study in detail the interaction of the headgroup with surrounding water molecules. A study that employed GIXD has been conducted earlier on tri-chain phospholipids,²² which concentrated on the impact of headgroup methylation on chain order/disorder. In the current study, we take advantage of state-of-the-art data evaluation techniques and the potential of a third generation synchrotron source to determine the headgroup organization of lipid/water interfaces in great detail.

2. Experimental

2.1. Materials

Dipalmitoylphosphatidylethanolamine (DPPE), dipalmitoylphosphatidylethanolamine-N-methyl (DPPE-N-Me), dipalmitoylphosphatidylethanolamine-N-dimethyl (DPPE-N-Me₂), and dipalmitoylphosphatidylcholine (DPPC) from Avanti Polar Lipids (Alabaster, AL) were used as received. These lipids were dissolved in chloroform/methanol (3 : 1, Merck, HPLC grade) in concentrations of ∼6 mM, and spread in 100 μl volumes on a clean water surface in a Langmuir trough of local design. At least 10 min were allowed for solvent evaporation before the computer-controlled Teflon (PTFE) barrier of the trough was set to compress the monolayer film at a rate of 1 Ų molecule⁻¹ min⁻¹). Ultra-pure water was obtained from a Milli-Q system coupled to a Milli-RO reverse osmosis unit (Millipore) with a residual specific resistance of 18.2 MΩ cm. The surface tension γ was measured with an ash-free filter paper used as a Wilhelmy plate, and monitored as a function of the surface area A at a temperature of 20 °C for DPPE, DPPE-N-Me and DPPE-N-Me₂. To ensure that DPPC is in the same phase as the remaining phospholipids under investigation, lecithin monolayers were prepared at 10 °C, in order to avoid the LE/TC phase¶ transition observed at a surface pressure, π ≈ 5 mN m⁻¹ at 20 °C. Assuming a temperature dependence of 1.5 mN m⁻¹ per K,²³ the transition pressure should have dropped to zero at this temperature. As we show below, however, subtle differences still persist between DPPC and DPPE-N-Me or DPPE-N-Me₂.

2.2. Scattering experiments

X-ray reflectivity (XR) experiments and GIXD were carried out at the undulator beamline BW1²⁴ of the DORIS III bypass at HASYLAB (DESY, Hamburg, Germany) at a positron energy of ∼4.6 GeV. The setup of BW1 has been described in detail.^25–28 X-ray wavelengths were between λ = 1.38 Å and 1.45 Å and the maximum beam footprint on the sample was ∼5 × 50 mm². Experiments were performed using a custom-built Langmuir film balance (surface area, 16 × 30 cm²) incorporated in a gas-tight, thermostated aluminum container with Kapton windows for the X-ray beam.²⁹ A polished (λ/10) Pyrex (boron silicate) glass block was inserted into the subphase to diminish surface waves in the film balance. GIXD was performed with a He atmosphere over the sample film.

2.3. Reflectivity data analysis

The reflectivity R(q_z) of a film-covered interface is a function of the electron density ρ_e(z), where z is the distance from the interface, q_z denotes momentum transfer and R_F is the Fresnel reflectivity, i.e. the hypothetical reflectivity of the ideal surface in vacuum. Due the lack of phase information, R(q_z) cannot be directly inverted. Rather, the optical parameters are determined by data modeling. The simplest approach uses layer models (“box models”), motivated by the propensity of amphiphilic molecules for supramolecular self-organization into molecular surface films. Two boxes represent the hydrophobic chains and the hydrated hydrophilic headgroups in contact with the aqueous bulk subphase. These boxes are blurred along z with a roughness parameter σ_cw to account for thermal capillary waves.

We have recently developed an alternate parameterization, the volume-restricted distribution function (VRDF) approach,³⁰ and have demonstrated that it overcomes deficiencies of the box-model particularly in describing the headgroup region of phospholipids.³¹ In short, the aliphatic chains are described within the VRDF model as a “box” profile, smeared by an error function with a width, σ_cw; the headgroup is parsed into submolecular fragments (three fragments, GC, P, and N, see inset in Fig. 1, where GC is the lipid’s glycerol–carbonyl backbone, P its phosphate and N its terminal, methylated or unmethylated, amine function). Their positions along z are represented by Gaussian distributions that describe the deviation from their average position due to capillary waves at the surface and due to thermal disorder within the monolayer (). Since GC is attached to the lower end of the chain box, there is no adjustable parameter describing its position. The full details of the VRDF approach have been described earlier.^30,31

Fig. 1 Surface isotherms, chemical structures and definition of submolecular fragments used in the VRDF modeling approach. Ch: acyl chains, GC: glycerol–carbonyl backbone, P: phosphate, N: ethanolamine, ethanolamine-N-methyl, ethanolamine-N-dimethyl, or choline, respectively. Isotherms were recorded on pure water at T = 20 °C (a: DPPE, b: DPPE-N-Me and c: DPPE-N-Me2) and at 10 °C (d: DPPC).

To keep the number of adjustable parameters reasonably low, the area per molecule, A_lipid, has been determined from GIXD rather than estimating it from the reflectivity models. To establish A at any π, we have determined A at selected π values in GIXD measurements,³² and have interpolated other values using the isotherm. In the original implementation of the VRDF model,³⁰ adjustable Gaussian heights of the headgroup fragments described their water association. A penalty function was then required³⁰ to satisfy the volume restrictions in conjunction with volumetric information.³³ In the current implementation, volume filling is more rigorously established by determining the void volume at any given distance from the interface and filling these voids with water. The hydration of a molecular subfragment, ξ = {Ch, GC, P or N}, was then quantified by measuring the propensity of encountering water molecules at the same distance z from the interface:

p_water^ξ = ∫n_ξ(z)n_water(z)dz (2.1)

where n(z) are number densities.

Confidence limits on the determined model parameters given the quality of the experimental data were estimated by χ² mapping as described earlier.^30,31 As the criterion for the evaluation we chose an increase of 10% over the minimum value of least-square difference between the experimental data and the model reflectivity. As we have explicitly shown earlier,³¹ this constitutes a conservative estimate of the true confidence limits.

3. Results and discussion

We studied the conformation of DPPE, DPPE-N-Me, DPPE-N-Me₂, and DPPC (molecular structures, see inset in Fig. 1) in monolayers on pure water by measuring Langmuir isotherms and surface-sensitive X-ray scattering, XR and GIXD, at various surface pressures. Experiments on DPPE, DPPE-N-Me and DPPE-N-Me₂ were performed at T = 20 °C, while DPPC monolayers were measured at T = 10 °C to obviate the LE/TC phase transition which is encountered at room temperature in DPPC, but not in theDPPE species. Isotherms are rather unexciting (see Fig. 1), indicating only a slight expansion of the monolayers as one proceeds along the homologous series, DPPE → DPPE-N-Me → DPPE-N-Me₂ → DPPC, at any constant pressure.

3.1. X-ray reflectivity and GIXD data

Fig. 2a shows representative data of Fresnel-normalized XRs for DPPE-N-Me and DPPE-N-Me₂ monolayers along their isotherms (top and center), as well as the reflectivities of all 4 species at π = 30 mN m⁻¹. At q_z ≤ 0.4 Å⁻¹, the errors are generally smaller than the plot symbols. At high momentum transfer, e.g. at q_z > 0.7 Å⁻¹, off-specular contributions inflate the apparent reflectivity values to some extent. While we determine (and subtract) background at each q_z by measuring the detector signal as the detector arm is rotated out of the specular position by ≈3°, off-specular contributions are not discriminated against. Due to the large error bars in this regime, however, they exert a negligibly small influence on the models in the data interpretation.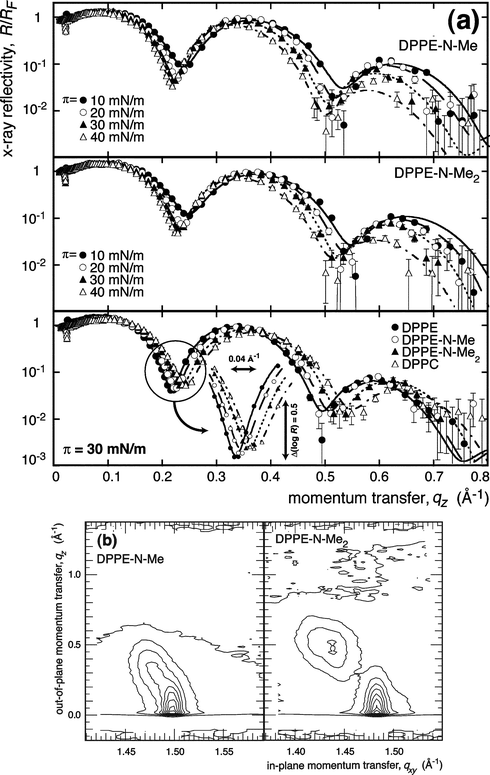

Fig. 2 (a) Top panels: Representative XR data of methylated DPPE surface monolayers on water as indicated. Bottom: Homologous series of lipids at the same surface pressure, π = 30 mN m⁻¹. The inset exemplifies the systematic shift of XR curves with increasing headgroup size. Error bars were determined from counting statistics. Lines show best fits derived from VRDF models. (b) Representative results on grazing-incidence X-ray diffraction from monolayers of DPPE-N-Me and DPPE-N-Me₂ at π = 40 mN m⁻¹ on water (T = 20 °C).

The data indicate a systematic shift of the interference features to lower q_z as the PE headgroup contains a sequentially larger number of methyl groups. A detailed analysis reveals subtle differences in the structures as a function of surface pressure (see below). By quantifying the constants of the hexatic acyl chain lattice in the TC or SC phase, GIXD measurements (results not shown, except for some representative data in Fig. 2a) provided precise estimates of A_lipid, which were used in the XR data modeling. DPPE and DPPC data were generally consistent with data reported in the literature.^34,35

3.2. XR data modeling and electron density profiles

XR data evaluation was performed in two steps: (a) a model-independent approach and (b) the VRDF approach as an explicit chemical model.

(a) The model-independent data modeling approach of Hamley and Skov Pedersen,^36,37 based on a constrained least-squares optimization of B-spline functions that define the relevant electron density distributions across the surface, was used to obtain a general impression of the monolayer structures. As expected, this procedure showed that the experimentally determined reflectivities can be interpreted in electron density distributions that resemble those of other lipid surface monolayers.³¹ These density profiles (data not shown) followed systematic trends that reflect the systematic development of the XR data (cf.Fig. 2) along the homologous sequence.

(b) The VRDF approach^30,31 subsequently brought the data evaluation to the structural level. Component volumes from the literature³³ (V_GC = 146.8 ų, V_P = 53.7 ų, V_Ch = 120.4 ų) or from molecular volume calculations (V_N = 55.4 ų, V_N–Me = 80.0 ų, V_N–Me2 = 103.6 ų) in Chem3D (CambridgeSoft, UK) were used, see also Table 1. The latter calculations were performed on MM2 optimized molecular models using the Connolly solvent-excluded volume option.³⁸ Care was taken that the lipid headgroups were in their most extended configuration for these estimates.

Table 1 Component volumes and distance between centers of gravity of lipid headgroup fragments

Fragment	Volume/Å^3	Electrons	Distance/Å^b
a From molecular dynamics simulations.^33b From MM2 optimized molecular models.
Glycerol–carbonyl	146.8^a	67
Phosphate	53.7^a	48	GC–P: 5.3
Ethanolamine	55.4^b	26	P–N: 4.5
Ethanolamine-N-methyl	80.0^b	34	P–N: 4.75
Ethanolamine-N-dimethyl	103.6^b	42	P–N: 4.85
Choline	120.4^a	50	P–N: 5.0

---

Fig. 3 shows electron density profiles retrieved from the VRDF refinement for all lipid monolayers at π = 30 mN m⁻¹ and, as an example, a decomposition of the electron density fragment contributions for DPPC. The origin of the z axis is located at the interface between the acyl chains and the GC backbone. Water distributions were obtained from filling the available space with water molecules, assumed to be of the same electron density as bulk water. The resultant (rugged) distributions were subsequently subject to the surface roughness, thus arriving at the smooth distributions presented in the plot. Similar profiles as the ones shown in Fig. 3 were derived from data sets at 10, 20 and 40 mN m⁻¹ and for unmethylated DPPE and DPPE-N-Me and DPPE-N-Me₂ (for all electron density profiles, see electronic supplementary information, ESI).

Fig. 3 Left: VRDF-derived electron density profile describing the XR of DPPE, DPPE-N-Me, DPPE-N-Me₂ and DPPC monolayers at π = 30 mN m⁻¹ (cf.Fig. 2). The interface between the hydrophobic chains and the GC subfragment defines the origin of the z axis. Right: Close-up of the thermal distributions of the ethanolamine fragments for all molecular species at this pressure together with the respective water distributions. While the water distributions at the DPPE-N-Me, DPPE-N-Me₂ and DPPC headgroups are indistinguishable, it is distinctively different for the DPPE headgroup.

To minimize the number of independent fit parameters, the GC fragment was strictly coupled to the chain slab in the model.³⁰ More specifically, it was assumed that the center position of this fragment (projected on the z axis) is located at z_GC = σ_int. In contrast, the z positions of the P and N(-Me_n) fragments were determined as independent parameters in the model. Thus, only six model parameters were adjusted in the course of the refinement: The global (capillary waves) and intrinsic roughness parameters, σ_cw and σ_int, the thickness of the alkane slab, d_Ch, the center positions of the phosphate and of the amine fragments, z_p and z_N, respectively, and the water filling level, z_dry. Parameters of the refined models are given in Table 2. Confidence limits on the parameters were evaluated for every individual model refinement. They were (typically): ∼1% for σ_cw; ∼5% for σ_int at low π and ∼10% for σ_int at high π; ∼5% for d_Ch; <10% for z_p; ≲20% for z_N; and ≲1 Å for z_dry (for details, see ESI†).

Table 2 Structural parameters describing the lipid molecules in a Langmuir monolayer on pure water as derived from VRDF modeling of XR data

Lipid	π/mN m^−1	Alipid/Å^2	σcw/Å	σint/Å	dCh/Å	zp/Å	zN/Å	zdry/Å
DPPE	10	44.8	2.69	1.69	17.0	−4.52	−6.51	−3.30
	20	42.8	2.88	1.78	17.7	−4.48	−7.25	−2.86
	30	41.1	3.13	2.03	18.3	−4.14	−7.61	−1.99
	40	39.9	3.54	2.26	19.1	−3.69	−7.79	−1.90
DPPE-N-Me	10	45.0	2.75	1.62	16.4	−4.65	−5.52	−4.84
	20	43.9	2.82	1.58	17.3	−4.64	−5.53	−4.66
	30	42.3	3.07	1.61	17.9	−4.67	−5.68	−5.24
	40	41.1	3.44	2.21	18.6	−4.03	−5.17	−5.99
DPPE-N-Me2	10	48.8	2.72	1.77	15.3	−4.63	−5.35	−4.80
	20	46.7	2.81	1.69	16.3	−4.44	−5.73	−5.03
	30	44.9	3.00	1.54	16.8	−4.69	−5.58	−5.05
	40	43.6	3.34	2.22	17.5	−3.89	−5.49	−5.32
DPPC	10	51.9	2.59	1.80	14.2	−4.33	−8.62	−1.87
	20	49.1	2.74	1.66	15.6	−4.04	−5.87	−4.48
	30	47.3	3.01	1.93	16.2	−3.70	−5.94	−4.62
	40	45.3	3.27	2.44	17.0	−3.75	−4.82	−6.23

---

A comparison of the model parameters for different molecular species at a given π, and hence of decomposed electron density profiles such as the one shown in Fig. 3, reveals systematic changes with molecular structure. The local order of the acyl chains is expected to be similar in different molecular species at a given π as long as they are in a similar phase state. Hence d_Ch should be inversely related to A_lipid, which in turn depends on the “bulkiness” of the headgroup. Indeed, d_Ch follows the sequence, DPPC → DPPE-N-Me₂ → DPPE-N-Me → DPPE, faithfully. Since the CG position is coupled to the lower interface of the chain slab in the model, these fragments coincide in their distribution across the interface regardless of surface pressure or molecular constitution of the monolayer. More surprising, however, is the near coincidence of the phosphate distributions in all molecular species at a given π. This indicates that both the molecular organization of the lipid backbone and the hydration of the phosphate is independent of the molecular constitution. It is thus exclusively the amine function which is responsible for structural differences between the different molecular species – the probability distributions of the (methylated) ethanolamines and their water associations is what discriminates their molecular structure.

3.3. “Composition-space refinement” and the significance of differences between data sets

How significant are these minute differences? If we had no information about the chemical constitution of the surface, the resolution one would expect to achieve in a reflectometry experiment is the “canonical” resolution,³⁹ Δz ≈ π/q_z^max (q_z^max: maximum momentum transfer in a measurement). In the data reported here, q_z^max ≈ 0.7 Å⁻¹, so that Δz ≈ 5 Å. Δz signifies the uncertainty in the localization of an object in space, given the possibility that the data truncation at q_z^max lets us miss small features in the SLD distribution. Thus, Δz is the resolution attained in model-free data evaluation approaches.³⁶ On the other hand, as discussed extensively for the case of Bragg diffraction from multilamellar membrane stacks,³⁹ explicit molecular models of the surface structure, based on the chemical constitution of the constituent molecules and “chemical intuition” about their supramolecular self-organization, may boost the effective resolution significantly, in particular if one analyzes X-ray and neutron data sets of different contrasts in a joint refinement of the corresponding data.⁶ Such approaches have been also successfully adapted to surface monolayer structure determination,^30,31,40 and dubbed “composition-space refinement”.^39,40 Conclusions from such an analysis are, of course, model dependent. In an earlier assessment of precision associated with the VRDF implementation of composition-space refinement of monolayer structures,³⁰ we determined that the center of a Gaussian function describing the thermal distribution of a lipid subfragment within the surface film may be typically localized within ±0.5 Å in high-resolution X-ray work at a third generation synchrotron source. The distribution width in such a situation can be typically specified to within ±0.1 Å. Since features that are missed due to the data truncation do not affect the average SLD of the interface film, the derived conclusions are robust against slight variations of the model parameters as long as the model is a reasonable description of the structure. As explicitly shown in earlier work,³¹ box models often fail to provide a realistic description of monolayer structures since the implicit assumption of a homogeneous composition of the phospholipid headgroup slab is questionable. Thus an evaluation of the same data using a box model or a VRDF approach may lead to contradictory conclusions.³¹ Finally, we note that differences in model parameters may be evaluated with even higher precision than their absolute values if consistent models are used in their evaluation. This may be rationalized in an analogy to either single molecule tracking in optical microscopy, where the location of maximum emission intensity of a fluorophore, and hence its trajectory in space, may be tracked with much higher precision than the optical wavelength would suggest,⁴¹ or IR spectroscopy where the precision of determining a band position also greatly exceeds resolution.⁴²

3.4. Data interpretation

The decomposed electron densities reveal a wealth of microscopic information on the molecular systems.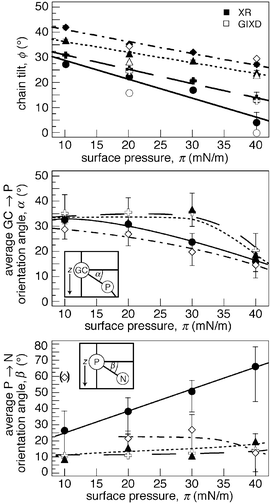

(1) Acyl chains. One fundamental structural parameter determined from the VRDF model is the thickness of the slab, d_Ch, that contains the palmitoyl chains. It is generally smaller than the extended length of such a chain, l_palmitoyl = 19.15 Å,⁴⁰ except for the most condensed monolayers, e.g., for DPPE at high π, where d_Ch = l_palmitoyl. d_Ch < l_palmitoyl is due to local chain disorder or, for a hexatic phase, to a collective tilt of the chains from the surface normal, and may hence be described in terms of an (average) chain tilt angle, ϕ = arccos(d_Ch/l_palmitoyl).⁴⁰ For hexatic phases, ϕ may be independently determined from GIXD.³² Chain tilt angles obtained from GIXD and XR as a function of π are shown in Fig. 4a. Their independently determined values correspond well with each other. For all lipids, ϕ values decrease monotonically, and for the most part linearly, with π, indicative of a progressive increase in molecular ordering. While DPPE shows an average chain tilt of ϕ ∼ 26 ± 1° at π = 10 mN m⁻¹, and becomes essentially untilted at 40 mN m⁻¹, the bulkier DPPC headgroup dictates a larger average inclination at a given π, ϕ ∼ 39 ± 2° at 10 mN m⁻¹ and ϕ ∼ 29° at 40 mN m⁻¹. ϕ angles for the other lipids lie systematically between those limiting values for DPPE and DPPC. Thus, the average chain tilt correlates clearly with the volume of the headgroup: The more methyl groups are attached to the amine group, the larger ϕ.

Fig. 4 Legend: DPPE (●), DPPE-N-Me (), DPPE-N-Me₂ (▲) and DPPC (◇). Above (a): Chain tilt angles ϕ, as obtained from GIXD and XR, respectively, are visualized as a function of the surface pressure. Middle (b) and bottom (c): Average GC → P and P → N orientation angles α and β as functions of π for the four molecular species in surface monolayers on water. Error bars are retrieved from confidence limits of the determined model parameters. Broken lines are guides for the eye.

(2) Headgroup conformation. The lipid backbone and phosphate positions, z_GC (≡ σ_int) and z_p, stay approximately constant along the homologous series for a given π. Both the amplitudes and widths of their distributions grow slightly as the molecular density rises. The only significant differences observed between distinct molecular species at a particular π are in the distributions of the terminal amino fragments for different methylation. This is exemplified for π = 30 mN m⁻¹ in the inset in Fig. 3. These differences can be categorized as follows. The positions of the N fragments indicate distinctive organizations of methylated ethanolamines (DPPE-N-Me, DPPE-N-Me₂ and DPPC) on the one hand and the parent DPPE on the other. In any situation for π = 20–40 mN m⁻¹, the amine fragment of DPPE is more deeply embedded in the water phase, and thus presumably more hydrated, than are the methylamine fragments of the other species, suggesting a substantially stronger interaction of the DPPE headgroup with water than in the other cases. (An exception to this general rule concerns DPPC at π = 10 mN m⁻¹: It is conceivably in a different phase state than the other species, even at the lower temperature, 10 °C, of the measurement).

In the same approach as in the determination of an average chain tilt angle ϕ, a comparison of the distances between the center positions of the headgroup fragments, Δz_GC–P or Δz_P–N, with their respective 3D distances in a molecular model (e.g., l_GC–P = 5.3 Å),³⁰ yields an estimate of the average inclination angles α (of the GC → P orientation) or β (of the P → N orientation), as in Fig. 4b/c. The distinctive behavior of DPPE is clearly visible: While β is rather flat with π for DPPE-N-Me, DPPE-N-Me₂ and DPPC, it increases steadily for DPPE. In fact, if one again separates out the data point for DPPC at 10 mN m⁻¹, the DPPE headgroup is always more extended toward the aqueous subphase than its counterparts at any given π.

(3) Headgroup water. The water distributions (inset in Fig. 3) confirm the trend observed for the amine fragments: For DPPE-N-Me, DPPE-N-Me₂ and DPPC they are indistinguishable from each other, while the distinctive organization of the DPPE headgroup indicates a considerably higher hydration of the amine fragment. These differences, slight as they are, are significant given the sensitivity of the method and the reproducibility within the framework of the model (see also ESI†).

3.5. Hydration

The distinctive molecular organization of the DPPE headgroup in terms of its propensity for interaction with water can also be quantitatively demonstrated (Fig. 5). The quantity ∫_zn_ξ(z)n_w(z)dz provides a convenient measure of water exposure of a headgroup fragment, ξ. (Strictly speaking, p_water^ξ is proportional to the probability that a particular headgroup fragment at position z neighbors a water molecule located at the same distance from the interface). Such an evaluation shows that the (methylated) ethanolamines account for at least 50% of the headgroup interaction with water. Along an isotherm, this interaction diminishes only slightly with monolayer compression (typically by less than 10% between 10 and 40 mN m⁻¹). However, the difference in headgroup-water interaction between DPPE and the methylated species is much larger: On average, the DPPE headgroup is about 25% more exposed to water than any other lipid headgroup at a given π.

Fig. 5 Legend: a: DPPE, b: DPPE-N-Me, c: DPPE-N-Me₂ and d: DPPC. Propensity for water interaction of the molecular subfragments in the different molecular species as a function of π, quantified as the overlap integral, p_water^ξ between the fragment and water number distributions. The bar quantifying DPPC hydration at 10 mN m⁻¹ has been greyed because the monolayer is presumably in a different phase state there than in the other situations. For some of the data points (DPPE and DPPC at 30 mN m⁻¹), error bars have been determined from the confidence limits of the structural parameters.

Just how much of the distinctive molecular organization of DPPE and the methylated PE species is due to differences in hydration, e.g. in terms of the number and strength of hydrogen bonds between H₂O and PE, and how much is due to the increased headgroup hydrophobicity upon methylation is an interesting question. On the one hand, PE and PC are distinct in their susceptibility for hydration in that PC cannot donate hydrogens bond while PE can. This argument, however, would place DPPE-N-Me and DPPE-N-Me₂ closer to DPPE than DPPC, since the remaining hydrogens on their headgroups can engage in hydrogen bonds. This suggests that hydrophobicity also plays an important role once a methyl is attached. In that case, the methylethanolamine function associates closer with the interface than the ethanolamine in unmethylated PE (bottom panel in Fig. 4). It thus remains to be determined what the relative proportions of the hydration and hydrophobicity effects are in controlling the organization of these lipid headgroups.

Some insight into that problem is gained from well-established bulk studies of phospholipid membrane organization. The conventional thinking about lipid hydration, derived from early gravimetric results⁴³ and borne out in classical X-ray diffraction work,^44,45 is that PE bilayers are significantly less hydrated than PC bilayers. In other words, the inter-bilayer space in lipid multibilayer systems contains much more water at all water activity values for PC than for PE.⁴⁶ Similar conclusions were drawn from NMR^47–49 and conductivity⁵⁰ measurements. Moreover, it has been reported that (mono-) methylethanolamines behave more similarly to PCs, in adsorbing significantly larger amounts of water, than to PEs.⁵¹ McIntosh has argued that while the steric repulsion⁵² between bilayers is similar for PC and PE⁵³ the reported differences in hydration reflect the PE’s propensity for hydrogen bonding, i.e., a water-mediated interaction between the quarternary amine in one bilayer and the phosphate in the apposed bilayer, in line with molecular dynamics simulation results of lipid bilayers.^54,55 As a result, the water-mediated hydrogen bonding leads to an adhesion term between the leaflets for PE-containing membranes which is absent in PC multibilayers⁴⁵ and helps explain the fusion-mediation effect of PE lipids on a molecular scale. While at first sight the results reported here appear in contradiction with these established views, it is important to realize that they describe molecular structure in the absence of an apposing membrane surface, showing how hydrogen bonding affects lipid headgroup organization. We argue thus that our observations actually fortifies the established, apparently paradoxical conclusion that enhanced interaction of the PE headgroup with water leads to a stronger interaction between apposing membrane surfaces in multilayer systems, and thus to an effective dehydration of these surfaces. Our results may thus also have potential to give a deeper understanding of the membrane fusion process.

4. Conclusions

Our work elucidated how the step-by-step substitution of methyl groups for hydrogens on the terminal ethanolamine of DPPE impacts lipid organization within membranes. One methyl substitution already exerts a large influence on the packing of the overall lipid molecule: The flexibility of the headgroup is restricted and the chain tilt increases. A detailed picture emerges from this study for the structure of DPPE and its methylated derivatives on pure water. The degree of methylization of the amine fragment has a significant impact on the lipid’s organization within the membrane as a function of monolayer pressure. While one might naively assume that the lipid headgroup would be further extended toward the subphase the larger its volume, to accommodate space limitations imposed by the aliphatic chains that maximize their van der Waals interactions when packed in areas as small as 40 Ų per lipid molecule, the opposite is actually observed: The smallest headgroup, PE, extends furthest toward the bulk, thus maximizing its hydration, while the P → N orientations align progressively closer to the lipid/water interface as bulkiness of the headgroups increases. This organization of the lipid headgroups reflects thus their interaction with water, in terms of the capability to donate hydrogen bonds and/or their relative hydrophobicities, rather than their relative volumes. This also implies that the chain packing of a lipid within a membrane is as much determined by its capability to interact with water as by its sheer size.

Acknowledgements

We thank D. J. McGillivray for his comments on the manuscript. Beamtime at HASYLAB (DESY, Hamburg, Germany, project no. II-01-042) is gratefully acknowledged. This work was supported by the NSF (grant no. 0304062), the Volkswagen Foundation (I/77709), the National Institutes of Health (1RO1 RR14812) and The Regents of the University of California.

References

1. S. H. White and W. C. Wimley, Annu. Rev. Biophys. Biomol. Struct., 1999, 28, 319–365.
2. H. Möhwald, Rev. Phys. Chem., 1990, 41, 441–476.
3. H. M. McConnell, Rev. Phys. Chem., 1991, 42, 171–195.
4. C. M. Knobler and R. C. Desai, Rev. Phys. Chem., 1992, 43, 207–236.
5. H. Möhwald, H. Baltes, C. A. Helm, G. Brezesinski and H. Haas, Jpn. J. Appl. Phys., 1995, 34, 3906–3913.
6. M. C. Wiener and S. H. White, Biophys. J., 1992, 61, 434–447.
7. J. Als-Nielsen, D. Jacquemain, K. Kjaer, M. Lahav, F. Leveiller and L. Leiserowitz, Phys. Rep., 1994, 246, 251–313.
8. T. L. Kuhl, J. Majewski, P. B. Howes, K. Kjaer, A. von Nahmen, K. Y. C. Lee, B. Ocko, J. N. Israelachvili and G. S. Smith, J. Am. Chem. Soc., 1999, 121, 7682–7688.
9. D. Vaknin, J. Am. Chem. Soc., 2003, 125, 1313–1318.
10. K. Kjaer, J. Als-Nielsen, C. A. Helm, L. A. Laxhuber and H. Möhwald, Phys. Rev. Lett., 1987, 58, 2224–2228.
11. P. Dutta, J. B. Peng, B. Lin, J. B. Ketterson and M. Prakash, Phys. Rev. Lett., 1987, 58, 2228–2231.
12. J. Als-Nielsen and K. Kjaer, in Phase Transitions in Soft Condensed Matter, ed. T. Riste and D. Sherrington, Plenum, New York, 1989, pp. 113–138.
13. J. Als-Nielsen and H. Möhwald, in Handbook on Synchrotron Radiation, ed. S. Ebashi, M. Koch and E. Rubinstein, Elsevier, Amsterdam, North-Holland, 1991, pp. 1–53.
14. J. Penfold and R. K. Thomas, J. Phys., Condens. Matter, 1990, 246, 1369–1412.
15. D. Vaknin, J. Als-Nielsen, M. Piepenstock and M. Lösche, Biophys. J., 1991, 60, 1545–1552.
16. J. N. Israelachvili and H. Wennerström, Nature, 1996, 379, 219–226.
17. B. Bechinger and J. Seelig, Chem. Phys. Lipids, 1991, 58, 1–5.
18. A. S. Ulrich and A. Watts, Biophys. J., 1994, 66, 1441–1449.
19. Z. Zhou, B. G. Sayer, D. W. Hughes, R. E. Stark and R. M. Epand, Biophys. J., 1999, 76, 387–399.
20. H. Wennerström and E. Sparr, Pure Appl. Chem., 2003, 75, 905–912.
21. W. Pohle, D. R. Gauger, M. Bohl, E. Mrazkova and P. Hobza, Biopolymers, 2004, 74, 27–31.
22. G. Brezesinski, F. Bringezu, G. Weidemann, P. B. Howes, K. Kjaer and H. Möhwald, Thin Solid Films, 1998, 327–329, 256–261.
23. O. Albrecht, H. Gruler and E. Sackmann, J. Phys. (France), 1978, 39, 301–313.
24. R. Frahm, J. Weigelt, G. Meyer and G. Materlik, Rev. Sci. Instrum., 1995, 66, 1677–1680.
25. I. Weissbuch, R. Povovitz-Biro, M. Lahav, L. Leiserowitz, K. Kjaer and J. Als-Nielsen, in Advances in Chemical Physics, ed. I. Prigogine and S. Rice, Wiley, New York, 1997, vol. 102, pp. 39–120.
26. S. A. W. Verclas, P. B. Howes, K. Kjaer, A. Wurlitzer, M. Weygand, G. Büldt, N. A. Dencher and M. Lösche, J. Mol. Biol., 1999, 287, 837–843.
27. T. R. Jensen and K. Kjaer, in Studies in Interface Sciences, ed. D. Möbius and R. Miller, Elsevier, Amsterdam, 2001, vol. 11, pp. 205–254.
28. P. Krüger, M. Schalke, J. Linderholm and M. Lösche, Rev. Sci. Instrum., 2001, 72, 184–192.
29. M. Lösche, M. Piepenstock, A. Diederich, T. Grünewald, K. Kjaer and D. Vaknin, Biophys. J., 1993, 65, 2160–2177.
30. M. Schalke, P. Krüger, M. Weygand and M. Lösche, Biochim. Biophys. Acta, 2000, 1464, 113–126.
31. M. Schalke and M. Lösche, Adv. Colloid Interface Sci., 2000, 88, 243–274.
32. K. Kjaer, Physica B, 1994, 198, 100–109.
33. R. S. Armen, O. D. Uitto and S. E. Feller, Biophys. J., 1998, 75, 734–744.
34. C. A. Helm, P. Tippmann-Krayer, H. Möhwald, J. Als-Nielsen and K. Kjaer, Biophys. J., 1991, 60, 1457–1476.
35. H. Haas, W. Caetano, G. P. Borissevich, M. Tabak, M. I. Mosquera Sanchez, O. N. Oliveira, Jr., E. Scalas and M. Goldmann, Chem. Phys. Lett., 2001, 335, 510–516.
36. I. W. Hamley and J. Skov Pedersen, J. Appl. Crystallogr., 1994, 27, 29–35.
37. J. Skov Pedersen and I. W. Hamley, J. Appl. Crystallogr., 1994, 27, 36–49.
38. M. L. Connolly, J. Appl. Crystallogr., 1983, 16, 548–558.
39. M. C. Wiener and S. H. White, Biophys. J., 1991, 59, 174–185.
40. D. Vaknin, K. Kjaer, J. Als-Nielsen and M. Lösche, Biophys. J., 1991, 1325–1332.
41. G. S. Harms, L. Cognet, P. H. M. Lommerse, G. A. Blab, H. Kahr, R. Gamsjäger, H. P. Spaink, N. M. Soldatov, C. Romanin and T. Schmidt, Biophys. J., 2001, 81, 2639–2646.
42. R. Mendelsohn, J. W. Brauner and A. Gericke, Annu. Rev. Phys. Chem., 1995, 46, 305–334.
43. P. H. Elworthy, Chem. Soc. J., 1962, 4897–4900.
44. R. P. Rand, N. Fuller, V. A. Parsegian and D. C. Rau, Biochemistry, 1988, 27, 7711–7722.
45. T. J. McIntosh, Chem. Phys. Lipids, 1996, 81, 117–131.
46. J. F. Nagle and M. C. Wiener, Biochim. Biophys. Acta, 1988, 942, 1–10.
47. E. G. Finer and A. Darke, Chem. Phys. Lipids, 1974, 12, 1–16.
48. B. Bechinger and J. Seelig, Chem. Phys. Lipids, 1991, 58, 1–5.
49. K. Gawrisch, D. Ruston, J. Zimmerberg, V. A. Parsegian, R. P. Rand and N. Fuller, Biophys. J., 1992, 61, 1213–1223.
50. G. L. Jendrasiak, Biophys. Biochim. Acta, 1976, 424, 149–159.
51. G. L. Jendrasiak, Nutritional Biochem., 1996, 424, 599–609.
52. T. J. McIntosh and S. A. Simon, Langmuir, 1987, 12, 1622–1630.
53. T. J. McIntosh, A. D. Magid and S. A. Simon, Langmuir, 1987, 12, 1622–1630.
54. K. V. Damodaran and K. M. Merz, Jr., Biophys. J., 1994, 66, 1076–1087.
55. F. Zhou and K. Schulten, J. Phys. Chem., 1995, 99, 2194–2207.

---

Footnotes

† Electronic supplementary information (ESI) available: Table S1 shows the confidence limits on all adjusted parameters presented in Table 2. Figs. S1 and S3 are color versions of Figs. 2 and 3. Moreover, Fig. S2 shows all the experimental reflectivity data sets for the four molecular species at four different pressures, π, thus complementing Figs. 2 and S1. Fig. S4a–d shows comparisons of the decomposed electron density distributions of the four molecular species at constant π = 10, 20, 30 and 40 mN m⁻¹. See http://www.rsc.org/suppdata/cp/b4/b410863a/

‡ Present address: Fraunhofer Institute for Non-Destructive Testing, D-01326 Dresden, Germany

§ Present address: CNBT consortium, National Institute of Standards and Technology, NIST Center for Neutron Research, Gaithersburg MD 20899, USA

¶ Monolayer phases are commonly denoted gaseous (G), liquid expanded (LE), tilted condensed (TC), or solid condensed (SC).

---