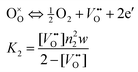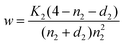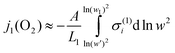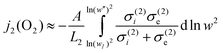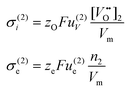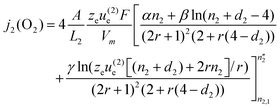Modeling of dense ceramic bilayer membranes
Received
13th April 2004
, Accepted 16th September 2004
First published on 29th November 2004
Abstract
A numerical analysis of the transport properties and the chemical stability of bilayer membranes with the compositions La0.9Sr0.1FeO3/Ce0.8Gd0.2O2 and La1−xSrxCoO3/Ce0.8Gd0.2O2 was carried out. For each membrane layer, the oxygen permeation flux was derived as a function of the defect concentrations and defect mobilities. The defect concentrations were calculated from point defect models. Coupling of the flux equations via the continuity condition yields the overall permeation flux of the bilayer membrane and the oxygen chemical activity at the layer interface, which serves as a criterion for the stability of the membrane under reducing conditions.
1. Introduction
Separation of oxygen from air by permeation through dense membranes is considered an efficient way to supply oxygen for hydrocarbon oxidation processes, such as the catalytic conversion of methane to syn-gas.1 The transfer of oxygen across a dense membrane occurs via reduction of oxygen molecules to oxygen ions on the air side, transport of oxygen ions and electronic charge carriers inside the membrane, and re-oxidation of the ions to neutral oxygen on the hydrocarbon reaction side. Suitable membrane materials are therefore required to be mixed ionic electronic conductors (MIEC) with high oxide-ion conductivity. To date, a large number of MIEC oxides with perovskite structure2–13 and related structures14–16 have been identified, which exhibit high permeability for oxygen. In order to attain sufficiently large permeation fluxes, dense membranes are operated at temperatures >700 °C. In this temperature range, the kinetics of catalytic hydrocarbon oxidation reactions are fast enough to allow high conversion rates. A dense membrane reactor is therefore considered a viable way to realize a continuous, single-step conversion of methane to syn-gas with air as oxygen supply, which was in fact demonstrated on a laboratory scale.17,18 During operation in a syn-gas reactor, the membrane has to endure extremely demanding conditions. The membrane surfaces are exposed to an air feed on one side and, on the hydrocarbon feed side, to a gas stream containing strongly reducing product gases such as hydrogen and carbon monoxide. As a consequence, a large gradient of oxygen chemical activity is imposed upon the membrane material. While this is beneficial in terms of oxygen permeation, it also causes a variation of lattice expansion across the membrane, which leads to build-up of mechanical stress and may cause membrane failure.19,20 Furthermore, highly permeable MIEC such as perovskite-structured oxides A1−xA′xB1−yB′yO3 with A,A′
= La,Ca,Sr,Ba and B,B′
= Co,Ni are particularly prone to undergo reduction as they contain significant amounts of transition metal ions in high oxidation states.21–23 Under strongly reducing conditions, these oxides were observed to form oxide or metallic secondary phases that exhibit low permeability for oxygen24 and cause deterioration of the permeation flux. To overcome these problems, attempts have been made to replace the mixed conductor by a material which is chemically and mechanically more stable in reducing environments: (a) Oxygen ‘pumps’ made of solid oxide-ion electrolytes, such as yttria-stabilized zirconia (YSZ), were used to separate oxygen by means of an applied electrical field.25 However, the necessary electrodes and external wiring may affect the catalytic properties of the surfaces and limit the flexibility in membrane shaping. (b) Dual phase membranes are composed of an oxide-ion phase and a noble metal phase. Typical examples are YSZ/Pd,25 Bi2−xErxO3/Ag,26 Ce2−xSmxO2/Pd and La1−xSrxGa1−yMgyO3/Pd.27 As the metal phase provides an internal electronic short-circuit, these membranes do not require electrodes. However, the large amount of noble metal which is necessary to form a percolative network is a major drawback of this type of membrane.
Recently, a new approach to strengthen oxide membranes against reduction was introduced and experimentally verified.23,28–30 Bilayer membranes were formed by depositing a protective coating of samarium-doped ceria on La1−xSrxCoO3, La1−xSrxB1−yNiyO3
(B = Co, Fe), and La1−xSrxCo1−yFeyO3 substrates. When these membranes were exposed with the coated side to a reducing atmosphere, they retained a constant permeation flux for several days whereas uncoated membranes of the same substrate deteriorated within several hours.30 The protective effect was explained by the fact that the coating establishes an oxygen activity aI(O2) at the inner interface of the membrane which is larger than the critical activity acr(O2) below which the MIEC substrate layer would decompose.23,29 The interfacial activity depends on the partial ionic and electronic conductivities of both layer materials as well as on the layer thickness ratio. Whereas the critical activity acr(O2) of MIEC oxides is experimentally accessible or may be calculated from thermodynamic data, it is difficult to measure aI(O2). For the case of solid oxide fuel cells, aI(O2) of bilayer electrolytes was calculated by assuming constant partial conductivities31 or simple oxygen activity dependences of the partial conductivities32 in both electrolyte layers. In this paper, a transport model of a mixed-conducting bilayer membrane is presented that relies on detailed defect chemical descriptions of both layer materials and takes into account the oxygen activity dependence of the ionic and electronic partial conductivities in both layers. The model yields quantitative results of the interfacial oxygen activity and the permeation flux as a function of the oxygen activities at the surfaces of the membrane.
2. Theory section
In this section, phenomenological equations of the oxygen transport in each layer of a bilayer membrane will be derived in a general form. Coupling of the transport equations then yields the steady state permeation flux and the interfacial oxygen activity as a function of the oxygen activities at the surfaces of the membrane. Subsequently, the transport equations will be reformulated using microscopic quantities based on defect model calculations for a bilayer membrane with a perovskite-type oxide of the general composition La1−xSrxBO3 as substrate and acceptor-doped ceria Ce1−xGdxO2 as coating.
2.1 Phenomenological transport equations and coupling conditions
The membrane is composed of a ‘substrate’ layer of a mixed conducting oxide with high oxygen permeability (hereafter indexed by 1), and a protective coating of a less permeable oxide (hereafter indexed by 2) which is chemically stable even under strongly reducing conditions. Exposure of the membrane to an oxygen-rich gas atmosphere on the substrate side and to an oxygen-lean atmosphere on the coating side creates a gradient of oxygen activity, which acts as driving force for the oxygen permeation (Fig. 1). The overall permeation process involves oxygen exchange at the outer membrane surfaces, ionic and electronic transport in the bulk of both layers, and transfer of oxygen across the layer interface. For the sake of simplicity, the following assumptions will be made:
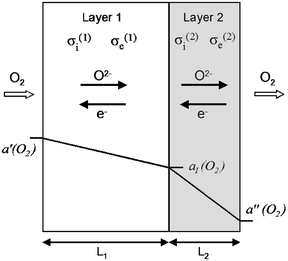 |
| | Fig. 1 Schematic representation of a bilayer membrane in a gradient of oxygen activity. The surface oxygen activities a′(O2) and a″(O2) and the transport properties of both layers determine the oxygen activity aI(O2) at the layer interface. | |
(i) The transfer of oxygen across the gas/solid interfaces and the interface of layers 1 and 2 is fast so that the oxygen permeation through the membrane is limited by the bulk transport of oxygen in both layers. Then, the permeation flux in each layer may be expressed according to Wagner:33
| |  | (1) |
| |  | (2) |
where
A
=
RT/16
F2.
L is the thickness of the layer,
T is the temperature,
R the gas constant,
F is Faraday’s constant.
a′(O
2),
a″(O
2) and
aI(O
2) are the oxygen activities on the oxygen-rich side, the oxygen-lean side, and the layer interface of the membrane, respectively (
cf.
Fig. 1). The ambipolar conductivity of each layer is given by the partial ionic and electronic conductivities:
| |  | (3) |
(ii) The transport properties of the layers are affected neither by interdiffusion of cations at the layer interface nor by chemical reaction of the layer oxides. In this case, the membrane can reach a steady state where the permeation flux across the membrane j(O2) is constant and equal to the partial fluxes through both layers:
| | | j(O2)
=
j1(O2)
=
j2(O2) | (4) |
Combination of
eqns. (1), (2) and (4) yields:
| |  | (5) |
By solving
eqn. (5), the interfacial activity
aI(O
2) is obtained as a function of the surface activities
a′(O
2),
a″(O
2), provided that
L1 and
L2 and the ambipolar conductivities
σ(1)amb and
σ(2)amb are known. Subsequently, the overall flux
j(O
2) through the membrane may be calculated from
eqns. (1) or (2). In general, the ambipolar conductivity of a mixed conducting
oxide is itself dependent on the oxygen activity. As an operating membrane is always subjected to a gradient of oxygen activity,
σ(1)amb and
σ(2)amb are expected to vary along the membrane cross section. However, the more simple case of constant ambipolar conductivities will be considered first as it provides some insight into how the variation of the ambipolar conductivities and the thickness ratio of the membrane layers affect the interfacial activity and the permeation flux. For constant
σ(1)amb and
σ(2)amb, integration of
eqn. (5) yields:
| |  | (6) |
Two limiting cases may be distinguished:
†| | | L1σ(2)amb/L2σ(1)amb
≫ 1 ⇒
aI(O2)
≈
a″(O2) | (7) |
| | | L1σ(2)amb/L2σ(1)amb
≪ 1 ⇒
aI(O2)
≈
a′(O2) | (8) |
In the first case, the interfacial activity
aI(O
2) is close to the oxygen activity on the oxygen-lean side of the membrane, which means that the protective layer does not protect the substrate material from
reduction. In the second case,
aI(O
2) is in the oxidizing regime and the coating provides optimum protection, however, the permeation flux of the coated membrane is small compared to the flux of an uncoated membrane of the same thickness because the driving force for the oxygen transport is small. Consequently, there is a trade-off between membrane flux and protection of the substrate material.
2.2 Microscopic transport model
For a rigorous calculation of the interfacial activity by means of eqn. (5), the partial conductivities of each layer compound must be derived as a function of T and a(O2). In order to achieve this, the partial conductivities will be expressed as functions of the concentrations and mobilities of mobile defects present in each layer. For layer 1 (substrate layer), a defect model typical of an acceptor doped mixed conducting oxide with perovskite structure is adopted. Such a model has been applied to a number of oxides containing different transition metal elements, e.g. La1−xSrxCoO3, La1−xSrxFeO3 and La1−xSrxCrO3.34,35 For layer 2, (coating layer) we will use a defect model that was applied to the acceptor doped binary metal oxides Ce2−xSmxO2 or Ce2−xGdxO2 with fluorite structure.36
2.2.1 Defect model of layer 1.
Oxides of the type La1−xAxBO3, where A is an acceptor dopant and B is a transition metal, are oxygen-deficient and can exhibit a large variation of oxygen stoichiometry.37,38 Oxygen vacancies V˙O, acceptor ions A′, electron holes h˙ and electrons e′ are assumed to be predominant defects. Table 1 summarizes the defect equilibrium reactions and the corresponding relations between the defect concentrations. For the sake of simplicity we replace the usual bracket notation for the defect concentrations by d1
=
[A′], p
=
[h˙], and n1
=
[e′], and we substitute w
=
a(O2)1/2. For the oxygen exchange reaction at the surface, we obtain:| |  | (9) |
The B-site cations in La1−xAxBO3 undergo significant charge disproportionation. By assuming that the electron and hole concentrations are small compared to the concentration of non-disproportionated B, we write| | | nil ⇔
h˙
+ e′ Kel
=
pn1 | (10) |
Table 1 Model parameters for layer 1 and 2 at 1173 K
| Layer 1 |
Layer 2 |
| Parameter |
La1−xSrxFeO3 |
La1−xSrxCoO3 |
|
Parameter |
Ce1−xGdxO2 |
| Values for K1 and Kel in layer 1 and for K2 in layer 2 were calculated from fits to nonstoichiometry data for La1−xSrxFeO3,39 for La1−xSrxCoO3,34 and for Ce1−xGdxO2.36uV(1),* was calculated from vacancy diffusion coefficients DV obtained from Ishigaki et al.40 For d1
= 0.5, uV(1),* was estimated from permeation data.8uV(2),* and ue(2),* were taken from Wang et al.41 |
|
d
1
=
x |
0.1 |
0.1 |
0.5 |
d
2
=
y |
0.2 |
|
V
m/m3 mol−1 |
3.6 × 10−5 |
3.4 × 10−5 |
3.5 × 10−5 |
V
m
(m3 mol−1) |
2.4 × 10−5 |
|
K
1/bar1/2 |
2.7 × 10−2 |
1.2 × 10−2 |
1.2 |
K
2
(bar1/2) |
3.1 × 10−12 |
|
K
el
|
2.8 × 10−7 |
3.8 × 10−3 |
4.0 × 10−3 |
u
V
(2),*
(m2V−1s−1) |
1.8 × 10−8 |
|
u
V
(1),*/m2 V−1 s−1 |
8.9 × 10−9 |
1.1 × 10−8 |
1.4 × 10−8 |
u
e
(2),*
(m2V−1s−1) |
2.2 × 10−7 |
The electroneutrality condition reads
| | | 2[V˙˙O]
+
p
=
n1
+
d1 | (11) |
Inserting
eqns. (9) and (10) into
eqn. (11) yields:
| |  | (12) |
From eqn. (12), w is obtained as a function of the electron hole concentration p provided the equilibrium constants K1 and Kel are known. The corresponding vacancy and electron concentrations of vacancies and electrons can be calculated from eqns. (9), (10), and (11).
2.2.2 Defect model of layer 2.
The model system Ce1−xAxO2 containing the acceptor dopant A exhibits prevailing ionic conductivity in oxidizing conditions but develops significant n-type electronic conduction in reducing atmospheres. Oxygen vacancies and electrons are assumed to be the prevailing defects in this layer. The defect concentrations are obtained from the surface oxygen exchange reaction and electroneutrality condition.| | 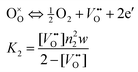 | (13) |
d2 denotes the dopant fraction and n2 the electron concentration. Combination of eqns. (13) and (14) yields:| | 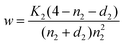 | (15) |
If n2 is chosen as an independent variable for this layer, we obtain w from eqn. (15) and the corresponding vacancy concentration from eqn. (14).
2.2.3 Transport equations.
Although mixed conducting materials such as La1−xSrxCoO3 exhibit high oxide-ion conductivity even when compared to oxide-ion electrolytes, they are prevailing electronic conductors, i.e.tel
≈1. The permeation flux is therefore mainly governed by the ionic partial conductivity. According to eqn. (1) we write for the permeation flux in layer 1:| | 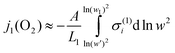 | (16) |
A similar simplification cannot be made for layer 2 because of the significant electronic contribution to the conductivity in the reducing regime. Therefore, we adopt eqn. (2) in full to describe the flux in this layer:
| | 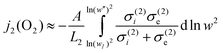 | (17) |
The partial conductivities of layer 1 and 2 may be written in terms of the vacancy and electron mobilities and concentrations. We obtain:
| |  | (18) |
| | 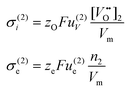 | (19) |
zO and
ze denote the charge numbers of oxygen ions in layer 1 and electrons in layer 2, respectively.
u(1)V and
u(2)V are the mobilities of vacancies in the substrate and protective layer, and
u(2)e is the electron mobility in the protective layer. Inserting
eqn. (18) into
eqn. (16) and
eqn. (19) into
eqn. (17) yields
| |  | (20) |
and
| |  | (21) |
By differentiating eqns. (12) and (15), we obtain for layer 1
| |  | (22) |
and for layer 2:
| |  | (23) |
Finally, inserting eqn. (9) for [V˙˙O], eqn. (12) for w, and eqn. (22) for dw into flux eqn. (20) yields the permeation flux in layer 1 as a function of the electron hole concentration p.
| |  | (24) |
p′ and
pI are the electron hole concentrations at the oxygen-rich surface and the layer interface of the membrane, respectively. Likewise, by combining
eqns. (14), (15), (23) and (21) we obtain the permeation flux in layer 2 after integration:
| | 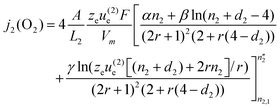 | (25) |
where
| | | α
= 2 +
(8 −
d2)
r
+
(8 − 2d2)r2 | (26) |
| | | β
=
d2
− 4 + 4(d2
− 4)
r
(r
+ 1) | (27) |
| | | γ
=
d2
(−1 + 2r
+
(8 − 2d2)
r2) | (28) |
r contains the ratio of the electronic and vacancy mobility:
r
=
zeu(2)e/
zOu(2)V.
n″2 and
n2,I are the electron concentrations in layer 2 at the layer interface and at the oxygen-lean surface, respectively.
2.2.4 The bilayer membrane.
In steady state, the interfacial oxygen activity of the bilayer membrane becomes independent of time. If the transfer of oxygen from one layer to the other is fast compared to the bulk transport in each layer, no drop of the oxygen activity occurs at the interface and therefore, a(1)I(O2)
=
a(2)I(O2) holds. From eqns. (12) and (15) for w in each layer it follows that:| |  | (29) |
Continuity of the oxygen flux along the membrane cross section requires j1(O2)
=
j2(O2)
(cf. eqn. (4)). By equating expressions (24) and (25), we obtain:| |  | (30) |
In order to calculate the interfacial oxygen activity aI(O2) from the surface oxygen activities a′(O2) and a″(O2), the set of eqns. (29) and (30) has to be solved numerically. By doing so, we obtain the electronic charge carrier concentrations pI in layer 1 and n2,I in layer 2 at the layer interface for given concentrations p′ and n2″. The latter concentrations correspond to a′(O2) and a″(O2), whereas the interfacial oxygen activity aI(O2) is obtained from pI or n2,Iviaeqn. (12) or (15), respectively. Finally, the oxygen permeation flux across the membrane is obtained from flux eqn. (24) or (25).
3. Numerical calculations
The interfacial activity and the permeation flux were numerically calculated for the model system La1−xSrxFeO3 with x
= 0.1. Although exhibiting a lower permeability than the corresponding cobalt-based compound, this oxide was chosen as reference systen because it is stable over a wide range of oxygen partial pressure (p(O2)
≥10−17 atm.) and the dilute defect model described in the previous section can be employed in this range.35 This allows us to assess situations where the interfacial activity of the bilayer membrane is close to the oxygen surface activity on the oxygen-lean side. On the other hand, the use of cobalt-based oxides La1−xSrxCoO3 as substrate should provide for a bilayer membrane with better performance. Results obtained for La1−xSrxCoO3 with x
= 0.1 and x
= 0.5 at 900 °C will be presented for comparison, but are valid only for a range of oxygen activity larger than the critical activity acr(O2) of these oxides. It is emphasized that for x
= 0.5, a simple defect model as employed in this work may not be valid, however, the model was appropriate to fit nonstoichiometry data taken from.34 The model parameters for both layer materials are collected in Table 1. u(1),*V, u(2),*V, and u(2),*e denote the vacancy mobilities of layers 1 and 2 and the electron mobility of layer 2, respectively, as obtained from experimental data reported in refs. 8, 40 and 41.
4. Results
The stability and the permeation properties of a bilayer membrane depend on various factors: the transport properties of each layer material, represented by the defect concentrations and mobilities, the thickness of each layer, and the gradient of oxygen activity applied on the membrane. In Fig. 2, the effect of the dopant fraction d2 in layer 2 (coating layer) on the permeation flux j(O2) and the interfacial oxygen activity aI(O2) is presented. At constant vacancy mobility μ(1)V, aI(O2) increases with decreasing dopant fraction. The opposite trend is observed for the oxygen permeation flux, which is shown in Fig. 3 for the same conditions. At low oxygen activities (a(O2)
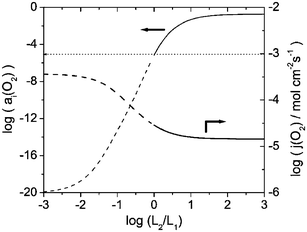
= 10−20), the oxygen vacancy and electron concentrations in layer 2 are of the same order of magnitude. However, under these conditions, the oxide is a prevailing electronic conductor, which is due to the higher mobility of the electrons as compared to the vacancy mobility.‡ Consequently, the ionic migration is the rate-limiting process for the permeation of oxygen through layer 2. Reducing the dopant level of the oxide in the coating layer diminishes the vacancy concentration, and the concomitant decrease of the ionic conductivity inhibits the permeation flux and increases the interfacial oxygen activity. Another way to modify the ionic conductivity is variation of the vacancy mobility μV(1). As seen in Figs. 2 and 3, a coating made of an oxide with a lower vacancy mobility would protect the substrate layer more effectively against reduction, but at the cost of a lower oxygen flux. The material in layer 1 is a prevailing electronic conductor over the entire range of oxygen activities considered, and the permeation flux is limited by the oxide-ion conductivity, which is proportional to the vacancy mobility (cf. eqn. (18)). Fig. 4 shows how the interfacial oxygen activity and permeation flux of the bilayer membrane is affected by the vacancy mobility in layer 1. As the mobility increases, both the permeation flux and the oxygen activity aI(O2) increase. Therefore, a substrate material with a higher ionic conductivity would not only enhance the membrane performance but also the protective effect of the coating layer. Fig. 5 shows the results for aI(O2) and j(O2) of a La0.9Sr0.1FeO3/Ce0.8Gd0.2O2 bilayer membrane with constant total thickness for a variation of the layer thickness ratio of the layers. A substantial protective effect is observed only if layer 2 is thicker than layer 1. The flux of a membrane that consists of a thick layer 2 and a thin layer 1 is larger than that of a membrane with a thick substrate layer and a thin protective layer. This unexpected result is due to the fact that the substrate material La0.9Sr0.1FeO3 has a lower permeability than the coating material. In this case, it would not be reasonable to employ a bilayer membrane because a single layer membrane made of the coating material would exhibit a larger permeation flux. The situation is different if a substrate material with a higher permeability is used. Figs. 6 and 7 depict results for aI(O2) and j(O2) of La1−xSrxCoO3/Ce0.8Gd0.2O2 bilayer membranes with different substrate composition but equal total thickness. For both membranes, the oxygen flux decreases with increasing thickness of layer 2. It is noted at this point that although the calculations were carried out for the full range of 0.21 ≤
aI(O2)
≤ 10−20, the results are valid only in the region aI(O2) >10−5 where the substrate material is stable. For lower interfacial activities, the results are to be regarded only as a qualitative trend. Fig. 6 shows that in a La0.5Sr0.5CoO3/Ce0.8Gd0.2O2 bilayer membrane, layers 1 and 2 must be of approximately equal thickness in order to reach the required minimum interfacial oxygen activity of aI(O2)
= 10−5. In case of the less permeable La0.9Sr0.1CoO3 substrate (Fig. 7), the model predicts that the thickness of layer 2 would have to be more than 10 times larger than that of layer 1.
 |
| | Fig. 2 Effect of the variation of the dopant fraction d2 in layer 2 on the interfacial oxygen activity aI(O2) for a′(O2)
= 0.21 bar and a″(O2)
= 10−20 bar. Layer thickness: L1
= 90 μm and L2
= 10 μm. Reference parameters for La1−xSrxFeO3
(layer 1) and Ce1−xGdxO2
(layer 2) taken from Table 1. | |
 |
| | Fig. 3 Effect of the variation of the dopant fraction d2 in layer 2 on the interfacial oxygen permeation flux j(O2) for a′(O2)
= 0.21 bar and a″(O2)
= 10−20 bar. Layer thickness: L1
= 90 μm and L2
= 10 μm. Reference parameters for La1−xSrxFeO3
(layer 1) and Ce1−xGdxO2
(layer 2) taken from Table 1. | |
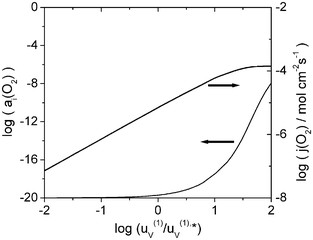 |
| | Fig. 4 Dependence of the interfacial oxygen activity aI(O2) and the oxygen permeation flux j(O2) on the vacancy mobility in layer 1 for a′(O2)
= 0.21 bar and a″(O2)
= 10−20 bar. L1
= 90 μm and L2
= 10 μm. Reference parameters for La1−xSrxFeO3
(layer 1) and Ce1−xGdxO2
(layer 2) taken from Table 1. | |
 |
| | Fig. 5 Dependence of the interfacial oxygen activity aI(O2) and the oxygen permeation flux j(O2) on the layer thickness ratio of a La0.9Sr0.1FeO3/Ce0.8Gd0.2O2 bilayer membrane. Total thickness of the membrane is 100 μm. a′(O2)
= 0.21 bar and a″(O2)
= 10−20 bar. Parameters were taken from Table 1. | |
 |
| | Fig. 6 Dependence of the interfacial oxygen activity aI(O2) and the oxygen permeation flux j(O2) on the layer thickness ratio of La1−xSrxCoO3
(x
= 0.5)/Ce0.8Gd0.2O2 bilayer membranes. Total thickness of the membrane is 100 μm. a′(O2)
= 0.21 bar and a″(O2)
= 10−20 bar. Parameters were taken from Table 1. | |
 |
| | Fig. 7 Dependence of the interfacial oxygen activity aI(O2) and the oxygen permeation flux j(O2) on the layer thickness ratio of La1−xSrxCoO3
(x
= 0.1)/Ce0.8Gd0.2O2 bilayer membranes. Total thickness of the membrane is 100 μm. a′(O2)
= 0.21 bar and a″(O2)
= 10−20 bar. Parameters were taken from Table 1. | |
5. Discussion
The results presented in the previous section indicate that the stability and the permeation properties of a bilayer membrane are greatly affected by the bulk transport properties and the thickness of both layers. As a general trend, the stability and the permeation flux is enhanced if a material with larger oxide-ion conductivity is used as a substrate (layer 1). Increasing the ionic or electronic conductivity of the coating material (layer 2) has the same effect on the permeation flux, however, it is detrimental to substrate protection because the interfacial oxygen activity decreases. An experimental study30 demonstrated that bilayered La0.5Sr0.5CoO3/Ce0.8Sm0.2O2 membranes with a total thickness of 520 μm were stable in a 5 vol-% methane/helium feed on the coating side, even though the coatings were as thin as 1.2 μm, which corresponds to log(L1/L2)
=
−2.64. According to Fig. 6, a membrane with this geometry should not be stable as the interfacial activity is very close to the surface oxygen activity a″(O2) on the reducing side of the membrane. In another work,29 2 mm thick La0.6Sr0.4Co0.8Fe0.2O3/Ce0.9Sm0.1O2 bilayer membranes with a coating thickness ranging from 0.1 to 0.29 μm were shown to retain a stable oxygen flux in a 6 vol% methane/helium feed at 900 °C for more than 30 h. The discrepancy between the experimental results and the analysis of this work may have several reasons. In both experimental studies the exact oxygen activity on the methane side was not measured and may not have been as low as in our calculations. Furthermore, the calculations are based on dilute defect models for both layers, which may not be valid for oxides with larger dopant contents. Vacancy ordering and the formation of defect associates may occur particularly at low oxygen partial pressures close to the stability limit.42 Vacancy ordering is expected to diminish the oxide-ion conductivity and has also been suggested to explain the maximum in the doping-level dependence of the ionic conductivity of yttria-doped ZrO243 which is isostructural to Ce0.8Gd0.2O2. According to the present analysis, vacancy ordering in the substrate layer lowers the interfacial oxygen activity whereas vacancy ordering in the coating layer has the opposite effect. Apart from this, the permeation process may not only be limited by bulk transport but also affected by sluggish oxygen exchange kinetics at the membrane surfaces. Surface limited permeation was discussed in the case of La1−xSrxCoO3 with dopant fractions larger than x
= 0.28 and other perovskite-structured mixed conductors.44 With bilayer membranes, surface limitations may exist not only at the outer surfaces but also at the layer interface. Fig. 8 depicts three possible scenarios. If the oxygen exchange at the oxygen-rich surface is sluggish, the surface oxygen activity a′S(O2) is lower than the equilibrium activity a′eq(O2). This causes the interfacial oxygen activity to drop, as depicted in Fig. 8a. In this case, the protective effect of the coating will be diminished. Fig. 8b shows a situation where the oxygen-lean surface is sluggish. In this case the surface oxygen activity a″S(O2) is larger than the equilibrium activity a″eq
(O2). As a consequence, the electronic conductivity of the coating material is diminished and the coating layer is more effective in blocking the permeation, thereby raising the interfacial oxygen activity to a higher level. Fig. 8c depicts a situation where the oxygen transfer across the layer interface is sluggish. In this case, different interfacial oxygen activities exist in both layers. However, the interfacial oxygen activity a(1)S(O2) in layer 1 is larger than the activity that would be established if the interfacial exchange reaction were in equilibrium, whereas a(1)S(O2) in layer 2 is smaller. In general, all three mechanisms mentioned above may affect the permeation process.
 |
| | Fig. 8 Schematic representation of the variation of the oxygen chemical activity in the presence of surface and interface oxygen exchange limitations: (a) sluggish oxygen exchange at the oxygen-rich surface, (b) sluggish oxygen exchange at the oxygen-lean surface and (c) sluggish exchange kinetics at the layer interface. | |
6. Conclusion
Chemical and mechanical durability of membrane materials is a key issue for oxygen separation applications that utilize dense ceramic membranes. Bilayer membranes may be employed in situations where highly permeable mixed conducting oxides cannot be used because they would undergo decomposition. The numerical analysis carried out in this work illustrates how the bulk transport properties and the thickness of the membrane layers affect the stability and the oxygen flux of a bilayer membrane. However, comparison of the model calculations with experimental results suggests that the assumption of a bulk-limited transport is not sufficient. Rather, the influence of sluggish surface reactions must be considered. In contrast to single-layered membranes, the permeation may also be affected by the transfer of oxygen across the membrane layer interface. If this transfer is slow compared to the bulk transport, a substantial drop of the oxygen activity exists at the layer interface. This may contribute to the stabilization of the substrate layer.
Acknowledgements
Part of this work is based on results that have been obtained during a post-doctoral stay of the author at the University of Texas at Austin, TX, which was generously supported by the Deutsche Forschungsgemeinschaft (DFG) in form of a research scholarship, and the Welch Foundation, Houston, Texas.
References
- J. R. Rostrup-Nielsen, Catal. Today, 2000, 63, 159 CrossRef CAS.
- Y. Teraoka, T. Nobunaga and N. Yamazoe, Chem. Lett., 1988, 503 CAS.
- Y. Teraoka, H. M. Zhang, K. Okamoto and N. Yamazoe, Mater. Res. Bull., 1988, 23, 51 CrossRef CAS.
- T. H. Lee, Y. L. Yang, A. J. Jacobson, B. Abeles and M. Zhou, Solid State Ionics, 1997, 100, 77 CrossRef.
- C. H. Chen, H. Kruidhof, H. J. M. Bouwmeester and A. J. Burggraaf, J. Appl. Electrochem., 1997, 27, 71 CrossRef CAS.
- S. Kim, Y. L. Yang, R. Christoffersen and A. J. Jacobson, Solid State Ionics, 1998, 109, 187 CrossRef CAS.
- H. Ullmann and N. Trofimenko, Solid State Ionics, 1999, 119, 1 CrossRef CAS.
-
K. Q. Huang, M. Schroeder and J. B. Goodenough, in Proceedings of the International Symposium “Solid State Ionic Devices”, ed. E. D. Wachsman, J. R. Akridge, M. Liu and N. Yamazoe, The Electrochemical Society Proceedings Series, 1999, 99–13, p. 95 Search PubMed.
- Z. Shao, W. Yang, Y. Cong, H. Dong, J. Tong and G. Xiong, J. Membr. Sci., 2000, 172, 177 CrossRef CAS.
- Y. Teraoka, Y. Honbe, J. Ishii, H. Furukawa and I. Moriguchi, Solid State Ionics, 2002, 152–153, 681 CrossRef CAS.
- T. Ishihara, Y. Tsuruta, C. Yu, T. Todaka, H. Nishiguchi and Y. Takita, J. Electrochem. Soc., 2003, 150, E17 CrossRef CAS.
- S. Lee, K. S. Lee, S. K. Woo, J. W. Kim, T. Ishihara and D. K. Kim, Solid State Ionics, 2003, 158, 287 CrossRef CAS.
- S. Diethelm and J. van Herle, J. Eur. Ceram. Soc., 2004, 24, 1319 CrossRef.
- U. Balachandran, B. Ma, P. S. Maiya, R. L. Mieville, J. T. Dusek, J. J. Picciolo, J. Guan, S. E. Dorris and M. Liu, Solid State Ionics, 1998, 108, 363 CrossRef CAS.
- T. Armstrong, F. Prado and A. Manthiram, Solid State Ionics, 2001, 140, 89 CrossRef CAS.
- V. V. Kharton, A. P. Viskup, A. V. Kovalevsky, E. N. Naumovich and F. M. B. Marques, Solid State Ionics, 2001, 143, 337 CrossRef CAS.
- U. Balachandran, J. T. Dusek, P. S. Maiya, B. Ma, R. L. Mieville, M. S. Kleefisch and C. A. Udovich, Catal. Today, 1997, 36, 265 CrossRef CAS.
- D. C. Zhu, X. Y. Xu, S. J. Feng, W. Liu and C. S. Chen, Catal. Today, 2003, 82, 151 CrossRef CAS.
- P. V. Hendriksen, P. H. Larsen, M. Mogensen, F. W. Poulsen and K. Wiik, Catal. Today, 2000, 56, 283 CrossRef CAS.
- A. Atkinson and T. Ramos, Solid State Ionics, 2000, 129, 259 CrossRef CAS.
- T. Nakamura, G. Petzow and L. J. Gauckler, Mater. Res. Bull., 1979, 14, 649 CrossRef.
- L. G. Tejuca, J. L. G. Fierro and J. M. D. Tascon, Adv. Catal., 1989, 36, 237 CAS.
-
M. Schroeder, K. Q. Huang, H. Q. Yin and J. B. Goodenough, in Proceedings
of the International Symposium “Solid State Ionic Devices”, ed. E. D. Wachsman, J. R. Akridge, M. Liu, N. Yamazoe, The Electrochemical Society Proceedings Series, Pennington, NJ, 1999, vol. 99–13, p. 121 Search PubMed.
- H. J. M. Bouwmeester, Catal. Today, 2003, 82, 141 CrossRef CAS.
- T. J. Mazanec, T. L. Cable and J. G. Frye Jr., Solid State Ionics, 1992, 53–56, 111 CrossRef CAS.
- J. E. ten Elshof, N. Q. Nguyen, M. W. den Otter and H. J. M. Bouwmeester, J. Electrochem. Soc., 1997, 144, 4361 CAS.
- K. Huang, M. Schroeder and J. B. Goodenough, Electrochem. Solid-State Lett., 1999, 2, 375 CrossRef CAS.
-
T. L. Clites and E. D. Wachsman, in Proceedings of the International Symposium “Solid State Ionic Devices”, ed. E. D. Wachsman, J. R. Akridge, M. Liu, N. Yamazoe, The Electrochemical Society Proceedings Series, Pennington, NJ, 1999, 99–13, p. 110 Search PubMed.
- E. D. Wachsman, Solid State Ionics, 2002, 152–153, 657 CrossRef CAS.
-
M. Schroeder, K. Q. Huang and J. B. Goodenough, in Mass and Charge Transport in Inorganic Materials. Fundamentals to Devices, Advances in Science and Technology, ed. P. Vincencini, V. Buscaglia, Faenza, 2000, vol. 29, p. 1507 Search PubMed.
- A. V. Virkar, J. Electrochem. Soc., 1991, 138, 1481 CAS.
- S. H. Chan, X. J. Chen and K. A. Khor, Solid State Ionics, 2003, 158, 29 CrossRef CAS.
- C. Wagner, Progr. Solid State Chem., 1975, 10, 3 Search PubMed.
- J. Mizusaki, Y. Mima, S. Yamauchi and K. Fueki, J. Solid State Chem., 1989, 80, 102 CrossRef CAS.
- B. A. van Hassel, T. Kawada, N. Sakai, H. Yokokawa, M. Dokiya and H. J. M. Bouwmeester, Solid State Ionics, 1993, 66, 295 CrossRef CAS.
- S. Wang, H. Inaba, H. Tagawa and T. Hashimoto, J. Electrochem. Soc., 1997, 144, 4076.
- J. Mizusaki, Solid State Ionics, 1992, 52, 79 CrossRef CAS.
- H. U. Anderson, Solid State Ionics, 1992, 52, 33 CrossRef CAS.
- J. Mizusaki, M. Yoshihiro, S. Yamauchi and K. Fueki, J. Solid State Chem., 1985, 58, 257 CrossRef CAS.
- T. Ishigaki, S. Yamauchi, K. Kishio, J. Mizusaki and K. Fueki, J. Solid State Chem., 1988, 73, 179 CrossRef CAS.
- S. Wang, T. Kobayashi, M. Dokiya and T. Hashimoto, J. Electrochem. Soc., 2000, 147, 3606 CrossRef CAS.
- L. M. van der Haar, M. W. den Otter, M. Morskate, H. J. M. Bouwmeester and H. Verweij, J. Electrochem. Soc., 2002, 149, J41 CrossRef CAS.
-
T. Takahashi, Solid Oxide Fuel Cells (Theoretics and Experiments) in: Physics of Electrolytes, 1977, vol. 2, p. 980 Search PubMed.
- S. Kim, S. Wang, X. Chen, Y. L. Yaug, N. Wu, A. Ignatiev, A. J. Jacobson and B. Abeles, J. Electrochem. Soc., 2000, 147, 2398 CrossRef CAS.
Footnotes |
| † Strictly speaking, these cases should be considered only for σ(1)amb > σ(2)amb. If the opposite were true, the protective coating would have a larger permeability for oxygen than the substrate and could be used itself as a single layer membrane. |
| ‡ From eqn. (19) it follows that σ(2)e/σ(2)i
=
rn2/[V˙˙O]2. Using the mobilities u(2),*V and u(2),*e reported in Table 1, r
=
zeu(2),*e/zOu(2),*V
≈ 6.1 is obtained. Furthermore, at low a(O2), eqn. (14) yields n2/[V˙˙O]2
≈2. |
|
| This journal is © the Owner Societies 2005 |
Click here to see how this site uses Cookies. View our privacy policy here.