Laser-induced fluorescence excitation and dispersed fluorescence spectroscopy of the Ã(¹B₁)–X̃(¹A₁) transition of dichlorocarbene

Abstract

The Ã(¹B₁)–X̃(¹A₁) transition of jet-cooled CCl₂ has been investigated using both laser-induced fluorescence (LIF) excitation and dispersed fluorescence (DF) spectroscopy. DF spectra were taken from over 90 emitting vibronic states over the breadth of the LIF spectrum. 68 ground state vibrational levels were assigned in the C³⁵Cl₂ isotopomer and 47 in C³⁵Cl³⁷Cl. The ground state frequencies were fit to an anharmonic potential yielding: ω^″₁ = 736 cm⁻¹, ω^″₂ = 338 cm⁻¹, ν^″₃ = 760 cm⁻¹, x^″₁₁ = −3.19 cm⁻¹, x^″₂₂ = −0.29 cm⁻¹, x^″₁₂ = −1.80 cm⁻¹, x^″₁₃ = −5.70 cm⁻¹ and x^″₂₃ = −3.80 cm⁻¹. This is the first gas phase measurement of ν^″₃. Despite the close frequency match between ν^″₁ and 2ν^″₂ there was no evidence for Fermi resonance. The intensities of transitions in the DF spectra were analysed to identify the nature of the emitting state. Levels below T₀₀ + 2500 cm⁻¹ in the à state could be assigned simply as combinations and overtones of ν^′₁ and ν^′₂. Between T₀₀ + 2500 and T₀₀ + 5300 cm⁻¹ the emission revealed an increasing mixing between levels within the same polyad, i.e., (m,n,0), (m + 1,n − 2,0), (m + 2,n − 4,0) etc, presumably due to Fermi resonance. This mixing becomes so extensive that simple assignment of the emitting states is not possible. Above T₀₀ + 5300 cm⁻¹ only K′ = 0 states could be identified, indicating that the Renner–Teller intersection between the X̃ and à states had been exceeded. This intersection is therefore 22 600 cm⁻¹ above the ground state, in excellent agreement with a previous theoretical calculation of 23 000 cm⁻¹.

---

Introduction

Carbenes have provided a fertile area of study for spectroscopists and theoreticians with many hundreds of papers published over more than four decades. One of the principle reasons for this extended interest is the extreme sensitivity of the electronic energies to substitution about the carbene site. This sensitivity is caused by the interaction of two non-bonding, carbon-centred electrons, which may be paired in the same orbital (the “carbene” configuration), or in two separate orbitals (the “biradical” configuration). The ground state configuration, and indeed the relative energy of all states involving these electrons, varies enormously with the other substituents on the central carbon atom. For example, the prototypical carbene, methylene (CH₂) has a triplet biradical ground state with the singlet carbene configuration lying 3165 cm⁻¹ higher in energy.¹ The singlet biradical lies about 12 000 cm⁻¹ above the triplet state.² All other hydrogen or halogen containing carbenes have a singlet carbene ground state, with the possible exception of CHI.³ In CF₂, this singlet carbene configuration is so stable that the triplet lies about 20 000 cm⁻¹ higher in energy^4,5 and the singlet biradical state 37 000 cm⁻¹ above the ground state.^6,7

More recently, both experimentalists and theorists have turned their attention to the photochemistry and photophysics of the à state. This has been motivated, in part, by increasing recognition that carbenes are present in a wide range of complex chemical environments, for example in flames and combustion^8,9 and in the atmosphere.^10–14 There is also interest in carbenes because their à and X̃ states are Renner–Teller (RT) components of the same ¹Δ state in the linear configuration, which often has an excitation energy similar to the bond dissociation energy of one of the C-ligand bonds. This has the potential to lead to a fascinating interplay between photochemistry (bond breaking) and photophysics (state mixing in the RT region). The RT coupling has been examined in CHF^15,16 and CHBr^17,18 in some detail, while photodissociation has been explored in CFBr¹⁹ and CFCl.²⁰

The subject of this paper is CCl₂. The first experimental study of CCl₂ was carried out by Milligan and Jacox in 1967.²¹ IR-absorption spectroscopy provided values of 748 and 721 cm⁻¹ for the symmetric and antisymmetric stretching frequencies, although no firm assignment was made as to which was which. They were also able to obtain the C³⁵Cl³⁷Cl isotopomer stretching frequencies of 726 and 700 cm⁻¹. Several more matrix studies have been performed since.^22–27 Andrews²² performed an experiment similar to that of Milligan and Jacox, and obtained consistent results, but was able to assign the lower frequency to the symmetric stretch (ν₁). Shirk²⁸ excited matrix isolated CCl₂ with 514.5 nm radiation from an argon ion laser and recorded the dispersed fluorescence (DF) spectrum, making the first assignment of the bending frequency ν^″₂ = 341 cm⁻¹. In 1975, Tevault and Andrews refined the value of ν^″₂ to 326.5 cm⁻¹ and calculated x^″₁₁ = −3 cm⁻¹ using DF spectroscopy. In 1977, Bondybey²⁷ measured both emission and excitation spectra of CCl₂ and calculated ω^″₁ = 726 cm⁻¹, ω^″₂ = 333 cm⁻¹, ω^″₃ = 745 cm⁻¹, x^″₁₁ = −3.7 cm⁻¹, x^″₂₂ = −2.2 cm⁻¹, x^″₁₂ = 0.2 cm⁻¹ and T₀₀ = 17 092 cm⁻¹. Bondybey also measured the laser induced fluorescence (LIF) excitation spectrum from which he was able to calculate many of the à state vibrational constants and a fluorescence lifetime of 3.6 μs. Matrix studies have provided all three ground state frequencies and all anharmonicities associated with ν₁ and ν₂, as well as ω₁, ω₂, x₁₁, x₂₂ and x₁₂ in the excited state.

Since 1977, when Huie et al. recorded an LIF spectrum of CCl₂ in a bulb²⁹, there have been many gas phase studies,^30–36 the most comprehensive of which was by Clouthier and Karolczak in 1991.³⁵ They used a pyrolysis nozzle to produce jet-cooled CCl₂ in the vacuum chamber, measuring the electronic transition origin at T₀₀ = 17 255.672 cm⁻¹ and several rotational constants. They also assigned several ground state vibrations from an analysis of hot band structure in the spectrum.

The most recent spectroscopic study of CCl₂ was a DF investigation reported by Liu et al. in 2003.³⁷ They recorded DF spectra from four vibrational bands in C³⁵Cl₂ and two vibrational bands in C³⁵Cl³⁷Cl. In all, 76 ground state vibrational levels were assigned for C³⁵Cl₂ and twelve for C³⁵Cl³⁷Cl. An anharmonic analysis was included, which reported all harmonic and anharmonic constants involving ν^″₁ and ν^″₂. At energies near 6000 cm⁻¹, extra transitions were observed, which were interpreted as mixing with the triplet state.

Bauschlicher et al.³⁸ carried out the first theoretical study of CCl₂ in 1976. They computed the energies, bond angles and bond lengths in the lowest energy singlet and triplet states. In 1985, Nguyen et al. published theoretical values for the vibrational frequencies of CCl₂ in the ground and excited singlet states.³⁹ Since then several theoretical studies have been undertaken.^5,40–45 The most recent calculations of the vibrational frequencies of CCl₂ were performed by Demaison et al.⁴⁵ who used the CCSD(T) method with a cc-pV5Z basis set and reported a full set of vibrational parameters including anharmonicity constants. Sendt and Bacskay⁵ examined the photochemically interesting region of the à state and calculated the Renner–Teller intersection to lie near 23 300 cm⁻¹ above the X̃ state zero-point level, or 6000 cm⁻¹ above the zero-point energy of the à state. The C–Cl dissociation energy was calculated to be a further 3000 cm⁻¹ above the Renner–Teller intersection.

In this work we start a comprehensive analysis of the Ã-X̃ spectroscopy of CCl₂. We have measured the LIF spectrum from 18 000 to 24 000 cm⁻¹, which is much further than any previous work. To assign the multitude of vibronic states over this range, we therefore measured 90 different DF spectra. Analysis of the spectra results in new X̃ state vibrational frequencies and anharmonicity constants, identification of extensive Fermi resonance in the à state, and measurement of the energy of the Renner–Teller intersection.

Experimental

Chloroform (l, 298 K) was seeded in argon (25 bar) and the mixture flowed to a pulsed nozzle (Precision Instruments) attached to an alumina oven heated to 1500 K.⁴⁶ The sample then entered the vacuum chamber (pumped to 2 × 10⁻⁶ mbar with the nozzle off and 1 × 10⁻³ mbar with the nozzle on) via a free-jet expansion, cooling the fragments to 5–10 K (based on rotational temperature). The vacuum system comprised a Varian VHS-6 diffusion pump backed by a mechanical pump (Alcatel 2033). The expansion was intersected 8–12 mm downstream by an Excimer-pumped dye laser (Lambda Physik Lextra-200, XeCl at 308 nm and Lambda Physik LPD-3001E). A number of laser dyes (C540A, C503, C480, C460, C450, C440 and Exalite 428, all from Exciton) were used to produce light in the range λ = 410–550 nm. The laser frequency was calibrated using a Coherent Wavemaster wavemeter. All frequencies are reported in vacuum wavenumber and should be accurate to within ±1 cm⁻¹.

LIF spectra were recorded by imaging the CCl₂ emission with an f = 50 mm quartz lens into a monochromator (Spex Minimate) with no slits (band pass 60 nm). A photomultiplier (EMI 9816QB) connected to the exit slit of the monochromator, detected the fluorescence. The photomultiplier signal was sent to a preamplifier (Stanford Research, SR-240) and then passed to a gated boxcar averager (SR-250). Although CCl₂ has a long fluorescence lifetime^27,29,30 we were only able to observe a small part of it as the molecules drifted in and out of the viewing region while still fluorescing. For this reason our gate was typically 100–500 ns. The output was passed through an A/D converter (SR-245) before being recorded by a PC using SR-272 software. The timing was controlled a digital delay generator (Stanford Research, DG-535).

DF spectra were measured by replacing the small monochromator with a Spex 0.75 m double monochromator with slits set typically at 1 mm (band pass 18 cm⁻¹). The excitation laser was fixed on a peak from the LIF spectrum and the monochromator was scanned to produce the DF spectra. Only one half of the double monochromator was used. The large monochromator was calibrated with the emission lines from a mercury lamp. Data collection and processing remained the same as for the LIF spectrum.

Results and analysis

Overview of the LIF spectrum

The à ← X̃ fluorescence excitation spectrum of jet-cooled CCl₂, spanning 6500 cm⁻¹, is shown in Fig. 1. The peak intensities have been normalised to laser power, and normalised between different laser dyes; however, because seven laser dyes were used, the intensities should be considered semi-quantitative. Our spectrum does not extend further to the red than 17 700 cm⁻¹, corresponding to the region of the 2²₀ transition, because the Franck–Condon intensity is decreasing strongly and glow from the pyrolysis nozzle interfered with our detection. The two non-contiguous parts of the excitation spectrum at the lowest frequency could only be obtained by measuring the fluorescence through the larger 0.75 m monochromator, which was set 335 cm⁻¹ (= ν^″₂) below the laser frequency and scanned at the same rate as the laser. This provided effective discrimination against the nozzle glow, but as a consequence, intensities are less reliable than the rest of the spectrum.

Fig. 1 LIF spectrum of CCl₂. The spectrum has been divided into three Regions (see text). Region 1: vibrational assignments are straightforward, and are shown below the spectrum; Region 2: emission is characteristic of mixed vibrational states where simple assignment is not possible; Region 3: a significant change in structure indicates that the Renner–Teller (RT) energy has been exceeded. The inferred energy of the RT intersection is indicated.

We have divided the spectrum into three regions for reasons that will become apparent. In essence, Region 1 comprises all of the previous assignments in the à state (except for Gao et al., which we shall comment further upon later). In all cases in Region 1 we are able to make secure rotational, vibrational and isotopic assignments through analysis of the DF spectra and modelling of the LIF contours. Vibrational assignments are shown below the spectrum in Fig. 1 and reported in Table 1.

Table 1 Vibrational assignments, frequencies and A rotational constants for transitions in CCl₂ throughout Region 1. Parentheses indicate tentative assignments

	Frequency/cm^−1	Frequency/cm^−1	A rotational constant/cm^−1
Assignment	C^35Cl2	C^35Cl^37Cl	C^35Cl2
a These levels show evidence of mixing, however their vibronic character is mostly as assigned. b These levels are not assigned, the levels map to a mixture of the available assignments.
(0,0,0)
(0,1,0)
(0,2,0)	17 861.25	17 853.25	3.8
(1,0,0)
(0,3,0)	18 164.4	18 155.1	4.0
(1,1,0)	18 187.8		3.9
(0,4,0)	18 467	18 455	4.1
(1,2,0)	18 488.3	18 478.4	3.95
(2,0,0)	18 510	18 502.2	3.8
(0,5,0)	18 770.1	18 755.7	4.3
(1,3,0)	18 789.2	18 776.3	4.1
(2,1,0)	18 808.7	18 797.8	3.95
(0,6,0)	19 072.6	19 056.1	4.55
(1,4,0)	19 090.9	19 074.8	4.25
(2,2,0)	19 108.1	19 094.1	4.1
(3,0,0)
(0,7,0)
(1,5,0)	19 392.5	19 373.7	4.43
(2,3,0)	19 408.0	19 390	4.2
(3,1,0)	19 422.5	19 403.1	4.1
(0,8,0)
(1,6,0)	19 693.6	19 672.4	4.65
(2,4,0)	19 708.1	19 687.6	4.35
(3,2,0)	19 720.9	19 696.94	4.2
(4,0,0)	19 750.1
(0,9,0)^a
(1,7,0)^a	19 997.8	19 972.7	4.75
(2,5,0)^a	20 008.3	19 985	4.55
(3,3,0)^a	20 020.1	19 997.1	4.35
(4,1,0)^a	20 030.2		4.2
(0,10,0)^a		(20 307.4)
(1,8,0)^a	(20 301.0)		5.1
(2,6,0)^a		20 282.2	4.5
(3,4,0)^a	20 327	20 293.8	4.32
(4,2,0)^a	20 333		4.2
(5,0,0)^a
(1,10,0)^b
(2,8,0)^b
(3,6,0)^b	20 599.5		4.5
(4,4,0)^b		20 608	4.3
(5,2,0)^b	20 627.5		4.5
(6,0,0)^b	20 635.8		4.3

---

In Region 2 the DF spectra from the various à vibronic states are increasingly complex, which indicates anharmonic mixing. Throughout this region we are able to assign the isotope and rotational structure, however conventional vibrational assignments are no longer really meaningful.

The LIF spectrum qualitatively changes in Region 3. The rotational structure cannot be modelled as it was throughout Regions 1 and 2 and we believe that the energy is now above that of the Renner–Teller intersection, where the molecule now has an averaged linear geometry.

The differentiation of the LIF spectrum into these three qualitatively different regions is based on a detailed analysis of 90 DF spectra spanning the entire CCl₂ LIF spectrum. We shall discuss general features of DF spectra first, and then return to the assignment of features and regions in the LIF spectrum.

Dispersed fluorescence (DF) spectra

DF spectra were recorded from rovibronic levels over the whole range of the LIF spectrum. For ease of analysis the fluorescence spectra were all calibrated relative to the excitation frequency. In this way the DF spectra provide a “map” of the ground state energy levels with the (0,0,0) level at 0 cm⁻¹. The only exceptions are the spectra featuring peaks at negative relative wavenumbers, which are easily assigned as originating from hot bands.

Each spectrum provides the same information about the X̃ state vibrational frequencies. Much of this information was published recently in a detailed analysis of the DF spectrum of CCl₂ by Liu et al.³⁷ In that work, many X̃ vibrational levels up to 6000 cm⁻¹ were assigned, resulting in harmonic and anharmonic constants that provided an excellent model of the observed frequencies. Our analysis is quantitatively similar to this previous work and so we shall be brief in this part of our analysis, and will concentrate on features that are different.

Fig. 2 shows a DF spectrum following excitation at 20025.14 cm⁻¹, at the top end of Region 1. This wavenumber corresponds to overlapped transitions in the rotational contours of the 1³₀2³₀ and 1²₀2⁵₀ bands. The resolution in the spectrum is 18 cm⁻¹ FWHM. The peak at 0 cm⁻¹ with the asterisk corresponds to the excitation frequency. The intensity of this peak contains a contribution due to scattered light and its intensity is not indicative of its relative transition strength. All DF spectra were corrected for the wavelength dependent sensitivity of the PMT, which was obtained from the manufacturer.

Fig. 2 Dispersed fluorescence spectrum of CCl₂. The excitation wavenumber is 20 025.14 cm⁻¹. Assignments for the long progressions in ν₁ and ν₂ are shown underneath. Weak emission assigned as due to ν₃ is shown expanded in the inset.

As described by several previous authors,^27,37 the spectrum is dominated by long progressions in the symmetric stretch (ν₁) and the bend (ν₂). Assignments for almost every vibrational level up to 5000 cm⁻¹ are shown below the spectrum and reported in Table 2 and are quantitatively consistent with assignments by Liu et al.³⁷ The near equivalence of ν₁ and 2ν₂ means that the peaks in the spectrum clump together to form polyads. When assignments involving all possible combinations of ν₁ and ν₂ had been exhausted there were a few bands that remained unassigned. These have been assigned to transitions involving levels containing two quanta of ν₃, the asymmetric stretch. (Transitions involving odd quantum changes in ν₃ are symmetry-forbidden.) The inset in Fig. 2 shows two of these peaks in greater detail.

Table 2 Assigned vibrational frequencies in the X̃ state of CCl₂ for two isotopomers and comparison with model frequencies

		C^35Cl2 frequency/cm^−1			C^35Cl^37Cl frequency/cm^−1
Assignment		Expt.	Model	Diff.	Expt.	Model	Diff.
2n	00	0	0	0	0	−1	−1
progression	21	335	335	0	331	331	0
	22	669	669	0	661	662	1
	23	1003	1003	0	992	992	0
	24	1337	1336	−1	1322	1321	−1
	25	1668	1669	1	1647	1650	3
	26	2002	2001	−1	1981	1977	−4
	27	2333	2332	−1	2307	2304	−3
	28	2663	2663	0	2629	2630	1
	29	2993	2993	0	2954	2954	0
	210	3323	3323	0	3278	3278	0
	211	3649	3652	3	3600	3601	1
	212	3979	3980	1	3920	3923	3
	213	4308	4308	0
	214	4633	4636	3
112n	1120	727	726	−1	723	723	0
progression	1121	1059	1059	0	1053	1053	0
	1122	1391	1391	0	1381	1382	1
	1123	1723	1723	0	1710	1710	0
	1124	2053	2055	2	2039	2037	−2
	1125	2386	2386	0	2365	2364	−1
	1126	2717	2716	−1	2688	2689	1
	1127	3046	3045	−1	3010	3014	4
	1128	3375	3374	−1	3342	3337	−5
	1129	3703	3703	0	3665	3660	−5
	11210	4032	4031	−1
	11211	4360	4358	−2
	11212	4684	4685	1
	11213	5014	5011	−3
	11214	5337	5336	−1
122n	1220	1445	1445	0	1441	1440	−1
progression	1221	1775	1777	2	1767	1768	1
	1222	2106	2107	1	2095	2095	0
	1223	2437	2438	1	2417	2421	4
	1224	2766	2767	1	2743	2746	3
	1225	3097	3096	−1	3065	3070	5
	1226	3425	3424	−1	3395	3394	−1
	1227	3752	3752	0	3716	3716	0
132n	1320	2159	2159	0	2153	2150	−3
progression	1321	2489	2488	−1	2473	2476	3
	1322	2817	2817	0	2799	2801	2
	1323	3145	3145	0	3121	3125	4
	1324	3474	3473	−1	3451	3448	−3
	1325	3802	3800	−2	3776	3770	−6
	1326	4128	4127	−1
	1327	4454	4453	−1
142n	1420	2866	2865	−1	2858	2853	−5
progression	1421	3194	3193	−1	3179	3177	−2
	1422	3521	3520	−1	3497	3500	3
	1423	3849	3847	−2	3821	3822	1
	1424	4171	4173	2
	1426	4826	4823	−3
152n	1520	3567	3566	−1	3549	3550	1
progression	1521	3891	3892	1	3870	3871	1
	1522	4214	4217	3
	1523	4541	4542	1
	1524	4862	4866	4
	1525	5187	5190	3
162n	1620	4260	4260	0
progression	1621	4584	4584	0
	1622	4908	4908	0
	1623	5228	5231	3
172n	1720	4950	4948	−2
progression	1721	5272	5270	−2
2n32	2032	1509	1511	2	1491	1494	3
progression	2132	1839	1838	−1	1820	1817	−3
112n32	112032	2227	2225	−2	2214	2211	−3
progression	112132	2549	2551	2	2530	2532	2

---

We have assigned 47 vibrational frequencies of the C³⁵Cl³⁷Cl isotopomer. Twelve of these were also reported by Liu et al.³⁷ and agree quantitatively.

The DF spectra also provide a positive assignment of the Cl isotopic composition of the emitting species because the frequencies are shifted according to the isotope effect. We attributed 63 of our DF spectra to emission from C³⁵Cl₂ while the remaining 27 were attributed to C³⁵Cl³⁷Cl. These correspond to distinct vibrational levels; however, due to the extensive mixing in Regions 2 and 3, they could not all be uniquely assigned and not all have been included in Table 1. No fluorescence spectra from transitions involving the C³⁷Cl₂ isotopomer were recorded.

When measured at higher resolution, the K_a value of the emitting state can also be determined from the DF spectrum. The upper spectrum in Fig. 3 is an LIF spectrum of one of the polyads in Region 1. High resolution (6 cm⁻¹ FWHM) DF spectra were measured after exciting the three transitions indicated on the LIF spectrum. A short section of each of these DF spectra is shown below. Each DF spectrum shows a single vibrational transition. The upper DF spectrum is characterised by emission from K^′_a = 1 and shows a splitting due to the ΔK = ±1 selection rule. This splitting is numerically approximately equal to 4A″. Emission from levels with K^′_a = 2 and 3, with splittings of about 8A″ and 12A″, respectively, are shown below. This information is not very useful for measuring ground state rotational parameters (these constants are already known to much higher precision^32,47), but it is invaluable for identifying the emitting state. The assignment of the K-state of the emitting level is an important check for the assignment of the LIF spectrum, such as shown in the top panel. This information is even more valuable higher up the vibrational ladder where assignments become more difficult.

Fig. 3 High resolution dispersed fluorescence spectra taken after exciting the three features indicated in the LIF spectrum at the top. The structure in each DF spectrum arises from a single vibrational transition. The splitting arises from excitation of different K^′_a states with and the subsequent ΔK = ±1 selection rule in emission.

Anharmonic analysis. Assignments for all observed peaks in the DF spectra are listed in Table 2. The frequencies were fit to a three-dimensional anharmonic (Morse) potential, whose energy levels are given by⁴⁸Vibrational levels involving at least two quanta of each vibrational mode were observed in the spectra, with the exception of ν^″₃. This means that the harmonic frequencies ω^″₁ and ω^″₂ could be determined, as could 5 of the 6 anharmonicity constants. x^″₃₃ was initially set to zero, and the fitted harmonic frequency, ω^″₃, includes the x₃₃ anharmonicity in its value. The values of all the spectroscopic constants are reported in Table 3. For comparison with other literature values, the anharmonic frequencies, which are simply the difference between υ = 1 and υ = 0 for each vibration, are also included in Table 3. These values do not differ much from the harmonic values because the anharmonicity constants are not large. The vibrational frequencies that are predicted by this model are shown in Table 2 and show a typical RMS deviation of <4 cm⁻¹, which is less than the resolution in the spectrum.

Table 3 Experimental and theoretical spectroscopic parameters for C³⁵Cl₂ and C³⁵Cl³⁷Cl

	Current			Previous
	C^35Cl2			Experimental^b		Theory^c
Parameter/cm^−1	x ^″33 = 0	Theory x^″33^a	C^35Cl^37Cl	C^35Cl2	C^35Cl^37Cl	C^35Cl2
a Our data was refit with x^″33 set to the value calculated by Demaison et al. (ref. 45). b These values are derived from ref. 37, refit to eqn. (1). c Ref. 45.
ν ^″1	726 ± 1	726 ± 1	724 ± 2	726	722	727.4
ν ^″2	335 ± 1	335 ± 1	332 ± 1	334	329	332.6
ν ^″3	759.5 ± 1.2	763 ± 1	751.4 ± 2.5	—	—	748.9
ω ^″1	735.7 ± 0.8	736.1 ± 0.7	733.3 ± 2.2	736.45	730.20	735.3
ω ^″2	338.2 ± 0.5	338.5 ± 0.5	336.0 ± 1.2	337.74	334.40	335.9
ω ^″3	—	783.9 ± 1.2	—	—	—	769.6
x ^″11	−3.18 ± 0.06	−3.20 ± 0.06	−3.4 ± 0.3	−3.385	−2.545	−2.24
x ^″22	−0.29 ± 0.02	−0.29 ± 0.02	−0.45 ± 0.05	−0.3303	−0.5066	−0.18
x ^″33	≡0	≡−7.89	≡0	—	—	−7.89
x ^″12	−1.79 ± 0.05	−1.81 ± 0.06	−2.0 ± 0.2	−1.959	−2.095	−1.63
x ^″13	−5.15 ± 0.8	−5.55 ± 0.7	−3.4 ± 1.5	—	—	−5.49
x ^″23	−3.8 ± 0.7	−4.1 ± 0.8	−4.4 ± 1.5	—	—	−4.36

---

Franck–Condon (FC) factors. The intensities of transitions in the DF spectra are, in the Born–Oppenheimer limit, proportional to the product of the Einstein A-coefficient and the FC factor. We have examined the intensities of all observed transitions in the DF spectra; a total of well over 3000 transitions between these 90 upper states and typically 30–40 lower states. The Einstein A-coefficient was taken to be proportional to ν³, while the FC factors were treated in the harmonic limit. 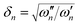The harmonic FC factors are parameterised for each vibrational mode in terms of , where the ω_n are the harmonic frequencies for each mode, n and D_n, which is a dimensionless parameter measuring the displacement of the normal coordinate upon electronic excitation.⁴⁹ As ω″ and ω′ are known for ν₁ and ν₂ the δ_n parameter is fixed for these modes, while D₁ and D₂ are treated as adjustable parameters.

We found that the intensities of all transitions for DF spectra originating in à state levels below 19 800 cm⁻¹ (i.e. Region 1) can be fit by just these two parameters, with optimal values being D₁ = 2.4 ± 0.1 and D₂ = 3.6 ± 0.1. Fig. 4 shows the experimental and model results, using these values of D_n. The error bars on the experimental intensities are 1σ from all available experimental data. Where there are no error bars, only a single measurement was available; however, errors of 10–20% are appropriate. The agreement between the model and experimental intensities is quite satisfactory. In general, values of D within ±0.1 of the values reported above also provided reasonable agreement with the experimental intensities. One important consequence of the agreement between the model and observed intensities is that although there is a near match between 2ν^″₂ and ν^″₁ (which results in polyads all the way up the X̃ state vibrational ladder), there is not any substantial anharmonic mixing between these states.

Fig. 4 Measured and calculated Franck–Condon (FC) factors. The measured FC factors are the average from many spectra and progressions (error = 1σ). The calculated FC factors are based on harmonic oscillator wavefunctions.

A. Detailed picture of the LIF spectrum and à state vibronic Structure

Above, we presented an overview of the LIF spectrum, which was divided into three Regions. We now return to the LIF spectrum armed with detailed knowledge of the emitting state that analysis of the DF spectra provides. This information includes the Cl isotope distribution of the emitting species, the value of K^′_a, the vibrational character of the emitting state (leading to a unique assignment in many cases), and whether the transition in the spectrum is a hot or cold band.

Region 1. Fig. 5 shows a high resolution scan of one of the vibronic polyads from Region 1 of Fig. 1. This spectrum, and indeed the entire CCl₂ spectrum, is complicated by the presence of an open rotational structure, several overlapping vibrational progressions, transitions arising from the three isotopomers C³⁵Cl₂, C³⁵Cl³⁷Cl and C³⁷Cl₂ (present in a 9 : 6 : 1 ratio), and occasional hot bands. This part of the CCl₂ spectrum near 19400 cm⁻¹ is towards the upper end of the assignments offered by Clouthier et al.³⁵ and overlaps that reported in Liu et al.³⁷ and Gao et al.³⁶ Transitions to four states should occur in this polyad: (3,1,0), (2,3,0), (1,5,0) and (0,7,0). The DF spectra obtained after exciting each of these single vibronic levels display the expected intensity distributions (FC factors) for these four levels, thereby confirming their identities and their previous assignments. Shown below the experimental spectrum are two simulations. One is for the rotational structure of a particular vibrational band (1,5,0) of the C³⁵Cl₂ isotopomer. The other is the sum of four such simulations and those of the corresponding bands in C³⁵Cl³⁷Cl. Throughout Region 1 our DF spectra confirm all previous assignments.

Fig. 5 Expanded region of the LIF spectrum from Regions 1, 2 and 3. Simulations underneath the Region 1 spectrum show four members of a polyad, each with three isotopomers contributing to the spectrum. The simulation for a single vibronic band is shown underneath. The spectrum from Region 2 can likewise be identified and model as a set of overlapping vibronic transitions (one shown underneath), however the assignment of the constituent bands is complex. The rotational structure is completely changed in Region 3, indicating that the Renner–Teller intersection has been exceeded (see text).

Region 2. DF spectra from vibrational states above about 20000 cm⁻¹ do not fit the harmonic FC intensity pattern so well. The first indication in the 20 000 cm⁻¹ polyad is that the FC factors are no longer orthogonal. For example, following excitation of the transition at 20 020 cm⁻¹, which has been assigned previously as a part of the 1³₀2³₀ band,³⁵ the intensity distributions in the 1³₀2³_n and 1³₁2³_n progressions are somewhat different. DF spectra from the other vibrational states in this polyad were likewise perturbed from the expected FC intensity distribution. We have analysed the intensities in these DF spectra and the 20 020 cm⁻¹ band seems to be explained by Fermi resonance between the levels (3,3,0) and (2,5,0). A similar analysis of the level excited at 20 008 cm⁻¹ indicates that this vibronic state is mostly of (2,5,0) vibronic character, but with an amount of (1,7,0) mixed in. Throughout this polyad, the mixing is not too strong, and the vibrational labels in Table 1 and used by previous authors are adequate.

The variance from the harmonic FC intensities increases for DF spectra obtained from higher vibrational states. Even one rung higher in the ladder, near 20 300 cm⁻¹, where absorption to the set of states (5,0,0) : (4,2,0) : (3,4,0) : (2,6,0) : (1,8,0) : (0,10,0) would be expected to occur, the set of DF spectra reveal extensive mixing. This is the highest that Clouthier et al., and Liu et al. have assigned. DF spectra from the next polyad are more complex again and are not readily identifiable as any simple harmonic vibrational assignment. In this region of the vibrational ladder the combination-differences no longer follow the same simple pattern as they do lower down. While the polyads appear regular throughout this region, the DF spectra demonstrate conclusively that anharmonic mixing is significant above about 20 000 cm⁻¹, and that this mixing is what is responsible for the misbehaviour of the combination-differences above about 20 000 cm⁻¹. We are currently evaluating the level mixing higher up the ladder in CCl₂ and will report on this later.

Throughout Region 2, the rotational structure of the vibronic bands is preserved. A higher resolution scan from a polyad near 21 250 cm⁻¹, in the middle of Region 2, is shown in Fig. 5. While the vibronic complexity increases throughout this Region, and we cannot offer a simple vibrational assignment for this polyad, or any polyad beyond 20 000 cm⁻¹, the individual vibronic bands can be clearly identified. The DF spectra continue to indicate the value of K^′_a in the emitting state and the chlorine isotope distribution of the emitting species.

Region 3. Above about 22 600 cm⁻¹ the character of the LIF spectrum changes qualitatively, as shown in Fig. 5. The rotational structure changes significantly over only a couple of polyads between 22 000 and 22 600 cm⁻¹. DF spectra in this region confirm that the emitting species is CCl₂, but the emitting state cannot be uniquely identified (as in Region 2). Perhaps one of the most striking features of the LIF spectra above 22 600 cm⁻¹ is that all the structure in this region appears to correspond to K^′_a = 0. We believe that at energies above 22 600 cm⁻¹, the transition accesses a region of the à potential energy surface above the Renner–Teller intersection between the X̃ and à states, where the à state is strongly coupled to the X̃ state. The RT interaction depends strongly on K_a. States with K_a > 0 have increasing X̃ state character and hence a weaker transition moment in absorption and fluorescence and a much longer fluorescence lifetime. In our experiment where we integrate only the first couple of hundred nanoseconds of fluorescence, we are biased significantly against the detection of such weak, long-lived states.

The A′ rotational constants for each vibronic level of the C³⁵Cl₂ isotopomer are also listed in Table 1. The constants generally increase with increasing quanta of the bending vibration, ν₂, and to a lesser extent the symmetric stretch, ν₁. This is characteristic of the average bond angle increasing for higher ν₂ and consistent with the presence of the RT intersection near 22 600 cm⁻¹. This trend in A′ constants becomes obscured for the highest levels in the table, as the vibronic mixing becomes more prevalent.

Discussion

In this work we have measured the LIF spectrum and many DF spectra of jet-cooled CCl₂. The DF spectra reveal a wealth of detail about the emitting state, as well as vibrational frequencies in the ground electronic state. There have been many previous experimental and theoretical investigations of this prototypical carbene, so we begin our discussion with a comparison and extension of the previous work, then consider the unanswered questions posed by this work.

Comparison with previous ground (X̃) state studies

In some regards the experiment and results reported here mirror those published recently by Liu et al.³⁷ and it is appropriate to comment on the differences between our measurements. Liu et al. measured DF spectra from a small number of initial à states, with similar resolution to ours. They measured a larger number of X̃ vibrational levels, importantly many higher lying vibrational states, and identified a region where state mixing seems to indicate the presence of the triplet state near these energies. We were unable to measure this region, due to interference by the glow from the pyrolysis nozzle.

In the present study, we have excited many more initial à vibronic states with the initial aim of assigning the emitting state. The frequencies in our DF spectra agree quantitatively (typically within 1 cm⁻¹) with those published by Liu et al. We have extended the assignments of the X̃ state vibrational levels in two important ways. First, we have assigned emission to levels involving ν^″₃, allowing the first measurement of the asymmetric stretch frequency in the gas phase. Second, we have measured significantly more levels in the C³⁵Cl³⁷Cl isotopomer than previously. The addition of ν₃ to the list of assigned levels changes the vibrational constants somewhat. These constants are summarised in Table 3.

Liu et al. fit their data to a slightly different form of the anharmonic equation:

where ω_i⁰ are the vibrational frequencies at the zero-point level. Eqns. (1) and (2) yield the same fit to the data, with the same anharmonicity constants. The harmonic frequencies, ω_i, evaluated using eqn. (1) differ from the ω_i⁰ in eqn. (2) by:The size of the anharmonicity constants in Table 3 means that there is a non-negligible difference between ω_i and ω_i⁰. We have chosen to use ω_i because it is the direct analogue of ω_e in the anharmonic equation for a diatomic molecule, which corresponds to the frequency of vibration for an infinitesimal displacement about the equilibrium point. It is also the harmonic frequency that is provided by theoretical calculations. In Table 3, for comparison with our data, we have refit Liu’s³⁷ data using eqn. (1).

There is a relatively good agreement between the current spectroscopic constants and those reported previously. Because we have measured levels involving ν₃ we were able to extract x₁₃ and x₂₃. The inclusion of these two anharmonicity constants has an effect on the rest of the constants, which accounts for the small differences between our results and other gas phase measurements.

A comparison of the current spectroscopic constants with the most recent ab initio calculations⁴⁴ shows quite extraordinary agreement. There has been no experimental measurement of x₃₃ which, according to calculation, is quite large at x₃₃ = −7.89 cm⁻¹. If this one theoretical value is used, and the rest of the constants re-fit according to eqn. (1), a new set of “experimental” constants are obtained as shown in Table 3. The effect on most of the other constants was negligible but it allows an estimate of the previously intractable ω^″₃, which becomes 784 cm⁻¹, and is now in reasonable agreement with the calculated value of 769.9 cm⁻¹. The agreement between the experimental and ab initio values is extraordinarily good and we believe that these constants are a good representation of the vibrational level structure of all levels in the ground state up to about 5000 cm⁻¹.

Comparison with previous excited (Ã) state studies

There have been several previous investigations of the CCl₂ absorption and fluorescence excitation spectrum.^27,31–36 The most extensive report was that of Clouthier et al., who assigned almost every vibrational level up to 20 300 cm⁻¹ (i.e. Region 1). This is the region where the DF spectra could be interpreted by harmonic Franck–Condon factors, and where analysis of the intensities provides an unambiguous assignment of the emitting state. Our DF spectra confirm all assignments of Clouthier, and have provided several new measurements, particularly for C³⁵Cl³⁷Cl.

Gao et al. assigned the LIF spectrum to significantly higher energy than Clouthier (Region 2), assigning up to 16 quanta of bending vibration and 8 quanta of symmetric stretch. The analysis of our DF spectra does not support that assignment. Above 20 300 cm⁻¹ assignment of the vibronic state becomes more and more complex. The vibrations no longer behave as overtones and combinations of normal modes and the DF spectra show clear character of emission from mixed states. One picture is that the vibrations are increasingly anharmonically mixed due to the fairly close resonance between 2ν^′₂ ≈ ν^′₁, which has been suggested by previous workers.^33,37 We are exploring and modelling this interaction further.

There have been no assignments for the LIF spectrum throughout Region 3. Indeed the whole nature of the spectrum has changed from the Region below. We have recorded about 30 DF spectra throughout this region. Every emitting state was shown to be due to CCl₂ (by the characteristic frequencies) and we have no reason to believe that any other species contributes to the spectrum in Fig. 1. The spectrum still shows what looks like polyad structure, though the polyads now have so many members that the spread of frequencies within a polyad now matches the spacing between them.

The most characteristic observation about this region of the LIF spectrum, however, is that every emitting state appears to have K′ = 0. We believe that this indicates that the Renner–Teller intersection has been exceeded. There has been an ab initio theoretical estimate of several key energy points on the à state surface.⁵ The energy to C–Cl bond cleavage on this surface was calculated to be 26 681 cm⁻¹, which is above the limit of the spectrum in Fig. 1, and therefore probably not optically accessible due to poor Franck–Condon overlap. The energy of the Renner–Teller intersection, however was calculated to lie at 23 000 cm⁻¹, in remarkable agreement with the boundary between Regions 2 and 3.

Conclusions

We have measured the ÖX̃ LIF excitation spectrum of jet-cooled CCl₂ from 17700–24000 cm⁻¹. Ninety dispersed fluorescence spectra were measured within this range. Analysis of the frequencies in the DF spectra have provided assignments of 68 vibrational levels in C³⁵Cl₂ and 47 in C³⁵Cl³⁷Cl, including the first gas phase measurement of ν^″₃ = 760 cm⁻¹. A full set of anharmonic constants was extracted for both isotopomers.

Analysis of the intensities in the DF spectra provided identification or characterisation of the emitting à vibronic state. Levels below about 20 000 cm⁻¹ (T₀₀ + 2300 cm⁻¹) can be assigned simply as combinations of ν^′₁ and ν^′₂. Excitation of levels between 20 000 and 22 600 cm⁻¹ result in DF spectra that cannot be assigned in the Franck–Condon limit and show evidence of increasing Fermi resonance. Levels above 22 600 cm⁻¹ show a collapsed rotational structure in the LIF spectrum, with only transitions terminating in K^′_a = 0 rotational states evident in the spectrum. This places the energy of the Renner–Teller intersection between the X̃ and à states at about 22 600 cm⁻¹, in excellent agreement with a previous theoretical calculation of 23 000 cm⁻¹.

Acknowledgements

This research was supported by an Australian Research Council Discovery grant. CAR and JSG gratefully acknowledge PhD stipends from an Australian Post-graduate Award and a University of Sydney, School of Chemistry Research Scholarship, respectively. KN acknowledges an ARC Post-doctoral Fellowship. All of us thank Dr George Bacskay and Dr Timothy Schmidt for stimulating discussions about various aspects of this work.

References

1. T. J. Sears, P. R. Bunker and A. R. W. McKellar, J. Chem. Phys., 1982, 77, 5363.
2. W. H. Green Jr., N. C. Handy, P. J. Knowles and S. Carter, J. Chem. Phys., 1991, 94, 118.
3. K. K. Murray, D. G. Leopold, T. M. Miller and W. C. Lineberger, J. Chem. Phys., 1988, 89, 5442.
4. S. Koda, Chem. Phys. Lett., 1978, 55, 353.
5. K. Sendt and G. B. Bacskay, J. Chem. Phys., 2000, 112, 2227.
6. D. S. King, P. K. Schenck and J. C. Stephenson, J. Mol. Spectrosc., 1979, 78, 1.
7. C. W. Mathews, Can. J. Phys., 1967, 45, 2355.
8. K. Sendt, E. Ikeda, G. B. Bacskay and J. C. Mackie, J. Phys. Chem. A, 1999, 103, 1054.
9. M. Martoprawiro, G. B. Bacskay and J. C. Mackie, J. Phys. Chem., 1999, 103, 3923.
10. R. E. Rebbert and P. J. Ausloos, J. Photochem., 1975, 4, 419.
11. M. J. Molina and F. S. Rowland, Nature, 1974, 249, 810.
12. W. Hack, M. Wagner and K. Hoyermann, J. Phys. Chem., 1995, 99, 10847.
13. B. T. Beiderhase, K. Hoyermann and W. Hack, Z. Phys. Chem., 2000, 214, 95.
14. W. Hack, B. Wagner and K. Hoyermann, Z. Phys. Chem., 2000, 214, 741.
15. T. W. Schmidt, G. B. Bacskay and S. H. Kable, Chem. Phys. Lett., 1998, 292, 80.
16. T. W. Schmidt, G. B. Backsay and S. H. Kable, J. Chem. Phys., 1999, 110, 11277.
17. B.-C. Chang, M. L. Costen, A. J. Marr, G. Ritchie, G. E. Hall and T. J. Sears, J. Mol. Spec., 2000, 202, 131.
18. H.-G. Yu, J. T. Muckerman and T. J. Sears, J. Chem. Phys., 2002, 116, 1435.
19. P. T. Knepp and S. H. Kable, J. Chem. Phys., 1999, 110, 11789.
20. J. S. Guss, O. Votava and S. H. Kable, J. Chem. Phys., 2001, 115, 11118.
21. D. E. Milligan and M. E. Jacox, J. Chem. Phys., 1967, 47, 703.
22. L. Andrews, J. Chem. Phys., 1968, 48, 979.
23. M. E. Jacox and D. E. Milligan, J. Chem. Phys., 1970, 53, 2688.
24. H. Fan, I. Ionescu, C. Annesley, J. Cummins, M. Bowers, J. Xin and S. A. Reid, Chem. Phys. Lett., 2004, 378, 548.
25. A. K. Maltsev, O. M. Nefedov, R. H. Hauge, J. L. Margrave and D. Seyferth, J. Phys. Chem., 1971, 75, 3984.
26. D. E. Tevault and L. Andrews, J. Mol. Spec., 1975, 54, 110.
27. V. E. Bondybey, J. Mol. Spectrosc., 1977, 64, 180.
28. J. S. Shirk, J. Chem. Phys., 1971, 55, 3608.
29. R. E. Huie, N. J. T. Long and B. A. Thrush, Chem. Phys. Lett., 1977, 51, 197.
30. J. J. Tiee, F. B. Wampler and W. W. Rice, Chem. Phys. Lett., 1979, 65, 425.
31. D. A. Predmore, A. M. Murray and M. D. Harmony, Chem. Phys. Lett., 1984, 110, 173.
32. J.-I. Choe, S. R. Tanner and M. D. Harmony, J. Mol. Spectrosc., 1989, 138, 319.
33. D. J. Clouthier and J. Karloczak, J. Phys. Chem., 1989, 93, 7542.
34. Q. Lu, Y. Chen, D. Wang, Y. Zhang, S. Yu, C. Chen, M. Koshi, H. Matsui, S. Koda and X. Ma, Chem. Phys. Lett., 1991, 178, 517.
35. D. J. Clouthier and J. Karolczak, J. Chem. Phys., 1991, 94, 1.
36. Y.-D. Gao, C.-J. Hu, R. Qin, C. Yang and C.-X. Chen, Acta Phys.-Chim. Sin., 2002, 18, 112.
37. M. L. Liu, C. L. Lee, A. Bezant, G. Tarczay, R. J. Clark, T. A. Miller and B. C. Chang, Phys. Chem. Chem. Phys., 2003, 5, 1352.
38. C. W. Bauschlicher Jr., H. F. Schaefer III and P. S. Bagus, J. Am. Chem. Soc., 1977, 99, 7106.
39. M. T. Nguyen, M. C. Kerins, F. Hegarty and N. J. Fitzpatrick, Chem. Phys. Lett., 1985, 117, 295.
40. G. L. Gutsev and T. Ziegler, J. Phys. Chem., 1991, 95, 7220.
41. K. K. Irikura, W. A. Goddard III and J. L. Beauchamp, J. Am. Chem. Soc., 1992, 114, 48.
42. N. Russo, E. Sicillia and M. Toscano, J. Chem. Phys., 1992, 97, 5031.
43. Z.-L. Cai, X.-G. Zhang and X.-Y. Way, Chem. Phys. Lett., 1993, 210, 481.
44. M. Born, S. Ingemann and N. M. M. Nibbering, J. Am. Chem. Soc., 1994, 116, 7210.
45. J. Demaison, L. Margules, J. M. L. Martin and J. E. Boggs, Phys. Chem. Chem. Phys., 2002, 4, 3282.
46. M. R. Cameron and S. H. Kable, Rev. Sci. Instrum., 1996, 67, 283.
47. H. E. Fujitake M., J. Chem. Phys., 1989, 91, 3426.
48. G. Herzberg, Molecular Spectra and Molecular Structure III. Electronic spectra of polyatomic molecules, Van Nostrand, New York, 1966, vol. 3.
49. J. R. Henderson, M. Muramoto and R. A. Willett, J. Chem. Phys., 1964, 41, 580.

---