Activity of surface active substances determined from their surface excess
Gunther
Andersson
*a,
Thomas
Krebs
b and
Harald
Morgner
b
aWilhelm-Ostwald Institute for Physical and Theoretical Chemistry, Leipzig University, Linnéstr. 2, 04103 Leipzig, Germany. E-mail: g.andersson@rz.uni-leipzig.de; Fax: +49-342-9736090
bWilhelm-Ostwald Institute for Physical and Theoretical Chemistry, Leipzig University, Linnéstr. 3, 04103 Leipzig, Germany
First published on 25th November 2004
Abstract
Commonly, the surface excess is determined from surface tension measurements via the Gibbs equation. This equation relates the activity (chemical potential), the surface excess, and the surface tension. When knowing two out of the three quantities, the third one can be calculated. Unfortunately, in the case of surface active components the concentration is in most cases too low to determine the activity from a measurable change in the bulk properties and thus assumptions are made about the activity coefficients. However, if the surface excess is measured directly and the surface tension is known, the activity can be determined making use of the Gibbs equation. The surface excess is the quantity of a surfactant solution which changes most strongly with the concentration. Thus it is obvious that this procedure should be used to determine activity coefficients of surfactants. One of the few techniques for determining the surface excess directly is neutral impact collision ion scattering spectroscopy (NICISS). With NICISS concentration depth profiles can be measured in the surface near region with a depth resolution of a few angströms. The surface excess and the activities are investigated here for the system tetrabutylphosphonium bromide (Bu4PBr) dissolved in the polar solvent formamide.
Introduction
In the case of solutions or mixtures of liquids the surface composition is different than that of the bulk and is characterized by the surface excess. Commonly, the surface excess is determined from a thermodynamic relation. The Gibbs equation provides the relation between the activity (chemical potential), the surface excess and the surface tension. Knowing two out of the three quantities allows the third one to be calculated. For example, if the surface tension is measured and the activity is known the excess can be determined. The surface tension is a macroscopic quantity that can be measured with a great variety of methods. The determination of the activity is a basic task in physical chemistry. Activities are determined from the variation of bulk properties as function of the composition. Common methods are measurement of lowering the freezing point (cryoscopy) and those that rely on changes of the vapor pressure, such as the increase of the boiling point or the isopiestic method. However, in the case of surface active components, their bulk concentration is in most cases too low to cause a measurable change in the bulk properties. Thus, either the activity coefficient is assumed to be constant,1–6 or is calculated in the case of ionic surfactants from the Debye–Hückel limiting law.1 The assumption that the activity coefficient is constant is especially not fulfilled close to the critical micelle concentration (c.m.c.), since the interaction of the surfactant molecules cannot be ignored at concentrations lower but close to the c.m.c.7 due to the fact that the aggregation of the molecules is due to their interaction. The use of the Debye–Hückel limiting law for the calculation of the activities of large molecules like surfactants suffer from the shortcoming that only the electrostatic interaction is considered and that the ions are treated as point charges which is oversimplistic, especially for larger molecules.One of the experimental methods used to directly determine the surface excess, i.e. without using a thermodynamic relation like the Gibbs equation, is neutron reflectivity (NR).8–12 The goal of these investigations is to compare the surface excess determined via the Gibbs equation with that determined directly with NR. The results reported are varying. Eastoe et al.10 found that NR and the Gibbs equation analysis of the surface tension of different anionic surfactants in water yield the same surface excess. However, An et al.9 and Downer et al.12 found that NR studies of aqueous solutions of perfluorooctanoate and perfluorononanoate yield an excess which is lower by more or less a constant factor unlike that determined via the Gibbs equation. In all these cases the activity was calculated with the Debye–Hückel limiting law. Li et al.11 also found in solutions with cationic gemini surfactants a discrepancy between the results of both methods when they used concentrations instead of activities for the calculation.
Another method used to determine the amount of adsorbed surfactants at the liquid–vapor interface are nonlinear optical methods (NLO). Motschmann et al. and Bae et al. investigated with second harmonic generation (SHG)13,14 the surface of 1-alcyl-4-dimethylaminopyridinium bromide solutions in water. The SHG signal of the C12 compound was calibrated with that of the C20 and C22 surfactant, which in contrast to the C12 compound are insoluble in water. The amount of the C12 surfactant determined with this method at the surface is only 64% of the excess determined with the Gibbs equation.
The deviations between the amounts of adsorbed surfactants determined with NR or NLO and the Gibbs equation is explained in some cases by the assumption that the ionic surfactants might not be dissociated fully at the surface. It is argued that undissociated species at the surfaces have to be treated in the thermodynamic relation (Gibbs equation) as one species and not as separated ions, i.e. 2 species for a 1 : 1 electrolyte, and thus the Gibbs equation would have to be modified.13,14 Other explanations for the discrepancy are cationic impurities in the case of anionic surfactants12,15 or the limited depth range of the method so that molecules adsorbed at the surface in deeper layers might not be seen by the method used.9,11 In the latter case the fact that fewer molecules are detected with NR than determined via the Gibbs equation is attributed to counter ions which are adsorbed in deeper layers, although this would result in a very large surface energy that is not observed. From the difference between these results a degree of dissociation of the ionic surfactant is computed.
The aim of this paper is to show how the thermodynamic properties surface excess and activity can be determined with the experimental method neutral impact collision ion scattering spectroscopy (NICISS). NICISS is used to determine for all species the concentration depth profiles and thus their surface excesses. It is shown that knowing the surface tension and the surface excess the activity can be determined using the Gibbs equation. This procedure is especially important for surfactants because the surface excess is a quantity which changes strongly upon changing the surfactant concentration. In the case of surfactants the surface excess and the Gibbs equation provide a surprisingly powerful tool to determine activities and activity coefficients.
We show how this procedure can be applied by investigating solutions of the surface active compound tetrabutylphosphonium bromide (Bu4PBr) in the polar solvent formamide. The concentration of Bu4PBr is sufficiently great that for this surfactant solution even a change in the bulk properties can be measured and thus activities can also be determined the usual way.
Further we carry out potential measurements (EMF). The hope was that the activity can be measured with a second method independently and the results can be compared. Nevertheless, determining activity coefficients by measurements of the cell potentials suffer from the uncertainty of whether not only the Volta potential but also the surface potential of the electrode change by changing the concentration of the solute. A second shortcoming could be caused by the fact that it cannot be controlled, whether the activity of the electrode is constant or not. The latter is eventually the case for the polymer electrode used. Both shortcomings cannot be circumvented. Their influence can be estimated by measuring cell potentials not only of solutions of Bu4PBr in formamide but also of tetrabutylammonium bromide (Bu4NBr) in water and comparing the activity coefficients determined from the latter system with data from literature.
Theory
Gibbs equation
The change of the surface tension at constant temperature is given by the Gibbs adsorption isotherm16 | (1) |
| Γjxi − Γixj = const. | (2) |
 | (3) |
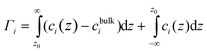 | (4) |
| Γexcesssolute = Γsolute | (5) |
 | ||
| Fig. 1 Schematic illustration of the concept of the Gibbs dividing plane according to Adamson.16 The position of the Gibbs dividing plane is chosen in a way that Γexcesssolute is equal to zero, i.e. the areas left and right of the Gibbs dividing plane marked with solid lines are equal. Γexcesssolute is the difference between the areas marked by dashed lines right and left of the Gibbs dividing plane. | ||
For a solution with a 1 : 1 electrolyte the chemical potential of the solute is defined as
 | (6) |
 | (7) |
 | (8) |
Cell potential
The dependence of the potential of an electrode on the concentration of a solute is given by the Nernst equation. For a 1 : 1 electrolyte the difference in the potentials is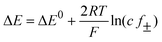 | (9) |
Experimental
Materials
We have investigated 0.01 to 1.5 molal solutions of Bu4PBr in formamide. Formamide was chosen as solvent due to two reasons: first it has a low vapour pressure (6 × 10−3 mbar at 6 °C) and can be handled in vacuum; and second it is a polar solvent with high surface tension. Bu4PBr was purchased from Merck with a purity >99%. The substance was used after purification by recrystallization in toluene, which was purchased from Lancaster. Purification by recrystallization was necessary since the impurity Bu4PO had to be removed. The supplier for the toluene had to be chosen carefully in order to exclude contamination of the Bu4PBr during the purification with the impurity surfactant siloxane. Siloxane is commonly used to tighten glass tubes during the fabrication of chemicals.NICISS
We have previously investigated the surfaces of several pure liquids and surfactant solutions with neutral impact collision ion scattering spectroscopy (NICISS).17,18,20 The method is used to determine elemental concentration depth profiles up to a depth of 200 Å with a depth resolution far below 10 Å.17,18 The details are described elsewhere.17 The target is bombarded with a pulsed beam of inert gas ions—mostly helium ions—with a kinetic energy of several keV. The energy of the projectiles back scattered from the atoms in the target is determined by their time of flight (TOF) from the target to the detector. The projectiles lose energy during the back scattering process, and the extent of energy transfer depends on the mass of the target atom. Additionally, the projectiles lose energy on their trajectory through the bulk, with a magnitude proportional to the depth of the target atom. The energy loss in the bulk is calibrated with self assembled monolayers of alkanethiolates on gold and silver single crystals.19 The depth that can be investigated with this method is limited by the broadening of the beam in the bulk due to low angle scattering. At an energy of 5 keV the maximum depth which can be investigated, is about 300 Å. The dose of the He ions for this investigation was about 1010 ions cm−2. Thus damage of the surface and the influence of the impinging ions on the surface structure can be neglected.The liquid surface is generated as a liquid film with a thickness of several tenths of a millimeter on a rotating disk, which is partially immersed into a reservoir filled with the investigated liquid. After emerging from the reservoir the disk passes by a skimmer. At this position a fresh surface is created.
Surface tension
The surface tension was measured with a Wilhelmy plate (Krüss K12). The measurements were carried out at a thermostated liquid at a temperature of 6 ± 0.1 °C in a dry nitrogen atmosphere in order to exclude condensation of moisture. The reproducibility of the measurements is 0.1 mN m−1.Cell potential
Cell potentials of solution of Bu4PBr in water and formamide were determined with an electrode of potassium–tetraphenylchloroborate in a poly(vinylchloride) matrix and a silver bromide electrode. The sensitivity of the electrode is due to the specific interaction of the Bu4PBr with the potassium–tetraphenylchloroborate and its surface morphology. The measurements were carried out at 20 °C in the case of water as solvent and at 6 °C in the case of formamide as solvent. For each concentration the potential was determined at which no current flow could be observed. The time needed to establish the equilibrium in the cell was up to 1 h.Results
NICISS
The NICIS spectra of the Bu4PBr solutions using helium ions with a kinetic energy of 3 keV as projectiles are given in Fig. 2. A detailed description of the nature of the NICIS spectra is given elsewhere.17 In general, the spectra consist of a broad distribution of sputtered hydrogen, which has its onset at about 2.5 μs, and steps for each element in the target which are due to the helium projectiles back scattered from the different elements of the target except for hydrogen. The onset of each step is determined by the mass of the detected element. The TOF of the onset of a step decreases with increasing mass of the element. | ||
| Fig. 2 NICIS spectra of the Bu4PBr solutions at different concentrations. The onset of the steps with respect to the elements oxygen (O), nitrogen (N), carbon (C), phosphorous (P) and bromine (Br) are indicated with vertical bars. | ||
Since we have improved the procedure used to extract the concentration depth profiles from the NICIS spectra, we provide details here. In order to obtain the concentration depth profiles of solute and solvent, the spectra have to be decomposed into contributions of the sputtered hydrogen and the steps due to the depth profiles of all elements. The procedure is based on two basic assumptions. First, the background of the sputtered hydrogen is a smooth curve. This is evident from the spectra of alkanes, which show only one step and before and after the onset of the carbon step a smooth distribution. Upon adding the solute the distribution of the sputtered hydrogen remains smooth. As long as the concentration of heavy elements is small, the shape of the recoil hydrogen distribution does not change and can be used for the evaluation of the spectra of the solutions. Second, the shape of each step is determined only by the depth profile of the desired element apart from the cross section of the back scattered projectiles and the detector sensitivity.
In the first step of the procedure, we calculate the steps for all elements according to their bulk concentration. The steps are subtracted from the measured spectra and the only free parameter is the intensity ratio between the sputtered hydrogen and the backscattered helium projectiles, i.e. the steps in the spectra.
| Isteps = Ispectrum − aIbackground | (10) |
 | (11) |
 | ||
| Fig. 3 The background of the sputtered hydrogen is determined by subtracting a step corresponding to the bulk concentration of oxygen from the NICIS spectrum. The intensity ratio between back scattered helium (step) and sputtered hydrogen is determined so that the distribution remaining after subtracting is a smooth curve, i.e. does not show a step. The intensity of a step in the TOF spectra of an element with a constant concentration depth profile decreases with increasing TOF due to the non-linearity between depth and TOF. | ||
 | ||
| Fig. 4 The background of the sputtered hydrogen is determined by subtracting steps corresponding to the bulk concentration of phosphorus and bromine from the NICIS spectrum. The intensity ratio between back scattered helium (steps) and sputtered hydrogen is determined so that the distribution remaining after subtracting (crosses) fits to that of the spectrum of pure formamide (solid line). | ||
The concentration depth profile of the pure solvent is shown in Fig. 5. The concentration depth profiles of cation and anion of the 0.2 molal solution are shown in Fig. 6. The shape of the onsets is a consequence of the distribution of the desired element at the surface and the experimental resolution of the method. The depth profiles could be deconvoluted, as shown in ref. 18. Since deconvolution does not affect the evaluation of the surface excess, deconvolution is not carried out here. The amount of adsorbed cation and anion is the same within the statistical error of the measurement. This is expected since an unbalanced charge distribution would result in a huge increase in surface energy. The observation of an equal amount of adsorbed bromine and phosphorus containing species is also important with respect to the cleanliness of the surface. If not purified solute was used we found that the excess of the phosphorus containing species was greater than that of bromine, which could be attributed to the contamination of the solute with the surface active impurity Bu4PO. The purification of the solute by recrystallisation in toluene introduced in some cases siloxane as a further impurity.
 | ||
| Fig. 5 Concentration depth profile of formamide (represented by oxygen) of the pure solvent and the Gibbs dividing plane. The depth profile of the oxygen is broadened due to the NICISS method and the reasons are known quantitatively.17 The depth profiles could be deconvoluted. Since in this case we would not gain additional information the deconvolution is not carried out. | ||
 | ||
| Fig. 6 Depth profiles of the cation Bu4P+ and the anion Br−. The depth profiles overlap within the statistics of the measurements. Thus the amount of adsorbed cation and anion is the same. | ||
The depth profiles of solvent and solute together with the Gibbs dividing plane are shown in Fig. 7. The position of the Gibbs dividing plane was determined using (4) with Γsolvent = 0. For the 0.2 molal solution this is shown schematically in Fig. 7a. The position is chosen so that the area marked with solid lines and that marked with crossed lines are equal. The surface excess of anion and cation was derived from the depth profiles with (4) and is marked in Fig. 7b with solid lines. The excess is shown in Fig. 8 and is the same for cation and anion within the error bars. The activity is calculated using (8) with the excess of the bromine, since its error bars are smaller than those of the cation. The activity at the lowest concentration of 0.01 molal is set equal to the concentration, i.e. the activity coefficient at that concentration is set equal to unity. The activity coefficients are shown in Fig. 9. They drop from unity to 0.18 ± 0.03 at the highest concentration of 1.5 molal.
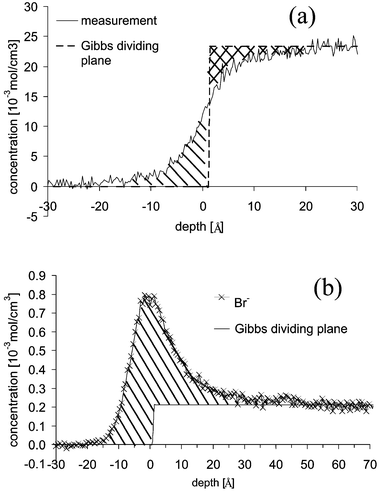 | ||
| Fig. 7 Depth profile of the solvent (a) and solute (b) with the Gibbs dividing plane of the 0.2 molal solution. | ||
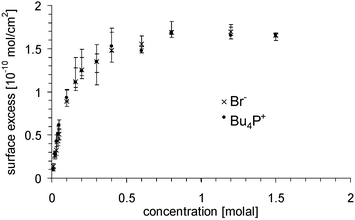 | ||
| Fig. 8 Surface excess of the cation Bu4P+ (filled circles) and the anion Br− (crosses) as a function of the bulk concentration. | ||
 | ||
| Fig. 9 Surface tension (a) and activity of the solute Bu4PBr in formamide (b) as determined from the surface excess from Fig. 8 and (8). | ||
Cell potential
In order to estimate whether cell potential measurements using the potassium tetraphenylchloroborate electrode can be used to determine activity coefficients, we investigated first solutions of Bu4NBr in water with concentrations from 0.2 × 10−3 to 0.8 molal. The measured cell potentials are shown in Fig. 10. The data points for the concentrations from 0.2 to 7 × 10−3 molal lie on a straight line within the error bars. Thus it may be assumed that the activity for these concentrations is constant and a straight line can be fitted to these data points. The gradient was found to be 49.4 ± 1.2 mV. It is known that the gradient for polymer electrodes might be slightly different from that for inorganic electrodes, although the reasons for that are not fully known. The activity coefficients are determined using (9) from the difference of the cell potential in the case of a constant activity coefficient (straight line) and the measured potentials. The error of the activity coefficients determined by the EMF measurements shown in Fig. 10b is mainly due to the uncertainty with which the gradient of the straight line can be determined. The activity coefficients are gauged so that data points lying on the straight line are unity. For comparison, activity coefficients determined from isopiestic measurements21 are also shown in Fig. 10b. | ||
| Fig. 10 Cell potential of Bu4NBr solutions in water (a) and activity coefficients (b) determined by the measurement of the cell potential (open circles) and from isopiestic measurements (crosses).21 The data points marked with crosses in (a) (0.2 to 7 × 10−3 molal) are lying on a straight line within the error bars. Thus, it may be assumed that the activity coefficient for these concentrations is constant and a straight line can be fitted to these data points. The error of the activity determined by these EMF measurements shown in (b) is mainly due to the uncertainty with which the gradient of the straight line can be determined. | ||
Measurements of the cell potentials of Bu4PBr solutions in formamide for concentrations from 1.8 × 10−3 to 1.3 molal are shown in Fig. 11. The data points for concentrations from 1.8 to 7 × 10−3 molal are lie on a straight line within the error bars. The activity coefficients are determined in the same way as for the solutions in water. At a concentration of 0.01 molal, which is the lowest concentration investigated using NICISS, the activity coefficients determined with NICISS and with the cell potential are the same and thus no further gauging of the activity coefficients has to be applied for comparing the results of each method.
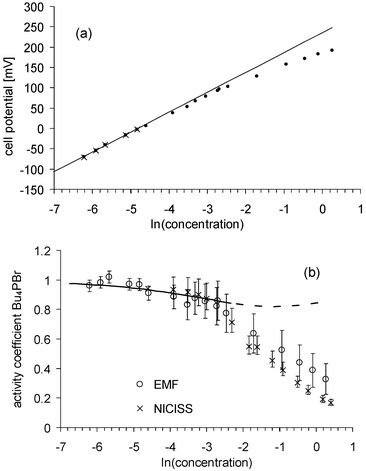 | ||
| Fig. 11 Cell potential of Bu4PBr solutions in formamide (a) and activity coefficients (b) determined by the measurement of the cell potential (open circles). For comparison, the activity coefficients determined from the NICIS measurements (crosses) are also shown. The data points marked with crosses in (a) (1.8 to 7 × 10−3 molal) are lying on a straight line within the error bars. Thus, it may be assumed that the activity for these concentrations is constant and a straight line can be fitted to these data points. The error of the activity determined by these EMF measurements shown in (b) is mainly due to the uncertainty with which the gradient of the straight line can be determined. The solid line represents the activity coefficients calculated by the extended Debye–Hückel theory. The extension of the calculation to concentrations greater than 0.1 molal is shown as a dashed line. | ||
Discussion
We have shown that the surface excess of solutions can be determined from concentration depth profiles measured with NICISS. Using the Gibbs equation, the activities can be evaluated. Since this method for determining the activity is new, we have to discuss both its accuracy and whether the results can be validated with established methods. Established methods in general make use of a measurable change in the bulk properties of the solution. Solutions of Bu4PBr in formamide are in this respect a suitable system since the solute is both surface active and the concentration is sufficiently high that a measurable change in the bulk properties of the solution occurs.The accuracy of the surface excess determined from the concentration depth profiles measured with NICISS is mainly given by the accuracy with which the background of the sputtered hydrogen can be determined. The uncertainty of the cross section, the detector sensitivity, the gauging of the depth scale, and the statistics are of minor importance. The error bars in all graphs concerning results using the NICISS measurements take all these uncertainties into account.
The error of the activity coefficients determined from the cell potential measurements is caused mainly by the accuracy with which the straight line representing the potentials with constant activity coefficients can be fitted to the measurements. Both the selection of the data points used for the fit and the accuracy of the cell potential measurement determine the accuracy. The error bars of the activity coefficients are calculated taking into account these uncertainties. Additionally, the cell potentials could be influenced by two other factors. First, the activity of the polymer electrode itself could change upon changing the concentration of the Bu4PBr solution. At the polymer electrode there is an exchange of ions. When Bu4P+ adsorbs to the polymer electrode, K+ desorbs. If the number of sites where the Bu4P+ is able to adsorb is significantly reduced, the activity of the polymer electrode itself might not be constant. Second, the potential between the solution and the polymer electrode is the Galvani potential which is the sum of the Volta potential and the surface potential. For the electrochemical potential and thus for the electrochemical force needed to transfer a charged particle from the solution to the electrode only the Volta potential is important. Unfortunately, only the sum of both can be measured. In the case when the surface potential changes with the concentration of the solution, e.g. by the occurrence or the change of dipoles at the surface of the electrode by reorientation of the solvent molecules, the measured potential, i.e. the Galvani potential, would change differently from the Volta potential. Both factors possibly influencing the cell potentials can not be separated. Moreover, the reliability of the cell potential measurements suffers from the fact that the gradient of the cell potential at low concentrations is lower for the polymer electrode than the theoretical value of 55.4 mV at 6 °C. This discrepancy can not be explained.
In order to estimate whether these effects influence the measurements we also measured the potentials of Bu4NBr solutions in water (see Fig. 10). Comparison of the activity coefficients with those measured isopiestically21 show good agreement. This shows that the response of the electrode in aqueous solutions is linear to the Bu4N+ ions most likely due to the specific interaction of the Bu4N+ ions to the electrode. Nevertheless, it cannot be excluded that using formamide as solvent the polymer electrode could react differently with respect to the two mentioned sources for uncertainties. Actually, we are not able to prove this influence, and thus the measurements of the cell potential can be used only to estimate whether there is a contradiction with the results determined with NICISS concerning the general trend but not for a severe comparison.
The activities determined with the cell potential and with NICISS are the same within the error bars up to a concentration of 0.6 molal. At 1.3 molal they differ by about 50%. In the case that the difference between the activity coefficients is due to the first reason, the activity of the polymer electrode itself would change up to 50% at a concentration of 1.3 molal. If the difference is due to the second reason the surface potential of the polymer electrode would increase up to 28 mV at a concentration of 1.3 molal.
In order to validate the activity coefficients determined by NICISS, we tested further methods that also rely on changes of the bulk properties with changes in the concentration of the solute. Unfortunately all other tested methods failed. Cryoscopy (measurement of the freezing point) cannot be used since we found in the solid phase solute up to several tens of percent of the concentration in the liquid phase. Thus the requirements for using this method are not met. All methods which make use of the change of the vapor pressure, e.g. isopiestic etc., cannot be used since the vapor pressure of the solvent is too low. Measuring the increase of the boiling point is not suitable, since both the boiling point of 216 °C is too far away from that used for the NICISS investigations and the solute is not stable above 50 °C.
For calculations of the activity coefficients of ionic surfactants the Debye–Hückel limiting law is often used.8–12 In Fig. 11 activity coefficients calculated with the extended Debye–Hückel law are shown assuming the minimum distance between the ions as 10 Å, which was calculated from the sum of the ion radii. It is commonly assumed that the Debye–Hückel limiting law is valid only up to concentrations of 0.01 molal and the extended Debye–Hückel law up to concentrations of 0.1 molal. The calculated activity coefficients are the same within the error bars as both those determined from cell potential measurements and NICISS, but the slope of the curve is different. This discrepancy nearly does not change if the minimum distance between the ions—the only parameter which can be varied—is changed between 5 and 20 Å, which are reasonable boundaries. A shortcoming for the Debye–Hückel theory is that the charges are treated as point charges and that the activity coefficients of greater ions, as it is the case for ionic surfactants, are not calculated correctly.
Conclusions
We show that from concentration depth profiles measured with NICISS the surface excess can be determined. Surface tension measurements then yield the activity of the surfactant via the Gibbs equation. The surface excess as a function of the concentration, as shown in Fig. 8, is the adsorption isotherm. The surface excess of Bu4PBr in formamide as polar solvent reaches its maximum with a value of (1.7 ± 0.06) × 10−10 mol cm−2 at the concentration of about 0.8 molal. The activity coefficient drops to 0.18 if the activity coefficient at dilute solutions is set to 1. The activity coefficients determined with NICISS show deviations from those determined by measurements of the cell potentials. It could not be clarified whether two of the requirements which have to be made using the cell potential measurements (constant activity of the electrode and constant surface potential) are met. Thus we classify the activity coefficients determined with NICISS as more reliable than those determined by cell potential measurements. The general trend of the activity coefficients is similar for both methods.The activity coefficients calculated with the extended Debye–Hückel theory are for concentrations less than 0.1 molal within the error bars of both experimental methods but the gradient of the curve is different. We attribute this deviation to the shortcoming in the theory, which treats the charges only as point charges, which is in general not the case for large molecules like surfactants.
We wish to emphasize here that activity coefficients should be determined from phenomena that yield for the desired system the most significant change of a measurable parameter. In the case of surfactants this is without doubt the surface excess. Our method to determine activity coefficients is thus suitable in general for solutions with surfactants as solutes. The method should also be suitable for non-ionic surfactants. Especially here the assumption that the activity coefficients were constant up to the respective c.m.c. cannot be expected to be fulfilled since the interaction of the surfactant molecules in the bulk is the cause for aggregation and, thus, plays a role even at concentrations lower than the c.m.c. but close to it.7
Experimental results reported in the literature seem to show in several cases a discrepancy between surface excess determined directly and via the Gibbs equation.
Our experimental results do not show a discrepancy with the Gibbs equation. In our opinion, there is no reason to modify the Gibbs equation from a thermodynamic point of view.
Acknowledgements
We are grateful to Mrs Alexeeva and Mr Grekovitsch for providing us with the polymer electrodes, and to Mrs Kirmse for the surface tension measurements.References
- A. J. Prosser and E. I. Franes, Colloids Surf., 2001, A 178, 1 Search PubMed.
- V. B. Fainerman, S. A. Zholob, E. H. Lucassen-Reynders and R. Miller, J. Colloid Interface Sci., 2003, 261, 180 CrossRef CAS.
- R. P. Borwankar and D. T. Wasan, Chem. Eng. Sci., 1988, 43, 1323 CrossRef CAS.
- B. Janczuk, M. L. González-Martin, J. M. Bruque and C. Dorado-Calasanz, Colloids Surf., 1998, A137, 15 Search PubMed.
- V. B. Fainerman, R. Miller and H. Möhwald, J. Phys. Chem., 2002, B106, 809 Search PubMed.
- V. B. Fainerman, E. H. Lucassen-Reynders and R. Miller, Colloids Surf., 1998, A143, 141 Search PubMed.
- R. Strey, Y. Viisanen, M. Aratono, J. P. Kratohvil, Q. Yin and S. Friberg, J. Phys. Chem., 1999, B103, 9112 Search PubMed.
- J. Penfold, R. K. Thomas, J. R. Lu, E. Staples, I. Tucker and L. Thompson, Pysica B (Amsterdam), 1994, B198, 110 Search PubMed.
- S. W. An, J. R. Lu, R. K. Thomas and J. Penfold, Langmuir, 1996, 12, 2446 CrossRef CAS.
- J. Eastoe, S. Nave, A. Downer, A. Paul, A. Rankin, K. Tribe and J. Penfold, Langmuir, 2000, 16, 4511 CrossRef CAS.
- Z. X. Li, C. C. Dong and R. K. Thomas, Langmuir, 1999, 15, 4392 CrossRef CAS.
- A. Downer, J. Eastoe, A. R. Pitt, J. Penfold and R. K. Heenan, Colloids Surf., 1999, A156, 33 Search PubMed.
- H. Motschmann, R. Teppner, S. Bae, K. Haage and D. Wantke, Colloid Polym. Sci., 2000, 278, 425 Search PubMed.
- S. Bae, K. Haage, D. Wantke and H. Motschmann, J. Phys Chem., 1999, B103, 1045 Search PubMed.
- J. Eastoe, S. Nave, A. Downer, A. Paul, A. Rankin, K. Tribe and J. Penfold, Langmuir, 2000, 16, 4511 CrossRef CAS.
- A. W. Adamson and A. P. Gast, in Physical Chemistry of Surfaces, John Wiley & Sons, New York, 6th edn., 1997, p. 71 Search PubMed.
- G. Andersson and H. Morgner, Surf. Sci., 1998, 405, 138 CrossRef CAS.
- G. Andersson and H. Morgner, Surf. Sci., 2000, 445, 89 CrossRef CAS.
- G. Andersson and H. Morgner, Nucl. Instrum. Methods, 1999, B155, 357 Search PubMed.
- G. Andersson, H. Morgner and K.-D. Schulze, Nucl. Instrum. Methods, 2002, B190, 222 Search PubMed.
- S. Lindenbaum and G. E. Boyd, J. Phys. Chem., 1964, 68, 911 CAS.
| This journal is © the Owner Societies 2005 |
