Tetrathiafulvalene–phosphine-based iron and ruthenium carbonyl complexes: Electrochemical and EPR studies

Abstract

The radical cation of the redox active ligand 3,4-dimethyl-3′,4′-bis-(diphenylphosphino)-tetrathiafulvalene (P2) has been chemically and electrochemically generated and studied by EPR spectroscopy. Consistent with DFT calculations, the observed hyperfine structure (septet due to the two methyl groups) indicates a strong delocalization of the unpaired electron on the central S₂C=CS₂ part of the tetrathiafulvalene (TTF) moiety and zero spin densities on the phosphine groups. In contrast with the ruthenium(0) carbonyl complexes of P2 whose one-electron oxidation directly leads to decomplexation and produces P2˙⁺, one-electron oxidation of [Fe(P2)(CO)₃] gives rise to the metal-centered oxidation species [Fe^(I)(P2)(CO)₃], characterized by a coupling with two ³¹P nuclei and a rather large g-anisotropy. The stability of this complex is however modest and, after some minutes, the species resulting from the scission of a P–Fe bond is detected. Moreover, in presence of free ligand, [Fe^(I)(P2)(CO)₃] reacts to give the complex [Fe^(I)(P2)₂(CO)] containing two TTF fragments. The two-electron oxidation of [Fe(P2)(CO)₃] leads to decomplexation and to the P2˙⁺ spectrum. Besides EPR spectroscopy, cyclic voltammetry as well as FTIR spectroelectrochemistry are used in order to explain the behaviour of [Fe(P2)(CO)₃] upon oxidation. This behaviour notably differs from that of the Ru(0) counterpart. This difference is tentatively rationalized on the basis of structural arguments.

---

1. Introduction

Tetrathiafulvalene (TTF) and its derivatives constitute a well-known class of redox active compounds extensively studied in the search for molecular conductors and superconductors.^1–3 The functionalization of a TTF core with heteroatom-based ligands,^4–7 capable to coordinate a metallic center, has developed steadily during the past decade, since it offers interesting perspectives on the modulation of architecture and collective electronic properties of molecular solids,^7,8 but also on the spectroscopic studies in solution,⁹ with respect to the redox activity of the TTF based ligand, and eventually, to that of the coordinated metallic fragment. Among the different class of ligands, we have been particularly interested in chelating diphosphines,^10,11 because of their capacity to coordinate various metallic centers, and, especially, metal carbonyl fragments.¹² The latter have led very recently to the synthesis of the first radical cation salt of a TTF based phosphine metal complex with an interesting magnetic behavior in the solid state.¹³ In this case, the organometallic moiety was a Mo(CO)₄ fragment, whose oxidation occurs at much higher potentials than that of the TTF core. Nevertheless, the TTF oxidation influenced the electronic density of the metallic center, as deduced from infrared spectroscopy. Indeed, absorptions for carbonyl ligands were measured at higher frequencies for the oxidized complex than for the neutral one, a consequence of the weaker π-back donation in the former, related to the lower electronic density on the metallic center. Another interesting situation is that when the oxidation of the metal carbonyl fragment occurs before that of the TTF moiety. In this case, after generation of the paramagnetic metal-based species, access to the TTF based radical cation should be still possible, thus creating the opportunity of having a paramagnetic metallic center in the vicinity of an organic TTF based radical. Fe(CO)₃¹² and Ru(CO)₃¹⁴ fragments probably present the required properties. The first oxidation potential of the corresponding complexes are expected to be sufficiently cathodic, and, in the case of [Fe(L2)(CO)₃] (where L2 is a bidentate phosphorus ligand) it is known that oxidation in non-coordinating solvents (e.g. CH₂Cl₂) is a one-electron reversible process leading to the paramagnetic 17-electron species.^15,16

Due to the large atomic hyperfine constants¹⁷ of ³¹P, EPR is a very efficient method of determining the localization of the unpaired electron in the reduction or oxidation compounds of transition metal complexes of organophosphorus ligands.^18,19 We, therefore, decided to investigate by EPR the oxidation behavior of the iron and of the ruthenium complexes of the redox active chelating diphosphine 3,4-dimethyl-3′,4′-bis-(diphenylphosphino)-tetrathiafulvalene (P2).

It will be shown from the EPR spectra, that the behaviours of these two complexes, [Fe(P2)(CO)₃] and [Ru(P2)(CO)₃], are in fact quite different: whereas a single type of signal could be detected for the ruthenium complex, four different spectra could be observed for the iron compound. The main purpose of the present study is to identify the various paramagnetic intermediates formed from the iron complex and to determine their electronic structure. This identification could be achieved by combining the results obtained with several techniques: EPR, cyclic voltammetry, FTIR spectroelectrochemistry and DFT calculations. Finally, a comparison between the crystal structures of the neutral Ru and Fe complexes explains, in part, the differences observed in their oxidation processes.

2. Experimental section

2.1. General

P2 and [Fe(P2)(CO)₃] were prepared by published procedures.¹² Ru₃(CO)₁₂ was purchased from Acros and used as received. Nuclear magnetic resonance spectra were recorded on a Bruker Avance DRX 500 spectrometer operating at 500.04 MHz for ¹H, 125.75 MHz for ¹³C and 202.43 MHz for ³¹P. Chemical shifts are expressed in parts per million downfield from external TMS (¹H and ¹³C) and 85% H₃PO₄ (³¹P). Coupling constants J are expressed in Hz. The following abbreviations are used: s, singlet; m, multiplet, t, triplet, b, broad, v, virtual. Mass spectrometry was performed on an HP 5989A spectrometer in the EI mode, with ionization energy of 70 eV. Infrared spectroscopy was measured on a FTIR NICOLET 20 SXC spectrometer. Elemental analysis were performed by the “Service d’analyse du CNRS”, at Gif/Yvette, France.

2.2. Synthesis and characterization of [3,4-bis(diphenylphosphino)-3′,4′-dimethyl-tetrathiafulvalene][tricarbonyl]ruthenium, [Ru(P2)(CO)₃]

P2 (300 mg, 0.50 mmol) and Ru₃(CO)₁₂ (106 mg, 0.17 mmol) were weighed in the glove-box in a Schlenk tube, then toluene (15 ml) was added. The mixture was heated for a period of 3 h, at 80 °C, under magnetic stirring. The completeness of the reaction was checked by ³¹P NMR spectroscopy. After cooling down to room temperature, the red solution was filtered through celite on a glass frit and then the solvent was removed under vacuum. After extraction with hexane and removing the solvent on a rota-evaporator, an orange solid was recovered. Recrystallization in hexane yielded bright orange crystals of complex (180 mg, 46%). Anal. calcd. for C₃₅H₂₆O₃P₂S₄Ru˙(C₆H₁₄)_1/2 (found); C, 55.06 (55.21); H, 4.01 (3.98). IR (KBr, cm⁻¹): ν_CO 1920, 1934, 2011. ³¹P NMR (C₇D₈) δ 57.0. ¹H NMR (CDCl₃) δ 1.88 (s, 6H, CH₃), 7.45 (bs, 12H, H_meta, H_para), 7.62–7.66 (m, 8H, H_ortho). ¹³C NMR (C₇D₈) δ 12.9 (s, CH₃), 114.0 (s, S₂C=CS₂), 114.5 (s, S₂C=CS₂), 122.8 (s, CH₃C=), 129.0 (vt, X part of an ABX system, ∑J_CP = 10.2 Hz, C_meta), 130.6 (s, C_para), 132.7 (vt, X part of an ABX system, ∑J_CP = 13.6 Hz, C_ortho), 135.6 (vt, X part of an ABX system, ∑J_CP = 48.5 Hz, C_ipso), 150.7 (vt, X part of an ABX system, ∑J_CP = 78.0 Hz, PC=CP), 209.9 (t, ²J_CP = 22.9 Hz, CO). MS (EI) m/z (ion, rel. intensity) 786 (M, 1), 758 (M − CO, 13), 730 (M − 2CO, 30), 702 (M − 3CO, 90), 600 (M − Ru(CO)₃, 40).

2.3. X-Ray crystallography

Data were collected on a Stoe-IPDS imaging plate system. The structure of [Ru(P2)(CO)₃] was solved by direct methods (SHELXS) and refined (SHELXL-97)²⁰ by full-matrix least-squares methods. The complex crystallized as a hemi-hexane solvate located on an inversion center. Hydrogen atoms were introduced at calculated positions (riding model), included in structure factor calculations and not refined. All the heavy atoms, excepting those of the solvate, were refined anisotropically.

Details about data collection and solution refinement are given in Table 1.

Table 1 Crystallographic data for [Ru(P2)(CO)₃]·(C₆H₁₄)_1/2

	[Ru(P2)(CO)3]·(C6H14)1/2
Empirical formula	C35H26O3P2RuS4, 0.5(C6H14)
Formula mass	828.89
Crystal dimensions/mm	0.6 × 0.4 × 0.35
Crystal system	Triclinic
Space group	P1̄
Temperature/K	293
a/Å	8.5098(8)
b/Å	11.5298(10)
c/Å	21.3180(18)
α/°	79.409(10)
β/°	79.189(10)
γ/°	72.778(10)
V/Å^3	1944.0(3)
Z	2
d calc/g cm^−3	1.416
μ/mm^−1	0.735
Data collected	6886
Indep. data	6886
R int	0.040
Observed data	4742
Param. refined	418
R(F)	0.0385
wR(F^2)	0.0880
GOF(obs)	0.866
Residual d/e Å^−3	0.66, −0.35

---

2.4. Electrochemistry

Cyclic voltammetry of [Ru(P2)(CO)₃] was carried out at room temperature, under dry argon atmosphere, in dried CH₂Cl₂ (0.1 M tetra-n-butylammonium hexafluorophosphate (TBAHP)) with a BAS electrochemical station (Model CV-50W). A standard three electrode cell was used, equipped with a platinum working electrode (diameter: 1 mm), a platinum wire counter-electrode and a SCE reference electrode. Measurements for [Fe(P2)(CO)₃] were performed, at room temperature, inside a glove box containing dry, oxygen-free (<1 ppm) argon, in a three-electrode cell equipped with a platinum millielectrode of 0.126 cm² area and a platinum wire counter-electrode. A silver wire served as a pseudo-reference electrode and its potential was checked against the ferrocene/ferrocenium couple (Fc/Fc⁺) before and after each experiment. Electrochemical experiments were carried out in CH₂Cl₂ (0.5 mol l⁻¹ of TBAHP) with an EGG PAR 273A potentiostat with positive feedback compensation. Based on repetitive measurements, absolute errors on potentials were found to be around 5 mV.

2.5. Electrolytic cell and EPR measurements

A quartz electrolytic cell, derived from the cell described by Peake et al.²¹ was designed to be inserted inside the EPR cavity and to allow measurements at controlled potential by using an Ag/AgCl electrode as a pseudo-reference. The solution could be directly degassed in the cell and all the measurements were performed under nitrogen atmosphere. This electrochemical device was equipped with a EGG PAR 362 potentiostat; both the working-electrode and the counter electrodes were in platinum. TBAHP (0.1 M) was used as an electrolyte. THF was freshly distilled on Na and CH₂Cl₂ on P₂O₅. Solutions were degassed by several freeze–pump–thaw cycles. Prior to EPR measurements, a cyclic voltammogram was recorded with this cell in order to locate the various oxidation waves. Chemical oxidations were performed in a glove box by reacting the TTF derivative with AgClO₄ or with bistrifluoroacetoxyiodobenzene (BTI).

EPR and ENDOR spectra were recorded on a Bruker ESP 300 spectrometer (X-band) equipped with a variable temperature attachment. Optimizations and simulations of the frozen solution spectra were carried out with a program²², based on the Levenberg–Marquardt least-squares fit, which compares the position of the experimental resonance lines with those calculated by second-order perturbation theory.

2.6. Spectroelectrochemistry

A spectroelectrochemistry experiment consists in monitoring in situ and in real time the FTIR signal of a solution at the surface of the working electrode of an electrochemistry setup while a cyclic voltammetry experiment is being carried out. The resulting IR spectra are collected at regular time intervals and are assembled in a 3D plot called spectroelectrogram. The spectroelectrochemical cell and methodology have been described elsewhere.²³ The solutions of P2 and [Fe(P2)(CO)₃] (1 × 10⁻³ M in CH₂Cl₂) were studied in thin layer (∼100 μm) conditions, therefore at low scanning rate (∼2 mV s⁻¹), so that the electrochemical process took place in quasi-electrolysis conditions. The potentiostat was an Autolab PGSTAT model 100 connected to a PC and monitored by the electrochemical software GPES v.4.8. The FTIR spectrometer was a Bruker model Tensor 27 equipped with a MCT detector cooled at the temperature of liquid nitrogen. The resolution was ∼4–8 cm⁻¹. The spectroscopic window was CaF₂ (∼50 000–1000 cm⁻¹).

2.7. DFT calculations

DFT calculations were performed with the Gaussian 98 package²⁴ using the UB3LYP functional²⁵ and 6-31G* standard basis sets. The Fermi contact and dipolar contributions to the hyperfine tensors were calculated after optimization of the complex or radical cation. A frequency analysis was carried out for each optimized structure (all frequencies real). The SOMO were represented by using the Molekel program.^26,27

3. Results

3.1. Structure of [Ru(P2)(CO)₃]

The infrared spectrum shows the three characteristic bands of a [Ru(L2)(CO)₃] complex, where L2 is a chelating diphosphine.^28,29 The fluxional behavior of the complex in solution is evidenced by the unique resonance in ³¹P NMR spectrum and the triplet observed for the carbonyl carbon atoms in ¹³C NMR spectrum. As in the case of pentacoordinate iron complexes,^30,31 the corresponding ruthenium complexes show a fast interconversion occurring in solution at the NMR time scale, between a trigonal bipyramidal and a square pyramidal geometry.²⁸ The solid state structure of [Ru(P2)(CO)₃] was determined by X-ray diffraction. The complex crystallized in the triclinic system, space group P1̄, with one molecule in general position and one molecule of hexane located on an inversion center. This latter is definitively trapped between the planes defined by the donors, since no desolvation occurs within months. Bond lengths and angles in the coordination sphere of Ru are listed in Table 2.

Table 2 Selected bond distances and angles in [Ru(P2)(CO)₃][hexane]_1/2

Bond lengths/Å
Ru–C(33)	1.905(4)	Ru–P(2)	2.330(1)
Ru–C(34)	1.908(6)	C(33)–O(1)	1.142(5)
Ru–C(35)	1.920(5)	C(34)–O(2)	1.150(6)
Ru–P(1)	2.328(1)	C(35)–O(3)	1.142(5)
Bond angles/°
C(33)–Ru–C(34)	93.73(19)	C(35)–Ru–P(1)	125.25(15)
C(33)–Ru–C(35)	90.24(19)	C(33)–Ru–P(2)	174.72(14)
C(34)–Ru–C(35)	120.2(2)	C(34)–Ru–P(2)	90.68(13)
C(33)–Ru–P(1)	91.21(13)	C(35)–Ru–P(2)	90.03(13)
C(34)–Ru–P(1)	114.27(16)	P(1)–Ru–P(2)	84.33(3)

---

The coordination geometry around the metallic center is intermediate between trigonal bipyramid, with apical phosphorus and carbonyl ligands, and square pyramid with an apical carbonyl ligand. In order to define to what extent the coordination geometry deviates from a perfect trigonal bipyramid, one can apply the τ criterion,^32,33 where τ = (α − β)/60, and α and β defining the largest angle and second largest angle, respectively, about the coordinated metallic center. Values of τ range from 0 for a perfect square pyramid to 1 for a perfect trigonal bipyramid. In our case τ amounts about 0.83, thus defining a distorted trigonal bipyramid, whereas in the case of Ru(dppe)(CO)₃,²⁸ with τ = 0.33, a distorted square pyramid is observed. The five-membered ring metallacycle defined by the diphosphine and the ruthenium atom is almost planar, as observed in Fig. 1, with a dihedral P(1)–C(1)–C(2)–P(2) angle of only 1°. This is somewhat surprising since also both dithiole moieties of the TTF core are essentially planar, with dihedral angles along the S⋯S hinges within 2.5°. Indeed, much larger folding angles, up to about 25°, along P⋯P or S⋯S hinges were observed for different P2 complexes.^11,12,34

An ORTEP representation of the complex is shown in Fig. 1.

Fig. 1 ORTEP view of [Ru(P2)(CO)₃] and side view of the complex.

3.2. Cyclic voltammetry

Cyclic voltammetry studies of P2, and of some of its transition metal complexes (Fe, W, Re, Mo)¹² have already been reported. They showed that coordinating the two phosphine groups of P2 drastically increases the oxidation potential of the TTF system. Whereas the two oxidation waves of P2 appear at E¹_P2 = 0.27 V and E²_P2 = 0.81 V, for [Fe(P2)(CO)₃] the first oxidation wave, centered on Fe, appears at E¹_P2Fe = 0.28 V while the oxidation waves centered on the TTF moiety appear at E²_P2Fe = 0.68 V and E³_P2Fe = 1.18 V. Nevertheless, these data did not allow us to conclude on the stability of the electrogenerated oxidized species.

In the present study, additional measurements have been carried out on [Fe(P2)(CO)₃] to obtain more detailed information on the electrochemical behaviour of this complex. As shown in Fig. 2A and 2D, at high scan rate (2 V s⁻¹), [Fe(P2)(CO)₃] indeed presents a nice reversible first oxidation wave (0.28 V) assigned to the formation of [Fe^(I)(P2)(CO)₃]. However, as shown in Fig. 2, repeated cycling shows that the two oxidation waves assigned to the TTF moiety (Fig. 2B, E and Fig. 2C, F) are split and that the intensity of the oxidation wave attributed to the metal moiety decreases during the negative reverse scan.

Fig. 2 Cyclic voltammograms (A, B and C) and deconvoluted voltammograms (D, E and F) of 1 mM [Fe(P2)(CO)₃] in 0.5 M TBAHP/CH₂Cl₂ at 2 V s⁻¹.

Cyclic voltammetry of [Ru(P2)(CO)₃], even at high scan rates, is characterized by an irreversible oxidation peak at E¹_P2Ru = 0.39 V and reversible peaks at E²_P2Ru = 0.71 V and E³_P2Ru = 1.22 V.

3.3. FTIR spectroelectrochemistry

The spectroelectrogram of P2 returns reversible absorption bands at 1558 and 1365 cm⁻¹ that can be assigned to (P2)˙⁺ and (P2)²⁺, respectively (see electronic supplementary information (ESI)).† These values are in good agreement with values recently reported for the TTF molecule.³⁵ The spectroelectrogram of [Fe(P2)(CO)₃] in the region of CO absorption frequencies is presented in Fig. 3.

Fig. 3 3D spectroelectrogram of [Fe(P2)(CO)₃]; the arrow indicates the potential sweep direction.

Additionally, the IR spectra obtained at potentials corresponding to the first (a), second (b) and third (c) oxidation waves are also reported in Fig. 4. There are two negative peaks that appear at 1907 and 1992 cm⁻¹ in all three spectra. They correspond to the disappearance of [Fe(P2)(CO)₃] during the electrochemical process and are assigned to C–O vibrations on the basis of previously reported data.¹² The same carbonyl vibrations are upshifted to 2019 and 2079 cm⁻¹ in spectrum (a). Spectrum (b) displays peaks at 1535 (assigned to the TTF⁺˙ moiety), 2073, 2112 and 2134 cm⁻¹, these latter values being assigned to carbonyl vibrations. The same vibrations are also met in curve (c) at 2077, 2106 and 2140 cm⁻¹. Additionally, a peak located at 1309 cm⁻¹ can be assigned to a TTF²⁺ species.

Fig. 4 Difference absorbance FTIR spectra of [Fe(P2)(CO)₃] at 0.4 (a), 0.8 (b) and 1.3 V (c) with respect to the spectrum of [Fe(P2)(CO)₃] at 0 V. The baselines have been arbitrarily shifted in order to ensure a better readability of the curves.

3.4. EPR spectroscopy

3.4.1. Spectra obtained by oxidation of the ligand P2.
Electrochemical oxidation. A solution of P2 in CH₂Cl₂ or THF was oxidized, at room temperature, in situ in the EPR cavity. A signal appears at g = 2.011 at a potential superior to that of the first oxidation wave. Increasing the voltage does not lead to another type of spectrum. As shown in Fig. 5a, the hyperfine structure is clearly due to a coupling of 0.96 G with six equivalent protons.

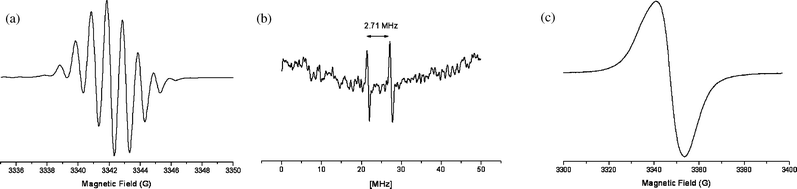Fig. 5 (a) EPR spectrum obtained at room temperature after electrochemical oxidation of P2 in CH₂Cl₂ (ν_klystron = 9.407 GHz). (b) ¹H-ENDOR spectrum obtained at 190 K after oxidation of P2 with AgClO₄ in CH₂Cl₂. (c) EPR frozen solution spectrum obtained at 115 K after oxidation of P2 with AgClO₄ in CH₂Cl₂.

Chemical oxidation. Oxidation of P2 in CH₂Cl₂ or THF with AgClO₄ leads, at room temperature, to the septet produced by electrochemical oxidation. The corresponding ENDOR spectrum obtained at 190 K, is shown in Fig. 5b. It confirms the ¹H-coupling of 0.96 G (2.71 MHz) and does not reveal additional hyperfine interaction. The EPR spectrum recorded at 115 K is a broad line (Fig. 5c), without any resolved hyperfine structure, centered at g = 2.010.

3.4.2. Spectra obtained by oxidation of the transition metal complexes.
Oxidation of the Ru complex. In accord with cyclic voltammetry results, measurements with the electrolytic EPR cell show that the first oxidation wave (E¹_P2Ru) of [Ru(P2)(CO)₃] appears at a potential approximately equal to half the value found for the second oxidation wave of the free ligand P2 (vide supra). Whereas no EPR signal could be detected for a potential inferior to E¹_P2Ru, a septet exhibiting a coupling constant of 2.71 MHz was detected for any potential higher than this value. The same spectrum was obtained by chemical oxidation with AgClO₄.
Oxidation of the Fe complex.
Electrochemical oxidation. The first EPR signal was obtained when the voltage was set ca. 200 mV above the first oxidation wave (E¹_P2Fe) of the complex. The corresponding spectrum, obtained at room temperature, is shown in Fig. 6a. It is characterized by a coupling of 22.5 G with two equivalent spin 1/2 nuclei and by a g-value equal to 2.054. At a potential slightly superior (ca. 100 mV) to that of the second oxidation wave (E²_P2Fe), this EPR spectrum disappears and is replaced by the septet (splitting = 1 G) centered at g = 2.011 and already observed by oxidation of P2.

Fig. 6 EPR spectra obtained after electrochemical one-electron oxidation of a solution of [Fe(P2)(CO)₃] in CH₂Cl₂ (a) at room temperature (ν_klystron = 9.410 GHz), b) at 120 K (ν_klystron = 9.417 GHz).

Chemical oxidation. Oxidation at room temperature of a solution of [Fe(P2)(CO)₃] in CH₂Cl₂ or THF with one equivalent of AgClO₄ led to the same spectrum as this one shown in Fig. 6a. This spectrum is attributed to [Fe(P2)(CO)₃]⁺, this identification will be confirmed by DFT (vide infra). The corresponding frozen solution spectrum was recorded at 110 K and is shown in Fig. 6b. It could be simulated by using almost isotropic hyperfine tensors with two equivalent ³¹P and an axial g-tensor whose average value is equal to the value determined in liquid solution (see Table 3). When the oxidation was carried out with two equivalents of AgClO₄, the liquid solution spectrum was identical to the septet recorded after oxidation of P2.

Table 3 EPR parameters for the various species formed by oxidation of [Fe(P2)(CO)₃]

	Liquid solution spectra			Frozen solution spectra
Species	Hyperfine structure	A iso/G	g	g	T/G		Anisotropic constants τaniso/G
P2˙^+	Heptet	(6x^1H) 1.0	2.011	g = 2.010
[Fe(P2)(CO)3L]^+	Doublet	(1x^31P) 20.2	2.014	g x = 2.0150
		(6x^1H) 0.7		g y = 2.0241
				g z = 2.0046
				g average = 2.0145
[Fe(P2)(CO)3]^+	Triplet	(2x^31P) 22.5	2.054	g x = 2.0755	(2x^31P)	T x = 22.60	τ aniso,x = 0
				g y = 2.0755		T y = 22.60	τ aniso,y = 0
				g z = 2.0051		T z = 22.60	τ aniso,z = 0
				g average = 2.0520		A iso = 22.6
[Fe(P2)2(CO)]^+	Quintet	(4x^31P) 21.1	2.054	g x = 2.0780	(4x^31P)	T x = 23.00	τ aniso,x = 1.2
				g y = 2.0695		T y = 20.50	τ aniso,y = −1.3
				g z = 2.0073		T z = 21.80	τ aniso,z = 0.0
				g average = 2.0516		A iso = 21.8

---

Stability of the oxidation products of [Fe(P2)(CO)₃]. At room temperature, the intensity of the triplet observed by chemical or electrochemical oxidation of [Fe(P2)(CO)₃] slowly decreased with time (Fig. 7a) and was replaced by a doublet (splitting = 20.2 G) of septets (splitting = 0.7 G) centered at g = 2.014 (Fig. 7b). One hour after electrochemical oxidation, this latter signal was very intense and the triplet had practically disappeared. It is worthwhile remarking that this decrease in the triplet intensity is much more rapid in THF than in CH₂Cl₂.

Fig. 7 (a) EPR spectra recorded at room temperature as a function of time after oxidation of [Fe(P2)(CO)₃] with AgClO₄ in CH₂Cl₂t₁ = 1 mn, t₂ = 30 mn, t₃ = 1 h. (b) EPR spectrum recorded at room temperature 1 h after electrochemical oxidation of [Fe(P2)(CO)₃] in CH₂Cl₂ (ν_klystron = 9.423 GHz).

The rather large coupling with a spin 1/2 nucleus suggests the formation of a complex with a single coordination phosphorus–iron bond.

Oxidation of [Fe(P2)(CO)₃] in the presence of P2. The spectrum shown in Fig. 8a was obtained after oxidation with AgClO₄ or BTI, at room temperature, of a solution of [Fe(P2)(CO)₃] containing a small amount of P2. CH₂Cl₂ or THF were used as solvents. The hyperfine structure is clearly due to a coupling of 21.1 G with four spin 1/2 nuclei. The corresponding frozen solution is shown in Fig. 8b, this spectrum was simulated by using the tensors given in Table 3.

Fig. 8 EPR spectra obtained after oxidation with 1 equivalent of AgClO₄ of a CH₂Cl₂ solution containing [Fe(P2)(CO)₃] and P2. (a) at room temperature (ν_klystron = 9.747 GHz). (b) at 120 K (ν_klystron = 9.397 GHz).

3.5. DFT calculations

DFT calculations were performed to confirm the analysis of the EPR spectra and to point out the geometrical modifications induced by the oxidation of P2 and [Fe(P2)(CO)₃]. Due to the large size of P2, calculations were carried out on the P2′ model where the phenyl groups were replaced by hydrogen atoms (Fig. 9). Some important geometrical parameters calculated for the optimised structures of P2′, P2′˙⁺, [Fe(P2′)(CO)₃] and [Fe(P2′)(CO)₃]⁺ are given in Table 4 together with the values determined from the crystal structure of [Fe(P2)(CO)₃]. For the ligand, n₁, n₂, n₃, n₄ and n₅ represent the normals to the planes S2C4C5S3, S2C1S3, S9C8S10, S9C11C12S10 and PC11C12P, respectively. In [Fe(P2′)(CO)₃], n₆ represents the normal to the PFeP plane. For all structures, the four sulfur atoms and the two central carbon atoms are coplanar ([n₂,n₃] angle ≈0°). In the neutral structures (P2′ or [Fe(P2′)(CO)₃]), the dithiafulvalene rings are not perfectly planar (the [n₁,n₂] and [n₃,n₄] angles are between 12 and 17°). In contrast with P2′ which becomes planar when an electron is removed, oxidation of [Fe(P2′)(CO)₃] leads only to a slight diminution of the [n₁,n₂] angle and to an appreciable increase of the [n₃,n₄] angle. For both P2′ and [Fe(P2′)(CO)₃], oxidation causes an increase in the C1–C8 bond length; this elongation is more marked for the free ligand (0.047 Å) than for the complex (0.008 Å). It is worthwhile mentioning a drastic conformation change induced by the oxidation of [Fe(P2′)(CO)₃]: whereas in the neutral compound the iron coordination is close to a trigonal bipyramid (τ = 0.88) with one of the two apical positions occupied by a phosphorus atom, as observed in the crystal structure of [Fe(P2)(CO)₃] (τ = 0.70) , in [Fe(P2′)(CO)₃]⁺ the coordination of Fe becomes a square pyramid (τ = 0.001) with the axial position occupied by a carbonyl group as shown in Fig. 9b.

Fig. 9 DFT optimized structure of (a) P2′˙⁺. b) [Fe(P2′)(CO)₃]⁺.

Table 4 Calculated geometrical parameters for the model systems P2′ and [Fe(P2′)(CO)₃]

			Angles/°
System		C1–C8/Å	(n2,n3)	(n1,n2)	(n3,n4)	(n4,n5)	(n5,n6)	τ
P2′	Neutral	1.349	0.5	13.5	13.7	1.9
	Oxidized	1.396	0.0	0.0	0.0	0.0
[Fe(P2′)(CO)3]	Neutral	1.349	0.3	12.5	17.4	2.0	0.1	0.88
	Oxidized	1.357	0.4	8.2	24.2	3.0	0.8	0.001
[Fe(P2)(CO)3]	Crystal	1.346	1.9	8.2	12.9	4.4	12.9	0.70

---

The SOMO represented in Fig. 10a indicates that in P2′˙⁺ the unpaired electron is mainly delocalized on the central part of the TTF moiety. Accordingly, the calculated ¹H and ³¹P couplings given in Table 5 are very small, they agree with the methyl hyperfine structure detected on the EPR and ENDOR spectra and are consistent with the absence of any ³¹P splitting.

Fig. 10 Representation of the SOMO for (a) P2′˙⁺, (b) [Fe(P2′)(CO)₃]⁺.

Table 5 Calculated hyperfine couplings for the one-electron oxidation compounds of P2′ and [Fe(P2′)(CO)₃]

		Hyperfine coupling/G
Species	Nucleus	A iso	τ aniso,1	τ aniso,2	τ aniso,3
a Average value for the protons of the two methyl groups.
P2′˙^+
	^1H^a	0.96	−0.34	−0.26	0.60
	^31P	0.14	−0.30	0.14	0.16
[Fe(P2′)(CO)3]^+
	^1H^a	0.05	−0.03	−0.03	0.02
	^31P	21.53	−2.77	1.05	1.64

---

For [Fe(P2′)(CO)₃]⁺, however, there is a large contribution of the iron orbital to the SOMO (Fig. 10b). As shown in Table 5, this spin localisation on the metal considerably modifies the hyperfine constants of the ligand as compared to those calculated for P2′˙⁺: the methyl couplings are now particularly small whereas the ³¹P hyperfine tensors are almost isotropic with a A_iso value close to 22 G. These properties agree with the EPR spectra recorded in both liquid and frozen solutions: absence of ¹H coupling, isotropic ³¹P hyperfine tensors, large anisotropy of the g-tensor.

4. Discussion

It is clear, from the above results, that oxidation of [Ru(P2)(CO)₃] leads only to the spectrum of the oxidized free ligand whereas oxidation of [Fe(P2)(CO)₃] gives rise to a variety of paramagnetic species. We will first elucidate the mechanisms leading to the oxidation species of the iron complex, then we will try to rationalize the difference in the electrochemical behaviour of [Ru(P2)(CO)₃] and [Fe(P2)(CO)₃].

As shown by DFT calculations, there is no doubt that one-electron oxidation of [Fe(P2)(CO)₃] is metal-centered, the resulting Fe(I) complex exhibits coupling with two ³¹P in good accordance with the experimental spectrum which, furthermore, is characterized by a rather large anisotropy of the g-tensor (Fig. 6b). The redox reaction is accompanied by an appreciable change in the coordination shape of the metal that passes from a trigonal bipyramid to a square pyramid. However, as shown in Fig. 7, at room temperature, the resulting structure is not very stable; a scission of one of the two phosphorus–iron bonds occurs giving rise to hyperfine coupling with only one ³¹P nucleus. In this secondary complex, [Fe(P2)(CO)₃L]⁺ (L = solvent), the detection of a small coupling with the methyl protons together with the decrease in the g_average value suggest that the unpaired electron delocalises onto the TTF moiety.

For a potential slightly superior to the second oxidation potential of [Fe(P2)(CO)₃], or for an oxidation with two equivalent of AgClO₄, the spectrum of the primary Fe(I) complex is replaced by the spectrum of the oxidized ligand P2˙⁺. No signal is observed which could be due to a stable species bearing two oxidized moieties: an Fe(I) site and a TTF centered radical cation. Therefore, decomplexation probably occurs. Such a process is in good accordance with the splittings of the second and third oxidation waves detected by cyclic voltammetry at high scan rates (Fig. 2). These splittings, observed within repetitive cycling, indicate that in addition to the ligand oxidation of the [Fe(P2)(CO)₃] complex, the oxidation of a second TTF-containing species occurs. At high scan rates, the oxidation potential values for this second species, which amount to 0.55 V and 1.05 V, hence largely superior to those of the free P2, suggest that an intermediate monocoordinated species is involved. Very likely, this latter is related to the monocoordinated species detected by EPR (vide supra). Moreover, on this hypothesis, the much higher oxidation potential of a [Fe(phosphine)(CO)₃L] (with L = CO, solvent) complex³⁶ agrees with the disappearance of the iron centered oxidation wave (E = 0.28 V). FTIR spectroelectrochemical measurements, performed in thin layer conditions, show unambiguously the signature of the iron based oxidized species [Fe(P2)(CO)₃]⁺ in the CO absorption region, as can be observed in spectrum (a), Fig. 4 (2019 and 2079 cm⁻¹ for ν_CO), with important upshifts when compared with the starting neutral complex (1907 and 1992 cm⁻¹). This trend is in agreement with a weaker π-back donation from the metal to the π^*_CO orbital, according to the Dewar–Chatt–Duncanson model.³⁷ At higher potentials such as 0.8 V and 1.3 V (Fig. 4), allowing for the oxidation of the TTF moiety, the three ν_CO absorption peaks present in spectra b and c, appear at 2073, 2112, 2134 and 2077, 2106 and 2140 cm⁻¹, respectively. Very likely, these absorptions can be attributed to a (monophosphine)Fe(CO)₃L (L = CO, solvent) cationic species. Indeed, the presence of absorption peaks at 1535 and 1309 cm⁻¹, characteristic for the central C=C bond in TTF⁺˙ and TTF²⁺ based species and different from those of the free P2˙⁺ and P2²⁺ (vide supra), is also an argument in the favour of a P2 monocoordinated iron carbonyl complex at this stage, and confirms the interpretation of the EPR spectra.

As shown in Fig. 8, when the primary Fe(I) complex is formed in presence of free ligands P2, coordination between iron and a second ligand can occur, giving rise to [Fe(P2)₂(CO)]⁺, a new metal centered complex with a large coupling with four ³¹P nuclei value and a large g-anisotropy.

The formation of these various oxidation products detected by EPR is summarized in Scheme 1.

Scheme 1

Unlike the iron complex [Fe(P2)(CO)₃], cyclic voltammetry measurements of the ruthenium complex [Ru(P2)(CO)₃], performed in the same conditions as for the iron counterpart, show only an irreversible oxidation peak at 0.39 V even at high scan rates, corresponding either to a decomposition or to other processes such as dimerization of the electrogenerated Ru(I) paramagnetic species. For example, a Ru₂ complex was isolated upon chemical oxidation of the [Ru(dppe)(CO)₃] complex.²⁸ In our case, the differences within the electrochemical behaviors are, very likely, due to a lower electron density on the ruthenium(0) centre when compared with the iron(0) one, hence a much lower stability of the paramagnetic oxidized species Ru(I) than Fe(I). Striking spectroscopic and structural differences between the two unoxidized complexes support this hypothesis. Indeed, the three infrared absorption frequencies of the carbonyl ligands appear at higher wave numbers for [Ru(P2)(CO)₃] than for [Fe(P2)(CO)₃],¹² as follows: ν_CO (cm⁻¹) 1920, 1934, 2011 and 1901, 1925, 1991, respectively. This trend can be easily rationalized in terms of a lower degree of π-back donation from metal-d to CO-π* orbitals, as a consequence of the lower electron density on the Ru(0) center than on the Fe(0) center, according to the Dewar–Chatt–Duncanson model.³⁷ Also, X-ray structural parameters are in good agreement with this difference in π-back donation, since the C≡O average distance amounts at 1.145 Å within the Ru(0) complex, whereas the same distance increases at 1.155 Å in the case of the Fe(0) complex. Indeed, a strong π-back donation leads to a partial filling of the π*-CO orbitals, hence a lengthening of the C≡O bond. Very likely, the electron density on the Ru(0) center, and, consequently the stability of the electrogenerated paramagnetic Ru(I) species, could be increased by the use of more electron-rich phosphines, such as dialkyl instead of diphenylphosphines, a much appealing situation which would eventually allow the EPR study of the paramagnetic Ru(I) complex. Moreover, in the case of the iron complexes, the replacement of diphenyl with dialkylphosphines could prevent the phosphine decomplexation subsequent to the second oxidation step, thus generating the very interesting situation of the coexistence of two radical sites on the same molecule. This is the subject of current and future work in our groups.

Acknowledgements

Support from the Fonds “Germaine de Staël” (Schweizerische Akademie der Technischen Wissenschaften, French Ministry of Foreign Affairs) is gratefully acknowledged. We thank the Swiss National Science Foundation and the Centre National de la Recheche Scientifique for support of this research.

References

1. J. M. Williams, J. R. Ferraro, R. J. Thorn, K. D. Carlson, U. Geiser, H. H. Wang and A. M. Kini, in Organic Superconductors (Including Fullerenes), Synthesis, Properties and Theory, ed. P. Hall, 1992.
2. M. R. Bryce, J. Mater. Chem., 1995, 5, 1481.
3. J. L. Segura and N. Martin, Angew. Chem., Int. Ed. Engl., 2001, 40, 1372.
4. R. Andreu, I. Malfant, P. G. Lacroix and P. Cassoux, Eur. J. Org. Chem., 2000, 737.
5. S.-X. Liu, S. Dolder, M. Pilkington and S. Decurtins, J. Org. Chem., 2002, 67, 3160.
6. J.-P. Griffiths, R. J. Brown, P. Day, C. J. Matthews, B. Vital and J. D. Wallis, Tetrahedron Lett., 2003, 44, 3127.
7. T. Devic, N. Avarvari and P. Batail, Chem. Eur. J., 2004, 10, 3697.
8. F. Iwahori, S. Golhen, L. Ouahab, R. Carlier and J.-P. Sutter, Inorg. Chem., 2001, 40, 6541.
9. S. Campagna, S. Serroni, F. Puntoriero, F. Loiseau, L. De Cola, C. J. Kleverlaan, J. Becher, A. P. Sorensen, P. Hascoat and N. Thorup, Chem. Eur. J., 2002, 8, 4461.
10. M. Fourmigué and P. Batail, Bull. Soc. Chim. Fr., 1992, 129, 29.
11. M. Fourmigué, C. E. Uzelmeier, K. Boubekeur, S. L. Bartley and K. R. Dunbar, J. Organomet. Chem., 1997, 529, 343.
12. N. Avarvari, D. Martin and M. Fourmigué, J. Organomet. Chem., 2002, 643–644, 292.
13. N. Avarvari and M. Fourmigué, Chem. Commun., 2004, 1300.
14. S. J. Sherlock, D. C. Boyd, B. Moasser and W. L. Gladfelter, Inorg. Chem., 1991, 30, 3626.
15. P. K. Baker, N. G. Connelly, B. M. R. Jones, J. P. Maher and K. R. Somers, J. Chem. Soc., Dalton Trans., 1980, 579.
16. J. H. MacNeil, A. C. Chiverton, S. Fortier, M. C. Baird, R. C. Hynes, A. J. Williams, K. F. Preston and T. Ziegler, J. Am. Chem. Soc., 1991, 113, 9834.
17. J. R. Morton and K. F. Preston, J. Magn. Reson., 1978, 30, 577.
18. S. Choua, H. Sidorenkova, T. Berclaz, M. Geoffroy, P. Rosa, N. Mézailles, L. Ricard, F. Mathey and P. Le Floch, J. Am. Chem. Soc., 2000, 122, 12227.
19. L. Cataldo, S. Choua, T. Berclaz, M. Geoffroy, N. Mézailles, N. Avarvari, F. Mathey and P. Le Floch, J. Phys. Chem. A, 2002, 106, 3017.
20. G. M. Sheldrick, in Programs for the Refinement of Crystal Structures, University of Göttingen, Germany, 1997.
21. K. R. Fernando, A. J. McQuillan, B. M. Peake and J. Wells, J. Magn. Reson., 1986, 68, 551.
22. E. Soulié, T. Berclaz and M. Geoffroy, AIP Conference Proceedings 330, Computational Chemistry, 1996, p. 627.
23. V. Bellec, M. DeBacker, E. Levillain, F. X. Sauvage, B. Sombret and C. Wartelle, Electrochem. Commun., 2001, 3, 483.
24. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery Jr., R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, P. Salvador, J. J. Dannenberg, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Cioslowski, J. V. Ortiz, A. G. Baboul, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, C. Gonzalez, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, J. L. Andres, C. Gonzalez, M. Head-Gordon, E. S. Replogle and J. A. Pople, in GAUSSIAN 98, (Revision A.7), ed. P. P., Gaussian Inc., USA, Pittsburgh PA, 1998.
25. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
26. P. Flukiger, Development of Molecular Graphics Package MOLEKEL, PhD Thesis, University of Geneva, Switzerland, 1992.
27. S. Portmann and H. P. Luthi, Chimia, 2000, 54, 766.
28. S. J. Skoog, A. L. Jorgenson, J. P. Campbell, M. L. Douskey, E. Munson and W. L. Gladfelter, J. Organomet. Chem., 1998, 557, 13.
29. K. A. Bunten, D. H. Farrar, A. J. Poee and A. J. Lough, Organometallics, 2000, 19, 3674.
30. R. S. Berry, J. Chem. Phys., 1960, 32, 933.
31. F. A. Cotton, K. I. Hardcastle and G. A. Rusholme, J. Coord. Chem., 1973, 2, 217.
32. D. K. Mills, Y. M. Hsiao, P. J. Farmer, E. V. Atnip, J. H. Reibenspies and M. Y. Darensbourg, J. Am. Chem. Soc., 1991, 113, 1421.
33. A. W. Addison, T. N. Rao, J. Reedijk, J. Van Rijn and G. C. Verschoor, J. Chem. Soc., Dalton Trans., 1984, 1349.
34. C. E. Uzelmeier, S. L. Bartley, M. Fourmigué, R. Rogers, G. Grandinetti and K. R. Dunbar, Inorg. Chem., 1998, 37, 6706.
35. C. Wartelle, P. M. Viruela, R. Viruela, E. Orti, F. X. Sauvage, E. Levillain, F. Le Derf and M. Sallé, Phys. Chem. Chem. Phys., 2003, 5, 4672.
36. S. W. Blanch, A. M. Bond and R. Colton, Inorg. Chem., 1981, 20, 755.
37. (a) M. J. S. Dewar, Bull. Soc. Chim. Fr., 1951, C71; (b) J. Chatt and L. A. Duncanson, J. Chem. Soc., Abstr., 1953, 2939.

---

Footnote

† Electronic supplementary information (ESI) available: 3D spectroelectrogram of P2. See http://www.rsc.org/suppdata/cp/b4/b409958c/

---