High-resolution absorption cross sections of formaldehyde at wavelengths from 313 to 320 nm

Abstract

Absorption cross sections have been measured for the 2²₀4³₀ and 2³₀4¹₀ vibrational bands of the ùA₂–X̃¹A₁ electronic transition of formaldehyde in the wavelength range 313–320 nm. Accurate values are of considerable importance for atmospheric monitoring and to understand the photochemistry of this compound. The 0.10 cm⁻¹ FWHM wavenumber resolution of the experiments is determined by the bandwidth of the ultraviolet laser used, and is a factor of 10 or more higher than any previously reported data. The absorption cross section data are thus obtained at a spectrometer resolution close to the Doppler broadening limit at 294 K of 0.07 cm⁻¹ FWHM, for isolated rotational lines, but lifetime broadening effects contribute a further ∼0.5 cm⁻¹ of width. Our spectral resolution is thus higher than required to resolve the sharpest spectral features and, as a consequence, the cross sections peak at greater values than previous studies of these structured rovibronic bands conducted at much lower spectrometer resolutions. Previous data can be quantitatively reproduced by convolution of the newly obtained spectra with lower-resolution instrument functions. Pressure broadening of regions of the spectra in the presence of up to 500 Torr of N₂ is examined and the effects on peak absorption cross sections are very small. The influence of reduced temperature on the spectrum is also explored through experimental measurements and spectral simulations.

---

Introduction

Formaldehyde (H₂CO) is a key atmospheric compound, central to the chemistry of ozone, HO_x and NO_x species. It is an intermediate product in the oxidation of methane, the most abundant atmospheric hydrocarbon, which is found ubiquitously in the lower atmosphere.¹ The high (∼1.72 parts per million by volume, ppmv, tropospheric average²) concentrations of methane result in a global tropospheric background of H₂CO, but it is also formed from the oxidation of most other hydrocarbons, including isoprene, which is emitted in large quantities by biogenic sources.³ Fossil fuel and biomass burning release formaldehyde directly into the atmosphere. The lifetime of H₂CO with respect to its two major loss pathways, photolysis and reaction with the hydroxyl radical (OH), is on the order of a few hours.⁴ Measured concentrations of H₂CO are ∼50 pptv (parts per trillion by volume) in clean Antarctic tropospheric air in winter,⁵ 15–20 ppbv (parts per billion by volume) in the London urban area,⁶ and ≤70 ppbv in the Los Angeles area.⁷ A recent summary of sources, sinks and concentrations of formaldehyde in different environments was given by Meller and Moortgat.⁸

H₂CO absorbs UV radiation in the wavelength range from 260–360 nm, with the S₁ ← S₀ electronic transition giving rise to the ùA₂–X̃¹A₁ band system.⁹ This electronic transition is formally electric-dipole forbidden, but becomes allowed through vibronic coupling. Absorption cross sections are thus relatively small for an electronic transition in a small molecule, but H₂CO is nevertheless photochemically active in the troposphere. Following absorption of a photon, photodissociation can occur through two distinct and competing channels:

H₂CO + hν → H₂ + CO (λ < 360 nm) (1)

H₂CO + hν → HCO + H (λ < 330 nm) (2)

The wavelengths in brackets are derived from the threshold energies for the opening of each dissociation channel,¹⁰ which correspond to the barrier height for channel (1) and the asymptotic energy for C–H bond breaking for channel (2). Both sets of products are atmospherically important: the further oxidation of CO to CO₂ has implications for greenhouse gas budgets, and both HCO and H atom products from the second channel produce HO₂ radicals by reaction with O₂:

HCO + O₂ → HO₂ + CO (3)

H + O₂ + M → HO₂ + M (4)

HO₂ interconverts rapidly with OH, which is the major atmospheric oxidant.

Various investigations of the absorption cross sections of formaldehyde have been undertaken over the years,^8,11–13 and Meller and Moortgat provided a comprehensive listing of the experimental procedures and conditions used for all these different studies.⁸ Prior to the current work, laser methods had not been employed and instrument resolution was thus much lower than the fine structure present in the absorption spectrum that results from partially resolved rotational features of this asymmetric top molecule. Previously reported absorption cross sections are thus strongly dependent upon the resolving powers of the various spectrometers employed. The highest instrumental resolution used to date was 1.00 cm⁻¹ (∼0.001 nm at 310 nm).¹³ This extensive study was carried out in the temperature range 223 to 293 K and the wavelength range 300 to 360 nm, thus capturing the temperatures and wavelengths of importance to tropospheric formaldehyde photochemistry. Peak cross sections were, in general, higher than reported in previous studies because of the superior resolution of sharply structured rotational features in many vibronic absorption bands, some of which may have widths close to the Doppler broadened limit (0.070 cm⁻¹ at 320 nm and 294 K).

Accurate formaldehyde absorption cross sections at higher resolution are, however, now needed so that ground-based and satellite-based spectrometers can retrieve more precise atmospheric formaldehyde concentrations. The higher the spectral resolution, the greater the likelihood of finding suitable absorption lines for atmospheric monitoring in a free spectral window. H₂CO concentration profiles obtained from satellite data can then be used as proxies for other atmospheric hydrocarbons including isoprene,¹⁴ because of their interlinked chemistry. Accurate cross sections are also essential for deriving wavelength dependent quantum yields for channels (1) and (2), and thus assessing correctly the impact of formaldehyde photochemistry on HO_x and ozone yields and other chemical processes in the troposphere.

Quantifying the effects of pressure broadening on atmospheric spectra is necessary if lineshape analysis is to be used in the retrieval of altitude-dependent mixing ratios. If pressure broadening is sufficiently pronounced, the wings of an isolated spectral line can provide data on concentrations lower in the atmosphere where the pressure is higher. H₂CO column concentrations have been measured from space by the Global Ozone Monitoring Experiment (GOME)¹⁵ over North America¹⁶ and Southeast Asia.¹⁷ The North American study used laboratory spectra from Cantrell et al.¹³ as reference data, but the Southeast Asia study did not specify which H₂CO reference spectra were employed.

The results presented in this paper are part of a wider project currently underway in our laboratory to measure quantum yields for H₂CO photolysis viaprocess (2) over a range of atmospherically relevant UV wavelength, pressure and temperature conditions, and at a resolution approaching the Doppler limit. A necessary first stage of this project involves measuring H₂CO absorption cross sections at this wavelength resolution. Towards these goals, and to supply improved data to the Earth observation community, we report here absorption cross sections obtained at an instrument resolution of 0.10 cm⁻¹, using Beer–Lambert law type measurements with a tuneable UV laser beam, and measured under conditions of low partial pressure of H₂CO (<1 Torr). The effects of temperature and of N₂ induced pressure broadening are also explored, and interpreted with the aid of simulations of the structures of the vibronic bands.

Experimental

H₂CO spectra were obtained using a purpose designed and engineered spectrometer consisting of a tuneable UV laser source and an absorption chamber evacuated by a mechanical vacuum pump and equipped with pressure gauges and thermocouple temperature sensors. A schematic diagram of the experiment is shown in Fig. 1. The intensity of the UV laser light was measured before and after the absorption chamber by independent photodiodes, enabling quantification of both fluctuations in the laser power and the change in intensity resulting from passage through the spectrometer. This latter intensity change is a consequence of H₂CO absorption, scattering losses from the vacuum cell windows, and Rayleigh scattering from added pressures of N₂; the absorption and scattering losses were distinguished by repeating all wavelength scans in the absence of H₂CO but under otherwise identical experimental conditions.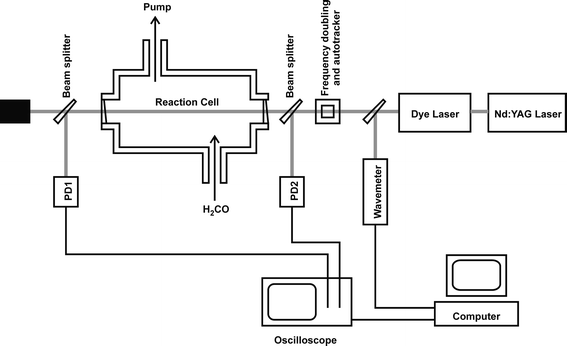

Fig. 1 A schematic diagram of the experimental apparatus. PD1 and PD2 denote photodiodes.

The rectangular spectrometer chamber was constructed from stainless steel, with external dimensions of 600 × 200 × 300 mm. The UV laser beam entered the chamber through windows mounted on short extension arms and crossed the chamber along its long axis, giving an internal path length of 767 mm. The windows were made from wedged quartz discs to eliminate interference effects that otherwise contributed an underlying fringe pattern to absorption spectra. The UV laser light was generated from the frequency doubled output of a dye laser (Sirah Cobra Stretch) pumped by the 532 nm second harmonic of an Nd:YAG laser (Continuum Surelite III). Frequency doubling was achieved using a KDP crystal that was angle-tuned to maintain efficient UV generation using a home-made auto tracker. The linewidth of the fundamental beam from the dye laser was estimated to be 0.07 cm⁻¹ by comparing experimentally measured low-pressure iodine laser induced fluorescence spectra to simulations, and the UV bandwidth is thus estimated to be ∼0.10 cm⁻¹. Wavelength calibration of the dye laser fundamental was achieved using a combination of a wavemeter (Coherent Wavemaster) and an etalon (with free spectral range of 2.05 cm⁻¹), with transmission fringes monitored by a photodiode. The energy of the UV laser light prior to the absorption chamber was typically 0.1 mJ pulse⁻¹ in a circular beam of diameter ∼3 mm. The pulse energy was varied in initial experiments to ensure there were no problems occurring due to power saturation either in the photodiode signals or in the H₂CO absorption. Light intensities before and after the absorption chamber were measured using fast photodiodes in photovoltaic mode. A fraction (∼5%) of the laser beam was split from the main beam into each photodiode, using quartz wedges (wedge angle 2°) as beam splitters. Wedged optics were necessary to prevent fringing from interference effects as the laser wavelength was scanned, as was observed for plane parallel beam splitters. Quartz diffusers were placed in front of both photodiodes and care was taken to ensure linear response of the photodiodes to changes in the laser intensity.

H₂CO was prepared in the manner of Spence and Wild.¹⁸ Briefly, para-formaldehyde (Aldrich prills, 95%) was heated to temperatures in excess of 383 K where it sublimes to gaseous monomeric H₂CO. The gas was collected in a liquid nitrogen trap. A first stage of purification was achieved by passing the gas through a dry ice/acetone trap (195 K) to remove thermal decomposition impurities with vapour pressures lower than H₂CO such as acetone and acetaldehyde. The remaining gas, including any formaldehyde, was then passed through a tube immersed in a liquid nitrogen/ethanol slush (156 K) to collect H₂CO but not any higher volatility impurities such as CO₂. Finally, trap-to-trap distillation was performed with liquid nitrogen to remove any residual O₂ or N₂. H₂CO was admitted to the absorption chamber via PTFE tubing either directly, by warming of the cryogenically trapped sample, or by vapour collection in a glass bulb to which further N₂ diluent was added up to pressures as high as 760 Torr. Pressures of the formaldehyde and other bath gases in the absorption chamber were measured using calibrated capacitance manometer gauges (0–10 Torr and 0–1000 Torr, Edwards Barocel pressure sensors). The absorption chamber was temperature controlled by passing cooled fluid from a thermostat (Huber Unistat 360) through internal loops of copper piping. The temperature of the sample gas was measured with two type-K thermocouples and a Pt100 probe. The temperature was measured at multiple points along the laser beam axis to ensure there were no temperature gradients. The signals from the photodiodes monitoring the laser intensity, the wavemeter, and the etalon photodiode were digitised using an oscilloscope (LeCroy 6030) and transferred to a PC via a GPIB interface for data accumulation and analysis. The computer also controlled the wavelength scanning of the dye laser.

Results and discussion

The formaldehyde absorption cross sections (σ) at each wavelength are derived from the Beer–Lambert law:

I = I₀exp{−σl[H₂CO]} (5)

where I₀ and I are, respectively, the normalized (see below) intensities measured by a photodiode (PD1) located after the absorption chamber, with or without a known concentration of H₂CO ([H₂CO]). The length of the absorption path through the gas sample was l = 767 mm. The ratio of the two intensities in eqn. (5) compensates for additional losses caused by the chamber windows and other scattering processes (such as Rayleigh scatter in the presence of N₂). The intensity of every laser pulse was monitored before entering the vacuum chamber by photodiode PD2, and each signal recorded by PD1 was normalised for fluctuating laser power by division by the equivalent signal from PD2.

Spectra were recorded using a static sample of gas at fixed formaldehyde partial pressure in the absorption chamber. Extensive tests were carried out to ensure that no complications arose from this static set up: possible problems might include loss of gaseous H₂CO by UV laser photolysis, subsequent reaction with photolysis products, and H₂CO adsorption on internal surfaces, with re-polymerisation to para-formaldehyde. Intensities of absorption spectra were unchanged when using the static gas samples over periods as long as 1 h, demonstrating negligible photodegradation of the sample under the conditions of low UV laser power, and no discernible effects of the chamber walls. Comparisons were made with flowing samples using H₂CO pre-diluted in N₂ to known mixing ratios, and results were found to be the same. Careful attention was paid to the partial pressures of H₂CO used in experiments because, as reported previously by others,^8,12 measured absorption cross sections were observed to decline at higher partial pressures (in this instance above 1 Torr). This decline is perhaps a consequence of formation of volatile dimers or larger oligomers of formaldehyde and experiments were thus conducted at pressures of 1 and 0.5 Torr to ensure reliable and consistent results.

Fig. 2 shows the room temperature (294 K) absorption spectrum of H₂CO in the wavenumber range 31250–31950 cm⁻¹ (320–313 nm). This spectral region covers two vibrational bands, denoted conventionally as 2²₀4³₀ and 2³₀4¹₀ (see ref. 9), that are part of the extensive progression of bands in the ùA₂–X̃¹A₁ electronic absorption spectrum. The spectrum is plotted as absolute absorption cross sections (in cm² molecule⁻¹) against vacuum wavenumber (in cm⁻¹), with cross sections determined at the resolution of the probe laser beam. Peak values reach the range of 2.0–2.5 × 10⁻¹⁹ cm² molecule⁻¹. As shown in the lower resolution, but broader wavenumber coverage spectra of Cantrell et al.,¹³ these are two of the stronger vibrational bands in the near UV region of the H₂CO absorption spectrum. As a result of their wavelengths and relative strengths, these will be important absorption bands for the photochemical activity of formaldehyde in the troposphere.

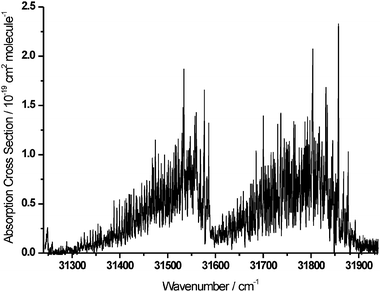Fig. 2 Rotationally resolved absorption cross-sections of the 2²₀4³₀ (left) and 2³₀4¹₀ (right) vibrational bands of the ùA₂–X̃¹A₁ electronic transition of H₂CO.

The peak cross sections in Fig. 2 are larger than the corresponding values reported by Cantrell et al. from a lower resolution spectrum.¹³ A comparison of the current experimental results with the two previous highest-resolution studies in the literature is shown in Fig. 3. The stated instrumental resolutions of spectra obtained by Cantrell et al.¹³ and Meller and Moortgat⁸ were, respectively, 1.00 cm⁻¹ and 2.73 cm⁻¹ (the latter specified as 0.028 nm at wavelengths around 320 nm). The improvement in wavenumber resolution that is achieved in this study brings the resolution very close to the limit of Doppler broadening of rotational linewidths. In such highly structured bands, as is evident from the figure, absorption cross sections are severely underestimated unless the resolution of the spectrometer closely approaches the widths of the sharpest spectral features. On the strongest peaks in the spectral region studied, an increase of ∼30% in absorption cross sections over the 1.00 cm⁻¹ resolution measurements is obtained, while for some of the lower intensity lines towards the high-wavenumber end, the increase can be as much as ∼100%. The higher measured absorption cross sections could influence whether certain spectral lines can be observed experimentally in the atmosphere by ground based, airborne or satellite instruments.

Fig. 3 A comparison of measurements of H₂CO absorption cross sections from the current study with data obtained previously at lower spectrometer resolutions. Top panel: laser absorption spectrum with a resolution of 0.1 cm⁻¹. Middle panel: spectrum obtained from a FT spectrometer with stated resolution of 1.00 cm⁻¹ (from ref. 13). Bottom panel: spectrum obtained from a diode array spectrometer with stated wavelength resolution of 0.028 nm at 320 nm (from ref. 8).

To demonstrate further the effects of spectrometer resolution and the advantages of making measurements at the highest possible resolution, and to enable a fully quantitative comparison with the earlier absorption cross section measurements, the data for the 2³₀4¹₀ vibronic band obtained in the current study were convoluted with an instrument function chosen to mimic the lower resolution of the experiments in ref. 13. The instrument function was assumed to be Gaussian in form, with a FWHM set to the stated value of 1.00 cm⁻¹. A comparison of the convoluted spectrum with the data of Cantrell et al.¹³ is shown in Fig. 4. The quantitative correspondence between the two data sets is remarkable across the full extent of the band. The difference between the two spectra is plotted in the lowest panel as a function of wavenumber, and the average of the magnitudes of the differences for both the 2²₀4³₀ and 2³₀4¹₀ bands is 7.0 × 10⁻²¹ cm² molecule⁻¹. The same approach was used to reduce the resolution of our data for comparison with measurements of Meller and Moortgat⁸ and, again, excellent agreement was observed. Fig. 5 shows a more detailed comparison, over a 100 cm⁻¹ wavenumber portion of the 2³₀4¹₀ band, between our data, convoluted with Gaussian functions of the appropriate FWHM, and spectra from refs. 8 and 13. In Table 1 we present integrated absorption cross sections for the 2²₀4³₀ and 2³₀4¹₀ bands, with integrations performed numerically using the trapezoidal method over respective wavenumber ranges of 31275–31600 cm⁻¹ and 31600–31900 cm⁻¹. The results are compared with the values for the data from Cantrell et al.¹³ and those obtained by integration of the spectra of Meller and Moortgat.⁸

Fig. 4 The effects of convolution of spectra from the current study with an instrument function of reduced resolution. Top panels: comparison of a spectrum of the 2³₀4¹₀ band obtained by convoluting our data with a 1.00 cm⁻¹ FWHM Gaussian function (panel A) with part of the spectrum from Cantrell et al.¹³ (panel B). Bottom panel: the A − B difference spectrum (on the same vertical scale).

Fig. 5 Expanded view of a portion of the 2³₀4¹₀ band, showing the detailed effects of convolution of spectra from the current study with instrument functions of reduced resolution. Top row: our data convoluted with 1.00 cm⁻¹ (panel A) and 2.73 cm⁻¹ (panel B) FWHM Gaussian functions. Bottom row: absorption cross-section data from Cantrell et al.¹³ (panel C) and Meller and Moortgat⁸ (panel D).

Table 1 Integrated absorption cross sections for the 2²₀4³₀ and 2³₀4¹₀ bands over the respective wavenumber ranges 31275–31600 cm⁻¹ and 31600–31900 cm⁻¹. Values obtained from this work are compared with results from Cantrell et al.^13a and results obtained by integration of the spectra of Meller and Moortgat⁸

	10^17 × Integrated absorption cross section/cm^2 molecule^−1 cm^−1
	2^204^30	2^304^10
a There is a typographical error in the exponents of the integrated absorption cross sections reported in ref. 13.
This work (293 K)	1.15	1.43
This work (263 K)	1.19
Cantrell et al. (293 K)	0.976	1.32
Cantrell et al. (263 K)	0.905	1.22
Meller and Moortgat (293 K)	1.02	1.37

---

Vibrational-level-dependent rotational constants for the X̃¹A₁ and ùA₂ electronic states are given in the literature, and the most comprehensive and recent sets⁹ were used in spectral simulations that employed the program PGOPHER.¹⁹ Simulations of the 2³₀4¹₀ band are satisfactory, but there are clear shortcomings when simulated spectra of the 2²₀4³₀ band are compared in detail with experimental data, either from the current study or from Cantrell et al.; the overall band shapes and features are, however, quite well reproduced. Discrepancies may be a consequence of imprecise upper state rotational constants or local perturbations, and attempts to refine the simulations by fits to the new experimental spectra are in progress. Simulations of both bands, performed at a wavenumber resolution of 0.10 cm⁻¹ (a Gaussian function designed to mimic the laser lineshape), show considerably more rotational structure than is evident even in our high resolution spectra. As the simulations shown in Fig. 6 demonstrate, it is necessary to introduce a Lorentzian component with a FWHM of 0.5–0.6 cm⁻¹ to reproduce the experimentally observed shapes of spectral lines. Although a precise determination of this line-broadening component requires better simulations of line positions, the calculated spectra definitively demonstrate a substantial lifetime broadening that dominates Doppler broadening effects. Simulations of the data of Cantrell et al., with a Gaussian resolution function of width 1.0 cm⁻¹ (corresponding to their instrumental resolution) are much improved if an additional Lorentzian component of FWHM 0.5 cm⁻¹ is also incorporated. We conclude that the rotational levels of the excited state have lifetimes of ∼10 ps, which is consistent with the known photochemistry of formaldehyde as represented in eqns. (1) and (2). The S₁ level lifetimes are probably controlled by the rates of internal conversion, which results from coupling to broad resonances of the S₀ state that lie higher in energy than the thresholds of the two dissociation channels. The lifetime broadening is sufficiently large that it is not necessary to know the exact bandwidth and lineshape of our laser to interpret the absorption cross sections. All data are recorded at a resolution that is greater than the sharpest features in the spectrum and thus our measurements should correspond to true absorption cross sections even though we are not quite at the Doppler broadening resolution limit. The same is not true, however, for the data of Cantrell et al.¹³, Meller and Moortgat,⁸ and others, who all employed spectrometers with instrument functions broader than the Lorentzian broadening components of the rovibrational spectral lines.

Fig. 6 Comparison of the experimental spectrum with spectral simulations with different lineshape functions. Top panel: a simulated spectrum with lineshape contributions from Doppler broadening and a laser bandwidth of 0.1 cm⁻¹. Bottom panel: the lower figure is an experimental spectrum, and the upper one is a simulation that also incorporates a 0.5 cm⁻¹ FWHM Lorentzian contribution to the lineshape to account for lifetime broadening. The simulation is offset vertically for clarity.

Absorption cross sections of formaldehyde are of greatest use in atmospheric monitoring and photochemistry if the effects of an ambient pressure of bath gas are quantified. Pressure broadening is well-known to reduce peak absorption cross sections in structured spectra and to cause nearby lines to merge. First measurements of added pressures of nitrogen gas on the H₂CO ùA₂–X̃¹A₁ 2³₀4¹₀ band are shown in Fig. 7 over a narrow wavenumber range to illustrate the effects on linewidths and peak intensities. The bath gas has very little effect on the overall magnitudes of the absorption cross sections at peaks of absorption, even at pressures of 500 Torr, but can be seen to induce a modest degree of pressure broadening in the line shapes (estimated to be ∼0.2 to 0.3 cm⁻¹ atm⁻¹). These observations are consistent with the lines already being substantially broadened by the short lifetimes of levels of the ùA₂ state: the mean intervals between collisions at 500 Torr are greater than the estimated 10 ps natural lifetimes of the excited state levels. Even at 500 Torr, the lines are still considerably sharper than the instrument resolutions used in previous studies, and precise determination of absorption cross sections necessitates high resolution studies of the type reported here.

Fig. 7 Absorption cross sections for a small portion of the 2³₀4¹₀ band of the ùA₂–X̃¹A₁ transition of H₂CO, showing data taken at three different pressures of added N₂ bath gas: (a) 500 Torr; (b) 200 Torr; (c) 0 Torr.

Formaldehyde is distributed throughout the troposphere and thus knowledge of the temperature variation of the absorption spectrum is also required. This information can, in principle, be obtained from accurate spectral simulations given precise knowledge of the rotational constants of the ground and excited vibronic states (and any perturbations of rotational energy levels). In the absence of fully reliable simulations, however, the spectrum can be recorded in absorption using a cooled sample chamber, and typical results are shown in Fig. 8 for the absorption cross sections of the H₂CO ùA₂–X̃¹A₁ 2²₀4³₀ band at 294 and 263 K. The bottom panel shows the difference between the two spectra, and an increase in absorption cross sections is evident towards lower wavenumbers (longer wavelengths) in the lower temperature spectrum. Some considerable care has to be taken in interpreting such spectra because of the presence of overlapping bands at both ends of the wavenumber scale. For example, the strong peaks at wavenumbers around 31250 cm⁻¹ come from a different vibronic band, as has been demonstrated by spectral modelling. In the wavenumber region from 31300 to 31350 cm⁻¹, the intensities of rotational lines arising from higher J″ levels are observed to decrease with reduction in the temperature.

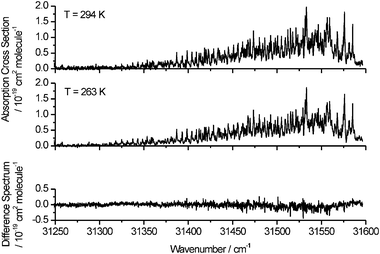Fig. 8 Top panel: Absorption cross sections of the H₂CO ùA₂–X̃¹A₁ 2²₀4³₀ band at temperatures of 294 and 263 K. Bottom panel: the difference spectrum obtained by subtraction of the 263 K data from the 294 K data.

Although the above results and discussion have highlighted the benefits of measurement of formaldehyde cross sections at instrument resolutions approaching closely the Doppler limit, there are also disadvantages associated with our experimental approach. Most obvious is that the data acquisition rate is slow, being limited by the laser repetition rate (10 Hz) and scanning speed. The laser based method measures absorbance at each wavelength individually, and cannot compete for efficiency with spectrometers using Fourier transform methods.

This study does, however, show the power of using a scanning laser technique for high-resolution absorption studies, and will now be extended to cover other bands within the ùA₂–X̃¹A₁ electronic excitation spectrum. The lower energy region, towards the 360 nm long-wavelength limits of the spectrum, may well contain the most useful bands for the Earth observation community because they suffer least from overlap with ozone absorption, and should contain sharper spectral features. As well as a greater wavelength range, further relevant temperature and pressure regimes will be investigated, as will the effects of added air (rather than N₂) on spectral line broadening. Data files of wavelength dependent absorption cross sections obtained under the various experimental conditions described in this paper, and convoluted with 0.1, 0.2 and 1.0 nm FWHM Gaussian functions are available as electronic supplementary information (ESI).† The cross sections obtained for 1.0 nm wavelength resolution should be treated with caution at the low and high wavenumber ends because the contributions from neighbouring vibronic bands are not incorporated.

Acknowledgements

Funding for this work from the NERC Upper Troposphere and Lower Stratosphere programme is gratefully acknowledged. We thank M. I. Mazurenka for his contributions to the early stages of this work, K. N. Rosser and Dr C. Murray for considerable technical assistance, and Dr D. E. Shallcross for many valuable discussions.

References

1. G. P. Brasseur, J. L. Orlando and G. S. Tyndall, Atmospheric Chemistry and Global Change, Oxford University Press, 1999.
2. D. J. Wuebbles and K. Hayhoe, Earth Sci. Rev., 2002, 57, 177.
3. M. Sprengnether, K. L. Demerjian, N. M. Donahue and J. G. Anderson, J. Geophys. Res., 2002, 107, 4269.
4. W. B. DeMore, S. P. Sander, D. M. Golden, R. F. Hampson, M. J. Kurylo, C. J. Howard, A. R. Ravishankara, C. E. Kolb and M. J. Molina, Data for Use in Stratospheric Modelling, Evaluation No. 12, JPL Publ. 97-4, Jet Propulsion Laboratory, Pasadena, CA, 1997.
5. K. Riedel, R. Weller and O. Schrems, Phys. Chem. Chem. Phys., 1999, 1, 5523.
6. I. D. Williams, D. M. Revitt and R. S. Hamilton, Sci. Total Environ., 1996, 189/190, 475.
7. D. Grosjean and R. D. Swanson, Sci. Total Environ., 1983, 29, 65.
8. R. Meller and G. K. Moortgat, J. Geophys. Res., 2000, 105, 7089.
9. D. J. Clouthier and D. A. Ramsay, Annu. Rev. Phys. Chem., 1983, 34, 31.
10. L. R. Valachovic, M. F. Tuchler, M. Dulligan, Th. Droz-Georget, M. Zyrianov, A. Kolessov, H. Reisler and C. Wittig, J. Chem. Phys., 2000, 112, 2752.
11. A. M. Bass, L. C. Glasgow, C. Miller, J. P. Jesson and D. L. Filkin, Planet. Space Sci., 1980, 28, 675.
12. J. D. Rogers, J. Phys. Chem., 1990, 94, 4011.
13. C. A. Cantrell, J. A. Davidson, A. H. McDaniel, R. E. Shetter and J. G. Calvert, J. Phys. Chem., 1990, 94, 3902.
14. P. I. Palmer, D. J. Jacob, A. M. Fiore, R. V. Martin, K. Chance and T. P. Kuroso, J. Geophys. Res., 2003, 108, 4180.
15. J. P. Burrows, M. Weber, M. Buchwitz, V. Rozanov, A. Ladstätter-Weißenmayer, A. Richter, R. DeBeek, R. Hoogen, K. Bramstedt, K. Eichmann and M. Eisinger, J. Atmos. Sci., 1998, 56, 151.
16. K. Chance, P. I. Palmer, R. J. D. Spurr, R. V. Martin, T. P. Kuroso and D. J. Jacob, Geophys. Res. Lett., 2000, 27, 3461.
17. W. Thomas, E. Hegels, S. Slijkhuis, R. Spurr and K. Chance, Geophys. Res. Lett., 1998, 25, 1317.
18. R. Spence and W. J. Wildm, J. Chem. Soc., 1935, 1, 338.
19. C. M. Western, PGOPHER, spectral simulation program, University of Bristol.

---

Footnote

† Electronic supplementary information (ESI) available: Wavelength-dependent cross sections acquired at 293 K and 263 K. See http://www.rsc.org/suppdata/cp/b4/b414183k/

---