Photochemical α-cleavage of ketones: revisiting acetone

Abstract

The photochemical α-cleavage of acetone is analyzed in view of recent results obtained for the isolated molecule in supersonic jets. The fluorescence decay time of the isolated molecule spans a range of more than six orders of magnitude, from ∼10⁻⁶ s near the origin of the S₀–S₁ transition to less than 10⁻¹² s at about 20 kcal mol⁻¹ excess energy. In contrast, the decay time of the excited singlet (S₁, ¹nπ*) in the bulk is around 10⁻⁹ s and independent of excitation wavelength. Initial excitation to the ¹nπ* state is followed by internal conversion (IC) to the ground state and intersystem crossing to the lowest-lying triplet. The rate constants of these processes are comparable to the radiative decay rate constant for excess energy up to 7 kcal mol⁻¹ above the origin of the S₀–S₁ transition. Beyond that energy, the triplet state becomes dissociative and the ISC rate becomes much larger than other processes depleting S₁. The primary reaction on the triplet surface is a barrier-controlled α-cleavage to form the triplet radical pair CH₃˙ + CH₃CO˙. Direct reaction from the S₁ is negligible, and the non-quenchable reaction (by triplet quenchers) observed in the bulk gas phase is due to hot triplet molecules that dissociate on the timescale of 10⁻¹² s or less. The singlet-state decay time measured in the bulk (∼1–2 ns) arises from collision-induced processes that populate low-lying levels of S₁. The analysis is aided by detailed state-resolved studies on related molecules (in particular formaldehyde and acetaldehyde) whose photophysics and photochemistry parallel those of acetone.

---

Yehuda Haas

Yehuda Haas was born and educated in Israel. After a period as a post-doctoral researcher (1973–1975) at the University of California, Berkeley, USA, he joined the Hebrew University of Jerusalem, where he is a Professor of Physical Chemistry. His current research interests include experimental and theoretical studies of photochemical reactions in supersonic jets and cryogenic matrices, the role of conical intersections in molecular photochemistry, light-induced electron transfer, laser processing of materials, high energy density materials and science teaching.

---

I Introduction

The photochemical decomposition of acetone and other aliphatic ketones following excitation of the nπ* state is one of the most comprehensively investigated reactions; some authors claim that it is the most thoroughly studied organic photo-reaction.¹ It has even been stated that “The photolysis of acetone is undoubtedly the most studied reaction in gas phase kinetics”.² The primary process of this reaction is the cleavage of the CC bond α to the carbonyl group to form an acetyl and a methyl radical:³

CH₃C(O)CH₃ → CH₃CO˙ + CH₃˙ (1)

The radicals proceed to form final products by a variety of secondary reactions^4–6. Analogous reactions are known for many ketones, both aliphatic and aromatic, as well as for aldehydes.

The first detailed mechanistic studies were carried out by Norrish and co-workers.^3,7,8 His contribution is acknowledged in the naming of the reaction as the Norrish type I process, and the mechanism he proposed is still the basis for analyzing the reaction.⁴ The parent carbonyl compound, formaldehyde, is also known to undergo α-cleavage following nπ* excitation, but in this case, a molecular dissociation channel is also observed:

H₂CO → H₂ + CO Molecular channel (2)

H₂CO → H˙ + HCO˙ Radical channel (3)

In acetaldehyde photolysis, the dominant primary reaction is CC bond cleavage;⁹ other primary reactions, CH₃C(O)–H cleavage and molecular dissociation (to CH₄ and CO), for instance, are minor channels.

The molecular channel forming ethane and carbon monoxide is not observed for acetone, which serves as a prototype ketone for this reaction. Other primary reactions, such as reactions 4 and 5, have been proposed,¹⁰ but not observed in the bulk gas phase or under collision-free conditions¹¹ (in this context, the term ‘bulk’ means any environment in which collisions affect the system; in practice, all environments except free jet expansion).

(CH₃)₂CO → H˙ + CH₃C(O)CH₂˙ (4)

(CH₃)₂CO → CH₄ + CH₂CO (5)

The major end products in the gas phase photolysis at room temperature are CO, ethane and methane, while biacetyl and some higher oxygenated compounds are observed as minor products. The product distribution of the photochemical reaction is different from the thermal one, although the initiation reaction (α-cleavage) is the same, indicating different dominant secondary processes. It is of some interest to explore the reasons for this diifference, as they may be helpful in elucidating the photochemical mechanism.

In the thermal pyrolysis reaction, which is also initiated by α-CC bond cleavage, the major end products are CO, methane and ketene.² Minor products are ethane, butanone and 2,5-hexanedione. These observations were rationalized by the Rice–Herzfeld mechanism,¹² summarized in the following sequence of reactions.

(CH₃)₂CO → CH₃˙ + CH₃CO˙ (1)

CH₃CO˙ → CH₃˙ + CO (6)

CH₃˙ + (CH₃)₂CO → CH₄ + CH₃C(O)CH₂˙ (7)

CH₃C(O)CH₂˙ → CH₂CO + CH₃˙ (8)

2CH₃˙ → C₂H₆ (9)

CH₃˙ + CH₃C(O)CH₂˙ → CH₃C(O)CH₂CH₃ (10)

2CH₃C(O)CH₂˙ → [CH₃C(O)CH₂]₂ (11)

The chain propagation reactions (reactions 6–8) lead to the major products and the minor ones arise from the chain terminating radical recombination reactions (reactions 9–11).

In the photolysis reaction, the photon energy is often large enough to form the nascent acetyl radical with enough energy to release a CO molecule, and the major products are ethane, methane and CO in the gas phase. Ketene is not observed at ambient temperatures. The quantum yield of the reaction is temperature dependent, reaching 100% conversion in the gas phase at about 100–130 °C (3130 Å radiation).⁴ At shorter irradiation wavelengths, e.g. 2534 Å, the yield is 100% at room temperature. The yield of the reaction is severely reduced in the liquid phase^13–15 and essentially blocked in cryogenic matrices.

A very large amount of data are available for the acetone photolysis reaction, leading to a detailed proposed mechanism. The key processes believed to be important are summarized in the following sequence of reactions:

(CH₃)₂CO + hν → CH₃˙ + CH₃CO˙ (1)

CH₃CO˙ → CH₃˙ + CO (6)

CH₃˙ + (CH₃)₂CO → CH₄ + CH₃C(O)CH₂˙ (7)

CH₃C(O)CH₂˙ → CH₂CO + CH₃˙ (8)

2CH₃˙ → C₂H₆ (9)

CH₃˙ + CH₃C(O)CH₂˙ → CH₃C(O)CH₂CH₃ (10)

2CH₃C(O)CH₂˙ → [CH₃C(O)CH₂]₂ (11)

2CH₃CO˙ → (CH₃CO)₂ (12)

2CH₃CO˙ → CH₂CO + CH₃CHO (13)

CH₃˙ + CH₃CO˙ → (CH₃)₂CO (14)

CH₃˙ + CH₃CO˙ → CH₄ + CH₂CO (15)

All the reactions postulated in the thermal pyrolysis mechanism (Rice–Herzfeld) are included. Important bimolecular reactions excluded from the Rice–Herzfeld mechanism involve acetyl radicals (reactions 12–15). In the hot environment of the pyrolysis reaction, the concentration of acetyl radicals is too small for these reactions to be important, as the barrier to reaction 6 is very low (∼17 kcal mol⁻¹).¹⁶ In photochemical reactions carried out in bulk gas phase at room temperature, some nascent acetyl radicals are cooled by collisions and their concentration is high enough to make the contribution of recombination and other reactions of this radical non-negligible. Consequently, biacetyl is an observed product under these conditions, in contrast to the thermal case. On the other hand, some reactions that are important in the pyrolysis may be neglected at the much lower temperature at which the photolysis is carried out. Thus, reactions 7, 8, 10 and 11 are unimportant normally, and ketene is not obtained as an end product. At temperatures exceeding 200 °C, these reactions become observable and ketene, as well as other products arising from the acetonyl [CH₃C(O)CH₂˙] radical, are observed.¹⁷

Early work concentrated mainly on bulk samples, primarily in the gas phase (neat acetone or mixed with other gases). Data on the photo-reactions of truly isolated acetone became available only after the advent of modern techniques, such as molecular beams (mid 1980s) using laser-induced fluorescence (LIF) and resonance-enhanced multiphoton ionization (REMPI), and more recently, femtosecond excitation (as of the mid 1990s). These novel technologies allowed real-time monitoring of the processes relevant to the reaction under collision-free conditions. The elimination of collisional processes helped the analysis of the data and makes it possible, in principle, to monitor single quantum state behavior. At present, such detailed investigations of acetone photophysics are still impractical, but much can be learned from recent work on the smaller carbonyl molecules formaldehyde and acetaldehyde. The spectroscopy and dynamics of formaldehyde in particular were studied in great detail thanks to the experimental and theoretical efforts of a large number of people, notably Moore and co-workers.^18,19

The energy parameters and thermochemical quantities for acetone in the gas phase, as well as the energies of a few frequently used UV light sources, are listed in Table 1.

Table 1 Energetics of the acetone system (relative to the ground state)

	Energy/kcal mol^−1	Ref.
H3C–C(O)CH3 bond	84	2
H–CHC(O)CH3 bond	98	20
S1 origin	87	21
T1 origin	80	11, 22
Barrier on T1	94	23
Hg lamp, 313 nm line	91
Quadrupled Nd:YAG laser, 266 nm	107
Hg lamp, 254 nm line	112
KrF excimer laser, 248 nm	115

---

The purpose of this review is to summarize the emerging developments in acetone photochemistry (and, by deduction, of other aliphatic ketones). First, the classic views of acetone photochemistry as portrayed in original papers, reviews and textbooks will be considered. A comparison of the data with the information obtained by more recent techniques will follow. The subsequent analysis shows that some current conjecture, particularly concerning direct dissociation on the singlet surface, should be revised.

II The outlook on the photochemical α-cleavage of acetone before 1985

IIa Mechanism and quantum yields

Overall quantum yields of acetone photolysis were determined early on in the gas phase.^24,25 The primary quantum yield was found to depend on the excitation wavelength and the temperature:⁴ it is essentially 1 at 2534 Å, while irradiation at 3130 Å, the most extensively studied excitation wavelength, leads to a lower yield at room temperature. The yield increases with temperature, reaching 1 at above 100 °C. In the bulk, the reaction is complicated by the fact that biacetyl, produced by recombination of two acetyl radicals, absorbs at the irradiation wavelength and the resulting secondary reactions make analysis more difficult.²⁶ Moreover, biacetyl efficiently quenches the acetone triplet state, effectively reducing the quantum yield.

Radicals, postulated by early workers on the basis of kinetic data, were eventually directly observed in water solution by chemically induced dynamic nuclear polarization (CIDNP).²⁷ They could, however, be formed by bimolecular reactions of electronically excited molecules with ground-state ones. CIDNP and EPR were later used to unambiguously detect the primary radicals in the photolysis of higher ketones:^28–31 in fact, it is easier to observe the nascent radicals formed in the reactions of higher ketones, as their bonds cleave more easily.⁵ The identity of the primary step in acetone photolysis being thus firmly established, attention turned to the nature of the excited state(s) involved.

IIb Properties of the excited states: triplet and singlet

In organic photochemistry, a reaction is traditionally described as either a singlet- or triplet-type, according to the nature of the excited state that ‘forms’ the products.^6,32 This categorization should be used with care, as it is known today that in many photochemical reactions the chemical change actually takes place on the ground-state surface after rapid internal conversion or intersystem crossing.^33–35 A correct definition of a photochemical reaction as being singlet- or triplet-type should refer to the identity of the excited state leading to the final products, either directly or via the ground state. The properties of the excited state linked directly with the ground-state products significantly affect the product distribution and the energy disposal into the various degrees of freedom; therefore, the clarification of its nature is one of the major tasks of photochemical studies.

In the proposed early mechanism (reactions 1 and 6–15), light was presumed to cause the dissociation of the molecules to two radicals in one step. However, the initial optical excitation is always to S₁, and the question of whether the system proceeds directly to dissociation on one of the singlet surfaces or first undergoes intersystem crossing to the triplet is of central mechanistic importance.

The discovery of the molecular nature of the triplet state in the 1940s³⁶ led to extensive investigations into its involvement in photochemical reactions of carbonyl compounds.^37,38 The nature of the initially excited state (S₁) was comprehensively studied for the parent carbonyl molecule formaldehyde.^39,40 A similarly detailed analysis was unrealistic for acetone (though it is likely to become less so in the future), but it is believed that the basic properties of the excited states are comparable for all aliphatic carbonyls. The S₀–S₁ transition is symmetry forbidden (typical molar absorption coefficients of 10 M⁻¹ cm⁻¹) and the absorption spectrum is relatively broad (240–340 nm), indicating a significant change in geometry. In molecular orbital (MO) theory, the optical transition is assigned to the promotion of the non-bonding electron of the oxygen atom to an anti-bonding π* orbital. The excited state is therefore also termed the nπ* state, which may exist as a singlet (S₁, ¹nπ*) or as a triplet (T₁, ³nπ*). The weakening of the CO bond leads to lengthening and to pyramidalization of the excited state at the carbonyl carbon atom—these are the main structural changes. Both S₁ and T₁ have a double-well potential surface; the symmetry of formaldehyde is thus reduced from C_2v to C_s. The direct optical transition from the ground state to the triplet (S₀–T₁ transition) is highly forbidden, and is of no practical importance in the photochemistry of acetone as a route to populate the triplet. However, the triplet state is readily observed in emission as phosphorescence^4,24,41,42 and by triplet–triplet absorption.³⁷

The singlet nπ* state cannot cleave directly to the ground-state radical pair; in the Franck–Condon region, it is a bound state, as shown by the fact that it fluoresces. Its energy is high enough to break the C–C bond, but it correlates with a high-lying alkoxy biradical, (CH₃)₂C(↑)O(↓), and not with the required C(↑)H₃ + C(↓)H₃CO radical pair. The two states that can produce the carbon atom-centered radical pair are the ground state (S₀), in which the spins of two radicals are paired, and a triplet state (T₁), which yields a parallel-spin pair. The triplet associated with the nπ* transition is low lying in the Franck–Condon region, but like its singlet counterpart, correlates with a high-lying alkoxy biradical, (CH₃)₂C(↑)O(↑), as the CO bond is lengthened. The triplet that correlates directly with the ground triplet state C(↑)H₃ + C(↑)H₃CO radical pair is a σσ* (σ*_C–C excitation) state,¹¹ which is high lying in the Franck–Condon region. A schematic representation is shown in Fig. 1.

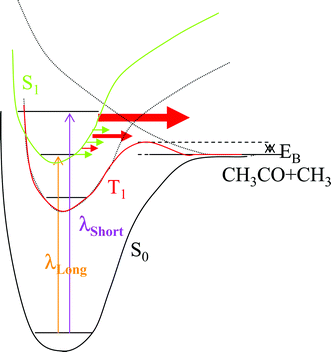Fig. 1 Schematic energy level diagram of acetone along the CC bond stretch. E_b is the barrier on the triplet surface and λ_long and λ_short are typical excitation wavelengths near the origin and above the triplet barrier, respectively. Green and red arrows symbolize IC and ISC from S₁ to S₀ and T₁, respectively. The size of the arrow is a measure of the relative value of the rate constant.

Thus, it is clear that the photochemical process must involve one or more radiationless processes that transform the initially excited singlet state to either the ground singlet state or the triplet manifold. In the triplet manifold, at least two states must be involved as the reaction proceeds. Much of the effort to understand the α-cleavage reaction was directed at elucidating these processes.

IIc Decay mechanisms of S₁ and T₁

The processes governing the decay of the S₁ state are fluorescence (rate constant k_f⁰), intersystem crossing (ISC) to T₁ (rate constant k_ISC) and internal conversion (IC) to S₀, (rate constant k_IC).

The observed decay time, τ_f, is given by

τ_f = 1/(k_f⁰ + k_ISC + k_IC) (16)

Intersystem crossing from the initially excited ¹nπ* (S₁) state to the triplet state ³nπ* (T₁), although symmetry forbidden,⁴³ does in fact take place, probably due to some small degree of mixing of ππ* character into the singlet state. The ISC rate constant (k ≈ 10⁹ s⁻¹) is much smaller than that found for allowed S–T transitions; for instance, in aromatic ketones (k ≈ 10¹¹ s⁻¹). The ³nπ* state is the only triplet state energetically accessible near the low-lying vibrational levels of S₁. That the radiationless transition takes place is evident from the fact that phosphorescence is observed in the gas phase⁴¹ and in condensed phases.⁴² Triplet–triplet absorption was observed by flash spectroscopy following optical excitation of acetone.³⁷ If the radicals are formed from the triplet state, they should be observable by magnetic spectroscopic methods such as EPR and CIDNP. This was indeed verified experimentally for many ketones subsequent to ¹nπ* excitation.⁶

A standard method for characterizing a reaction as singlet- or triplet-type is by energy transfer: some sensitizers or quenchers are highly specific for the triplet state and often do not affect the singlet state. By using a specific triplet sensitizer or triplet quencher, it is possible to establish the involvement of a triplet state in a photochemical reaction. Typical triplet quenchers are molecules containing heavy atoms such as I or Br, and molecules having low-lying triplet states, such as piperylene (trans- or cis-penta-1,3-diene) or biacetyl. Molecular oxygen (whose ground electronic state is a triplet) is also an effective triplet quencher. Triplet acetone was indeed found to be efficiently quenched by dienes in solution³⁸ and in the gas phase,⁴¹ by monitoring the emission yield. HBr was found to partly quench gas-phase acetone photolysis, but some excited molecules were not quenchable.⁴⁴ The system was analyzed in terms of two types of triplet states: a quenchable and a ‘vibrationally excited’ triplet state, which is non-quenchable. From an Arrhenius-type analysis based on an RRK fit, the Arrhenius parameters listed in Table 2 were deduced.

Table 2 Arrhenius parameters for gas-phase photolysis of acetone in the presence of HBr

	Log A(s^−1)	E a/kcal mol^−1
Quenchable triplet	11	9–10
‘Vibrationally excited’ triplet	15	17

---

These data led to a mechanism based on the energy level diagram reproduced in Fig. 2. Initial excitation to S₁ is followed by rapid intersystem crossing (rate constant k_ISC) to a highly excited triplet (T**). This state can either dissociate with a large rate constant, k**, or relax via collisions to the thermally equilibrated triplet T. The latter can be thermally activated to energies above the dissociation barrier, E_b, which was determined to be ∼17 kcal mol⁻¹.⁴⁴ The rate constant for dissociation of the thermalized triplet, k_d, was considered to be pseudo-first order. The highly excited triplet is not fully quenchable by conventional triplet quenchers due to its high reactivity.

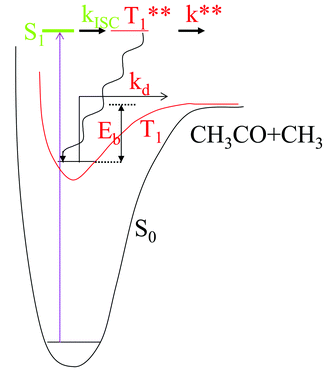Fig. 2 Mechanism suggested by ref. 44 to account for the observed kinetics of acetone photochemistry. Initial excitation is to a high-lying S₁ state that intersystem crosses to T₁. Some of the molecules are vibrationally relaxed to the bottom of the triplet potential surface (wavy line). From there, they subsequently react by thermally overcoming the barrier, with the rate constant k_d. Some of the initially prepared vibrationally excited triplet molecules react directly with a much larger rate constant (k**).

These results were in line with previous work by Cundall and Davis,⁴⁵ in which the photochemistry (under 2537 and 3130 Å excitation) of acetone was studied in the gas phase. From the variation of the product yield with pressure and temperature, they deduced two sets of Arrhenius parameters. For the quenchable triplet, A = 1.25 × 10¹⁰ s⁻¹, E_a = 6 kcal mol⁻¹, and for the non-quenchable part, which they assigned to singlet (S₁) reaction, A = 2.5 × 10¹⁶ s⁻¹, E_a = 16 kcal mol⁻¹.

Larson and O'Neal's⁴⁴ depiction of the highly reactive species as an ‘unquenchable’ triplet was not generally accepted: the consensus appears to be that the ‘unquenchable’ state is in fact the nπ* singlet.^6,32,33 As a corollary of this consensus, it has been assumed that the different activation energies obtained from the analysis of the temperature and wavelength dependence of the yield^44,45 should be interpreted as barriers on the triplet (9 kcal mol⁻¹) and singlet (17 kcal mol⁻¹) surfaces. This ‘experimental’ result was difficult to explain theoretically. Attempts using correlation diagrams have appeared in the literature^46–48 and in textbooks.^6,32,33 A measure of their ambiguity is the fact that close inspection shows that different correlation diagrams were put forward by different authors. One of the weak points in these analyses was the fact that the CH₃˙ + CH₃CO˙ singlet radical pair was proposed to correlate to an electronic excited state of acetone, rather than to the ground singlet state. A 1976 review considers the difference in rate constants and activation energies as a puzzle “to this day” (i.e. in 1976).⁵

In a subsequent paper, O'Neal and Larson⁴⁹ expressed some doubts concerning the validity of the RRK parameters and proposed a somewhat different mechanism in which an electronically excited dissociative singlet state (not specified) participates. This interpretation is untenable, as there is no singlet state that correlates with the singlet C(↑)H₃+C(↓)H₃CO radical pair, apart from the ground state.

IId Direct measurement of S₁ decay rates

The main experimental evidence supporting direct singlet-state dissociation came from the analysis of fluorescence lifetime measurements. The advent of single photon counting in the late 1960s allowed the measurement of fluorescence lifetimes down to about 1 ns. Many measurements were made for acetone (and other ketones). Some representative data are summarized in Table 3.

Table 3 Fluorescence decay times of acetone and other ketones (pre-1980 values)

Molecule	Solvent	λ exc/nm	τ/ns	Ref.
a Values in parentheses are for the per-deuterated molecule. b trans-DMCP = trans-3,4-dimethylcyclopentanone.
Acetone	Gas		2.5	50, 51
	Gas (O2 added)	260	>1.6	52
		280	1.7	52
		295	2.1	52
		313	2.7	52
	Hexane		>1.6	52
	Hexane		2	53
	Cyclohexane		1.7	50
	Various		2.5	42
Acetone-d6	Gas		3.4	50
	Neat liquid		1.7	50
	Cyclohexane		2.3	50
	Benzene		2.3	50
Cyclobutanone	Gas	<310	≪1	52
		320	4.7	52
Cyclopentanone (d8)^a	Gas	260	<1.8 (3.2)	52
		280	2.1 (3.5)	52
		300	2.25 (3.6)	52
		320	2.4 (4.1)	52
trans-DMCP^b	Gas	320	4.8	52
Cyclohexanone	Gas	270	2.9	52
		295	2.9	52
		320	3.2	52

---

Several generalizations can be made: (1) the fluorescence lifetime of acetone is practically the same in the gas phase as it is in many solvents (a value of 2 ± 1 ns is almost universal); (2) moreover, this value is approximately the same for other small ketones; (3) there is a small, but measurable, isotope effect—the decay time of acetone-h₆ is shorter than that of acetone-d₆; (4) there is a small wavelength dependence for acetone—the lifetime decreases somewhat as the excitation wavelength is decreased; (5) substitution of methyl groups on cyclopentanone increases the lifetime slightly (by a factor of two).

Similar results were obtained for many other ketones. From these results, Breuer and Lee concluded that the lifetime of singlet states is an intrinsic property, determined by the intersystem crossing rate constant.⁵² This conclusion rests on the assumption that the most efficient process in aliphatic ketones is intersystem crossing to the triplet, which takes place with nearly 100% efficiency.

However, other experiments appeared to show that S₁ states of aliphatic ketones do not decay by intersystem crossing alone. Thus, Wettack et al.⁵³ used very high concentrations of piperylene (up to 10 M) to study the quenching of acetone fluorescence. They found a decrease in the measured lifetime, from which a quenching rate constant of 9 × 10⁷ M⁻¹ s⁻¹ was deduced. This should be compared with the rate constant for triplet quenching, which is about 10¹⁰ M⁻¹ s⁻¹, i.e. two orders of magnitude bigger. In a similar paper, the photochemistry of methyl tert-butyl ketone was studied.⁵⁴ From a comparable quenching experiment, it was concluded that the rate constant for α-cleavage from the triplet state is also two orders of magnitude larger than the singlet-state rate constant. These and similar considerations⁵⁵ have been accepted as the basis for the theoretical analysis of the system.^6,46–48

The calculation of the reactivity of the singlet state was centered on its measured fluorescence lifetime, of the order of 10⁻⁹ s (Table 3). Thus, the upper limit for the rate constant for α-cleavage from the excited singlet state was assumed to be around 10⁹ s⁻¹. This line of reasoning is based on the notion that the reaction takes place on the thermalized S₁ potential surface. As revealed in recent femtosecond experiments (Section III), this is not necessarily the case, and the real lifetime of vibrationally excited S₁ levels may be much shorter due to intersystem crossing or internal conversion to S₀.

A final remark needs to be made concerning the controversy that was raised by direct measurements of the fluorescence lifetime, τ_f, and the fluorescence yield, ϕ_f. The radiative lifetime, τ_f⁰, can be calculated from these quantities using the relation τ_f⁰ = τ_f/ϕ_f. Using the measured nanosecond lifetime, τ_f⁰ turns out to be about 1 µs. Another method of calculating the lifetime is from the absorption spectrum, using the Einstein relation connecting the integrated absorption coefficient, ∫ε dν, with the rate constant for radiative emission, A = 1/τ_f⁰.⁵⁶ This method yielded a value that was an order of magnitude larger (τ_f⁰ ≈ 10 µs). The source of this disagreement was not clear.⁵⁷

To summarize, the following points remained to be resolved in the early 1980s: (1) what is the correct radiative lifetime of an isolated acetone molecule? (2) Why are the decay times in a collision-dominated system always around 1 ns? (3) What is the nature of the reacting non-quenchable excited state of acetone? Is a direct reaction from the S₁ state important? (4) Is there a barrier on the triplet surface and what is its value? (5) What are the relative contributions of ISC and IC to the non-radiative decay of S₁?

More recent experiments appear to provide answers to all these queries, paving the way to a coherent explanation of acetone photochemistry.

III The photohysics of isolated acetone molecules

The first indications that the true collision-free photophysics of acetone require much lower pressures than previously assumed came from bulk experiments in the milliTorr pressure range.⁵⁸ It was found that the fluorescence decay time of acetone is much longer than had previously been believed. Doubts about the earlier interpretation of the photophysics of acetone arose when it was found that the lifetime was much longer than previously measured: near the origin, the decay time of acetone-h₆ was found to be ∼0.8 µs and that of acetone-d₆ nearly 3.3 µs. These results had immediate consequences concerning the controversy over the radiative lifetime of acetone (see above); obviously a radiative lifetime of 1 µs is not realistic, and the value derived from the integrated absorption coefficient (∼10 µs) must be the correct one.

Regrettably, the room temperature decay times exhibited a grossly non-exponential decay; more precise analysis was hampered by the fact that several different vibrational and rotational levels of acetone were probably simultaneously excited under these conditions. Single vibrational level (SVL) excitation of acetone fluorescence became possible only after the widespread introduction of supersonic jet cooling. This technique allowed for the first time the probing of truly collision-free molecules in the gas phase; an added bonus was that the low vibrational and rotational temperature of such samples removed much of the spectral congestion characterizing the room temperature work. The first study of the S₀–S₁ transition of jet-cooled acetone²¹ immediately yielded the precise frequency of the 0–0 band, and of several low-lying vibronic levels of S₁. Subsequently, a rotationally resolved spectrum of a few low-lying vibronic levels of acetone-h₆ was recorded.⁵⁹ The 0–0 band was fully analyzed and about 600 lines could be assigned; each rotational band was found to be a multiplet, mostly a triplet due to splitting by the methyl group. The 0–0 band was found to be an A-type transition, resolving a controversy about the polarization of the transition.²¹ Higher bands were found to be more difficult to analyze due to complications arising from various interactions (Coriolis, interactions with triplet levels) and some still await a complete assignment.

Zuckermann et al.²³ measured the decay times of single vibronic levels of jet-cooled acetone at medium resolution (0.4 cm⁻¹)—many rotational lines were simultaneously excited. In view of the detailed work on formaldehyde (see below), the data obtained must be regarded as average values over many eigenstates. Nonetheless, a clear trend was observed, as shown in Fig. 3. In contrast to the previous bulk data,⁵⁸ the fluorescence decay curves were very nearly exponential and numerical estimates could be extracted with more confidence. At the origin, the long lifetimes of acetone-h₆ and acetone-d₆ were firmly established. The decay times of deuterated acetone were consistently longer than those of the protonated molecule. Rate constants measured for both isotopomers moderately decreased as the excitation energy was increased up to about 2200 cm⁻¹ above the S₁ origin. At that energy, the decay rates suddenly increased, so that the observed decay times were smaller than the time resolution of the apparatus (∼10 ns) over an interval of ∼100 cm⁻¹.

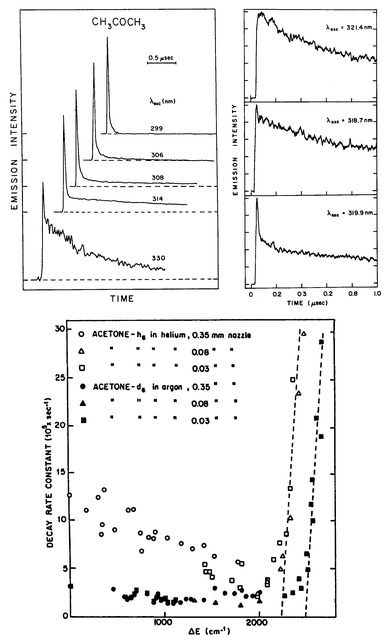Fig. 3 Fluorescence decay of acetone. Top left: data obtained for low pressure bulk acetone. A short lived component is observed at all excitation wavelengths.⁵⁸ Top right: data obtained for jet-cooled acetone. The short-lived component near the origin is absent.⁶⁰ When higher resolution excitation is used, the decays are exponential. Bottom: the fluorescence rate constants of jet-cooled acetone as a function of excess energy.²³

The interpretation offered for these data^23,61 was that near the origin, non-radiative transitions to S₀ and to T₁ dominate the decay of S₁. The isotope effect was assigned primarily to coupling to S₀ rather than to T₁: the larger quantum of the CH oscillator (compared to the CD one) makes the transition more effective, in agreement with the energy gap law.⁶² Similar results were known for long-lived electronically excited states; for instance, formaldehyde,¹⁸ aromatic hydrocarbons^63,64 and Eu³⁺ solutions.⁶⁵ As long as the triplet state is bound, intersystem crossing rates are slow;¹⁸ once the barrier for triplet dissociation is exceeded, the width of the triplet levels coupled to S₁ levels increases dramatically, and with it the ISC rate. Assuming that the triplet state lies at 80 kcal mol⁻¹, this translates to a 14 kcal mol⁻¹ dissociation barrier on the triplet surface. Significantly, it also means that there is a 10 kcal mol⁻¹ barrier for the recombination of the two radicals on the triplet surface. This result is in agreement with a low pressure bulk measurement of acetone phosphorescence in the gas phase,⁶⁶ in which a sharp decrease in the intensity upon excitation in the same energy range was detected. At excitation energies above this threshold, ISC completely dominates the decay of S₁.

The first truly collision-free photo-dissociation experiment on acetone was conducted by Waits et al.²² in a molecular beam. Excitation was at 266 nm (excess energy above the S₀ 107 kcal mol⁻¹). It was found that the molecule cleaved exclusively to yield the acetyl and methyl radicals. The dissociation was found to be isotropic, in contrast to the results of a previous bulk experiment.⁶⁷ Analysis of the velocity of the products indicated that the average energy release to product translation is about 14 kcal mol⁻¹. This large fraction of the available energy released to translation indicates that the dissociation is mediated by a barrier on the outgoing channel. The similarity to the value determined by Zuckermann et al.²³ suggests that the dissociation takes place primarily on the triplet surface. A few years later, Lee et al.¹¹ re-examined the system using 248 nm excitation (corresponding to 115 kcal mol⁻¹ excess energy above the S₀). In spite of the extra 8 kcal mol⁻¹ energy input, the translational energy release was again found to be ∼14 kcal mol⁻¹, supporting the idea of an exit-channel barrier. Also in agreement with the previous study, the spatial distribution was found to be isotropic. In these studies, no indication for a 17 kcal mol⁻¹ second barrier over the S₁ origin could be detected. At 266 nm irradiation, the excess energy is only 3 kcal mol⁻¹ (see Table 1), which may make it difficult to monitor a kinetic effect. However at 248 nm, the photon energy would be 11 kcal mol⁻¹ over the presumed barrier.⁶ The large exit barrier should have appeared as an extra peak in the translational energy release, but none was found.

The first sub-picosecond experiment on acetone photo-dissociation was published in 1995⁶⁸ and used a two-photon process that excited states higher than the nπ* state. Later, two groups used single-photon excitation to probe the ultrafast dissociation of acetone at 259⁶⁹ and 266 nm.⁷⁰ Both groups reported that acetone dissociated within the pulse width, namely, in less than 150 fs. This result now closes a cycle: the decay time of a truly isolated acetone molecule at an excess energy of 107 kcal mol⁻¹ is less than a picosecond, more than three orders of magnitude shorter that the value assigned to the singlet state by bulk studies.⁵⁷ On the other hand, the decay time of acetone near the origin is three orders of magnitude longer than the bulk lifetime of ∼1 ns.

Table 4 lists the observed decay times of acetone upon excitation to different excess energies in S₁. Evidently, the decay rate of the isolated acetone molecule after excitation to different vibrational levels of S₁ is far from uniform: it spans a range of at least six orders of magnitude (from less than 10⁶ to more than 10¹² s⁻¹) over an energy range of 24 kcal mol⁻¹ (Table 4). These results can be used now to analyze the higher pressure (as well as the solution phase) data. Before attempting that, it is instructive to survey the photophysics of the simpler members of the carbonyl family, particularly formaldehyde, which were studied in great detail and are more amenable to direct comparison with theory. In the smaller H₂CO molecule, the details of the IC (S₁–S₀) and ISC (S₁–T₁) processes can be studied down to the level of single eigenstates.

Table 4 Fluorescence decay times of acetone (post-1980 values, supersonic jet)

Molecule	λ exc/nm	Excess energy/cm^−1	τ/ns	Ref.
Acetone	Origin	0	800	23
	305	2300	∼50	23
	266	7100	0.00015	70
Acetone-d6	Origin	0	3300	23

---

IV Diversion: a brief survey of the photophysics of formaldehyde and acetaldehyde

Comparison of the acetone photophysics with that of the simpler carbonyl compounds formaldehyde and acetaldehyde is vindicated by noting the many similarities between these molecules. The electronic transitions of all three molecules are to an nπ* state and the properties of the transitions are very similar: they are symmetry forbidden (vibronically allowed) and occur at about the same energy with approximately the same absorption cross-section. All three molecules exhibit fluorescence and phosphorescence in the gas phase, and all are dissociated by α-cleavage. It turns out that in all three molecules, the low-lying electronic excited state and the reaction thresholds lie within a rather small energy range. Table 5 lists the relevant values for formaldehyde, which can be seen to be similar to those reported in Table 1 for acetone. Thus, the origin of the S₁ and T₁ states, the threshold to radical dissociation and the barrier to molecular dissociation on S₀, as well as the barrier for radical dissociation on the triplet surface, are all found within a 14 kcal mol⁻¹ range. This state of affairs (which may be a coincidence) complicated the full analysis of the system on one hand, but also allowed a very detailed energy-resolved study on the other.

Table 5 Energetics of the formaldehyde system

	Energy/kcal mol^−1	Ref.
H–CHO bond	86.5	71
S0 barrier to H2 + CO	79.2	72
S1 origin	80.5	40
T1 origin	71.8	40
Barrier on T1	91.2	71

---

Formaldehyde has only six normal modes, and its UV absorption and fluorescence spectra have been fully analyzed.^39,40 The substantial vibrational spacing allows easy access to separate vibronic levels, whose assignment is firmly established. Moreover, the relatively large rotational constants allow access to single rotational lines with full JKM resolution, making it possible to study the photophysics of individual eigenstates of S₁. Since the 1980s much progress was made towards the goal of elucidating the mechanism of formaldehyde photo-dissociation. The following brief summary of some data obtained for formaldehyde following nπ* excitation (which is by no means intended to be comprehensive) is presented in order to put the results for acetone in the proper perspective.

The radical dissociation channel (reaction 3) produces hydrogen atoms that can be monitored by LIF using Lyman-α VUV radiation (L_α, 121.51 nm). Chuang et al.⁷¹ used this technique in conjunction with a tunable nanosecond UV laser (5 ns pulse duration, 0.4 cm⁻¹ bandwidth). The L_α source was also generated by a nanosecond laser and the two pulses were overlapped spatially in a flow cell, wherein formaldehyde was kept at 10–100 mTorr pressure. Fixing the probe laser on the peak of the hydrogen (or deuterium) atom L_α line and scanning the UV laser produced a photofragment excitation (PHOFEX) spectrum.

The threshold for H˙ + HCO˙ formation was determined by comparing the absorption spectrum (obtained using photoacoustic spectroscopy) with the PHOFEX spectrum. It was found that the threshold was between 85.91 and 86.75 for H₂CO and between 88.53 and 88.69 for D₂CO. These values agree very well with previous determinations of the dissociation on the ground-state surface,⁷³ and are therefore assigned to reaction on the S₀ surface, reached by IC from the S₁ state. The width of the H atom fluorescence excitation line is determined by its velocity due to the Doppler effect. Monitoring the width as a function of the photolysis laser excitation wavelength allows the determination of the translational energy release in the reaction as a function of excess energy. It was found that the width increased rather steeply over a relatively narrow range for both H and D atoms produced by dissociation of HDCO. In the interval between approximately 31 000 and 32 000 cm⁻¹, the increase in translational energy amounted to 80% of the total increase in excitation energy. This sudden upsurge, not consistent with a statistical distribution among all degrees of freedom, was assigned to the launching of an additional dissociation channel on the triplet surface. The barrier on the triplet surface adds a ‘kick’ that makes translation the dominant energy release channel. The barriers for both CH and CD bond dissociation reactions on the triplet surface were determined to be 92 and 93.5 kcal mol⁻¹ (above the ground state), respectively.

In addition to the radical channel, the molecular dissociation channel is observed in formaldehyde photochemistry (reaction 2). Its products correlate with the ground state through a barrier that is almost isoenergetic with the 0–0 band of S₁. Apart from fluorescence, this reaction is the only truly dissipative route that can deplete S₁ levels below the onset of the radical route. The fluorescence decay times of formaldehyde in this region are known to decrease as the excess energy is increased near the origin, though not necessarily in a regular fashion. It was found that different JKM sublevels of a given vibronic state may have widely different decay times. In order for an S₁ state to interact efficiently with an S₀ state, the two must be isoenergetic within their natural width, determined, in the case of S₀, by the dissociation reaction. In the unperturbed free molecule, such overlaps are accidental, but it is possible to cause the states to overlap using the Stark effect. The dipole moment of formaldehyde in the excited state (1.46 D) is smaller than that of the ground state (2.33 D).⁴⁰ Applying an electric field therefore shifts the levels of S₀ and S₁ to a different extent, and can be used to tune S₁ levels to resonance with S₀ ones. This technique was used by Polik and co-workers^72,74 to measure the decay times of D₂CO molecules near the threshold of the molecular channel. The deuterated molecule was used since, in the protonated analog, the decay times turn out to be already too short in the first observed band. It was found that at about 28 370 cm⁻¹, there are over 400 S₀ states per cm⁻¹, an order of magnitude more than calculated on the basis of the harmonic approximation, or even with anharmonicity taken into account. This large discrepancy indicates that radiationless transitions in this molecule are more efficient than previously estimated. In these experiments, S₀ energy levels were separated from each other by more than the linewidth, so that no quantum beats were observed; the decay was strictly exponential.

The work on formaldehyde showed that, even in a small molecule, coupling of the discrete S₁ levels to the S₀ and T₁ manifolds is possible in the isolated molecule. Near the origin, the coupling is weak, but it becomes much stronger as the dissociation rate constants of the dissociating molecules on the lower surface become larger. Statistical theories can be used to calculate these rate constants and, hence, the fluorescence decay times; such calculations lead to values that are found to be in reasonable agreement with experiment. It is noted that, in this case, no curve crossing takes place (at low energies), so that the interaction between the coupled states is weak. The resulting relatively small rate constants can still be measured for D₂CO, because the competing radiative process is even slower (due to the forbidden nature of the S₀–S₁ transition). These detailed effects could not have been discerned if the optical transition were fully allowed.

The research on formaldehyde also revealed that as the decay times of the S₀ and T₁ levels (due to dissociation) become shorter the linewidths of the S₀–S₁ absorption spectrum become larger. The spacing between adjacent levels of S₀ and T₁ decreases upon increasing the excitation energy as the density of states increases. At a certain point, the lower state becomes a true continuum (when the line widths become larger than the spacing between them), and the decay time of S₁ levels coupled to it becomes very short. It was also found that, as in the case of acetone, the radical recombination reaction has a barrier on the T₁ surface, but not on the S₀ one.

Studies on acetaldehyde (CH₃CHO) were not as extensive as on formaldehyde, though state-resolved measurements are beginning to emerge. The radical channel producing CH₃˙ + CHO˙ is dominant (93% of the dissociated molecules).⁹ At room temperature, a sharp energy onset for HCO˙ production was found at 89.3 kcal mol⁻¹,⁷⁵ concurrent with a drop in the fluorescence intensity.⁷⁶ Work in supersonic jets monitoring the HCO˙ product by PHOFEX showed that the threshold for the dissociation is at 320.5 nm (88.8 kcal mol⁻¹), corresponding to a barrier on the triplet surface of 12.3 kcal mol⁻¹.⁷⁷ Gejo et al.⁷⁸ measured the fluorescence decay of jet-cooled acetaldehyde as a function of excitation wavelength (cf. a similar experiment on acetone²³). The laser linewidth was such that two or more triplet states were coupled to a single S₁ state, resulting in quantum beats. A moderate increase in the fluorescence lifetime was recorded as the excitation energy was increased near the origin. This was interpreted as better coupling to non-dissociating triplet states. As in formaldehyde and acetone, the fluorescence of protonated molecules decayed much faster than that of deuterated ones. At an excess energy of about 2000 cm⁻¹ over the S₁ origin, there was a sharp decrease in the decay time over a very small energy range. Thus, the system behaves much like both formaldehyde and acetone under collision-free conditions. The rate of appearance of the HCO˙ fragment was directly measured near threshold by Huang et al.⁷⁹ using LIF of HCO˙. The appearance times of HCO˙ were rather long near the threshold, more than 100 ns. As the energy is increased, the rate becomes much faster, reaching 665 ps at 266 nm.⁸⁰Table 6 lists some energy values relevant to acetaldehyde photochemistry.

Table 6 Energetics of the acetaldehyde system

	Energy/kcal mol^−1	Ref.
H3C–COH bond	83	9
H–CH2COH bond	87	9
S1 origin	83	21
T1 origin	76	81
Barrier on T1	88.8	77

---

The experiments summarized in this section show that the photophysics and photochemistry of the three small carbonyl compounds—formaldehyde, acetaldehyde and acetone—are very similar, particularly as far as the radical dissociation channel is concerned. An important common feature is that as soon as the triplet dissociation channel opens, it becomes the dominant one. No direct dissociation from S₁ is observed for any molecule. Therefore, the much more detailed understanding of the photophysics of formaldehyde can be used to help interpret the data for acetone.

V The impact of collision-free data on the interpretation of bulk experiments

The results of recent experiments on isolated acetone molecules may be summarized as follows: (1) in the Franck–Condon region, the only singlet state accessible in the 240–340 nm excitation range is the bound ¹nπ* state. (2) At the same (or similar) geometry, only the ground state and the ³nπ* state are energetically accessible from the ¹nπ* state. (3) The only important dissociation channel within this energy range is radical dissociation, which can yield either a singlet or a triplet radical pair. (In contrast to formaldehyde, the rates of other dissociation channels are negligibly slow.) (4) The triplet state that correlates with the radical pair at infinite separation is a ³σσ* state, which, in the FC region, is very high lying. (5) The ground electronic state correlates with the singlet radical pair at infinite separation (in analogy with formaldehyde). The singlet radical pair is formed on the ground state surface following IC. (6) On the exit channel of the triplet surface, there is a barrier of about 14 kcal mol⁻¹. At energies exceeding this value, the dominant S₁ depletion channel is ISC leading to dissociation. (7) No direct dissociation from the S₁ state occurs.

Above the barrier for triplet dissociation, the rate constant of the triplet channel is much larger than on the ground state. This is consistent with measured rate constants: for the ground state, the pre-exponential factor is very large, as is the activation energy [log A(s⁻¹) = 17.9 and E_a = 84 kcal mol⁻¹, respectively²]. For the triplet, a slightly lower pre-exponential factor may be assumed (most vibrational frequencies are very similar to those of S₀, except the CO stretch and out-of-plane bend), but the activation energy is much smaller [log A(s⁻¹) = 16.0^37,38 and E_a = 14 kcal mol^−1 22,60]. Using these parameters, the triplet dissociation rate constant at 400 K (a temperature at which the quantum yield becomes 1) is 10^8.4 s⁻¹, very close to the ‘universal’ S₁ decay rate constant in solution and bulk gas phase. The S₀ rate constant is negligibly small compared to this value.

Experiments under collision-free conditions reveal that in S₁ state of acetone has a range of decay times determined by the excitation energy. Three main regions may be distinguished (Table 7): (I) below the triplet barrier, 87 < E_exc/kcal mol⁻¹< 91, the decay time is determined by coupling to S₀ (a dissociative state) and T₁ (bound). In the protonated molecule, coupling to S₀ manifolds is more efficient than in the deuterated one, as a smaller number of vibrational quanta are needed to achieve resonance (see below). In the case of the deuterated molecule, the decay at the origin is quite slow and the radiative decay rate constant is almost as large as the non-radiative one. Coupling to the triplet is also operative, as made obvious by the lengthening of the decay time with energy; (II) above the barrier, but at relatively low energies, 91 < E_exc/kcal mol⁻¹ ≲ 100, the decay time is much faster, but emission can still be detected until the dissociation rate is of the order of 10⁹–10¹⁰ s⁻¹, leading to a quantum yield of fluorescence of 10⁻⁴–10⁻⁵; (III) in the third region, E_exc ≫ 100 kcal mol⁻¹, the dissociation is so rapid that practically no emission is observed.

Table 7 Dependence of S₁ decay channel rate constants on excess energy (schematic)

Region	Rate constant relationships	Observed decay times/ns
(I) S1 origin < E < Eb(T)	k f ^0 ∼ kIC ∼ kISC	1000
(II) Eb(T) < E < Eb(T) + dE	k f ^0 ∼ kIC < kISC	1
(III) E ≫ Eb(T)	k f ^0 < kIC ≪ kISC	<0.001

---

The bulk results can now be analyzed with these facts in mind. In the bulk, collisions mediate all kinetics. Collisions can affect both IC and ISC by broadening the S₀ and T₁ levels; however, the main new feature is vibrational relaxation that leads to thermalization within a given bound electronic state, regardless of the initial excitation energy. Traditionally, it has been assumed that vibrational relaxation is rapid enough to compete with any process, so that all photophysical and photochemical processes can be assumed to proceed from the thermalized electronic state. This presumption must be qualified when ultrafast reactions are involved. A reasonable estimate for the vibrational relaxation rate in solution is 10¹² s⁻¹, while in the gas phase, it is pressure dependent and could be slower. The dissociation of acetone excited at 266 nm or shorter wavelengths is probably 10 times faster. Thus, some of the radicals are formed in the bulk (upon excitation at these wavelengths) in competition with vibrational relaxation, rather than subsequent to it. It transpires that O'Neal's description⁴⁴ of the unquenchable triplet better matches our current understanding of the system than the assumption that the singlet state has a separate reaction channel.

The low quantum yield of photolysis in solution is probably due to the fact that even the ‘hot’ singlet state initially arrived at are mostly relaxed to low-lying levels. In liquids, the cage effect is much more pronounced than in the gas phase, so that geminate radical pairs tend to recombine efficiently.¹⁵

The ‘limiting’ decay rate constant of S₁, as measured by fluorescence, can also be understood in terms of this scheme. Fluorescence from a weak absorber such as acetone can be observed above the noise level if the quantum yield exceeds roughly 10⁻⁴. The radiative lifetime is 10⁵ s⁻¹ (Section III). Thus, observing fluorescence when the competing processes have rates exceeding 10⁹ s⁻¹ is not practical. Consequently, in solution and bulk gas phase measurements, the observed fluorescence is dominated by the low-lying levels of S₁. These levels are in rapid thermal equilibrium with higher levels that dissociate over the low barrier on the triplet surface. All levels having a shorter lifetime are not contributing to fluorescence. This scenario is supported by the fact that at very low pressures (∼10⁻³ Torr) the decay time of bulk acetone is much longer than in the Torr range.⁵⁸

The upshot of this account is that the nanosecond decay time of singlet acetone in the bulk is determined by ISC, as traditionally believed. What has to be remembered is that different vibrational triplet levels vary with respect to the rate of dissociation: below the barrier to dissociation, ISC does take place and is accompanied by an increase in the S₁ decay time. On the other hand, the dissociation rate of high-lying levels is so rapid that even vibrational relaxation cannot compete with it.

VI Summary

The present state of the art of acetone photochemistry may be summarized as follows: (1) in the isolated molecule, the decay of the initially prepared S₁ levels is determined by radiative decay, internal conversion to S₀ and intersystem crossing to T₁. (2) Near the origin, the dominant pathway for acetone-h₆ is IC, mediated by the high frequency vibrational modes (CH stretch). For acetone-d₆, the radiative and the IC rate constants are approximately equal. (3) In the energy range of up to δE ≈ 2000 cm⁻¹, ISC becomes more important with increasing energy. The coupling is to bound triplet levels, causing a slight decrease in the fluorescence decay lifetime. (4) In this energy range, dissociation can only occur on the ground state surface, following IC. The reaction, resulting in a singlet radical pair, has a very small rate constant; in the bulk, the reaction is strongly impeded by vibrational relaxation. (5) At an excess energy of 2200 cm⁻¹ (∼6 kcal mol⁻¹) with respect to the origin of the S₀–S₁ transition, the triplet dissociation channel opens up. This causes a sudden increase in the decay rate of S₁ and the appearance of products, acetyl and methyl triplet radical pairs. This energy corresponds to a barrier of approximately 14 kcal mol⁻¹ on the triplet surface. This implies a 10 kcal mol⁻¹ back-reaction (recombination of the two radicals) barrier. (6) The lowest-lying triplet state (T₁) has primarily nπ* character near the Franck–Condon region, and essentially a σσ* character as the CC bond is extended. (7) No direct dissociation of S₁ is observed at excess energies up to 27 kcal mol⁻¹ (irradiation at 248 nm). Correlation diagrams advanced in an attempt to account for the barrier for radical dissociation on the singlet surface are therefore needless. (8) The decay of S₁ at these high energies takes place in less than 0.15 ps, most probably primarily by ISC.

In the presence of collisions: (9) radiationless transitions depopulating S₁ are made more effective by collisions, due to the broadening of S₀ and T₁ energy levels. This helps to couple more dissociative states into resonance with S₁ levels, resulting in a faster decay (this conclusion is based on experiments performed on formaldehyde). (10) The measured decay rate in the bulk, around 10⁻⁹ s⁻¹, is due to thermally equilibrated acetone molecules in the S₁ state. Fluorescence from high-lying vibrational states of acetone is not observed. (11) The equilibrated triplet state can be quenched by the usual triplet quenchers. (12) The non-quenchable reaction is due to high-lying triplet states that react too rapidly to be intercepted by the quenchers. (13) The contribution of high-lying vibrational levels of S₀ to the reaction yield is negligible compared to T₁ under collisional conditions, as in the isolated molecule.

While these conclusions seem to be consistent with all the known data on acetone, the story may still unfold as further experiments are carried out. Based on past experience, novel techniques time and again open up new research directions and future work may well lead to better understanding of the reaction.

Acknowledgments

Y. H. thanks the Israel Science Foundation and the Farkas Center for Light-Induced Processes, which is supported by the Minerva Gesellschaft mbH, for their generous support of the work carried out in Jerusalem. My special thanks to Prof. David Klug and his group for their hospitality at Imperial College, London, UK, where much of this paper was prepared. I am indebted to my research associates, whose names appear in the references; their skill and zeal made this work possible.

References

1. J. G. Calvert and J. N. Pitts, Photochemistry, Wiley, New York, 1966, p. 379.
2. J. A. Kerr and M. J. Patronage, Evaluated Kinetic Data on Gas Phase Hydrogen Transfer Reactions of Methyl Radicals, Butterworth, London, 1976, p. 171, cited by: S. H. Mousavipour and P. D. Pacey, Initiation and abstraction reactions in the pyrolysis of acetone, J. Phys. Chem., 1996, 100, 3593.
3. R. G. W. Norrish, H. G. Crone and O. D. Saltmarsh, Primary photochemical reactions. Part V. The spectroscopy and photochemical decomposition of acetone, J. Chem. Soc., 1934, 1456.
4. A. Noyes, Jr., G. B. Porter and E. Jolley, The primary photochemical process in simple ketones, Chem. Rev., 1956, 56, 49.
5. P. J. Wagner, Chemistry of excited triplet organic carbonyl compounds, Curr. Top. Chem., 1976, 66, 1.
6. N. J. Turro, Modern Molecular Photochemistry, Benjamin/Cummings, Menlo Park, CA, 1978.
7. R. G. W. Norrish, The primary photochemical production of some free radicals, Trans. Faraday Soc., 1934, 30, 103.
8. R. G. W. Norrish and F. W. Kirkbride, Primary photochemical reactions. Part I. The decomposition of formaldehyde, J. Chem. Soc., 1932, 1518.
9. A. Horowitz, C. J. Karshner and J. G. Calvert, Primary processes in the photolysis of acetaldehyde at 3000 Å and 25 °C, J. Phys. Chem., 1982, 86, 3094.
10. P. D. Lightfoot, S. P. Kirwan and M. J. Pilling, Photolysis of acetone at 193.3 nm, J. Phys. Chem., 1988, 92, 4938.
11. S. W. North, D. A. Blank, J. D. Gezelter, C. A. Longfellow and Y. T. Lee, Evidence for stepwise dissociation dynamics in acetone at 248 and 193 nm, J. Chem. Phys., 1995, 102, 4447.
12. F. O. Rice and K. F. Herzfeld, The thermal decomposition of organic compounds from the standpoint of free radicals. VI. The mechanism of some chain reactions, J. Am. Chem. Soc., 1934, 284.
13. E. J. Bowen and E. L. A. E. de la Praudiere, The photoreactions of liquid and dissolved ketones, part I, J. Chem. Soc., 1934, 1503.
14. P. E. Frankenberg and W. A. Noyes, Photochemical studies, XLVII. Liquid acetone-oxygen and liquid acetone-heptane-oxygen, J. Am. Chem. Soc., 1953, 75, 2847.
15. G. S. Hammond and N. J. Turro, Organic photochemistry, Science, 1963, 142, 1541.
16. W. A. Watkins and W. M. Word, Addition of methyl radicals to carbon monoxide: chemically and thermally activated decomposition of acetyl radical, Int. J. Chem. Kinet., 1974, 6, 855.
17. R. C. Ferris and S. Haynes, Formation of ketene in the photolysis of acetone, J. Am. Chem. Soc., 1950, 72, 893.
18. C. B. Moore and J. C. Weisshaar, Radiative, collisional and dissociative processes in triplet acetone, Annu. Rev. Phys. Chem., 1983, 34, 525.
19. C. B. Moore and I. W. M. Smith, State-resolved studies of reactions in the gas phase, Centennial Issue, J. Phys. Chem., 1996, 100, 12 848.
20. CRC Handbook of Chemistry and Physics, CRC Press, Boca Raton, 60th edn., 1980, p. F-232.
21. M. Baba, I. Hanazaki and U. Nagashima, The S₁(n, π*) states of acetaldehyde and acetone in supersonic nozzle beam: methyl internal rotation and C=O out-of-plane wagging, J. Chem. Phys., 1985, 82, 3938.
22. L. D. Waits, R. J. Horwitz and J. A. Guest, Translational energy study of CH₃ photofragments following (n, π*) excitation of acetone, Chem. Phys., 1991, 155, 149.
23. H. Zuckermann, B. Schmitz and Y. Haas, Acetone photophysics in seeded supersonic molecular beams, J. Phys. Chem., 1989, 93, 4083.
24. J. Heicklen and W. A. Noyes, Jr., The photolysis and fluorescence of acetone and acetone-biacetyl mixtures, J. Am. Chem. Soc., 1959, 81, 3858.
25. G. H. Damon and F. Daniels, The photolysis of gaseous acetone and the influence of water, J. Am. Chem. Soc., 1933, 35, 2363.
26. M. E. S. Appleyard and R. G. W. Norrish, J. Chem. Soc., 1934, 1456.
27. S. P. Vaish, R. D. McAlpine and M. Cocivera, Photochemistry of acetone in liquid phase studied by CIDNP [chemically induced dynamic nuclear polarization], J. Am. Chem. Soc., 1974, 96, 1683.
28. H. Schuh, E. J. Hamilton, H. Paul and H. Fisher, Reaction rates of t-butyl and pyvaloyl radicals in solution, Helv. Chim. Acta, 1974, 57, 2011.
29. K. Muller and G. L. Closs, Effect of nuclear spin relaxation on intensity pattern of multiplet spectra in chemically induced dynamic nuclear polarization, J. Am. Chem. Soc., 1972, 94, 1002.
30. G. L. Closs and C. E. Doubleday, Chemically induced dynamic nuclear spin polarization derived from biradicals generated by photochemical cleavage of cyclic ketones, and the observation of a solvent effect on signal intensities, J. Am. Chem. Soc., 1972, 94, 9248.
31. M. Tomkiewicz, A. Goren and M. Cocivera, Nuclear spin polarization during the photolysis of di-t-butyl ketone, J. Chem. Phys., 1972, 56, 5850.
32. A. Gilbert and J. Baggot, Essentials of Molecular Photochemistry, CRC Press, Boca Raton, 1991.
33. M. Klessinger and J. Michl, Excited States and Photochemistry of Organic Molecules, VCH, New York, 1995.
34. F. Bernardi, M. Olivucci and M. A. Robb, Predicting forbidden and allowed cycloaddition reactions: potential surface topology and its rationalization, Acc. Chem. Res., 1990, 23, 405.
35. S. Zilberg and Y. Haas, Conical intersections in molecular photochemistry – the role of phase change, Chem. Phys., 2000, 259, 249.
36. G. N. Lewis and M. Kasha, Phosphorescence and the triplet state, J. Am. Chem. Soc., 1944, 66, 2100.
37. G. Porter and M. Windsor, The triplet state in fluid media, Proc. R. Soc. London, Ser. A, 1958, 245, 238.
38. G. S. Hammond, N. J. Turro and P. A. Leermakers, The mechanisms of photoreactions in solution. IX. Energy transfer from the triplet states of aldehydes and ketones to unsaturated compounds, J. Phys. Chem., 1962, 66, 1144.
39. V. Sethuraman and K. K. Innes, The 3500 Å A¹A₂–X¹A₁ transition of formaldehyde h₂, d₂ and hd, J. Mol. Spectrosc., 1969, 30, 365.
40. D. J. Clouthier and D. A. Ramsay, The spectroscopy of formaldehyde and thioformaldehyde, Annu. Rev. Phys. Chem., 1983, 34, 31.
41. R. E. Rebbert and P. Ausloos, Triplet-state energy transfer from acetone to aliphatic aldehydes in the gas phase, J. Am. Chem. Soc., 1964, 86, 4803.
42. R. F. Borkman and D. R. Kearns, Electronic relaxation processes in acetone, J. Chem. Phys., 1966, 44, 945.
43. M. A. El-Sayed, Spin–orbit coupling and the radiationless processes in nitrogen heterocyclics, J. Chem. Phys., 1963, 38, 2834.
44. C. W. Larson and H. E. O'Neal, The gas phase photolysis of acetone at 3130 Å in the presence of hydrogen bromide. A study of the primary photochemical decomposition processes of acetone, J. Phys. Chem., 1966, 70, 2475.
45. R. B. Cundall and A. S. Davis, The mechanism of the gas phase photolysis of acetone, Proc. R. Soc. London, Ser. A, 1966, 290, 563.
46. L. Salem, Surface crossings, and surface touchings in photochemistry, J. Am. Chem. Soc., 1974, 96, 3486.
47. W. G. Dauben, L. Salem and N. J. Turro, Classification of photochemical reactions, Acc. Chem. Res., 1975, 8, 41.
48. N. J. Turro, W. E. Farneth and A. Devaquet, Salem diagrams as a device for the elucidation of photochemical reaction mechanisms. Applications to the cleavage of cyclic alkanones, J. Am. Chem. Soc., 1976, 98, 7425.
49. H. E. O'Neal and C. W. Larson, Primary processes in the acetone photochemical system, J. Phys. Chem., 1969, 73, 1011.
50. A. M. Halpern and W. R. Ware, Excited singlet radiative and nonradiative transition probabilities for acetone, acetone-d6, and hexafluoroacetone in the gas phase, in solution and in the neat liquid, J. Chem. Phys., 1971, 54, 1271.
51. G. M. Breuer and E. K. C. Lee, Fluorescence decay times of cyclic ketones, acetone, and butanal in the gas phase, J. Phys. Chem., 1971, 75, 989.
52. D. A. Hansen and E. K. C. Lee, Radiative and nonradiative transitions in the first excited singlet state of symmetrical methyl-substituted acetones, J. Chem. Phys., 1975, 62, 183.
53. F. S. Wettack, G. D. Renkes, M. G. Rockley, N. J. Turro and J. C. Dalton, Quenching of alkyl ketone fluorescence by 1,3-dienes, J. Am. Chem. Soc., 1970, 92, 1793.
54. N. C. Yang, E. D. Feit, M. H. Hui, N. J. Turro, and J. C. Dalton, Photochemistry of di-tert-butyl ketone and structural effects on the rate and efficiency of intersystem crossing of aliphatic ketones, J. Am. Chem. Soc., 1970, 92, 6974.
55. J. C. Dalton, K. Dawes, N. J. Turro, D. S. Weiss, J. A. Barltrop, J. D. Coyle and J. Molecular, Photochemistry. XLVIII. Type I and type II photochemical reactions of some five- and six-membered cycloalkanones, J. Am. Chem. Soc., 1971, 93, 7213.
56. S. J. Strickler and R. A. Berg, Relationship between absorption intensity and fluorescence lifetime of molecules, J. Chem. Phys., 1962, 37, 814.
57. E. K. C. Lee and R. S. Lewis, Photochemistry of simple aldehydes and ketones in the gas phase, Adv. Photochem., 1980, 12, 1.
58. G. D. Greenblat, S. Ruhman and Y. Haas, Fluorescence decay kinetics of acetone vapor at low pressures, Chem. Phys. Lett., 1984, 112, 200.
59. H. Zuckermann, Y. Haas, M. Drabbels, J. Heinze, W. L. Meerts, J. Reuss and J. van Bladel, Acetone, a laser-induced fluorescence study with rotational resolution at 320 nm, Chem. Phys., 1992, 163, 193.
60. O. Anner, H. Zuckermann and Y. Haas, Fluorescence decay of jet-cooled acetone, J. Phys. Chem., 1985, 89, 1336.
61. Y. Haas and H. Zuckermann, Photodynamics of small aliphatic ketones in a supersonic jet expansion, Isr. J. Chem., 1989, 29, 405.
62. R. D. Levine and R. B. Bernstein, Molecular Reaction Dynamics, Oxford University Press, Oxford, 1974, ch. 5.
63. G. W. Robinson and R. P. Frosch, Electronic excitation transfer and relaxation, J. Chem. Phys., 1962, 38, 1187.
64. W. Siebrand, Radiationless transitions in polyatomic molecules. I. Calculation of Franck–Condon factors, J. Chem. Phys., 1967, 46, 440.
65. Y. Haas and G. Stein, Pathways of radiative and radiationless transitions in europium(III) solutions. The role of high energy vibrations, J. Phys. Chem., 1971, 75, 3677.
66. R. A. Copeland and D. R. Crossley, Radiative, collisional and dissociative processes in triplet acetone, Chem. Phys. Lett., 1985, 115, 362.
67. J. Solomon, C. Jonah, P. Chandra and R. Bersohn, Photolysis mapping studies of aliphatic carbonyl compounds, J. Chem. Phys., 1971, 55, 362.
68. S. K. Kim, S. Pedersen and A. H. Zewail, Direct femtosecond observation of the transient intermediate in the cleavage reaction of (CH₃)₂CO to 2CH₃ + CO: resolving the issue of concertedness, J. Chem. Phys., 1995, 103, 477.
69. Q. Zhong, L. Poth and A. W. Castleman, Jr., Ultrafast dissociation dynamics of acetone: a revisit to the S₁ state and 3s Rydberg state, J. Chem. Phys., 1999, 110, 192.
70. J. C. Owrutski and A. P. Baronawski, Ultrafast photodissociation dynamics of the S₁and S₂ states of acetone, J. Chem. Phys., 1999, 110, 11 206.
71. M.-C. Chuang, M. F. Foltz and C. B. Moore, T ₁ barrier height, S₁–T₁ intersystems crossing rate, and S₀ radical dissociation threshold for H₂CO, D₂CO, and HDCO, J. Chem. Phys., 1987, 87, 3855.
72. W. F. Polik, D. R. Gruyer and C. B. Moore, Stark level-crossing spectroscopy of S₀ formaldehyde eigenstates at the dissociation threshold, J. Chem. Phys., 1990, 92, 3453.
73. R. Walsh and S. W. Benson, Kinetics and mechanism of the gas phase reaction between iodine and formaldehyde and the carbon-hydrogen bond strength in formaldehyde, J. Am. Chem. Soc., 1966, 88, 4570.
74. F. Polik and C. B. Moore, A transition state theory-based statistical distribution of unimolecular decay rates with application to unimolecular decomposition of formaldehyde, J. Chem. Phys., 1990, 93, 5657.
75. R. J. Gill and G. H. Atkinson, Wavelength dependence of HCO formation in the photolysis of acetaldehyde, Chem. Phys. Lett., 1979, 64, 426.
76. M. Noble and E. K. C. Lee, The singlet π*←n spectrum of jet-cooled acetaldehyde, J. Chem. Phys., 1982, 78, 2219.
77. T. Kono, M. Takayanagi, T. Nishiya and I. Hanazaki, Photodissociation of acetaldehyde studied by photofragment excitation spectroscopy in a supersonic free jet, Chem. Phys. Lett., 1993, 201, 166.
78. T. Gejo, H. Bitto and J. R. Huber, Quantum beats in the S₁ dynamics of acetaldehyde, Chem. Phys. Lett., 1996, 261, 443.
79. C.-H. Huang, V. Chien, C.-K. Ni, A. H. Kung and I-C. Chen, State-resolved dynamics of dissociation of triplet acetaldehyde: rate of appearance of fragment HCO and decay of excited states of parent molecule, J. Phys. Chem., 2000, 104, 10 362.
80. O. K. Abu Zied and J. D. McDonald, Picosecond real time study of the bimolecular reaction O(³P) + C₂H₄ and the unimolecular photodissociation of CH₃CHO and H₂CO, J. Chem. Phys., 1998, 109, 1293.
81. J. S. Yadav and J. D. Goddard, Acetaldehyde photochemistry: the radical and molecular dissociations, J. Chem. Phys., 1986, 84, 2682.

---