Absorption and scattering of light by suspensions of cells and subcellular particles: an analysis in terms of Kramers–Kronig relations
K. Razi Naqvi*a, M. N. Merzlyakb and T. B. Meløa
aDepartment of Physics, Norwegian University of Science and Technology (NTNU), N-7491 Trondheim, Norway. E-mail: razi.naqvi@phys.ntnu.no
bDepartment of Physiology of Microorganisms, Faculty of Biology, Moscow State University, 119992 GSP-2 Moscow, Russia
First published on 22nd October 2003
Abstract
An analysis of light scattering from suspensions of pigmented cells and particles is undertaken, and a practicable method, requiring only the experimentally measured extinction spectra, is documented. The analysis is based on two premises: Absorption and selective scattering from a single pool of pigments satisfy the Kramers–Kronig relations, which imply that one can be derived from the other; pigment-free domains contribute only nonselective scattering. This approach succeeds in simulating the spectra of many systems (human erythrocytes, chloroplasts and sub-chloroplast particles, algal cells) over a wide spectral range. Other, less favourable, cases are also examined, but even here the apparent discrepancy between theory and experiment provides some clues that cannot be gleaned from absorption data alone.
Introduction
The optical properties of animal tissues, plant leaves, vegetative canopies, and natural waters are determined to a large extent by the absorption and scattering properties of individual cells and/or pigmented particles.1–12 A reliable apportioning of the total extinction of light to absorption and scattering losses is crucial for solving any problem involving photon transport through an absorbing-and-scattering medium. Methods for separating the contribution made by scattering to the total attenuation have been available for a long time,1,3–5 but a prescription for extracting various quantities of interest (particularly the absorption and scattering cross sections) from extinction data is still missing. Past attempts6b,8 have amounted to using analytically tractable models, capable of providing a good deal of physical insight but unable to simulate measured spectra over the whole spectral range of interest. Now that large data sets can be collected and manipulated with the aid of commercial software, and the true absorption spectrum of a turbid sample can be found using standard spectrophotometric equipment,11–13 the time has come to place the analysis of light scattering on a firmer foundation. Here we take a first step in this direction by formulating a quantitative description of the shape of the scattering spectrum in terms of two ingredients: (i) a pivotal hypothesis that the absorption and scattering of light by a pool of pigments are subject to the Kramers–Kronig relationship,14,15a,b and (ii) an inconsequential assumption about scattering from non-pigmented domains.The approach outlined above and described in greater detail below suffers from a limitation, but this can be traced, not to any inherent shortcoming in our standpoint, but to spectrophotometry itself, which performs a spatial averaging over the volume defined by the measuring beam. The hypothetic relation between absorption and scattering cannot be applied indiscriminately to an object as heterogeneous as a cell, comprising (in general) of many absorbing structures, each of which may in turn contain several pools, differing in pigment composition as well as in size. Examining a single cell by resorting to microspectrometry would not solve the problem, for the measured absorbance would still refer to the entire cell rather than a much smaller, submicrometer region within the cell. In the light of these remarks, the important questions are the following. Is there a recipe for computing the spectral properties of a single pool of pigments? Secondly, if the answer to the first question is in the affirmative, does heterogeneity in the sizes and pigment compositions of the pools invalidate the reasoning behind the recipe?
After presenting our prescription for calculating the scattering spectrum, we will answer the above questions by examining red blood cells (erythrocytes) and a wide variety of photosynthetic systems, ranging from isolated pigment-protein complexes and chloroplasts to prokaryotic cyanobacteria and eukaryotic algae. The red blood cell is particularly well suited for testing our approach, for it contains only one type of pigment, and all pigments are encapsulated within a single refractive structure (plasma membrane). As the paper is written with an eye towards applications, the choice of the photosynthetic species was based as much on the rich variety in the pigment content, size and shape of the selected organisms as on their ecological relevance8 and biotechnological significance.16
Terminology, background and the new approach
When an absorbing-and-scattering specimen (containing particles comparable in size to the wavelength of visible light) is placed in the sample chamber of a conventional (UV-visible) absorption spectrophotometer, the recorded spectrum (to be called the extinction spectrum) is contaminated by scattering losses; the extent of the contamination depends on γ, the half-angle subtended by an on-axis light detector at the suspension,5,6 and γ can be easily varied by changing the distance between the cuvette and the detector or the collection element. We will denote an extinction spectrum by E(λ;γ), the corresponding true absorption spectrum by A(λ), and the difference, E(λ;γ) − A(λ), to be called the scattering spectrum corresponding to the collection angle γ, by C(λ;γ). Thanks to a strategy devised by Latimer and Eubanks,5 a serviceable approximation to A(λ) is easily obtained.11,12 For the sake of notational simplicity, the γ-dependence of the experimental spectra will no longer be explicitly indicated.To explain our analysis of the spectra of turbid samples, it will be well to display a set of extinction spectra recorded by placing a suspension of human red blood cells (erythrocytes) at various distances from the entrance port of an integrating sphere (Fig. 1(a)). As the distance becomes larger, scattering (as judged from the measured extinction at wavelengths longer than 600 nm, where haemoglobin does not absorb) increases, whereas absorption (as judged from the heights, above the rising background, of the three peaks) suffers a decline. In dealing with scattering from cells it has become customary to distinguish between two types,6,7 nonselective and selective, neither of which has so far been shown to be amenable to a quantitative analysis. For a brief explanation of the terminology, we turn to a sentence in the paper where selective scattering from plant cells was reported for the first time: “The light scattering by the cells is due: (1) to colorless structures, which scatter with a relatively uniform wavelength dependence (not unlike the scattering by bleached cells …), and (2) to highly pigmented chloroplasts (or grana), the index of refraction of which changes sharply with wavelength, as described approximately by the classical dispersion formula”. The contribution made by selective scattering can be evaluated, we claim, from the absorption spectrum itself; we also claim that lack of precise knowledge of the wavelength dependence of nonselective scattering need not discourage one from deciphering the scattering spectrum. Our approach can be enunciated in terms of the following equation
| E(λ) = a0 + a1A(λ) + a2S(λ) + a3N(λ), | (1) |
 | ||
| Fig. 1 Spectra of an erythrocyte suspension. Panel a shows A(λ), the absorption spectrum (curve 0), and a set of extinction spectra, E(λ), recorded by placing the sample at increasing distance from an integrating sphere11 (curves 1–5). The three curves in panel (b), all derived from the data plotted in panel (a), display the shapes of the following spectra: A(λ), the absorption spectrum; X(λ) = α + βC(λ), the rescaled and vertically shifted experimental scattering spectrum; and S(λ), the Hilbert transform of A(λ); The measured (green) and simulated (red) scattering spectra are compared in panel (c). | ||
Since A(λ) can be found experimentally, it only remains to provide recipes for calculating S(λ) and N(λ). We adopt, on the basis of some observations to be summarised at the end of this section, the working hypothesis that A(λ) and S(λ) are related by a Hilbert transformation in the following manner:
 | (2) |
 denotes the Cauchy principal value of the integral, and ĤA(λ) signifies the Hilbert transform14e,15b of A(λ). Should this prescription prove to be effective, it would pave the way for a model-independent approach to selective scattering from heavily pigmented cells. The relation between a function and its Hilbert transform is commonly known as Kramers–Kronig relationship;14e it follows from eqn. (2) that the Hilbert transform of a function remains unchanged if a constant term is added to the function; the application of two Hilbert transforms in succession returns the negative of the original function.15b This means that we are at liberty to displace the Hilbert transform along the vertical axis, which is one reason for the inclusion of the constant term a0 in eqn. (1).
denotes the Cauchy principal value of the integral, and ĤA(λ) signifies the Hilbert transform14e,15b of A(λ). Should this prescription prove to be effective, it would pave the way for a model-independent approach to selective scattering from heavily pigmented cells. The relation between a function and its Hilbert transform is commonly known as Kramers–Kronig relationship;14e it follows from eqn. (2) that the Hilbert transform of a function remains unchanged if a constant term is added to the function; the application of two Hilbert transforms in succession returns the negative of the original function.15b This means that we are at liberty to displace the Hilbert transform along the vertical axis, which is one reason for the inclusion of the constant term a0 in eqn. (1).As to nonselective scattering from particles of our interest, there appears to be no broad guiding principles, apart from the general observation that it increases with decreasing wavelengths. We have chosen a two-parameter relation of the form
| N(λ) = b1λ−1 + b2λ−2, | (3) |
The intimate link between absorption, reflection and scattering, and the relevance of the Kramers–Kronig relations, have been emphasized by Kliger et al.14c in the following words: “A second application of the Kramers–Kronig relation occurs in light scattering samples. … This can be understood by considering scattering as the limit of reflection from small particles. Since strength of reflection depends on refractive index, anything that affects refractive index will also affect the strength of scattering”. Our own investigations of light scattering began with an examination of the spectra of the light-harvesting complex LHCII isolated from the photosystem II of green plants.11 We noticed, soon after obtaining our spectra, that the scattering C(λ) spectrum bore a striking resemblance to the Hilbert transform of the corresponding absorption spectrum. To substantiate this claim we draw the reader's attention to Fig. 2: the upper panel shows A(λ), and another curve which need not be discussed now, whereas the lower panel shows three spectra, one of which is the scattering C(λ) spectrum, and each of the other two is S(λ), the Hilbert transform of A(λ), calculated in different ways (which will be explained later). In this example, C(λ) is dominated by selective scattering, and corresponds rather closely to S(λ); another extreme, where A(λ) makes the largest contribution to C(λ) is exemplified by erythrocytes (see Fig. 1(b)); we have also come across systems, not germane to the present discussion, in which non-selective scattering accounts for the bulk of scattering losses. The foregoing discussion is not intended to be rigorously logical; its main purpose is to suggest that eqns. (1) and (2) constitute a plausible starting point for scrutinising scattering spectra of pigmented cells. If we find that a great many systems conform to our provisional viewpoint, we will end up with a body of cumulative confirmatory evidence, each item of which gains credence by corroborating the rest.
 | ||
| Fig. 2 The upper panel shows A(λ), the absorption spectrum of a suspension of LHCII, and Ã(λ), a fit obtained by resolving A(λ) into Gaussian peaks. The lower panel compares the shape of C(λ) with that of the Hilbert transform of Ã(λ); the transform has been calculated in two different ways, analytically and numerically (see Materials and methods), and it has been suitably scaled and vertically displaced. | ||
The presumed interrelationship between A(λ) and S(λ) in a given suspension of particles will hold only if each particle behaves as a single spectral entity–as one giant chromophore, so to speak. When applied to a cell (a composite particle containing different pools of pigments, each situated in a different refractive environment and making its own contribution to the overall absorption and scattering), this assumption can hardly be expected to hold. The results presented below show that in many cases, the simplified picture appears to be satisfactory, and that even when it fails, one is able to draw some significant conclusions.
We would like to emphasise that we are occupied with spectra rather than cross sections. This means that rescaling of a spectrum, or its displacement along the vertical axis, is not of the essence; only the shape of a particular spectrum is important. It is also worth bearing in mind that, though the magnitudes of the coefficients in eqn. (1) will increase with γ, the collection angle, the shapes of the scattering spectra of the sample investigated here are almost independent of the collection angle;12 it is sufficient, therefore, to examine the scattering spectrum for one value of γ, which explains why the γ-dependence of C(λ) and S(λ) has been suppressed.
Materials and methods
Preparation of samples
Approximately 150 µl of freshly collected human peripheral blood was added to 5 ml of 0.6% NaCl solution containing 7 mM trisodium citrate as an anticoagulant. Erythrocytes were sedimented by centrifugation at 1000 g for 5 min, washed twice and resuspended in 0.6% NaCl.Preparations of LHC II11 and BBY17 particles from spinach were supplied by Drs G. Garab (Szeged, Hungary) and B.N. Ivanov (Puschino, Moscow region, Russia), respectively. Chloroplasts and thylakoids were isolated from pea plants using standard procedures. The cell suspensions of the following photosynthetic microorganisms were used in the study: the cyanobacteria Anabaena variabilis Kutz and Anacystis nidulans Menighini (Cyanophyceae), the yellow-green alga Monodus subterraneus Petersen (Eustigmatophyta), the green algae Chlorella stigmatophora Butcher, Dunaliella maritima and Haematococcuspluvialis Flotow (Chlorophyceae), the diatom Thalassiosiraweissflogii (Grunow) Fryxell & Hasles (Bacillariophyceae) and the red alga Porphyridiumcruentum (Ag.) Näg (Rhodophyceae). The cells were cultivated under optimal growth conditions and collected at logarithmic phase, either in Moscow University or obtained from Drs I. P. Maslova (H. pluvialis and P. cruentum) and Yu. V. Balnokin (C. stigmatophora). Green and red types of H. pluvialis were obtained by cultivation under low and high light conditions, respectively. Cell suspensions were washed with and measured against the growth medium.
Determination of true absorption spectra
Apart from red blood cells and LHC II, the scattering-free spectra (in the 350–800 nm region) of all samples were recorded in Moscow, using the instrument and methods described in earlier publications.11,12 Two different instruments were used for measurements in Trondheim: A Hitachi Model 3010 spectrophotometer (equipped with a 150 mm diameter integrating sphere attachment) provided spectra in the 300–800 nm range, and a Shimadzu Model UV-160A spectrophotometer,11 which had a lower signal-to-noise ratio, covered a wider spectral range (200–1100 nm). Suspensions of red blood cells were examined in both instruments, and an absorption spectrum covering the 200–1100 nm range was constructed by piecing together the output of the two instruments.Calculation of Hilbert transforms and curve fitting
The true absorption spectrum calculated by following the procedure described above was extended to 1200 nm by adding dummy data points (consisting of zeros) to the absorbance readings. Hilbert transforms of these extended spectra were calculated by using the commercial software programme Matlab. The reliability of this numerical approach to calculating the Hilbert transform was checked as follows. A given absorption spectrum is first decomposed into a sum of n Gaussian peaks:18 | (4) |
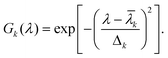 | (5) |
The parameters ak, ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) k and Δk determine (respectively) the height, location and width of the k-th peak in the spectrum. An example of this decomposition is given in Fig. 2(a). Once a fit has been performed, the Hilbert transform of the spectrum can be expressed as15a,c
k and Δk determine (respectively) the height, location and width of the k-th peak in the spectrum. An example of this decomposition is given in Fig. 2(a). Once a fit has been performed, the Hilbert transform of the spectrum can be expressed as15a,c
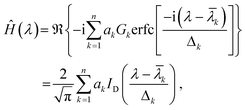 | (6) |
 | (7) |
The analytical method of calculation has the advantage that the spectrum does not need any padding at the long wavelength end. Fig. 2(b) provides a comparison of the analytical transform of the fitted spectrum and its numerical counterpart; one sees that the two are in very good agreement. That the short wavelength end of the spectrum still needs padding has been taken into account by recording the absorption spectrum up to 350 nm and discarding the transform in the 350–400 nm region. We have also checked, by padding the absorption spectrum (analytically or numerically) to still shorter wavelengths, that the output (at wavelengths longer than 400 nm) is rather insensitive to the padding. In any case, the residual discrepancy, caused by the finite range of experimental data, between the calculated transform and its (unknown) exact counterpart is absorbed in the evaluation of N(λ), the featureless part of the scattering spectrum.
With the true absorption spectrum and its Hilbert transform at hand, the measured extinction spectrum (for a particular collection angle) was fitted to eqn. (1) by linear regression analysis; the details pertaining to this analysis are available elsewhere.18 In treating multi-chromophoric systems, a two-parameter fit for N(λ) was preferred only if a one-parameter fit tried (with b1 or b2 set to zero) failed to provide an acceptable fit.
Results and discussions
We return now to the set of spectra displayed in Fig. 1(a) and show, in panel (b), three spectra derived from this set: A(λ), S(λ), and a third curve, X(λ) = α + βC(λ), where C(λ) ≡ E(λ) − A(λ), and the constants (α and β) permit vertical displacement and rescaling, respectively. It will be noticed that in this case A(λ) makes by far the largest contribution to C(λ). Having finished with the preliminaries, we proceed to check if the extinction spectrum of erythrocytes can be simulated by using eqn. (1). A one-parameter fit (with b2 = 0) between E(λ) and Ẽ(λ) is so good that deviations between the two curves cannot be perceived on the scale of the figure; we have therefore plotted, in the bottom panel of Fig. 1,![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) (λ), the simulated scattering curve, and C(λ)
≡
E(λ)
−
A(λ), the measured scattering curve. We mention here, without showing the corresponding simulated spectra, that the fit does not deteriorate significantly if one uses the expression N(λ)
=
bnλ−n and changes the exponent to n
= 1/2 or even to n
= 2; of course, these changes do affect the values of the retrieved parameters, but the outcomes for ã1 and ã2 change very little, showing the robustness of a one-parameter fit in this case.
(λ), the simulated scattering curve, and C(λ)
≡
E(λ)
−
A(λ), the measured scattering curve. We mention here, without showing the corresponding simulated spectra, that the fit does not deteriorate significantly if one uses the expression N(λ)
=
bnλ−n and changes the exponent to n
= 1/2 or even to n
= 2; of course, these changes do affect the values of the retrieved parameters, but the outcomes for ã1 and ã2 change very little, showing the robustness of a one-parameter fit in this case.Suspensions of isolated chloroplasts, thylakoid membranes, BBY particles, and aggregates of LHC II (the light-harvesting complex associated with photosystem II of plants) have been found to comply with eqn. (1). The results pertaining to LHC II and chloroplasts are plotted in Fig. 3; the spectra for the other suspensions are not shown, but we would like to record here two observations concerning chloroplasts and sub-chloroplast membranes/particles: though these systems are not strictly homogeneous (according to the definition given above), departure from homogeneity is hardly noticeable in LHC II, and is not sufficiently serious in the other cases; secondly, nonselective scattering makes a larger contribution in thylakoids than in any of the other systems. It is also relevant to point out here that the shape of the 90°-scattering spectrum of LHC II, recorded with the aid of a fluorescence spectrometer,11 agrees with that obtained by means of absorption spectrophotometry.
 | ||
Fig. 3 Spectra of suspensions of LHC II (panel (a)) and isolated chloroplasts (panel (b)). Each panel shows the following plots: A(λ), the absorption spectrum, in blue; C(λ), the experimental scattering curve, in green; ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) (λ), the simulated scattering curve, in red. The left scale applies to absorption (blue curves); the right scale, to the experimental and simulated scattering spectra (green and red curves, respectively). The simulated spectra are two-parameter fits. (λ), the simulated scattering curve, in red. The left scale applies to absorption (blue curves); the right scale, to the experimental and simulated scattering spectra (green and red curves, respectively). The simulated spectra are two-parameter fits. | ||
We move to more complex systems and present, in Fig. 4, the scattering spectra of cells of four species, whose pigments are listed within the parentheses following the name: the yellow-green alga Monodus subterraneus (Chla, Chlc, Car), the green algae Chlorella stigmatophora (Chla, Chlb, Car), the diatom Thalassiosiraweissflogii (Chla, Chlc, Car–mainly fucoxanthin), and the red alga Porphyridiumcruentum (Chla, Car, phycobilins–mainly phycoerythrin). One can see that, despite the diversity of the cells (in respect of size, shape, morphology and pigment content), the quality of the fits for the first three species is comparable to that for chloroplasts and sub-chloroplast particles (Fig. 3); the exception, occupying the bottom panel, will be discussed shortly.
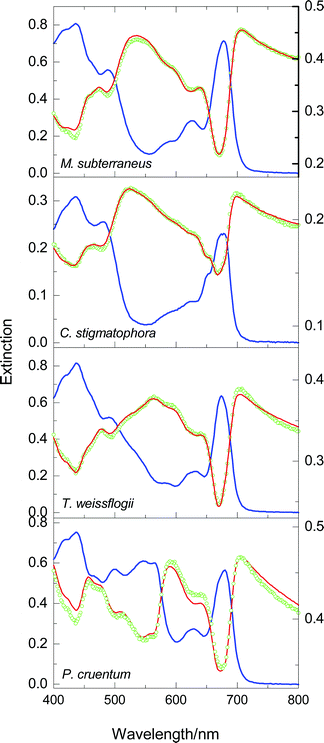 | ||
| Fig. 4 Spectra of cell suspensions of M. subterraneus, C. stigmatophora, , T. weissflogii and P. cruentum. The simulation in the top panel is a one-parameter fit; the others are all two-parameter fits. Other details as in Fig. 4. | ||
Among the photosynthetic systems analysed here, only LHC II and the cell suspension of M. subterraneus could be described satisfactorily by a one-parameter fit, and both come close to being homogeneous. Since LHC II is a single pigment-protein complex, its homogeneity is easily understood, but that of Monodus warrants an explanation. To this end, let us recall first that the published absorption spectra of the two pigment-protein complexes (LHC I and LHC II) of Pleurochloris meiringensis, which account for the bulk of the pigments (Chla, Chlc, and Car–mainly diadinoxanthin and heteroxanthin) in this yellow–green alga,19 happen to be remarkably similar; it follows that the shapes of the selective scattering spectra of the two antenna complexes, SI(λ) and SII(λ), must resemble each other, and any linear combination of SI(λ) and SII(λ). Secondly, the absorption spectrum20 of cell suspensions of P. meiringensis bears a striking resemblance to the absorption spectrum of M. subterraneus (shown in the top panel of Fig. 4). If the above mentioned spectral similarity holds, as seems highly likely, also for the two complexes of M. subterraneus, the attempt to simulate its extinction spectrum should meet with the same degree of success as in the case of chloroplasts and LHC II of higher plants. The good correspondence between E(λ) and Ẽ(λ), evident from the spectra of Monodus appearing in Fig. 4 (top panel), supports our reasoning and conjecture.
We return now to the case of P. cruentum (bottom panel of Fig. 4), and note first that the cyanobacteria Anabaena variabilis and Anacystis nidulans, which contain high amounts of phycocyanins, behave likewise (data not shown). The persistent discrepancy between E(λ) and Ẽ(λ) in the spectra of these cells is ascribed to the presence, on the cytoplasmic side of the thylakoid membranes, of phycobilisomes, the water soluble antenna complexes of red algae21 and cyanobacteria.22 The following considerations suggest that these antennae are anomalous inasmuch as they scatter only weakly, and their selective scattering cannot be identified with the Hilbert transform of the absorbance. Morphologically, a phycobilisome (PBS) is almost hemispherical, with a diameter around 50 nm, consisting of a core complex and several rod-like segments protruding from the core; dynamically, it is highly mobile, diffusing as a single entity, implying the absence of a stable complex and a reaction centre.23,24 Though nothing is known about their scattering properties in vivo, the absorption spectra of aqueous suspensions of isolated phycobilisomes, and of other aggregates of similarly small size (for instance, chlorosomes, the light-harvesting complexes of green bacteria25) reveal no perceptible scattering losses;26 what is more, 90°-scattering spectra of such small particles (not reported here), termed resonance light scattering by Pasternack et al.,27 indicate that eqn. (1) cannot describe the shapes of the scattering spectra of these systems.
Continuing in the same vein, we present another example involving anomalous pigment pools. As a preamble, we recall that cells of the green alga Haematococcus pluvialis are green in the normal, motile form, and their dominant Car pigments are β-carotene and lutein; in response to a variety of environmental stresses, the cells accumulate large amounts of esterified forms of a secondary carotenoid, astaxanthin, in lipid globules located outside the chloroplast, and turn into so-called red cysts.28 Unlike the other green algae examined by us, namely C. stigmatophora (Fig. 4) and Dunaliella maritima (data not shown), H. pluvialis does not comply with eqn. (1); this is illustrated in Fig. 5(a), which displays the results of a two-parameter fit, and a one-parameter (with b2 = 0) segmental fit covering the 550–800 nm segment, where Car pigments do not absorb. Since the only other noncompliant examples pertain to cells possessing extra pigmentation, we hypothesise that even the normal Haematococcus cells contain pools of such pigments; it seems plausible that these pools are astaxanthin-containing globules. It will hardly come as a surprise that the spectra of the red cyst also proved to be noncompliant; to illustrate this behaviour, two segmental fits are included in Fig. 5(b).
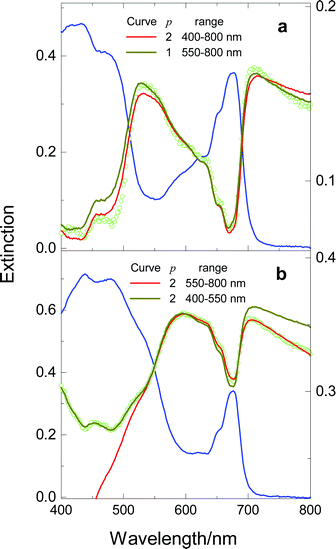 | ||
| Fig. 5 Spectra of cell suspensions of the green cells (panel (a)) and red cysts (panel (b)) of H. pluvialis. The value p of indicates whether the simulation results from a one-parameter or a two-parameter fit; the spectral range used for fitting is also shown for each fit. Other details as in Figs. 3 and 4. | ||
Concluding remarks
The examples presented above suffice to demonstrate that, using routine measurements and straightforward data analysis, light scattering of cell suspensions can be subjected to a satisfactory analysis. The principal assumption–that one is dealing with a single absorbing-and-scattering entity–must be relaxed when one is dealing with a situation where the heterogeneity (in the sizes and pigment compositions) of different subcellular domains gives rise to a substantial discrepancy between simulation and experiment. To this extent, therefore, if no further, scattering provides a clue that cannot be extruded from the absorption spectrum. To go further, one would need to resolve, using additional pieces of information, the overall absorbance into contributions from different pools of pigments, assign unequal weights to the calculated scattering spectra of different pools, and seek agreement between theory and experiment.Latimer and Rabinowitch,6b envisaged “the possibility of obtaining from studies of scattered light information about the distribution and packing of pigment molecules in vivo”. The foregoing evidence shows that we have come closer to this goal.
Acknowledgements
The authors are grateful to Drs G. Garab (Szeged, Hungary), B. N. Ivanov (Puschino, Moscow region, Russia), S. I. Pogosyan (Faculty of Biology, Moscow State University), I. P. Maslova, Yu. V. Balnokin (both from Institute of Plant Physiology, Russian Academy of Sciences, Moscow) and Dr I. F. Khozin (Ben-Gurion University of the Negev, Ber-Sheva, Israel) for providing samples and to Drs O.B. Chivkunova and T.V. Shigalova (Faculty of Biology, Moscow State University) for assistance in some experiments. This work was supported by a grant for M. N. M. from the Research Council of Norway (NFR).References
- K. Shibata, A. A. Benson and M. Calvin, The absorption spectra of suspensions of living micro-organisms, Biochim. Biophys. Acta, 1954, 15, 461–470 CrossRef CAS.
- L. N. M. Duysens, The flattering of the absorption spectrum of suspensions, as compared to that of solutions, Biochim. Biophys. Acta, 1956, 19, 1–12 CAS.
- D. Keilin and E. F. Hartree, Spectrophotometric study of suspensions of pigmented particles, Biochim. Biophys. Acta, 1958, 27, 173–184 CrossRef CAS.
- J. Amesz, L. N. M. Duysens and D. C. Brandt, Methods for measuring and correcting the absorption spectrum of scattering suspensions, J. Theor. Biol., 1961, 1, 59–74 CAS.
- P. Latimer and C. A. H. Eubanks, Absorption spectrophotometry of turbid suspensions: a method of correcting for large systematic distortions, Arch. Biochem. Biophys., 1962, 98, 274–285 CAS.
- (a) P. Latimer and E. Rabinowitch, Selective scattering of light by pigment-containing plant cells, J. Chem. Phys., 1956, 24, 480 CAS; (b) P. Latimer and E. Rabinowitch, Selective scattering of light by pigments in vivo, Arch. Biochem. Biophys., 1959, 84, 428–441 CAS.
- W. L. Butler, Absorption spectroscopy in vivo: theory and application, Annu. Rev. Plant Physiol., 1964, 15, 451–470 CrossRef CAS.
- A. Bricaud and A. Morel, Light attenuation and scattering by phytoplanktonic cells: a theoretical modelling, Appl. Opt., 1986, 25, 571–580.
- G. B. J. Dubelaar, J. M. W. Visser and J. M. Donze, Anomalous behaviour of forward and perpendicular light scattering of a cyanobacterium owing to intracellular gas vacuoles, Cytometry, 1987, 8, 405–412 CAS.
- P. Taroni, A. Pifferi, A. Torricelli, D. Comelli and R. Cubeddu, In vivo absorption and scattering spectroscopy of biological tissues, Photochem. Photobiol. Sci., 2003, 2, 124–129 RSC.
- K. Razi Naqvi, T. B. Melø, B. B. Raju, T. Jávorfi and G. Garab, Comparison of the absorption spectra of trimers and aggregates of chlorophyll a/b light-harvesting complex LHC II, Spectrochim. Acta, Part A, 1997, 53, 1925–1936 CrossRef.
- M. N. Merzlyak and K. Razi Naqvi, On recording the true absorption spectrum and the scattering spectrum of a turbid sample: application to cell suspensions of the cyanobacterium Anabaena variabilis, J. Photochem. Photobiol. B: Biol., 2000, 58, 123–129 CrossRef CAS.
- M. N. Merzlyak, O. B. Chivkunova, T. B. Melø and K. Razi Naqvi, Does a leaf absorb radiation in the infra red (780–900 nm)? A new approach to quantifying optical reflection, absorption and transmission of leaves, Photosynth. Res., 2002, 72, 263–270 CrossRef CAS.
- (a) H. M. Nussenzveig, Causality and Dispersion Relations, Academic Press, New York, 1972, pp. 3–53 Search PubMed; (b) A. B. Pippard, The Physics of Vibration, Cambridge University Press, 1978, vol. 1, pp. 105–113 Search PubMed; (c) D. S. Kliger, J. L. Lewis and C. E. Randall, Polarized Light in Optics and Spectroscopy, Academic Press, Boston, 1990, pp. 256–268 Search PubMed; (d) K. Yamamoto and H. Ishida, Kramers–Kronig analysis applied to reflection-absorption spectroscopy, Vib. Spectrosc., 1997, 15, 27–36 CrossRef CAS; (e) F. Castro and B. Nabet, Numerical computation of the complex dielectric permittivity using Hilbert transform and FFT techniques, J. Franklin Inst., 1999, 336B, 53–64 CrossRef.
- (a) J. A. Schellman, Circular dichroism and optical rotation, Chem. Rev., 1975, 75, 323–331 CrossRef; (b) R. N. Bracewell, The Fourier Transform and its Applications, Mc-Graw Hill, New York, 2nd edn., 1986, p. 267 Search PubMed; (c) M. Abramowitz and I. A. Stegun, Handbook of Mathematical Functions, Dover, 1965, pp. 297 and 319 Search PubMed.
- Chemicals from Microalgae, ed. Z. Cohen, Taylor & Francis Ltd., London, 1999 Search PubMed.
- D. A. Berthold, G. T. Babcock and C. F. Yocum, A highly resolved, oxygen-evolving photosystem-II preparation from spinach thylakoid membranes: EPR and electron-transport properties, FEBS Lett., 1981, 134, 231–234 CrossRef CAS.
- K. Razi Naqvi, T. Hj. Hassan, Z. M. Said and Y. A. Naqvi, Expeditious implementation of two new methods for analysing the pigment composition of photosynthetic specimens, 2002, CPS: analchem/0203001 (http://preprint.chemweb.com/CPS/).
- C. Büchel and C. Wilhelm, Isolation and characterization of a photosystem I-associated antenna (LHC I) and a photosystem I-core complex from the chlorophyll c-containing alga Pleurochloris meiringensis (Xanthophyceae), J. Photochem. Photobiol. B: Biol., 1993, 20, 87–93 CrossRef.
- C. Büchel, C. Wilhelm and I. Lenartz-Weiler, The molecular analysis of the light adaptation reactions in the yellow-green alga Pleurochloris meiringensis (Xanthophyceae), Bot. Acta, 1988, 101, 306–310 Search PubMed.
- L. Talarico and G. Maranzana, Light and adaptive responses in red macroalgae: an overview, J. Photochem. Photobiol. B: Biol., 2000, 56, 1–11 CrossRef CAS.
- A. R. Grossman, D. Bhaya and Q. He, Tracking the light environment by cyanobacteria and the dynamic nature of light harvesting, J. Biol. Chem., 2001, 276, 11449–11452 CrossRef CAS.
- C. W. Mullineaux, M. J. Tobin and G. R. Jones, Mobility of photosynthetic complexes in thylakoid membranes, Nature, 1997, 390, 421–424 CrossRef CAS.
- M. Sarcina, M. J. Tobin and C. W. Mullineaux, Diffusion of phycobilisomes on the thylakoid membranes of the cyanobacterium Synechococcus 7042, J. Biol. Chem., 2001, 276, 46830–46834 CrossRef CAS.
- J. M. Olson, Chlorosome organization and function in green photosynthetic bacteria, Photochem. Photobiol., 1998, 67, 61–75 CAS.
- J. B. Arrelano, T. B. Melø, C. M. Borrego and K. Razi Naqvi, Bacteriochlorophyll e monomers, but not aggregates, sensitize singlet oxygen: implications for self-photoprotection mechanism in chlorosomes, Photochem. Photobiol., 2002, 76, 373–380 CrossRef.
- (a) R. F. Pasternack and K. F. Schaefer, Resonance light-scattering studies of porphyrin diacid aggregates, Inorg. Chem., 1994, 33, 2062–2065 CrossRef CAS; (b) R. F. Pasternack and P. J. Collings, Resonance light scattering: a new technique for studying chromophore aggregation, Science, 1995, 269, 935–939 CAS; (c) R. F. Pasternack, C. Flemin, S. Herring, P. J. Collings, J. de Paula, G. DeCastro and E. J. Gibbs, Aggregation kinetics of extended porphyrin and cyanine aggregates, Biophys. J., 2000, 79, 550–560 CAS.
- S. Boussiba, Carotenogenesis in the green alga Haematococcus pluvialis: Cellular physiology and stress response, Physiol. Plant., 2000, 108, 111–117 CrossRef CAS.
| This journal is © The Royal Society of Chemistry and Owner Societies 2004 |
