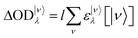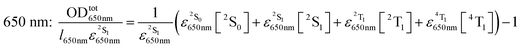Ultrafast studies of the excited-state dynamics of copper and nickel phthalocyanine tetrasulfonates: potential sensitizers for the two-photon photodynamic therapy of tumors
Received
10th March 2003
, Accepted 17th July 2003
First published on 4th September 2003
Abstract
In order to evaluate the potential of copper and nickel phthalocyanine tetrasulfonates as sensitizers for two-photon photodynamic therapy, we conducted kinetic femtosecond measurements of transient absorption and bleaching of their excited state dynamics in aqueous solution. Samples were pumped with 620 nm and 310 nm laser light, which allowed us to study relaxation processes from both the first and second singlet (or doublet for the copper phthalocyanine) excited states. A second excitation from the first excited triplet state, approximately 685 and 105 ps after the first excitation for copper and nickel phthalocyanine tetrasulfonate respectively, was the most efficient way to bring the molecules to an upper triplet state. Presumably this highest triplet state can inflict molecular damage on adjacent biomolecules in the absence of oxygen, resulting in the desired cytotoxic cellular response. Transient absorption spectra at different fixed delays indicate that optimum efficiency would require that the second photon has a wavelength of approximately 750 nm.
Introduction
Photodynamic therapy (PDT) is a promising new treatment of cancer1–3 as well as several non-malignant conditions such as age related macular degeneration (AMD).4 The treatment requires three components, a photosensitizer, visible light and molecular oxygen.5,6 Upon systemic or topical administration the photosensitizer localizes in the target tissue where it is activated by visible light. The photosensitizer being brought to its excited electronic triplet state may react via a type I or a type II mechanism.7 The type I mechanism involves interaction with substrate molecules via hydrogen abstraction or electron transfer to yield radical and ionic species that in turn may react with molecular oxygen to give cytotoxic reactive oxygen species (ROS). Alternatively the triplet sensitizer may react via energy transfer with ground state molecular oxygen to yield singlet oxygen (type II mechanism) that can react with a large number of biological substrates to initiate oxidative damage via peroxidative chain reactions. Both mechanisms rely on the presence of oxygen, with the type II pathway being the most widely accepted mechanism leading to cell death.8,9 The necessity for molecular oxygen in either pathway can greatly limit the potential of PDT in solid tumors where important hypoxic regions may exist.2 There is however evidence that an oxygen-independent photodynamic effect is possible from the upper excited triplet state Tn of photosensitizers such as rose bengal and a substituted magnesium phthalocyanine.10,11 There is increasing interest in the application of simultaneous biphotonic activation of photosensitizer molecules using two NIR photons.12–15 However little work has been reported to demonstrate the cytotoxic effect of such Tn species in a biological system.
Among several classes of second-generation photosensitizers that are advanced for PDT, phthalocyanines have been studied extensively due to their strong absorption (ε
= 105 M−1 cm−1) in the far-red region of the spectrum (λ
≈ 680 nm) where tissue transparency is optimal.16,17 Also many time-resolved studies on phthalocyanine molecules have been reported.18–27 For the present study we selected two water-soluble sulfonated phthalocyanines containing paramagnetic central metal ions, i.e. copper and nickel phthalocyanine tetrasulfonates (CuPcS4 and NiPcS4). Only little work has recently been conducted on the latter molecules.28 Such paramagnetic ions greatly shorten the lifetime of the triplet state (≈ ns) rendering the complexes far less effective photosensitizers for PDT as compared to phthalocyanines chelated with diamagnetic metal ions (Al3+, Ga3+, Zn2+), whose triplet lifetimes are much longer.29 The absence of a type I or II photodynamic process should simplify studies on the cytotoxicity of the the upper excited triplet states generated via a sequential biphotonic activation of the photosensitizers. Furthermore their solubility in water facilitates their formulation for potential clinical applications. Selecting the optimal parameters for two-photon PDT in vivo requires an understanding of the excited-state dynamics of CuPcS4 and NiPcS4 in aqueous solution. Although several studies report on the excited-state dynamics of CuPc and NiPc complexes,21,22,25,26 data on the ultrafast excited-state dynamics for the water-soluble tetrasulfonated derivatives are not available.
Experimental
Photosensititizers
NiPcS4 and CuPcS4 were prepared via the condensation method adapted from Weber and Bush.30 Briefly this involved the following.
NiPcS4 sodium salt (MW 978g): a mixture of nickelous chloride hexahydrate (MW 237.7 g, 4.4 g, 18.4 mmol), triammonium sulfophthalic acid (MW 297 g, 10.87 g, 36.6 mmol), ammonium chloride (MW 53 g, 0.35 g, 6.5 mmol), ammonium molybdate (0.1 g) and urea (MW 60 g, 10 g, 0.16 mmol) was heated for 3 h at 200 °C, triturated with 1 N HCl in brine, filtered and washed with water, dialyzed, evaporated to dryness and oven-dried to give 7.16 g of NiPcS4. λmax in DMF 669 nm (ε
= 155,000 M−1 cm−1).
CuPcS4 sodium salt (MW 983.5 g): a mixture of copper diacetate monohydrate (MW 200 g, 8 g, 40 mmol), triammonium sulfophthalic acid (MW 297 g, 39.92 g, 134 mmol), ammonium chloride (MW 53 g, 8 g), ammonium molybdate (40 mg) and urea (MW 60 g, 40 g, 0.64 mmol) in water (10 mL) was heated for 4 h at 190–200 °C, triturated with 1 N HCl in brine, filtered and washed with water, dialyzed, evaporated to dryness and oven-dried to give 18.32 g of CuPcS4. λmax in MeOH 666 nm.
CuPcS4 and NiPcS4 were dissolved in water at a concentration of about 3 × 10−4 M. Absorption spectra of the samples were recorded with a spectrophotometer (HITACHI, U-2000). A fresh solution was prepared from the solid powder before each experiment and circulated in a 2 mm thick cell at constant flow to avoid photoinduced damage. The metallophthalocyanine tetrasulfonate structure is illustrated in Fig. 1.
 |
| | Fig. 1 Metallophthalocyanine tetrasulfonate structure. | |
Transient absorption experiments
There are two possible pathways to bring the photosensitizer molecule to an upper triplet state via sequential two-photon excitation (Fig. 2). Femtosecond time-resolved transient absorption spectroscopy was used for kinetic studies of the excited-state dynamics of CuPcS4 and NiPcS4. First order rate constants in the relaxation process as well as relative molar absorption coefficients for each state were computed from the kinetic results using a normal three level model for NiPcS4 and a four-state model for the CuPcS4 as developed by Ake and Gouterman31 for Cu-centered porphyrins. A simulation using these parameters was conducted to obtain the population evolution in time of each quantum state for both molecules. Kinetic studies were done with both 620 and 310 nm pump-laser beams in order to obtain data on the relaxation process from both the first and the second excited singlet states, respectively (doublet states for the CuPcS4 molecule).
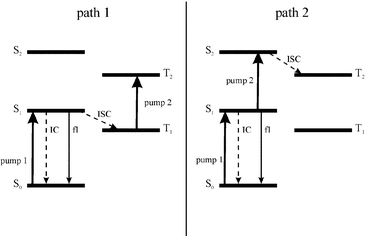 |
| | Fig. 2 Two possible ways of populating the upper triplet state T2. | |
The pump–probe experimental setup used for our kinetic studies is shown in Fig. 3. The incident 620 nm laser beam was extracted from a colliding pulse mode-lock (CPM) dye laser followed by four stages of amplification in sulforhodamine and kiton-red dye cells pumped by a 10 Hz frequency doubled Q-switched Nd:YAG (Lumonics) laser. After subsequent compression by a grating pair, typical pulses of 150 fs duration and 0.5 mJ energy are obtained. A more complete description can be found elsewhere.32 This incident laser beam is split in two with a beamsplitter. The first beam (pump), has a fixed optical path length and is focused in the sample solution. The second beam (probe), has a variable optical path length. A moving retroreflector is used to introduce a controlled pump–probe delay. The apparatus has a displacement capacity of 1.5 ns and a mechanical precision of 0.1 µm, i.e. a precision of two thirds of 1 fs in the pump–probe delay. It is then focused in a cell containing ethanol in order to generate a spectral continuum. The wavelengths of interest are extracted using bandpass interference filters (Andover Corp.) and attenuated to the desired intensities with neutral density filters. The probe pulse is finally focused in the cell containing the dye solution, where it overlaps the pump focus. Increasing this delay gives information on the relaxation rate of the molecules in an excited state after absorption of photons from the pump pulse.
 |
| | Fig. 3 The pump–probe experimental setup. The incident beam is split into two beams, the pump and the probe. A moving mirror controls the pump–probe delay. The probe beam is focused in ethanol for continuum generation, then filtered. Thereafter, it is focused in the sample cell, spatially overlapping the pumping beam. A monochromator and photodiode (PD) analyze the output light. | |
The transmitted probe signal is directed at the entrance of a 0.32 m spectrophotometer (Instruments SA, model HR320) for spectral analysis. The output signal is sent on a silicon photodiode selector (EG & G, DT 10). A small sample of the probe signal is sampled with another photodiode in order to reference the shot-to-shot intensity fluctuation. The effect of the long term signal decay from the main laser source is avoided by alternately blocking and enforcing the pump pulse, with a chopper triggered at the same rate as the main laser. The end result of this procedure is the transient optical density (ΔOD) computed as follows : ΔOD = log10[(P0/R0)/(P/R)], where the P values represent the transmitted probe intensities and R the reference readings. The zero (0) subscript refers to the case where the pump is obstructed. Insertion of a KDP (potassium dihydrogen phosphate) crystal in the pumping beam path was done for SHG (second-harmonic generation) in the second kinetic experiment in which a 310 nm pump is used.
Molecular energy level models
A four-level model31 was used to fit data from the excited-state dynamics of CuPcS4
(Fig. 4a), while a three-level model (S1, S1 and T1) was used for the NiPcS4 molecule (Fig. 4b). For the CuPcS4 molecule, the unpaired electron in a d orbital splits singlet states into doublets (S0
→
2S0 and S1
→
2S1) while the normal triplet state splits into a doublet (trip-doublet 2T1) and a quadruplet (4T1). By solving the differential equation system associated with the relaxation process of each molecule, the kinetic behavior of every electronic state population is obtained. The solutions for the CuPcS4 molecule are shown in the set of equations (1),| | 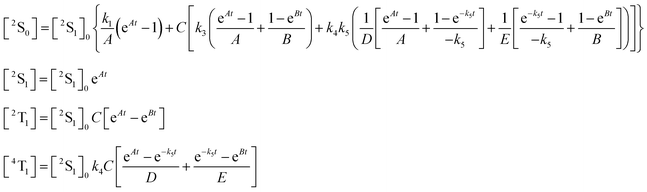 | (1) |
where [2S1]0 is the concentration of molecules in the 2S1 state at time zero, A
=
−(k1
+
k2), B
=
−(k3
+
k4), C
=
k2/(−k1
−
k2
+
k3
+
k4), D
=
(−k1
−
k2
+
k5) and E
=
(−k3
−
k4
+
k5).
 |
| | Fig. 4 Energy level diagram for CuPcS4
(a) and NiPcS4
(b). The latter features one odd electron in a d orbital. The normal triplet state is split into a trip-doublet (2T1) and a quadruplet (4T1). For both molecules the k1 transition takes into account both radiative and non-radiative processes. | |
For the NiPcS4 molecule, the solutions are given in the set of equations (2).
| |  | (2) |
A generalization of the Beer–Lambert law applied to the transient absorption problem gives:
| | 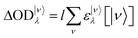 | (3) |
where
l is the overlapping optical path,
ε|ν〉λ is the molar absorption coefficient of a molecule in the |
ν〉 state and at wavelength
λ and [|
ν〉] is the concentration of the molecules in the |
ν〉 state. The Σ symbol is used because the contributions of every absorbing quantum state must be summed.
Eqns. (1) and (2) were fitted with the ΔOD data. The net result was the kinetic behavior of every [|ν〉], i.e. the first order rate constants kn. Since the experimental data had to be normalized because of mathematical constraints in the fitting procedure, relative values for the molar absorption coefficients were also obtained.
Side effects
The pump pulse with an estimated 1013 W cm−2 power density at the focal point in the active volume lies within the non-linear regime. Such intensity induces a strong local electric field, favoring the generation of long-lived electrons,33 along with coherent effects such as induced grating effects at zero pump–probe delay and two-photon absorption. Stimulated and inverse Raman peaks at specified wavelengths when pumping at 620 nm can also be present.34 Corrections for these side effects were made when necessary.
Results
Ground state as well as excited-state absorption spectra at different fixed delays were taken and are illustrated in Fig. 5. The absorption spectrum for both products presents two strong bands, i.e. the Soret band in the near UV (λmax
= 335 nm for both molecules) and the Q-band in the visible region (λmax
= 630 and 625 nm for CuPcS4 and NiPcS4, respectively). The spectrum reveals good absorption at 620 and 310 nm, which is well suited for the kinetic measurements mentioned above. The superimposed transient absorption spectra show strong bleaching in the Q-band region while a transient absorption is clearly visible for other tested wavelengths. The maximum transient absorption occurs around 720 nm in the therapeutic window region (700 to 1050 nm, approximately) for both sensitizers. It is also noted that transient absorption seems quite stable over time for CuPcS4 while in the case of NiPcS4 quick bleaching of the absorbency around 630 nm is evident.
Kinetic ultrafast transient absorption studies
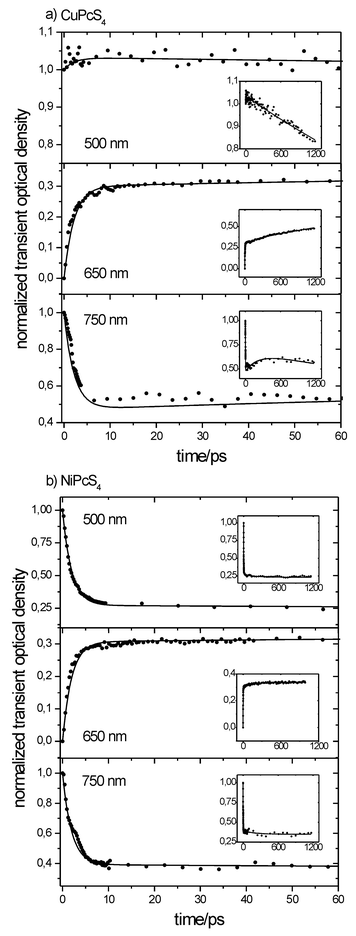
Kinetics at three different wavelengths (500, 650 and 750 nm) using a 620 nm pumping pulse were recorded for analysis. They were corrected for the non-linear and coherent effects mentioned earlier and are shown in Figs. 6a and 6b. The 500 and 750 nm kinetics represent the time evolution of the excited-state absorption spectra alone, while at 650 nm the bleaching of the ground state must also be taken into account along with the excited-state transient absorption.
 |
| | Fig. 6 Transient absorption kinetics for the CuPcS4
(a) and NiPcS4
(b) molecules for three different wavelengths: 500 nm, 650 nm and 750 nm. The experimental conditions are: solution concentration c
= 3 × 10−4 M; pH = 7.0 ± 0.1; excitation wavelength λexc
= 620 nm, of 150 fs duration and energy 250 µJ. | |
Discussion
CuPcS4
The absorption curves clearly indicate a many-exponential decay. At 750 nm, the first and rapid decay relates to the transition from the 2S1 state to both the 2T1 and the fundamental states with rate constants of 460 ± 120 × 109 s−1
(≈2.2 ps time constant) and 2.0 ± 0.5 × 109 s−1
(≈500 ps time constant), respectively. The 2S1
→
2T1 transition time constant is consistent with that reported by Dongho et al.18 for Cu(etioporphyrin) and Cu(TPP) in toluene. It is important to note that the decreasing transient absorption of the depleting 2S1 state is offset by that of the increasing population of the 2T1 state. The latter will then depopulate to the fundamental state with a rate constant of 2.3 ± 0.9 × 109 s−1
(≈435 ps time constant) as well as undergo intersystem crossing to the 4T1 state with a rate constant of 2.5 ± 1.0 × 109 s−1
(≈400 ps time constant). This is still consistent with the result of Dongho et al.18 of approximately 450 ps. The quadruplet state will finally deplete back to the ground state on a longer time scale (0.2 ± 0.1 × 109 s−1). A time constant of approximately 5 ± 2.5 ns was obtained for the 4T1
→
2S0 transition, which is consistent with the result of 5.7 ± 1 ns for the Cu(crown)Pc cofacial dimer.21 The key feature lies in the subsequent increase of the transient absorption around 250 ps. As demonstrated by the population dynamic simulations, this likely results from the presence of the third excited state (4T1) whose population is increasing at a slower rate. At 500 nm, the first transient absorption overshoot is not clearly visible, which implies that the molar absorption coefficient of the 2T1 state at 500 nm is comparable to that of the 2S1 state. At 650 nm, a transient bleaching occurs. It correlates well with the transient absorption data at other wavelengths assuming that bleaching is countered by a transient absorption of the excited states.
The four-state model for kinetic behavior of the transient optical density (i.e. the concentration) superimposed with the experimental data is shown in Fig. 7. The data are compatible with our model, indicating that the 2S1
→
2T1
→
4T1 transitions are discernable, with 2.2 ± 0.2 ps and 400 ± 60 ps time constants respectively. This suggests that the rate constant for the 2S1
→
2T1/4T1 transition might not be as fast as suggested for Cu-centered porphyrins.19 A similar conclusion has also been drawn by Rodgers et al.21 using kinetic transient absorption data for CucrPc, although the authors do not conclude on their capacity to resolve the 2S1
→
2T1
→
4T1 transitions. Consequently, they associate the 2.2 × 109 s−1 rate constant (2.9 × 109 s−1 in their case) with either a charge transfer state CT →
4T1 or the 2T1
→
4T1 triplet transition. This transition (2T1
→
4T1) seems to take place on a longer time scale (≈400 ps). The presence of a CT state can neither be supported nor invalidated by our present data, and accordingly we assume this to be the 2T1 state. A summary of the rate constants is given in Table 1. The exact kinetic behavior for the excited-state population evolution with time was calculated and the results are shown in Fig. 8a.
 |
| | Fig. 8 Simulated population dynamics for CuPcS4
(a): solid line for the 2S1 state, (■) for the 2T1 state and (•) for the 4T1 state; NiPcS4
(b): solid line for the S1 state and (•) for the T1 state. The y-axis represents the relative population of each quantum state in time, normalized to the initial first excited singlet (doublet for CuPcS4) state population. | |
The fact that the kinetic results do not seem to depend upon the pumping wavelength that was used suggests that the 2S2
→
2S1 transition occurs within the time resolution of the apparatus (≈210 fs, considering gaussian shaped laser pulses of 150 fs duration) and hence a 2S2
→ Tn transition seems quite improbable. Alluding to Fig. 2, only the first excitation scheme would be efficient in populating the upper triplet state.
NiPcS4
The population dynamics of the three-state model representing NiPcS4 is shown in Fig. 8b. At 500 nm, a rapid transient absorption overshoot is well visible. The subsequent decay is fitted with the three-state model, involving three exponentials. The S1
→ S0 transition has a rate constant of 22 ± 3 × 109 s−1
(45.5 ± 6.2 ps), while the S1
→ T1 transition has a rate constant of 31 ± 9 × 109 s−1
(≈32 ps time constant) and the T1
→ S0 transition has a 0.17 ± 0.15 × 109 s−1
(< 10 ns time constant). A large error arises from the fact that a nanosecond scale event is being evaluated with a maximum delay of 1.2 ns. Millard and Greene26 measured a lifetime of 2.8 ± 0.2 ps for the ground state recovery of uncrowned NiPc, though the authors used a single exponential for the evaluation and pointed out that the ground-state bleaching did not completely recover to the initial zero level.
Like the Cu complex, the transient absorption kinetics for NiPcS4 does not show a great difference whether the pumping wavelength is 620 nm or 310 nm. This again leads to the conclusion that the S2
→ S1 transition occurs within the time resolution of the apparatus (≈210 fs), a conclusion that was also been drawn by Rodgers et al.22 from their studies with the analogous NicrPc. Hence the most efficient sequential biphotonic excitation path is the first one (Fig. 2).
Relative molar absorption coefficients
The relative molar absorption coefficient values given in Table 1 clearly indicate that the excited-state absorption is not negligible. For CuPcS4, the quadruplet state absorption is even higher than the excited doublet absorption at 750 nm. The triplet state absorption for the NiPcS4 molecule is smaller than that of the excited singlet state S1 at 750 nm. Overall, there is no significant difference in absorption for the excited states between the two photosensitizer molecules.
Upper triplet state
Several attempts were made to measure the absorption and lifetime of the upper triplet state by adding a second pump beam (see Fig. 2) to the transient kinetic experimental setup. Unfortunately, the upper triplet state could not be seen and no conclusion regarding its lifetime could be drawn. It is possible that the lifetime in question is shorter than the time resolution of the apparatus. To certify on the efficiency of the photosensitizers, in vitro experiments are presently being conducted on living cells.
Exact excited-state population dynamics
Using the rate constants from Table 1, an analytic evaluation of the excited-state population dynamics can be given. Fig. 8 features the curves representing the build up of each state population in time, for both sensitizer molecules. It can be seen that the maximum triplet state occupation occurs around 105 ps for NiPcS4, while it happens around 685 ps for CuPcS4
(4T1 state). Considering the relative absorption of 4T1 to 2T1 of 2.6 (refer to Table 1), their maximum combined absorption occurs around 425 ps. To boost the 2T1 state to an upper triplet state by sequential biphotonic excitation within living cells would require testing of both delays to compare their respective efficiency.
Conclusions
In summary this study presents a first step to evaluate the potential of CuPcS4 and NiPcS4 as photosensitizers for 2 photon photodynamic therapy (2ph-PDT). Different rate constants involved in the relaxation process were determined, which allowed us to obtain the exact excited state population dynamics. Using the optimal parameters provided by this study we have projected 2ph-PDT in living cells in vitro and subsequently in in vivo tumor models.
Acknowledgements
Funding for this research was provided by the Canadian Institutes of Health Research (CIHR) grant no. MGP-37768 (J. E. v. L.), the Canadian Institute for Photonics Innovations (D. H.) and by the Intelligent Materials and Systems Institute of the Université de Sherbrooke (D. H.).
References
- T. J. Dougherty, Photosensitizers: therapy and detection of malignant tumors, Photochem. Photobiol., 1987, 45, 879–889 CAS.
- T. J. Dougherty, C. J. Gomer, B. W. Henderson, G. Jori, D. Kessel, M. Korbelik, J. Moan and Q. Peng, Photodynamic therapy, J. Natl. Cancer Inst., 1998, 90, 889–905 CrossRef CAS.
- W. M. Sharman, C. M. Allen and J. E. van Lier, Photodynamic therapeutics: Basic principles and clinical applications, Drug Discovery Today, 1999, 4, 507–517 CrossRef CAS.
- H. van den Bergh, Photodynamic therapy of age-related macular degeneration: History and principles, Semin. Ophthalmol., 2001, 16, 181–200 Search PubMed.
- I. Rosenthal, C. M. Krishna, P. Riesz and E. Ben-Hur, The role of molecular oxygen in the photodynamic effect of phthalocyanines, Radiat. Res., 1986, 107, 136–142 CAS.
- J. Spikes, Photodynamic action: From paramecium to photochemotherapy, Photochem. Photobiol., 1997, 65, 142–147.
- C. S. Foote, Definition of type I and type II photosensitized oxidation, Photochem. Photobiol., 1991, 54, 659 CAS.
- K. R. Weishaupt, C. J. Gomer and T. J. Dougherty, Identification of singlet oxygen as the cytotoxic agent in photo-inactivation of a murine tumor, Cancer Res., 1976, 36, 2326–2329 CAS.
- W. M. Sharman, C. M. Allen and J. E. van Lier, Role of activated oxygen species in photodynamic therapy, Methods Enzymol., 2000, 319, 376–400 CAS.
- G. W. Smith, G. McGimpsey, M. C. Lynch, I. E. Kochevar and R. W. Redmond, An efficient oxygen independent two-photon photosensitization mechanism, Photochem. Photobiol., 1994, 59, 135–139 CAS.
- H. Stiel, K. Teuchner, A. Paul, W. Freyer and D. Leupold, Two-photon excitation of alkaly-substituted magnesium phthalocyanine: radical formation via higher excited states, J. Photochem. Photobiol., A, 1994, 80, 289–298 CrossRef CAS.
- R. L. Goyan and D. T. Cramb, Near-infrared two-photon excitation of photoporphyrin IX: photodynamics and photoproduct generation, Photochem. Photobiol., 2000, 72, 821–827 CAS.
- W. G. Fisher, W. P. Partridge, Jr., C. Dees and E. A. Wachter, Simultaneous two-photon activation of type-I photodynamic therapy agents, Photochem. Photobiol., 1997, 66, 141–155 CAS.
- J. D. Bhawalkar, N. D. Kumar, C.-F. Zhao and P. N. Prasad, Two-photon photodynamic therapy, J. Clin. Lasers Med. Surg., 1997, 15, 201–204 Search PubMed.
- R. S. Bodaness, D. F. Heller, J. Krasinski and D. S. King, The two-photon laser induced fluorescence of the tumor localizing photosensitizer hematoporphyrin derivative, J. Biol. Chem., 1986, 261, 12098–12101 CAS.
- H. Ali and J. E. van Lier, Metal complexes as photo- and radiosensitizers, Chem. Rev., 1999, 99, 2379–2450 CrossRef.
- C. M. Allen, W. M. Sharman and J. E. van Lier, Current status of phthalocyanines in the photodynamic therapy of cancer, J. Porphyrins Phthalocyanines, 2001, 5, 161–169 CrossRef CAS.
- K. Dongho, D. Holten and M. Gouterman, Evidence from picosecond transient absorption and kinetic studies of charge-transfer states in copper(II) porphyrins, J. Am. Chem. Soc., 1984, 106, 2793–2798 CrossRef.
- J. Rodriguez, C. Kirmaier and D. Holten, Optical properties of metalloporphyrins excited states, J. Am. Chem. Soc., 1989, 111, 6500–6506 CrossRef CAS.
- L Howe and J. Z. Zhang, The effect of biological substrates on the ultrafast excited-state dynamics of zinc phthalocyanine tetrasulfonate in solution, Photochem. Photobiol., 1998, 67, 90–96 CAS.
- A. V. Nikolaitchik, O. Korth and M. A. J. Rodgers, Crown ether substituted monomeric and cofacial dimeric metallophthalocyanines. 1. Photophysical studies of the free base, zinc(II), and copper(II) variants, J. Phys. Chem., 1999, 103, 7587–7596 Search PubMed.
- A. V. Nikolaitchik and M. A. J. Rodgers, Crown ether substituted monomeric and cofacial dimeric metallophthalocyanines. 2. Photophysical studies of the cobalt(II) and nickel(II) variants, J. Phys. Chem., 1999, 103, 7597–7605 Search PubMed.
- Q. Zhong, Z. Wang, Y. Liu, Q. Zhu and F. Kong, The ultrafast dynamics of phthalocyanine and porphyrin derivatives, J. Chem. Phys., 1996, 105, 5377–5379 CrossRef CAS.
- A. P. Pelliccioli, K. Henbest, G. Kwag, Terri, R. Carvagno, M. E. Kenney and M. A. J. Rodgers, Synthesis and excited state dynamics of μ-oxo group IV metal phthalocyanine dimers: a laser photoexcitation study, J. Phys. Chem., 2001, 105, 1757–1766 Search PubMed.
- A. D. Kirk, C. H. Langford, C. S. Joly, R. Lesage and D. K. Sharma, Sub-nanosecond processes in the quenching of a copper phthalocyanine dye absorbed on TiO2, J. Chem. Soc., Chem. Commun., 1984, 961–962 RSC.
- R. R. Millard and B. I. Greene, Direct determination of nonradiative relaxation rates in nonfluorescent metallophthalocyanines, J. Phys. Chem., 1985, 89, 2976–2978 CrossRef CAS.
- L. Howe and J. Z. Zhang, Ultrafast studies of excited-state dynamics of phthalocyanine and zinc phthalocyanine tetrasulfonate in solution, J. Phys. Chem., 1997, 101, 3207–3213 Search PubMed.
- K. Arnold, T. S. Balaban, M. N. Blom, O. T. Ehrler, S. Gilb, O. Hampe, J. E. van Lier, J. M. Weber and M. M. Kappes, Electron Autodetachment from Isolated Nickel and Copper Phthalocyanine-Tetrasulfonate Tetraanions: Isomer Specific Rates, J. Phys. Chem. A, 2003, 107, 794–803 CrossRef CAS.
-
J. E. van Lier and J. D. Spikes, in Photosensitising Compounds: Their Chemistry, Biology and Clinical Use, eds. G. Bock and S. Harnett, Wiley and Sons Ltd., Chichester, 1989, pp.17–32 Search PubMed.
- J. H. Weber and D. H. Bush, Complexes derived from strong field ligands. XIX. Magnetic properties of transition metal derivatives of 4,4′,4″,4‴-tetrasulfophthalocyanines, Inorg. Chem., 1965, 4, 469–471 CrossRef CAS.
- R. L. Ake and M. Gouterman, Porphyrins XIV. Theory for the luminescent state in VO, Co, Cu complexes, Theor. Chim. Acta, 1969, 15, 20–42 CrossRef CAS.
- S. Marengo, C. Pépin, T. Goulet and D. Houde, Time-gated transillumination of objects in highly scattering media using a subpicosecond optical amplifier, IEEE J. Sel. Top. Quantum Electron., 1999, 5, 895–901 CrossRef CAS.
- C. Pépin, D. Houde, H. Remita, T. Goulet and J.-P. Jay-Gerin, Evidence for resonance-enhanced multiphoton ionization of liquid water using 2-eV laser light: variation of hydrated electron absorbance with femtosecond pulse intensity, Phys. Rev. Lett., 1992, 69, 3389–3392 CrossRef CAS.
- D. Houde., C. Pépin, T. Goulet and J.-P. Jay-Gerin, Dynamics of solvated electrons in polar liquids using 2-eV femtosecond laser pulses, Proc. SPIE-Int. Soc. Opt. Eng., 1993, 2041, 139–151 Search PubMed.
|
| This journal is © The Royal Society of Chemistry and Owner Societies 2004 |
Click here to see how this site uses Cookies. View our privacy policy here.