How does Mg²⁺ affect the binding of anhydrotetracycline in the TetR protein?

Abstract

The binding of anhydrotetracycline (atc) in wild-type TetR(D), TetR(B), and four single tryptophan mutants of TetR(B) was investigated by UV/vis absorption, steady-state, and time-resolved fluorescence spectroscopy. From absorption titration experiments with Mg²⁺, we conclude that binding of one [atc–Mg]⁺ complex in the homodimer causes changes in the protein conformation around the second binding pocket. In the presence or absence of Mg²⁺, several different groups of atc-protein arrangements must exist, each with a characteristic atc fluorescence decay time. Taking into account the results of molecular dynamics (MD) simulations, we propose as one possible origin for such a differentiation the extent of hydrogen bonding between atc and the surrounding amino acids. Binding of Mg²⁺ should change the arrangement of the surrounding amino acids such that some of the excited atc molecules do not undergo the relaxation processes typical for free atc. The MD simulations also show that the pattern of intra- and intermolecular hydrogen bonding in the two monomeric units is not correlated, thereby leading to different fluorescence kinetics for atc in the two monomeric units. Furthermore, it is suggested that hydrogen bonding between Arg104 and O10 of anhydrotetracycline could regulate the relaxation processes of excited anhydrotetracycline.

---

1 Introduction

The most prominent resistance mechanism against tetracycline (tc)-type antibiotics in Gram-negative bacteria relies on the regulation of the synthesis of an antiporter protein, TetA, by the Tet repressor protein TetR.^1,2 The latter protein binds, in the absence of tc, to operator DNA (tetO) and thus prevents the transcription of the genes encoding TetR and TetA. Upon binding of tc complexed with divalent metal ions, like Mg²⁺ or Ca²⁺, in the binding pockets of the TetR dimer, conformational changes are induced in TetR,^3–5 which lower the TetR/tetO binding constant by up to ten orders of magnitude.⁶ After dissociation, the expression of the genes TetR and TetA can proceed.

More recent investigations by Hillen and coworkers^7,8 proved that, in contrast to the established assumption, anhydrotetracycline (atc) is bound by TetR, even in the absence of divalent metal ions, although with a binding constant some 4 orders of magnitude lower than in the presence of Mg²⁺ (6.5 × 10⁷ M⁻¹versus 9.8 × 10¹¹ M⁻¹ in the presence of Mg²⁺). Furthermore, it was shown that induction occurs in wild-type TetR(D), and in the mutants TetR H100A and E147A, but not in mutant TetR T103A, in which Thr 103 is replaced by Ala. Therefore, it was concluded that the induction mechanism must be different in the presence and absence of Mg²⁺.⁷

In this contribution, we report the results of steady-state and time-resolved fluorescence spectroscopic studies aimed at achieving a better understanding of the influence of divalent metal ions on anhydrotetracycline (atc) binding and induction of the allosteric changes in protein conformation. Investigations were performed with both TetR(B) and TetR(D) proteins to separate class-specific and general phenomena. Furthermore, molecular dynamics (MD) simulations were carried out to model the time-dependent interaction between bound atc and the surrounding amino acids.

2 Materials and methods

2.1 Materials

The preparation and purification of TetR(B), TetR(D), and TetR(B) mutants are described in detail in previous publications.^9–11 The concentration of TetR dimer was always about 2 × 10⁻⁵ M in Tris buffer at pH 8.0. atc was purchased from ACROS Chimica (Beerse, Belgium). To control the ionic strength, 0.15 M NaCl was added, along with 1 × 10⁻³ M β-mercaptoethanol as an antioxidant. Further information regarding the sample composition is presented in Table 1.

Table 1 Preparation procedures and concentrations of various samples investigated by time-resolved fluorescence measurements

Sample	Starting compound	Additive 1	Additive 2	Additive 3
α	TetR(B) (37 µM)	atc (40%)	—	—
β	TetR(B) (30 µM)	EDTA (10 mM)	atc (40%)	—
γ	TetR(B)	atc (80%)	EDTA	—
β′	TetR(B)	EDTA	atc (40%)	Mg^2+
γ′	TetR(B)	atc (80 %)	EDTA	Mg^2+
δ (≡ β′)	TetR(B)	EDTA	atc (40%)	Mg^2+
δ′	TetR(B)	EDTA	atc (40%)	Mg^2+ + atc (40%)
ρ′	W170	Mg^2+	atc	—
σ′	W171	Mg^2+	atc	—
τ′	W172	Mg^2+	atc	—
ω′	W173	Mg^2+	atc	—
ε	TetR(D)	EDTA	atc	—
ε′	TetR(D)	EDTA	atc	Mg^2+

---

2.2 Steady-state spectroscopy

UV/vis absorption spectra were recorded on a Perkin Elmer Lambda 2 spectrometer. Steady-state fluorescence spectra were monitored on Jobin Yvon Fluoromax 3 or Perkin Elmer LS50B spectrometers, and were spectrally corrected.

2.3 Time-resolved fluorescence spectroscopy

Our home-built experimental set-up comprises a grating monochromator with an attached microchannel plate photomultiplier, whose output is fed into standard single-photon timing circuitry exhibiting an instrumental response of about 50 ps full width at half maximum.¹² Fluorescence from the thermostatted sample (T = 295 K) is detected under 90° through an analyser set at the magic angle with respect to the polarisation of the excitation beam.

Samples are excited by the frequency-doubled output (400 nm) of a cavity-dumped Ti:Sapphire laser, pumped by continuous wave Nd:YAG laser (pulse repetition rate 800 kHz, pulse width ∼100 fs, single pulse energy ∼5 nJ).

2.4 Data analysis

The fluorescence decay curves were analysed on the basis of a multi-exponential decay law, R(t), by using a nonlinear least-squares reconvolution procedure involving both the Marquardt and (for the final fit) the Simplex algorithm.^13,14

R(t, λ) = ΣA_i(λ) exp(−t/τ_i)

The number of exponentials was progressively increased until the fit was considered appropriate, as judged from the reduced χ² value, the distribution of weighted residuals and their autocorrelation function. Relative intensities of the individual fluorescence components are expressed as

F_i(λ) = [A_i(λ)τ_i]/[ΣA_i(λ)τ_i]

2.5 Model generation and molecular dynamics simulations

As a spatial basis for the model generation, we used an X-ray structure of the tetracycline repressor (TetR) dimer.³ The model contains two identical monomers generated by symmetry transformation. Each monomer consists of the repressor protein (Ala 2 to Ile 207) co-crystallised with one tetracycline (tc) molecule and one Mg²⁺ ion. Furthermore, there are 66 water molecules present, three of them coordinated to the active site magnesium ion. Because there are no TetR structures in complexes with anhydrotetracycline available, the coordinates of tc served, after removing the 6-OH group of ring C, as the geometrical basis for atc (see Scheme 1). To account for effects caused by the presence of the metal ion, which is coordinated to His 100 in the original X-ray structure, two additional systems were generated by removing the metal ion and (a) leaving the histidine residue unchanged (i.e. neutral, abbreviated to HID) or (b) protonating the histidine (abbreviated to HIP) to take into account its pK_a value of ∼6.5.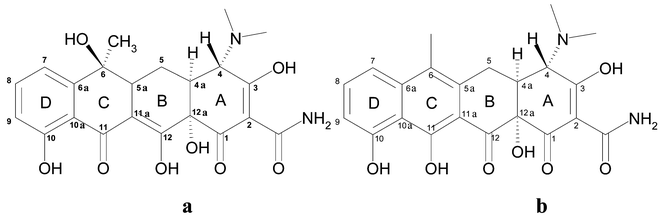

Scheme 1 Structures of tetracycline (a) and anhydrotetracycline (b) and numbering of atoms.

All molecular mechanics calculations were performed using the AMBER-94 force field parameters (parm94) of Cornell et al.,¹⁵ as implemented in the AMBER 5.0 software package.¹⁶ Charges for the ligand in the zwitteranionic form were derived after geometry optimisation with the AM1 Hamiltonian¹⁷ implemented in the semiempirical program package VAMP 7.0a¹⁸ using the VAMP restrained electrostatic potential fit procedure VESPA.¹⁹ The total system was subjected to 250 steps of steepest descent optimisation, followed by 11 750 steps of conjugate gradient minimisation, leading to an RMS gradient of <0.01 kcal mol⁻¹ Å⁻¹.

Using the energy-minimised coordinates as starting configuration, the system was equilibrated for 200 ps, raising the temperature gradually to 298 K by coupling to a temperature bath with a time constant of 5.0 ps, according to Berendsen. This equilibration part of the MD trajectories was not evaluated further. The final production run was carried out for 3 ns at 298 K. For all molecular dynamics simulations, we used an integration step size of 2 fs. Atomic coordinates, temperatures, and energies were recorded every 2 ps and used for subsequent analyses. SHAKE was employed to keep all bonds involving hydrogen atoms rigid. A cutoff of 8 Å applied to non-bonding interactions was used during all simulations, the 1–4 electrostatic and 1–4 van der Waals interactions were scaled by 1/1.2 and 1/2, respectively. The calculations were run using a distance-dependent dielectric constant (ε) of 4 because no bulk solvent molecules, apart from the crystal water molecules, were present and no periodic boundary conditions were applied. For this reason, the water molecules were prevented from evaporating by applying a weak harmonic restraint with a force constant of 1.0 kcal mol⁻¹ Å⁻² on the oxygen atoms, allowing reorientation and optimisation of the hydrogen-bond network. Preceding test simulations showed that the DNA-binding helix–turn–helix motif and the long loop connecting helices 8 and 9 (this loop is not resolved in all the available Tet repressor X-ray structures) are extremely flexible and do not maintain their tertiary structure in the absence of bulk water. Therefore, we additionally applied weak harmonic restraints (10.0 kcal mol⁻¹ Å⁻²) to the main chain atoms of the terminal amino acids Ala 2 to Arg 3 and Leu204 to Ile 207, and to the loop residue Glu 164. This procedure maintains the solute conformations close to their initial structures without affecting the flexibility in the inducer-binding and inter-domain connecting regions. Because the termini of the protein were almost fixed in Cartesian space, centre-of-mass translational motion never became substantial.

3 Results

3.1 Steady-state absorption and emission spectroscopy

The introduction of an additional double bond in anhydrotetracycline (atc) versus the parent tetracycline (for structures, see Scheme 1) causes a bathochromic shift of the longest wavelength transition by about 70 nm, but does not change its appearance as a broad and structureless band with only one distinct maximum (Fig. 1, top). Complexation of atc with one Mg²⁺ ion (the binding constant at pH 8 is about 10⁴ M⁻¹)²⁰ causes a further red shift of about 12 nm, again without much change in the band shape, but with a reduction in ε_max of about 15% (Fig. 1, bottom).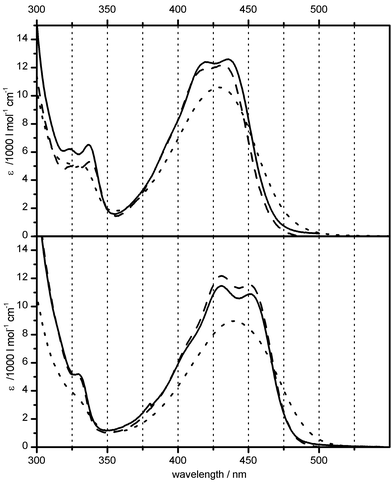

Fig. 1 Comparison of UV/vis absorption spectra of anhydrotetracycline (atc) in buffer solution (pH 8.0) (⋯) and when bound in TetR(D) (––) or TetR(B) ([dash dash, graph caption]) dimer, both without Mg²⁺ (top) and in the presence of excess Mg²⁺ (bottom).

In the next step, atc was mixed with about twice the equimolar amount of TetR(D) dissolved in buffer containing millimolar EDTA for complexation of all divalent metal ions. This was done because it had been speculated that binding of atc without addition of Mg²⁺ is mediated by divalent metal ions that can be present in the protein preparation for various reasons. The resulting absorption spectra show the appearance of a double peak in the range of the atc red absorption band, with maxima at about 420 and 436 nm. At the same time, the long wavelength tail of the red band is reduced. Furthermore, the weak band around 330 nm also splits up into two weak peaks at around 325 and 340 nm (Fig. 1, top). If, on the other hand, the complexes of atc with Mg²⁺ ions are added to the roughly 2 ∶ 1 TetR(D)–atc solution, then both ‘red’ maxima seem to be shifted bathochromically, the new locations being around 431 and 451 nm (Fig. 1, bottom). In other words, the two maxima seen in the spectrum of the Mg²⁺-free TetR(D)–atc complex apparently experience a similar shift (around 11 and 15 nm, respectively), as does the absorption maximum of free atc (around 10 nm) upon Mg²⁺ complexation.

To elucidate the origin of the double peak observed in the absorption spectra of atc bound in TetR protein and to assure ourselves that both maxima indeed shift in parallel, we performed titration experiments by adding MgCl₂ stock solution to the EDTA-containing mixture of atc and TetR(D). By also taking the spectra obtained for concentration ratios in between those shown in Fig. 2 into consideration, it can be stated that addition of small amounts of Mg²⁺ (trace B) causes a reduction in the intensity of the weak bands around 325 and 340 nm. Furthermore, the peak around 420 nm is reduced to a shoulder barely visible at the short wavelength side of a ‘new’ band maximum around 435 nm and the long wavelength tail starts to increase in intensity. Once the ratio [EDTA]/[Mg²⁺] is reduced to about 19 (trace C), then only one maximum is seen around 432 nm. When the ratio is below 4.5, which means a much higher concentration of free Mg²⁺, two pronounced maxima can be located at about 432 and 452 nm. The weak shoulder on the short wavelength side of the absorption band seems to persist, but is also shifted by about the same amount (12 nm).

Fig. 2 Mg²⁺-titration of EDTA-containing mixtures of atc and TetR(D) with EDTA/Mg²⁺ molar ratios of 174 (A), 58 (B), 19 (C), 4.5 (D) and 2.3 (E); pH 8.

A careful inspection also shows that two sets of isosbestic points can be identified: one set, for very low Mg²⁺ concentrations, comprises λ₁ = 320.5 nm and λ₂ = 445.5 nm, while the second set, for very large Mg²⁺ concentrations, includes λ₁′ = 320.0 nm and λ₂′ = 443.0 nm. As will be confirmed later by titration experiments with TetR(B), a possible explanation is that this shift of the isosbestic point manifests the Mg²⁺ complexation of the first and second atc bound in the dimeric TetR. It should be mentioned explicitly that the spectral changes induced by addition of Mg²⁺ are largely reversible if excess EDTA is added to the solution. Because of its large binding constant, EDTA complexes free Mg²⁺ effectively and thus partially eliminates it also from the binding equilibrium with atc in TetR(D).⁴

The appearance of the double peak in the ‘red’ absorption band of atc when bound in the TetR protein could arise for different reasons:

(i) It could be due to a heterogeneity of the chromophore–protein arrangement. Different types of protein conformations could result in a modified chromophore–protein interaction causing a change in electronic excitation energy. Further evidence for such an interpretation can be seen in the splitting of the band around 325 nm.

(ii) The broad, structureless absorption band of free atc could be caused by inhomogeneous broading due to a variety of different chromophore conformations (e.g. rotation of the amide group, tautomeric structures) or different intermolecular hydrogen-bonding patterns. Upon introduction into the binding pocket, the structural diversity of the functional groups of ring A could be greatly reduced due to strong interaction with the conserved amino acids (His64, Asn82, Phe86 and Gln116). Under this assumption, the modulation of the absorption profile would represent a vibronic structure. In favour of such an interpretation is the magnitude of the band splitting (about 990 cm⁻¹) and the conservation of the shoulder at the short wavelength slope upon Mg²⁺ complexation.

A well-established method for detecting the existence of two or more non-interconverting species in a solution makes use of the analysis of fluorescence spectra recorded with different excitation wavelengths or excitation spectra recorded at different detection wavelengths. Consequently, both types of spectra (not shown) were monitored for the samples whose absorption spectra are displayed in Fig. 2. It was generally found that the spectral distribution of the fluorescence is independent of the excitation wavelength, whether Mg²⁺ is absent or present in excess.

In accordance with the changes observed in the absorption spectra, the fluorescence spectra vary with the amount of Mg²⁺ available for binding to atc. Fig. 3 (trace B) illustrates that in the absence of Mg²⁺, the TetR(D)-bound atc exhibits a broad and unstructured fluorescence spectrum with only one maximum around 557 nm, despite the double peak seen in the absorption spectra. Compared to free atc, the maximum is blue shifted by about 28 nm, thus showing a smaller (but still unusually large) Stokes shift in the TetR(D)-bound state. At the same time, the fluorescence yield is increased by about a factor of 30. Upon increasing the concentration of Mg²⁺, a new fluorescence contribution grows in at the short wavelength side without obviously changing the spectral distribution at the long wavelength tail significantly (traces C and D). At the highest Mg²⁺ concentration investigated (when all atc should be complexed by Mg²⁺ because there were no further spectral changes), an indication for the appearance of two additional maxima at shorter wavelength (488 and 515 nm) is seen. The energetic splitting of about 1000 cm⁻¹ resembles that found in the absorption spectra.

Fig. 3 Normalised fluorescence spectra of free atc (A) and TetR(D)-bound atc in the absence of Mg²⁺ (B), and with increasing concentrations of Mg²⁺ (C and D); λ_ex = 430 nm, pH 8.0

In the intermediate Mg²⁺ concentration range, a pronounced excitation wavelength dependence is observed for the intensity ratio of the original red emission and the Mg²⁺-induced blue contribution (Fig. 4). The latter increases if the excitation wavelength approaches the maximum connected with the atc–Mg²⁺ complex (450 nm). Noteworthy is the large reduction in the fluorescence Stokes shift upon Mg²⁺ complexation, if the fluorescence maximum around 488 nm is correlated with the absorption maximum around 450 nm (Δ[small nu, Greek, tilde] ≈ 1730 cm⁻¹). The reported results provide, at the limits of free and completely Mg²⁺-complexed atc embedded in TetR(D), no evidence for more than one independently absorbing or emitting species.

Fig. 4 Excitation wavelength dependence of the normalised fluorescence spectrum of a sample containing both TetR(D)–atc and TetR(D)–atc–Mg²⁺ complexes; λ_ex = 395 (A), 420 (B), 432 (C), and 452 nm (D), [EDTA]/[Mg²⁺] = 20, pH 8.0.

In Fig. 1, we have also included the absorption spectra of atc and the atc–Mg²⁺ complex when bound in a TetR(B) dimer. The general appearance of the two spectra is similar to that of the corresponding TetR(D) spectra. The titration experiment (Fig. 5) reveals, however, a subtle difference. Whereas in the case of TetR(D), the location of the long wavelength maximum of the Mg²⁺-free TetR(D)–atc binary complex (λ = 435 nm) is clearly different from that of the short wavelength maximum of the ternary TetR(D)–atc–Mg²⁺ complex (λ = 430 nm), the corresponding two maxima of Mg²⁺-free atc and Mg²⁺-complexed atc are essentially superimposed in the case of TetR(B) complexes (λ ≈ 432 nm). In the Mg²⁺-complexed form, the two long wavelength absorption maxima of atc observed in the two different TetR proteins are nearly at the same location (λ = 451 nm). But a protein-specific interaction is manifested by comparison of the fluorescence spectra displayed in Fig. 6 and Fig. 3. Without Mg²⁺, the emission maximum of atc bound in TetR(B) appears at 550 nm (trace B) versus 557 nm in TetR(D). In contrast, in the presence of excess Mg²⁺, the fluorescence spectrum exhibits a rather broad region with comparable high intensity (trace D) and therefore barely represents a mirror image of the absorption spectra. It is also worth noting that in the case of TetR(B), binding of Mg²⁺ causes a significant red shift of the long wavelength tail of the fluorescence. The fluorescence excitation spectra, which appear to be independent of detection wavelength, closely resemble the absorption spectra (Fig. 7). In particular, the overlap of the maxima at 435 nm of the first peak of the Mg²⁺-free sample and the second peak of the Mg²⁺-incubated sample is nicely evidenced. The detection wavelength independence of the fluorescence excitation spectra could point to a rapid excited-state reaction by which two (or more) different emitters are formed at a fixed ratio (excited-state equilibrium). One of the emitting species must be formed by the same relaxation process which causes the extremely large Stokes shift of atc or atc–Mg²⁺ complexes in aqueous solution. This relaxation process must be prohibited by protein-specific interaction with the amino acids surrounding the chromophore. Depending on the model assumption chosen to explain the double peak in the absorption spectra, the two peaks seen in the ‘blue’ part of the fluorescence spectra must be taken as evidence for a reduced heterogeneity of the chromophore's structure or for the existence of a heterogeneity in the arrangement of the surrounding amino acids (e.g. formation of intramolecular hydrogen bonding).

Fig. 5 Mg²⁺ titration of an EDTA-containing mixture of atc and TetR(B); [EDTA]/[Mg²⁺] = 370 (A), 29 (B), 10 (C), 7 (D) and 2 (E), pH 8.0.

Fig. 6 Normalised fluorescence spectra of free atc (A) and TetR(B)-bound atc in absence of Mg²⁺ (B), and with increasing concentrations of Mg²⁺ (C and D); λ_ex = 430 nm, pH 8.0.

Fig. 7 Fluorescence excitation spectra of atc bound in TetR(B) in the absence (A; λ_det = 575 nm) and presence (B; λ_det = 550 nm) of Mg²⁺.

3.2 Time-resolved fluorescence

In the range 2 ≤ pH ≤ 10, anhydrotetracycline can be subject to three different protonation/deprotonation equilibria:

cation ↔ zwitterion ↔ anion ↔ dianion

atcH₃⁺ ↔ atcH₂ ↔ atcH⁻ ↔ atc²⁻

Since the macroscopic acidity constants have been determined to be pK_a1 = 3.93, pK_a2 = 5.94 and pK_a3 = 8.48,²⁰ atc will preferentially exist in solution at pH ∼8.0 as the mono-anion, accompanied by some dianions. Both atc ions can complex Mg²⁺ ions, thereby resulting, in principle, in a mixture of various metal ion-free and metal ion-complexed atc species in different states of protonation. Because of lack of information as to which of these species is (preferentially) incorporated in the binding pocket of TetR, we have to consider the possibility of a heterogeneity of the state of protonation for the bound atc and atc–Mg²⁺ complex, respectively. Consequently, we performed our time-resolved fluorescence measurements at several different detection wavelengths, covering the whole emission range. In most cases, the variation of deduced lifetimes was small. This could indicate either that the state of protonation is very uniform or that the fluorescence lifetimes do not vary significantly with the state of protonation of the dimethylamino group. The results given in Table 2 represent averages over the results obtained for different detection wavelengths. Under the conditions employed, a tri-exponential or tetra-exponential fluorescence decay law proved generally necessary and sufficient for a proper fit of the experimentally recorded intensity profiles. The third or fourth component, respectively, contributes only very little to the total fluorescence. Although the product A₃ × τ₃ is reproduced fairly well in fits with different starting values, the resulting values of τ₃ (of the order of 100 ps) and A₃ are subject to large errors. Therefore, we concentrate our discussion on the lifetimes and amplitudes of the two major components and especially the fractions F_i of these two components. In order to allow the reader to judge the signal-to-noise ratio obtained and the quality of the fit, the results obtained for the TetR(B)–atc–Mg²⁺ complex (sample γ′ in Table 1) are shown in Fig. 8.

Fig. 8 Time-resolved fluorescence profile recorded for a TetR(B)–atc–Mg²⁺ complex (sample γ′), with the corresponding residuals and autocorrelation functions for the bi- and tri-exponential fits, respectively. The solid line represents the optimised fit curve employing a tri-exponential decay law (λ_ex = 400 nm, λ_det = 550 nm).

Table 2 Fluorescence decay times (τ_i) and relative fractions (F_i = A_iτ_i/ΣA_iτ_i) determined for the samples α–ε′ specified in Table 1. (Note F₁ + F₂ < 100% if a small, very shorter-lived component is also detected.) Measurements were generally performed at pH 8, numbers in parentheses signify measurements at pH 7

Sample	τ 1/ns	τ 2/ns	F 1 (%)	F 2 (%)
α	3.9	1.6	78	14
β	5.1 (4.7)	2.6 (2.3)	48 (40)	48 (52)
γ	3.5	1.4	69	16
β′	3.8	2.2	85	14
γ′	3.6	1.4	88	7
δ (≡ β′)	3.8	2.2	85	14
δ′	3.6	2.3	89	11
ρ′	3.2	2.2	33	67
σ′	3.8	2.3	84	16
τ′	3.9	2.2	78	22
ω′	3.9	2.3	51	49
ε	5.0 (5.2)	2.4 (2.7)	78 (72)	20 (26)
ε′	4.7	1.5	97	3

---

If a TetR(B) protein sample prepared according to the previously described procedure^9–11 is incubated with metal ion-free atc (0.4 equimolar, sample α in Table 1), then the fluorescence decay curve can be fitted well with a tri-exponential decay law comprising a slow component with τ₁ ≃ 4 ns and a faster component with τ₂ ≃ 1.6 ns as the dominant ones (Table 2). In accordance with the generally observed increase in fluorescence intensity upon protein binding, one could speculate that the longer-lived component, which contributes about 80% to the total steady-state fluorescence, originates from atc bound within the protein, whereas the second component is due to metal ion-free atc not imbedded in the TetR(B) binding pocket. The fluorescence lifetimes previously determined for aqueous solutions of atc and tc do not favour this hypothesis.^21,22 Alternatively, it could be assumed that both components originate from TetR-bound atc; but in one case, atc is complexed with divalent metal ions already present, for whatever reason, in the protein preparation.

Further evidence for the latter hypothesis can be seen in the fact that, upon addition of EDTA to the protein before incubation with atc (sample β), the relative contribution of the longer-lived species is reduced to about 50% and the contribution of the shorter-lived species increased accordingly. However, the fact that both decay times change significantly (they increase by roughly 1 ns to about 5 and 2.6 ns, respectively) is at variance with this. The assignment of these two components to metal ion-free and metal ion-complexed atc would require that the interaction of both species with the surrounding protein is modified by a change in protein conformation coupled to the presence of divalent metal ions somewhere within the protein.

If, on the other hand, EDTA is added to a mixture of TetR(B) and atc (0.8 equimolar) (sample γ) then only small changes in the apparent decay times and the relative contributions of both fluorescence components are observed. Since there is strong evidence that EDTA is capable of removing Mg²⁺ from atc–Mg²⁺ complexes, this result, and also those described above, are in favour of an alternative model: the two fluorescence components found in sample β originate from atc molecules which are not complexed with metal ions, but exhibit a different chromophore–protein arrangement.

If the latter model applies, then addition of Mg²⁺ to these two different types of binary TetR(B)–atc complexes could yield different ternary TetR(B)–atc–Mg²⁺ complexes, except if the binding of Mg²⁺ to atc results in so strong an interaction that the two originally different protein conformations are adapted and similar final states are reached. If TetR(B) is exposed to EDTA before addition of atc (sample β), then both apparent fluorescence decay times decrease slightly upon addition of Mg²⁺, whereas the relative fractions (and amplitude ratio) change in favour of the longer fluorescence decay time (sample β′, Table 2). In the second sample, in which EDTA was added to the binary TetR(B)–atc mixture (sample γ), the fluorescence decay times appear to be fairly insensitive to Mg²⁺ addition and the relative contributions of both components change in favour of the longer-lived species (sample γ′).

If TetR(D) is treated with EDTA before addition of atc (sample ε, Table 2), then the fluorescence of the binary complex is characterised by two components with lifetimes similar to those measured for TetR(B) (sample β), namely τ ≈ 2.4 and 5 ns. Upon addition of Mg²⁺ to this binary mixture of EDTA-treated TetR(D) and atc (sample ε′), the shorter-lived component decays much faster (1.5 ns); the second decay time (4.7 ns) shows less shortening of the fluorescence decay time upon Mg²⁺ complexation than is observed for sample β′. The difference in the distribution of the fluorescence between the shorter- and longer-lived components is also noteworthy. In the case of TetR(D), the contribution of the shorter-lived component is much smaller than in TetR(B) independent of the presence or absence of Mg²⁺. Since the decay times and the changes brought about by Mg²⁺ complexation are very similar for the two types of protein, this pattern of relative intensity changes can be taken as another piece of evidence for the proposed model: the two fluorescence components originate from atc chromophores with different interactions with the surrounding protein. Complexation of atc by Mg²⁺ has a minor effect only on the chromophore's fluorescence lifetime and a small but significant effect on the equilibrium between the two protein conformations.

Changing the pH of the buffer can significantly modify the equilibrium between the two different types of chromophore–protein arrangements. Reducing the pH from 8 to 7 results in an enhancement of the amplitude of the shorter-lived fluorescence component of Mg²⁺-free atc by about 8% in TetR(D) and 10% in TetR(B), accompanied by small changes in the derived decay times (values in parentheses in Table 2).

3.3 Fluorescence of single trp mutants of TetR(B)

In Fig. 9, the absorption and (normalised) steady-state emission spectra of the TetR–atc–Mg²⁺ ternary complexes of four single tryptophan (trp) mutants of the TetR(B) class are shown for comparison. The absorption spectra show the same features as the absorption spectrum of the wild type (e.g. the double peak around 430 and 455 nm). The results of modelling studies based upon the X-ray structure of TetR(D) confirm the conclusions from stationary trp fluorescence spectra: In the mutants W170 and W173, the indole ring of trp points into the protein interior, in mutants W171 and W172, it points more towards the protein surface.^23,24 This difference in structure also manifests itself in the steady-state fluorescence spectra of atc–Mg²⁺ complexes bound within these mutants: the emission maxima of W170 and W173 are located further to the red than those of W171 and W172. The larger shift of the atc fluorescence in W170 and W173 probably reflects a stronger interaction with the indole ring of the mutated trp.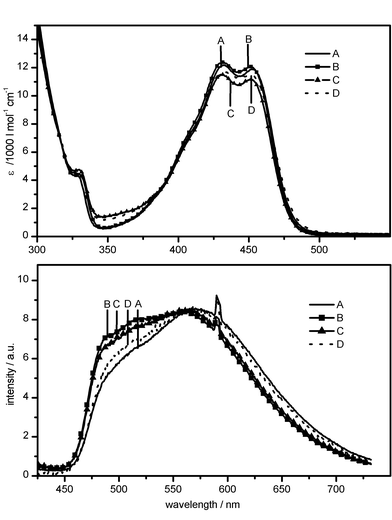

Fig. 9 Steady-state absorption (top) and normalised fluorescence spectra (bottom; λ_ex = 295 nm) of the atc–Mg²⁺ complex bound to mutants TetR(B) W170 (A), W171 (B), W172 (C) and W173 (D).

It is noteworthy in the context of the present investigation that the contribution in the blue spectral region of the fluorescence spectrum, which is strongly correlated with binding of Mg²⁺, varies with the site of mutation (Fig. 9, bottom). The additional two emission maxima can be identified more clearly in W171 and W172. The analysis of the fluorescence decay curves of the atc–Mg²⁺ complex also reflects the discussed structural difference. In all samples (protein incubated with atc–Mg²⁺ complexes), the decay can be fitted by a multi-exponential with one decay time close to 2.2 ns (Table 2). The second decay time varies with detection wavelength, the spread being larger in W170 and W173 than in W171 and W172. In the latter two mutants, the amplitude of the slower decaying components dominates, whereas in the former two mutants, the reverse is true.

Consequently, these time-resolved measurements favour the assumption of a significant heterogeneity of the protein arrangement around the inductor species. The structural heterogeneity can be classified according to the effect of the interaction on the fluorescence kinetics of the atc chromophore. A certain type of interaction results in the differentiation of the chromophores in one group with decay times below about 2.5 ns and a second group with decay times above 3 ns. Within these two groups, a further differentiation mechanism is effective, and it leads to small variations in conformationally averaged τ values and, additionally, to detection wavelength-dependent lifetimes.

4 Discussion

The goal of this section is to present the characteristics of a model that can explain the observations and conclusions described above:

(1) In aqueous solution, both the red absorption band and the fluorescence of atc are unstructured. A very large Stokes shift is observed (Δλ ∼ 160 nm).

(2) Upon binding in the protein, a splitting of the red absorption band of atc occurs in the absence of Mg²⁺. The fluorescence spectra are still unstructured and show a Stokes shift similar to that of free atc. Complexation of the protein-bound atc by Mg²⁺ results in a similar bathochromic shift of the two peaks of the ‘red’ absorption band and the shoulder on its short wavelength tail. In the fluorescence spectra, Mg²⁺ complexation results in an additional ‘blue’ component.

(3) Incubation of the first binding pocket of a TetR dimer with one atc–Mg²⁺ complex induces structural changes in the second binding pocket, as indicated by small shifts of the two isosbestic points observed upon titration of the TetR–atc complex with Mg²⁺.

(4) Several different ground electronic states (types of chromophore–protein arrangements) could exist, even if both binding pockets are filled with an atc–Mg²⁺ complex.

(5) Since the fluorescence emission spectra of the ternary complexes are independent of excitation wavelength, and because the fluorescence excitation spectra are independent of observation wavelength, an excited-state reaction leading to only one emitting state or to an equilibrium between several emitting chromophore–protein arrangements must be considered.

(6) The heterogeneity in chromophore–protein interaction can be classified according to the effect on the fluorescence decay time (and fluorescence yield) of the inductor molecule.

(7) Mg²⁺ complexation of atc has only a minor effect on the fluorescence decay times, but affects the distribution of the emitting states into two groups characterised by their fluorescence decay times. The pH variation of the surrounding buffer can also change the distribution of the emitting states somewhat.

Recently, a series of X-ray structures have been published for TetR(D) without an inducer, with [^7ClTc Mg]⁺ complexes in both binding pockets of the homodimer and with Mg²⁺ being removed from one pocket afterwards.^3–5 Additionally, the X-ray structure of TetR(D) bound to operator DNA (tetO) has been determined.⁵ By comparison of these structures, a model has been developed to explain the induction of allosteric conformational changes upon inductor binding and the concomitant change in distance and orientation of the two helix–turn–helix binding motifs. According to this model, the substitution pattern of the tc (especially on ring A) causes the binding specificity of its metal ion complex to TetR, while Mg²⁺ is primarily responsible for induction. Mg²⁺ is bound to the imidazole N(ε) of His100 and octahedrally coordinated to the 1,3-keto-enolate group of tc and three water molecules. One of these water molecules forms a hydrogen bond to the O(γ) hydroxyl group of Thr103 (Fig. 10). Although it is not yet clear whether exactly the same binding pattern applies to atc, since it induces in the absence of divalent metal ion, its adoption is a good starting point for the following discussion.

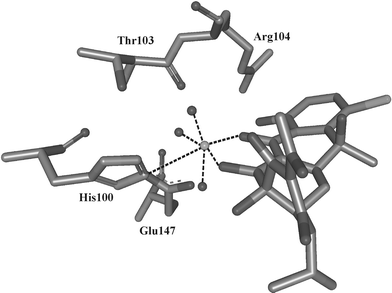Fig. 10 X-Ray structure of the 7-chlorotetracycline-bound Tet repressor (after ref. 4).

The X-ray structures also reveal that upon binding of a ^7Cltc–Mg²⁺ complex, a movement of α-helix 9 occurs, thereby bringing it closer to the side of tc that is not complexed with Mg²⁺. In the ‘fully induced’ form, the shift of α-helix 9 (amino acids 168–178) in both subunits amounts to about 2 Å versus the ‘uninduced’ form. If Mg²⁺ is eliminated from one TetR-bound [Tc–Mg]⁺ complex only, the corresponding shift in that subunit amounts only to about 1.2 Å (‘half-induced’ form). Upon induction, the position of the strongly interacting amino acids His100, Thr103 or Arg104 also changes markedly; more in the ‘fully induced’ form than in the ‘half-induced’ form, of course.^4,5

Keeping this structural information in mind, it is not surprising that the UV/vis absorption spectra of atc in the ‘singly complexed’ (of the two binding pockets, only one contains an atc–Mg²⁺ complex, the other one an Mg²⁺-free atc) and ‘doubly complexed’ (both binding pockets are occupied by an atc–Mg²⁺ complex) forms are slightly different. If we furthermore assume that, in the absence of Mg²⁺, the time-averaged absorption spectra of the atc molecules in both subunits are equal, then it is obvious that Mg²⁺ complexation of the first atc must yield an isosbestic point slightly shifted from that obtained by Mg²⁺ complexation of atc in the modified binding pocket (‘singly complexed’ protein conformation).

In view of the numerous functional groups of tc and atc, which can be subject to formation of hydrogen bonds (or protonation/deprotonation), one can speculate that interaction via hydrogen bonds is the origin of a heterogeneity in the electronic ground state and in the excited-state relaxation kinetics. Because the band splitting is also observed in the Mg²⁺-free samples, the relevant interaction must occur without the direct involvement of Mg²⁺. Therefore, it seems that the equilibrium between the different forms is only slightly influenced by the presence of Mg²⁺, except if a (large) excess of Mg²⁺ binds somewhere to the protein and induces significant changes in tertiary structure. Conformational differences in the protein could be such that they favour or disfavour the formation of hydrogen bonds between it and specific functional groups of atc. The latter conclusion is also favoured by fact that (i) the extent of the shift of the maximum varies slightly from one class of TetR to the other and (ii) the equilibrium distribution between the different groups of chromophore–protein arrangements can be varied by changing the pH without significantly affecting the shape of the steady-state absorption or emission spectra.

The alternative interpretation, namely that the weak structure in the UV/vis absorption spectra represents a manifestation of vibronic structure, makes obsolete the assumption that at least two different chromophore–protein arrangements with different excitation energies of the atc chromophore exist. The latter interpretation would also immediately account for the fact that the fluorescence spectra are independent of the excitation wavelength and that the excitation spectra match the absorption spectra.

However, we also cannot exclude a third possibility, namely that the absorption spectra represent the superposition of the spectra of two groups of chromophore–protein arrangements. One group, in which atc exhibits a broad and structureless absorption band, and a second group, in which, due to a specific interaction, a promoting mode appears in the absorption band of atc. As in the first case, the equilibrium between the different chromophore–protein arrangements must be established very effectively.

Depending on which model we choose to explain the features observed in the UV/vis absorption spectra, we must make different assumptions and, concomitantly, draw different conclusions in order to explain the steady-state emission spectra. If atc is bound without Mg²⁺ in the protein, then the fluorescence spectrum shows a broad and structureless band with a similar Stokes shift, as in case of free atc. This implies that the protein-bound atc must be subject to the same relaxation processes [e.g. excited-state intramolecular proton transfer (ESIPT), deprotonation in the excited state, charge transfer, etc.]²⁵ which occur in free atc. The fluorescence spectrum of the protein-bound Mg²⁺–atc complex, on the other hand, contains at least three contributions. One contribution exhibits nearly the same spectral distribution as the protein-bound atc without Mg²⁺ complexation. The other part in the ‘blue’ spectral region, with indications of two weakly expressed maxima, could be considered as the superposition of the fluorescence from the two different chromophore–protein arrangements that give rise to the two peaks in the UV/vis absorption spectra. Alternatively, one could interpret the weak structure as the mirror image of the vibrational structure seen in the absorption spectra. This means that the ‘blue’ contribution is due to atc molecules, whose geometries are better fixed by intermolecular interaction with the protein in the electronic ground state. In the excited state, a smaller fraction of the atc molecules cannot, due to a specific interaction with the surrounding amino acids, undergo the relaxation processes which cause the large fluorescence Stokes shift of the majority of atc molecules. Binding of Mg²⁺ can therefore induce changes in the chromophore–protein arrangement which prevents a fraction of the atc molecules undergoing the relaxation processes typical for free atc. (Remember that the site of complexation of atc by Mg²⁺ is the same for free atc and protein-bound atc.²⁶)

The results of the time-resolved fluorescence experiments are in accord with a model that assumes a heterogeneity in the chromophore–protein arrangement in the electronic ground state and different relaxation pathways in the excited state of atc. It was found that the shorter of the two fluorescence decay times (τ₂ ≈ 2–2.5 ns) is fairly well conserved for all preparations, including different classes of wild-type TetR and single trp mutants of TetR(B). Therefore, this component should be assigned to that chromophore–protein arrangement that is not determined by specific interactions.

The second, longer-lived component is assigned to the chromophore–protein arrangement whose structure may be influenced by the formation (or breaking) of hydrogen bonds. Since the latter depends on the actual sequence of amino acids and, consequently, on the spatial arrangement of the protein backbone, the variation of the longer lifetime, τ₁, with protein structure can easily be rationalised. Furthermore, one can also understand why the spread of the values of τ₁ with detection wavelength is larger in certain mutants. The results of previous investigations on TetR suggest that the protein backbone in the neighbourhood of the binding pocket is not very rigid and can adopt different conformations with comparable total free energy (ΔA ≤ RT).

In addition, we know that the large amino acid residue (indole ring) of tryptophan (trp) looks inside the binding pockets of the mutants TetR(B)W170 and TetR(B)W173.^27,28 The steric interactions between the indole ring and the atc–Mg²⁺ complex should affect the dynamics and structural heterogeneity of the binding pockets of the TetR(B)W170–atc–Mg²⁺ and TetR(B)W173–atc–Mg²⁺ ternary complexes, respectively.^27,28 This perturbation can manifest itself in a spread in fluorescence decay times about a characteristic value and in a change in the fluorescence spectrum (Fig. 9).

In order to learn more about the nature and kinetics of the interaction between anhydrotetracycline and the surrounding amino acids, extensive molecular dynamics calculations are presently in progress. To illustrate the model outlined above further, we report here the results obtained for intermolecular hydrogen bonding to O10. There is good reason to assume that this could have a significant effect on the rate of radiationless deactivation of tetracyclines, either directly or indirectly, by changing the intramolecular hydrogen-bonding pattern. Excited-state intramolecular proton transfer (ESIPT) has been quoted as a possible reason for the large Stokes shift of the fluorescence and/or the low fluorescence quantum yield.²⁵ Our recent DFT calculations provide evidence that in the case of tetracycline, ESIPT is governed by the intramolecular hydrogen-bonding pattern.²²

The X-ray structure suggests a persistent hydrogen-bond interaction between N(ε)H of Arg104 and O10 of tetracycline. The MD simulations show that one can distinguish between at least three different arrangements. The first closely resembles the binding situation found in the crystalline state of the [TetR–Tc–Mg] ternary complex [Fig. 11(a), HE]. As a consequence of rotation around the C(δ)–N(ε) single bond, the diamino group of Arg104 is rearranged such that a hydrogen-bonding interaction between O10 and the hydrogens of one amino group is established [Fig. 11(b), HH]. However, the side chain of Arg104 can also rotate as a whole, with the effect that no relevant interaction between Arg104 and atc results [Fig. 11(c)]. It is important to note that all other proposed hydrogen-bond interactions between atc and the protein are found to be >85% occupied, and therefore considered stable during all simulations.

Fig. 11 Distinct atc–Arg104 arrangements found during the MD simulations: hydrogen bonding to O10 via N(ε)H (a) as in the X-ray structure and (b) via one amino group hydrogen. There is no interaction in case (c).

The MD simulations point to a second important aspect. Although in the starting configuration a hydrogen bond N(ε)H–O10 was assumed to exist in both monomers, the structure of the protein develops such that (at least during the time interval covered by the actual calculation) the binding situation is different for most of the time in the two subunits (Fig. 12). Displayed is the fraction of time (in %) during which the hydrogen bonding described exists in the two monomeric units for the three simulated systems (Mg²⁺, HIP, and HID cases). It is apparent that the motions within the two monomeric subunits of the system are not coupled, at least in the time window of 3 ns investigated. For the metal-containing system, we encounter all three possible cases: no hydrogen bonding at all, hydrogen bonding via N(ε)H (termed HE) and hydrogen bonding via the amino group hydrogens (termed HH). One can therefore state that, in the presence of Mg²⁺, the probability for hydrogen bonding between Arg104 and O10 of atc is about 0.15. Removing the metal changes the situation so that we see a preference for the formation of a hydrogen-bond interaction between Arg 104 and O10 via the amino group. In the case of protonated histidine, only one monomer shows this behaviour. Nevertheless, these interactions cannot be considered as persistent.

Fig. 12 Percentage of time during which hydrogen bonding between N(ε)H (denoted HE) or one amino group of Arg104 and O10 of atc (denoted HH) is present during the 3 ns production phase in monomers M1 and M2, respectively. Mg²⁺ denotes the metal-containing system, HIP the case where His100 is protonated and HID the case where His100 is neutral.

The effect of Mg²⁺ on the intramolecular hydrogen-bonding pattern is demonstrated in Fig. 13, where the variation in time of the dihedral angle H–O10–C10–C10a is shown, which can be taken as an indicator of OH10–O11 intramolecular hydrogen bonding. As might be expected in view of the results described above, the formation of this intramolecular hydrogen bond in monomers Mon 1 and Mon 2, respectively, is not correlated. Secondly, there are abrupt changes of fairly short periods in which the bond is established or in which it is broken. Thirdly, the binding of Mg²⁺ significantly affects the distribution of the ‘on’ and ‘off’ periods for hydrogen bonding. Although we would not claim that the hydrogen-bonding interaction discussed above is the exclusive or predominant parameter governing the excited-state kinetics of atc, it nevertheless provides strong evidence that the fluorescence kinetics of inducer molecules embedded in the binding pocket of TetR cannot be understood on the basis of the static protein structure provided by X-ray diffraction alone.

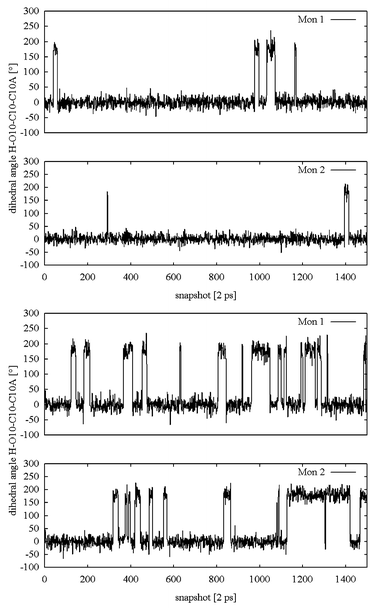Fig. 13 Variation of H–O10–C10–C10a dihedral angle characterising the intramolecular OH10⋯O11 hydrogen bond during the molecular dynamics simulation production phase of the system (a) in the absence of Mg²⁺, but with protonated His100, and (b) in the presence of Mg²⁺ with neutral His100. Every 2 ps, a snapshot containing the actual geometry was recorded, resulting in a total data acquisition time of 3 ns for 1500 trajectory entries. The labels Mon 1 and Mon 2 refer to the individual monomers within the tetracycline repressor dimer, which behave independently.

5 Conclusions and outlook

The spectroscopic experiments, described in this contribution, provide additional evidence for the conclusions drawn from a comparison of the X-ray structures of ‘uninduced’, ‘half-induced’ and ‘fully induced’ TetR(D). Mg²⁺ complexation of atc in one binding pocket of the TetR homodimer causes a small but significant change in the protein arrangement of the second monomer. However, the protein conformation in solution can, in addition, depend on the presence or absence of a divalent metal ion in the protein before atc is added. Consequently, the results of steady-state and time-resolved fluorescence experiments depend on the pretreatment of the protein sample, e.g. whether EDTA is added to the protein before mixing with atc and Mg²⁺. It is concluded that atc and the atc–Mg²⁺ complex are bound in different groups of chromophore–protein arrangements, with the equilibrium between them being established quickly. Because of the dependence of this equilibrium on pH, it is postulated that hydrogen bonding is an important factor for the discrimination of the different groups of excited-state conformations. Mg²⁺ can influence the hydrogen-bonding pattern, but is not directly involved in the differentiation. The shorter-lived fluorescence component should be related to the chromophore–protein arrangement which is less affected by specific interactions.

In a previous study employing high pressure as an additional experimental parameter, we showed that TetR must have a very rough energy landscape, thus giving rise to a significant heterogeneity in the arrangement of the indole ring of tryptophan (fluorophore) versus the location of other possibly quenching amino acids.²⁸ The regions of the conformational phase space that the protein adopts at ambient pressure and temperature obviously depend sensitively on the presence of divalent metal ions. These can change the interaction between the amino acids located at different sites on the same or on the second monomer, and thus modify the tertiary protein structure and, concomitantly, the interaction with the embedded inducer molecules. Consequently, work is presently in progress to learn more about the factors governing the chromophore–protein arrangement and the nature of the relaxation processes by studying a series of mutants using fluorescence spectroscopy under high pressure¹² and by performing further MD simulations. It seems impossible to understand the fluorescence kinetics of either tryptophan or any inducer molecule just on basis of the static protein structure provided by X-ray diffraction. Weak interactions, like hydrogen bonding, will exert only a small effect on energetic parameters. But they can have a dramatic effect on the relaxation processes which occur when the inducer molecule is in the electronically excited state.

We have fitted our fluorescence decay curves with a multi-exponential decay law. The latter is adequate only if the fluorescence represents the emission of a small number of distinct species. In view of the above-mentioned possibility of atc to establish several different (weak) hydrogen-bonding interactions, one must suspect that the multi-exponential decay law does not provide an appropriate description. Therefore, we will re-analyse the fluorescence data presented herein by the maximum entropy method.^29,30 We hope that this, together with the analysis of the spectroscopic data obtained for further mutants, will allow us to gain a better understanding of the effect of metal ions on the distribution of chromophore–protein arrangements in the electronic ground state and the relaxation processes induced by electronic excitation of the inducer molecules.

Acknowledgements

Financial support by Deutsche Forschungsgemeinschaft (SFB 473) and Fonds der Chemischen Industrie is gratefully acknowledged.

References

1. W. Hinrichs and Ch. Fenske, Gene regulation by the tetracycline-inducible Tet repressor-operator system — molecular mechanics at atomic resolution, in Tetracyclines in Biology, Chemistry and Medicine, ed. R. A. Greenwald, W. Hillen and M. Nelson, Birkhäuser, Basel, Switzerland, 2001.
2. W. Hillen and C. Berens, Mechanisms underlying expression of TN10 encoded tetracycline resistance , Annu. Rev. Microbiol., 1994, 48, 345–369.
3. W. Hinrichs, C. Kisker, M. Duvel, A. Müller, K. Tovar, W. Hillen and W. Saenger, Structure of the Tet repressor-tetracycline complex and regulation of antibiotic resistance, Science, 1994, 264, 418–420.
4. P. Orth, W. Saenger and W. Hinrichs, Tetracycline-chelated Mg²⁺ ion initiates helix unwinding in Tet repressor induction, Biochemistry, 1999, 38, 191–198.
5. P. Orth, D. Schnappinger, W. Hillen, W. Saenger and W. Hinrichs, Structural basis of gene regulation by the tetracycline inducible Tet repressor–operator system, Nat. Struct. Biol., 2000, 7, 215–219.
6. T. Lederer, M. Takahashi and W. Hillen, Thermodynamic analysis of tetracycline-mediated induction of Tet repressor by a quantitative methylation protection assay, Anal. Biochem., 1995, 232, 190–196.
7. O. Scholz, P. Schubert, M. Kintrup and W. Hillen, Tet repressor induction without Mg²⁺, Biochemistry, 2000, 39(35), 10 914–10 920.
8. O. Scholz, Induktorerkennung und Induktion des Tet Repressors, Ph.D. Thesis, Universität Erlangen-Nürnberg, Germany, 2002.
9. N. Ettner, G. Muller, C. Berens, H. Backes, D. Schnappinger, T. Schreppel, K. Pfleiderer and W. Hillen, Fast large-scale purification of tetracycline repressor variants from overproducing Escherichia coli strains, J. Chromatogr., A, 1996, 742, 95–105.
10. O. Landt, H. P. Grunert and U. Hahn, A general method for rapid site-directed mutagenesis using the polymerase chain reaction, Gene, 1990, 96, 125–128.
11. C. Berens, D. Schnappinger and W. Hillen, The role of the variable region in Tet repressor for inducibility by tetracycline, J. Biol. Chem., 1997, 272, 6936–6942.
12. D.-Th. Marian, TetR Protein Dynamics and Effector Binding Studied by Steady-State and Time-Resolved Fluorescence Spectroscopy at Variable Pressure, Ph.D. Thesis, Universität Erlangen-Nürnberg, Germany, 2003.
13. P. Bevington and D. Robinson, Data Reduction and Error Analysis for the Physical Sciences, McGraw Hill, Boston, 1992.
14. W. H. Press, S. A. Teukolsky, W. T. Vetterling and B. P. Flannery, Numerical Recipes in C: The Art of Scientific Computing, Cambridge University Press, Cambridge, 2nd edn., 1992.
15. W. Cornell, P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, Jr, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, A second generation force field for the simulation of proteins, nucleic acids, and organic molecules, J. Am. Chem. Soc., 1995, 117, 5179–5197.
16. D. A. Case, D. A. Pearlman, J. W. Caldwell, T. E. Cheatham III, W. S. Ross, C. L. Simmerling, T. A. Darden, K. M. Merz, R. V. Stanton, A. L. Cheng, J. J. Vincent, M. Crowley, D. M. Ferguson, R. J. Radmer, G. L. Seibel, U. C. Singh, P. K. Weiner and P. A. Kollman, AMBER 5.0, University of California, San Fransisco, USA, 1997.
17. M. J. S. Dewar, E. G. Zoebisch, E. F. Healy and J. J. P. Stewart, Development and use of quantum mechanical molecular models. 76. AM1: a new general purpose quantum mechanical molecular model, J. Am. Chem. Soc., 1985, 107, 3902–3909.
18. T. Clark, A. Alex, B. Beck, J. Chandrasekar, P. Gedeck, A. Horn, M. Hutter, B. Martin, G. Rauhut, W. Sauer, T. Schindler and T. Steinke, VAMP 7.0, Oxford Molecular Group Plc, Oxford, UK, 1998.
19. B. Beck, T. Clark and R. C. Glen, VESPA: a new, fast approach to electrostatic potential-derived atomic charges from semiempirical methods , J. Comput. Chem., 1997, 18, 744–756.
20. M. O. Schmitt and S. Schneider, Spectroscopic investigation of complexation between various tetracyclines and Mg²⁺ or Ca²⁺, PhysChemComm, 2000, 3(9), 42–55.
21. S. Schneider, M. O. Schmitt, G. Brehm, N. Fritz, P. Matousek and M. Towrie, Photophysical primary processes of anhydrotetracycline in aqueous solution, Rutherford Appleton Lab., [Rep.] RAL, 2003 , in press.
22. S. Schneider, M. O. Schmitt, G. Brehm, M. Reiher, P. Matousek and M. Towrie, Fluorescence kinetics of aqueous solutions of tetracycline and its complexes with Mg²⁺ and Ca²⁺, Photochem. Photobiol. Sci., 2003, 2 10.1039/b304523b.
23. M. Kintrup, P. Schubert, M. Kunz, M. Chabbert, P. Alberti, E. Bombarda, S. Schneider and W. Hillen, Trp scanning analysis of Tet repressor reveals conformational changes associated with operator and anhydrotetracycline binding, Eur. J. Biochem., 2000, 267, 821–829.
24. M. Kunz, M. Kintrup, W. Hillen and S. Schneider, Conformational changes induced in the Tet repressor protein TetR(B) upon operator or anhydrotetracycline binding as revealed by time-resolved fluorescence spectroscopy on single tryptophan mutants, Photochem. Photobiol., 2000, 72, 35–48.
25. H. Morrison, G. Olack and C. Ciao, Organic photochemistry. 93. Photochemical and photophysical studies of tetracycline, J. Am. Chem. Soc., 1991, 113, 8110–8118.
26. C. F. Leypold, Spektroskopische Untersuchungen von Tetrazyklinderivaten und deren Bindung in Tet Repressoren, Ph.D. Thesis, Universität Erlangen-Nürnberg, Germany, 2003.
27. B. Vergani, M. Kintrup, W. Hillen, H. Lami, E. Piémont, E. Bombarda, P. Alberti, S. M. Doglia and M. Chabbert, Backbone dynamics of Tet repressor α8∩α9 loop, Biochemistry, 2000, 39, 2759–2768.
28. D.-Th. Marian, C. Leypold, M. Kunz, S. Schneider, P. Schubert, O. Scholz and W. Hillen, Pressure effect on the structure of the Tet repressor protein TetR(B), Photochem. Photobiol. Sci., 2002, 1, 841–851.
29. J.-C. Brochon, Maximum entropy method of data analysis in time-resolved spectroscopy, Methods Enzymol., 1994, 240, 262–311.
30. C. Laboulais, E. Deprez, H. Leh, J.-F. Mouscadet, J.-C. Brochon and M. L. Bret, HIV-1 integrase catalytic core: molecular dynamics and simulated fluorescence decays, Biophys. J., 2001, 81, 473–489.

---