Complementary hydrogen bonding in a new tridentate Schiff base ligand: X-ray, DFT and solution NMR studies

Abstract

The X-ray crystal structure of a novel mono(pyrrole)-containing tridentate Schiff base ligand, N-[(1E)-1H-pyrrol-2-ylmethylene]benzene-1,2-diamine (3), shows unexpected hydrogen bond complementarity between neighbouring pairs of molecules in the solid state (monoclinic space group C2). The supramolecular structure is best described as a hinged dimer in which the dihedral angle between the two ligand planes measures 65(1)° and is stabilized by a pair of hydrogen bonds involving the pyrrole N–H proton on one molecule and the N atom of the aryl amino group on the neighbouring molecule. The experimental H_(pyrrole)⋯N_(amine) H-bond distances are equivalent at 2.40(2) Å. The ¹H NMR spectrum of 3 in CDCl₃ shows concentration-dependent features that are consistent with endergonic dimerization by intermolecular hydrogen bonding at higher concentrations [K_D = 0.89(16) M⁻¹ at 25 °C]. DFT calculations at the B3LYP/6-31G** level of theory correctly predict the main geometrical features of the dimer, which has slightly inequivalent H_(pyrrole)⋯N_(amine) distances of 2.31 and 2.33 Å in the calculated structure. The DFT-calculated dimer shows some conformational differences from the X-ray structure that primarily reflect the fact that the individual molecules of 3 in the in vacuo model are twisted about the C=N–C=C torsion angle involving the imine group and adjacent phenyl ring (C5–N2–C6–C7) by 4–8° more than is the case for the experimental structure. These conformational differences reflect the role that crystal packing plays in fine-tuning the supramolecular structure of 3.

---

Introduction

Schiff base ligands produced from condensation reactions between pyrrole-2-carboxaldehyde and an alkyl- or arylamine contain the bidentate chelate group 1 as one or more of the primary chelating motifs in the ligand. (Structures based on 1 are N-[(1E)-1H-pyrrol-2-ylmethylene]alkyl/arylamine derivatives, see Scheme 1.)

Scheme 1 Schiff bases containing pyrrole groups.

Ligand groups such as 1 are attractive as synthons since metallation of the chelate with concomitant deprotonation of the pyrrole ring affords an anionic ligand, a useful strategy for stabilizing metal ions in high oxidation states. Indeed, a search of the Cambridge Structural Database (CSD) reveals that there are well over 100 crystallographically characterized complexes of transition and main group metal ions that have been complexed with macrocycles or polydentate chelates based on fragment 1. Two simple, yet exemplary, derivatives of this system are the 3d transition metal complexes bis(N-t-butylpyrrole-2-carbaldimino)copper(II)¹ and cis-dichlorobis[2-(ethyliminomethyl)pyrrolide]titanium(IV).²

One of our current objectives is to use the tetradentate Schiff base ligand 2 {N,N′-bis[(1E)-1H-pyrrol-2-ylmethylene]benzene-1,2-diamine} as a porphyrin-like chelate for the complexation of metal ions to complement the work we have being doing with porphyrins.^3,4 Our interest in compound 2 is based on two observations. First, porphyrins may formally be considered to comprise two trans pyrrole nitrogens and two trans imine-type nitrogens—the donor atom combination of 2 is thus an analogue of this pattern that has the imine nitrogen pair cis or adjacent in the ligand. Second, the electronic structure of the ligand is not unlike that of a porphyrin since the pyrrole and imine nitrogens are also capable of π-bonding with the metal dπ orbitals. There are some obvious differences between porphyrins and 2, including the 5-membered chelate rings of 2 (porphyrins contain 6-membered chelate rings) and the fact that 2 is not a macrocycle. These fundamental differences are in fact of some significance because they may provide tractable clues, such as differences in metal ion affinity constants, as to the functional importance of the four equivalent 6-membered chelate rings and the macrocyclic structure that typify porphyrins.

Tetradentate Schiff base derivatives such as 2 are normally prepared by reacting 2 equiv. of pyrrole-2-carboxaldehyde and the appropriate diamine in ethanol or dichloromethane.⁵ It occurred to us during this work that the tridentate mono(pyrrole) Schiff base ligand 3 {N-[(1E)-1H-pyrrol-2-ylmethylene]benzene-1,2-diamine} would also be easy to prepare by reaction of the diamine with 1 equiv. of the appropriate aldehyde. Compound 3 is interesting because it is an asymmetric tridentate ligand that may be further functionalized by reaction with a range of aldehydes of varying complexity. In effect, 3 is a potentially important synthon for the synthesis of asymmetric or chiral tridentate/tetradentate ligands with applications in enantioselective catalysis, currently a highly active field of inquiry.^6–10

Schiff base 3 crystallizes from dichloromethane–hexane in the monoclinic space group C2 and displays an interesting supramolecular structure that involves complementary hydrogen bonding between neighbouring pairs of molecules (Fig. 1). In this paper, we describe the synthesis and X-ray crystal structure of 3 as well as density functional theory (DFT) calculations aimed at elucidating the intermolecular interactions between molecules of 3 in the solid state. Moreover, we have been able to show that Schiff base 3 forms H-bonded dimers at high concentrations in CDCl₃ by ¹H NMR spectroscopy. Significantly, the spectroscopic evidence suggests that the solid state supramolecular structure is probably also favoured in solution.

Fig. 1 Schematic illustration of the H-bond complementarity found in the X-ray crystal structure of 3.

Experimental

General

Hexane was distilled over sodium/benzophenone and dichloromethane over CaH₂. Pyrrole-2-carboxaldehyde and 1,2-diaminobenzene (Aldrich) were used as received. CDCl₃ for NMR spectroscopy was dried before use by passage down a short column (5 × 15 mm) of activated basic alumina. Electronic spectra were recorded with a Perkin–Elmer Lambda 45 double beam spectrophotometer using dichloromethane solutions in 1.0 cm path length cuvettes. Samples for IR spectroscopy were KBr mulls of polycrystalline material. FT-IR spectra were recorded with a Perkin–Elmer Spectrum One spectrometer (4 scans, spectral resolution = 1.0 cm⁻¹). Microanalytical data were obtained from a polycrystalline sample of 3 using a LECO CHNS-932 instrument. NMR spectra were recorded at various concentrations of 3 in CDCl₃ with a 500 MHz Varian Unity Inova spectrometer equipped with an Oxford magnet (11.744 T). Standard pulse sequences were employed. The proton and carbon NMR spectra were assigned using 2D COSY, HSQC, and HMQC data as well as calculated shielding tensors (vide infra).

Synthesis of N,N′-bis[(1E)-1H-pyrrol-2-ylmethylene]benzene-1,2-diamine, Schiff base 3

Pyrrole-2-carboxaldehyde (2.853 g, 15 mmol) and 1,2-diaminobenzene (1.600 g, 15 mmol) were refluxed in ethanol (15 ml) for 1 h. The solution was cooled and the solvent removed by rotary evaporation to obtain an orange-yellow solid. The solid was dissolved in dichloromethane (CH₂Cl₂) and n-hexane and allowed to recrystallize by slow rotary evaporation at reduced temperature and pressure. This process was repeated twice until a fluffy yellow powder (1.8504 g, 9.990 mmol, 67% crude yield) was obtained. The crude product was chromatographed on a short column of silica gel using 5% acetone in dichloromethane as the mobile phase to remove compound 2 and a purple contaminant, yielding 0.9418 g of 3 (35%) after final recrystallization from dichloromethane–n-hexane. X-Ray quality crystals of 3 were obtained by slow diffusion of n-hexane into a CH₂Cl₂ solution of the compound over 5 days at room temperature.

Anal. calcd for C₁₁H₁₁N₃: C, 71.3; H, 5.99; N, 22.7; found: C, 70.9; H, 5.97; N, 22.5. UV-vis (CH₂Cl₂) λ_max/nm: 245, 301, 365. δ_H (500 MHz, CDCl₃): 4.26 (2H, s, br, a), 6.30 (1H, dd, ³J₁ 3.4, ³J₂ 2.5, b), 6.71 (1H, dd, ³J 3.4, ⁴J 1.6, c), 6.74 (1H, m, d), 6.79 (1H, dd, ³J 8.1, ⁴J 1.2, e), 6.85 (1H, td, ³J 7.8, ⁴J 1.2, f), 7.07 (1H, dd, ³J 7.8, ⁴J 0.93, g), 7.11 (1H, td, ³J 8.1, ⁴J 1.2, h), 8.33 (1H, s, i), 10.25 (1H, s, br, j). δ_C (125 MHz, CDCl₃): 110.16 (C-1), 115.38 (C-2), 116.54 (C-3), 117.58 (C-4), 118.62 (C-5), 123.34 (C-6), 126.67 (C-7), 130.77 (C-8), 137.55 (C-9), 141.21 (C-10), 148.62 (C-11). IR (KBr pellet, cm⁻¹): 3454w ν_a(NH₂), 3352w ν_s(NH₂), 3296w br ν(N–H, pyrrole), 3103w ν(C–H), 3024w ν(C–H), 1616s ν(C=N), 1599s δ(NH₂), 1493m, 1416m, 1326m, 1298w, 1262m, 1121m, 1088m, 1031s, 883w, 824w, 741vs, 604w, 593w, 469w.

X-Ray crystallography

X-Ray diffraction data from a flat yellow needle-shaped crystal of 3 with the approximate dimensions 0.1 × 0.4 × 0.8 mm³ were collected on an Oxford Diffraction Xcalibur2 CCD 4-circle diffractometer equipped with an Oxford Instruments Cryojet operating at 122(2) K. The data were collected with Mo Kα (λ = 0.71073 Å) radiation at a crystal-to-detector distance of 50 mm using omega scans at θ = 29.389° with 35 s exposures taken at 2.78 kW X-ray power with 0.75° frame widths. The data were reduced with the program CrysAlis RED¹¹ using outlier rejection, scan speed scaling, as well as standard Lorentz and polarization correction factors. A total of 4084 reflections were merged to give 2065 unique data with an average redundancy of 2.5 and a mean F²/σF² of 24.43. The internal R index for the data set after reduction was 0.03(2) and the resolution of the data was to 0.68 Å with an impressive mean F²/σ(F²) of 4.06 for the high angle data (0.72–0.68 Å resolution).

The structure was solved in the monoclinic space group C2 using direct methods in WinGX's¹² implementation of SHELXS-97.¹³ All non-H atoms were located in the E-map and refined anisotropically with SHELXL-97.¹³ The data set was of sufficiently high quality that all H atoms were located in the final difference Fourier synthesis cycle. The coordinates of the H atoms attached to the pyrrole and amino nitrogens of 3 were refined isotropically without constraints; however, the isotropic U_ij values were fixed at 1.2 times the U_eq values of the nitrogen atoms. All other H atoms were calculated using the standard riding model of SHELXL-97 (HFIX 44 instruction), which allows the X–H distances to vary during refinement. The absolute configuration of 3 could not be determined unambiguously from the value of the Flack parameter.¹⁴ Selected crystal data and refinement details are given in Table 1.‡

Table 1 Crystal data and structure refinement details for 3

a w = 1/[σ^2(F^2o) + (0.0759P)^2 + 0.0298P], where P = (F^2o + 2F^2c)/3
Chemical formula	C11H11N3
M r	185.23
Cell setting	Monoclinic
Space group	C2
a/Å	18.373(8)
b/Å	5.489(4)
c/Å	11.369(4)
β/°	124.22(3)
U/Å^3	948.1(9)
Z	4
μ/mm^−1	0.08
T/K	122 (2)
Total reflections	4084
Independent reflections	2065
Observed reflections [I > 2σ(I)]	1936
R int	0.030
R [F^2 > 2σ(F^2)]	0.036
wR (F^2)^a	0.102

---

DFT calculations

Density functional theory calculations were carried out using the X-ray coordinates of 3 as input with the B3LYP functional,¹⁵ 6-31G** basis set,¹⁶ and a medium grid in Titan 1.08.¹⁷ Spin-restricted DFT wave functions (RDFT) were used on the lowest-lying doublet states of the X-ray structures (monomer and H-bonded dimer), which were analyzed by single point calculations as well as full geometry optimizations with the convergence criteria 4.500 × 10⁻⁴ (max. gradient), 3.000 × 10⁻⁴ (rms gradient) and 5.000 × 10⁻⁵ (max. energy difference) between successive steps. All converged DFT wave functions were analyzed with Weinhold's NBO 4M program,¹⁸ which uses the first-order reduced density matrix of the wave function to obtain natural atomic orbitals (NAOs) and natural electron populations for the system. NMR shielding tensors were calculated at the B3LYP/6-31G** level of theory using gauge-independent atomic orbitals¹⁹ with Gaussian 98.²⁰ Frequency calculations were carried out on all minimum energy structures with Gaussian 98; none yielded imaginary vibrational modes (implying that all refined geometries were true minima).

Results and discussion

Synthesis and molecular structure of 3

Although somewhat inelegant, the synthesis of the tridentate Schiff base 3 was straightforward using a 1∶1 mole ratio of 1,2-diaminobenzene and pyrrole-2-carboxaldehyde. However, we did find that the crude reaction product contained ∼35% of the tetradentate Schiff base 2 since this reaction product is statistically feasible, even under conditions chosen to favour formation of the mono(pyrrole) adduct. Successive recrystallization of the crude reaction product from a mixture of dichloromethane and hexane afforded a substantially purer (85% compound 3) pale yellow microcrystalline material. The solid was then further purified in a convenient manner using regular column chromatography on silica gel. Good quality single crystals suitable for an X-ray diffraction experiment were obtained by slow liquid diffusion with dichloromethane and hexane as the solvent system.

The X-ray crystal structure of 3 (Fig. 2) confirms that the E isomer of the Schiff base is obtained from the condensation reaction. Inspection of the space-filling plot of the structure reveals that this isomer is probably preferred on steric grounds since the Z isomer would require rotation about the N2–C5 bond by 180° and this would lead to rather severe nonbonded repulsion between H7 and H1A. Interestingly, the E isomer of 3 is not completely planar. There is a 4.0(2)° twist about the C7–C6–N2–C5 torsion angle that apparently reflects a conformational adjustment to alleviate an unfavourable steric interaction between H7 and H5 (H7⋯H5 = 2.05 Å). Moreover, as shown in the schematic diagram of Fig. 2(b), the out-of-plane displacements of the non-H atoms of 3 are consistent with the molecule adopting a somewhat bowed conformation in which the two aromatic rings partly dip below the 14-atom mean plane. (The imine group atoms N2 and C5 are displaced above the mean plane.)

Fig. 2 (a) Labelled ORTEP diagram of 3. Displacement ellipsoids are drawn at the 60% probability level; H atoms are drawn as spheres with equal, though arbitrary radii. (b) Diagram illustrating the perpendicular displacements of selected atoms from the 14-atom (non-H) mean plane of 3. (c) Partly labelled space-filling view (van der Waals radii) of 3 approximately perpendicular to the phenyl ring plane.

The refined coordinates of the amino group H atoms show that the N atom has mainly sp³-hybridized character. However, it is interesting to note that the values of the bond angles C11–N3–H3A and C11–N3–H3B (Table 2) are actually between those expected for an unsubstituted sp³ hybridized N atom (107°) and an sp² hybridized N atom (120°). Thus, although H1A and H1B are located above the 14-atom mean plane of 3, the amino group is somewhat flatter than expected for a purely sp³-hybridized N atom. The X-ray data therefore suggest that the hybridization of N3 is best described as an sp³/sp² admixture. This interpretation is in fact confirmed by the in vacuo DFT-calculated structure of 3 (vide infra).

Table 2 Selected bond distances (Å) and angles (°) for 3^a

a The s.u. of each value is given in parentheses.
C (1)–N(1)	1.367(2)	C(6)–C(11)	1.414(2)
C(1)–C(2)	1.383(2)	C(7)–C(8)	1.392(2)
C(2)–C(3)	1.416(2)	C(8)–C(9)	1.394(2)
C(3)–C(4)	1.388(2)	C(9)–C(10)	1.394(2)
C(4)–N(1)	1.375(2)	C(10)–C(11)	1.404(2)
C(4)–C(5)	1.439(2)	C(11)–N(3)	1.386(2)
C(5)–N(2)	1.282(2)	N(1)–H(1A)	0.88(2)
C(6)–C(7)	1.399(2)	N(3)–H(3A)	0.88(2)
C(6)–N(2)	1.414(2)	N(3)–H(3B)	0.88(2)
N(1)–C(1)–C(2)	108.3(1)	C(10)–C(9)–C(8)	120.8(1)
C(1)–C(2)–C(3)	107.2(1)	C(9)–C(10)–C(11)	120.0(1)
C(4)–C(3)–C(2)	107.2(1)	N(3)–C(11)–C(10)	121.8(1)
N(1)–C(4)–C(3)	107.8(1)	N(3)–C(11)–C(6)	118.7(1)
N(1)–C(4)–C(5)	121.9(1)	C(10)–C(11)–C(6)	119.4(1)
C(3)–C(4)–C(5)	130.1(1)	C(1)–N(1)–C(4)	109.3(1)
N(2)–C(5)–C(4)	120.8(1)	C(1)–N(1)–H(1A)	125.5(1)
C(7)–C(6)–N(2)	126.2(1)	C(4)–N(1)–H(1A)	125.2(1)
C(7)–C(6)–C(11)	119.6(1)	C(5)–N(2)–C(6)	121.8(11)
N(2)–C(6)–C(11)	114.2(1)	C(11)–N(3)–H(3A)	118(1)
C(8)–C(7)–C(6)	120.7(1)	C(11)–N(3)–H(3B)	116(1)
C(7)–C(8)–C(9)	119.5(1)	H(3A)–N(3)–H(3B)	114(2)

---

The unit cell packing for 3 (Fig. S1, Electronic supplementary information) clearly indicates that the central pair of molecules within the unit cell constitutes a hydrogen-bonded dimer in which there is a complementary interaction between the amino group lone pair (N3) of one molecule and the pyrrole NH group H atom (H1A) of the neighbouring molecule. The angle between the non-H 14-atom mean planes of the two molecules in the H-bonded pair measures 65(1)°. This reflects the projection of the lone pair of electrons that belong to N3 at an angle that is close to orthogonal to the benzene ring. Such a location of the H-bond acceptor site, which has significant sp² hybrid character as a result of hyperconjugation of the lone pair of electrons with the aryl ring π-electrons, essentially precludes any co-planar alignments for the hydrogen bond donor molecule.

The intriguing arrangement of H-bonding interactions in the crystal structure of 3 is illustrated graphically in Fig. 3. The two complementary H bonds between the molecules that constitute the dimer have an atomic separation that measures 2.386(2) Å (N3⋯H1Aⁱ) and an interaction angle of 160.11(7)° (N1ⁱ–H1Aⁱ⋯N3) [symmetry code: (i) −x + 1, y, −z + 1]. There is also a second, more unusual type of H-bonding interaction between each member of the dimer and the closest neighbouring molecule in the unit cell. More specifically, the X-ray data suggest that a somewhat weaker hydrogen bond between the pyrrole nitrogen lone pair of a neighbouring molecule (which is formally part of the delocalised π-electron system of the ligand) and the donor hydrogen atom H3A is likely. The H-bond distance measures 2.740(2) Å (N1ⁱⁱ⋯H3A) and has an interaction angle of 156.19(7)° (N3–H3A⋯N1ⁱⁱ) [symmetry code: (ii) −x + 1, y − 1, −z + 1]. A noteworthy caveat is that the latter contact distance is very close to the sum of the van der Waals radii of H and N (2.75 Å). Furthermore, the true position of the H atom in question is never completely certain even from high-resolution low-temperature X-ray diffraction data. Nevertheless, the geometry of this unconventional H bond is not altogether unreasonable if one considers the electrostatics of the interaction. Indeed, it may even be argued that hydrogen atom H3A interacts to some extent with the delocalized π-electron cloud of the neighbouring pyrrole ring.

Fig. 3 H-bonding interactions between neighbouring molecules of 3 in the solid state.

Interestingly, the recent X-ray crystal structure of 4,5-dimethyl-1,2-bis(2-pyrrolylmethylimino)phenylene, the 4,5-dimethyl analogue of 2, also shows a complementary H-bonding relationship between two Schiff base units within a discrete dimer.⁵ The H bonding is, however, quite different in that four H bonds exist between the pair of molecules in the dimer, consistent with there being two imine type nitrogen H-bond acceptor sites and two pyrrole NH group H-bond donor sites in the tetradentate Schiff base derivative. Furthermore, the tridentate Schiff base 1-{(E)-[(2-hydroxyethyl)imino]methyl}-2-naphthol, which has the donor atom combination ONO, also forms intermolecular H-bonded dimers in the solid state by virtue of a suitable combination of H-bond donor and acceptor sites within the molecule.²¹ A number of tri- and tetradentate Schiff base systems (both free bases and metal complexes²²) therefore appear to be predisposed towards self-recognition by intermolecular H-bonding.²³

NMR spectroscopy: solution structure of 3

A pertinent question is whether or not the complementary hydrogen-bonding pattern observed in the solid state is maintained in solution. In general, H-bonded alcohol and amino groups display concentration dependent chemical shifts and line widths that reflect intermolecular H bonding. In most cases, the chemical shift of the resonance is deshielded as a result of an H-bonding association and the line width is normally sharper due to slower exchange and/or relaxation on the proton NMR timescale as a result of the association.²⁴

Fig. 4 shows selected proton NMR spectra of 3 as a function of the total concentration of the Schiff base in solution. At low concentrations, the pyrrole NH proton resonance is very broad (line width = 275 ± 83 Hz at 0.047 M) as a result of rapid relaxation in CDCl₃ solution. Association by hydrogen bonding as the concentration of 3 in solution increases leads to a downfield shift of the signal and concomitant narrowing of the line width (to 67 ± 4 Hz at 0.90 M), consistent with a slower relaxation and/or exchange rate for the pyrrole NH proton(s) in the dimer complex. It is also noteworthy that a single resonance is observed for the pyrrole NH proton at all concentrations. This suggests that the exchange rate for the monomer ↔ dimer equilibrium is fast on the 500 MHz ¹H NMR time scale and that the spectrum is a weighted time-average of that due to each species in solution. Importantly, the methine proton resonance of the imine group (δ_H = 8.33) retains its Larmor frequency and line width at all concentrations. Indeed, protons that do not change their magnetic environment with concentration are expected to give concentration independent signals. This signal therefore serves as an intense, visible reference point in the ¹H NMR spectrum of 3 and highlights the marked changes in the pyrrole NH proton resonance that are brought about by intermolecular hydrogen bonding.

Fig. 4 Selected scans of the pyrrole NH proton resonance for Schiff base 3 as a function of the total concentration in CDCl₃ at 25 °C. The inset shows a non-linear least-squares fit of a simple equilibrium dimerization model [eqn. (1)] to the experimental data.

The ¹H NMR spectra strongly suggest that Schiff base 3 dimerizes in solution according to the simple equilibrium shown in Scheme 2. If we assume that the observed chemical shift for the pyrrole NH proton is the equilibrium-weighted average of the chemical shifts of the monomer and dimer, then eqn. (1) can be used to fit the concentration dependence of the resonance in question:

δ_obs = δ_M × f_M + δ_D × f_D (1)

where δ_obs, δ_M and δ_D are the chemical shifts of the equilibrium mixture, monomer and dimer, respectively. The association (dimerization) constant, K_D, may be given by eqn. (2):

f_D = 1 − f_M (4)

The fractions of the monomer and dimer in solution, f_M and f_D, are then given by eqns. (3) and (4), where [L]_T is the total concentration of the Schiff base. As shown in Fig. 5, the fit of eqn. (1) to the observed concentration dependence of the chemical shift of the pyrrole NH proton resonance is quite satisfactory (correlation coefficient = 0.999, sum of squares of errors = 1.9 × 10⁻³ ppm) and affords the following parameter estimates: δ_M = 9.46(3), δ_D = 11.10(8) and K_D = 0.89(16) M⁻¹ at 25 °C [ΔG²⁹⁷ = +0.29(4) kJ mol⁻¹]. The association constant is close to 1 and the reaction possibly exergonic if one considers the s.u. (standard uncertainty) of the measured value of K_D. However, without measured values of ΔH and ΔS for the reaction, we cannot determine the slope of the Gibbs–Helmholtz function for this system. It is thus difficult to say whether at 25 °C the system has just become endergonic or is about to become exergonic—a property that can only be revealed by variable temperature studies of the system. The bottom line is that the room temperature reaction (25 °C) has a ΔG value that is close to zero in CDCl₃. However, even though forcing conditions are required to bring about dimerization of 3 in solution, the NMR data clearly demonstrate that the association is via intermolecular H bonds involving the pyrrole NH proton, as seen in the solid state.

Scheme 2

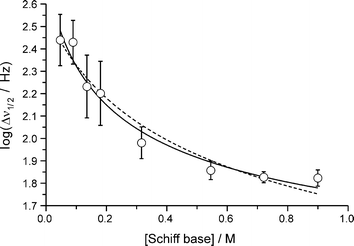Fig. 5 Unconstrained (solid line) and constrained (dashed line) non-linear least-squares fits of eqn. (5) to the concentration dependence of the pyrrole NH proton resonance line width in CDCl₃ (25 °C).

As noted above, the pyrrole NH proton resonance shows a marked decrease in line width with increasing concentration. Eqn. (1) may therefore be rewritten to fit the concentration dependence of the line width:

log(Δν_1/2) = log(Δν_M) × f_M + log(Δν_D) × f_D (5)

where Δν_1/2, Δν_M and Δν_D are the widths at half height of the observed, monomer and dimer pyrrole NH proton resonances, respectively. As shown in Fig. 5, an unconstrained fit of the data by eqn. (5) affords a suitable description of the experimental line width variation in this system. The parameter estimates were log(Δν_M) = 2.7(2), log(Δν_D) = 1.2(2) and K_D = 2(2) M⁻¹. Although the fit yields a poor estimate of the association constant, which fails a statistical student's T-test as reflected by the large s.u., the limiting line widths for the monomer and dimer species are statistically reliable. Since Δν_1/2 = (πT₂)⁻¹,²⁴ where T₂ is the transverse (spin–spin) relaxation time, the estimated effective transverse relaxation times for the pyrrole NH proton in the monomer and dimer are 6.35(2) × 10⁻⁴ and 1.89(6) × 10⁻² s, respectively. The relaxation rate of the pyrrole NH proton is thus about two orders of magnitude slower in the dimer as a result of its association with the amino N atom lone pair in the neighbouring molecule and, presumably, slower chemical exchange. The dashed line in Fig. 5 shows the fit of eqn. (5) to the data with K_D fixed at 0.89 M⁻¹. Given the s.u.'s of the experimental line widths, this curve also gives a reasonable fit of the concentration dependence of the line width and yields limiting line widths of log(Δν_M) = 2.6(1) and log(Δν_D) = 0.8(6), the latter unfortunately being statistically insignificant (high s.u.).

A further point worth mentioning is that the line widths increased somewhat at Schiff base concentrations >1.0 M [e.g., log(Δν_1/2) = 1.89(3) at a concentration of 1.54 M]. Evidently, additional line broadening over and above that expected from intrinsic transverse relaxation occurs at the highest concentrations studied. The most likely origin of this effect is instrumental since larger volumes of solvent were used to acquire spectra from the most concentrated solutions and some magnetic field inhomogeneity is likely if part of the solution lies outside the NMR probe receiver coils. We also examined the effect of adding water to the solution and found that although the pyrrole NH proton resonance broadened significantly with increasing H₂O content, the chemical shift of the signal remained constant (Fig. S2, ESI). The latter experiments confirmed (1) that our procedure for drying CDCl₃ by passage down a short column of activated basic alumina is adequate for removal of all but a trace quantity of H₂O and (2) that the plot of chemical shift vs. Schiff base concentration shown in Fig. 4 indisputably reflects dimerization of 3 in this system rather than a water-dependent exchange process. However, we cannot rule out the possibility that some of the line width variation evident in Fig. 5 might be due to slight variations in the trace water content of the solutions used for the NMR study.

Gas-phase DFT-calculated structure of 3

The gas-phase structure of 3 calculated at the B3LYP/6-31G** level of theory is, on the whole, in reasonable agreement with the crystallographically observed conformation (Fig. 6). However, there are two key differences between the structures that predominantly reflect the intermolecular interactions present in the experimental structure. First, the calculated structure is more twisted than the X-ray structure by virtue of the larger torsion angle C7–C6–N2–C5, which measures 29.2° in the DFT-calculated conformation but only 4.1(1)° in the X-ray structure. We believe that this may well reflect the geometric constraints imposed by the pair of H bonds between the interacting units of the dimer in the experimental structure (Fig. 3). More specifically, the experimental conformation is flatter than the gas-phase structure because this conformation favours optimal H bonding between the two units comprising the dimer. Secondly, the lone pair of electrons belonging to the ArNH₂ group of the DFT-calculated structure is twisted in the opposite direction to that of the experimental structure. The torsion angles C6–C11–N3–H3B and C10–C11–N3–H3A, which may be used to effectively gauge the degree of tilt of the ArNH₂ lone pair, measure 16.8° and 28.2° in the calculated structure. These same angles, however, measure 27.2(1)° and 17.4(1)° in the X-ray conformation of 3. Again, this difference in the calculated and experimental structures probably reflects a local conformational adjustment that favours optimal H bonding between the two units of the dimer, as is evident from Fig. 3.

Fig. 6 Least-squares fit of the DFT-calculated (grey) and experimental (black) structures of 3. The RMSD between the two conformations is 0.374 Å for all atoms.

As noted earlier, the ArNH₂ group N atom has mixed sp² and sp³ hybrid character if the experimental bond angles subtended at the nitrogen atom are taken as being sufficiently accurate. We find that the values of the bond angles C11–N3–H3A and C11–N3–H3B measure 114.0° and 116.3°, respectively, for the in vacuo DFT-calculated conformation of 3. These calculated bond angles are within 2–4° of the experimental angles and support the notion that the amino group of 3 has a mixed hybridization state. An intriguing question is whether H bonding with the lone pair of electrons in the dimer structure of 3 changes the C–N–H bond angles, that is the relative contributions of sp² and sp³ hybrid character for the amino group N atom. As discussed below, we have been able to obtain evidence in support of this idea from the calculated structure of the H-bonded dimer of 3.

DFT-calculated dimer geometry for 3

A priori calculation of the structure of a dimer, particularly when the interaction is noncovalent, is usually not a straightforward matter when one is dealing with relatively complex molecules.²⁵ In this case, however, the X-ray structure of the H-bonded dimer of 3 provided a suitable set of input atomic coordinates for a full geometry optimization at the B3LYP/6-31G** level of theory. The geometry of the dimer calculated in the gas-phase was, on the whole, in good agreement with that of the X-ray structure (Fig. 7).

Fig. 7 Least-squares fit of the DFT-calculated (grey) and experimental (black) dimer structure of 3. The RMSD between the dimer structures is 0.413 Å for all atoms.

Three geometrical features of the dimer were reasonably well modelled in the calculated structure: (1) the H bond distances, (2) the conformation of each monomer unit making up the dimer and (3) the hinged arrangement of the interacting monomer units. Thus, the mean calculated N3⋯H1A distance was 2.32(1) Å while the dihedral angle between the 14-atom mean planes of the two calculated monomer units measured 79.8°. The H bond distance deviates from the experimental distance by only 0.07 Å and is well within the expected level of performance of the B3LYP method for H-bond calculations.²⁵ The calculated dihedral angle between the two planes of the interacting monomers deviates from the experimental value by some 15°. We attribute this mainly to the absence of steric or other crystal packing interactions in the simulation. In particular, it appears that the absence of packing interactions in the in vacuo simulation allows a significant degree of twisting of the molecule about the C7–C6–N2–C5 torsion angle (as noted above in the case of the monomer structure of 3). The driving force for this intramolecular twist is probably the nonbonded repulsion between H7 and H5, which is not damped to any significant extent in the simulated structure since the molecules are not in close contact with neighbouring molecules.

Interestingly, the conformation of each molecule within the dimer is calculated to be somewhat flatter than the in vacuo structure of the monomer itself. More specifically, the dihedral angle C7–C6–N2–C5 measures 8.6° and 12.8° for the two molecules making up the dimer. (The X-ray structure of the dimer comprises symmetry equivalent molecules, while the calculated structure of the dimer has C₁ symmetry and thus independent monomer conformations.) These calculated values are within 4.5° and 8.7° of the experimental values, respectively. The better agreement between the calculated and experimental conformations of 3 when H bonding to at least one of the neighbouring molecules in the lattice is taken into account clearly shows that H bonding and nonbonded intermolecular interactions fine-tune the crystallographically observed conformation of this compound.

The mean calculated C–N–H angle for the ArNH₂ group of 3 measures 113(2)° and compares favourably with the mean experimental value of 117(1)°. Interestingly, the calculated structure of the H-bonded dimer exhibits an amino group geometry that is somewhat closer to being pyramidal (sp³ hybridized) than planar (sp² hybridized). This finding suggests that the H bond to the nitrogen lone pair of electrons slightly changes the character of the nitrogen atom relative to the in vacuo monomer. Indeed, comparison of the natural atomic orbital populations for N3 in the monomer and dimer structure of compound 3 shows that the 2s and 2p orbital populations are highest for the dimer (Table 3), consistent with a more localized set of hybrid orbitals on the nitrogen atom. Ultimately, the lower valence electron population for N3 of the monomer is best viewed as reflecting a slightly higher degree of hyperconjugation of the N atom lone pair with the aryl ring π-electron system.

Table 3 Calculated natural atomic orbital electron populations for the amino group nitrogen atom N3 of compound 3

Natural atomic orbital	Monomer	Dimer
2s	1.3436	1.3699
2px	1.3773	1.6956
2py	1.7294	1.3781
2pz	1.3819	1.4249
Σ2p	4.4885	4.4986
Σ(valence electrons)	5.8322	5.8685

---

The natural atomic charge distributions for the monomer and dimer (Fig. 8) clearly indicate the favourable (complementary) electrostatics of the H-bonding interactions in the dimer. Thus, the amino group nitrogen atom (N3) carries a significant negative charge that approaches a full electron. The pyrrole NH group hydrogen atom (H1A) is seen to carry the highest fractional positive charge in both the monomer and the dimer. It therefore stands to reason that these regions of high opposite fractional charge should interact favourably in the H-bonded dimer and, we propose, succinctly explain the driving force behind the formation of the dimer (at least in the solid state). Interestingly, N3 and H1A achieve a slightly higher charge polarization in the dimer relative to the monomer. The increase in negative charge on the amino group nitrogen atom in the dimer amounts to about 0.037 of an electron and possibly reflects a slight increase in sp³ hybrid character for this N atom.

Fig. 8 Natural atomic charges for (a) the monomer and (b) the H-bonded dimer structures of compound 3.

The DFT-calculated energies in Table 4 may be used to estimate the energy of formation of the H-bonded dimer, ΔE_complexation, in the gas phase. Taking into account the appropriate counterpoise correction²⁶ to eliminate basis set superposition errors, we found that formation of the dimer was strongly favoured on thermodynamic grounds in the gas phase (ΔE_complexation = −9.33 kcal mol⁻¹). The favourable complexation energy is, furthermore, paralleled by an increase in the frontier orbital energy gap, ΔE_{(LUMO–HOMO)}, of 0.04 eV over that for the monomer, consistent with net stabilization of the system. If one compares the calculated gas phase complexation energy to the value of ΔG measured for the associative interaction in solution by NMR spectroscopy (vide supra), then it is clear that solvation has a pronounced effect on the process and severely diminishes the stability of the H-bonded complex.

Table 4 Selected DFT-calculated energy parameters for 3^a

	Monomer	Dimer	Molecule A	Molecule B
a All energies are in eV. b Formation energy of the dimer in the gas phase calculated as the total energy of the dimer minus the sum of the energies of its non-interacting constituent molecules (Molecules A and B). The BSSE (basis set superposition error) correction to this energy is +0.1563 eV.
E total	−16056.4141	−32113.2963	−16056.3651	−16056.3706
HOMO − 3	−6.81787	−5.91499	−6.85732	−6.86739
HOMO − 2	−6.48833	−5.90655	−6.68916	−6.66603
HOMO − 1	−5.75743	−5.04993	−5.78056	−5.77702
HOMO	−4.94734	−5.01510	−4.97564	−4.97646
LUMO	−1.27269	−1.30180	−1.35106	−1.34561
LUMO + 1	0.55947	−1.28058	0.55648	0.55484
ΔE(HOMO − LUMO)	3.67465	3.71329	3.62459	3.63084
ΔEcomplexation^b		−0.5606

---

Finally, it is noteworthy that the dimer structure of 3 does not comprise two separate molecules at the electronic level. As shown by a plot of the HOMO for the dimer (Fig. 9), the highest filled molecular orbital has π-symmetry and spans both molecules. Importantly, the MO coefficients for chemically equivalent atoms in each molecule are significantly different, consistent with the symmetry of the dimer and the idea that this system does not simply consist of two “isolated monomers”. Notwithstanding the fact that we have used a basis set without diffuse functions that may have partly limited the accuracy of the calculations as a result, the best description for the dimer structure of 3 is that of a single supramolecular system with substantially delocalized π-electrons. As indicated by the data in Table 4, the HOMO is near degenerate with the HOMO − 1. The latter orbital is roughly the inversion-related analogue of the HOMO. This trend is evident for the other frontier orbitals, which are seen to occur in near-degenerate pairs. In the limit of exact inversion symmetry for the dimer, one would expect these orbitals to be doubly degenerate.

Fig. 9 Drawing of the HOMO for the geometry-optimized (gas phase) dimer of 3.

Conclusions

We have synthesized and characterized a new tridentate Schiff base ligand that comprises a pyrrole group, an adjacent imine group, and an aryl amino group, namely N-[(1E)-1H-pyrrol-2-ylmethylene]benzene-1,2-diamine. The X-ray crystal structure indicates that the molecule is near planar and involved in a notable complementary hydrogen-bonding interaction with a neighbouring molecule in the solid state. The pyrrole NH and ArNH₂ groups act as the H-bond donor and H-bond acceptor sites, respectively, in the dimer. The supramolecular H-bonded dimer structure is apparently also favoured at high concentration in deuterated chloroform, as evidenced by concentration-dependent changes in the pyrrole NH proton NMR line width and chemical shift. Finally, gas-phase DFT simulations show that the H-bonded dimer is energetically feasible and that crystal packing interactions modulate the observed solid state conformation by flattening the molecular structure beyond that predicted in the absence of lattice interactions.

Acknowledgements

We gratefully acknowledge financial support from the University of Natal (URF), SASOL, and the National Research Foundation (NRF, Pretoria).

References

1. C. H. Wei, Inorg. Chem., 1972, 11, 2315–2321.
2. Y. Yoshida, S. Matsui, Y. Takagi, M. Mitani, T. Nakano, H. Tanaka, N. Kashiwa and T. Fujita, Organometallics, 2001, 20, 4793–4799.
3. O. Q. Munro, S. C. Shabalala and N. J. Brown, Inorg. Chem., 2001, 40, 3303–3317.
4. O. Q. Munro, P. S. Madlala, R. A. F. Warby, T. S. Seda and G. Hearne, Inorg. Chem., 1999, 38, 4724–4736.
5. F. Franceschi, G. Guillemot, E. Solari, C. Floriani, N. Re, H. Birkedal and P. Pattison, Chem.-Eur. J., 2001, 7, 1468–1478.
6. A. Heckel and D. Seebach, Helv. Chim. Acta, 2002, 85, 913–926.
7. M. Nielsen and K. V. Gothelf, J. Chem. Soc., Perkin. Trans. 1, 2001, 2440–2444.
8. P. R. Woodman, I. J. Munslow, P. B. Hitchcock and P. Scott, J. Chem. Soc., Dalton Trans., 1999, 4069–4076.
9. H. L. Kwong, W. S. Lee, T. S. Lai and W. T. Wong, Inorg. Chem. Commun., 1999, 2, 66–69.
10. R. I. Kureshy, N. H. Khan, S. H. R. Abdi, S. T. Patel and P. Iyer, J. Mol. Catal. A: Chem., 1999, 150, 175–183.
11. CrysAlis CCD and CrysAlis RED, Version 170, Oxford Diffraction Ltd., Abingdon, UK, 2002.
12. L. J. Farrugia, J. Appl. Crystallogr., 1999, 32, 837–838.
13. G. M. Sheldrick, SHELXS-97, Program for solution of crystal structures, University of Göttingen, Germany, 1997; G. M. Sheldrick, SHELXL-97, Program for refinement of crystal structures, University of Göttingen, Germany, 1997.
14. (a) H. D. Flack, Acta Crystallogr. Sect. A, 1983, 39, 876–881; (b) G. Bernardinelli and H. D. Flack, Acta Crystallogr., Sect. A, 1985, 41, 500–511.
15. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
16. R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728.
17. Titan, Version 1.08, Wavefunction, Inc. and Schrödinger, Inc., Irvine, CA, USA and Portland, OR, USA, 1999.
18. (a) F. Weinhold, NBO 4M, Theoretical Chemistry Institute, University of Wisconsin, Madison, WI, 1999; (b) J. E. Carpenter and F. Weinhold, J. Mol. Struct. (Theochem), 1988, 169, 41–62; (c) J. P. Foster and F. Weinhold, J. Am. Chem. Soc., 1980, 102, 7211–7218.
19. K. Wolinski, J. F. Hilton and P. Pulay, J. Am. Chem. Soc., 1990, 112, 8251–8265.
20. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery, Jr., R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Cioslowski, J. V. Ortiz, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, C. Gonzalez, M. Challacombe, P. M. W. Gill, B. G. Johnson, W. Chen, M. W. Wong, J. L. Andres, M. Head-Gordon, E. S. Replogle and J. A. Pople, GAUSSIAN 98 (Revision A.7), Gaussian, Inc., Pittsburgh, PA, 1998.
21. B. Kaitner and G. Pavlovic, Croat. Chem. Acta, 1999, 72, 607–620.
22. (a) A. Mukhopadhyay, G. Padmaja, S. Pal and S. Pal, Inorg. Chem. Commun., 2003, 6, 381–386; (b) V. M. Leovac, V. S. Jevtovic and G. A. Bogdanovic, Acta Crystallogr. Sect. C, 2002, 58, M514–M516; (c) S. A. Warda, Acta Crystallogr. Sect. C, 1998, 54, 1754–1755.
23. C. Y. Su, X. P. Yang, B. S. Kang, K. B. Yu and Y. X. Tong, Bull. Chem. Soc. Jpn, 1999, 72, 2217–2222.
24. R. K. Harris, Nuclear Magnetic Resonance Spectroscopy: A Physicochemical View, 2nd edn., Longman Scientific & Technical, Harlow, UK, 1986.
25. F. Jensen, Introduction to Computational Chemistry, 1st edn., Wiley, Chichester, UK, 1999.
26. F. B. van Duijneveldt, J. G. C. M. van Duijneveldt-van de Rijdt and J. H. van Lenthe, Chem. Rev., 1994, 94, 1873–1885.

---

Footnotes

† Electronic supplementary information (ESI) available: unit cell packing diagram for 3 (Fig. S1) and ¹H NMR spectra of 3 as a function of the concentration of added H₂O in CDCl₃ solution (Fig. S2). See http://www.rsc.org/suppdata/nj/b3/b305946d/

‡ CCDC reference number 219663. See http://www.rsc.org/suppdata/nj/b3/b305946d/ for crystallographic data in .cif or other electronic format.

---