Hydrodynamic simulation of cell docking in microfluidic channels with different dam structures

Abstract

The immobilization of biological cells in micro-devices requires high efficiency and easy control while maintaining cell viability. One approach for cell immobilization is to utilize constriction structures such as dams to trap cells in microfluidics. In this paper, we present a comprehensive hydrodynamic analysis of two different types of constriction structures for cell immobilization: dams either in perpendicular or in parallel to the main flow route. Various structural models and experimental conditions were compared for cell docking and alignment, and the pressure and velocity profiles of the flow in the micro-channels and the hydrodynamic force and shear stress on the docked cells were calculated based on fluid dynamic theory and numerical simulation. The effects of the dam structures and cell docking on the flow properties, the transportation efficiency, and the induced stress on the docked cells were analyzed. Improved hydraulic pressure profiles in the auxiliary inlets were discussed for the modulation of the flow characteristics and attenuation of hydrodynamic forces exerted on the cells. Furthermore, a new design combining the advantages of perpendicular and parallel dam structures was proposed for cell-based microfluidics.

---

Introduction

Cell-based assays are widely applied in cell biology, pharmacology, toxicology, and drug screening. As microfluidics offer significant advantages in terms of analytical speed, separation efficiency, reduced sample/reagent consumption, and elimination of contamination, the development of microfluidic devices for cell-based analysis has attracted growing interest in the area of lab-on-a-chip research.¹ A number of microfluidic devices for cell sampling and transportation, cell trapping and sorting, and cellular studies have been demonstrated based upon mechanical and electrical principles.^2–5 While some applications have relied on the flow characteristics of cells for on-chip cell manipulation, others have focused on the immobilization of target cells on microfluidic structures for culturing and assay purposes.^2,6–11

The immobilization of biological cells in micro-devices requires high efficiency and easy control while maintaining cell viability. Previous attempts have included the immobilization of cells on surfaces or micro-chambers by chemical or physical interaction prior to the sealing of microfluidics.^9,11–14 However, the alignment and bonding of the cell-immobilized substrates with peripheral microfluidic structures involves complex processes and may lead to the damage of immobilized cells. Multiple laminar flow technique is used as a simple and flexible method to form patterned cells in capillary networks,¹⁵ which requires specific surface modification and is difficult to form special laminar patterns within complex microfluidic networks. Cells could be manipulated by negative dielectrophoresis (nDEP) where AC current or rotating electric fields were used to focus, trap and separate eukaryotic cells.¹⁶ However, the fabrication and alignment of three-dimensional microelectrode systems is complicated and the applied electric field may affect cellular viability and cell-based reactions.

One approach for cell immobilization is to utilize constriction structures such as dams to trap cells in microfluidics. For example, an array of channels with variable lengths and diameters slightly smaller than target cells was used to trap and fractionate white blood cells.⁴ Other customized constriction architectures have been demonstrated for cell entrapment and immobilization.⁶ In these structures, the fluidic pathway at a particular region of a microfluidic device was narrowed down to hold back the targeted cells but let the fluid flow through. Because the constriction is usually perpendicular to the main flow route, the major limitation of this approach is the possible blocking of the micro-channels by the trapped cells, and the increasing hydrodynamic force exerted on the cells. Recently, we had demonstrated that a dam structure constructed between two parallel channels could be used to trap cells.² Cells flowing in micro-channels may be controlled to dock along the dam to form a regular single layer under suitable hydraulic pressure with little impact on the flow characteristics, and the docked cells were easily removed after each assay for subsequent reuse of the device.

In this paper, we present a comprehensive hydrodynamic analysis of two different types of constriction structures for cell immobilization: dams either in perpendicular or in parallel to the main flow route. Various structural models and experimental conditions were compared for cell docking and alignment, and the pressure and velocity of the flow in the micro-channels and the hydrodynamic force on the docked cells were calculated based on fluid dynamic theory and numerical simulation.^17,18 The effects of the dam structures and cell docking on the flow properties, the transportation efficiency, and the induced stress on the docked cells were analyzed. Improved hydraulic pressure profiles in the auxiliary inlets were discussed for the modulation of the flow characteristics and attenuation of hydrodynamic forces exerted on the cells. Furthermore, a new design combining the advantages of perpendicular and parallel dam structures was proposed for cell-based microfluidics.

Theory and simulation

When designing microfluidics for cell-based assays, the overwhelming concern is the reliable control of cell docking and the viability of the cells after immobilization, which are affected by the hydrodynamic force and the impact of cell immobilization on the flow.

Effect of dam structure and cell docking on the microfluidic flow

In a microfluidic channel, introduction of a constriction structure and immobilization of cells inevitably narrows the fluidic pathway, which increases flow resistance and affects the flow characteristics. According to classical hydrodynamic theory, the hydraulic pressure difference (ΔP) between two ends of a channel is the product of the flow resistance R and the average flow velocity v in the channel:

ΔP = Rv (1)

where the flow resistance is inversely proportional to the sectional area (A) of the channel:

R ∝ 1/A (2)

The presence of a dam structure and immobilized cells leads to the increase of flow resistance and pressure difference, which inevitably affects the flow velocity. Therefore, the dam height and the quantity of docked cells are very important in the control of the dam-dependent cell docking process.

If a cell is treated as a small sphere with radius a, the Reynolds number Re of the flow around a cell docking in an even, infinite fluidic field with flow velocity U (from −x to +x direction) is given by:

R_e = 2Ua/γ (3)

where the flow velocity U is in the order of 10⁻⁴m s⁻¹ under cell docking experiments controlled by liquid pressure difference, the kinematic viscosity γ of water is 10⁶ m² s⁻¹, and the radius a for a mammalian cell is about 10⁻⁵m. Because the Reynolds number Re is very low (<<1), Stokes equations can be used to estimate the pressure and velocity profiles of the flow and the hydrodynamic force exerted on the docked cell.¹⁹ In a spherical coordinate, Stokes equations are simplified as the continuity equation:and the momentum eqns (5) and (6) in the radial and tangential direction, respectively.Where μ is the dynamic viscosity, p, v_R, v_θ are the pressure, the radial flow velocity and the tangential flow velocity at point (R,θ), respectively. According to aforesaid boundary conditions, eqns (4–6) can be solved to give the flow velocity and pressure profiles in the fluidic field and the distribution of stress on the cellular surface.

Hydrodynamic force exerted on the docked cell surface

Assuming that the hydrodynamic force F exerted on the cell is in the +x direction due to the symmetry of the flowing field, and that the cell is docked in an infinite and even fluidic field, F can be given by the integration of the stress according to eqn. (7),in which F is composed of the pressure force (related to hydrostatic pressure on the cellular surface) and the viscous force (related to shear stress on the cellular surface and dependent on the velocity gradient).

When a cell is trapped by a dam structure, the hydrodynamic force will induce cell distortion. While the normal fraction of the force tends to push the cell through the narrowed pathway, the shear stress may affect the viability of the cell.¹⁸ Therefore, it is important in microfluidic designs to decrease the force on the cell in order to maintain the viability and prevent the cell from leaking through the dam.

Perpendicular and parallel dam structures

Based on eqn. (7), the hydrodynamic force is in direct proportion to the flow velocity (U), the cellular radius (a), and the dynamic viscosity (μ). In the design with the dam structure perpendicular to the channel (hereafter called “perpendicular dam”, Fig. 1a), the only way to decrease the force is by decreasing the flow velocity, which inevitably leads to a decrease in cell transportation efficiency. On the other hand, in the design with the dam structure situated between two parallel channels (hereafter called “parallel dam”, Fig. 1b), the flow velocity for cell docking is different from the velocity for the main flow and cell transportation. A decrease in the docking flow will have little impact on the main flow. Furthermore, in the dam structure, the normal hydrodynamic force applied to the cell docked on the parallel dam is only a fraction of that on the perpendicular dam. It is possible to change the docking flow direction by adjusting the pressure distribution between the two parallel channels.

Fig. 1 Perspective diagram of the perpendicular dam (a) and the parallel dam (b). The normal fraction of hydrodynamic force on cell docking along the parallel dam is called normal force, and another one parallel to the dam is called tangential force. In all simulation models, the origin of the coordinate system is at the symmetrical center of the dams instead of that shown here.

Microfluidic flow simulation

The flow velocity and force profiles in different microfluidic models were simulated using a commercial computational fluid dynamic package FLUENT 6.0 (Fluent, Lebanon, NH). For the FLUENT simulation, the grid patterns had more than 400 000 nodes for the perpendicular dam model and more than 800 000 nodes for the parallel dam model, respectively. The finest grid, where the distance between nodes was about 1 µm, was located at the dam area where the local flow velocity and pressure gradients are varying significantly. The flows were assumed as steady-state laminar flows and the cell suspensions were assumed to be Newtonian and homogeneous. A cell docking against a dam was treated as a rigid sphere with 15 µm diameter. The inlets and outlets were defined as pressure-inlet and pressure-outlet, respectively. Convergence criterions of residual monitor for all quantities (continuity, x-, y- and z- flow velocity) were 10⁻⁵. The pressure and flow velocity profiles within the micro-channels and the hydrodynamic forces (including both the pressure and the viscosity components) on the cell surface were considered in final analysis.

Simulation models

The perpendicular and the parallel dam structures were used as models for simulation (Fig. 1). A dam is a constriction structure protruding from the top wall of a microchannel and has the same size in both models. The distance from the top wall of the channel to the bottom of the dam is defined as the dam height. The flow direction is indicated by the inlet and outlet. Fluid containing cells was loaded into the inlet and flowed to the outlet driven by a hydraulic pressure. In the parallel dam model (Fig. 1b), the main channel was used to flow the cell suspension and the auxiliary channel was used to adjust the docking flow. Inlet 1 of the main channel was used to load the cell suspension, and Inlet 2 of the auxiliary channel was used to load the controlling flow. All channels were designated 1000 µm long, 100 µm wide and 20 µm deep. The hydraulic pressure in the cell-loading inlet was maintained at a constant of 20 Pa, and the hydraulic pressure in all outlets was zero. These pressures were used in actual cell docking experiments.² In the parallel dam model, the hydraulic pressure in Inlet 2 could be adjusted according to different control modes. The pressure in Inlet 2 was designated 10 Pa unless otherwise specified.

Both the perpendicular and the parallel dam structures were 100 µm in width (z direction in Fig. 1a, x direction in Fig. 1b) and 10 µm long (x direction in Fig. 1a and z direction in Fig. 1b). In each model, seven cases with different dam heights were simulated, denoted as DAM06, DAM08, DAM10, DAM12, DAM14, DAM16 and DAM18 for dam heights of 6, 8, 10, 12, 14, 16, 18 µm, respectively. Since the cell diameter was assumed as 15 µm and the channel depth was 20 µm, only dams with a height greater than 6 µm were assumed to be able to trap the cells. In addition, two different cell-docking conditions were considered, including a single layer of docked cells and multiple layers of docked cells.

Results and discussion

Effect of dam height and cell docking on the flow pressure

According to eqn (2), the hydraulic pressure decreases along the channel due to flow resistance. Dams with different heights produce different flow resistance and hydraulic pressure difference. In the perpendicular dam model, the flow resistance created by a dam with a height less than 10 µm had little impact on the pressure difference across the dam (less than 1 Pa, Fig. 2). When the dam was higher than 16 µm, a large pressure difference was generated across the dam. The pressure difference across DAM18 was greater than 50% of the total hydraulic pressure difference between the two ends of the microchannel (20 Pa in the simulation), which would significantly affect the flow property.

Fig. 2 The simulated hydraulic pressure difference across the dams with different height and docking a single layer of cells or multiple layers cells. In the figures of this paper A denotes the results of the perpendicular dam (of 6–18 µm height), B, a parallel dam (of 6–18 µm height), C, perpendicular dam docking a single layer of cells, D, perpendicular dam docking a multi-layer of cells, E, parallel dam docking a single layer of cells.

With increasing numbers of cells docked along the dam, the fluidic pathway became smaller and large flow resistance was produced. When a single layer of cells was docked on a dam of 6 µm height, the effect on the pressure difference across the dam was comparable to that of a dam of 16 µm height (DAM16, Fig. 2). Moreover, because the docked cells significantly blocked the fluid pathway, more and more cells were accumulated at the dam to form multi-layers (3 layers of cells were simulated here). This led to even greater flow resistance and the net effect on the pressure difference across the dam was equivalent to that of a dam of 18 µm height, indicating an almost complete blockage of the channel.

In the parallel dam model, the simulation result indicated that the flow resistance of the dam has little impact on the pressure profile in the channel (Fig. 2). In the absence of docked cells, the pressure difference across the highest dam (at DAM18) was less than 10% of the driven pressure in Inlet 1 (20 Pa, Fig. 1b), which could be further attenuated by adjusting the pressure in Inlet 2 (discussed in a later section). In the presence of a single layer of docked cells, the flow resistance of the dam increased and the docking flow decreased quickly, such that all subsequent cells would flow to the Outlet 1 with the main flow without the formation of multi-layer cells, as demonstrated by the experimental results described in a previous report.² The docking of a single layer of cells along the parallel dam resulted in little change in the pressure profile in the channel, as compared to the perpendicular dam (Fig. 2).

Effect of dam height and cell docking on the flow velocity

The presence of different types of dams with the same height resulted in different impacts on the average flow velocity (Fig. 3). With a dam height less than 14 µm, there was no obvious difference in the flow velocity between the two models in the absence of docked cells. When the dam height was 18 µm, the flow velocity decreased by more than 50% for the perpendicular dam but by less than 10% for the parallel dam.

Fig. 3 The simulated average flow velocity in two models with different dams and docking a single layer of cells or multi-layers of cells.

Transportation efficiency of cells and analyte solutions is an important factor in cell-based microfluidics, which is decided by the flow velocity in microchannels. In the presence of single layer and multi-layer docked cells, the flow velocity decreased dramatically in the perpendicular dam (Fig. 3), leading to a reduction in transportation efficiency. In the parallel dam model, however, the flow resistance created by the dam only affected the docking flow across the dam but not the flow in the main channel. As a result, the docking of a single layer of cells did not cause much change in the flow velocity in the main channel and the transportation efficiency remained unaffected.

Hydrodynamic force and shear stress on docked cells

Cells docking in a dam structure bear two different hydrodynamic forces: pressure force and viscous force. The former was decided by the pressure profile, and the latter was decided by the shear stress, hence the flow velocity gradient near the cell. In this section, the hydrodynamic forces exerted on cells at initial docking, forming single and multiple layers (for the perpendicular dam) were simulated and compared. In both dam models, the viscous force exhibited little change among different dam heights and was much smaller than the pressure force. The change in hydrodynamic force mainly resulted from the change in the pressure force. For both dam structures, the hydrodynamic force increased rapidly with increasing dam height (Fig. 4a). The hydrodynamic force increased from 52.5 pN (p denotes 10⁻¹²) to 418 pN for the perpendicular dam and from 33.2 pN to 234 pN for the parallel dam, respectively, when the dam height increased from 6 to 18 µm. Since the pressure force was determined by pressure and pressure-effecting surface area, there were two reasons for the change of the force: an increase in the pressure gradient near the cells, and an increase in the contacting area between the docked cell and the dam leading to a decrease in the pressure-effecting area. Higher dams induced greater pressure gradients across the docked cells and thus greater normal pressure force. The decrease in the downstream pressure-effecting surface reduced the reverse pressure force, which also added to the increase in the absolute value of the pressure force. For the perpendicular dam, both the force and the effecting area contributed to the increase in the hydrodynamic force. For the parallel dam, only the effecting area provided major contribution to the increase in the hydrodynamic force. As shown in Fig. 4a, the presence of a single- or multi-layer cells in the perpendicular dam caused a much more significant increase in the hydrodynamic force than that in the parallel dam.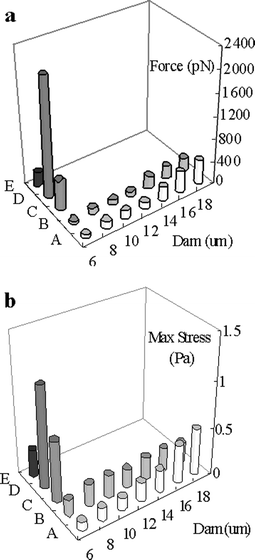

Fig. 4 Simulated hydraulic forces (a) and simulated maximal shear stress (b) on cellular surface. A and B denote different dams docking only one cell (at the beginning of cell-docking process).

Shear stress is one of the main factors for cellular damage in microfluidics.¹⁸ For the perpendicular dam, shear stress increased with the dam height (Fig. 4b). After cells fully docked along the dam, there was a great increase in shear stress, especially under multi-layer conditions. However, for the parallel dam, shear stress was much smaller and did not change with the dam height during the initial docking or after the fully docking of cells (single layer, Fig. 4b).

Based on the above analysis, it is apparent that the parallel dam provides a better structure for cell docking than the perpendicular dam, as having been demonstrated experimentally previously.² While a parallel dam with a greater height may have a smaller gap, making it difficult for cells to escape, it may also generate a greater pressure force that is damaging to cells.^20–22 Alternatively, a parallel dam with a smaller height may have a wider gap for cells to escape, especially under high pressure and flow velocity generated after cellular docking. One approach to decrease the hydrodynamic force and shear stress on the docked cells is by adjusting the pressure in the auxiliary channel on the other side of the parallel dam, as discussed in the following section.

Fine-tuning the pressure in the auxiliary channel of the parallel dam

The hydrodynamic force and shear stress generated upon cell docking may cause distortion and damage of the docked cells. By adjusting the pressure in the auxiliary channel on the other side of the parallel dam (Inlet 2 in Fig. 1b), it is possible to decrease the force and stress on the cells without significantly affecting the flow velocity and transportation efficiency. As shown in Fig. 5a, when the pressure in Inlet 2 was increased from 10 Pa to 18 Pa, the hydrodynamic force and the shear stress on a fully docked, single layer of cells decreased from 240 pN to 67.1 pN (Fig. 5a) and from 0.30 Pa to 0.131 Pa (Fig. 5b), respectively. These values were comparable to or less than those during the initial docking of cells (one cell only) under initial pressure (10 Pa at Inlet 2). Additionally, the increase in Inlet 2 pressure had little effect on the flow velocity in the main channel (Fig. 5c). Mammalian cells exhibited certain effects such as enhancing metabolism, altering cellular function, and activating G protein under shear stress greater than 1 Pa,^23–26 and became damaged under shear stress greater than 10 Pa.¹⁸ The simulation results showed that when a single layer of cells were fully docked along a 6 µm parallel dam, the maximal shear stress was less than 0.13 Pa by using suitable pressures in the main channel and the auxiliary channel (20 Pa in Inlet 1 and 16 Pa in Inlet 2, Fig. 5b). In order to prevent the docked cells from being pushed back to the main flow and driven away to the outlet, sufficient force in the normal direction must be maintained. This presents the maximal limit on the pressures in the auxiliary channel.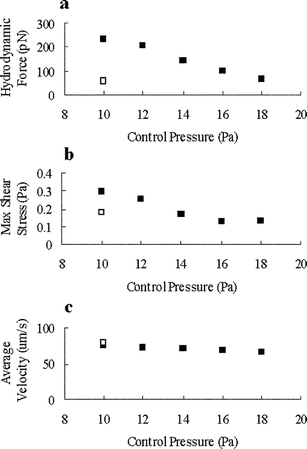

Fig. 5 In parallel dam model, the hydrodynamic force, maximal shear stress on cellular surface and average flow velocity in microchannel at different adjusting modes. ■ is the result of a single layer of docked cells and □ denotes the result of only one docked cell (at the beginning of cell-docking process).

New dam structures

While the parallel dam structure has clear advantages over the perpendicular dam for cell docking, it is more difficult to fabricate and control. Here we proposed a new structure for cell docking combining the features of both parallel and perpendicular dams. In this design, the region in the midway of a channel was expanded to a circular shape and a dam in perpendicular to the main flow of the channel was positioned in the region (Fig. 6a). For example, a circular region of 300 µm diameter was designed in a channel of 100 µm in width, with a 100 µm (variable) wide dam. The dam actually consisted of two levels, a middle section with greater height (the real dam) and the two flanking sections with smaller height (for controlling flow rates). For comparison with the above models, the hydraulic pressure in the inlet and outlet was 20 Pa and zero, respectively. Initially, the flow towards the middle of the channel had a higher velocity than that towards the walls because of the viscosity force of the channel wall. Cells moving in the main flow were stopped by the dam (Fig. 6b left). After the cells were fully docked along the dam to form a single layer, the flow resistance generated by the docked cells reduced the flow velocity towards the dam. The fluid and cells would bypass the dam and flow through the flanking sides near the wall to the outlet (Fig. 6b right). In order to realize this process, two conditions must be satisfied: (1) the initial flow resistance of the dam should be sufficiently low so that cells would dock towards the dam; (2) the flow resistance after a single layer cell docking should be sufficiently high so that additional cells would bypass the dam to avoid the formation of multi-layer cells.

Fig. 6 A top view diagram of optimized microfluidic system and a side view of the dam (a). Flow rate within this system before and after cellular full docking (b) this is the flow profile in the y = 0 plane, no dam and flank shown here).

It is apparent that the ratio of the flow rates across the dam and the bypass determines the docking efficiency. The ratio is 1 if the flow rate in the middle and the bypass are the same. If the ratio is less than 0.2, most cells flow through the bypass without docking. A higher dam resulted in greater resistance and smaller ratio, which may reduce the docking capacity. Simulation was carried out for dams with seven different heights plus two flanks of 4 µm in height (this brought the best docking effect as described next). The lengths of the dam and the flanks are 100 µm (Fig. 6a). When the dam height was changed from 6 µm to 18 µm, the ratio decreased to approach zero (Fig. 7a). Only the 6 µm dam gave a ratio greater than 1, which could be used to effectively dock cells.

Fig. 7 (a) The impact of dam height to the ratio of the flow rates across the dam and the bypass, □ denotes the result of a single layer of docked cells along the dam. (b) The impact of the height of flank to the ratio at 6 µm dam.

Adding two flanks to the dam would decrease the difference of resistance between the dam and the bypass and prevent cells from flowing through the bypass at the beginning, in order to improve docking capacity. In this simulation, the cell flow pathway was assumed to be 16 µm (cell diameter 15 µm). The height of the flanks should be less than 4 µm (in the channel of 20 µm depth) to avoid serious blocking. Here, the 6 µm dam with different flanks from 0–4 µm was compared. When the flank height changed from 0 to 4 µm, the ratio increased with the 4 µm flank giving the best docking capacity (Fig. 7b). Because all ratio values were greater than 1, a 6 µm dam without flanks could also be chosen to decrease blocking.

In the optimized model (6 µm dam with 4 µm flank), the simulated results showed that there was no obvious change of flow velocity in the channel (64.1 to 62.9 µm S⁻¹) after full cell docking. The hydrodynamic force and maximal shear stress on the cells were 47.1 pN and 0.0387 Pa, respectively, which were much smaller than those in either the perpendicular dam model (536 pN and 0.656 Pa) or the parallel dam (67.1 pN and 0.13 Pa). After a single layer of cells docked along the dam, the flow ratio became less than 0.2, and all additional cells flowed through the bypass without blocking. Experiments are underway to verify the validity of the proposed design as an effective dam structure for cell docking.

Conclusion

Hydrodynamic analysis of two different types of dam structures for cell immobilization were carried out to compare the effects of dam dimensions and cell docking on the pressure and velocity of the flow in the micro-channels as well as the hydrodynamic force and shear stress on the docked cells. It is apparent that the parallel dam provides a better structure for cell docking than the perpendicular dam. By adjusting the pressure in the auxiliary channel of the parallel dam, it is possible to decrease the hydrodynamic force and shear stress on the cells without significantly affecting the flow velocity and transportation efficiency. A new dam structure for cell docking combining the features of both parallel and perpendicular dams was proposed and shown to be suitable for cell-based microfluidics. The simulation results also provide a guideline for designing microfluidic structures and for controlling the hydraulic pressures that are suitable for cell docking and maintaining cell viability during the dam-dependent docking process.

Acknowledgements

This work was supported by the Innovation and Technology Fund, Hong Kong SAR Government (Project No. ITS/015/02).

References

1. H. Andersson and A. van den Berg, Sens. Actuators, B., 2003, 92, 315.
2. M. S. Yang, C. W. Li and J. Yang, Anal. Chem., 2002, 74, 3991.
3. P. C. H. Li and D. J. Harrison, Anal. Chem., 1997, 69, 1564.
4. R. H. Carlson, C. V. Gabel, S. S. Chan, R. H. Austin, J. P. Brody and J. W. Winkelman, Phys. Rev. Lett., 1997, 79, 2149.
5. S. Fiedler, S. G. Shirley, T. Schnelle and G. Fuhr, Anal Chem., 1998, 70, 1909.
6. D. J. Beebe, I. K. Glasgow and M. B. Wheeler, US patent 6,193,647, 1999 Microfluidic embryo and/or oocyte handling device and method.
7. S. A. Sundberg, Curr. Opin. Biotech., 2000, 11, 47.
8. L. Bousse, Sens. Actuators, B., 1996, 34, 270.
9. T. Vo-Dinh, B. M. Cullum and D. L. Stokes, Sens. Actuators, B., 2001, 74, 2.
10. S. Takayama, E. Ostuni, P. LeDue, K. Naruse, D. Ingber and G. Whitesides, Nature, 2001, 411, 1016.
11. I. Inoue, Y. Wakamoto, H. Moriguchi, K. Okano and K. Yasuda, Lab Chip, 2001, 1, 50.
12. P. M. St. John, R. Davis, N. Cady, J. Czajka, C. A. Batt and H. G. Craighead, Anal. Chem., 1998, 70, 1108.
13. C. S. Chen, M. Mrksich, S. Huang, G. M. Whitesides and D. E. Ingber, Science, 1997, 276, 1425.
14. B. D. DeBusschere and G. T. A. Kovacs, Biosens. Bioelectron., 2001, 16, 543.
15. S. Takayama, J. C. McDonald, E. Ostuni, M. N. Liang, P. J. A. Kenis, R. F. Ismagilov and G. M. Whitesides, P. Natl. Acad. Sci. USA, 1999, 96, 5545.
16. T. Muller, G. Gradl, S. Howitz, S. Shirley, T. Schnelle and G. Fuhr, Biosens. Bioelectron., 1999, 14, 247.
17. D. P. Gaver and S. M. Kute, Biophys. J., 1998, 75, 721.
18. N. N. Ma, K. W. Koelling and J. J. Chalmers, Biotechnol. Bioeng., 2002, 80, 428.
19. I. G. Currie, Fundamental Mechanics of Fluids, McGraw-Hill, Inc. Press, 2nd edn., 1993, pp. 246–267.
20. N. Gregoriades, J. Clay, N. Ma, K. Koelling and J. J. Chalmers, Biotechnol. Bioeng., 2000, 69, 171.
21. M. S. Croughan and D. I. C. Wang, Biotechnol. Bioeng., 1989, 33, 731.
22. M. A. Garcia-Briones, R. S. Brodkey and J. J. Chalmers, Chem. Eng. Sci., 1994, 49, 2301.
23. K. K. Chittur, L. V. McIntire and R. R. Rich, Biotechnol. Progr., 1988, 4, 89.
24. M. U. Nollert, S. L. Diamond and L. V. McIntire, Biotechnol. Bioeng., 1991, 38, 588.
25. S. L. Diamond, S. G. Eskin and L. V. McIntire, Science, 1989, 243, 1483.
26. V. Ranjan, R. Waterbury, Z. H. Xiao and S. L. Diamond, Biotechnol. Bioeng., 1996, 49, 383.

---