Atomistic study of dopant site-selectivity and defect association in the lanthanum gallate perovskite
M. Saiful
Islam
* and
R. Andrew
Davies
Materials Chemistry Group, Chemistry Division, University of Surrey, Guildford, GU2 7XH, UK. E-mail: m.islam@surrey.ac.uk
First published on 21st November 2003
Abstract
Advanced modelling techniques have been used to investigate the defect properties of the LaGaO3 ionic conductor on the atomic-scale. The present study addresses a variety of topics, but focuses on the site-selectivity of a wide range of dopants, the influence of A-site deficiency, the nature of dopant–vacancy association, and the energetics of oxidation in the transition-metal doped oxide. Ion size trends are found for both divalent and trivalent dopant incorporation at La and Ga sites. Certain trivalent dopants may show “amphoteric” behaviour in which the dopant can occupy either site, and is found to be influenced by A-site deficiency. The M4+
(Ti, Sn, Zr, Hf) and M5+
(Nb, Ta) dopants are predicted to substitute for Ga with La vacancy compensation. Dopant–vacancy clusters for a wide range of dopant ions have been examined. A minimum in the binding energy occurs for Sr2+ on La3+, which would be beneficial to oxygen ion conductivity. Dopant–vacancy association for isovalent (M3+) substitution indicates elastic strain effects. We have considered complex clusters ( ) of x up to 12 within 2D and 3D structures, which may be related to possible “nano-domain” formation at higher dopant regimes. Favourable oxidation on energetic grounds is found for Ni2+ and Cu2+ doping, suggesting p-type conductivity at increasing oxygen partial pressures.
) of x up to 12 within 2D and 3D structures, which may be related to possible “nano-domain” formation at higher dopant regimes. Favourable oxidation on energetic grounds is found for Ni2+ and Cu2+ doping, suggesting p-type conductivity at increasing oxygen partial pressures.
1. Introduction
Oxygen ion transport in ceramic oxide materials has attracted considerable interest due to the promising electrochemical applications such as solid oxide fuel cells (SOFCs), oxygen separation membranes and partial oxidation reactors. In this field, high oxygen ion conductivity has been reported in the LaGaO3-based perovskite,1,2 which is superior to that found in the conventional Y/ZrO2 electrolyte at lower temperatures. It is apparent that a significant decrease in the SOFC operating temperature would be an important practical advance. The incorporation of cation dopants to form the system La1−xSrxGa1−yMgyO3−δ (often termed LSGM), gives rise to the highly mobile oxygen vacancies that are responsible for the observed ionic conductivity.Following the initial discovery by Ishihara et al.,1,2 numerous experimental studies have been carried out on the LaGaO3-based (LSGM) material, which include reports covering oxygen ion conductivity,3–13 structural properties,14–23 electrolyte performance within SOFCs24–27 and the effect of transition-metal doping.28–36 Such doping with multivalent transition-metal cations in order to introduce electronic conductivity is of interest for developing applications of mixed conductors (e.g. SOFC electrodes, hydrocarbon oxidation reactors). Other perovskite oxides such as (La, Sr)MnO3 and (La, Sr)(Co, Fe)O3 are already known to exhibit either mixed or electronic conductivities. More recently, there have been a few studies of cation diffusion37–39 (including creep behaviour) and of cation non-stoichiometry in LSGM.40 It is apparent that variations in the A/B cation ratio of ABO3 perovskites can have a significant affect on their properties.
However, despite the investigations referred to above, there is only limited information on the fundamental microscopic factors that control the macroscopic properties, such as lattice defects, dopant-site selectivity and redox processes. Furthermore, there is conflicting debate as to the extent and nature of the association between dopant ions and oxygen vacancies.
This detailed study attempts to provide further insight into these problems by using atomistic simulation techniques, which are now well established tools in solid state chemistry. The reliability of such an approach has been demonstrated by our simulation studies of defects, ion transport and surface structures of other perovskite oxides (e.g. LaMnO3, LaCoO3).41–44 Results from our earlier investigation of the LaGaO3 system45 indicate that oxygen vacancy migration follows a curved pathway in which the saddle-point of the migrating oxygen ion sits just outside the edge of the GaO6 octahedron and away from the adjacent Ga ion (leading to a calculated activation energy of 0.73 eV). This study also finds that Sr2+ on La3+ and Mg2+ on Ga3+ are the most favourable acceptor dopants on energetic grounds. A recent neutron scattering study23 of doped LaGaO3 provides evidence for our predicted curved pathway. De Souza46 has also employed simulation methods to investigate impurity incorporation and, in particular, cation defect migration in LaGaO3.
The present study builds and extends upon this earlier work by turning attention to the site-selectivity of a wider range of dopants (including Co, Fe, Ni, Mn, In, Nb), the influence of A/B cation non-stoichiometry, the nature of dopant–vacancy association, and the energetics of oxidation.
2. Simulation techniques
The computational techniques used in this work are well established and have been reviewed in detail elsewhere.47 Hence, only a brief summary is given here.The calculations are based upon the Born model of ionic solids with ions assigned integral charges corresponding to their formal oxidation states. The interactions between the ions are formulated in terms of long-range Coulombic forces and short-range forces that account for electron cloud overlap (Pauli repulsion) and dispersion (van der Waals) interactions. The short-range interactions are modelled with a Buckingham potential of the form:
| Vij(r) = Aijexp(−r/ρij) − Cij/r6 | (1) |
An important feature of these calculations is the treatment of lattice relaxation about the point defect or migrating ion. The Mott–Littleton approach is to partition the crystal lattice into two regions so that ions in a spherical inner region surrounding the defect are relaxed explicitly. In contrast, the remainder of the crystal, where the defect forces are relatively weak, is treated by more approximate quasi-continuum methods. In this way, local relaxation is effectively modelled and the crystal is not considered simply as a rigid lattice through which ion species diffuse.
The potential parameters for LaGaO3 are exactly the same as in our previous study,45 which were derived by empirical procedures using the observed orthorhombic perovskite structure.48 This structure is built upon a framework of corner-linked GaO6 octahedra; the orthorhombic phase can be considered as due purely to tilts of these octahedra from the ideal cubic configuration. The potentials for the La–O and O–O interactions were transferred directly from the analogous simulation study of the LaMO3 (M = Cr, Mn, Fe, Co) perovskites.43 We note that the interatomic potentials for the dopant ions are exactly those of the corresponding binary metal oxides49 that have been applied to analogous studies of the LaMO3 perovskites.41,43
Energy minimisation methods identify the static configuration of lowest energy and are essentially ‘zero Kelvin’ calculations, with no representation of thermal effects. It is possible to add a treatment of the vibrational properties of the system via the quasi-harmonic approximation as discussed by Catlow.47 Despite these features, minimisation techniques have been readily applied to materials with large complex unit cells and have been used to refine approximate crystal structures. In essence, the empirical interatomic potentials are derived within the context of a room temperature or higher temperature experimental structure.
Before carrying out defect calculations, the crystal structure of LaGaO3 was simulated using energy minimisation procedures. The calculated bond distances and lattice parameters are compared with experimental values in Table 1. Examination of the differences shows good agreement between experimental and simulated structures, as well as reasonable accord with the measured dielectric constant.50 These results provide support for the validity of our potential model for the subsequent defect simulations.
3. Results and discussion
3.1. Dopant substitution in LaGaO3
In terms of modes of “solution” into the LaGaO3 material, dopant ions can substitute at either La3+ or Ga3+ sites with the creation of charge-compensating defects. This raises key questions in relation to the favoured substitution site, the type of compensating defect and the influence, if any, of A and B site cation size. Our simulation methods can probe these issues by generating quantitative estimates of the relative energies of different modes of solution. Although the prediction of the precise amount of dopant that can be incorporated is less straightforward, our results can provide a useful systematic guide to the site-selectivity for different dopant species and to trends in dopant solubility. Such an approach has been applied successfully to a variety of oxides.41,51,52We have therefore examined a wide range of dopants in LaGaO3 including divalent (e.g. Sr2+, Ni2+, Cu2+), trivalent (e.g. Co3+, Fe3+, Mn3+, In3+), tetravalent (e.g. Ti4+, Zr4+, Th4+) and pentavalent (e.g. Nb5+, Ta5+) ions. The results are discussed in the following sub-sections.
 | (2) |
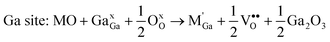 | (3) |
 | ||
| Fig. 1 Calculated solution energies as a function of ion radius for divalent (M2+) dopants at both La and Ga sites in LaGaO3. (The lines are guides to the eye). | ||
Examination of the results (Fig. 1) reveals three main points. First, low favourable solution energies are found for Sr2+ at the La site and Mg2+ at the Ga site, in accord with conductivity studies and with recent calorimetry measurements.22 There are clear correlations with dopant size with unfavourable values for substitution of the large Ba2+ in line with the observed low solubility. These results provide support for the validity of our simulation approach and are compatible with previous calculations.45,46
Second, the transition-metal dopants, Co2+, Ni2+ and Cu2+ are predicted to occupy the Ga site, as expected. However, the precise oxidation state of the Co dopant is still unclear from experiment. As noted previously,45 we find a low solution energy for Cu2+ at the Ga-site making it a potential candidate for use as an effective acceptor dopant, although we recognise the possible electronic contribution from mixed-valency. In our view, the dopant energies will not be modified significantly by crystal field terms of transition metal dopants since these effects are included implicitly in the interatomic potential model. We note that the potentials have been derived to reproduce the observed structures of the corresponding binary oxides.
Finally, a key point is that based on low energetics, the favourable incorporation of dopant ions (such as Sr2+) will enhance oxygen diffusivity owing to the increase in the population of oxygen vacancies.
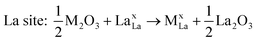 | (4) |
 | (5) |
The calculated solution energies for a series of trivalent dopants are represented in Fig. 2. The results clearly confirm that cation size is a key factor: smaller ions of radius ≤0.8 Å (including Al3+, Co3+, Cr3+, Fe3+, Sc3+) are predicted to be highly soluble at the Ga site, while larger rare-earth dopants (e.g. Gd3+, Nd3+) substitute preferentially at the La site. Our calculations are in accord with structural studies that show Gd3+ and Nd3+ incorporation into the La sublattice,2 and transition metal doping at the Ga site.29–32 The recent microstructural work of Kimpton et al.15 also verifies that In3+ substitutes for Ga.
However, an interesting result is found for Yb3+, which sits at the “crossover” point in Fig. 2. It is therefore difficult to make firm predictions for this dopant, since it may substitute at either La or Ga sites. Indeed, there is evidence of “amphoteric” dopant ions that can occupy either A or B sites (depending on the A/B ratio) in other perovskite oxides such as BaTiO3.55 We note that the influence of cation non-stoichiometry on dopant site-selectivity is examined in Section 3.2.
 | ||
| Fig. 2 Calculated solution energies as a function of ion radius for trivalent (M3+) dopants at both La and Ga sites in LaGaO3. | ||
With regard to the possibility of simultaneous occupancy of both La and Ga sites, we examined the incorporation of Yb3+ into LaGaO3 according to the following defect reaction (in which there is equal partition between the two sites):
 | (6) |
It is found that the calculated solution energy is about 0.5 eV less favourable than occupancy at only La and Ga sites, which is largely due to dopant–dopant interactions between neighbouring sites. However, this does not rule out simultaneous occupancy of both sites by another mechanism and requires further investigation.
M4+ at La with La vacancy compensation:
 | (7) |
M4+ at La with Ga vacancy compensation:
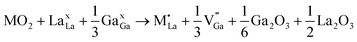 | (8) |
M4+ at Ga with La vacancy compensation:
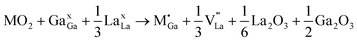 | (9) |
M4+ at Ga with Ga vacancy compensation:
 | (10) |
Therefore, the precise mode of site-substitution is critical and can be difficult to probe by experiment alone. In Table 2, we present calculated solution energies for the different modes of solutions for the cations Ti4+, Sn4+, Zr4+, Hf4+, Th4+, Nb5+ and Ta5+; this constitutes a much wider survey than current experimental reports.
| Dopant | La site | Ga site | ||
|---|---|---|---|---|
| La vacancy compensation | Ga vacancy compensation | La vacancy compensation | Ga vacancy compensation | |
| Ti4+ | 6.04 | 6.96 | −0.83 | 0.09 |
| Sn4+ | 4.11 | 5.03 | −1.09 | −0.17 |
| Zr4+ | 4.10 | 5.02 | −0.70 | 0.22 |
| Hf4+ | 3.77 | 4.69 | 0.42 | 1.34 |
| Th4+ | 1.56 | 2.48 | 3.88 | 4.80 |
| Nb5+ | 5.27 | 7.11 | 0.25 | 2.09 |
| Ta5+ | 5.61 | 7.45 | −0.48 | 1.36 |
Three main points emerge. Firstly, all the M4+ and M5+ dopants (except Th4+) show a preference for substitution at the Ga site with La vacancy (V‴La) compensation; in general substitution at the La site is energetically unfavourable. Secondly, the largest cation considered, Th4+, is the only dopant predicted to occupy the La site (with La vacancy compensation). Finally, the incorporation of these dopants would either have no effect or decrease the oxygen ion diffusivity. However, cation diffusion in M4+/M5+ doped LaGaO3 would be facilitated by the increase in the La vacancy concentration. We note that De Souza42,46 has presented a detailed simulation study of cation vacancy migration in LaGaO3 (and LaMnO3). Although there are limited experimental data for direct comparison, Kharton et al.36 find that the Ti and Nb-doped gallate materials exhibit lower oxygen ion conductivity.
3.2. M3+ dopants in A-site deficient lanthanum gallate
It is known that deviations from A/B stoichiometry in perovskite oxides can strongly influence their dopant behaviour, sintering properties and chemical stability. For example, cation non-stoichiometry in the SOFC material (La,Sr)MnO356 and the proton-conducting cerates (ACeO3)57 has been used to modify their properties. Luecke and Armstrong39 recently investigated the creep behaviour of lanthanum gallate deliberately prepared to give A-site deficient non-stoichiometry, although the precise defect model for creep was unresolved. In general, there has been limited experimental or simulation work that has focused on dopant substitution and cation non-stoichiometry in the gallate perovskite.Our results on M3+ dopant incorporation in stoichiometric LaGaO3 (Fig. 2) show that Yb3+ sits on the “crossover” point, which suggests possible “amphoteric” behaviour with occupancy of either La or Ga sites. We therefore decided to investigate the possible influence of cation non-stoichiometry on dopant site occupancy for Yb3+, as well as another dopant close in size (In3+). More specifically, we have calculated the solution energies for these two dopants (based on eqns. 4 and 5) in A-site deficient La0.83GaO2.75; our simulation methods allow this non-stoichiometric system to be represented by cation vacancies compensated by oxygen vacancies using a supercell of La10Ga12O33. The resulting energies are presented in Table 3 in which they are compared with values for stoichiometric LaGaO3.
| Dopant | LaGaO3 | La0.83GaO2.75 |
|---|---|---|
| In3+ La-site | 2.66 | 0.67 |
| In3+ Ga-site | 0.94 | −0.92 |
| Yb3+ La-site | 0.38 | −1.01 |
| Yb3+ Ga-site | 0.37 | −1.99 |
Examination of the results reveal that A-site (La) deficiency is predicted to have a strong influence on Yb dopant site-selectivity, making Ga-site occupancy energetically more favourable. It is interesting to note that we have calculated opposite trends for A2+B4+O3 perovskites such as BaCeO3 and BaZrO3 in which A-site deficiency promotes A-site occupancy for trivalent dopants at the “crossover” point. In any case, these results suggest that the site occupancy of Yb3+ will be particularly sensitive to the precise La/Ga ratio and hence to the experimental processing conditions. We stress that although we are able to construct these non-stoichiometric models, certain compositions may be difficult to synthesise in practice. Our main objective here is to examine trends in dopant substitution, with further work being planned on this topic.
Although there is limited related experimental work on lanthanum gallate for direct comparison, it is well known that conductivity measurements and microstructural studies of the BaTiO3 ferroelectric perovskite demonstrate that certain dopants (e.g. Y3+, Er3+) can occupy either A or B sites depending on the Ba/Ti ratio.55
In the context of A-site deficiency, we have also made preliminary simulations on the possible association between oppositely-charged lanthanum and oxygen vacancies: the calculated binding energy of the (V‴LaV••O) pair cluster is found to be favourable (−0.33 eV defect−1), which could be another factor inhibiting oxygen ion conductivity. This is consistent with related work of Berenov et al.56 who speculate that the mobility of oxygen vacancies in A-site deficient LaMnO3 may be reduced due to the formation of (V‴LaV••O) defect complexes.
3.3. Dopant–vacancy association
LaGaO3 materials are typically acceptor-doped with divalent ions (Sr2+, Mg2+) with the creation of charge-compensating oxygen vacancies that are crucial to the observed ionic conductivity. It is well known that in fluorite-structured oxides (e.g. doped CeO2 and ZrO2) interactions between dopant ions and their opposite-charged compensating defects leads to the formation of distinct clusters (or associates).12,58 This adds a binding (association) energy term to the conduction activation energy. Dielectric relaxation measurements by Nowick et al.59 of acceptor-doped KTaO3 and CaTiO3 perovskites also provide evidence of dopant–vacancy pairs.However, there has been conflicting debate as to whether there are any significant dopant–vacancy interactions in the lanthanum gallate perovskite. Conductivity measurements of LSGM find significant differences in activation energy as a function of Sr and Mg content.4 Huang et al.7 have noted the possible “trapping” of an oxygen vacancy at a divalent cation dopant on the Ga site. However, detailed experimental determination of the atomic structures of defect clusters can be difficult.
In an attempt to shed light on this problem we have extended our previous studies41,45 by performing a wide series of calculations on defect clusters in the LaGaO3 system comprised of dopant substitutions and oxygen vacancies. For this task our simulation methods are well suited as they model accurately the Coulomb and polarisation energies, which are the predominant terms in any local association process.
The cluster binding energies (Ebind) were calculated using the general relation:
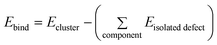 | (11) |
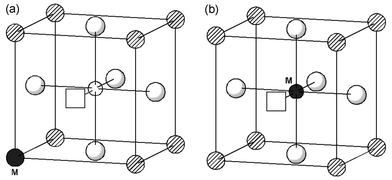 | ||
| Fig. 3 Dopant–vacancy pair clusters showing the oxygen vacancy at nearest-neighbour positions: (a) dopant at La site; (b) dopant at Ga site. | ||
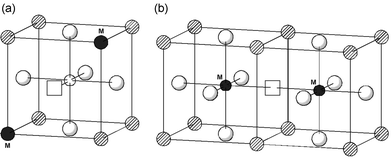 | ||
| Fig. 4 Dopant–oxygen vacancy trimer-clusters: (a) dopants on La-site; (b) dopants on Ga-site. | ||
Three main points emerge from the calculated binding energies reported in Table 4 and Fig. 5. First, the magnitude of the binding energy varies greatly for the different dopants with the lowest value for Sr2+ on the La site. Indeed, a near-zero binding energy is calculated for both Sr-vacancy pair and trimer clusters, and is predicted to be a major factor in promoting the free oxygen vacancy population and the high ionic conductivity, which we noted in our previous work.41,45 This may be relevant to all LaMO3 perovskites in which acceptor doping is achieved by partial replacement of La by Sr, as discussed by Kilner.58
 | ||
| Fig. 5 Calculated binding energies for dopant–oxygen vacancy clusters as a function of dopant ionic radius for M+ and M2+ ions. (Lines are a guide to the eye). | ||
| Dopant | (M′LaV••O) Pair | (M′LaV••OM′La) Trimer |
|---|---|---|
| (a) M2+ at La site | ||
| Ca2+ | −0.08 | −0.10 |
| Sr2+ | 0.00 | 0.04 |
| (b) M2+ at Ga site | ||
|---|---|---|
| (M′GaV••O) Pair | (M′GaV••OM′Ga) Trimer | |
| Ni2+ | −0.91 | −1.23 |
| Mg2+ | −0.90 | −1.22 |
| Cu2+ | −0.65 | −0.88 |
| Zn2+ | −1.00 | −1.35 |
| Co2+ | −0.94 | −1.27 |
| Fe2+ | −0.98 | −1.32 |
| (c) M+ at La site | ||
|---|---|---|
| (M″LaV••O) Pair | ||
| Na+ | −0.75 | |
| K+ | −0.80 | |
Second, dopant–vacancy clusters involving Mg2+ or divalent transition metal ions at the Ga site are found to have significant binding energies, which points to greater trapping of oxygen vacancies. The lowest value relative to Mg2+ is for the Cu2+ dopant, which may be beneficial to conductivity. It has been suggested that Mg doping has an important rôle in promoting the incorporation of a higher concentration of Sr into lanthanum gallate. In the case of the cobalt dopant, we should note that it is not certain that the dopant is introduced purely in the divalent state since Co3+ doping would not lead to charge-compensation.
Third, the trimer clusters (M′GaV••O M′Ga) for all the divalent dopants on the Ga site are slightly more stable than the pair clusters (Table 4); the symmetric linear configuration with an oxygen vacancy midway between two dopant ions (Fig. 4) probably maximises the favourable interactions.
Our results for Mg are consistent with the observed increase in the conduction activation energy at higher Mg doping levels in LSGM.4,7 This would lead to two regions in the conductivity Arrhenius plot (ln σ versus 1/T) as found from conductivity measurements.7,10,34 The high temperature region relates to purely the oxygen migration energy, whereas the low temperature region relates to both migration and binding energy terms, i.e. Mg-vacancy association contributes to the observed increase in activation energy at low temperatures. More recently, Norby and Haavik12 have employed simple defect models to rationalise the temperature-dependent conductivity of LSGM and derive a defect association enthalpy of −65 ± 5 kJ mol−1 which is compatible with our calculated binding energies.
Finally in this section, we also considered neutral pair clusters (M″LaV•O) for both Na+ and K+ dopants at the La site, although we recognise that the solubility of monovalent ions is believed to be low. The resulting binding energies of up to −0.8 eV (Table 4 and Fig. 5) suggest strong association between these monovalent ions and oxygen vacancies, which would have a detrimental effect on ionic conductivity. Indeed, the studies of Thangadurai and Weppner11 have indicated that replacement of Sr2+ by K+ in LSGM decreases the electrical conductivity and increases the activation energy to about 1.4 eV.
The calculated binding energies for pair clusters (MxV••O) are presented in Fig. 6. The results indicate a degree of association for all the trivalent dopants at either La or Ga sites, with binding energies ranging from about −0.1 to −0.45 eV. These results suggest the importance of elastic strain effects. The binding energy is dependent upon the ion size “mis-match” between host and isovalent dopant causing local perturbation with the expectation of a minimum when the ionic radii are approximately the same. This is borne out here with the greater ion size mismatch for In3+ (0.80 Å) on the small Ga3+ site (0.62 Å), and Y3+ (0.90 Å) on the large La3+ site (1.03 Å). These results suggest that In3+ and Y3+ dopants, in particular, would have a detrimental effect on oxygen ion conductivity in which defect association would be a key factor. This is consistent with findings of Kimpton et al.15 that show In3+ occupying the Ga-site and that the electrical conductivity decreases with increasing In content.
 | ||
| Fig. 6 Calculated binding energies for dopant–oxygen vacancy clusters as a function of dopant ionic radius for M3+ ions. (Values for Sr2+ and Mg2+ are included as reference points). | ||
The lowest binding energies are calculated for Co3+ and Cr3+ at Ga, and for Nd3+ at La (Fig. 6). These results are analogous to the fluorite-structured oxides (e.g. doped CeO2) in which the minimum in the binding energy occurs when the ionic radius of the host and the dopant are close to each other.58 It is worth noting that Co3+ is closer in size to Ga3+ than Co2+, and that the cluster involving Co3+ has a much lower calculated binding energy than Mg2+. This suggests that Co3+ (and Cr3+) doping would be beneficial to ionic conductivity in LSGM, although the precise oxidation state of the Co dopant is still not clear.
Recent work on substitution of Co for Mg in LSGM has shown a small enhancement of ionic conductivity at low levels.29,32 In addition, Ishihara et al.2 have observed that for rare-earth doped LaGaO3 the ionic conductivity decreases in the order Nd3+ > Gd3+ > Y3+. These findings are compatible with our results in which the calculated binding energy increases in the same order.
We have therefore examined, for the first time, the energetics of larger clusters focusing on Mg on the Ga site with oxygen vacancies at nearest-neighbour sites. Neutral configurations based on ( ) were considered with the number of Mg dopants ions (x) ranging from 2 to 12. Examples of possible 2D (in-plane) and 3D configurations are shown in Figs. 7 and 8 respectively. The calculated binding energies are presented in Fig. 9 for a range of 2D and 3D clusters as a function of the number of Mg2+ ions.
) were considered with the number of Mg dopants ions (x) ranging from 2 to 12. Examples of possible 2D (in-plane) and 3D configurations are shown in Figs. 7 and 8 respectively. The calculated binding energies are presented in Fig. 9 for a range of 2D and 3D clusters as a function of the number of Mg2+ ions.
 | ||
| Fig. 7 2D (in-plane) arrays of large neutral Mg2+–vacancy clusters (a) (4M′Ga2V••O); (b) (12Mg′Ga6V••O). (Filled circles represent Mg and open squares vacancies; occupied oxygen sites are omitted for clarity). | ||
 | ||
| Fig. 8 3D structures of large neutral Mg2+–vacancy clusters (a) (8M′Ga4V••O); (b) (12Mg′Ga6V••O). (Filled circles represent Mg and open squares vacancies; occupied oxygen and La sites are omitted for clarity). | ||
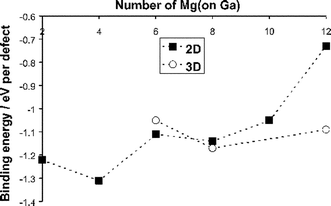 | ||
Fig. 9 Calculated binding energies for 2D and 3D configurations of neutral Mg–vacancy clusters ( ) as a function of the number of Mg2+ ions. ) as a function of the number of Mg2+ ions. | ||
Two main points emerge. First, all the clusters show relatively favourable binding energies with the magnitude varying for the different structures. The strongest binding energy is found for the (4Mg′Ga2V••O) configuration (Fig. 7). Second, the 3D structures show greater stability than the 2D arrays for the largest nano-scale (12Mg′Ga6V••O) cluster. These results suggest that such complex clusters may form at higher dopant concentrations and may be important as precursors to possible short-range ordering or “nano-domain” formation. We note that recent electron diffraction studies of Politova and Irvine60 have suggested nano-domains of dopant ions and oxygen vacancies in the zirconia-based oxygen ion conductor.
3.4. Hole formation in the transition-metal doped oxide
Doping with transition-metal cations in order to introduce electronic conductivity has been of interest for developing applications of mixed conductors. We have therefore examined the energetics of hole formation in Sr/Mg and transition-metal doped LaGaO3via the following oxidation reaction: | (12) |
We focused our calculations on the oxidation process within the La0.8Sr0.2Ga0.8Mg0.1M0.1O3−δ system where M is the dopant ion. Using the hole terms, the energies of the oxidation reaction (12) were calculated for all three systems and are reported in Table 5. Our analysis has included all the key terms in the solution and redox processes. There are, however, uncertainties in the absolute values due to the free-ion energies employed. Nevertheless, our concern here is to understand trends in the formation of hole species; for this task our modelling methods have proved to be reliable.
| Cation, M | E ox/eV hole−1 |
|---|---|
| Mg2+ | 2.18 |
| Ni2+ | −3.29 |
| Cu2+ | −2.28 |
| Cr3+ | 0.90 |
| Mn3+ | 2.17 |
| Fe3+ | 2.18 |
| Co3+ | 1.70 |
First, the calculated oxidation energy for Sr and Mg doped LaGaO3 (with oxygen hole formation) suggests an unfavourable process. This result indicates that ionic rather than electronic compensation (and hence ionic rather than p-type conductivity) predominates in LSGM which is in agreement with tracer experiments.6 Such redox behaviour is in contrast to that found in LaMO3 perovskites containing transition-metal ions at the B-site, in which a key factor for conduction behaviour is the relative ‘redox stability’ of the transition-metal cation. In general, our calculations are consistent with experimental findings that show that Sr/Mg-doped LaGaO3 system is mainly an ionic conductor with an ionic transport number close to unity.
Second, the oxidation energy for Ni and Cu doped LaGaO3 suggests a thermodynamically favourable reaction (Table 5). Thus, we would expect holes (Ni3+ or Cu3+) to form at increasing oxygen partial pressures and that oxidation will enhance the solubility of these two dopants in the LaGaO3 host. Based on the oxidation reaction (eqn. 12) the pO2 dependence is expected to be +¼. These results are consistent with conductivity studies of Long et al.30 that show increasing p-type electronic conductivity at high pO2 with increasing Ni content. Ishihara31 also find that the Ni-doped gallate produced the highest oxygen permeation rate. The magnitude of the calculated oxidation energy for Co3+ doped LSGM is greater than for Ni2+ or Cu2+ doped materials, suggesting that it is comparatively resistant to oxidation.
Finally, we calculate relatively unfavourable energetics for Fe3+ or Mn3+ doped LaGaO3. While no measured values are available for direct comparison, these results are consistent with experiments31 that find that the transport number of the oxide ion is almost unity in undoped or Fe-doped LaGaO3, whereas that of the Ni-doped material is lower than one due to hole conduction.
4. Conclusions
Advanced simulation techniques have been used to investigate dopant site-selectivity, dopant–vacancy association and hole formation in LaGaO3-based perovskites. Our detailed studies have produced atomic-scale information that is of relevance to the electrochemical behaviour of the gallate and of other LaMO3 perovskites. The main points are as follows:(1) Favourable energetics for dopant substitution are found for Sr2+ at La and Mg2+ at Ga in accord with general observation including recent calorimetry measurements.22 Size is important for trivalent dopant incorporation: cations of radius ≤0.8 Å (e.g. Fe, Mn, Sc, In) are favourable on the Ga site, while larger rare-earth ions (e.g. Gd, Nd) substitute preferentially on the La site.
(2) The Yb3+ dopant is found to sit at the “crossover” point in our calculated energies for La versus Ga substitution. This suggests possible “amphoteric” behaviour in which the dopant can occupy either site. Our first examination of A-site deficiency in the gallate material predicts a strong influence on the site-selectivity of Yb. Hence, dopant site-selectivity would be sensitive to the La/Ga ratio and hence to the experimental processing conditions.
(3) The M4+ (Ti, Sn, Zr, Hf) and M5+ (Nb, Ta) dopants are predicted to substitute for Ga with La vacancy compensation. Such “donor” doping may facilitate La vacancy diffusion. The favourable binding energy for the (V‴LaV••O) cluster of vacancies could be a factor inhibiting oxygen ion conductivity in samples that are M4+/M5+ doped or A-site deficient.
(4) Our results on dopant–vacancy association may have general relevance to other ABO3 perovskite oxides. The cluster binding energy (and hence activation energy) is dependent upon ion size effects and A/B site-occupancy. This is analogous to ion size effects in doped fluorite-oxides. A minimum in binding energy in LaGaO3 occurs when the ionic size of the host and dopant are close to each other (e.g. Sr2+ on La3+ and Co3+ on Ga3+), which would be beneficial to oxygen ion conductivity. In particular, incorporation of Sr2+ at La will optimise oxygen diffusivity owing to the negligible binding energy term and the free oxygen vacancy concentration. This may be relevant to all LaMO3 perovskites in which acceptor doping is achieved by partial replacement of La by Sr.
(5) Our prediction of strong Mg–vacancy association is consistent with the observed increase in the conduction activation energy at higher Mg doping levels and at low temperatures. This would lead to two regions in the conductivity Arrhenius plot.
(6) Dopant–vacancy association for isovalent (M3+) substitution indicates the importance of elastic strain effects, which depend upon the degree of ion size “mismatch” between host and dopant ion. The strongest binding energies are found for In3+ on Ga3+ and Y3+ on La3+, which would be detrimental to oxygen ion conductivity.
(7) We considered, for the first time, larger complex clusters ( ) of x up to 12 within 2D and 3D structures. These clusters may be important as precursors to possible short-range ordering or “nano-domain” formation at higher dopant regimes. Indeed, one of the aims of this work is to encourage further structural studies (e.g. electron microscopy, electron diffraction) to probe such defect features in perovskite oxides at the local level.
) of x up to 12 within 2D and 3D structures. These clusters may be important as precursors to possible short-range ordering or “nano-domain” formation at higher dopant regimes. Indeed, one of the aims of this work is to encourage further structural studies (e.g. electron microscopy, electron diffraction) to probe such defect features in perovskite oxides at the local level.
(8) Favourable oxidation to form hole species is found for Ni2+ and Cu2+ doping, but not for Fe3+ and Mn3+ doping. This suggests p-type conductivity at increasing oxygen partial pressure with a pO2 dependence of +¼. Our results confirm that Ni and Cu doped LSGM are possible candidates for applications of mixed ionic-electronic conductors (e.g. SOFC cathodes, oxygen separation membranes).
5. Acknowledgements
We wish to acknowledge the EPSRC, the Computational Chemistry Working Party, and the JREI for Compaq resources at RAL. We are also grateful to P. R. Slater, J. T. S. Irvine and A. Navrotsky for useful discussions.6. References
- T. Ishihara, H. Matsuda and Y. Takita, J. Am. Chem. Soc., 1994, 116, 3801 CrossRef CAS.
- T. Ishihara, H. Matsuda and Y. Takita, Solid State Ionics, 1995, 79, 147 CrossRef CAS.
- M. Feng and J. B. Goodenough, Eur. J. Solid State Inorg. Chem., 1994, 31, 663 CAS.
- P. Huang and A. Petric, J. Electrochem. Soc., 1996, 143, 1644 CAS.
- J. Drennan, V. Zelizko, D. Hay, F. T. Ciacchi, S. Rajendran and S. P. S. Badwal, J. Mater. Chem., 1997, 7, 79 RSC.
- T. Ishihara, J. A. Kilner, M. Honda and T. Takita, J. Am. Chem. Soc., 1997, 119, 2747 CrossRef CAS.
- K. Huang, R. S. Tichy and J. B. Goodenough, J. Am. Ceram. Soc., 1998, 81, 2565 CAS.
- D. Lybye, F. W. Poulsen and M. Mogensen, Solid State Ionics, 2000, 128, 91 CrossRef CAS.
- S. M. Choi, K. T. Lee, S. Kim, M. C. Chun and H. L. Lee, Solid State Ionics, 2000, 131, 221 CrossRef CAS.
- (a) S. Kim, M. C. Chun, K. T. Lee and H. L. Lee, J. Power Sources, 2001, 93, 279 CrossRef CAS; (b) K. T. Lee, S. Kim, G. D. Kim and H. L. Lee, J. Appl. Electrochem., 2001, 31, 1243 CrossRef CAS.
- V. Thangadurai and W. Weppner, J. Electrochem. Soc., 2001, 148, 1294 CrossRef CAS.
- (a) T. Norby, J. Mater. Chem., 2001, 11, 11 RSC; (b) C. Haavik, E. M. Uttesen and T. Norby, Solid State Ionics Search PubMed , to be published.
- E. Iguchi, S. Nakamura, F. Munakata, M. Kurumada and Y. Fujie Y, J. Appl. Phys, 2003, 93, 3662 CrossRef CAS.
- (a) P. R. Slater, J. T. S. Irvine, T. Ishihara and Y. Takita, Solid State Ionics, 1998, 107, 319 CrossRef CAS; (b) P. R. Slater, J. T. S. Irvine, T. Ishihara and Y. Takita, J. Solid State Chem., 1998, 139, 135 CrossRef CAS.
- J. Kimpton, T. H. Randle, J. Drennan and G. Auchterlonie, Mater. Res. Bull., 2001, 36, 639 CrossRef CAS.
- L. Vasylechko, V. Vashook, D. Savytskii, A. Senyshyn, R. Niewa, M. Knapp, H. Ullmann, M. Berkowski, A. Matkovskii and U. Bismayer, J. Solid State Chem., 2003, 172, 396 CrossRef CAS.
- T. Mathews, J. R. Sellar, B. C. Muddle and P. Manoravi, Chem. Mater., 2000, 12, 917 CrossRef CAS.
- A. Skowron, P. Huang and A. Petric, J. Solid State. Chem., 1999, 143, 202 CrossRef CAS.
- (a) A. Ahmad-Khanlou, F. Tietz and D. Stover, Solid State Ionics, 2000, 135, 543 CrossRef CAS; (b) P. J. Majewski, M. Rozumek, H. Schluckwerder and F. Aldinger, J. Am. Ceram. Soc., 2001, 84, 1093 CAS.
- H. Hayashi, M. Suzuki and H. Inaba, Solid State Ionics, 2000, 128, 131 CrossRef CAS.
- (a) S. Tao, F. W. Poulsen, S. Meng and O. T. Sorensen, J. Mater. Chem., 2000, 10, 1829 RSC; (b) T. L. Nguyen and M. Dokiya, Solid State Ionics, 2000, 132, 217 CrossRef.
- J. Cheng and A. Navrotsky, J. Mater. Res., 2003, 18, 2501 CAS.
- M. Lerch, H. Boysen and T. Hansen, J. Phys. Chem. Solids, 2001, 62, 445 CrossRef CAS.
- K. Huang, R. Tichy, J. B. Goodenough and C. Milliken, J. Am. Ceram. Soc., 1998, 81, 2581 CAS.
- G. C. Kostogloudis, C. Ftikos, A. Ahmad-Khanlou, A. Naoumidis and D. Stover, Solid State Ionics, 2000, 134, 127 CrossRef CAS.
- Y. H. Du and N. Sammes, Ionics, 2003, 9, 7 Search PubMed.
- (a) K. Huang, J. Wan and J. B. Goodenough, J. Mater. Sci., 2001, 36, 1093 CrossRef CAS; (b) K. Huang, J. Wan and J. B. Goodenough, J. Electrochem. Soc., 2001, 148, 788 CrossRef.
- J. Y. Yi and G. M. Choi, Solid State Ionics, 2002, 148, 557 CrossRef CAS.
- T. Ishihara, H. Furutani, M. Honda, T. Yamada, T. Shibayama, T. Akbay, N. Sakai, H. Yokokawa and Y. Takita, Chem. Mater., 1999, 11, 2081 CrossRef CAS.
- N. J. Long, F. Lecarpentier and H. L. Tuller, J. Electroceram., 1999, 3, 399 CrossRef CAS.
- T. Ishihara, T. Shibayama, H. Nishiguchi and Y. Takita, J. Mater. Sci., 2001, 36, 1125 CrossRef CAS.
- N. Trofimenko and H. Wellmann, Solid State Ionics, 1999, 124, 263 CrossRef CAS.
- H. Ullmann, N. Trofimenko, A. Naoumidis and D. Stover, J. Eur. Ceram. Soc., 1999, 19, 791 CrossRef CAS.
- P. S. Anderson, F. M. B. Marques, D. C. Sinclair and A. R. West, Solid State Ionics, 1999, 118, 229 CrossRef CAS.
- A. A. Yaremchenko, V. V. Kharton, A. P. Viskup, E. N. Naumovich, N. M. Lapchuk and V. N. Tikhonovich, J. Solid State Chem., 1999, 142, 325 CrossRef CAS.
- (a) V. V. Kharton, A. P. Viskup, A. A. Yaremchenko, R. T. Baker, B. Gharbage, G. C. Mather, F. M. Figueirido, E. N. Naumovich and F. M. B. Marques, Solid State Ionics, 2000, 132, 119 CrossRef CAS; (b) V. V. Kharton, A. A. Yaremchenko, A. P. Viskup, G. C. Mather, E. N. Naumovich and F. M. B. Marques, Solid State Ionics, 2000, 128, 79 CrossRef CAS.
- J. Wolfenstine, Solid State Ionics, 1999, 126, 293 CrossRef CAS.
- O. Schulz, M. Martin, C. Argirusis and G. Borchardt, Phys. Chem. Chem. Phys, 2003, 5, 2308 RSC.
- W. E. Luecke and T. R. Armstrong, J. Mater. Res., 2002, 17, 532 CAS.
- J. W. Stevenson, T. R. Armstrong, L. R. Pederson, J. Li, C. A. Lewinsohn and S. Baskaran, Solid State Ionics, 1998, 113–115, 571 CrossRef CAS.
- (a) M. S. Islam, J. Mater. Chem., 2000, 10, 1027 RSC; (b) M. S. Islam, Solid State Ionics, 2002, 154–155, 75 CrossRef CAS.
- (a) R. A. De Souza, M. S. Islam and E. Ivers-Tiffee, J. Mater. Chem., 1999, 9, 1621 RSC; (b) E. Ruiz-Trejo, M. S. Islam and J. A. Kilner, Solid State Ionics, 1999, 123, 121 CrossRef CAS.
- M. Cherry, M. S. Islam and C. R. A. Catlow, J. Solid State Chem., 1995, 118, 125 CrossRef CAS.
- (a) M. S. D. Read, M. S. Islam, G. W. Watson, F. King and F. E. Hancock, J. Mater. Chem., 2000, 10, 2298 RSC; (b) M. S. Islam, R. A. Davies and J. D. Gale, Chem. Mater., 2001, 13, 2049 CrossRef CAS.
- M. S. Khan, M. S. Islam and D. R. Bates, J. Phys. Chem. B., 1998, 102, 3099 CrossRef CAS.
- R. A. De Souza and J. Maier, Phys. Chem. Chem. Phys., 2003, 5, 740 RSC.
- (a) J. D. Gale and A. L. Rohl, Mol. Simul., 2003, 29, 291 Search PubMed; (b) C. R. A. Catlow, ed. Computer Modelling in Inorganic Crystallography, Academic Press, San Diego, 1997 Search PubMed.
- Y. Wang, X. Liu, G. D. Yao, R. C. Liebermann and M. Dudley, Mater. Sci. Eng., A., 1991, 132, 13 Search PubMed.
- G. V. Lewis and C. R. A. Catlow, J. Phys. C: Solid State Phys., 1985, 18, 1149 CrossRef CAS.
- D. C. Dube, H. J. Scheel, I. Reaney, M. Daglish and N. Setter, J. Appl. Phys., 1994, 75, 4126 CrossRef CAS.
- (a) M. O. Zacate, L. Minervini, D. J. Bradfield, R. W. Grimes and K.E. Sickafus, Solid State Ionics, 2000, 128, 243 CrossRef CAS; (b) M. T. Buscaglia, V. Buscaglia, M. Viviani and R. Nanni, J. Am. Ceram. Soc., 2001, 84, 376 CAS.
- (a) C. M. Freeman and C. R. A. Catlow, J. Solid State Chem., 1990, 85, 65 CAS; (b) N. L. Allan, P. S. Baram, A. Gurmezano and W. C. Mackrodt, J. Mater. Chem., 1994, 4, 817 RSC.
- F. A. Kroger, The Chemistry of Imperfect Crystals, Amsterdam, North-Holland, 1974 Search PubMed.
- R. D. Shannon, Acta Crystallogr., Sect. A, 1976, 32, 751 CrossRef.
- (a) Y. Tsur, A. Hitomi, I. Scrymgeour and C. A. Randall, Jpn. J. Appl. Phys., 2001, 40, 255 CrossRef CAS; (b) J. Zhi, A. Chen, Y. Zhi, P. M. Vilarinho and J. L. Baptista, J. Am. Ceram. Soc., 1999, 82, 1345 CAS; (c) K. Takada, E. Chang and D. Smyth, Adv. Ceram., 1987, 19, 147 Search PubMed; (d) L. A. Xue, Y. Chen and R. J. Brook, Mater. Sci. Eng., B., 1998, 1, 193 Search PubMed.
- (a) A. V. Berenov, J. L. MacManus-Driscoll and J. A. Kilner, Solid State Ionics, 1999, 122, 41 CrossRef CAS; (b) S. P. Jiang, J. G. Love, J. P. Zhang, M. Hiang, Y. Ramprakash, A. E. Hughes and S. P. S. Badwal, Solid State Ionics, 1999, 121, 1 CrossRef CAS.
- S. M. Haile, G. Staneff and K. H. Ryu, J. Mater. Sci., 2001, 36, 1149 CrossRef CAS.
- J. A. Kilner, Solid State Ionics, 2000, 129, 13 CrossRef CAS.
- A. S. Nowick, S. Q. Fu, W. K. Lee, B. S. Lim and T. Scherban, Mater. Sci. Eng., B., 1994, 23, 19 Search PubMed.
- S. García-Martín, M. A. Alario-Franco, D. P. Fagg, A. J. Feighery and J. T. S. Irvine, Chem. Mater., 2000, 12, 1729 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2004 |
