Effect of iron on delithiation in Li_xCo_1−yFe_yO₂. Part 2:in-situ XANES and EXAFS upon electrochemical cycling

Abstract

Li_xCo_1−yFe_yO₂ solid solutions were examined in an in-situ electrochemical X-ray absorption spectroscopy study using a plastic battery configuration. XANES and EXAFS were applied to elucidate the evolution of local symmetry and oxidation states of iron and cobalt upon electrochemical cycling of three particular stoichiometries: Li_xCo_0.9Fe_0.1O₂, Li_xCo_0.8Fe_0.2O₂ and Li_xCo_0.6Fe_0.4O₂. While the cobalt environment shows little variation, a distortion of the FeO₆ octahedra occurs quite rapidly for all three samples with a decrease in the next neighbour numbers from six to four. This is ascribed to the Jahn–Teller effect which affects Fe⁴⁺ (a d⁴ system), that is formed upon delithiation. No distortion is observed for cobalt. Along the delithiation process a simultaneous increase in the edge energy occurs for cobalt and iron in the case of y = 0.1 and to a lesser extent for iron than for cobalt for y = 0.4. This means that the oxidation of Fe³⁺ occurs together with the oxidation of the cobalt matrix in the cobalt-rich samples but becomes more difficult for iron-rich samples. In the case of the cobalt-rich samples, the edge-energy for both elements shifts back down at the end of charge, in spite of the continuing oxidation of the cations. This effect is probably related to the appearance of a new lithium-poor phase, that is not formed for y = 0.4, and confirms the in-situ X-ray diffraction results published in the first part of this series.

---

Introduction

LiCoO₂ is a very promising layered oxide material for use as cathode materials in 4 V-lithium batteries.^1–4 This is due to its superior stability upon prolonged cycling and ease of preparation but it does suffer from economic and ecological drawbacks, which made necessary the search for alternative materials. LiFeO₂ of the same structure type, cheap and non-toxic, exists,^5–9 besides several other isomorphs,^10–14 but up to now lithium could not be deintercalated reversibly from this material. LiCo_1−yFe_yO₂ could be an interesting alternative in this respect, if the stabilising effect of cobalt was maintained and indeed numerous works have been devoted to investigate this system. The synthesis and the structural and physicochemical characterisation of these compounds have already been discussed^15–26 in the first part of this series,²⁷ where the in-situ X-ray diffraction study of the LiCo_1−yFe_yO₂ solid solution is described. Upon oxidation of Fe³⁺, Fe⁴⁺ should be formed, which is a d⁴-high spin system, showing, in principle, a Jahn–Teller effect, i.e. an energetically favoured distortion of the FeO₆-octahedron under elongation of the ligand along the z-axis. It should be possible to monitor this distortion by a technique that probes the local environment of atoms: X-ray absorption spectroscopy (XAS).^28–31 Two energy ranges in the XAS spectrum can be defined: (1) The X-ray absorption near edge structure (XANES) area, which corresponds to the energy region within ca. 50 eV on both sides of the absorption edge, is very sensitive to the oxidation state of the investigated atom, its site symmetry and chemical environment. (2) The energy region above 50 eV above the absorption edge is the extended X-ray absorption fine structure (EXAFS) area. In this region, the interaction between the emitted and backscattered photo-electron waves leads to oscillations of the absorption coefficient, due to the surroundings of the absorbing atoms. The interpretation of these EXAFS oscillations gathers information about the local environment of the absorbing atoms: the coordination number N, the interatomic mean distances R and their distribution (the so-called Debye–Waller factors in the Gaussian distribution approximation). XAS has recently been applied to determine the evolution of both local environment and valence in transition metal oxides used in lithium batteries. In this domain, it is a very powerful technique because of its chemical selectivity, usable in-situ in thin batteries and applicable to both crystallised and amorphous materials.^32,33

A key asset of the XANES technique is its selectivity: by regarding both iron and cobalt edges, it allows to follow independently the variation in valence of the two elements during the electrochemical cycling and hence to determine whether Fe³⁺ is oxidised along with Co³⁺ or after it. This feature could be related to the structural transformations that occur during lithium deintercalation and would give precious information for the comprehension of the role of iron in this system and generally in LiMO₂ materials. EXAFS measurements should give important information about the local structure, as Fe⁴⁺ is a d⁷ ion and hence a Jahn–Teller deformation of the host material could be expected on its formation. The formation of Fe^3+/4+ pairs with a fast electron hopping has been already evidenced in LiNi_1−yFe_yO₂.³⁴

In order to elucidate these questions we undertook in-situ synchrotron X-ray diffraction and absorption during electrochemical delithiation–relithiation of Li_xCo_1−yFe_yO₂-samples for three different x values (0.1, 0.2 and 0.4). The results for these in-situ XANES and EXAFS experiments are presented and discussed in this paper, whereas the X-ray diffraction data are presented in the first article.²⁷

Experimental

The preparation of the samples and the plastic batteries has been carried out as described in detail previously.²⁷ The prepared LiCo_1−yFe_yO₂ compounds were used here as starting materials to study the delithiated Li_xCo_1−yFe_yO₂ systems with y = 0.1, 0.2 and 0.4. These compounds are abbreviated LCF1, LCF2 and LCF4, respectively. The cycling of the batteries was done with intermittent charge/discharge steps with a rate set to C/5. The acquisition of the X-ray absorption spectra was performed at the subsequent rest times of the batteries, i.e. at constant Li compositions (x). For details of the electrochemical behaviour of the LCF samples, see refs. 21 and 27.

in-situ X-Ray absorption

The plastic batteries were studied on the BM 29 absorption spectroscopy beamline at ESRF (Grenoble, France).³⁵ In order to cover both the Fe (7112 eV) and Co (7709 eV) K-edges, spectra were recorded between 6.9 and 8.7 keV with 0.3 eV steps at the absorption edges, using a double Si (311) monochromator. Metallic iron was used to calibrate the energies of the absorption edges for each spectrum. The absorption was measured in transmission mode using three argon/helium filled ionisation chambers for the measurements of the intensity of the incident beam I₀, the beam after the sample I₁ and the beam after the iron metallic reference I₂. The absorption coefficient of the sample is given by ln(I₀/I₁), that of the reference by ln(I₁/I₂). The simultaneous acquisition of both sample and reference spectra together with the use of a high resolution monochromator, allows an accurate analysis of the various XANES features (position of the edge, shape of the pre-edge). The primary slit used was of 0.4 mm, which permitted an energy resolution of about five times better than the natural broadening of the spectrum (for details see ref. 35).

The program package SEDEM³⁶ was used for the XAS analysis procedure. The atomic absorption, μ₀(E), was determined from a straight line in the pre-edge region and as a fourth-order polynomial (cubic spline) in the post-edge region. The shape of the atomic absorption was then computed with the Cromer & Liberman fPrime program and the oscillations normalised according to χ(E) = (μ(E) − μ₀(E))/μ₀(E). The normalised spectra were converted into k-space and the χ(k)-spectra were weighted by k in order to magnify the signals in the lower energy region, compared to classic analysis where the weighting is performed with k³. This procedure allows to put more weight on the information coming from the first shell. This was followed by Fourier-transforming the weighted spectra, kχ(k) into k-space in the ranges 1.9–12.0 and 1.8–16.0 Å⁻¹ for iron and cobalt, respectively. The shorter data range for iron results from the shorter spectral range available due to the close succession of the Fe and Co edges. Due to the absence of further neighbours and the rapidly declining backscattering amplitudes, the analysis is not influenced by this close succession. The F(R) obtained spectra were then back-transformed into k-space after filtering between 0.68 and 2.82 Å, to extract from the overall oscillations the information due to the first two shells around the central atoms. The curve fitting procedure was performed in the single scattering approximation with SEDEM³⁶ using ab initio backscattering phase and amplitude calculated from FEFF.³⁷

Results and discussion

1. X-Ray absorption near edge structure results

a. General features. The K-edge XANES spectra originate from different transitions of the 1s electron to vacant orbitals of different symmetries.^38–42 For the iron and cobalt K-edges, the near-edge spectra show three distinct features (see Fig. 1): a pre-edge peak, A, a shoulder on the main absorption peak, B and the main absorption peak, C.

Fig. 1 in-situ Fe-edge XANES for LCF1: (a) during electrochemical delithiation, (b) during relithiation. Note: For this and the following figures the spectra have been shifted vertically for clarity. Peaks A, B and C denote different features of the spectra that are explained in the text.

These peaks are located at about 7113, 7123 and 7133 eV for Fe and 7709, 7718 and 7727 eV for Co (see Figs. 1(a) and 2(a)). In Fig. 1(a) and (b) there is an irregular jump in absorption for the most delithiated composition. Such jumps are due to changed probe geometry, coming from a slight slipping of the sample or a slight gas evolution. In view of the type of battery used, such jumps are not surprising. For the EXAFS analysis these spectra have, however been excluded.

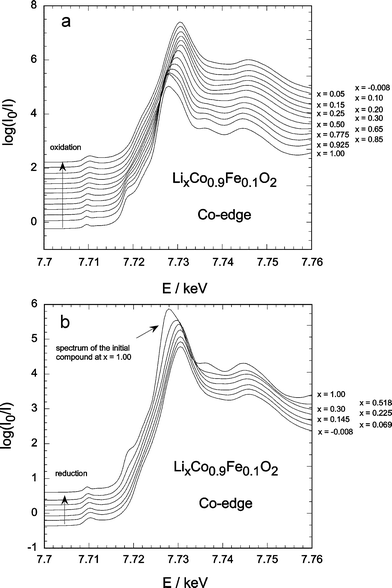Fig. 2 in-situ Co-edge XANES for LCF1: (a) during the electrochemical delithiation, (b) during the relithiation.

The pre-edge peak A is due to a 1s to 3d electric quadrupole transition. This transition is normally symmetry-forbidden for a centrosymmetric site such as a regular octahedron. In a non-centrosymmetric site, however, this weak peak A is commonly observed in the case of slight local distortions, related to 3d–4p orbital mixing, which attributes some electric dipole character to the transition.^41,43,44 An increase in the pre-edge intensity is therefore a sensitive indicator of a change in local environment or a local distortion around the central atom.

The B peak is due to a 1s to 4p transition followed by a ligand to metal transfer from the oxide anions⁴¹ (Fe 1s²3d⁵O 2p⁴ → Fe 1s¹3d⁵O 2p⁵ → Fe 1s¹3d⁶O 2p⁴) which is of relatively weak intensity.

The main peak is the peak C, which corresponds to the 1s to 4p transition without the shakedown process:^45–48 Fe 1s²3d⁵O 2p⁴ → Fe 1s¹3d⁵O 2p⁵.

The qualitative evolutions of the XANES features are the same for the three different iron concentrations. The XANES spectra obtained during electrochemical deintercalation and reintercalation for x = 0.1 are presented for the Fe and Co K-edges in Figs. 1 and 2, respectively.

b. Pre-edge region: the A-peak. For all three compounds and x > 0.7, the intensity of the A-peak is very weak, as expected for an octahedral environment, and actually shows two peaks. Such a feature has been acknowledged already in several Fe(III) compounds, as ferric sulfate, goethite or hematite, and has been explained with long-range order, including Fe–Fe pairs.^46,49

For x ≤ 0.7, the signal rapidly merges and its intensity first increases. This indicates a certain local distortion occurring upon lithium deintercalation. At the end of the deintercalation process (x ≤ 0.2), the intensity decreases again. This is consistent with a structural transformation into a CdI₂-type structure as shown by in-situ XRD,²⁷ obviously with a different iron surrounding.

During reintercalation, the A-peak height increases again but does not go back to its initial value. This is consistent with the electrochemical behaviour of the batteries used, which showed reversibility only up to x ∼ 0.5 upon re-intercalation.

For the cobalt A-peak (Fig. 2) the increase in intensity upon oxidation/reduction is almost negligible indicating a much lower tendency to distortion than the iron. The shift of the peak maximum upon oxidation is, again, clearly visible and only partially reversible, as the reduction process itself is not fully reversible.

For LCF2 and LCF4 the A peak evolution is rather similar, but the increase in intensity of the A-peak on charge is weaker than in LCF1. The decrease in peak intensity at the end of charge is less marked for LCF2 and disappears for LCF4. The absence of this effect for LCF4 can be explained by the absence of a structural transformation at the end of oxidation for LCF4.²⁷

c. Pre-edge region: the B-peak. In contrast to the A-peak, the B-peak shows decreasing intensity for increasing local disorder at the site of the probed atom. As shown in Figs. 1 and 2, a decreasing intensity is actually observed. This effect is strongest for LCF1, and is visible for both cobalt and iron, which indicates increasing disorder for both atom environments. This is not related to the Jahn–Teller-effect, as Co^3+/4+ does not show this effect, but to decreasing crystallinity of the sample. The spectra taken upon relithiation do not show a reincrease of the intensity of the B-peak, for any of the samples, indicating that this effect is irreversible.

d. The main absorption: the region around the C-peak. The region around the main absorption peak is shown for the cobalt and iron edges in all three compounds in Figs. 1–4. The first derivative of the absorption, the maximum of which represents the inflection point, is shown for the iron edge in LCF2 as an example in Fig. 5 (only the delithiation process is shown). It is sometimes taken as a measure for the energy shift, instead of the maximum of the absorption curve, as a clear relationship between this value and the oxidation state has been established in the case of manganese.⁵⁰

Fig. 3 in-situ XANES for LCF2 during delithiation: (a) Fe-edge, (b) Co-edge.

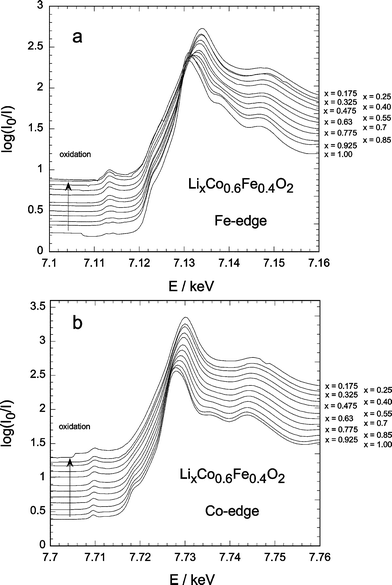Fig. 4 in-situ XANES for LCF4 during delithiation: (a) Fe-edge, (b) Co-edge.

Fig. 5 Derivative of the Fe-edge XANES for LCF2 (data from Fig. 3(a)).

The maximum of the derivative (Fig. 6) clearly shifts to higher energies with delithiation, for both cobalt and iron edges as expected for the simultaneous oxidation of both Co³⁺ and Fe³⁺. However at the end of oxidation (x < 0.3), the derivative maximum shifts back to lower energy values for both LCF1 and LCF2, whereas it remains at the higher energy value for LCF4. This illustrates the complexity of the edge position variation which actually depends on both the absorbers valence and symmetry changes. The observed decrease in edge energy is probably related to the appearance of a new, lithium-poor phase.²⁷ It starts, indeed, at the same lithium content x and does not occur for LCF4, for which no specific lithium-poor phase is found. This behaviour is partly reversible, as shown in Fig. 6.

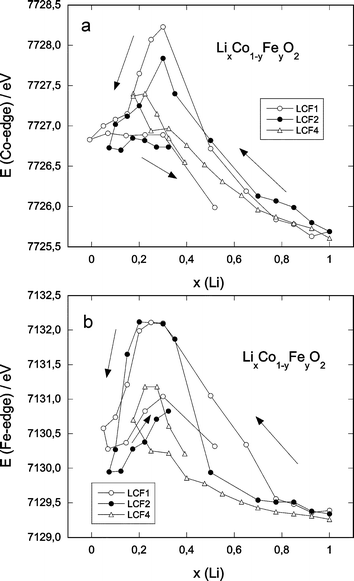Fig. 6 Edge energy (determined as the maximum of the first derivative of the XANES spectra) as a function of the lithium content: (a) Co-edge, (b) Fe-edge.

A faint peak after the main peak can be observed at around 7138 eV for iron and 7736 eV for cobalt (not shown), in the case of the lithiated samples. It disappears quite rapidly for both elements during the oxidation process and does not reappear upon the subsequent reduction. This peak is a sign of a certain long range order present in the samples which disappears upon oxidation and illustrates again a certain decrease in crystallinity of the compounds on lithium deintercalation.

2. Extended X-ray absorption fine structure results

a. Qualitative considerations. Qualitatively, the evolution of the EXAFS spectra is similar for LCF1, LCF2 and LCF4. As an example, we show the Fourier Transform modulus F(R) (Fig. 7) and filtered kχ(k) (Fig. 8) spectra obtained for the LCF2 set at the Co and Fe K-edges for selected lithium contents.

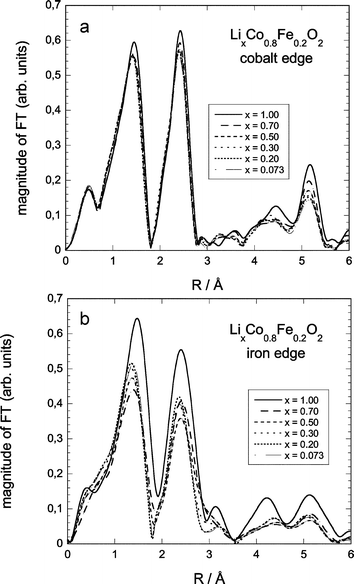Fig. 7 Fourier-transformed EXAFS-spectra for selected compositions of LCF2: (a) Co-edge, (b) Fe-edge.

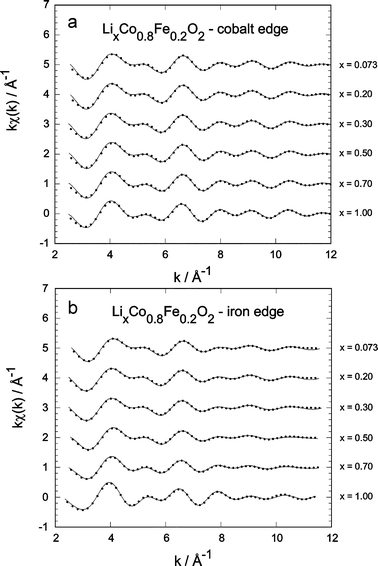Fig. 8 Comparison of the normalised kχ(k) as a function of lithium content (solid lines) for LCF2; points, experimental data: (a) Co-edge, (b) Fe-edge.

The F(R) modulus of the EXAFS signal is a pseudo-radial distribution function around the absorber atoms. The different peaks can be associated to various neighbour shells and the positions of the peak maxima are linked to the bonds lengths (uncorrected from the backscattering phase shift at this stage).

At the Co and Fe K-edges (Fig. 7), the F(R) spectra present the same main characteristics. A first peak at about 1.5 Å corresponds to the first oxygen neighbours; a second peak at about 2.4 Å corresponds to the second (transition metal) shell.

The peaks at higher distances (around 4.3 and 5.2 Å) are well defined, especially in the initial state (x = 1), indicating the good crystallinity of the samples.

With the decrease of the Li amount (x) in the samples, the heights of the different F(R) peaks decrease. Considering first cobalt, the Co–O and Co–Co peaks do not change in shape and the intensity decrease is gradual, meaning that the local surrounding of cobalt remains, in a first approximation, the same during the delithiation process. For iron, both shape and intensity of the first two peaks change considerably. This reflects an important change in local symmetry around the iron ions upon delithiation (cf. refs. 51 and 52), which will be addressed in the next section.

b. Simulation parameters and results. Simulations were performed on the filtered kχ(k) spectra. The filtering process was performed between 0.68 and 2.82 Å. Whereas the composition of the first neighbour shell around Co and Fe is straightforward (oxygen atoms only), the second shell contains Li (Z = 3), Fe (Z = 26) and Co (Z = 27). The contribution of the light Li atoms to the EXAFS signal can be considered negligible. Given the small difference in Z between Fe and Co, the simulations of the second shell were performed considering a cobalt layer.

Fig. 8 shows the experimental Fourier-filtered (points) and the simulated (continuous lines) kχ(k)-spectra for LCF2. In the whole composition range and for both Co and Fe, the agreement between experiment and model shows the quality of the fit. Much stronger variations are visible for iron. The main results are summarised in Figs. 9–12, showing the evolution of the main variables in the EXAFS fits: bond length distances d, mean square relative displacements σ² and nearest neighbour numbers N.

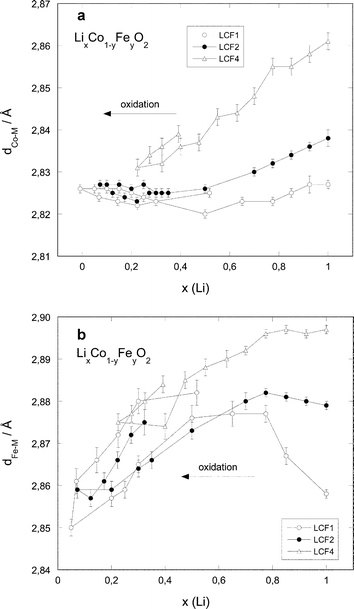
Fig. 9 Interatomic distances for the nearest neighbours (oxygen shell) around the central atom as a function of the lithium content: (a) Co-edge, (b) Fe-edge.

Fig. 10 Interatomic distances for the second nearest neighbours (transition metal shell) around the central atom as a function of the lithium content: (a) Co-edge, (b) Fe-edge.

Fig. 11 Mean square relative displacements as a function of the lithium content: (a) Co-edge, first and second shell, (b) Fe-edge, first and second shell.

Fig. 12 Neighbour numbers as a function of the lithium content, iron edge: (a) nearest neighbours (oxygen shell), (b) second nearest neighbours (transition metal shell).

Considering first the evolution of the M–O and M–M distances (Figs. 9 and 10), a decrease in the distances is observed along the oxidation process for all samples. The bond lengths are Fe-concentration dependent: they are larger for higher Fe concentrations. However, these differences tend to vanish for small x values: at the end of the oxidation process (x lower than 0.3), the different bond lengths are equal within the experimental error.

The variation of the M–O distances with the lithium content is approximately linear for x ≥ 0.25 and x ≥ 0.5 for cobalt and iron, respectively (see Fig. 9). The overall M–O distance variation is much stronger for iron (1.98–1.88 Å) than for cobalt (1.91–1.875 Å). For the M–M distances (Fig. 10), the evolutions are more different. The Co–M distances decrease regularly with decreasing x down to x ≈ 0.3, and then stabilise to a common value around 2.825 Å for all iron concentrations. The Fe–M distance evolution shows two distinct ranges: for x > 0.7, the distances remain constant for LCF2 and LCF4 and increase for LCF1. For x ≤ 0.7, the Fe–M distances decrease to reach a value around 2.86 Å in the region of low lithium content.

The σ²_M–O evolution is similar for Co and Fe (see Fig. 11). It exhibits a slight increase at the beginning of the charge (right side of the figures), then stabilises for x ≤ 0.8. The only exceptions to this trend are σ²_Fe–M for LCF1 and LCF2, where σ²_Fe–M decreases again in the highly oxidised region. It should also be noted that the σ² values are systematically higher for iron than for cobalt.

Regarding the nearest neighbour numbers, N around cobalt remains remarkably constant for all the three samples and in both, the first and second shells. But this is not the case for iron, as shown in Fig. 12. The nearest neighbour (N_Fe–O) and second nearest neighbour numbers (N_Fe–M) fall from six in the starting materials to about 4.5 in the delithiated products. It is important to note that this effect is nearly not reversible, except for LCF1.

General discussion

1. Bond length distances

The M–O and M–M distances are larger for increasing iron content, which is in agreement with the larger size of Fe³⁺ compared to Co³⁺ and the lattice parameters of the corresponding compounds.⁹

One can first explain the decrease in the M–O and M–M distances along the oxidation process considering the evolution of the cationic radii of Fe and Co. However, for cobalt, the difference is small between Co³⁺ (low spin: 0.545 Å) and Co⁴⁺ (high spin: 0.53 Å). The relatively similar behaviour of the Co–O distances in the cobalt series highlights the fact that the oxidation process proceeds in a comparable manner for all three samples. For iron, on the contrary, the difference is much larger between Fe³⁺ (high spin: 0.645 Å) and Fe⁴⁺ (high spin: 0.585 Å).⁵³ This is reflected in the steeper variation of the Fe–O distance than of the Co–O one upon oxidation and the much larger M–O distance contraction on delithiation in d_Fe–O (≈0.12 Å) than in d_Co–O (≈0.04–0.05 Å) (see Fig. 9).

There is a very strong resemblance between the evolutions of the Co–M distances determined by EXAFS and the a-lattice parameters determined by X-ray diffraction (cf. ref. 27) for the three compounds: the Co–M distances determined by EXAFS diminish by 1% for LCF4, by 0.3% for LCF2 and do not diminish for LCF1.

The a-parameter of the corresponding phases shows a contraction of 1.7% for LCF4, 0.7% for LCF2 and 0.3% for LCF1. This behaviour can be expected, as the a-lattice parameter only depends of the M–M distances.

Regarding the Fe–M distances, however the situation is completely different and does not mirror the evolution of the a-lattice constant. In order to explain this behaviour one must take into account another parameter, the Jahn–Teller-effect.

2. Local distortions and Jahn–Teller effect

In the initial state, the Fe atoms are surrounded by six O atoms. The Jahn–Teller effect, which occurs for uneven occupation of the e_g orbitals can be briefly described as follows: two (axial) Fe–O bonds are elongated whereas four (planar) Fe–O bonds are shortened. Ultimately, the number of neighbours in the first shell will be reduced to four. Such an effect is expected to occur in Fe⁴⁺ ions which has the same t_2g³e_g¹ configuration as the well-known Jahn–Teller ion Mn³⁺. In addition, in the LiCoO₂ structure, the nearest transition metal neighbour of a given Fe atom is located in a diagonal direction between two Fe–O bonds: one could be elongated and the other shortened. The elongation should be more pronounced than the shortening, so that the dominant effect could easily be an increase in Fe–M distance, as observed experimentally for LCF1 and LCF2 in the range 0.75 ≤ x ≤ 1.

A direct proof of the mentioned Jahn–Teller effect can be drawn from the evolution of the number of nearest and next-nearest neighbours (the Fe–O and Fe–M shells respectively), shown in Fig. 12. A decrease of the numbers of next neighbours for iron can be expected to occur for a JT-ion, whereas for cobalt such a decrease is not observed, the number of nearest neighbours and next nearest neighbours remain about six.

Moreover, these distortions of the Fe neighbourhood compared to Co are clearly evidenced in the σ² evolutions and in the XANES part of the signal. The bell-shaped variation observed for σ²_Fe–O and σ²_Fe–M (with the exception of LCF4) can be directly linked to the increasing intensity of the Fe K-edge A-peak, sign of a local distortion around the Fe ions. These distortions reflect the JT-effect (notably for the diluted iron systems) in the following manner: at the beginning the average Fe–M distances hardly change or slightly increase (LCF1 case, Fig. 10(b)), as only few JT-ions are formed. However the Debye–Waller factors increase significantly (see Fig. 11(b)). For a higher fraction of JT-ions the distance effect takes over, the active local environment of iron atoms is reduced to the four equatorial ligands; hence the observed decrease in the effective coordination number and simultaneous decrease in Debye–Waller factor, as the distance distribution becomes narrower again. The evolution of the Debye–Waller factor is closely linked to the M–O and M–M distances and supports the apparition of a distorted local environment for iron but not for cobalt upon oxidation.

The local distortion around cobalt atoms is indeed much weaker. The σ²_Co–M and σ²_Co–O values (Fig. 11(a)) are much lower than the iron ones (Fig. 11(b)). Moreover, the increase in intensity of the cobalt A-peak in XANES upon oxidation/reduction (Fig. 2) is much less marked than for iron, which confirms a lower distortion of cobalt.

This difference appears normal, as the Co⁴⁺-ion is a d⁵ system and as such not subject to the Jahn–Teller effect. The increase of σ²_Co–M and σ²_Co–O at the beginning of delithiation can, on the other hand, be explained taking into account the presence of two rhombohedral phases with relatively similar lattice parameters. The distances are less well defined, as the signal is an average of the values of both phases. Along the electrochemical lithium deintercalation also a certain decrease of crystallinity can be expected to occur which should increase the Debye–Waller factors.

The σ² values are systematically higher for iron than for cobalt, in agreement with the fact that the major site occupant (cobalt) “imposes” its size to the transition metal site in the structure, to which iron must adapt. It must, however, be kept in mind that the strong correlation of the nearest neighbour numbers and the Debye–Waller factor makes a reduction in the nearest neighbour number along with a low σ² in principle indistinguishable from a mere distortion of the regular coordination along with a high σ². This problem is enhanced by the limitation of the usable iron spectrum length because of the neighbouring cobalt edge. Nevertheless, the conclusion remains the same: the recognition of the distortion of the regular FeO₆ octahedron.

3. Oxidation process

The reduction of the edge-energies for both cobalt and iron for the highly delithiated regions coincides with the appearance of new delithiated phases.²⁷ The altered symmetry of these phases accounts for a lower energy value which counteracts the shift to higher energy upon oxidation of the cations. This effect is reversible with respect to the disappearance of these phases upon relithiation. For y = 0.1 the evolution of the edge position clearly shows a simultaneous oxidation process from the initial Fe³⁺ and Co³⁺ to Fe⁴⁺ and Co⁴⁺, respectively. The weaker variation of the edge energy of iron upon oxidation for the compounds with higher iron content (Fig. 6(b)) illustrates, however, a less easy oxidation of Fe³⁺ compared to Co³⁺, which indicates a certain matrix effect of cobalt. In all cases, the evolution of the Fe K-edge A-peak height is consistent with the change in the iron oxidation number upon lithium deintercalation and a partial reduction back upon reintercalation.

An interesting comparison can be made with the well-known LiNi_1−yM_yO₂ systems (M = Fe, Co). In the Ni/Fe systems,³⁴ the larger iron ions are supposed to be oxidised along with the oxidation of Ni³⁺, due to the compression of the lattice. In this system there is, however, a net difference in size between Ni³⁺ and Ni⁴⁺, which is not the case for Co³⁺ (low spin) and Co⁴⁺ (high spin). In the Ni/Co system⁵⁴ this size effect does not apply to Co^3+/4+, thus the Ni³⁺-ions are oxidised first and thereafter the Co³⁺-ions. In our case the oxidation of Fe³⁺ occurs simultaneously with the oxidation of Co³⁺. As the latter does not considerably reduce the mean ionic radius, the effect mentioned for the Ni/Fe system is expected to be much weaker, if present at all. This can be seen in comparing the difference in edge energy shift for iron and cobalt in the cobalt-rich (LCF1) and iron-rich compounds (LCF4). Nevertheless, a large amount of iron is effectively oxidised, even in LCF4, as seen for the number of neighbours in the two Fe–O and Fe–M shells. At the same time, however, the potential for lithium deintercalation rises notably with increasing iron content,²⁷ which indicates the energetically more difficult oxidation of iron.

No indication could be found in the present study about the effect that some iron can be found in tetrahedral sites as in the Ni/Fe system.⁵⁵ This somewhat peculiar location for Fe³⁺-ions could either come from synthesis or occur upon electrochemical oxidation. Such a migration would then also create iron with a coordination number of four, but which could not be separated from the iron experiencing the JT effect, as this effect affects the bulk of iron whereas wandering or disorder always remains at a marginal scale. We can not exclude this in our combined studies (cf. ref. 27), but do see good evidence to question the ease of iron ion oxidisability in iron containing layered compounds, when iron is present in an appreciable (>40%) amount, where template and dilution effects lose their influence.

Conclusions

The in-situ X-ray absorption technique is found to be an invaluable technique to probe separately the evolution of iron and cobalt along an electrochemical charge/discharge cycle. Changes of local symmetry and the evolution of the oxidation state of cobalt and iron have been monitored in the Li_xCo_1−yFe_yO₂ solid solutions. Upon oxidation of Fe³⁺ to Fe⁴⁺ (t_2g³e_g¹), evidence of Jahn–Teller distortion is found by an increase of the intensity of the iron pre-edge peak and the reduction of the nearest neighbour number from six to four. A bell-shaped variation of the Debye–Waller factors for iron supports the local distortion evolution around iron atoms. These effects do not take place for cobalt. The shift of the edge energies for both elements indicate that for y = 0.1 the oxidation of Co³⁺ and Fe³⁺ occurs simultaneously, whereas for y = 0.4 Fe³⁺-oxidation starts later than that for Co³⁺. This can be a sign of assisting matrix-effect of the cobalt lattice in the case of the diluted iron-system, whereas for the iron-richer sample this effect is less effective. A shift of the edge energies of both elements at the end of charge to lower values in the case of y = 0.1 and y = 0.2 reflects the structural transformation (for x < 0.27) already evidenced by in-situ X-ray diffraction,²⁷ which does not take place in the iron-rich sample.

Acknowledgements

The authors would like to express their gratitude to Dr Yves Chabre for the very helpful discussions and his valuable support. The experiment was carried out under the ESRF proposal number CH 1187. We kindly acknowledge the help of Ralph Weigel from the beamline support staff.

References

1. M. Winter, J. O. Besenhard, M. Spahr and P. Novak, Adv. Mater., 1998, 10, 725.
2. T. Nagaura, 4th International Rechargeable Battery Seminar, Deerfield Beach, FL, USA, 1990.
3. K. Mizushima, P. C. Jones, P. J. Wiseman and J. B. Goodenough, Mater. Res. Bull., 1980, 15, 783.
4. T. Ohzuku, A. Ueda, N. Nagayama, Y. Iwakoshi and H. Komori, Electrochim. Acta, 1993, 38, 1159.
5. J. B. Goodenough, W. A. England, K. Mizushima and P. J. Wiseman, Proc. Eur. Communities Meet. Adv. Batt., 1979, 185.
6. K. Ado, M. Tabuchi, H. Kobayashi, H. Kageyama, O. Nakamura, Y. Inaba, R. Kanno, M. Takagi and Y. Takeda, J. Electrochem. Soc., 1997, 144, L177.
7. T. Shirane, R. Kanno, Y. Kawamoto, Y. Takeda, M. Takano, T. Kamiyama and F. Izumi, Solid State Ionics, 1995, 79, 227.
8. B. Fuchs and S. Kemmler-Sack, Solid State Ionics, 1994, 68, 279.
9. M. Holzapfel, C. Haak and A. Ott, J. Solid State Chem., 2001, 156, 470.
10. R. Famery, P. Bassoul and F. Queyroux, J. Solid State Chem., 1985, 57, 178.
11. R. Famery, P. Bassoul and F. Queyroux, J. Solid State Chem., 1985, 61, 293.
12. R. Kanno, T. Shirane, Y. Inaba and Y. Kawamoto, J. Power Sources, 1997, 68, 145.
13. R. Kanno, T. Shirane, Y. Kawamoto, Y. Takeda, M. Takano, M. Ohashi and Y. Yamaguchi, J. Electrochem. Soc., 1996, 143, 2435.
14. Y. Sakurai, H. Arai, S. Okada and J. Yamaki, J. Power Sources, 1997, 68, 711.
15. H. Kobayashi, H. Shigemura, M. Tabuchi, H. Sakebe, K. Ado, H. Kageyama, A. Hirano, R. Kanno, M. Wakita, S. Morimoto and S. Nasu, J. Electrochem. Soc., 2000, 147, 960.
16. M. Tabuchi, K. Ado, H. Kobayashi, H. Sakaebe, H. Kageyama, C. Masquelier, M. Yonemura, A. Hirano and R. Kanno, J. Mater. Chem., 1998, 9, 199.
17. R. Alcántara, J. C. Jumas, P. Lavela, J. Olivier-Fourcade, C. Pérez-Vicente and J. L. Tirado, J. Power Sources, 1999, 81–82, 547.
18. R. Alcantara, P. Lavela, C. Pérez-Vicente, J. L. Tirado, J. Olivier-Fourcade and J. C. Jumas, Solid State Commun., 2000, 115, 1.
19. N. Li, J. Li, J. Yang, H. Gao, S. Li and B. Lin, Electrochim. Acta, 2000, 46, 717.
20. N. Kalaiselvi, P. Periasami, R. Thirunakaran, B. Ramesh Babu, T. Prem Kumar, N. G. Renganathan, M. Raghavan and N. Muniyandi, Ionics, 2001, 7, 451.
21. M. Holzapfel, R. Schreiner and A. Ott, Electrochim. Acta, 2001, 46, 1063.
22. E. Chappel, M. Holzapfel, G. Chouteau and A. Ott, J. Solid State Chem., 2000, 154, 451.
23. E. Chappel, M. Holzapfel, G. Chouteau and A. Ott, J. Magn. Magn. Mater., 2001, 226–230, 652.
24. E. Chappel, M. Holzapfel, N. Douakha, G. Chouteau and B. Ouladdiaf, J. Magn. Magn. Mater., 2002, 740, 242.
25. N. Douakha, M. Holzapfel, E. Chappel, G. Chouteau, L. Croguennec, A. Ott and B. Ouladdiaf, J. Solid State Chem., 2002, 163, 406.
26. H. Sakaebe, H. Shigemura, H. Kobayashi, H. Kageyama and M. Tabuchi, LiBD–Electrode Materials, abstract # 71, Arcachon, France, 2001.
27. M. Holzapfel, P. Strobel, C. Darie, J. Wright, M. Morcrette, E. Chappel and M. Anne, J. Mater. Chem., 2004, 14 10.1039/b307671g.
28. M. Balasubramanian, X. Sun, X.G. Yang and J. McBreen, J. Electrochem. Soc., 2000, 147, 2903.
29. I. Nakai and T. Nakagome, Electrochem. Solid State Lett., 1998, 1, 259.
30. W. E. O'Grady, K. I. Pandya, K. E. Swider and D. A. Corrigan, J. Electrochem. Soc., 1996, 143, 1613.
31. A. N. Mansour, J. McBreen and C. A. Melendres, J. Electrochem. Soc., 1999, 146, 2799.
32. A. Ibarra-Palos, P. Strobel, O. Proux, J. L. Hazemann, M. Anne and M. Morcrette, Electrochim. Acta, 2002, 47, 3171.
33. C. R. Horne, U. Bergmann, J. K. Kim, K. A. Striebel, A. Manthiram, S. P. Kramer and E. J. Cairns, J. Electrochem. Soc., 2000, 147, 395.
34. C. Delmas, G. Prado, A. Rougier and E. Suard, Solid State Ionics, 2000, 135, 71.
35. A. Filipponi, M. Borowski, D. T. Bowron, S. Ansell, S. De Panfilis, A. Di Cicco and J. P. Itié, Rev. Sci. Instrum., 2000, 71, 2422.
36. D. Aberdam, J. Synchrotron Radiat., 1998, 5, 1287.
37. M. Newville, P. Livins, Y. Yacoby, J. J. Rehr and E. A. Stern, Phys. Rev. B, 1993, 47, 14126.
38. I. J. Pickering, G. N. George, J. T. Lewandowski and A. J. Jacobson, J. Am. Chem. Soc., 1993, 115, 4137.
39. A. Manceau, A. I. Gorshkov and V. A. Drits, Am. Mineral., 1992, 77, 1133.
40. M. C. Martins Alves, J. P. Dodelet, G. Duay, M. Ladouceur and G. Tourillon, J. Phys. Chem., 1992, 96, 10898.
41. W. S. Yoon, K. K. Lee and K. B. Kim, J. Electrochem. Soc., 2002, 149, A146.
42. J. H. Choy, D. K. Kim, S. H. Hwang and G. Demazeau, Phys. Rev. B, 1994, 50, 16631.
43. M. Morcrette, P. Barboux, J. Perrière, T. Brousse, A. Traverse and J. P. Boilot, Solid State Ionics, 2001, 138, 213.
44. J. Garcia, M. C. Sanchez, G. Subias and J. Blasco, J. Phys.: Condens. Matter., 2001, 13, 3229.
45. M. Wilke, F. Farges, P. E. Petit, G. E. Brown, Jr. and F. Martin, Am. Mineral., 2001, 86, 714.
46. G. Dräger, R. Frahm, G. Materlik and O. Brummer, Phys. Status Solidi B, 1988, 146, 287.
47. T. E. Westre, P. Kennepohl, J. de Witt, B. Hedman, K. O. Hodgson and E. I. Solomon, J. Am. Chem. Soc., 1997, 119, 6297.
48. M. Y. Apte and C. Mande, J. Phys. C: Solid State Phys., 1980, 41, 307.
49. P. E. Petit, F. Farges, M. Wilke and V. A. Solé, J. Synchrotron Radiat., 2001, 8, 952.
50. M. Belli, A. Scafati, A. Bianconi, S. Mobilio, L. Palladino, A. Reale and E. Burattini, Solid State Comm., 1980, 38, 355.
51. A. N. Mansour, X. Q. Yang, X. Sun, J. McBreen, L. Croguennec and C. Delmas, J. Electrochem. Soc., 2000, 147, 2104.
52. T. Nonaka, C. Okuda, Y. Ukyo and T. Okamoto, J. Synchrotron Radiat., 2001, 8, 869.
53. R. D. Shannon, Acta Crystallogr., Sect. A, 1976, 32, 751.
54. I. Saadoune and C. Delmas, J. Solid State Chem., 1998, 136, 8.
55. G. Prado, L. Fournès and C. Delmas, Solid State Ionics, 2000, 138, 19.

---

Footnotes

† Part 1: ref. 27.

‡ Present address: Paul-Scherrer-Institut, CH-5232 Villigen PSI. E-mail: michael.holzapfel@psi.ch; Fax: +41.(0)56.310.4415; Tel: +41.(0)56.310.2116.

§ Present address: Herzogstr. 60, D-80803 München.

---