First local minimum of the formic acid dimer exhibits simultaneously red-shifted O–H⋯O and improper blue-shifted C–H⋯O hydrogen bonds
Jana
Chocholoušová
,
Vladimír
Špirko
and
Pavel
Hobza
*
J. Heyrovský Institute of Physical Chemistry, Academy of Sciences of the Czech Republic and Center for Complex Molecular Systems and Biomolecules, 18223 Prague 8, Czech Republic. E-mail: hobza@indy.jh-inst.cas.cz
First published on 25th November 2003
Abstract
The first local minimum of the formic acid dimer exhibits simultaneously red-shifted O–H⋯O and blue-shifted C–H⋯O hydrogen bonds. The improper, blue-shifted hydrogen bond was investigated by means of the NBO analysis, rehybridization model and optimization in the electric field. It was shown that the electrostatic model cannot describe the nature of the blue-shifted H-bond. From the NBO analysis it becomes evident that the formation of the O–H⋯O hydrogen bond and C–H⋯O improper hydrogen bond can be explained on the basis of an increase of electron density in the σ* antibonding O–H orbital and a decrease of electron density in the σ* antibonding C–H orbital. While the former effect is easily explained on the basis of hyperconjugation, the latter requires the existence of a new mesomeric structure characterized by delocalization of electron density from the C–H σ* antibonding orbital to the remaining part of the complex. The rehybridization model explains properly the formation of both hydrogen bonds but fails to interpret the changes of the other bonds.
I. Introduction
The potential energy surface of the formic acid dimer was investigated recently1 and it was shown that the cyclic structure (structure I in Fig. 1) possessing two O–H⋯O hydrogen (H)- bonds corresponds to the global minimum. This structure exists in a gas phase and nonpolar solvent but, surprisingly, not in helium droplets.2 The first local minimum (structure II in Fig. 1) is by about 5.5 kcal mol−1 less stable and coexists with structure I at low temperatures.1 Its population increases with temperature and is has a greater population than structure I at room temperature. Structure I of the dimer was detected in Ar matrix experiments3 and when the temperature was increased from 7 K to 40 K the existence of structure II was proved. Structure I is characterized by two very strong O–H⋯O H-bonds with typical large red-shifts of O–H stretch vibration frequencies. On the other hand structure II possesses one O–H⋯O and one C–H⋯O contacts and exhibits simultaneously the red-shifted H-bond (former contact) and blue-shifted H-bond (latter contact). The existence of blue-shifted H-bond in this dimer is surprising since it was mostly connected with C–H hydrogen donors containing halogen atoms and it was even speculated that this is a necessary condition for the existence of this unusual H-bond.4 The aim of the present work is to examine the spectral manifestation of both contacts and explain the nature of each.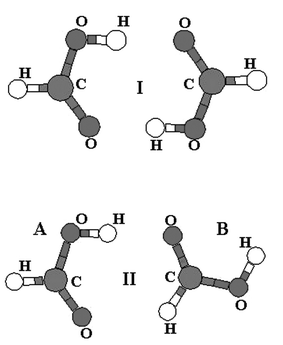 | ||
| Fig. 1 Structures of the global (I) and first local (II) minima of the formic acid dimer; subsystems A and B are designated with reference to structure II. | ||
II. Blue-shifted H-bonding
Improper blue-shifted H-bonds were first observed experimentally5–7 and theoretically4 for C–H hydrogen donors. Later this unusual H-bonding, exhibiting a manifestation opposite the standard H-bonding (contraction of the X–H bond instead of elongation, and blue-shift of the X–H stretch vibration frequency instead of red-shift), was also found for other types of hydrogen donors (F–H,9 N–H,8,10 Si–H,10 P–H10). Existing literature on blue-shifted H-bonding is already extensive and we will mention only a few recent studies explaining the nature of improper H-bonding. Schlegel et al.10 explained the blue-shifted H-bonding mainly in terms of electrostatic interaction and a balance between electrostatic attraction and Pauli repulsion. Similarly, Hermansson11 showed that reasons for improper, blue-shifted H-bonds are neither electron transfer shifts nor dispersion interactions but the sign of the dipole moment derivative for the isolated hydrogen donor combined with an electronic exchange overlap. Similarly Scheiner et al.12 and Masunov et al.13 concluded that there are no fundamental differences between standard and improper H-bonding and explained the differences solely on the basis of different behavior in the electric field. We are certainly aware of the role of negative dipole moment derivatives (the dipole moment of a subsystem increased upon contraction of a X–H bond) and we were the first to demonstrate it14 but we have also shown the limits of explaining improper H-bonding solely on the basis of the electric field.15 Certainly all of the arguments presented10–12 are justified but they do not explain all of the features and manifestations of improper H-bonding. The first dimer by we theoretically proved the existence of improper H-bonding was the benzene dimer16 (experiments are still uncompleted) but the benzene monomer did not exhibit the negative sign of the dipole moment derivative. The benzene dipole moment (zero at the optimum geometry) becomes larger upon elongation of the C–H bond than upon its contraction. Further, the dispersion energy is decisive for the sole existence of the dimer and without it any bonding (standard H-bonding or improper H-bonding) cannot exist. Further, we recently studied the guanine dimer,17 which exhibits a rather large blue-shift of the amino N–H stretch vibration frequency. It is true that planarization of the amino group in the guanine monomer exhibits a negative sign of the dipole moment derivative (the planar system, which is less stable energetically, has a larger dipole moment than the non-planar structure corresponding to the global minimum) but the problem is that some structures of the dimer having the improper blue-shifted H-bond exhibit dipole–dipole repulsion. This means that the negative sign of the dipole moment derivative is counteracting since it increases dipole–dipole repulsion and, evidently, another stabilizing contribution must take place. Finally, when shortening the O–H bond (by 0.1 Å) of the formic acid monomer, one obtains a decrease of the dipole moment (from 1.31 D to 1.29 D) and when similarly shortening the C–H bond the dipole moment is not changed. A new insight into the nature of improper, blue-shifted hydrogen bonding was presented recently by Alabugin et al.18 The authors have shown that improper H-bonding is not an aberration but a consequence of Bent's rule which predicts an increase in the s-character of the hybrid AO of the X–H bond upon X–H⋯Y hydrogen bond formation. The reason for this is the fact that hydrogen becomes more electropositive. It was shown that this “rehybridization” model describes all types of improper H-bonding including the O–H⋯Y one.III. Computations
The structure and harmonic vibration frequencies of the monomer, and dimer structures I and II (see Fig. 1) were studied using the second order Møller–Plesset (MP2) method with the cc-pVTZ basis set. This basis set is known to provide reasonable characteristics of hydrogen bonded systems since it contains first and second sets of polarization functions. It is well balanced and can therefore be used for geometry optimization. The stabilization energy of a dimer was determined at the same theoretical level adopting the function counterpoise method. The deformation energies were subtracted; these were calculated as the difference of the energy of the optimized subsystem and the energies of subsystems of the same geometry as within the complex.The natural bond orbital (NBO) analysis yields reliable values only if the wavefunction is fully defined, in other words, for use with either Hartree–Fock or density functional theory (DFT) wavefunctions. The NBO analysis performed at the MP2 level does not provide energy of hyperconjugative interaction (more later). In the present paper the NBO analysis was performed at the DFT/B3LYP/cc-pVTZ level using MP2-FC (frozen core)/cc-pVTZ geometries. The use of the DFT method is justified as the dispersion contribution (not covered by the DFT approach) is not significant regarding hydrogen bonded dimers. The interaction between filled orbitals of one subsystem and vacant orbitals of another subsystem represents a deviation of the complex from the Lewis structure and can be used as a measure of the intermolecular delocalization, also called hyperconjugation. The hyperconjugative interaction energy can be deduced from the second-order perturbation approach
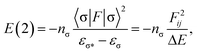 | (1) |
To establish the influence of the electrostatic field, the geometry of one subsystem was optimized in the electrostatic field of the other one which was generated by point charges evaluated by the Kollman–Merz procedure.19
The harmonic vibration frequencies, determined at the MP2/cc-pVTZ level, were scaled by the recommended factor of 0.943.20 The harmonic approach is limited with respect to formic acid and the vibration frequencies were therefore also determined at the anharmonic level. The anharmonic vibrational energies pertaining to the X–H (X![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O and C) stretching motions of the formic acid fragments were found as eigenvalues of the following one-dimensional Hamiltonians
O and C) stretching motions of the formic acid fragments were found as eigenvalues of the following one-dimensional Hamiltonians
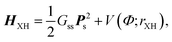 | (2) |
All calculations were performed with the Gaussian 98 suite of programs.21
IV. Results and discussion
a. Geometry, energy and vibration characteristics
Geometrical characteristics of formic acid monomer and formic acid dimer structures I and II are summarized in Table 1. Stabilization energy of structure I (the global minimum) is 14.23 kcal mol−1 which is about 5.8 kcal mol−1 more than that of the first local minimum, structure II (8.39 kcal mol−1). By examining Table 1 it becomes evident that O–H and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds in structure I are significantly elongated while C–O bonds are shortened. The C–H bonds are also shortened but to a negligible extent. These results support formation of two strong O–H⋯O
O bonds in structure I are significantly elongated while C–O bonds are shortened. The C–H bonds are also shortened but to a negligible extent. These results support formation of two strong O–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds characterized by the elongation of both chemical bonds. The harmonic vibration analysis (Table 2) supports the above mentioned results. Structure I exhibits a significant lowering of the O–H stretch frequencies; the red shift amounts to 587 and 490 cm−1 for symmetric and asymmetric stretch vibrations, respectively. The C–H stretch frequencies are almost untouched upon dimerization and their changes amount to −11 and +15 cm−1 for symmetric and asymmetric stretch vibrations, respectively.
C bonds characterized by the elongation of both chemical bonds. The harmonic vibration analysis (Table 2) supports the above mentioned results. Structure I exhibits a significant lowering of the O–H stretch frequencies; the red shift amounts to 587 and 490 cm−1 for symmetric and asymmetric stretch vibrations, respectively. The C–H stretch frequencies are almost untouched upon dimerization and their changes amount to −11 and +15 cm−1 for symmetric and asymmetric stretch vibrations, respectively.
| Parameter | Monomer | Global minimumab (I) | First local minimum (II)b |
|---|---|---|---|
| a Units A and B are identical. b Cf. Fig. 1. | |||
| Unit A | |||
| C–H | 1.092 | 1.091 | 1.093 |
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
1.203 | 1.222 | 1.211 |
| C–O | 1.345 | 1.311 | 1.327 |
| O–H | 0.969 | 0.999 | 0.987 |
| Unit B | |||
| C–H | 1.092 | 1.091 | 1.088 |
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
1.203 | 1.222 | 1.214 |
| C–O | 1.345 | 1.311 | 1.332 |
| O–H | 0.969 | 0.999 | 0.970 |
| Unit A | |||
H–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
125.3 | 121.8 | 123.5 |
| H–C–O | 109.5 | 111.6 | 110.4 |
| C–O–H | 106.0 | 109.4 | 108.1 |
| O–C–O | 125.1 | 126.6 | 126.1 |
| Unit B | |||
H–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
125.3 | 121.8 | 124.0 |
| H–C–O | 109.5 | 111.6 | 112.2 |
| C–O–H | 106.0 | 109.4 | 106.7 |
| O–C–O | 125.1 | 126.6 | 123.8 |
| Monomera | Global minimum (I)a | First local minimum (II)a | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ν harm | ν scharm | ν 1Dharm | ν 1Danharm | ν harm | ν scharm | ν 1Dharm | ν 1Danharm | ν harm | ν scharm | ν 1Dharm | ν 1Danharm | |
| a cf. Fig. 1 b Symmetric vibration c Antisymmetric vibration d Free XH stretch e Bound XH stretch | ||||||||||||
| OH | 3762 | 3548 | 3749 | 3582 | 3142b | 2961b | 3104b | 2991b | 3757d | 3543d | —d | —d |
| OH | — | — | — | — | 3245c | 3058c | —c | —c | 3407e | 3213e | 3399e | 2993e |
| CH | 3125 | 2947 | 3120 | 3003 | 3115b | 2936b | —b | —b | 3110d | 2933d | —d | —d |
| CH | — | — | — | — | 3130c | 2952c | 3134c | 3018c | 3180e | 2999e | 3170e | 3058e |
The situation in structure II is more complicated. One of the O–H⋯O motifs remains and again both O–H and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds are elongated. Both elongations are, however, smaller than those in structure I. The second bonding motif is of the C–H⋯O type. Here, again, the C
O bonds are elongated. Both elongations are, however, smaller than those in structure I. The second bonding motif is of the C–H⋯O type. Here, again, the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond is elongated but, surprisingly, the C–H bond is contracted and the contraction is not negligible. Both C–O bonds are, similar to structure I, contracted. The stretch vibration frequency of the free OH is practically unchanged while that of bound OH (asymmetric stretch) is red-shifted by 335 cm−1. The smaller red-shift in comparison with the red shifts in structure I is in accord with the smaller elongation of the O–H bond in structure II and also with smaller stabilization energy in structure II. The bound C–H stretch frequency is blue-shifted by 52 cm−1 while the free C–H stretch frequency is slightly red-shifted.
O bond is elongated but, surprisingly, the C–H bond is contracted and the contraction is not negligible. Both C–O bonds are, similar to structure I, contracted. The stretch vibration frequency of the free OH is practically unchanged while that of bound OH (asymmetric stretch) is red-shifted by 335 cm−1. The smaller red-shift in comparison with the red shifts in structure I is in accord with the smaller elongation of the O–H bond in structure II and also with smaller stabilization energy in structure II. The bound C–H stretch frequency is blue-shifted by 52 cm−1 while the free C–H stretch frequency is slightly red-shifted.
The anharmonic calculations were performed to check whether the harmonic analysis gives reasonable results especially for changes in vibration frequencies upon complexation. In Table 2 we can see that harmonic frequencies evaluated from the full analytical treatment and 1-D approximation agree reasonably well and supports the reliability of the 1-D anharmonic approximation. Table 2 further shows that anharmonicity affects the shift of OH frequency significantly. In the case of structure I the anharmonic red-shift is by 4 cm−1 larger than the shift from the harmonic, while for structure II it is by 254 cm−1 larger. Table 2 tells us, however, that the CH vibration is not affected by the anharmonic contributions. The CH vibration frequency shifts in structure I using harmonic and anharmonic approximations are +5 cm−1 and +15 cm−1, respectively. For structure II, the harmonic CH is blue-shifted by 52 cm−1 while the anharmonic blue shift is 55 cm−1. It is thus possible to rely on the harmonic approximation when describing the CH vibrations, while for OH vibrations, the anharmonicity should be considered. Let us recall here that blue shifts of C–H stretch frequencies of benzene upon formation of the T-shaped benzene dimer evaluated at harmonic and anharmonic levels were also practically identical.16
b. NBO analysis
To interpret and explain the above mentioned vibration frequency changes occurring upon dimerization, we performed the NBO analysis using the DFT wave functions and the respective results are presented in Tables 3 and 4. The situation with structure I is straightforward. The largest increase of electron density (ED) occurred at C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O σ* and the antibonding orbitals π* and O–H σ*. Consequently, these bonds become weaker and are elongated, and the respective stretch vibration frequencies are red-shifted. The principal donor of ED are lone electron pairs of carbonyl oxygens and this is why the C
O σ* and the antibonding orbitals π* and O–H σ*. Consequently, these bonds become weaker and are elongated, and the respective stretch vibration frequencies are red-shifted. The principal donor of ED are lone electron pairs of carbonyl oxygens and this is why the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds become weaker and are elongated. The increase of ED in the C–O bonding orbitals is in an opposite direction but these changes are smaller than those discussed above. Further, the ED in the C1–O4 σ* antibonding orbitals decreased upon dimerization which yields to strengthening the bond and its contraction. It is, however, difficult to explain this decrease and it can only be interpreted on the basis of intramolecular polarization and conjugation (more later). Analyzing the perturbation E2 charge-transfer energies (cf.Table 5) we found that their dominant contributions originate from the interaction of the second and first electron lone pairs of carbonyl oxygens and O–H σ* antibonding orbitals (22.08 and 8.63 kcal mol−1). A larger value of the former energy is due to a smaller difference in energies of electron donor and acceptor as well as in a more favorable geometry arrangement of these orbitals reflected by the larger Fij element (cf.Table 5). Neither of the remaining E2 charge transfer energies was larger than 0.5 kcal mol−1. Formation of both strong O–H⋯O H-bonds is thus a textbook example of hyperconjugation between carbonyl oxygen lone electron pairs and O–H σ* antibonding orbitals.
O bonds become weaker and are elongated. The increase of ED in the C–O bonding orbitals is in an opposite direction but these changes are smaller than those discussed above. Further, the ED in the C1–O4 σ* antibonding orbitals decreased upon dimerization which yields to strengthening the bond and its contraction. It is, however, difficult to explain this decrease and it can only be interpreted on the basis of intramolecular polarization and conjugation (more later). Analyzing the perturbation E2 charge-transfer energies (cf.Table 5) we found that their dominant contributions originate from the interaction of the second and first electron lone pairs of carbonyl oxygens and O–H σ* antibonding orbitals (22.08 and 8.63 kcal mol−1). A larger value of the former energy is due to a smaller difference in energies of electron donor and acceptor as well as in a more favorable geometry arrangement of these orbitals reflected by the larger Fij element (cf.Table 5). Neither of the remaining E2 charge transfer energies was larger than 0.5 kcal mol−1. Formation of both strong O–H⋯O H-bonds is thus a textbook example of hyperconjugation between carbonyl oxygen lone electron pairs and O–H σ* antibonding orbitals.
| Unit Ab | |
|---|---|
| a BD, LP and BD* means σ bonding, lone pair, σ*, and π* antibonding AO, respectively. b Both subunits in the symmetrical structure I are identical | |
| BD(C1–O3) | 0.00482 |
| LP1(O3) | −0.02038 |
| LP2(O3) | 0.00676 |
| LP(O4) | −0.00947 |
| BD*(C1–H2) | −0.00755 |
| BD*(C1–O3) | 0.00635 |
| BD*(C1–O3) | 0.05069 |
| BD*(C1–O4) | −0.02644 |
| BD*(C1–H5) | 0.0566 |
| Unit Bb | |
|---|---|
| BD(C7–O8) | 0.00306 |
| LP(O8) | −0.00972 |
| LP(O8) | 0.00727 |
| LP(O9) | −0.01719 |
| BD*(C7–H6) | −0.00938 |
| BD*(C7–O8) | 0.0122 |
| BD*(O4–H5) | −0.016 |
| Donor (i) | Acceptor(j) | E(2)a (kcal mol−1) | E(j)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) − −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E(i)b
(a.u.) E(i)b
(a.u.) |
F(i,j)c (a.u.) |
|---|---|---|---|---|
| a E(2) means energy of hyperconjugative interactions; cf.eqn. 1 b energy difference between donor and acceptor i and j NBO orbitals c F(i,j) is the Fock matrix element between i and j NBO orbitals | ||||
| Structure I | ||||
| From unit 1 to unit 2 | ||||
| LP(1) O3 | BD*(1) O8–H9 | 8.63 | 1.10 | 0.088 |
| LP(2) O3 | BD*(1) O8–H9 | 22.08 | 0.70 | 0.114 |
| From unit 2 to unit 1 | ||||
| LP (1) O7 | BD*(1) O4–H5 | 8.63 | 1.10 | 0.088 |
| LP (2) O7 | BD*(1) O4–H5 | 22.08 | 0.70 | 0.114 |
| Structure II | ||||
| From unit 1 to unit 2 | ||||
| LP(1) O3 | BD*(1) H6–C7 | 0.63 | 1.08 | 0.024 |
| LP(2) O3 | BD*(1) H6–C7 | 0.98 | 0.62 | 0.023 |
| From unit 2 to unit 1 | ||||
| LP(1) O8 | BD*(1) O4–H5 | 4.77 | 1.16 | 0.067 |
| LP(2) O8 | BD*(1) O4–H5 | 14.13 | 0.72 | 0.092 |
Formation of the O–H⋯O H-bond in structure II is similar to structure I. From Table 4 it becomes evident that now the ED also increased in C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and O–H σ* antibonding orbitals which leads to a weakening and elongation of these bonds though to a lesser extent than in structure I. Similarly as in the case of structure I the first lone pair of O8 is the important electron donor (which yields to a further weakening of the C
O and O–H σ* antibonding orbitals which leads to a weakening and elongation of these bonds though to a lesser extent than in structure I. Similarly as in the case of structure I the first lone pair of O8 is the important electron donor (which yields to a further weakening of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond) but from the table it becomes clear that a larger decrease of ED occurred from lone electron pair of O9. The C–H⋯O contact is associated with the ED increase at the lone electron pair of O3 as well as at the bonding orbitals of the C2
O bond) but from the table it becomes clear that a larger decrease of ED occurred from lone electron pair of O9. The C–H⋯O contact is associated with the ED increase at the lone electron pair of O3 as well as at the bonding orbitals of the C2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O3 carbonyl bond. Both these changes indicate strengthening and contraction of the bond. The ED in the C7–H6 σ* antibonding orbitals decreased upon dimerization which unambiguously meant strengthening and contraction of the bond and a blue-shift of the respective stretch vibration frequency.
O3 carbonyl bond. Both these changes indicate strengthening and contraction of the bond. The ED in the C7–H6 σ* antibonding orbitals decreased upon dimerization which unambiguously meant strengthening and contraction of the bond and a blue-shift of the respective stretch vibration frequency.
To this point, the NBO results fully explain the found red as well as the blue vibration frequency shifts in both dimer structures. The question arising, however, is how to explain the ED decrease in the C7–H6 σ* antibonding orbitals of structure II. Investigating the E2 energies (Table 5), we found large participation from the above discussed LP(O8)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ*(O–H) terms. The LP(O3)
σ*(O–H) terms. The LP(O3)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ*(C–H) contributions are smaller but definitely not negligible and give clear evidence of stabilization originating in the hyperconjugation between lone electron pair of O3 and C–H σ* antibonding orbitals. The consequence of this interaction should be an ED increase in the respective antibonding orbitals leading to the weakening of the respective bond. Investigating Table 4 we, however, found the opposite. The ED in the C7–H6 σ* antibonding orbitals decreased. The only possible scenario is the following: the ED is transferred from the LP(O3) to the σ*
(C–H) orbitals but then, in a second step, further. Do we have any evidence about this transfer? The answer is yes. First, the energy of C–H σ* antibonding orbital (0.35 Eh) in this subsystem (B) is higher than the energy of C–O σ* antibonding orbital (0.34 Eh) which supports the likelihood of the delocalization of ED from the C–H to the C–O region. (The energy of the C–H σ* antibonding orbital in subsystem A is lower than that of C–O σ* antibonding orbital (0.34 Ehvs. 0.38 Eh)). Furthermore, both C–H and C–O σ* antibonding orbitals can interact with a lone electron pair of O8 which is supported by the corresponding perturbation E2 energies within subsystem B which are very large (15.2 and 29.8 kcal mol−1).
σ*(C–H) contributions are smaller but definitely not negligible and give clear evidence of stabilization originating in the hyperconjugation between lone electron pair of O3 and C–H σ* antibonding orbitals. The consequence of this interaction should be an ED increase in the respective antibonding orbitals leading to the weakening of the respective bond. Investigating Table 4 we, however, found the opposite. The ED in the C7–H6 σ* antibonding orbitals decreased. The only possible scenario is the following: the ED is transferred from the LP(O3) to the σ*
(C–H) orbitals but then, in a second step, further. Do we have any evidence about this transfer? The answer is yes. First, the energy of C–H σ* antibonding orbital (0.35 Eh) in this subsystem (B) is higher than the energy of C–O σ* antibonding orbital (0.34 Eh) which supports the likelihood of the delocalization of ED from the C–H to the C–O region. (The energy of the C–H σ* antibonding orbital in subsystem A is lower than that of C–O σ* antibonding orbital (0.34 Ehvs. 0.38 Eh)). Furthermore, both C–H and C–O σ* antibonding orbitals can interact with a lone electron pair of O8 which is supported by the corresponding perturbation E2 energies within subsystem B which are very large (15.2 and 29.8 kcal mol−1).
To summarize, we expect the ED transfer first from LP(O3) to the σ* (C–H) orbitals and then either through a C–O σ* antibonding orbital to, or directly to LP(O8). In agreement with the mechanism proposed, the total charge on O8 increased upon dimerization by 0.057 e while that at the O3 increased only by 0.052 e. We wish to reiterate that these values contradict expectations since the O8⋯O–H interaction is stronger than O3⋯C–H and, therefore, a larger portion of ED is expected to be transferred from O8 than O3. Therefore, we can conclude that the unexpected blue-shift of the C–H stretch vibration frequency is due to a significant rearrangement of electrons in the donor characterized by a decrease of ED in the C7–H6 σ* antibonding orbitals. This formally resembles the situation in the guanine dimer characteristic by a blue shift of amino N–H stretch frequencies due to the decrease of ED at the amino nitrogen lone electron pair. This decrease was explained by improved conjugation where the amino group was planar over the non planar.
c. Role of electric field
Table 6 shows the geometry parameters of subsystems A and B of structure II optimized in the electric field of subsystem B and A, respectively. The particular changes are much larger than those found in the fully optimized dimer (values in parenthesis). The O–H bond in unit A is elongated by an electric field of subsystem B by unrealistic 0.203 Å while the C–H bond in subsystem B is contracted by an electric field of subsystem A by (again unrealistic) 0.107 Å. The corresponding values obtained from the fully optimized dimer are +0.018 and −0.004 Å, i.e., by more than one order of magnitude smaller. The C–O bond in both units is contracted in the dimer systematically while the electric field brings systematic elongation. The overall picture obtained from optimization in an electric field is entirely different from that found in full optimization and, apparently, the electrostatic approximation in this particular case fails completely.| Unit A | |
|---|---|
| C–H | 1.224 (1.093) |
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
1.217 (1.211) |
| C–O | 1.338 (1.338) |
| O–H | 1.252 (0.987) |
| Unit B | |
|---|---|
| C–H | 1.092 (1.088) |
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
1.201 (1.214) |
| C–O | 1.332 (1.332) |
| O–H | 0.971 (0.971) |
d. Rehybridization
Table 7 shows the changes of hybridization of the O–H and C–H hybrid orbitals in structures I and II. The perturbation E2 energies obtained for structure I (cf.Table 5) are very large, much larger than the 5 kcal mol−1 threshold (see ref. 18), which indicates the dominant role of the hyperconjugation. The same is true for O–H⋯O contact in structure II. Consequently, the lowering of the p-character of the O–H hybrid orbitals (which should lead to contraction of these bonds) is overbalanced by the hyperconjugation effect.| Monomer | Global minimum | Structure II | |
|---|---|---|---|
| a The changes presented are in the σ hybrid orbitals only. | |||
| Unit A | |||
| H–C | C(sp1.88) | C(sp1.97) | C(sp1.95) |
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Oa Oa |
C(sp1.75) | C(sp1.81) | C(sp1.77) |
| C–O | C(sp2.37) | C(sp2.19) | C(sp2.26) |
| O–H | O(sp3.59) | O(sp2.79) | O(sp2.91) |
| Unit B | |||
| H–C | C(sp1.97) | C(sp1.78) | |
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Oa Oa |
C(sp1.81) | O(sp1.85) | |
| C–O | C(sp2.19) | C(sp2.37) | |
| O–H | O(sp2.79) | O(sp3.61) | |
The situation in the C–H⋯O contact in structure II is different. The E2 energy is now well below the threshold mentioned which indicates that rehybridization will play the dominant role. Table 7 shows that the p-character of the C–H in unit B (bound CH) decreased from sp1.88 (isolated monomer) to sp1.78 which strengthens the bond and a concominant blue-shift of the respective C–H stretch frequency. As regards the free CH bond (unit A) the p-character of the hybrid orbital increased which indicates bond weakening and its elongation. From Table 1 it becomes evident that small elongation was in fact observed.
A different situation exists for CH bonds in the global minimum. Here the p-character of the CH hybrid orbital increased (by the same amount as the bound CH hybrid orbital in structure II decreased), which supports bond weakening and elongation but the bond become shorter. On the other hand the NBO analysis correctly shows the decrease of ED in the CH σ* antibonding orbital which indicates strengthening and contraction of the bond. This ED decrease occurred as a consequence of the formation of a new mesomeric state (see above).
V. Conclusions
The first local minimum of the formic acid dimer (structure II) exhibits simultaneously the O–H⋯O red-shifted hydrogen bond and C–H⋯O blue-shifted improper hydrogen bond. NBO analysis fully interprets these findings and provides an increase of ED in the σ* antibonding orbital of the OH bond and a decrease of ED in the σ* orbital of the CH bond. The former effect can be easily explained on the basis of hyperconjugation. The latter requires adoption of the existence of mesomeric structure characterized by delocalization of ED from C–H σ* antibonding orbital to the remaining part of the complex. The main features of the mechanism suggested by the NBO analysis are supported by the rehybridization model, but in some cases this model fails. The electrostatic model fails completely in this instance.Acknowledgements
Financial support by the Center for Complex Molecular Systems and Biomolecules, Czech Republic (Project LN00A032 of MSMT CR) is acknowledged.References
- J. Chocholoušová, J. Vacek and P. Hobza, Phys. Chem. Chem. Phys., 2002, 4, 2119 RSC.
- F. Madeja, M. Havenith, K. Nauta, R. E. Miller, J. Chocholoušová and P. Hobza, J. Chem. Phys., submitted Search PubMed.
- M. Gantenberg, M. Halupka and W. Sander, Chem. Eur. J., 2000, 6, 1865 CrossRef CAS.
- P. Hobza and Z. Havlas, Chem. Rev., 2000, 100, 4253 CrossRef CAS.
- G. T. Trudeau, J.-M. Dumas, P. Dupuis, M. Guerin and C. Sandorfy, Top. Curr. Chem., 1980, 93, 91 CAS.
- M. Buděšinský, P. Fiedler and Z. Arnold, Synthesis, 1989, 858 CAS.
- I. E. Bodeskul, I. F. Tsymbal, E. V. Ryltsev, Z. Latajka and A. J. Barnes, J. Mol. Struct., 1997, 167, 435.
- H. Satonaka, K. Abe and M. Hirota, Bull. Chem. Soc. Jpn., 1987, 60, 953 CAS.
- P. Hobza, Int. J. Quantum Chem., 2002, 90, 1071 CrossRef CAS.
- X. Li, L. Liu and H. B. Schlegel, J. Am. Chem. Soc., 2002, 124, 9636.
- K. Hermansson, J. Phys. Chem. A, 2002, 106, 4695 CrossRef CAS.
- Y. Gu, T. Kar and S. Scheiner, J. Am. Chem. Soc., 1999, 121, 9411 CrossRef CAS.
- A. Masunov, J. J. Dannenberg and R. Contreras, J. Phys. Chem. A, 2001, 105, 4737 CrossRef CAS.
- P. Hobza and Z. Havlas, Chem. Phys. Lett., 1999, 303, 447 CrossRef CAS.
- W. Zierkiewicz, D. Michalska, Z. Havlas and P. Hobza, ChemPhysChem, 2002, 3, 511 CrossRef CAS.
- P. Hobza, V. Špirko, H. L. Selzle and E. W. Schlag, J. Phys. Chem., 1998, 102, 2501 Search PubMed.
- P. Hobza and V. Špirko, Phys. Chem. Chem. Phys., 2003, 5, 1290 RSC.
- I. V. Alabugin, M. Manoharan, S. Peabody and F. Weinhold, J. Am. Chem. Soc., 2003, 125, 5973 CrossRef CAS.
- B. H. Besler, K. M. Merz and P. A. Kollman, J. Comput. Chem., 1990, 11, 431 CrossRef CAS.
- S. Scheiner, Hydrogen Bonding, Oxford University Press, New York, 1997 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery Jr., R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Cioslowski, J. V. Ortiz, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, C. Gonzalez, M. Challacombe, P. M. W. Gill, B. G. Johnson, W. Chen, M. W. Wong, J. L. Andres, M. Head-Gordon, E. S. Replogle and J. A. Pople, Gaussian 98, revision A.7, Gaussian, Inc., Pittsburgh, PA, 1998 Search PubMed.
| This journal is © the Owner Societies 2004 |
