Vibrationally excited states of NC4P: millimetre-wave spectroscopy and coupled cluster calculations†
Received
23rd September 2003
, Accepted 3rd November 2003
First published on 20th November 2003
Abstract
A fairly efficient method for the production of the unstable NC4P molecule has been found, based on copyrolysis of phosphorus trichloride and cyclopropyl cyanide. This allowed us to extend the study of the rotational spectrum of NC4P to a large number of vibrationally excited states lying between 450 and 750 cm−1, namely (v5v6v7v8v9)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (00100), (01000), (10000), (00020), (00101), (01001), (00110), and (01010). The strong Fermi resonance which couples the v5
(00100), (01000), (10000), (00020), (00101), (01001), (00110), and (01010). The strong Fermi resonance which couples the v5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and v8
1 and v8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 states and the l-type resonances between the different sublevels of the bending states have been taken into account in the analysis of the spectra. The identification of new excited-state spectra was facilitated by CCSD(T) calculations with the cc-pVQZ basis, which provided accurate predictions for a variety of spectroscopic constants, including harmonic vibrational wavenumbers, vibration–rotation coupling constants and l-type doubling constants. Accurate theoretical predictions for the equilibrium structure and the electric dipole moment of NC4P are also presented.
2 states and the l-type resonances between the different sublevels of the bending states have been taken into account in the analysis of the spectra. The identification of new excited-state spectra was facilitated by CCSD(T) calculations with the cc-pVQZ basis, which provided accurate predictions for a variety of spectroscopic constants, including harmonic vibrational wavenumbers, vibration–rotation coupling constants and l-type doubling constants. Accurate theoretical predictions for the equilibrium structure and the electric dipole moment of NC4P are also presented.
1. Introduction
The carbon chain 1-cyano-4-phosphabutadiyne (NC4P) was first detected by Kroto and coworkers by microwave spectroscopy in the pyrolysis products of a gaseous mixture of phosphorus trichloride (PCl3) and 1-cyanopropyne.1 The old centimetre-wave (cm-wave) measurements of Durrant et al.1 have been recently extended to the millimeter-wave (mm-wave) region, producing NC4P by copyrolysis of PCl3 and ortho-cyanotoluene, which is commercially available.2 The efficiency of this method is very low, and the number of side-products very large, so that mm-wave lines belonging to the ground and low-lying bending state (v8,v9)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (0,1), (0,2), (0,3), (0,4), (1,0), and (1,1) could be only detected and analysed. Subsequent pyrolysis experiments dealing with production of the isoelectronic molecule HC5P have shown that its amount can be greatly enhanced if an aliphatic ring precursor (cyclopentene) is used instead of an aromatic ring precursor (toluene).3, 4 This result motivated us to check whether a similar effect could be exploited to improve also the production of NC4P. We found indeed that if ortho-cyanotoluene is replaced by cyclopropyl cyanide, then a ten times higher concentration of NC4P is obtained, and in addition fewer interfering lines are present in the spectra. The improved production method gave us the possibility of extending the study of the rotational spectra of NC4P to eight further excited states lying approximately between 450 and 750 cm−1 above the vibrational ground state. These are (v5v6v7v8v9)
(0,1), (0,2), (0,3), (0,4), (1,0), and (1,1) could be only detected and analysed. Subsequent pyrolysis experiments dealing with production of the isoelectronic molecule HC5P have shown that its amount can be greatly enhanced if an aliphatic ring precursor (cyclopentene) is used instead of an aromatic ring precursor (toluene).3, 4 This result motivated us to check whether a similar effect could be exploited to improve also the production of NC4P. We found indeed that if ortho-cyanotoluene is replaced by cyclopropyl cyanide, then a ten times higher concentration of NC4P is obtained, and in addition fewer interfering lines are present in the spectra. The improved production method gave us the possibility of extending the study of the rotational spectra of NC4P to eight further excited states lying approximately between 450 and 750 cm−1 above the vibrational ground state. These are (v5v6v7v8v9)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (00100), (01000), (10000), (00020), (00101), (01001), (00110), and (01010).
(00100), (01000), (10000), (00020), (00101), (01001), (00110), and (01010).
The assignment of the new excited-state spectra has been facilitated by theoretical predictions obtained through large-scale coupled cluster calculations. A complete cubic force field has been calculated from which a variety of spectroscopic constants, including harmonic vibrational wavenumbers, vibration–rotation coupling constants and l-type doubling constants, have been obtained. The equilibrium structure and the electric dipole moment of NC4P have been also theoretically evaluated using different methods and basis sets.
The recorded spectra have been analysed taking into account l-type resonances and the Fermi resonance between the v5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and v8
1 and v8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 states. The new measurements allowed us to enlarge considerably the set of spectroscopic parameters experimentally known for this molecule, which now include also the α5, α6, and α7 vibration–rotation coupling constants, the xL(88), xL(79), xL(69), xL(78), and xL(68) anharmonicity constants, the ϕ588 normal coordinate cubic force constant, and the vibrational energy difference between the resonant v5
2 states. The new measurements allowed us to enlarge considerably the set of spectroscopic parameters experimentally known for this molecule, which now include also the α5, α6, and α7 vibration–rotation coupling constants, the xL(88), xL(79), xL(69), xL(78), and xL(68) anharmonicity constants, the ϕ588 normal coordinate cubic force constant, and the vibrational energy difference between the resonant v5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and v8
1 and v8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 states.
2 states.
2. Experimental details
In the present work NC4P has been generated through a high temperature reaction between PCl3 and cyclopropyl cyanide (Aldrich), using the same pyrolysis apparatus employed for a previous mm-wave spectroscopy study.2 The stable precursors were flowed through a quartz tube heated to 1170![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C, which was connected to the absorption cell of the mm-wave spectrometer. The spectra were recorded while pumping continuously the pyrolysis products through the cell. 50 mTorr of cyclopropyl cyanide and 175 mTorr of PCl3 were typically allowed to flow into the quartz reactor, corresponding to a total pressure of ca. 12 mTorr inside the cell. Good spectra of NC4P were also observed when PCl3 was copyrolyzed with crotononitrile (CH3CH
°C, which was connected to the absorption cell of the mm-wave spectrometer. The spectra were recorded while pumping continuously the pyrolysis products through the cell. 50 mTorr of cyclopropyl cyanide and 175 mTorr of PCl3 were typically allowed to flow into the quartz reactor, corresponding to a total pressure of ca. 12 mTorr inside the cell. Good spectra of NC4P were also observed when PCl3 was copyrolyzed with crotononitrile (CH3CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCN), which is as efficient a precursor nearly as cyclopropyl cyanide. The rotational spectra of NC4P were investigated in the frequency range 78–260 GHz using the same source modulation mm-wave spectrometer employed for previous measurements.2
CHCN), which is as efficient a precursor nearly as cyclopropyl cyanide. The rotational spectra of NC4P were investigated in the frequency range 78–260 GHz using the same source modulation mm-wave spectrometer employed for previous measurements.2
3. Coupled cluster calculations
The equilibrium structure of NC4P was calculated by four different methods and two different basis sets. Dunning's correlation consistent cc-pVTZ and cc-pVQZ basis sets5,6 were employed in these calculations. The ab initio methods used are Hartree–Fock self consistent field (SCF), second order perturbation theory according to Møller and Plesset (MP2), coupled cluster (CC) theory with single and double excitation operators (CCSD) and CCSD(T) which includes connected triple substitutions by means of perturbation theory.7 Throughout, the valence electrons were correlated in the post-Hartree–Fock calculations. The program system MOLPRO20008,9 was used in all electronic structure calculations of this work.
Calculated equilibrium bond lengths, total energies and rotational constants for NC4P are listed in Table 1. As is usually observed in systems with conjugated triple bonds (see for example the results for isoelectronic HC5P3), electron correlation effects strongly increase the lengths of the triple bonds, but reduce the lengths of the longer carbon–carbon bonds which are intermediate between single and double bonds. MP2 overestimates the correlation effects in both cases. An accurate equilibrium structure for NC4P was obtained by taking over corrections to the CCSD(T)/cc-pVQZ values, established through our earlier work on HC3P10 and NCCP11
(see also Table II of ref. 3) From the resulting equilibrium bond lengths given in the last line of Table 1, an equilibrium rotational constant of Be![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 873.1 MHz was obtained.
873.1 MHz was obtained.
Table 1
Ab initio equilibrium bond lengths (in Å), total energies and equilibrium rotational constants for NC4P
| Method |
Basis |
R
1e(NC(1)) |
R
2e(C(1)C(2)) |
R
3e(C(2)C(3)) |
R
4e(C(3)C(4)) |
R
5e(C(4)P) |
V
e/Eh |
B
e/MHz |
| SCF |
cc-pVTZ |
1.1289 |
1.3819 |
1.1866 |
1.3759 |
1.5173 |
−546.617596 |
888.9 |
| |
cc-pVQZ |
1.1276 |
1.3824 |
1.1853 |
1.3762 |
1.5137 |
−546.635045 |
890.3 |
| MP2 |
cc-pVTZ |
1.1812 |
1.3601 |
1.2345 |
1.3619 |
1.5798 |
−547.538103 |
859.2 |
| |
cc-pVQZ |
1.1781 |
1.3589 |
1.2316 |
1.3501 |
1.5738 |
−547.611777 |
866.0 |
| CCSD |
cc-pVTZ |
1.1590 |
1.3790 |
1.2131 |
1.3722 |
1.5508 |
−547.529772 |
868.8 |
| |
cc-pVQZ |
1.1555 |
1.3778 |
1.2097 |
1.3705 |
1.5443 |
−547.593092 |
872.9 |
| CCSD(T) |
cc-pVTZ |
1.1692 |
1.3743 |
1.2248 |
1.3658 |
1.5659 |
−547.591546 |
862.8 |
| |
cc-pVQZ |
1.1657 |
1.3729 |
1.2214 |
1.3639 |
1.5593 |
−547.658995 |
867.0 |
| Recommended |
|
1.1630 |
1.3680 |
1.2182 |
1.3590 |
1.5524 |
|
873.1 |
The complete cubic force field of NC4P was calculated by CCSD(T) with the cc-pVQZ basis set which comprises 364 contracted Gaussian type orbitals (cGTOs). The derived harmonic vibrational wavenumbers, vibration–rotation coupling constants, l-type doubling constants and the equilibrium quartic centrifugal distortion constant are reported in Table 2 for the normal isotopic species. As is usually observed for semirigid linear molecules the vibration–rotation coupling constants for stretching vibrations (αs, s![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1–5) have positive sign, while those of the bending vibrations (αt, t
1–5) have positive sign, while those of the bending vibrations (αt, t![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6–9) have negative sign. In the same Table 2 the calculated difference between the equilibrium and the ground-state rotational constant is reported:
6–9) have negative sign. In the same Table 2 the calculated difference between the equilibrium and the ground-state rotational constant is reported:
| | 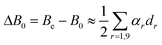 | (1) |
where
dr is the degeneracy factor of each vibrational mode.
Table 2 CCSD(T)/cc-pVQZ spectroscopic constants for NC4P.
|
See the text.
|
|
ω
1/cm−1 |
2281.5 |
α
1/MHz |
2.154 |
q
e6/MHz |
(0.007)a |
|
ω
2/cm−1 |
2159.8 |
α
2/MHz |
2.284 |
q
e7/MHz |
0.141 |
|
ω
3/cm−1 |
1591.3 |
α
3/MHz |
2.864 |
q
e8/MHz |
0.228 |
|
ω
4/cm−1 |
1022.1 |
α
4/MHz |
1.587 |
q
e9/MHz |
0.574 |
|
ω
5/cm−1 |
496.5 |
α
5/MHz |
(0.716)a |
|
|
|
ω
6/cm−1 |
501.5 |
α
6/MHz |
(−1.175)a |
q
6J/Hz |
(1.346)a |
|
ω
7/cm−1 |
459.6 |
α
7/MHz |
−0.995 |
q
7J/Hz |
−0.008 |
|
ω
8/cm−1 |
236.4 |
α
8/MHz |
−1.604 |
q
8J/Hz |
−0.055 |
|
ω
9/cm−1 |
90.1 |
α
9/MHz |
−1.690 |
q
9J/Hz |
−0.370 |
| |
|
ΔB0/MHz |
−0.661 |
D
e/Hz |
11.6 |
Combining the Be value obtained from the recommended equilibrium geometry with the ΔB0 value reported in Table 2, a ground-state rotational constant B0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 873.7 MHz results. It is only 0.2 MHz larger than the experimental value1,2 and thus gives support to the present recommended equilibrium structure.
873.7 MHz results. It is only 0.2 MHz larger than the experimental value1,2 and thus gives support to the present recommended equilibrium structure.
An extensive theoretical investigation of the electric dipole moment of NC4P (for which an approximate evaluation was only reported by Durrant et al.1) has been also carried out, and the results are summarized in Table 3. Three different basis have been used, which are the aug-cc-pVTZ and aug-cc-pVQZ basis sets of Dunning and coworkers5,6,12 plus an intermediate set termed “avqz-g” in Table 3, which corresponds to the aug-cc-pVQZ set exclusive of g functions. The CCSD(T) calculations with the largest basis are expected to produce the most reliable result, μe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.865 D. The dipole moment in the vibrational ground state may well differ from this value by a few hundredths of a Debye.
3.865 D. The dipole moment in the vibrational ground state may well differ from this value by a few hundredths of a Debye.
Table 3 Calculated equilibrium dipole moments for NC4P (in D)a
| Method |
Basisb |
μ
e
|
|
Throughout, electric dipole moments are evaluated at the recommended equilibrium structure from this work.
An obvious shorthand notation is employed to designate the basis sets; e.g., “avqz-g” stands for aug-cc-pVQZ exclusive of g functions.
|
| SCF |
avtz |
4.504 |
| SCF |
avqz-g |
4.532 |
| SCF |
avqz |
4.532 |
| MP2 |
avtz |
3.647 |
| MP2 |
avqz-g |
3.679 |
| MP2 |
avqz |
3.680 |
| CCSD |
avtz |
3.980 |
| CCSD |
avqz-g |
4.013 |
| CCSD |
avqz |
4.023 |
| CCSD(T) |
avtz |
3.829 |
| CCSD(T) |
avqz-g |
3.860 |
| CCSD(T) |
avqz |
3.865 |
4. Observed spectra and analysis
We have investigated rotational spectra of NC4P in the (v5v6v7v8v9)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (00100), (01000), (10000), (00020), (00101), (01001), (00110), and (01010) excited states. Partial cm-wave frequency data were only available for the (00020) state,1 for which we have extended the measurements to the mm-wave region, reaching a frequency as high as 260 GHz. On the contrary, no experimental information was available for all other states, whose mm-wave spectra have been assigned in the frequency range 78–190 GHz. With only the exception of the (10000) stretching state, all the states investigated involve excitation of at least one bending quantum, so that multiplets of rotational lines were always recorded for each J
(00100), (01000), (10000), (00020), (00101), (01001), (00110), and (01010) excited states. Partial cm-wave frequency data were only available for the (00020) state,1 for which we have extended the measurements to the mm-wave region, reaching a frequency as high as 260 GHz. On the contrary, no experimental information was available for all other states, whose mm-wave spectra have been assigned in the frequency range 78–190 GHz. With only the exception of the (10000) stretching state, all the states investigated involve excitation of at least one bending quantum, so that multiplets of rotational lines were always recorded for each J![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ←
←![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) J transition, owing to l-type resonance effects between the different l sublevels. The spectra have been analysed using the same formalism originally developed by Yamada et al.13 and already employed to fit the excited-state rotational spectra of HC3P14 and NCCP.15 Briefly, the ro-vibrational Hamiltonian is first represented using the unsymmetrized basis functions
J transition, owing to l-type resonance effects between the different l sublevels. The spectra have been analysed using the same formalism originally developed by Yamada et al.13 and already employed to fit the excited-state rotational spectra of HC3P14 and NCCP.15 Briefly, the ro-vibrational Hamiltonian is first represented using the unsymmetrized basis functions  , where k
, where k![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) l6
l6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) l7
l7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) l8
l8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) l9. Employing the simplified notation |l6,l7,l8,l9;k〉, the elements of the Hamiltonian matrix which are diagonal in the quantum numbers vt and lt are:
l9. Employing the simplified notation |l6,l7,l8,l9;k〉, the elements of the Hamiltonian matrix which are diagonal in the quantum numbers vt and lt are: | |  | (2) |
where Gv is the vibrational energy of the state.
The off-diagonal rotational l-type doubling terms (Δlt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±2, Δk
±2, Δk![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±2) have the general form:
±2) have the general form:
| |  | (3) |
while the off-diagonal vibrational
l-type doubling terms (Δ
lt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
=
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
±
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
2, Δ
lt′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
=
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
∓2, Δ
k![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
=
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
0) have the expression:
| |  | (4) |
In addition to
l-type resonance effects, the Fermi resonance which originates from the normal coordinate cubic force constant
ϕ58816 has also been considered in the analysis of the measured frequencies for the
v5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
=
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
1 and
v8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
=
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
2 states. The off-diagonal
matrix element is given by:
| |  | (5) |
The resulting energy
matrix can be factorized into symmetric and antisymmetric blocks adopting Wang-type linear combinations of wavefunctions.
13 Any sublevel belonging to a given vibrational state can be therefore labelled through its
k
(or
lt) value and by the “+” or “−” superscripts which designate which kind of symmetrized linear combination of wavefunctions has been chosen.
In the following subsections, some details dealing with the analyses performed for the various vibrational states investigated are given. About 500 transition frequencies have been analysed, and the complete list is available as ESI.†
4.1 The fundamental bending states (00100) and (01000)
The lines of the two fundamental bending levels near 500 cm−1 have been identified for the first time thanks to the availability of theoretical predictions and to the improved method for the production of NC4P. The recording of the J![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 55
55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ←
←![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 54 transition for both the v7
54 transition for both the v7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and v6
1 and v6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 states is reported in Fig. 1, which shows that these two states are characterized by nearly equal values of the αt vibration–rotation coupling constants and of the qtl-type doubling constants, as it was found for the corresponding pair of states v9
1 states is reported in Fig. 1, which shows that these two states are characterized by nearly equal values of the αt vibration–rotation coupling constants and of the qtl-type doubling constants, as it was found for the corresponding pair of states v9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and v8
1 and v8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 of the isoelectronic HC5P molecule.4 Measurements up to J
1 of the isoelectronic HC5P molecule.4 Measurements up to J![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 107 were performed for these states, and the observed frequencies have been analysed through eqns. (2,3) fitting the rotational constant B, the quartic centrifugal distortion constant D and the l-type doubling parameters qt and qtJ. The results of the least squares fits are listed in Table 4, where the experimental values of the vibration–rotation coupling constants α6 and α7 are also reported.
107 were performed for these states, and the observed frequencies have been analysed through eqns. (2,3) fitting the rotational constant B, the quartic centrifugal distortion constant D and the l-type doubling parameters qt and qtJ. The results of the least squares fits are listed in Table 4, where the experimental values of the vibration–rotation coupling constants α6 and α7 are also reported.
 |
| | Fig. 1 Recording of the J![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 55 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ← ←![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 54 rotational transition of NC4P in the vibrationally excited states (01000) and (00100)
(single scan with time constant 0.3 s and baseline subtracted). The weak unlabeled absorbption features belong to impurities. 54 rotational transition of NC4P in the vibrationally excited states (01000) and (00100)
(single scan with time constant 0.3 s and baseline subtracted). The weak unlabeled absorbption features belong to impurities. | |
Table 4 Spectroscopic constants determined for the (01000) and (00100) bending states of NC4P. Standard errors in units of the last digit are given in parentheses for the fitted parameters
| |
01000 |
00100 |
|
B/MHz |
874.519552(30) |
874.493890(25) |
|
α
t
/MHz |
−1.040 |
−1.014 |
|
D/Hz |
13.0507(23) |
13.0707(18) |
|
q
t
/MHz |
0.156618(60) |
0.145080(49) |
|
q
tJ
/Hz |
−0.0104(45) |
−0.0100(37) |
|
σ
fit/kHz |
13.9 |
11.2 |
| Number of lines |
51 |
48 |
|
J range |
44–107 |
44–107 |
4.2 The resonance system (10000)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) ≈
≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) (00020)
(00020)
The present CCSD(T) calculations predict a harmonic vibrational energy difference ω5–2ω8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 23.7 cm−1 and a normal coordinate cubic force constant |ϕ588|
23.7 cm−1 and a normal coordinate cubic force constant |ϕ588|![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 88.9 cm−1. This means that a strong Fermi resonance must occur between the v5
88.9 cm−1. This means that a strong Fermi resonance must occur between the v5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and v8
1 and v8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 vibrational states, which should produce a considerable low-frequency displacement of the rotational lines for the v8
2 vibrational states, which should produce a considerable low-frequency displacement of the rotational lines for the v8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, l
2, l![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 sublevel, paralleled by a high-frequency displacement of the v5
0 sublevel, paralleled by a high-frequency displacement of the v5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 transitions. A similar resonance, involving the lowest-energy stretching state, was observed for HC5P.4 A couple of lines of the unperturbed v8
1 transitions. A similar resonance, involving the lowest-energy stretching state, was observed for HC5P.4 A couple of lines of the unperturbed v8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, l
2, l![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2± sublevels were observed by Durrant et al.,1 who erroneously assigned the measured frequencies also to the transitions of the l
2± sublevels were observed by Durrant et al.,1 who erroneously assigned the measured frequencies also to the transitions of the l![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 sublevel. On the contrary, we found the v8
0 sublevel. On the contrary, we found the v8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, l
2, l![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 lines rather far from the respective l
0 lines rather far from the respective l![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2± lines, in correspondence of an effective B constant ca. 1.07 MHz smaller than the unperturbed value. A change of this amount due to Fermi resonance is sufficient to produce a negative effective value for the α5 vibration–rotation coupling constant, bringing the v5
2± lines, in correspondence of an effective B constant ca. 1.07 MHz smaller than the unperturbed value. A change of this amount due to Fermi resonance is sufficient to produce a negative effective value for the α5 vibration–rotation coupling constant, bringing the v5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 rotational lines at frequencies higher than those of the respective ground-state lines. We found indeed the v5
1 rotational lines at frequencies higher than those of the respective ground-state lines. We found indeed the v5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 transitions between the ground-state lines and the v7
1 transitions between the ground-state lines and the v7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 lines, in correspondence of an effective B constant 0.51 MHz larger than the ground-state rotational constant. Transition frequencies for the resonance system (10000)
1 lines, in correspondence of an effective B constant 0.51 MHz larger than the ground-state rotational constant. Transition frequencies for the resonance system (10000)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≈
≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (00020) were measured in the frequency range 78–260 GHz, from J
(00020) were measured in the frequency range 78–260 GHz, from J![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 44 to J
44 to J![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 146. Only one line was generally observed for the l
146. Only one line was generally observed for the l![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2± sublevels, produced by the superimposition of both components. A small splitting was only resolved for the transitions recorded above 180 GHz, corresponding to J values greater than 100, as shown in Fig. 2. The smallness of the 2+
2± sublevels, produced by the superimposition of both components. A small splitting was only resolved for the transitions recorded above 180 GHz, corresponding to J values greater than 100, as shown in Fig. 2. The smallness of the 2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2− splitting is due to the rather strong Fermi resonance existing between the v5
2− splitting is due to the rather strong Fermi resonance existing between the v5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and v8
1 and v8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 states, which causes a considerable lowering of the energy for the v8
2 states, which causes a considerable lowering of the energy for the v8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, l
2, l![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 sublevel in comparison to the l
0 sublevel in comparison to the l![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2+ sublevel, thus making the effect of rotational l-type resonance undetectable until very high J values are reached. The measured transition frequencies of the coupled states have been simultaneously analysed through eqns. (2), (3) and (5), and the fitted parameters are reported in Table 5 together with the derived unperturbed value of the α5 vibration–rotation coupling constant. It was possible to determine the B and D constants for both the v5
2+ sublevel, thus making the effect of rotational l-type resonance undetectable until very high J values are reached. The measured transition frequencies of the coupled states have been simultaneously analysed through eqns. (2), (3) and (5), and the fitted parameters are reported in Table 5 together with the derived unperturbed value of the α5 vibration–rotation coupling constant. It was possible to determine the B and D constants for both the v5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and v8
1 and v8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 vibrational states, the unperturbed vibrational energy difference between the two interacting states, ΔGv, the absolute value of the off-diagonal coupling term, W588, and the unperturbed xL(88) anharmonicity constant, which obviously turns out poorly determined. Our analysis establishes that the v5
2 vibrational states, the unperturbed vibrational energy difference between the two interacting states, ΔGv, the absolute value of the off-diagonal coupling term, W588, and the unperturbed xL(88) anharmonicity constant, which obviously turns out poorly determined. Our analysis establishes that the v5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 state is actually 61.3 cm−1 above the v8
1 state is actually 61.3 cm−1 above the v8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, l
2, l![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 sublevel, and since the unperturbed energy difference is ΔGv
0 sublevel, and since the unperturbed energy difference is ΔGv![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26.5 cm−1, this means that the v8
26.5 cm−1, this means that the v8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, l
2, l![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 sublevel is pushed by the Fermi resonance 17.4 cm−1 below the l
0 sublevel is pushed by the Fermi resonance 17.4 cm−1 below the l![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2± sublevels, while the v5
2± sublevels, while the v5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 state is symmetrically displaced by the same amount towards higher vibrational energies. Since the infrared spectrum of NC4P is so far unobserved, this is the first experimental information obtained for the vibrational energy pattern of this molecule.
1 state is symmetrically displaced by the same amount towards higher vibrational energies. Since the infrared spectrum of NC4P is so far unobserved, this is the first experimental information obtained for the vibrational energy pattern of this molecule.
 |
| | Fig. 2 Recording of the J![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 147 147![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ← ←![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 146 rotational transition of NC4P for the l 146 rotational transition of NC4P for the l![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2± sublevels of the (00020) vibrationally excited state (four scans with time constant 0.3 s). The smallness of the 2+–2− splitting is an indication of the large energy separation between the l 2± sublevels of the (00020) vibrationally excited state (four scans with time constant 0.3 s). The smallness of the 2+–2− splitting is an indication of the large energy separation between the l![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 and l 0 and l![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2+ sublevels. 2+ sublevels. | |
Table 5 Spectroscopic constants determined for the resonance system (10000)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≈
≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (00020) of NC4P. Standard errors in units of the last digit are given in parentheses for the fitted parameters
(00020) of NC4P. Standard errors in units of the last digit are given in parentheses for the fitted parameters
| |
10000 |
|
00020 |
|
Fixed in the analysis.
|
|
B/MHz |
872.920191(67) |
|
876.667248(25) |
|
α
5/MHz |
0.560 |
|
|
|
D/Hz |
12.9492(45) |
|
13.52869(83) |
|
H/μHz |
|
|
0.5205a |
|
x
L(88)/GHz |
|
|
9.5(13) |
|
q
8/MHz |
|
|
0.234376a |
|
q
8J/Hz |
|
|
−0.0550a |
| ΔGv/cm−1 |
|
26.524(39) |
|
| |W588|/cm−1 |
|
27.666(42) |
|
|
σ
fit/kHz |
|
13.2 |
|
| Number of lines |
20 |
|
60 |
|
J range |
44–107 |
|
20–146 |
4.3 The bending combination states (00101), (01001), (00110), and (01010)
The novel determination of the α6 and α7 vibration–rotation coupling constants made it possible to search for the lines of the bending combination states in which the v6 or v7 vibrational modes are excited. Notwithstanding the great spectral congestion due to the fact that α6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≈
≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α7 and α8
α7 and α8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≈
≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α9, the quadruplets of lines belonging to the four combination states (00101), (01001), (00110), and (01010), respectively, were successfully identified and assigned. Transition frequencies have been measured in the frequency range 78–170 GHz, and they were analysed through eqns. (2–4) taking into account both rotational and vibrational l-type resonances. The qt constants involved in the off-diagonal matrix elements were generally held fixed at the values determined for the singly excited bending states, but in some cases it was found useful to release them to improve the quality of the fits. The changes observed are always less than 1%, as expected for a normal vibrational dependence of the qt constants. The results of the four least-squares fits are collected in Table 6. It can be noted that the two combination states in which v8 is excited are characterized by larger values of the xL(tt′) anharmonicity constants, which produce larger energy separations between the different sublevels of a given state, and, as a consequence, a more compact rotational structure.
α9, the quadruplets of lines belonging to the four combination states (00101), (01001), (00110), and (01010), respectively, were successfully identified and assigned. Transition frequencies have been measured in the frequency range 78–170 GHz, and they were analysed through eqns. (2–4) taking into account both rotational and vibrational l-type resonances. The qt constants involved in the off-diagonal matrix elements were generally held fixed at the values determined for the singly excited bending states, but in some cases it was found useful to release them to improve the quality of the fits. The changes observed are always less than 1%, as expected for a normal vibrational dependence of the qt constants. The results of the four least-squares fits are collected in Table 6. It can be noted that the two combination states in which v8 is excited are characterized by larger values of the xL(tt′) anharmonicity constants, which produce larger energy separations between the different sublevels of a given state, and, as a consequence, a more compact rotational structure.
Table 6 Spectroscopic constants determined for the (00101), (01001), (00110), and (01010) bending combination states of NC4Pa. Standard errors in units of the last digit are given in parentheses for the fitted parameters
| |
00101 |
01001 |
00110 |
01010 |
|
For each combination state, t corresponds to the highest energy bending mode, and t′ to the lowest energy bending mode.
Fixed in the analysis.
|
|
B/MHz |
876.240381(29) |
876.266734(28) |
876.090952(34) |
876.112780(30) |
|
D/Hz |
13.7651(23) |
13.7456(23) |
13.3623(25) |
13.3335(23) |
|
x
L(tt′)/GHz |
3.9923(14) |
1.97844(29) |
13.812(55) |
10.10(19) |
|
d
JL(tt′)/kHz |
2.144(62) |
0.0b |
3.120(44) |
5.432(31) |
|
d
JL(99)/kHz |
−1.2831b |
−1.2831b |
— |
— |
|
q
t
/MHz |
0.145080b |
0.155686(33) |
0.145080b |
0.156618b |
|
q
tJ
/Hz |
−0.0100b |
−0.0104b |
−0.0100b |
−0.0104b |
|
q
t′/MHz |
0.594577(91) |
0.594286(33) |
0.234376b |
0.234376b |
|
q
t′J/Hz |
−0.3978b |
−0.3978b |
−0.0550b |
−0.0550b |
|
r
tt′/GHz |
−2.7384(13) |
−0.71644(58) |
−23.58(11) |
4.71(38) |
|
r
tt′J/kHz |
−1.353(22) |
−1.651(21) |
−6.119(25) |
−5.209(22) |
|
σ
fit/kHz |
13.2 |
13.4 |
15.6 |
14.2 |
| Number of lines |
76 |
81 |
78 |
80 |
|
J range |
44–94 |
44–94 |
44–96 |
44–96 |
5. Conclusions
Thanks to a much improved production method and to the availibility of theoretical predictions for vibrational energies and various vibration–rotation coupling parameters, this paper extends the study of the mm-wave spectra of NC4P to eight further vibrationally excited states which approximately lie between 450 and 750 cm−1. Novel determinations of the α5, α6, and α7 vibration–rotation coupling constants, and of the xL(88), xL(79), xL(69), xL(78), and xL(68) anharmonicity constants have been obtained from the analysis of the spectra. Nearly all the states investigated involve excitation of at least one bending quantum, so that l-type resonance effects had to be taken into account in the analysis of the spectra in order to obtain spectroscopic parameters with unambiguous physical meaning. In addition, the strong Fermi resonance which couples the v5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and v8
1 and v8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 states has been satisfactorily analysed. The rotational and centrifugal distortion constants fitted for the overtone state (00020), and for the combination states (00101), (01001), (00110), and (01010) are in excellent agreement with the values which is possible to extrapolate from the results obtained for the ground and singly excited bending states, thus supporting the reliability of the analyses performed. The analysis of the Fermi resonance between the v5
2 states has been satisfactorily analysed. The rotational and centrifugal distortion constants fitted for the overtone state (00020), and for the combination states (00101), (01001), (00110), and (01010) are in excellent agreement with the values which is possible to extrapolate from the results obtained for the ground and singly excited bending states, thus supporting the reliability of the analyses performed. The analysis of the Fermi resonance between the v5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and v8
1 and v8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 states has also yielded experimental evaluations of the unperturbed energy difference between the interacting states (ΔGv
2 states has also yielded experimental evaluations of the unperturbed energy difference between the interacting states (ΔGv![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26.5 cm−1) and of the normal coordinate cubic force constant responsible for the resonance (|ϕ588|
26.5 cm−1) and of the normal coordinate cubic force constant responsible for the resonance (|ϕ588|![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 78.3 cm−1). Both results agree well with the corresponding theoretical values: ω5–2ω8
78.3 cm−1). Both results agree well with the corresponding theoretical values: ω5–2ω8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 23.7 cm−1, and |ϕ588|
23.7 cm−1, and |ϕ588|![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 88.9 cm−1. The comparison between experimental and theoretically computed values of the αr, qt and qtJ constants of NC4P is summarized in Table 7. Excellent agreement between experiment and theory is observed for the spectroscopic constants of the v7
88.9 cm−1. The comparison between experimental and theoretically computed values of the αr, qt and qtJ constants of NC4P is summarized in Table 7. Excellent agreement between experiment and theory is observed for the spectroscopic constants of the v7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, v8
1, v8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and v9
1, and v9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 states, which are essentially unperturbed. Owing to the small difference ω5
1 states, which are essentially unperturbed. Owing to the small difference ω5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ω6
ω6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −5.0 cm−1, which is indicative of Coriolis resonance, the theoretical results for α5, α6, qe6 and q6J are not suited for proper comparison with the present experimental data. Simply removing the near-zero resonance denominators by setting the Coriolis coupling constant ζ56 equal to zero in the relevant equations provided by 2nd order perturbation theory,17 yields α5
−5.0 cm−1, which is indicative of Coriolis resonance, the theoretical results for α5, α6, qe6 and q6J are not suited for proper comparison with the present experimental data. Simply removing the near-zero resonance denominators by setting the Coriolis coupling constant ζ56 equal to zero in the relevant equations provided by 2nd order perturbation theory,17 yields α5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.601 MHz, α6
0.601 MHz, α6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −1.117 MHz, qe6
−1.117 MHz, qe6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.122 MHz, and q6J
0.122 MHz, and q6J![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −0.010 Hz. On the other hand, if the transition frequencies measured for the v5
−0.010 Hz. On the other hand, if the transition frequencies measured for the v5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and v6
1 and v6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 states are analysed treating variationally the corresponding Coriolis coupling, with ζ56 and ω5
1 states are analysed treating variationally the corresponding Coriolis coupling, with ζ56 and ω5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ω6 fixed at the respective CCSD(T) values (|ζ56|
ω6 fixed at the respective CCSD(T) values (|ζ56|![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.0785 and ω5–ω6
0.0785 and ω5–ω6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −5 cm−1), the following experimental results are obtained: α5
−5 cm−1), the following experimental results are obtained: α5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.592 MHz, α6
0.592 MHz, α6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −1.056 MHz, and qe6
−1.056 MHz, and qe6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.124 MHz, which agree very well with the theoretical estimates listed above.
0.124 MHz, which agree very well with the theoretical estimates listed above.
Table 7 Comparison between experimental and theoretically computed values of the vibration–rotation interaction constants (αr) and l-type doubling constants (qt and qtJ) of NC4P
| |
Experimental |
CCSD(T)/cc-pVQZ |
|
See the text.
From ref. 2.
|
|
α
5/MHz |
0.560 |
(0.716)a |
|
α
6/MHz |
−1.040 |
(−1.175)a |
|
α
7/MHz |
−1.014 |
−0.995 |
|
α
8/MHz |
−1.594b |
−1.604 |
|
α
9/MHz |
−1.741b |
−1.690 |
|
q
6/MHz |
0.157 |
(0.007)a |
|
q
7/MHz |
0.145 |
0.141 |
|
q
8/MHz |
0.234b |
0.228 |
|
q
9/MHz |
0.593b |
0.574 |
|
q
6J/Hz |
−0.010 |
(1.346)a |
|
q
7J/Hz |
−0.010 |
−0.008 |
|
q
8J/Hz |
−0.055b |
−0.055 |
|
q
9J/Hz |
−0.398b |
−0.370 |
Acknowledgements
L.B. and C.D.E. gratefully acknowledge financial support from MIUR, CNR, and from the University of Bologna (Funds for Selected Research Topics). P.B. thanks the Fonds der Chemischen Industrie for supporting this work.
References
- M. C. Durrant, H. W. Kroto, D. McNaughton and J. F. Nixon, J. Mol. Spectrosc., 1985, 109, 8 CrossRef CAS.
- L. Bizzocchi and C. Degli Esposti, J. Mol. Spectrosc., 2003, 221, 186 CrossRef CAS.
- L. Bizzocchi, C. Degli Esposti and P. Botschwina, J. Chem. Phys., 2003, 119, 170 CrossRef CAS.
- L. Bizzocchi, C. Degli Esposti and P. Botschwina, Phys. Chem. Chem. Phys., 2003, 5, 4090 RSC.
- T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007 CrossRef CAS.
- D. E. Woon and T. H. Dunning Jr., J. Chem. Phys., 1993, 98, 1358 CrossRef CAS.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479 CrossRef CAS.
-
R. D. Amos, A. Bernhardsson, A. Berning, P. Celani, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, C. Hampel, G. Hetzer, P. J. Knowles, T. Korona, R. Lindh, A. W. Lloyd, S. J. McNicholas, F. R. Manby, W. Meyer, M. E. Mura, A. Nicklass, P. Palmieri, R. Pitzer, G. Rauhut, M. Schütz, U. Schumann, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson and H.-J. Werner, MOLPRO, a package of ab initio programs designed by H.-J. Werner and P. J. Knowles, Version 2002.1, 2002 Search PubMed.
- C. Hampel, K. Peterson and H.-J. Werner, Chem. Phys. Lett., 1992, 190, 1 CrossRef CAS.
- L. Bizzocchi, C. Degli Esposti and P. Botschwina, Chem. Phys. Lett., 2000, 319, 411 CrossRef CAS.
- L. Bizzocchi, C. Degli Esposti and P. Botschwina, J. Chem. Phys., 2000, 113, 1465 CrossRef CAS.
- R. A. Kendall, T. H. Dunning, Jr. and J. Harrison, J. Chem. Phys., 1992, 98, 6796 CrossRef.
- K. M. T. Yamada, F. W. Birss and M. R. Aliev, J. Mol. Spectrosc., 1985, 112, 347 CrossRef CAS.
- L. Bizzocchi, C. Degli Esposti, L. Dore and G. Cazzoli, J. Mol. Spectrosc., 2001, 205, 164 CrossRef CAS.
- L. Bizzocchi, C. Degli Esposti, S. Thorwirth, H. S. P. Muller, F. Lewen and G. Winnewisser, Phys. Chem. Chem. Phys., 2001, 3, 3490 RSC.
- A. R. Hoy, I. M. Mills and G. Strey, Mol. Phys., 1972, 24, 1265 CAS.
-
D. Papousek, M. R. Aliev, Molecular Vibrational-Rotational Spectra, Elsevier, New York, 1982 Search PubMed.
|
| This journal is © the Owner Societies 2004 |
Click here to see how this site uses Cookies. View our privacy policy here. ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (00100), (01000), (10000), (00020), (00101), (01001), (00110), and (01010). The strong Fermi resonance which couples the v5
(00100), (01000), (10000), (00020), (00101), (01001), (00110), and (01010). The strong Fermi resonance which couples the v5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and v8
1 and v8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 states and the l-type resonances between the different sublevels of the bending states have been taken into account in the analysis of the spectra. The identification of new excited-state spectra was facilitated by CCSD(T) calculations with the cc-pVQZ basis, which provided accurate predictions for a variety of spectroscopic constants, including harmonic vibrational wavenumbers, vibration–rotation coupling constants and l-type doubling constants. Accurate theoretical predictions for the equilibrium structure and the electric dipole moment of NC4P are also presented.
2 states and the l-type resonances between the different sublevels of the bending states have been taken into account in the analysis of the spectra. The identification of new excited-state spectra was facilitated by CCSD(T) calculations with the cc-pVQZ basis, which provided accurate predictions for a variety of spectroscopic constants, including harmonic vibrational wavenumbers, vibration–rotation coupling constants and l-type doubling constants. Accurate theoretical predictions for the equilibrium structure and the electric dipole moment of NC4P are also presented.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (0,1), (0,2), (0,3), (0,4), (1,0), and (1,1) could be only detected and analysed. Subsequent pyrolysis experiments dealing with production of the isoelectronic molecule HC5P have shown that its amount can be greatly enhanced if an aliphatic ring precursor (cyclopentene) is used instead of an aromatic ring precursor (toluene).3, 4 This result motivated us to check whether a similar effect could be exploited to improve also the production of NC4P. We found indeed that if ortho-cyanotoluene is replaced by cyclopropyl cyanide, then a ten times higher concentration of NC4P is obtained, and in addition fewer interfering lines are present in the spectra. The improved production method gave us the possibility of extending the study of the rotational spectra of NC4P to eight further excited states lying approximately between 450 and 750 cm−1 above the vibrational ground state. These are (v5v6v7v8v9)
(0,1), (0,2), (0,3), (0,4), (1,0), and (1,1) could be only detected and analysed. Subsequent pyrolysis experiments dealing with production of the isoelectronic molecule HC5P have shown that its amount can be greatly enhanced if an aliphatic ring precursor (cyclopentene) is used instead of an aromatic ring precursor (toluene).3, 4 This result motivated us to check whether a similar effect could be exploited to improve also the production of NC4P. We found indeed that if ortho-cyanotoluene is replaced by cyclopropyl cyanide, then a ten times higher concentration of NC4P is obtained, and in addition fewer interfering lines are present in the spectra. The improved production method gave us the possibility of extending the study of the rotational spectra of NC4P to eight further excited states lying approximately between 450 and 750 cm−1 above the vibrational ground state. These are (v5v6v7v8v9)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (00100), (01000), (10000), (00020), (00101), (01001), (00110), and (01010).
(00100), (01000), (10000), (00020), (00101), (01001), (00110), and (01010).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and v8
1 and v8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 states. The new measurements allowed us to enlarge considerably the set of spectroscopic parameters experimentally known for this molecule, which now include also the α5, α6, and α7 vibration–rotation coupling constants, the xL(88), xL(79), xL(69), xL(78), and xL(68) anharmonicity constants, the ϕ588 normal coordinate cubic force constant, and the vibrational energy difference between the resonant v5
2 states. The new measurements allowed us to enlarge considerably the set of spectroscopic parameters experimentally known for this molecule, which now include also the α5, α6, and α7 vibration–rotation coupling constants, the xL(88), xL(79), xL(69), xL(78), and xL(68) anharmonicity constants, the ϕ588 normal coordinate cubic force constant, and the vibrational energy difference between the resonant v5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and v8
1 and v8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 states.
2 states.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C, which was connected to the absorption cell of the mm-wave spectrometer. The spectra were recorded while pumping continuously the pyrolysis products through the cell. 50 mTorr of cyclopropyl cyanide and 175 mTorr of PCl3 were typically allowed to flow into the quartz reactor, corresponding to a total pressure of ca. 12 mTorr inside the cell. Good spectra of NC4P were also observed when PCl3 was copyrolyzed with crotononitrile (CH3CH
°C, which was connected to the absorption cell of the mm-wave spectrometer. The spectra were recorded while pumping continuously the pyrolysis products through the cell. 50 mTorr of cyclopropyl cyanide and 175 mTorr of PCl3 were typically allowed to flow into the quartz reactor, corresponding to a total pressure of ca. 12 mTorr inside the cell. Good spectra of NC4P were also observed when PCl3 was copyrolyzed with crotononitrile (CH3CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCN), which is as efficient a precursor nearly as cyclopropyl cyanide. The rotational spectra of NC4P were investigated in the frequency range 78–260 GHz using the same source modulation mm-wave spectrometer employed for previous measurements.2
CHCN), which is as efficient a precursor nearly as cyclopropyl cyanide. The rotational spectra of NC4P were investigated in the frequency range 78–260 GHz using the same source modulation mm-wave spectrometer employed for previous measurements.2
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 873.1 MHz was obtained.
873.1 MHz was obtained.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1–5) have positive sign, while those of the bending vibrations (αt, t
1–5) have positive sign, while those of the bending vibrations (αt, t![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6–9) have negative sign. In the same Table 2 the calculated difference between the equilibrium and the ground-state rotational constant is reported:
6–9) have negative sign. In the same Table 2 the calculated difference between the equilibrium and the ground-state rotational constant is reported: 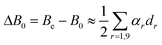
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 873.7 MHz results. It is only 0.2 MHz larger than the experimental value1,2 and thus gives support to the present recommended equilibrium structure.
873.7 MHz results. It is only 0.2 MHz larger than the experimental value1,2 and thus gives support to the present recommended equilibrium structure.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.865 D. The dipole moment in the vibrational ground state may well differ from this value by a few hundredths of a Debye.
3.865 D. The dipole moment in the vibrational ground state may well differ from this value by a few hundredths of a Debye.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (00100), (01000), (10000), (00020), (00101), (01001), (00110), and (01010) excited states. Partial cm-wave frequency data were only available for the (00020) state,1 for which we have extended the measurements to the mm-wave region, reaching a frequency as high as 260 GHz. On the contrary, no experimental information was available for all other states, whose mm-wave spectra have been assigned in the frequency range 78–190 GHz. With only the exception of the (10000) stretching state, all the states investigated involve excitation of at least one bending quantum, so that multiplets of rotational lines were always recorded for each J
(00100), (01000), (10000), (00020), (00101), (01001), (00110), and (01010) excited states. Partial cm-wave frequency data were only available for the (00020) state,1 for which we have extended the measurements to the mm-wave region, reaching a frequency as high as 260 GHz. On the contrary, no experimental information was available for all other states, whose mm-wave spectra have been assigned in the frequency range 78–190 GHz. With only the exception of the (10000) stretching state, all the states investigated involve excitation of at least one bending quantum, so that multiplets of rotational lines were always recorded for each J![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ←
←![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) J transition, owing to l-type resonance effects between the different l sublevels. The spectra have been analysed using the same formalism originally developed by Yamada et al.13 and already employed to fit the excited-state rotational spectra of HC3P14 and NCCP.15 Briefly, the ro-vibrational Hamiltonian is first represented using the unsymmetrized basis functions
J transition, owing to l-type resonance effects between the different l sublevels. The spectra have been analysed using the same formalism originally developed by Yamada et al.13 and already employed to fit the excited-state rotational spectra of HC3P14 and NCCP.15 Briefly, the ro-vibrational Hamiltonian is first represented using the unsymmetrized basis functions  , where k
, where k![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) l6
l6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) l7
l7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) l8
l8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) l9. Employing the simplified notation |l6,l7,l8,l9;k〉, the elements of the Hamiltonian matrix which are diagonal in the quantum numbers vt and lt are:
l9. Employing the simplified notation |l6,l7,l8,l9;k〉, the elements of the Hamiltonian matrix which are diagonal in the quantum numbers vt and lt are: 
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±2, Δk
±2, Δk![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±2) have the general form:
±2) have the general form: 
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, Δlt′
2, Δlt′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∓2, Δk
∓2, Δk![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0) have the expression:
0) have the expression: 
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and v8
1 and v8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 states. The off-diagonal matrix element is given by:
2 states. The off-diagonal matrix element is given by: 
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 55
55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ←
←![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 54 transition for both the v7
54 transition for both the v7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and v6
1 and v6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 states is reported in Fig. 1, which shows that these two states are characterized by nearly equal values of the αt vibration–rotation coupling constants and of the qtl-type doubling constants, as it was found for the corresponding pair of states v9
1 states is reported in Fig. 1, which shows that these two states are characterized by nearly equal values of the αt vibration–rotation coupling constants and of the qtl-type doubling constants, as it was found for the corresponding pair of states v9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and v8
1 and v8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 of the isoelectronic HC5P molecule.4 Measurements up to J
1 of the isoelectronic HC5P molecule.4 Measurements up to J![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 107 were performed for these states, and the observed frequencies have been analysed through eqns. (2,3) fitting the rotational constant B, the quartic centrifugal distortion constant D and the l-type doubling parameters qt and qtJ. The results of the least squares fits are listed in Table 4, where the experimental values of the vibration–rotation coupling constants α6 and α7 are also reported.
107 were performed for these states, and the observed frequencies have been analysed through eqns. (2,3) fitting the rotational constant B, the quartic centrifugal distortion constant D and the l-type doubling parameters qt and qtJ. The results of the least squares fits are listed in Table 4, where the experimental values of the vibration–rotation coupling constants α6 and α7 are also reported.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 55
55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ←
←![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 54 rotational transition of NC4P in the vibrationally excited states (01000) and (00100)
(single scan with time constant 0.3 s and baseline subtracted). The weak unlabeled absorbption features belong to impurities.
54 rotational transition of NC4P in the vibrationally excited states (01000) and (00100)
(single scan with time constant 0.3 s and baseline subtracted). The weak unlabeled absorbption features belong to impurities.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) ≈
≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) (00020)
(00020)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 23.7 cm−1 and a normal coordinate cubic force constant |ϕ588|
23.7 cm−1 and a normal coordinate cubic force constant |ϕ588|![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 88.9 cm−1. This means that a strong Fermi resonance must occur between the v5
88.9 cm−1. This means that a strong Fermi resonance must occur between the v5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and v8
1 and v8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 vibrational states, which should produce a considerable low-frequency displacement of the rotational lines for the v8
2 vibrational states, which should produce a considerable low-frequency displacement of the rotational lines for the v8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, l
2, l![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 sublevel, paralleled by a high-frequency displacement of the v5
0 sublevel, paralleled by a high-frequency displacement of the v5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 transitions. A similar resonance, involving the lowest-energy stretching state, was observed for HC5P.4 A couple of lines of the unperturbed v8
1 transitions. A similar resonance, involving the lowest-energy stretching state, was observed for HC5P.4 A couple of lines of the unperturbed v8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, l
2, l![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2± sublevels were observed by Durrant et al.,1 who erroneously assigned the measured frequencies also to the transitions of the l
2± sublevels were observed by Durrant et al.,1 who erroneously assigned the measured frequencies also to the transitions of the l![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 sublevel. On the contrary, we found the v8
0 sublevel. On the contrary, we found the v8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, l
2, l![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 lines rather far from the respective l
0 lines rather far from the respective l![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2± lines, in correspondence of an effective B constant ca. 1.07 MHz smaller than the unperturbed value. A change of this amount due to Fermi resonance is sufficient to produce a negative effective value for the α5 vibration–rotation coupling constant, bringing the v5
2± lines, in correspondence of an effective B constant ca. 1.07 MHz smaller than the unperturbed value. A change of this amount due to Fermi resonance is sufficient to produce a negative effective value for the α5 vibration–rotation coupling constant, bringing the v5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 rotational lines at frequencies higher than those of the respective ground-state lines. We found indeed the v5
1 rotational lines at frequencies higher than those of the respective ground-state lines. We found indeed the v5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 transitions between the ground-state lines and the v7
1 transitions between the ground-state lines and the v7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 lines, in correspondence of an effective B constant 0.51 MHz larger than the ground-state rotational constant. Transition frequencies for the resonance system (10000)
1 lines, in correspondence of an effective B constant 0.51 MHz larger than the ground-state rotational constant. Transition frequencies for the resonance system (10000)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≈
≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (00020) were measured in the frequency range 78–260 GHz, from J
(00020) were measured in the frequency range 78–260 GHz, from J![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 44 to J
44 to J![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 146. Only one line was generally observed for the l
146. Only one line was generally observed for the l![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2± sublevels, produced by the superimposition of both components. A small splitting was only resolved for the transitions recorded above 180 GHz, corresponding to J values greater than 100, as shown in Fig. 2. The smallness of the 2+
2± sublevels, produced by the superimposition of both components. A small splitting was only resolved for the transitions recorded above 180 GHz, corresponding to J values greater than 100, as shown in Fig. 2. The smallness of the 2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2− splitting is due to the rather strong Fermi resonance existing between the v5
2− splitting is due to the rather strong Fermi resonance existing between the v5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and v8
1 and v8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 states, which causes a considerable lowering of the energy for the v8
2 states, which causes a considerable lowering of the energy for the v8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, l
2, l![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 sublevel in comparison to the l
0 sublevel in comparison to the l![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2+ sublevel, thus making the effect of rotational l-type resonance undetectable until very high J values are reached. The measured transition frequencies of the coupled states have been simultaneously analysed through eqns. (2), (3) and (5), and the fitted parameters are reported in Table 5 together with the derived unperturbed value of the α5 vibration–rotation coupling constant. It was possible to determine the B and D constants for both the v5
2+ sublevel, thus making the effect of rotational l-type resonance undetectable until very high J values are reached. The measured transition frequencies of the coupled states have been simultaneously analysed through eqns. (2), (3) and (5), and the fitted parameters are reported in Table 5 together with the derived unperturbed value of the α5 vibration–rotation coupling constant. It was possible to determine the B and D constants for both the v5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and v8
1 and v8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 vibrational states, the unperturbed vibrational energy difference between the two interacting states, ΔGv, the absolute value of the off-diagonal coupling term, W588, and the unperturbed xL(88) anharmonicity constant, which obviously turns out poorly determined. Our analysis establishes that the v5
2 vibrational states, the unperturbed vibrational energy difference between the two interacting states, ΔGv, the absolute value of the off-diagonal coupling term, W588, and the unperturbed xL(88) anharmonicity constant, which obviously turns out poorly determined. Our analysis establishes that the v5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 state is actually 61.3 cm−1 above the v8
1 state is actually 61.3 cm−1 above the v8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, l
2, l![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 sublevel, and since the unperturbed energy difference is ΔGv
0 sublevel, and since the unperturbed energy difference is ΔGv![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26.5 cm−1, this means that the v8
26.5 cm−1, this means that the v8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, l
2, l![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 sublevel is pushed by the Fermi resonance 17.4 cm−1 below the l
0 sublevel is pushed by the Fermi resonance 17.4 cm−1 below the l![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2± sublevels, while the v5
2± sublevels, while the v5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 state is symmetrically displaced by the same amount towards higher vibrational energies. Since the infrared spectrum of NC4P is so far unobserved, this is the first experimental information obtained for the vibrational energy pattern of this molecule.
1 state is symmetrically displaced by the same amount towards higher vibrational energies. Since the infrared spectrum of NC4P is so far unobserved, this is the first experimental information obtained for the vibrational energy pattern of this molecule.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 147
147![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ←
←![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 146 rotational transition of NC4P for the l
146 rotational transition of NC4P for the l![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2± sublevels of the (00020) vibrationally excited state (four scans with time constant 0.3 s). The smallness of the 2+–2− splitting is an indication of the large energy separation between the l
2± sublevels of the (00020) vibrationally excited state (four scans with time constant 0.3 s). The smallness of the 2+–2− splitting is an indication of the large energy separation between the l![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 and l
0 and l![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2+ sublevels.
2+ sublevels.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≈
≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (00020) of NC4P. Standard errors in units of the last digit are given in parentheses for the fitted parameters
(00020) of NC4P. Standard errors in units of the last digit are given in parentheses for the fitted parameters
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≈
≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α7 and α8
α7 and α8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≈
≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α9, the quadruplets of lines belonging to the four combination states (00101), (01001), (00110), and (01010), respectively, were successfully identified and assigned. Transition frequencies have been measured in the frequency range 78–170 GHz, and they were analysed through eqns. (2–4) taking into account both rotational and vibrational l-type resonances. The qt constants involved in the off-diagonal matrix elements were generally held fixed at the values determined for the singly excited bending states, but in some cases it was found useful to release them to improve the quality of the fits. The changes observed are always less than 1%, as expected for a normal vibrational dependence of the qt constants. The results of the four least-squares fits are collected in Table 6. It can be noted that the two combination states in which v8 is excited are characterized by larger values of the xL(tt′) anharmonicity constants, which produce larger energy separations between the different sublevels of a given state, and, as a consequence, a more compact rotational structure.
α9, the quadruplets of lines belonging to the four combination states (00101), (01001), (00110), and (01010), respectively, were successfully identified and assigned. Transition frequencies have been measured in the frequency range 78–170 GHz, and they were analysed through eqns. (2–4) taking into account both rotational and vibrational l-type resonances. The qt constants involved in the off-diagonal matrix elements were generally held fixed at the values determined for the singly excited bending states, but in some cases it was found useful to release them to improve the quality of the fits. The changes observed are always less than 1%, as expected for a normal vibrational dependence of the qt constants. The results of the four least-squares fits are collected in Table 6. It can be noted that the two combination states in which v8 is excited are characterized by larger values of the xL(tt′) anharmonicity constants, which produce larger energy separations between the different sublevels of a given state, and, as a consequence, a more compact rotational structure.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and v8
1 and v8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 states has been satisfactorily analysed. The rotational and centrifugal distortion constants fitted for the overtone state (00020), and for the combination states (00101), (01001), (00110), and (01010) are in excellent agreement with the values which is possible to extrapolate from the results obtained for the ground and singly excited bending states, thus supporting the reliability of the analyses performed. The analysis of the Fermi resonance between the v5
2 states has been satisfactorily analysed. The rotational and centrifugal distortion constants fitted for the overtone state (00020), and for the combination states (00101), (01001), (00110), and (01010) are in excellent agreement with the values which is possible to extrapolate from the results obtained for the ground and singly excited bending states, thus supporting the reliability of the analyses performed. The analysis of the Fermi resonance between the v5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and v8
1 and v8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 states has also yielded experimental evaluations of the unperturbed energy difference between the interacting states (ΔGv
2 states has also yielded experimental evaluations of the unperturbed energy difference between the interacting states (ΔGv![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26.5 cm−1) and of the normal coordinate cubic force constant responsible for the resonance (|ϕ588|
26.5 cm−1) and of the normal coordinate cubic force constant responsible for the resonance (|ϕ588|![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 78.3 cm−1). Both results agree well with the corresponding theoretical values: ω5–2ω8
78.3 cm−1). Both results agree well with the corresponding theoretical values: ω5–2ω8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 23.7 cm−1, and |ϕ588|
23.7 cm−1, and |ϕ588|![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 88.9 cm−1. The comparison between experimental and theoretically computed values of the αr, qt and qtJ constants of NC4P is summarized in Table 7. Excellent agreement between experiment and theory is observed for the spectroscopic constants of the v7
88.9 cm−1. The comparison between experimental and theoretically computed values of the αr, qt and qtJ constants of NC4P is summarized in Table 7. Excellent agreement between experiment and theory is observed for the spectroscopic constants of the v7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, v8
1, v8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and v9
1, and v9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 states, which are essentially unperturbed. Owing to the small difference ω5
1 states, which are essentially unperturbed. Owing to the small difference ω5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ω6
ω6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −5.0 cm−1, which is indicative of Coriolis resonance, the theoretical results for α5, α6, qe6 and q6J are not suited for proper comparison with the present experimental data. Simply removing the near-zero resonance denominators by setting the Coriolis coupling constant ζ56 equal to zero in the relevant equations provided by 2nd order perturbation theory,17 yields α5
−5.0 cm−1, which is indicative of Coriolis resonance, the theoretical results for α5, α6, qe6 and q6J are not suited for proper comparison with the present experimental data. Simply removing the near-zero resonance denominators by setting the Coriolis coupling constant ζ56 equal to zero in the relevant equations provided by 2nd order perturbation theory,17 yields α5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.601 MHz, α6
0.601 MHz, α6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −1.117 MHz, qe6
−1.117 MHz, qe6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.122 MHz, and q6J
0.122 MHz, and q6J![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −0.010 Hz. On the other hand, if the transition frequencies measured for the v5
−0.010 Hz. On the other hand, if the transition frequencies measured for the v5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and v6
1 and v6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 states are analysed treating variationally the corresponding Coriolis coupling, with ζ56 and ω5
1 states are analysed treating variationally the corresponding Coriolis coupling, with ζ56 and ω5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ω6 fixed at the respective CCSD(T) values (|ζ56|
ω6 fixed at the respective CCSD(T) values (|ζ56|![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.0785 and ω5–ω6
0.0785 and ω5–ω6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −5 cm−1), the following experimental results are obtained: α5
−5 cm−1), the following experimental results are obtained: α5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.592 MHz, α6
0.592 MHz, α6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −1.056 MHz, and qe6
−1.056 MHz, and qe6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.124 MHz, which agree very well with the theoretical estimates listed above.
0.124 MHz, which agree very well with the theoretical estimates listed above.
