View PDF VersionPrevious ArticleNext Article
 
DOI: 10.1039/B311073G (Paper) Phys. Chem. Chem. Phys., 2004, 6, 138-143

From a pluripotent stem cell to an ensemble of differentiated cells: Elements of theoretical tissue engineering

Vladimir P. Zhdanov *ab and Bengt Kasemo a
aDepartment of Applied Physics, Chalmers University of Technology, S-412 96 Göteborg, Sweden
bBoreskov Institute of Catalysis, Russian Academy of Sciences, Novosibirsk, 630090, Russia. E-mail: zhdanov@catalysis.nsk.su; zhdanov@fy.chalmers.se

Received 10th September 2003 , Accepted 4th November 2003

First published on 1st December 2003

Abstract

We present Monte Carlo lattice simulations illustrating how the growth of stem and differentiated cells on a uniform surface can be governed (guided differentiation) by tuning long-range cell–cell communication. Due to spatial constraints on cell division, the growth rate is shown to strongly depend on the interplay of cellular division, diffusion, and signaling. With decreasing diffusion rate, the kinetics become slower. To increase the selectivity of the growth with respect to “desirable” cells, one can use induced messenger-mediated generation of these cells by stem cells. The simplest schemes based on this idea may, however, result in appreciable slowdown of the growth. A more optimal strategy may be simultaneous promotion of generation of desirable cells and stem cells.

1. Introduction

Depending on the source, stem cells have the potential to form one, many or all cell types of an organism (the diversity and abilities to evolve in different directions decrease from embryonic stem cells to “adult” stem cells) and accordingly can in principle be employed to build blocks for every tissue.1 Using this potential and bringing stem-cell therapies to the clinic demand a better understanding of the factors that maintain cells in a multipotent state or drive them to create differentiated cells.1,2 Specifically, there is a need to improve the control of differentiation of cells and to promote desirable division via external signals and suppress undesired differentiation, in order to reach suitable spatial cellular arrangements and composition.2–4 An additional challenge is to extend and sophisticate the tools, which can be employed to govern the tissue evolution. One of the opportunities here is to grow cells on specially designed solid surfaces on which the original cell culture(s) are deposited and eventually develop into a tissue.5 By changing the surface properties, one can influence cell division and mobility and also cell–cell communication. For example, supported lipid bilayers offer efficient reduction of nonspecific cell and protein binding and, if selectively functionalized, constitute one of the promising approaches.6 Alternatively or in parallel, one can use surfaces with heterogeneities fabricated on the μm or nm scale (for recent experimental studies of cell adsorption on such surfaces, see refs. 7–9). Such patterned surfaces have the potential to allow production of different cell types on different areas of the surface.

In addition to the experiments, it is of interest to form a basis of theoretical tissue engineering or, more specifically, to develop models describing the growth of ensembles of stem and differentiated cells. At present such models are in fact lacking (for a review, see ref. 10). In the nearest future, one can hardly expect the models constructed to be fully predictive. However, mathematical modelling in this area is still motivated, firstly because it may help to conceptually understand what may occur in real systems, and secondly it is a concise way of structuring existing knowledge. Thirdly, it is an invaluable tool to guide experiments.

The goal of our present Monte Carlo (MC) simulations is to illustrate how the 2D cellular growth on an uniform surface depend on and/or can be governed by varying the rate of cellular mobility and/or cell–cell communication. (For reviews of cellular mobility and communication, see refs. 11, 12 and 13, respectively.)

2. Model

In our simulations, we use a recently proposed coarse-grained lattice model10 including cell diffusion, division, and cell–cell communication. The former two processes are considered to be complicated by spatial constraints and cell–cell adhesion resulting usually in aggregation of similar cells and/or segregation of different cells. The cell–cell communication depends on the type of cells as well. Below, the symbol i (or j) indicating a cell type runs from 1 to 3. Cells of type 1 are assumed to be pluripotent, i.e., they are able to give rise to all three cell types. Cells of types 2 and 3 represent differentiated cells. The model parameters are chosen for these cells so that they tend to segregation. In addition, the communication of type-2 cells with stem cells is different compared to that of type-3 cells.

In principle, the number of cell types could be easily increased, but we believe that the 3-type case is generic because it makes it possible to illustrate various aspects of cellular growth with a minimal number of model parameters. In particular, a model with this number cell types can be used to show how the selectivity of the growth with respect to desirable cells (e.g. of type 2) depends on the details of diffusion, division, and cell–cell communication.

In the simulations, cells are located on a 2D L[thin space (1/6-em)]×[thin space (1/6-em)]L square lattice. Each lattice site is either vacant or occupied by one cell. This means that the reconfiguration of a single cell is not described explicitly (for the multi-site models making it possible to mimic changes of the cell shape, see ref. 14). The cell size is assumed to be slightly larger than the site size but smaller than the distance between the next-nearest-neighbour (nnn) sites. With this prescription, the interactions between nearest-neighbour (nn) and nnn cells, εnnij and εnnnij, should be repulsive and attractive due to deformation and adhesion, respectively. In addition, the attractive nnn interactions between similar cell should be stronger than that between different cells. These interactions, introduced to take into account softness, deformation, adhesion and segregation of cells, are of course “effective”.

Cell diffusion is realized via jumps (spreading) to vacant nn sites. A jump is allowed provided that in the final state (after the jump) the cell has at least one contact with other cells, i.e., after a jump at least one of the nn or nnn sites should be occupied (this condition is introduced in order to suppress rare events of escape of single cells from the central area where they are located; its role in the simulations is minor, because the probability of such events is low anyway). The normalized jump probability is defined by the standard Metropolis rule. In the case under consideration, the Metropolis algorithm is appropriate, because it correctly describes the tendency of cells to increase the number of adhesive contacts and segregate. One should however bear in mind that in our context the thermal energy, kBT, used in the Metropolis rule, is effective as well as the cell–cell interactions (for discussion of this aspect of the lattice models, see ref. 15).

In our previous general simulations,10 we allowed division of cells of all the types. Specifically, the division rate of differentiated cells was assumed to be higher that that of the stem cells. From the point of view of stem-cell tissue engineering, it is of interest to analyze the opposite case, because if the rate of division of differentiated cells were high, there would be no need of stem cells. For this reason, we prohibit division of differentiated cells. The division of a stem cell is allowed provided that (i) all the nn sites are vacant (the cells located in nn sites are deformed and accordingly the division probability in such cases is assumed to be negligibly small) and (ii) the newly-born cell located (after division) in one of the nn sites has at least one nn vacant site.

In reality, the rate of division of stem cells and, what is more important, the differentiation probabilities depend on cell–cell signaling including transport of messenger molecules between cells, signal transmission via the cell membrane, gene regulation, etc. The signaling may occur via ligand diffusion between cells12 or via the so-called gap-junction communication.13 In the former case, the cells may be far from each other. In the latter case, the cells should be in close contact. Earlier,10 we discussed both these schemes, but the simulations were performed for the simplest case of communication between adjacent (nnn) cells. The present simulations are focused on a more general case of long-range ligand-diffusion-mediated signaling.

The cell–cell communication is assumed to influence primarily the “decision-taking” process in stem cells, i.e. it changes the distribution of the newly born cells but does not change the division rate. Thus, the effect of signaling on the rate of division of these cells is neglected. The differentiation probabilities of stem cells are considered to depend on the signals arriving from cells of type 2 or, more specifically, on the signal molecule concentration due to signaling of type-2 cells (the signaling of cells of types 1 and 3 is for simplicity neglected). The signal molecule concentration near a given stem cell is represented as10

 
ugraphic, filename = b311073g-t1.gif(1)
where summation runs over sites occupied by cells of type 2 (rk is the distance between the stem cell and site k, A is a constant, and α is a factor dependent on the messenger diffusion coefficient and degradation rate). The probability that a stem cell gives birth to a cell of type i is defined as
 
ugraphic, filename = b311073g-t2.gif(2)
where χi[thin space (1/6-em)]=[thin space (1/6-em)]P0i[thin space (1/6-em)]+[thin space (1/6-em)]Bi∑k[thin space (1/6-em)]exp(−αrk)/rk, P0i is the birth probability in the absence of signaling, Bi∑k[thin space (1/6-em)]exp(−αrk)/rk is the signal-related term [cf.eqn. (1)], and Bi are the constants describing the signal efficiency. Eqn. (2) is constructed so that (i) with increasing messenger concentration the birth of cell of type i becomes more probable if Bi is larger for these cells than for cells of other types, and (ii) simultaneously ∑iPdivi[thin space (1/6-em)]=[thin space (1/6-em)]1. The former feature makes it possible to qualitatively mimic the effect of cell–cell communication on the division process. The latter guarantees that the communication does not change the total division rate (for the details, see below).

The probabilities Pdivi specify the distribution of cells after division but do not characterize the rate of division. To run MC simulations, we actually need a ratio of the rates of cell division and diffusion. To characterize the relative rates of these processes, we use a dimensionless parameter pdiv. During the simulations, the division and diffusion trials are performed with probabilities pdiv and 1[thin space (1/6-em)]−[thin space (1/6-em)]pdiv, respectively. In all the examples below, diffusion of cells is considered to be faster or much faster than division, i.e.pdiv[thin space (1/6-em)]≪[thin space (1/6-em)]1. In reality, diffusion of cells on surfaces is usually slow, but division is slow as well. Thus, the condition pdiv[thin space (1/6-em)]≪[thin space (1/6-em)]1 may be fulfilled.

3. Algorithm of simulations

With the specification above, our MC algorithm is as follows:

(1) A site is chosen at random. If the site is vacant, the trial ends. Otherwise, a cell located in the site has chances to diffuse irrespective of its type [item (2)] if ρ[thin space (1/6-em)]>[thin space (1/6-em)]pdiv, or to divide [item (3)] provided that it belongs to type 1 and ρ[thin space (1/6-em)]<[thin space (1/6-em)]pdiv, where ρ (0[thin space (1/6-em)]≤[thin space (1/6-em)]ρ[thin space (1/6-em)]≤[thin space (1/6-em)]1) is a random number.

(2) For diffusion, an adjacent site is randomly selected, and if the latter site is vacant, the cell is transferred to it provided that (i) in the final state the cell has at least one contact with other cells and (ii) ρ′[thin space (1/6-em)]<[thin space (1/6-em)]Pdifi, where ρ′ (0[thin space (1/6-em)]≤[thin space (1/6-em)]ρ′[thin space (1/6-em)]≤[thin space (1/6-em)]1) is a new random number, and Pdifi is the standard Metropolis jump probability dependent on cell–cell lateral interactions.

(3) Division of a stem cell may occur if all the nn sites are vacant. In this case, one of the nn sites (site 2) is selected at random and if this site has at least one vacant nn site the division is realized with unit probability. After division of a stem cell, there are two cells. One of them is a stem cell and another one is a stem or differentiated cell (the type of this cell is defined by probabilities Pdivi). The former cell occupies the site which was occupied by the stem cell before division. The latter cell is situated in site 2.

All the MC runs were started from the clean lattice with a single stem cell located in the center. During simulations, we used the so-called “no-flux” boundary conditions (this means that a MC trial ends if the nn site chosen for diffusion jump or division is located outside the L[thin space (1/6-em)]×[thin space (1/6-em)]L array of sites). The duration of the runs was usually selected so that in the end there were about 2000 cells.

Time was measured in MC steps (MCS). Usually, one MCS is defined as L[thin space (1/6-em)]×[thin space (1/6-em)]L MC trials. In our case, this definition would result in a time scale connected primarily with cell migration, because this process is considered to be rapid compared to cell division. Under such circumstances, the conventionally defined MC time is physically somewhat artificial. The situation here is similar to MF calculations of reaction kinetics, where the time scale is usually independent of the rate of reactant diffusion. For this reason, we define one MC step as L[thin space (1/6-em)]×[thin space (1/6-em)]L MC trials of cell division on average. Practically, this means that the MC time is calculated by dividing the total number of trials by L[thin space (1/6-em)]×[thin space (1/6-em)]L and multiplying by pdiv. One of the advantages of this choice is that we can directly, with the same MC time, compare the kinetics corresponding to very different rates of cell mobility.

The simulations presented are executed on a lattice with L[thin space (1/6-em)]=[thin space (1/6-em)]150. The energetic parameters are selected so that different cells tend to segregate and this process is not too slow. Practically, this means that the ratio of the effective cell–cell interactions and kBT should not be too large. In particular, we use εnnij/kBT[thin space (1/6-em)]=[thin space (1/6-em)]1, εnnn11/kBT[thin space (1/6-em)]=[thin space (1/6-em)]−1, εnnnii/kBT[thin space (1/6-em)]=[thin space (1/6-em)]−2 for i[thin space (1/6-em)]≥[thin space (1/6-em)]2, and εnnnij/kBT[thin space (1/6-em)]=[thin space (1/6-em)]−1 for i[thin space (1/6-em)]≠[thin space (1/6-em)]j. The stem-cell division probability, pdiv, is chosen to be a governing parameter and varied from 10−3 to 0.1 (this means that the ratio of the rates of cell diffusion and division is between one and three orders of magnitude). For single stem cells, the distribution of birth probabilities for the three cell types is considered to be P01[thin space (1/6-em)]=[thin space (1/6-em)]0.1, P02[thin space (1/6-em)]=[thin space (1/6-em)]0.5, and P03[thin space (1/6-em)]=[thin space (1/6-em)]0.4. To describe cell–cell communication, we measure distance in terms of the lattice spacing and employ α[thin space (1/6-em)]=[thin space (1/6-em)]0.1 (this means that the length scale of communication is about ten lattice spacings). The parameters Bi [in eqn. (2)] are varied in order to illustrate typical situations.

4. Results of simulations

One of the central goals of tissue engineering and cell-based therapies is to increase the selectivity of division of stem cells in order to obtain a desirable distribution/composition of cell types. Bearing this point in mind, our first example of cellular growth (Figs. 1 and 2) is chosen so that the cell–cell communication is negligible and the selectivity is low (specifically, the populations of cells of types 2 and 3 are comparable). Then, we illustrate how the selectivity with respect to cells of type 2 can be increased by employing tuned cell–cell communication. In all the examples, we use pdiv[thin space (1/6-em)]=[thin space (1/6-em)]0.1, 10−2, and 10−3.
Number of cells of types 1, 2, and 3 (thin solid, thick solid, and dashed lines) as a function of time for pdiv = 0.1 (a), 10−2 (b), and 10−3 (c) in the absence of cell–cell communication.
Fig. 1 Number of cells of types 1, 2, and 3 (thin solid, thick solid, and dashed lines) as a function of time for pdiv[thin space (1/6-em)]=[thin space (1/6-em)]0.1 (a), 10−2 (b), and 10−3 (c) in the absence of cell–cell communication.

[(a)–(c)] Patterns obtained in the end of the MC runs shown in Fig. 1 (a)–(c). Open circles, filled circles, and plus signs represent cells of types 1, 2, and 3, respectively.
Fig. 2 [(a)–(c)] Patterns obtained in the end of the MC runs shown in Fig. 1 (a)–(c). Open circles, filled circles, and plus signs represent cells of types 1, 2, and 3, respectively.

Typical results of the simulations for negligible cell–cell communication (Bi[thin space (1/6-em)]=[thin space (1/6-em)]0) are shown in Fig. 1. For all the values of pdiv, the characteristics of the cellular growth kinetics are similar. The distribution of cell types is the same as well, because in the absence of cell signaling it is defined simply by probabilities P0i. The times, characterizing the ensemble growth, and cellular patterns are however different. If cell mobility is relatively low (pdiv[thin space (1/6-em)]=[thin space (1/6-em)]0.1), the growth is slow (the 2000 cell population is reached after about 700 MCS). With increasing diffusion rate compared to rate of division, the growth becomes much faster. For pdiv[thin space (1/6-em)]=[thin space (1/6-em)]10−3, e.g., the 2000 cell population is observed already after about 80 MCS. This difference in the growth rate is related to the spatial constraints on cell division and also related to cell segregation. If cell diffusion is relatively slow (or, in other words, division is rapid), the cellular patterns are rather compact [Fig. 2 (a) and (b)], segregation is poor, stem cells are surrounded by other cells, the conditions for division of stem cells inside the cellular patch are as a rule not fulfilled, and accordingly the growth rate is relatively low. With increasing diffusion rate, the cell arrangement is less compact [Fig. 2(c)], segregation is better, and accordingly the kinetics are faster.

The simplest cell–cell communication favourable for production of cells of type 2 includes signal-molecule-mediated promotion of birth of these cells by stem cells due to signals from type-2 cells. Mathematically, this situation is described by using B1[thin space (1/6-em)]=[thin space (1/6-em)]B3[thin space (1/6-em)]=[thin space (1/6-em)]0 and B2[thin space (1/6-em)]>[thin space (1/6-em)]0. Typical results of the corresponding simulations, performed with B2[thin space (1/6-em)]=[thin space (1/6-em)]0.1 (this value is relatively small), are exhibited in Figs. 3 and 4. As expected, the self-promotion of type-2 cells is seen to result in an increase of their population (cf.Figs. 1 and 3). The price for this effect is that the kinetics become slower, especially for slow diffusion [cf.Figs. 1(a) and 3(a)], because type-2 cells suppress birth of stem cells. With increase of B2 up to 0.2 (Figs. 5 and 6), the population of type-2 cells further increases but not appreciably. The slowdown of the cellular growth for slow diffusion is in this case dramatic [cf.Figs. 1(a), 3(a), and 5(a)].


Number of cells of type 1, 2, and 3 (thin solid, thick solid, and dashed lines) as a function of time for pdiv = 0.1 (a), 10−2 (b), and 10−3 (c) and cell–cell communication with B1 = B3 = 0 and B2 = 0.1.
Fig. 3 Number of cells of type 1, 2, and 3 (thin solid, thick solid, and dashed lines) as a function of time for pdiv[thin space (1/6-em)]=[thin space (1/6-em)]0.1 (a), 10−2 (b), and 10−3 (c) and cell–cell communication with B1[thin space (1/6-em)]=[thin space (1/6-em)]B3[thin space (1/6-em)]=[thin space (1/6-em)]0 and B2[thin space (1/6-em)]=[thin space (1/6-em)]0.1.

[(a)–(c)] Snapshots obtained in the end of the MC runs presented in Fig. 3(a)–(c). The designations are as in Fig. 2.
Fig. 4 [(a)–(c)] Snapshots obtained in the end of the MC runs presented in Fig. 3(a)–(c). The designations are as in Fig. 2.

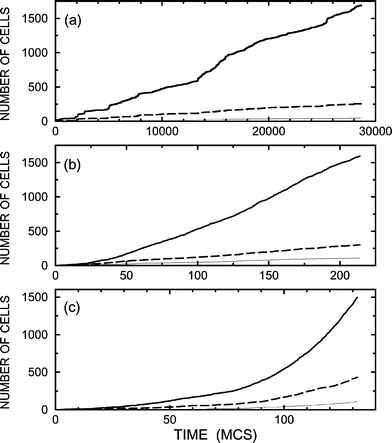As Fig. 3 for B2 = 0.2.
Fig. 5 As Fig. 3 for B2[thin space (1/6-em)]=[thin space (1/6-em)]0.2.

[(a)–(c)] Patterns obtained in the end of the MC runs shown in Fig. 5(a)–(c). The designations are as in Fig. 2.
Fig. 6 [(a)–(c)] Patterns obtained in the end of the MC runs shown in Fig. 5(a)–(c). The designations are as in Fig. 2.

To avoid the slowdown in growth, cell–cell communication can be tuned so that in addition to self-promotion the type-2 cells promote birth of stem cells. This situation is illustrated by employing B1[thin space (1/6-em)]=[thin space (1/6-em)]0.05, B1[thin space (1/6-em)]=[thin space (1/6-em)]0.05, and B3[thin space (1/6-em)]=[thin space (1/6-em)]0 (Figs. 7 and 8). In this case, the growth kinetics are rapid even if diffusion is relatively slow [Fig. 7(a)]. The price for this improvement is that the selectivity of production of type-2 cells becomes somewhat lower [cf.Figs. 5(a) and 7(a)].


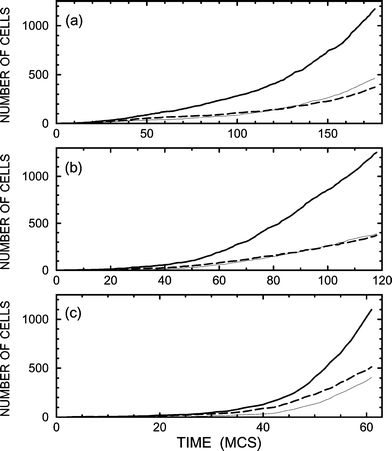As Fig. 3 for B1 = 0.05 and B2 = 0.1.
Fig. 7 As Fig. 3 for B1[thin space (1/6-em)]=[thin space (1/6-em)]0.05 and B2[thin space (1/6-em)]=[thin space (1/6-em)]0.1.

[(a)–(c)] Snapshots obtained in the end of the MC runs presented in Fig. 7(a)–(c). The designations are as in Fig. 2.
Fig. 8 [(a)–(c)] Snapshots obtained in the end of the MC runs presented in Fig. 7(a)–(c). The designations are as in Fig. 2.

5. Conclusion

We have presented the first MC simulations illustrating how the growth of stem and differentiated cells from a single stem cell on a uniform surface can be governed by tuning long-range cell–cell communication. The rate of this process is demonstrated to strongly depend on the interplay of cellular division, diffusion, and signaling, in the presence of spatial constraints on cell division. With decreasing diffusion rate, the kinetics become slower. To increase the selectivity of the growth with respect to desirable cells, one can use induced signal-molecule-mediated generation of these cells by stem cells. The simplest schemes based on this idea may, however, result in appreciable slowdown of the growth. A more optimal strategy may be simultaneous promotion of generation of desirable cells and stem cells. Other promising strategy, not discussed in detail here, may be based on the use of a specially designed heterogeneous surface.

Acknowledgements

Financial support for this work has been obtained from the Swedish Research Council (Contract 621-2001-2649) and from the SSF Biocompatible Materials Program (Contract A3 95:1).

References

  1. Stem Cells, Nature, 2001, 414, 87 Search PubMed.
  2. N. L. Parenteau and J. H. Young, Ann. NY Acad. Sci., 2002, 961, 27 CAS.
  3. A. Vats, A. Vats, N. S. Tolley, J. M. Polak and L. D. K. Buttery, Clin. Ontolaringology, 2002, 27, 227 Search PubMed.
  4. C. M. Ward, Expert Opin. Ther. Pat., 2002, 12, 1395 Search PubMed.
  5. B. Kasemo, Surf. Sci., 2002, 500, 656 CrossRef CAS.
  6. S. Swedhem, D. Dahlborg, J. Ekeroth, J. Kelly, F. Höök and J. Gold, Langmuir, 2003, 19, 6730 CrossRef.
  7. A. I. Teixeira, G. A. Abrams, C. J. Murphy and P. F. Nealey, J. Vac. Sci. Technol. B, 2003, 21, 683 CrossRef CAS.
  8. R. N. Orth, M. Wu, D. A. Holowka, H. G. Craighead and B. A. Baird, Langmuir, 2003, 19, 1599 CrossRef.
  9. F. Pfeiffer, B. Herzog, D. Kern, L. Scheideler, J. Geis-Gerstorfer and H. Wolburg, Microelectr. Eng., 2003, 67, 913 Search PubMed.
  10. V. P. Zhdanov and B. Kasemo, Phys. Chem. Chem. Phys., 2003, 5, 1433 RSC.
  11. D. A. Lauffenburger and A. F. Horwitz, Cell, 1996, 84, 359 CAS.
  12. M. Freeman and J. B. Gurdon, Annu. Rev. Cell. Dev. Biol., 2002, 18, 515 CrossRef CAS.
  13. M. Levin, J. Memb. Biol., 2001, 185, 177 Search PubMed.
  14. J. A. Glazier and F. Graner, Phys. Rev. E, 1993, 47, 2128 CrossRef; M. Zajac, G. L. Jones and J. A. Glazier, J. Theor. Biol., 2003, 222, 247 CrossRef.
  15. D. A. Beysens, G. Forgacs and J. A. Glazier, Proc. Natl. Acad. Sci. USA, 2000, 97, 9467 CrossRef CAS.
This journal is © the Owner Societies 2004
Click here to see how this site uses Cookies. View our privacy policy here.