Molecular dynamics tests of the Smoluchowski–Collins–Kimball model for fluorescence quenching of spherical molecules
Marek
Litniewski
and
Jerzy
Gorecki
Institute of Physical Chemistry of the Polish Academy of Science, Kasprzaka 44/52, 01-224 Warszawa, Poland
First published on 19th November 2003
Abstract
We test the Smoluchowski–Collins–Kimball (SCK) model of fluorescence quenching reaction in liquids. Our attention is focused on the description of diffusion controlled processes and we use the simplest microscopic model of binary de-excitation which occurs instantaneously. Molecular dynamics simulations have been performed for a wide range of densities and for various potentials of interparticle interactions. The large number of particles used (typically N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 681
681![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 472) allowed us to obtain quantitative results. The simulations show that at very short times the SCK model completely fails, especially if the distribution function of the reagents is not included in the model. Even if the short time data are excluded the diffusion constant obtained by fitting the simulation data with the SCK model may still be burdened with a 25% error when the distribution function is not taken into account. The error can be reduced to 10% level if this function is included in the model.
472) allowed us to obtain quantitative results. The simulations show that at very short times the SCK model completely fails, especially if the distribution function of the reagents is not included in the model. Even if the short time data are excluded the diffusion constant obtained by fitting the simulation data with the SCK model may still be burdened with a 25% error when the distribution function is not taken into account. The error can be reduced to 10% level if this function is included in the model.
1. Introduction
Typical fluorescence quenching reaction for the A molecule consists of three processes: initial excitation A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A*, spontaneous de-excitation A*
A*, spontaneous de-excitation A*![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A and de-excitation in the presence of a quencher, B, A*
A and de-excitation in the presence of a quencher, B, A*![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B
B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A
A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B. In this work our attention is focused only on the third reaction, which is diffusion controlled. There are many theoretical descriptions of diffusion controlled reactions.1–9 The most popular one is the Smoluchowski–Collins–Kimball (SCK)2,3 model based on the Smoluchowski equation.1,2 It gives a simple analytical formula for the reaction rate, which is widely used to interpret experimental data of fluorescence quenching.10–14 The model returns the parameters of the reaction: intrinsic rate constant (k0), the reaction radius (a) and the sum of the diffusion coefficients of the excited molecule and the quencher (DS). Many experiments15–18 show inconsistencies between the model and reality. The recent works of Krystkowiak and Maciejewski17,18 report significant differences between the parameters obtained by fitting the experimental results of fluorescence quenching with the SCK model and the values obtained by different methods. On the other hand, the report on consistency between the model and experimental results can be also found in the literature.19
B. In this work our attention is focused only on the third reaction, which is diffusion controlled. There are many theoretical descriptions of diffusion controlled reactions.1–9 The most popular one is the Smoluchowski–Collins–Kimball (SCK)2,3 model based on the Smoluchowski equation.1,2 It gives a simple analytical formula for the reaction rate, which is widely used to interpret experimental data of fluorescence quenching.10–14 The model returns the parameters of the reaction: intrinsic rate constant (k0), the reaction radius (a) and the sum of the diffusion coefficients of the excited molecule and the quencher (DS). Many experiments15–18 show inconsistencies between the model and reality. The recent works of Krystkowiak and Maciejewski17,18 report significant differences between the parameters obtained by fitting the experimental results of fluorescence quenching with the SCK model and the values obtained by different methods. On the other hand, the report on consistency between the model and experimental results can be also found in the literature.19
The purpose of our work is to test the SCK model applying it to fit simulation data of fluorescence quenching. We simulate reaction between A* and B using molecular dynamics (MD) and our assumptions match as closely as possible those of the SCK model: the microscopic model for reaction between A* and B molecules is the same as in the SCK, the reactants are spherical and the concentration of quencher is very low. Because most of the assumptions of the theory are satisfied the comparison of theory with simulation results gives us information on the scale and the origin of the inconsistencies coming from the application of the Smoluchowski equation. The simulations also allow us to estimate the errors caused by the neglect of spatial correlations between A* and B (gA*B(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) typical in analysis of experimental data. Our simulations have been performed for a wide range of the parameters (the liquid density, DS, a) and different types of intermolecular interactions so we believe that random coincidences are absent. The fact that the conditions of our computer experiments are much closer to the assumptions of the SCK model than it is for a real experiment allows us to treat the scale of deviations between the simulation results and the model as a minimum level of errors expected in applications of SCK to real experiments. Focusing our attention on the errors within the SCK model we have not concerned more realistic descriptions of the reaction cross section. Nevertheless, some of our results are also valid for the step function nonradiative lifetime model2,20
(SFNL) which assumes more realistic reaction cross section than the SCK model.
1) typical in analysis of experimental data. Our simulations have been performed for a wide range of the parameters (the liquid density, DS, a) and different types of intermolecular interactions so we believe that random coincidences are absent. The fact that the conditions of our computer experiments are much closer to the assumptions of the SCK model than it is for a real experiment allows us to treat the scale of deviations between the simulation results and the model as a minimum level of errors expected in applications of SCK to real experiments. Focusing our attention on the errors within the SCK model we have not concerned more realistic descriptions of the reaction cross section. Nevertheless, some of our results are also valid for the step function nonradiative lifetime model2,20
(SFNL) which assumes more realistic reaction cross section than the SCK model.
A large scale of our simulations (typically, the total number of molecules N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 681
681![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 472) has allowed us to make the quantitative test. Simple, qualitative simulations on both the Smoluchowski1,2 and the SCK model were performed over 10 years ago for a hard sphere liquid.21,22 The main conclusion was22 that the SCK model gave surprisingly good results, much better than the Smoluchowski one. Zhou and Szabo22 showed also that the agreement between the model and the simulations improved significantly when the shape of the two-particle radial distribution function was taken into account. This conclusion was only qualitative one and no quantitative analysis of differences between the model and the simulations have been performed. Ten years ago the scale of simulations was not sufficient for such an analysis. As a result, the scale of errors resulting from the standard assumption that the liquid is structureless as well as from the simplifications of the SCK model itself is still unknown.
472) has allowed us to make the quantitative test. Simple, qualitative simulations on both the Smoluchowski1,2 and the SCK model were performed over 10 years ago for a hard sphere liquid.21,22 The main conclusion was22 that the SCK model gave surprisingly good results, much better than the Smoluchowski one. Zhou and Szabo22 showed also that the agreement between the model and the simulations improved significantly when the shape of the two-particle radial distribution function was taken into account. This conclusion was only qualitative one and no quantitative analysis of differences between the model and the simulations have been performed. Ten years ago the scale of simulations was not sufficient for such an analysis. As a result, the scale of errors resulting from the standard assumption that the liquid is structureless as well as from the simplifications of the SCK model itself is still unknown.
The paper is organized as follows. Section 2 defines the model, presents the computational details and methods of describing the results. Section 3 gives the results of simulations and discussions. It starts with the analysis (Section 3.1) of errors in results presented in Section 3.2. Section 3.2, describes an “idealized” situation when the time of measurement is long so we can divide the obtained intensity curve and discard a part of data inconsistent with the remaining ones. As a result, we are able to extract the errors related to the Smoluchowski equation for times when the relative motion of reactants is dominated by diffusion. We also show the errors resulting from the standard simplification that the liquid is structureless. The “idealized” situation allows us to generalize some of results to the case when the reaction is described by the SFNL model. Section 3.3 is concerned with the problem of the early phase of fluorescence quenching. We discuss here the influence of non-diffusive motion which dominates at short times. We also consider situation frequent in experiments on fluorescence quenching: the time of measurement is short and data cannot be divided into parts corresponding to short time processes and purely diffusive motion (long times). An influence of such situation on the parameters obtained from the fitting is presented. The summary and final remarks are presented in Section 4.
2. Model, computational aspects and interpretation of results
Following the SCK model, we consider spherical molecules in three dimensional bulk liquid and a fluorescence quenching reaction in the form:A*![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) → →![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) hν hν | (2.1) |
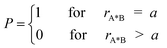 | (2.2) |
 | (2.3) |
According to the SCK model, the probability of finding the A* particle around the B particle at the interparticle distance r and at time t, p(r,t), satisfies the Smoluchowski equation1,2 for spherical molecules:
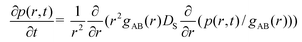 | (2.4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) gAB(r), where gAB(r) is the equilibrium pair distribution function which, according to our assumptions, is identical to gA*B(r). In the SCK model DS is independent of r and equal to the sum of the diffusion coefficients of bulk liquid. The model also assumes the radiation boundary condition of Collins and Kimball:2,3
gAB(r), where gAB(r) is the equilibrium pair distribution function which, according to our assumptions, is identical to gA*B(r). In the SCK model DS is independent of r and equal to the sum of the diffusion coefficients of bulk liquid. The model also assumes the radiation boundary condition of Collins and Kimball:2,3 | (2.5) |
 | (2.6) |
 | (2.7) |
In the case gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡
≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, eqn. (2.6) is the exact solution of the model for a whole range of t.
1, eqn. (2.6) is the exact solution of the model for a whole range of t.
The k0 constant is determined, following Zhou and Szabo,22 from the kinetic theory of gases:24,25
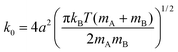 | (2.8) |
2.1. Simulations
The computer simulations were performed using standard molecular dynamics (MD) constant volume and energy (NVE) method.26 The cubic box and the periodic boundary conditions were applied.26 Most of the simulations were performed for the total number of particles N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 681
681![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 472. Several simulations for smaller N
(110
472. Several simulations for smaller N
(110![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 592 and 343
592 and 343![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) were also carried out. During a single simulation run the particles interacted via the potential of the same kind. Four various kinds of spherical interparticle potentials were considered. Most of simulations were performed for the two following potentials:
000) were also carried out. During a single simulation run the particles interacted via the potential of the same kind. Four various kinds of spherical interparticle potentials were considered. Most of simulations were performed for the two following potentials:
Lennard-Jones26 type (LJ):
 | (2.9) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and ε, σ are standard parameters of the potential; and the potential with an exponential repulsive term (R6e):
1 and ε, σ are standard parameters of the potential; and the potential with an exponential repulsive term (R6e):  | (2.10) |
The ci and di constants from eqns. (2.9) and (2.10) were adjusted so the derivative of u(r) (force) was differentiable at RS.
The cut-off distances, RC, were low. For the L-J type RC was always equal to 1.6 (RS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.25). For R6e three values of RC were applied: 1.65 (RS
1.25). For R6e three values of RC were applied: 1.65 (RS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.40), 1.95 (RS
1.40), 1.95 (RS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.65), 2.15 (RS
1.65), 2.15 (RS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.85). Such low values of RC made the time of computation sufficiently short. Any qualitative influence of the cut-off distance on the investigated problem was not observed.
1.85). Such low values of RC made the time of computation sufficiently short. Any qualitative influence of the cut-off distance on the investigated problem was not observed.
Two simulation runs for non-attracting potentials were also performed: soft spheres (SS, eqn. (2.9) for α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, RC
1, RC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.15, RS
1.15, RS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.0), and hard soft spheres (HSS–(2.9) for α
1.0), and hard soft spheres (HSS–(2.9) for α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5, RC
5, RC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.03, RS
1.03, RS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.985). The Newton equations of motion were solved applying the velocity Verlet algorithm26,27 with the time step Δt
0.985). The Newton equations of motion were solved applying the velocity Verlet algorithm26,27 with the time step Δt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.01σ(m/ε)1/2 except of HSS for which the time step was four times shorter. The temperature was evaluated directly from the average of the total kinetic energy26 of simulated systems.
0.01σ(m/ε)1/2 except of HSS for which the time step was four times shorter. The temperature was evaluated directly from the average of the total kinetic energy26 of simulated systems.
For all the investigated systems the reagents (A, A*, and B whose total number was NR) were mechanically identical (identical ε, σ, and mass m) and differed only by a chemical identification parameter. The reaction (2.1) were realized by simple re-labeling A* to A so the simulated system was always in the mechanical equilibrium state. At the beginning of each evolution (after equilibration) some of the reagents were randomly labeled as the B particles. In order to keep our simulations consistent with the SCK model the considered molar fraction of B was never larger than 0.0025 (see Table 1). The remaining particles were labeled as the A* particles but if the condition in eqn. (2.2) was fulfilled they were instantaneously relabeled as A (the reaction had occurred before the start of the simulation run). The mechanical identity of A and A* allows us to regard the single simulation as a set of NA*
(NX is the number of X-type particles) independent evolution runs for one excited particle (A*) in a mixture of the B and A particles (A*![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A does not lead to de-excitation). The names of the reagents (A, A*, B) were stored in an array (of the length of NR). Mechanical identity of A and B enabled us to lessen the statistical error by applying procedure similar to that proposed by Gorecki.28,29 During a single simulation run we considered simultaneously several sets of the reagents (nset is the number of the sets), each set described by a different array. Therefore, a single simulation run was approximately equivalent to NRnset evolutions for single A* particle.
A does not lead to de-excitation). The names of the reagents (A, A*, B) were stored in an array (of the length of NR). Mechanical identity of A and B enabled us to lessen the statistical error by applying procedure similar to that proposed by Gorecki.28,29 During a single simulation run we considered simultaneously several sets of the reagents (nset is the number of the sets), each set described by a different array. Therefore, a single simulation run was approximately equivalent to NRnset evolutions for single A* particle.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) for a0/σAB
1) for a0/σAB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.0, 1.13 respectively. The index ‘g
1.0, 1.13 respectively. The index ‘g![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡
≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1’ means gAB(r)
1’ means gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡
≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, the index ‘SIM’, gAB taken from the simulation (by eqns. (2.14)). The mark — in the last column means that the value has not been “measured”
1, the index ‘SIM’, gAB taken from the simulation (by eqns. (2.14)). The mark — in the last column means that the value has not been “measured”
| Run | Type | R C | ρ | k B T | 103xB | N | n set | t T | D 0 | ΔD(1.0, 1.13)g≡1 | ΔD(1.0, 1.13)SIM |
|---|---|---|---|---|---|---|---|---|---|---|---|
| a The mean value from the eight independent simulation runs. | |||||||||||
| #1 | LJ | 1.60 | 0.5787 | 1.00 | 1.00 | 681![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 472 472 |
4 | 464 | 0.1971 | 0.165, 0.371 | 0.084, −0.117 |
| #2 | LJ | 1.60 | 0.7830 | 1.00 | 1.00 | 681![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 472 472 |
4 | 576 | 0.0794 | 0.058, −0.009 | −0.085, −0.131 |
| #3 | HSS | 1.03 | 0.9358 | 1.00 | 1.00 | 343![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
6 | 576 | 0.0236 | −0.052, −0.122 | −0.086, −0.074 |
| #4 | SS | 1.15 | 0.9358 | 1.00 | 1.50 | 343![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
6 | 576 | 0.0401 | −0.002, −0.116 | −0.072, −0.088 |
| #5a | LJ | 1.60 | 0.9358 | 1.00 | 2.50 | 681![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 472 472 |
4 | 656 | 0.02782 | −0.020, −0.101 | −0.068, −0.061 |
| #5b | LJ | 1.60 | 0.9358 | 1.00 | 1.25 | 681![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 472 472 |
4 | 2184 | 0.02797 | −0.032, −0.107 | −0.076, −0.069 |
| #5c | LJ | 1.60 | 0.9358 | 1.00 | 0.625 | 681![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 472 472 |
4 | 738 | 0.02781 | −0.022, −0.101 | −0.068, −0.061 |
| #5d–k | LJ | 1.60 | 0.9358 | 1.00 | 0.10 | 110![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 592 592 |
8 | 1000 | 0.02763a | −0.009a, −0.089a | — |
| #6 | R6e | 2.15 | 0.9358 | 1.00 | 1.00 | 681![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 472 472 |
4 | 1080 | 0.01330 | −0.065, −0.106 | −0.038, −0.002 |
| #7a | R6e1.0 | 1.95 | 0.8594 | 1.00 | 0.50 | 681![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 472 472 |
6 | 3360 | 0.00287 | −0.198, −0.233 | −0.040, 0.030 |
| #7b | R6e1.0 | 1.95 | 0.8594 | 1.00 | 0.50 | 681![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 472 472 |
4 | 2864 | 0.00287 | −0.213, −0.247 | −0.056, 0.017 |
| #8a | R6e1.1 | 1.95 | 0.8594 | 1.25 | 1.50 | 681![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 472 472 |
2 | 2048 | 0.00616 | −0.215, −0.266 | −0.072, −0.025 |
| #8b | R6e1.1 | 1.95 | 0.8594 | 1.25 | 0.50 | 343![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
6 | 2736 | 0.00611 | −0.201, −0.243 | −0.056, −0.001 |
| #9 | R6e1.0 | 1.65 | 0.8594 | 1.50 | 0.50 | 681![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 472 472 |
6 | 1312 | 0.00942 | −0.168, −0.235 | −0.106, −0.074 |
| #10a | R6e1.5 | 1.65 | 0.8594 | 1.50 | 0.70 | 681![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 472 472 |
6 | 2320 | 0.00557 | −0.218, −0.246 | −0.022, 0.026 |
| #10b | R6e1.5 | 1.65 | 0.8594 | 1.50 | 0.70 | 343![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
6 | 3160 | 0.00559 | −0.213, −0.239 | −0.019, 0.032 |
From the mechanical point of view the reagent-only system is a simple liquid. To make our computer experiments more realistic we considered also the mixtures composed of the heavy components (10% molar fraction) and the light solvent, C, (90%). The parameters of the heavy particles were: σA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σB
σB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.35σC and mA
1.35σC and mA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mB
mB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (σA/σC)3mC. The σAC parameter (identical to σBC) of the A–C (or B–C) interaction satisfied the Lorentz–Berthelot rule:30
(σA/σC)3mC. The σAC parameter (identical to σBC) of the A–C (or B–C) interaction satisfied the Lorentz–Berthelot rule:30
σAC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (σAA (σAA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σCC)/2 σCC)/2 | (2.11) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ε
ε![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) m
m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.0) of A (or B) for the simple liquids and C for the mixtures. If the other units are used, it is explicitly written in the text.
1.0) of A (or B) for the simple liquids and C for the mixtures. If the other units are used, it is explicitly written in the text.
The reaction condition, eqn. (2.2), was checked at each time step. A comparison with additional simulations for Δt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.005σ(m/ε)1/2 showed that the error resulting from a finite value of Δt was much lower than the errors discussed in Section 3.1. During each simulation run a set of 21 fixed values of a, from σAB to over 3σAB, was considered and evolutions corresponding to 21 different reaction radii were obtained. The mechanical identity between A and A* enabled us to apply an efficient procedure analogous with the simultaneous simulations for different sets of reagents. In the following we denote the reaction radius for a given simulation as a0 to emphasis that this is a constant value and a is a parameter of SCK theory and it may be used as an argument of minimization procedure.
0.005σ(m/ε)1/2 showed that the error resulting from a finite value of Δt was much lower than the errors discussed in Section 3.1. During each simulation run a set of 21 fixed values of a, from σAB to over 3σAB, was considered and evolutions corresponding to 21 different reaction radii were obtained. The mechanical identity between A and A* enabled us to apply an efficient procedure analogous with the simultaneous simulations for different sets of reagents. In the following we denote the reaction radius for a given simulation as a0 to emphasis that this is a constant value and a is a parameter of SCK theory and it may be used as an argument of minimization procedure.
According to our assumptions DS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2D, where D is the diffusion coefficient of the A (or B) particle of a bulk liquid. The value of the coefficient, denoted by D0
(indexed by “0” because we treat the value as a constant parameter), was “measured” during simulations by using the Einstein formula:26
2D, where D is the diffusion coefficient of the A (or B) particle of a bulk liquid. The value of the coefficient, denoted by D0
(indexed by “0” because we treat the value as a constant parameter), was “measured” during simulations by using the Einstein formula:26
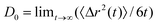 | (2.12) |
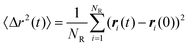 | (2.13) |
The limit in (2.12) was obtained by analyzing the time evolution of 〈Δr2(t)〉. This was not difficult because due to high N and the lengths of the simulation runs the fluctuations of 〈Δr2(t)〉/t were small. As an example the plot of 〈Δr2(t)〉/6t as a function of time (the simulation run labelled #10b in Table 1) is shown in Fig. 1. The presented simulation run has been performed for the lowest numbers of reagents (here NR![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1N
0.1N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34
34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300) so the fluctuations are much higher than for a typical run discussed in the work.
300) so the fluctuations are much higher than for a typical run discussed in the work.
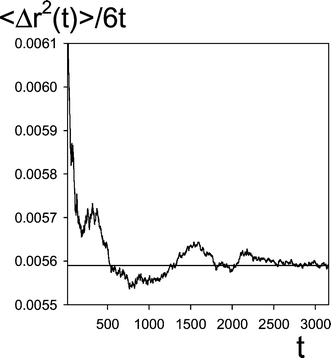 | ||
| Fig. 1 Asymptotic behavior of 〈Δr2(t)〉/6t, eqn. (2.13), as a function of time, t. The data from the simulation run marked by #10b in Table 1. The horizontal line corresponds to the value adopted as D0 (=0.00559). | ||
The radial distribution function of the reagents was obtained directly from simulation data using the standard formula:23
 | (2.14) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) r
r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) r2and 〈
r2and 〈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 〉t means an average over time. Δr was always equal to 0.0025σAB. Typical gAB(r) function is presented in Fig. 2.
〉t means an average over time. Δr was always equal to 0.0025σAB. Typical gAB(r) function is presented in Fig. 2.
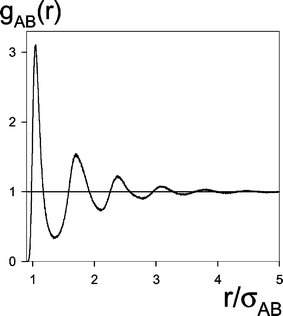 | ||
| Fig. 2 The partial radial distribution function of the reagents A* and B (gAB(r), eqn. (2.14)) as a function of the interparticle distance, r. The data from # 8a in Table 1. | ||
2.2. Interpretation of results
In this subsection we present the methods of describing and interpreting the results of simulations. Experimental data of fluorescence quenching are interpreted by analyzing time evolution of the survival probability. For example, the survival probabilities of A* as functions of time obtained from the simulations (solid line) and predicted by the SCK model (dashed line) for DS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2D0 and gAB(r)
2D0 and gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡
≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 are presented in Fig. 3
(a0
1 are presented in Fig. 3
(a0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σAB) and Fig. 4
(a0
σAB) and Fig. 4
(a0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.27σAB). The probabilities predicted by the SCK model have been obtained by numerical integration of formula (2.3) with k(t) given by (2.6)
(for gAB(r)
3.27σAB). The probabilities predicted by the SCK model have been obtained by numerical integration of formula (2.3) with k(t) given by (2.6)
(for gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡
≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, (2.6) is the exact solution of (2.4)). It can be noticed that the inconsistency between the model and the simulations is quite important not only in the vicinity of t
1, (2.6) is the exact solution of (2.4)). It can be noticed that the inconsistency between the model and the simulations is quite important not only in the vicinity of t![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0, but also for large t which is especially evident in Fig. 3. The differences between the solid and the dashed lines presented in Figs 3 and 4 indicate that there is a significant difference between kSCK(t)
(from (2.6)) and the time dependent rate constant, k(t), characterizing the reaction simulated by MD method. Detailed discussion on the difference is presented in Sections 3.2 and 3.3.
0, but also for large t which is especially evident in Fig. 3. The differences between the solid and the dashed lines presented in Figs 3 and 4 indicate that there is a significant difference between kSCK(t)
(from (2.6)) and the time dependent rate constant, k(t), characterizing the reaction simulated by MD method. Detailed discussion on the difference is presented in Sections 3.2 and 3.3.
 | ||
Fig. 3 The survival probability (NA*(t)/NA*(0)) as a function of t for a0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σAB. The solid line–the data from # 8a in Table 1; the dashed line, the SCK model eqn. (2.6) for gAB(r) σAB. The solid line–the data from # 8a in Table 1; the dashed line, the SCK model eqn. (2.6) for gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡ ≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, DS 1, DS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2D0, and a 2D0, and a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a0. a0. | ||
 | ||
Fig. 4 The survival probability (NA*(t)/NA*(0)) as a function of t for a0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.27σAB. Notation as in Fig. 3. 3.27σAB. Notation as in Fig. 3. | ||
In this work the simulation data are analyzed by calculating the time dependent rate constant, k(t), evaluated from eqn. (2.3) by omitting the higher order terms in δt:
 | (2.15) |
 | ||
Fig. 5 The time dependent rate constant, k(t), as a function of t for the case shown in Fig. 3. The circles: the results of simulation (evaluated from eqn. (2.15)) the dashed line: the SCK model for gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡ ≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and DS 1 and DS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2D0; the solid line: gAB(r) 2D0; the solid line: gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡ ≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and DS taken as double the “idealized” value of Dfit. 1 and DS taken as double the “idealized” value of Dfit. | ||
In order to describe the differences between the SCK model and the simulations quantitatively, we fitted the values of k(t) obtained from simulation runs using (2.15) to (2.6) by the least square method. The weights of “experimental” points were proportional to NA*(t). The minimization procedure was applied with respect to one of the parameters (D (≡ DS/2) at given a or a at given D), or with respect to both a and D. In further considerations, Dfit and afit denote the values corresponding to the best fit. The approximation in eqn. (2.15) may lead to considerably large errors if random fluctuations in NA* are high. But in our case eqn. (2.15) worked very well. We checked that for a wide range of δt (in eqn. (2.15)) its value did not have any significant influence on results of the minimizations.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∞, where tD
(discarded time) is the upper limit of the time interval {0, tD} that was not taken into account in the minimization. The results and discussion on the “idealized” values is given in Section 3.2. As an example, the solid line in Fig. 5 presents the kSCK(t) curve for a
∞, where tD
(discarded time) is the upper limit of the time interval {0, tD} that was not taken into account in the minimization. The results and discussion on the “idealized” values is given in Section 3.2. As an example, the solid line in Fig. 5 presents the kSCK(t) curve for a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a0
(=σAB) and D equal to the “idealized” value of Dfit. It is clearly seen that this curve fits the asymptotic data much better than the SCK formula for D0
(the dashed line). The “idealized” values are defined as the limits for tD
a0
(=σAB) and D equal to the “idealized” value of Dfit. It is clearly seen that this curve fits the asymptotic data much better than the SCK formula for D0
(the dashed line). The “idealized” values are defined as the limits for tD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∞ and we use such notation being aware that the total time of simulation, tT, however very long, is finite. The limit has been determined by analyzing the dependence of Dfit on tD. The problem is that the interval {tD, tT} should be sufficiently long to obtain reasonable results of the minimization. Thus, the value of tD must be significantly lower than tT. The problem has been overcome by increasing tT to very large values. The influence of tT on the determination of the limit is also discussed in Section 3.3.
∞ and we use such notation being aware that the total time of simulation, tT, however very long, is finite. The limit has been determined by analyzing the dependence of Dfit on tD. The problem is that the interval {tD, tT} should be sufficiently long to obtain reasonable results of the minimization. Thus, the value of tD must be significantly lower than tT. The problem has been overcome by increasing tT to very large values. The influence of tT on the determination of the limit is also discussed in Section 3.3.
 | ||
Fig. 6 The “idealized” values. Dfit/D0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) − −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at fixed a 1 at fixed a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a0 as a function of a0 for various xB for #5. Symbols: triangle down–#5a (xB a0 as a function of a0 for various xB for #5. Symbols: triangle down–#5a (xB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.0025), square–#5b (xB 0.0025), square–#5b (xB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.00125), triangle up–#5c (xB 0.00125), triangle up–#5c (xB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.000625), black circles connected by a line–5d–k (xB 0.000625), black circles connected by a line–5d–k (xB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.0001). The error bars have been estimated from the mean square deviation. 0.0001). The error bars have been estimated from the mean square deviation. | ||
For a typical experiment on fluorescence quenching all the measurements from t![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 to t
0 to t![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tT are taken into account in the minimization (i.e.tD
tT are taken into account in the minimization (i.e.tD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0). The “idealized” values have been obtained from the minimization over the time interval {tD
0). The “idealized” values have been obtained from the minimization over the time interval {tD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∞, tT} and, as a result, they are not burdened with an error due to non-diffusive processes that dominate k(t) for short times. Therefore, the errors of the “idealized” values should be treated as the minimum values of errors of parameters obtained from minimization. This error is not small. In the case presented in Fig. 5 the “idealized” value of Dfit is of about 22% lower than D0
(see also Section 3.2). In the case of gAB(r)
∞, tT} and, as a result, they are not burdened with an error due to non-diffusive processes that dominate k(t) for short times. Therefore, the errors of the “idealized” values should be treated as the minimum values of errors of parameters obtained from minimization. This error is not small. In the case presented in Fig. 5 the “idealized” value of Dfit is of about 22% lower than D0
(see also Section 3.2). In the case of gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≠
≠![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 eqn. (2.6) is valid only for sufficiently large t. For low D and a close to σAB, the convergence of eqn. (2.6) to the exact solution of eqn. (2.4) is poor. But the procedure of determination of the “idealized” values guarantees that the difference between k(t) evaluated from (2.6) and its real value is negligible. This has been confirmed by comparing k(t) obtained from the numerical solution of eqns. (2.4) and (2.5) with kSCK(t) at a0
1 eqn. (2.6) is valid only for sufficiently large t. For low D and a close to σAB, the convergence of eqn. (2.6) to the exact solution of eqn. (2.4) is poor. But the procedure of determination of the “idealized” values guarantees that the difference between k(t) evaluated from (2.6) and its real value is negligible. This has been confirmed by comparing k(t) obtained from the numerical solution of eqns. (2.4) and (2.5) with kSCK(t) at a0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σAB
(the worst convergence) for all the simulation points. The highest relative deviations in kSCK(t) found was only 0.0075 for t
σAB
(the worst convergence) for all the simulation points. The highest relative deviations in kSCK(t) found was only 0.0075 for t![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tT/3 and 0.0035 for t
tT/3 and 0.0035 for t![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tT.
tT.
The “idealized” values calculated within the SCK model may be used for the SFNL model, which assumes a more realistic form of reaction than eqn. (2.2). Szabo has shown2,20 that, for gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡
≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, the formula for k(t) of SFNL model transforms into that of kSCK(t) if t/τ
1, the formula for k(t) of SFNL model transforms into that of kSCK(t) if t/τ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∞ where τ is the nonradiative lifetime. As a consequence, we generalize some our results concerning the “idealized” values obtained from the SCK model to the SFNL one (Section 3.2).
∞ where τ is the nonradiative lifetime. As a consequence, we generalize some our results concerning the “idealized” values obtained from the SCK model to the SFNL one (Section 3.2).
3. Results of simulations and discussions
The parameters and some results of the simulations discussed in the work are presented in Table 1. The first column (Run) presents the number of the simulation run and the second column (Type) the symbol of the potential used. For the mixtures there are additional characters following the symbol (here R6e), which give the value of εAC (e.g. R6e1.1 means: the mixture, the potential (2.10), and εAC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) εBC
εBC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.1). In the following text we refer to a particular simulation run by its number in Table 1. The last two columns of Table 1 present pairs of values of ΔD
(≡
Dfit/D0
1.1). In the following text we refer to a particular simulation run by its number in Table 1. The last two columns of Table 1 present pairs of values of ΔD
(≡
Dfit/D0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) for a0/σAB
1) for a0/σAB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.0 and 1.13 (separated by comas) where Dfit are the “idealized” values. The second last column gives the values for gAB(r)
1.0 and 1.13 (separated by comas) where Dfit are the “idealized” values. The second last column gives the values for gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡
≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and the last one: for gAB(r) calculated from the simulation. All of the evolutions presented in Table 1 have been performed independently except of #7a and #7b. The two results were obtained on the basis of the same evolution run for different moments of initialization of reaction (2.1). The time difference between #7a and #7b is 496 time units.
1, and the last one: for gAB(r) calculated from the simulation. All of the evolutions presented in Table 1 have been performed independently except of #7a and #7b. The two results were obtained on the basis of the same evolution run for different moments of initialization of reaction (2.1). The time difference between #7a and #7b is 496 time units.
Further discussion of the simulations results is mainly focused on the minimization with respect to D. The value of Dfit/D0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 will be considered as a measure of the quality of the SCK approximation. Such an approach is motivated by the fact that the dependence of D on the distance between reactants is also interesting from theoretical point of view (see refs. 31,32). The second reason is given in Section 3.2: for the case of gAB(r)
1 will be considered as a measure of the quality of the SCK approximation. Such an approach is motivated by the fact that the dependence of D on the distance between reactants is also interesting from theoretical point of view (see refs. 31,32). The second reason is given in Section 3.2: for the case of gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡
≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (which is a standard assumption for fitting experimental data with eqn. (2.6))
Dfit and afit are strongly correlated and, as a result, deviations of Dfit from D0 give us also information about the deviations of afit. For a typical fluorescence quenching the reaction radius, a, is close to σAB. Thus, our attention is mainly focused on a
1 (which is a standard assumption for fitting experimental data with eqn. (2.6))
Dfit and afit are strongly correlated and, as a result, deviations of Dfit from D0 give us also information about the deviations of afit. For a typical fluorescence quenching the reaction radius, a, is close to σAB. Thus, our attention is mainly focused on a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5σAB
(called further the main region of a).
1.5σAB
(called further the main region of a).
3.1. Errors of the “idealized” values
The SCK theory assumes that the interactions between the B particles are negligible which is satisfied if the value of xB is very low. In order to estimate the possible influence of xB as well as of N (which may always occur in MD simulations) on results eleven evolutions have been performed for the same ρ and kBT. Eight of them, presented in Table 1 as a single run (#5d–k), were performed for the same xB and N and differed by the initial conditions only.First, let us discuss if the value of D0 obtained in the simulations is reliable. This is an important question because we treat D0 as a reference value so its error directly burdens the “idealized” values. We have noticed a weak dependence of D0 on N, but the effect is on the level of statistical errors and its influence can be neglected. One can see this dependence in Table 1 by considering the difference between D0 for #5a, b, c and D0 for #5d–k. The statistical error in D0 for sets #5d–k (sigma of the Gauss distribution) has been estimated from the mean square deviation as 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−5. This value is too small to explain the difference between #5a–c and #5d–k by a statistical deviation only. Nevertheless, the difference in D0 is small and, taking into account that the possible influence of N on D decreases with an increase of N, the effect for N
10−5. This value is too small to explain the difference between #5a–c and #5d–k by a statistical deviation only. Nevertheless, the difference in D0 is small and, taking into account that the possible influence of N on D decreases with an increase of N, the effect for N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 681
681![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 472 becomes negligible.
472 becomes negligible.
The value 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−5 seems to underestimate the error of D0 of #5d–k if compared with the dispersion of the results of #5a, b, c. The difference between D0 of #5b and #5a,c does not come from different tT. The values of D0 of #5b obtained by taking the limit in the Einstein formula for t
10−5 seems to underestimate the error of D0 of #5d–k if compared with the dispersion of the results of #5a, b, c. The difference between D0 of #5b and #5a,c does not come from different tT. The values of D0 of #5b obtained by taking the limit in the Einstein formula for t![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 656 (cf.
#5a) and t
656 (cf.
#5a) and t![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 738 (cf.
#5c) are very close to that for t
738 (cf.
#5c) are very close to that for t![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tT
(=2184). The dispersion of D0 for #5a, b, c shows that the random (statistical) deviation of D0 is more important than the hypothetical dependence on N. Examination of the results for #5a, b, c, #8a, b, and #10a, b enables us to estimate the error in D0 as not larger than 1%.
tT
(=2184). The dispersion of D0 for #5a, b, c shows that the random (statistical) deviation of D0 is more important than the hypothetical dependence on N. Examination of the results for #5a, b, c, #8a, b, and #10a, b enables us to estimate the error in D0 as not larger than 1%.
The “idealized” values of Dfit obtained by the minimization at the fixed a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a0 and gAB(r)
a0 and gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡
≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for #5a, b, c and #5d–k are presented in Fig. 6. The range of error bars in the Figure has been evaluated from the mean square deviation of the results of #5d–k. Fig. 6 shows that the dependence of Dfit on xB, however noticeable, is very weak. For the main region (a
1 for #5a, b, c and #5d–k are presented in Fig. 6. The range of error bars in the Figure has been evaluated from the mean square deviation of the results of #5d–k. Fig. 6 shows that the dependence of Dfit on xB, however noticeable, is very weak. For the main region (a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5σ) the maximal difference between the results for a very low xB
(the curve–#5d–k) and for low xB
(the symbols–#5a, b, c) amounts to 0.023 (#5b and #5d–k at a0
1.5σ) the maximal difference between the results for a very low xB
(the curve–#5d–k) and for low xB
(the symbols–#5a, b, c) amounts to 0.023 (#5b and #5d–k at a0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ) and, typically it is of about 0.01 - 0.015. Out of the main region, the differences increase with a0 but they do not exceed 0.06. The A and B particles of the mixtures are about 2.5 times larger than in the case of the simple liquids. But, the simulations for the mixtures have been usually performed for much lower xB. Therefore, the deviations due to a finite value of xB should be similar to that presented in Fig. 6. This agrees with the differences in ΔD between #8a (xB
σ) and, typically it is of about 0.01 - 0.015. Out of the main region, the differences increase with a0 but they do not exceed 0.06. The A and B particles of the mixtures are about 2.5 times larger than in the case of the simple liquids. But, the simulations for the mixtures have been usually performed for much lower xB. Therefore, the deviations due to a finite value of xB should be similar to that presented in Fig. 6. This agrees with the differences in ΔD between #8a (xB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.0015) and #8b (xB
0.0015) and #8b (xB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.0005) presented in Table 1.
0.0005) presented in Table 1.
The random errors (error bars) from Fig. 6 are very small (form 0.004 to 0.010 for a0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.0, 3.125, respectively) in spite of the total number of the B particles considered in #5d–k is 704 only; it is a few times less than for any of the remaining simulations. Therefore, we can assume that the random (statistical) errors for the remaining simulations are comparable to these from Fig. 6. In order to confirm it, the statistical errors (corresponding to sigma in the Gauss distribution) have been additionally estimated from the mean square deviation of the results of 6 sets of #10a. For a low a the obtained values are only slightly higher than that in Fig. 6. The highest statistical error for a0
1.0, 3.125, respectively) in spite of the total number of the B particles considered in #5d–k is 704 only; it is a few times less than for any of the remaining simulations. Therefore, we can assume that the random (statistical) errors for the remaining simulations are comparable to these from Fig. 6. In order to confirm it, the statistical errors (corresponding to sigma in the Gauss distribution) have been additionally estimated from the mean square deviation of the results of 6 sets of #10a. For a low a the obtained values are only slightly higher than that in Fig. 6. The highest statistical error for a0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5σAB amounts to 0.0055 for gAB(r)
1.5σAB amounts to 0.0055 for gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡
≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 0.0065 for gAB(r) taken from the simulation. We should note that the latter value contains also the error resulting from taking the limit for tD
1 and 0.0065 for gAB(r) taken from the simulation. We should note that the latter value contains also the error resulting from taking the limit for tD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∞ because for each set of the reagents the limit has been determined independently. The errors sharply increases with a and for a0
∞ because for each set of the reagents the limit has been determined independently. The errors sharply increases with a and for a0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.27σAB
(the highest value of a for the mixtures) the estimated statistical error amounts to 0.027. The statistical errors estimated for low a0 agree with the differences in Dfit between #10a and #10b presented in Table 1. But, the differences between #7a and #7b are nearly three times higher (the differences between #8a and #8b are also high but here xB is not the same) which shows that the adopted statistical errors may be slightly underestimated.
3.27σAB
(the highest value of a for the mixtures) the estimated statistical error amounts to 0.027. The statistical errors estimated for low a0 agree with the differences in Dfit between #10a and #10b presented in Table 1. But, the differences between #7a and #7b are nearly three times higher (the differences between #8a and #8b are also high but here xB is not the same) which shows that the adopted statistical errors may be slightly underestimated.
In the paragraph above we estimated the errors of “idealized” values. Although the estimation is very rough, the values of errors are much smaller than typical values of Dfit/D0-1 resulting form our simulations. Therefore, we can treat the results shown in Sec. 3.2 as a quantitative test of the SCK model. Section 3.3 presents the values of Dfit and afit that have been obtained for a finite tD without considering the limit. The errors of these values are not analyzed here but we believe that they are of the similar order as the errors of the “idealized” values. Therefore, taking into account that, the deviations between the SCK model and the simulations for the case presented in Sec. 3.3 are significantly larger than that analyzed in Sec. 3.2 we can treat the values of Dfit and afit presented in Sec. 3.3 also as quantitative ones but, their errors may be significantly larger then the errors of the “idealized” values.
3.2. The errors of the SCK model for long time phase of fluorescence quenching
All values of Dfit and afit presented in this subsection are the “idealized” values obtained by taking the limit for tD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∞. The results of the minimization at fixed a
∞. The results of the minimization at fixed a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a0 are presented as Dfitversusa0 in Figs. 7–9. We show the results for: Fig. 7, the simple liquids for various densities at a fixed interparticle potential; Fig. 8, the simple liquids for different interparticle potentials at a fixed density; Fig. 9–the mixtures for various temperatures, solute-solvent interactions, and RC. The filled symbols always show the results for gAB(r)
a0 are presented as Dfitversusa0 in Figs. 7–9. We show the results for: Fig. 7, the simple liquids for various densities at a fixed interparticle potential; Fig. 8, the simple liquids for different interparticle potentials at a fixed density; Fig. 9–the mixtures for various temperatures, solute-solvent interactions, and RC. The filled symbols always show the results for gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡
≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The empty symbols connected by a line show the results obtained by including gAB(r)
(evaluated from eqn. (2.14)) in eqn. (2.6). First, general conclusion from Figs. 7–9 agrees with the results of Zhou and Szabo.22 An inclusion of real gAB(r) significantly improves an agreement between the simulation data and the SCK model.
1. The empty symbols connected by a line show the results obtained by including gAB(r)
(evaluated from eqn. (2.14)) in eqn. (2.6). First, general conclusion from Figs. 7–9 agrees with the results of Zhou and Szabo.22 An inclusion of real gAB(r) significantly improves an agreement between the simulation data and the SCK model.
 | ||
Fig. 7 The “idealized” values. Dfit/D0–1 at fixed a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a0 as a function of a0 for the L-J potential and various densities. Symbols: triangle up–#1 (ρ a0 as a function of a0 for the L-J potential and various densities. Symbols: triangle up–#1 (ρ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5787), square–#2 (ρ 0.5787), square–#2 (ρ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.7830), triangle down–#5b (ρ 0.7830), triangle down–#5b (ρ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.9358). Filled symbols–gAB(r) 0.9358). Filled symbols–gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡ ≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.0, empty symbols connected by a solid line–gAB(r) taken from the simulations. 1.0, empty symbols connected by a solid line–gAB(r) taken from the simulations. | ||
 | ||
Fig. 8 The “idealized” values. Dfit/D0–1 at fixed a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a0 as a function of a0 for various potentials at the same state point (ρ a0 as a function of a0 for various potentials at the same state point (ρ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.9358, kBT 0.9358, kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.0). Symbols: triangle up–#3 (HSS), square–#4 (SS), triangle down–#5b (LJ), circle–#6 (R6e). Remaining notation as in Fig. 7. 1.0). Symbols: triangle up–#3 (HSS), square–#4 (SS), triangle down–#5b (LJ), circle–#6 (R6e). Remaining notation as in Fig. 7. | ||
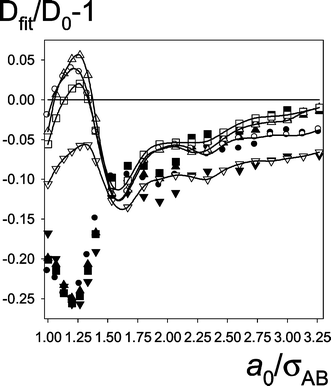 | ||
Fig. 9 The “idealized” values. Dfit/D0–1 at fixed a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a0 as a function of a0 for mixtures at various temperatures (kBT), cut-off distances (RC) and solute-solvent interactions (εAC). Symbols: triangle up–#7, square–#8b, triangle down–#9, circle–#10. Remaining notation as in Fig. 7. a0 as a function of a0 for mixtures at various temperatures (kBT), cut-off distances (RC) and solute-solvent interactions (εAC). Symbols: triangle up–#7, square–#8b, triangle down–#9, circle–#10. Remaining notation as in Fig. 7. | ||
For gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡
≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 the main conclusion is that for all the cases except of the largest diffusion (triangle up in Fig. 7, the case is discussed separately) the relative deviations of Dfit from D0
(Dfit/D0
1 the main conclusion is that for all the cases except of the largest diffusion (triangle up in Fig. 7, the case is discussed separately) the relative deviations of Dfit from D0
(Dfit/D0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) can be described by similar curves with a minimum at a/σAB
1) can be described by similar curves with a minimum at a/σAB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≈
≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.4 for the simple liquids and a/σAB
1.4 for the simple liquids and a/σAB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≈
≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.2 for the mixtures. The minimum values are about:–0.21 and–0.25 respectively. Both the shape of Dfit/D0
1.2 for the mixtures. The minimum values are about:–0.21 and–0.25 respectively. Both the shape of Dfit/D0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 curves and the minimum values are similar in spite of significant differences in densities and interparticle interactions. Therefore, we believe that the presented dependence of Dfit/D0 on a0 is generally held for spherical molecules if D0 is small. Some differences between the simple liquids and the mixtures occur in Dfit/D0
1 curves and the minimum values are similar in spite of significant differences in densities and interparticle interactions. Therefore, we believe that the presented dependence of Dfit/D0 on a0 is generally held for spherical molecules if D0 is small. Some differences between the simple liquids and the mixtures occur in Dfit/D0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at a0
1 at a0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≈
≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σAB. For the simple liquids (Fig. 8) the deviation at a0
σAB. For the simple liquids (Fig. 8) the deviation at a0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σAB is much closer to 0 than the value at the minimum. For the mixtures (Fig. 9), the deviations at a0
σAB is much closer to 0 than the value at the minimum. For the mixtures (Fig. 9), the deviations at a0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σAB are strongly negative and comparable with the value at the minimum (see also Table 1). According to our considerations from Sec. 2.2.1, we can also predict that, if gAB(r)
σAB are strongly negative and comparable with the value at the minimum (see also Table 1). According to our considerations from Sec. 2.2.1, we can also predict that, if gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡
≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 then the minimum values of deviations of Dfit from D0 for the SFNL model are very close to the values from Figs. 7–9.
1 then the minimum values of deviations of Dfit from D0 for the SFNL model are very close to the values from Figs. 7–9.
Fig. 7 shows that, the deviations in Dfit/D0-1 for gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡
≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at high D0
(#1 and, to some extent, #2) are qualitatively different form the discussed above. They are characterized not only by a minimum, but also by a maximum. For #1 the maximum is very sharp (+0.55 at a0
1 at high D0
(#1 and, to some extent, #2) are qualitatively different form the discussed above. They are characterized not only by a minimum, but also by a maximum. For #1 the maximum is very sharp (+0.55 at a0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.063σAB). The effect is additionally strengthened because ∂kSCK/∂DS
1.063σAB). The effect is additionally strengthened because ∂kSCK/∂DS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 for DS
0 for DS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∞. The sharp maximum is a consequence of gAB(r)
∞. The sharp maximum is a consequence of gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡
≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 because for gAB(r) taken from the simulation Dfit/D0
1 because for gAB(r) taken from the simulation Dfit/D0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at a0
1 at a0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.063σAB decreases to −.075 only.
1.063σAB decreases to −.075 only.
The deep minimum which appears in Dfit/D0 curves obtained for gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡
≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (black symbols) comes from the presence of the first coordination shell in the structure of real liquids. The shell is manifested by a sharp maximum in gAB(r) at r slightly above σAB
(e.g.Fig. 2). The screening by the first coordination shell decreases the probability of reaction between A* with B. Due to the finite size of particles the screening is effective at a range of distances larger than the width of the first peak of gAB(r)
(it can be seen as the first minimum of gAB(r)). As a result, Dfit calculated with the assumption gAB(r)
1 (black symbols) comes from the presence of the first coordination shell in the structure of real liquids. The shell is manifested by a sharp maximum in gAB(r) at r slightly above σAB
(e.g.Fig. 2). The screening by the first coordination shell decreases the probability of reaction between A* with B. Due to the finite size of particles the screening is effective at a range of distances larger than the width of the first peak of gAB(r)
(it can be seen as the first minimum of gAB(r)). As a result, Dfit calculated with the assumption gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡
≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for values of a0 in the range where screening is effective are significantly reduced if compared with the real ones. At very short distances the probability of collision with a screening particle decreases and the contribution to the transport process coming from ballistic motions becomes significant. As a result, the rate of approaches between A* and B increases. This explains why, for simple liquids, the values of Dfit/D0 are significantly higher for a0
1 for values of a0 in the range where screening is effective are significantly reduced if compared with the real ones. At very short distances the probability of collision with a screening particle decreases and the contribution to the transport process coming from ballistic motions becomes significant. As a result, the rate of approaches between A* and B increases. This explains why, for simple liquids, the values of Dfit/D0 are significantly higher for a0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σAB than at the minimum (see Figs. 7, 8 and ΔD(1.0,1.13)g≡1 from Table 1). For the mixtures (Fig. 9) the increase in Dfit/D0 for a0 approaching σAB is much less pronounced. We think that it is related to the presence of solvent. The C molecules, which are smaller than A (and B) ones, can efficiently screen B molecules at distances very close to σAB
(which is impossible for the simple liquids) and so reduce the increase of Dfit at small a. It is confirmed by the shape of gBC(r) function which has a sharp maximum for r
σAB than at the minimum (see Figs. 7, 8 and ΔD(1.0,1.13)g≡1 from Table 1). For the mixtures (Fig. 9) the increase in Dfit/D0 for a0 approaching σAB is much less pronounced. We think that it is related to the presence of solvent. The C molecules, which are smaller than A (and B) ones, can efficiently screen B molecules at distances very close to σAB
(which is impossible for the simple liquids) and so reduce the increase of Dfit at small a. It is confirmed by the shape of gBC(r) function which has a sharp maximum for r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≈
≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.9σAB. The maximum in the local probability density at small intermolecular distances is also present if molecules are non-spherical. Therefore, the decrease of Dfit if a is close to the distance of the maximum is expected in analysis of experimental results. Such tendency (Dfit lower than the value of diffusion coefficient) has been recently observed.17 However, the values of Dfit analyzed in this experiment were not the “idealized” ones and, as it is shown in Section 3.3, they may be burdened with large errors due to non-diffusive processes neglected by the SCK model.
0.9σAB. The maximum in the local probability density at small intermolecular distances is also present if molecules are non-spherical. Therefore, the decrease of Dfit if a is close to the distance of the maximum is expected in analysis of experimental results. Such tendency (Dfit lower than the value of diffusion coefficient) has been recently observed.17 However, the values of Dfit analyzed in this experiment were not the “idealized” ones and, as it is shown in Section 3.3, they may be burdened with large errors due to non-diffusive processes neglected by the SCK model.
Figs. 7–9 show that, the result of including the real gAB(r) in (2.6) depends on a0. In the main region (a0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5σAB), the inclusion significantly improves the agreement. The effect is especially strong for the potential R6e (the most realistic potential) for which Dfit/D0
1.5σAB), the inclusion significantly improves the agreement. The effect is especially strong for the potential R6e (the most realistic potential) for which Dfit/D0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for real gAB(r) is typically a few times lower than that for gAB(r)
1 for real gAB(r) is typically a few times lower than that for gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡
≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (compare ΔD from Table 1). Figs. 7–9 show also that, opposite to the case of gAB(r)
1 (compare ΔD from Table 1). Figs. 7–9 show also that, opposite to the case of gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡
≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, the curves obtained for real gAB(r) are similar only out of the main region of a. In the main region, the shapes of the curves visibly depend on the interparticle potential (Fig. 8) as well as on ρ
(compare Dfit/D0 for L-J potential in Figs. 7 and 8). All simulations for the mixtures were performed for the same density and for the fixed potential type, eqn. (2.10). As a result, the curves have similar shapes but the extreme values are different. Changes of εAC from 1.0 to 1.5 (#9 and #10 in Table 1), as well as the change of kBT from 1.0 to 1.5 or RC from 1.65 to 1.95, do not modify significantly the functional dependence of Dfit/D0 on a. The values of Dfit/D0 increase with the increase of liquid bonding (decrease of D0). In spite of significant differences between parameters of intermolecular interactions we have not observed qualitative changes in the behavior of Dfit for the mixtures. We think it is related to a high temperature of the system. Simulations at distinctly lower temperatures were beyond our computational facilities. In such case tT must be very large to attain equilibrium and perform credible measurements at a very low diffusion.
1, the curves obtained for real gAB(r) are similar only out of the main region of a. In the main region, the shapes of the curves visibly depend on the interparticle potential (Fig. 8) as well as on ρ
(compare Dfit/D0 for L-J potential in Figs. 7 and 8). All simulations for the mixtures were performed for the same density and for the fixed potential type, eqn. (2.10). As a result, the curves have similar shapes but the extreme values are different. Changes of εAC from 1.0 to 1.5 (#9 and #10 in Table 1), as well as the change of kBT from 1.0 to 1.5 or RC from 1.65 to 1.95, do not modify significantly the functional dependence of Dfit/D0 on a. The values of Dfit/D0 increase with the increase of liquid bonding (decrease of D0). In spite of significant differences between parameters of intermolecular interactions we have not observed qualitative changes in the behavior of Dfit for the mixtures. We think it is related to a high temperature of the system. Simulations at distinctly lower temperatures were beyond our computational facilities. In such case tT must be very large to attain equilibrium and perform credible measurements at a very low diffusion.
For a typical liquid system, the assumption gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡
≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 is a very rough simplification so the model improves significantly when the real gAB(r) is taken into account. The Smoluchowski approach treats reactants as large molecules moving in a Brownian medium and intermolecular interactions are incorporated only viagAB(r). This is also an approximation because it treats the interactions in a statistically averaged way. Nevertheless, it describes the presence of local correlations more realistically than the assumption that they are absent (gAB(r)
1 is a very rough simplification so the model improves significantly when the real gAB(r) is taken into account. The Smoluchowski approach treats reactants as large molecules moving in a Brownian medium and intermolecular interactions are incorporated only viagAB(r). This is also an approximation because it treats the interactions in a statistically averaged way. Nevertheless, it describes the presence of local correlations more realistically than the assumption that they are absent (gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡
≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). The observed deviations in Dfit/D0 as well as the differences between these deviations observed for various systems are the consequence of higher order correlations between molecules. In order to describe them one may consider distance dependent diffusion, DS(r) in eqn. (2.6). Some theoretical works on the distance dependent diffusion, D(r), were presented31,32 but the problem has not been solved yet. The results presented in Figs. 6–9 suggest that, especially for strongly bonded liquids with a low diffusion, the inclusion of a correct form of gAB function is more important than taking into account DS is a function of r. Out of the main region the Dfit curves from Figs. 6–9 qualitatively agree with the form of D(r) proposed by Northrup and Hynes.31 However, Fig. 7 shows that the deviations of Dfit from D0 depend on ρ, which was not considered in the mentioned paper. A more detailed analysis of the D(r) function on the basis of the presented results is impossible. Dfit(a0) obtained here from the fit of kSCK(t) for constant DS may be treated only as a very rough estimation of DS(a0) because if DS is a function of r, the formula for k(t) is slightly different23 than eqn. (2.6) taken to the minimization.
1). The observed deviations in Dfit/D0 as well as the differences between these deviations observed for various systems are the consequence of higher order correlations between molecules. In order to describe them one may consider distance dependent diffusion, DS(r) in eqn. (2.6). Some theoretical works on the distance dependent diffusion, D(r), were presented31,32 but the problem has not been solved yet. The results presented in Figs. 6–9 suggest that, especially for strongly bonded liquids with a low diffusion, the inclusion of a correct form of gAB function is more important than taking into account DS is a function of r. Out of the main region the Dfit curves from Figs. 6–9 qualitatively agree with the form of D(r) proposed by Northrup and Hynes.31 However, Fig. 7 shows that the deviations of Dfit from D0 depend on ρ, which was not considered in the mentioned paper. A more detailed analysis of the D(r) function on the basis of the presented results is impossible. Dfit(a0) obtained here from the fit of kSCK(t) for constant DS may be treated only as a very rough estimation of DS(a0) because if DS is a function of r, the formula for k(t) is slightly different23 than eqn. (2.6) taken to the minimization.
All the afit/a0 curves obtained from the minimization fixed D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D0 and gAB(r)
D0 and gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡
≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 are qualitatively similar to the curves from Figs. 6–9. As an example, the “idealized” values of afit/a0-1 and Dfit/D0
1 are qualitatively similar to the curves from Figs. 6–9. As an example, the “idealized” values of afit/a0-1 and Dfit/D0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 as a function of a0 for gAB(r)
1 as a function of a0 for gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡
≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 are presented in Fig. 10. The both curves are obtained from the minimization keeping the other parameter constant. The correlation between Dfit and afit is evident. The curves differ only by amplitudes, which for afit/a0-1 typically amounts to 70–80% of that of Dfit/D0
1 are presented in Fig. 10. The both curves are obtained from the minimization keeping the other parameter constant. The correlation between Dfit and afit is evident. The curves differ only by amplitudes, which for afit/a0-1 typically amounts to 70–80% of that of Dfit/D0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.
1.
 | ||
Fig. 10 The “idealized” values. Dfit/D0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) − −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at fixed a 1 at fixed a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a0
(triangles down) and afit/a0 a0
(triangles down) and afit/a0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) − −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at fixed D 1 at fixed D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D0
(triangles up) for gAB(r) D0
(triangles up) for gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡ ≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 as a function of a0 for #6. 1 as a function of a0 for #6. | ||
The minimization with respect to both D and a have been performed only for gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡
≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. As example, the “idealized” values of Dfit/D0 and afit/a0 as functions of a0 for #5b and #9 are presented in Fig. 11. The functional dependencies are typical for the simulated liquids. A comparison of Fig. 11 with Figs. 8 and 9 shows that, for a low a0, the minimization with respect to both D and a gives usually lower deviations than the fit for a single parameter. This is the result of the correlations between Dfit and afit
(see Fig. 10). The correlation can be also noticed analyzing the form of eqn. (2.6). For example, for low DS and t
1. As example, the “idealized” values of Dfit/D0 and afit/a0 as functions of a0 for #5b and #9 are presented in Fig. 11. The functional dependencies are typical for the simulated liquids. A comparison of Fig. 11 with Figs. 8 and 9 shows that, for a low a0, the minimization with respect to both D and a gives usually lower deviations than the fit for a single parameter. This is the result of the correlations between Dfit and afit
(see Fig. 10). The correlation can be also noticed analyzing the form of eqn. (2.6). For example, for low DS and t![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∞, kSCK(t)
∞, kSCK(t)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≈
≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4πDSa and the both parameters are fully correlated.
4πDSa and the both parameters are fully correlated.
 | ||
Fig. 11 The “idealized” values. Simultaneous fitting. Dfit/D0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) − −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (filled symbols) and afit/a0 1 (filled symbols) and afit/a0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) − −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (empty symbols) for gAB(r) 1 (empty symbols) for gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡ ≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 as a function of a0 for two simulations: square, #5b, triangle down, #9. 1 as a function of a0 for two simulations: square, #5b, triangle down, #9. | ||
3.3. The early phase of fluorescence quenching process
In order to compare the results presented in this subsection with a real experiment we assume the following values of the parameters of the A (≡ B) particles:mA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 amu, σAB 200 amu, σAB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) × ×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−8 cm, εAB 10−8 cm, εAB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300kB 300kB | (3.1) |
Figs. 12 and 13 show k(t)/k(0) as a function of time for the early phase of fluorescence quenching for a0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σAB. The values of k(0)
σAB. The values of k(0)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kSCK(0) have been evaluated from eqns. (2.5) and (2.8) taking gAB(σAB) from the simulations. k(t)/k(0) obtained from the simulations (circles) is compared with the theoretical results obtained from the numerical solution of eqns. (2.4) and (2.5) with the real gAB(r) taken from simulations (the solid line) and the formula (2.6) for gAB(r)
kSCK(0) have been evaluated from eqns. (2.5) and (2.8) taking gAB(σAB) from the simulations. k(t)/k(0) obtained from the simulations (circles) is compared with the theoretical results obtained from the numerical solution of eqns. (2.4) and (2.5) with the real gAB(r) taken from simulations (the solid line) and the formula (2.6) for gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡
≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (the dashed line). The theoretical curves have been calculated for DS
1 (the dashed line). The theoretical curves have been calculated for DS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2D0 and a
2D0 and a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σAB. According to Table 1 the values of ΔD for #6 (Fig. 12) and #7a (Fig. 13) are small except of #7a for gAB(r)
σAB. According to Table 1 the values of ΔD for #6 (Fig. 12) and #7a (Fig. 13) are small except of #7a for gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡
≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. As a result, except of the case mentioned, the influence of the errors coming from the fact that DS is a function of r
(see Section 3.2) can be neglected. The differences between the solid curve and the circles come from the fact that the SCK model neglects non-diffusive motion. For the case shown on Fig. 12
(larger D0) the curve obtained by the numerical solution matches the “experimental” points in a very wide range of times and the model fails just for t
1. As a result, except of the case mentioned, the influence of the errors coming from the fact that DS is a function of r
(see Section 3.2) can be neglected. The differences between the solid curve and the circles come from the fact that the SCK model neglects non-diffusive motion. For the case shown on Fig. 12
(larger D0) the curve obtained by the numerical solution matches the “experimental” points in a very wide range of times and the model fails just for t![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tB
(in this case
tB
(in this case![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≈
≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (mA/εA)1/2σAB
[7 ps]). This break down is also seen in Fig. 13 at t
(mA/εA)1/2σAB
[7 ps]). This break down is also seen in Fig. 13 at t![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tB close to that for #6 from Fig. 12. The break down can be explained considering the ballistic motions. At the very early stage of the reaction some A* and B molecules can come closer than a without colliding with another molecule (i.e.via ballistic motion). Such way of transport is much faster than diffusive one. As a result, for very short times, k(t) obtained from the simulations is significantly higher than that resulting from the model (which takes into account diffusion only). The effect lasts for a very short time because the time of the mean free flight for a dense liquid is very low (a few times shorter than (mA/εA)1/2σAB, which agrees with the value of tB). On Fig. 13 the differences between the solid curve and the circles for t
tB close to that for #6 from Fig. 12. The break down can be explained considering the ballistic motions. At the very early stage of the reaction some A* and B molecules can come closer than a without colliding with another molecule (i.e.via ballistic motion). Such way of transport is much faster than diffusive one. As a result, for very short times, k(t) obtained from the simulations is significantly higher than that resulting from the model (which takes into account diffusion only). The effect lasts for a very short time because the time of the mean free flight for a dense liquid is very low (a few times shorter than (mA/εA)1/2σAB, which agrees with the value of tB). On Fig. 13 the differences between the solid curve and the circles for t![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tB are larger than in Fig. 12
(the contribution from diffusive process decreases with D0) and the inconsistency between the model and simulations spreads for the time of an order of magnitude longer than tB. This inconsistency probably results from the higher order correlations between the reagents (for #7 the correlations are much stronger than for #6). However the effect is weaker than for t
tB are larger than in Fig. 12
(the contribution from diffusive process decreases with D0) and the inconsistency between the model and simulations spreads for the time of an order of magnitude longer than tB. This inconsistency probably results from the higher order correlations between the reagents (for #7 the correlations are much stronger than for #6). However the effect is weaker than for t![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tB.
tB.
 | ||
Fig. 12
k(t)/k(0) as a function of time for the early phase of fluorescence quenching for simulation run #6 at a0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σAB
(circles) and the SCK model for DS σAB
(circles) and the SCK model for DS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2D0 and a 2D0 and a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σAB. The solid line: the SCK model for gAB(r) taken from simulations (from the numerical solution of eqns. (2.4) and (2.5)). The dashed line: the SCK model for gAB(r) σAB. The solid line: the SCK model for gAB(r) taken from simulations (from the numerical solution of eqns. (2.4) and (2.5)). The dashed line: the SCK model for gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡ ≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. 1. | ||
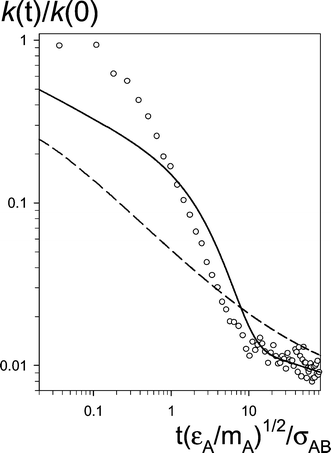 | ||
Fig. 13
k(t)/k(0) as a function of time for the early phase of fluorescence quenching of simulation run #7a at a0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σAB and the SCK model for DS σAB and the SCK model for DS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2D0 and a 2D0 and a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σAB. Notation as in Fig. 12. σAB. Notation as in Fig. 12. | ||
The inconsistency between the solid curves and the dashed ones in Figs. 12 and 13 is not smaller than the one coming from the neglect of non-diffusive processes (the solid line and the simulation data) and, for both #6 and #7a, the effect is observed for times an order of magnitude larger than tB. The inconsistency is an obvious consequence of the assumption that gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡
≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. From the physical point of view the most important conclusion is that using the simplification gAB(r)
1. From the physical point of view the most important conclusion is that using the simplification gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡
≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 it is not possible to describe the short time dependence of the “experimental”
k(t) even in a qualitative way. This means that such simplification neglects some basic processes important for a description of the early stage of fluorescence quenching.
1 it is not possible to describe the short time dependence of the “experimental”
k(t) even in a qualitative way. This means that such simplification neglects some basic processes important for a description of the early stage of fluorescence quenching.
In the following we discuss the influence of the inconsistencies discussed above on the results of minimization. The inconsistency can be eliminated taking the limit tD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∞
(the “idealized” values) but in a real experiment this is frequently impossible. Our attention is focused especially on the case of tD
∞
(the “idealized” values) but in a real experiment this is frequently impossible. Our attention is focused especially on the case of tD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 which means that all the obtained experimental data are treated as a whole, which is typical for analysis of experimental results. All the results of the minimization presented below have been obtained for gAB(r)
0 which means that all the obtained experimental data are treated as a whole, which is typical for analysis of experimental results. All the results of the minimization presented below have been obtained for gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡
≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. In a real experiment, the influence of initial stage of the fluorescence quenching on results of the minimization strongly depends on the parameters describing the system and the experimental setup, potentials of intermolecular interactions, the de-excitation process studied, and other experimental conditions, which are beyond the considered system. Therefore, we have decided to give two examples only (Figs. 14, 15) and present conclusions of a general character.
1. In a real experiment, the influence of initial stage of the fluorescence quenching on results of the minimization strongly depends on the parameters describing the system and the experimental setup, potentials of intermolecular interactions, the de-excitation process studied, and other experimental conditions, which are beyond the considered system. Therefore, we have decided to give two examples only (Figs. 14, 15) and present conclusions of a general character.
![D
fit/D0 − 1 at fixed a = a0 = σAB as a function of tD for various tT for the mixture #8a. D0 = 0.00616 [6.36 × 10−6 cm2 s−1]. Horizontal line–the limit of Dfit(tD) attained for tT ≥ 800 [2700 ps]
(the critical value). Lines with symbols: circles–tT = 25 [84 ps], triangles down–tT = 100 [340 ps], squares–tT = 400 [1350 ps].](/image/article/2004/CP/b308680a/b308680a-f14.gif) | ||
Fig. 14
D
fit/D0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) − −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at fixed a 1 at fixed a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a0 a0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σAB as a function of tD for various tT for the mixture #8a. D0 σAB as a function of tD for various tT for the mixture #8a. D0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.00616 [6.36 0.00616 [6.36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) × ×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−6 cm2 s−1]. Horizontal line–the limit of Dfit(tD) attained for tT 10−6 cm2 s−1]. Horizontal line–the limit of Dfit(tD) attained for tT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≥ ≥![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 [2700 ps]
(the critical value). Lines with symbols: circles–tT 800 [2700 ps]
(the critical value). Lines with symbols: circles–tT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 [84 ps], triangles down–tT 25 [84 ps], triangles down–tT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 [340 ps], squares–tT 100 [340 ps], squares–tT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 [1350 ps]. 400 [1350 ps]. | ||
![Simultaneous fitting. Dfit/D0 − 1 (empty symbols) and afit/a0–1 (filled symbols) as functions of tD for various tT for #5b. D0 = 0.02797 [2.50 × 10−5 cm2 s−1]. Lines and symbols: triangles down, tT = 100 [716 ps]; squares, tT = 420 [3000 ps]; triangles up, tT = 2184 [15 600 ps].](/image/article/2004/CP/b308680a/b308680a-f15.gif) | ||
Fig. 15 Simultaneous fitting. Dfit/D0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) − −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (empty symbols) and afit/a0–1 (filled symbols) as functions of tD for various tT for #5b. D0 1 (empty symbols) and afit/a0–1 (filled symbols) as functions of tD for various tT for #5b. D0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.02797 [2.50 0.02797 [2.50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) × ×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−5 cm2 s−1]. Lines and symbols: triangles down, tT 10−5 cm2 s−1]. Lines and symbols: triangles down, tT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 [716 ps]; squares, tT 100 [716 ps]; squares, tT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 420 [3000 ps]; triangles up, tT 420 [3000 ps]; triangles up, tT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2184 [15 2184 [15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 ps]. 600 ps]. | ||
The dependence of Dfit/D0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at fixed a for #8a on tD for three different total times of measurement, tT, are presented in Fig. 14. The deviations of Dfit from D0 at tD
1 at fixed a for #8a on tD for three different total times of measurement, tT, are presented in Fig. 14. The deviations of Dfit from D0 at tD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 are extremely large. The effect is only due to inconsistency of the model with experiment, i.e. from the fact that the ballistic motion is neglected. The simulated system is always in the mechanical equilibrium state and reaction (2.1) does not disturb it anyway (see Section 2.1). The values of Dfit/D0
0 are extremely large. The effect is only due to inconsistency of the model with experiment, i.e. from the fact that the ballistic motion is neglected. The simulated system is always in the mechanical equilibrium state and reaction (2.1) does not disturb it anyway (see Section 2.1). The values of Dfit/D0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 strongly decrease with an increase of tT, which is a consequence of the increased relative contribution coming from the diffusive processes. Analogically, a comparison between results of different simulation runs show that the deviation at tD
1 strongly decrease with an increase of tT, which is a consequence of the increased relative contribution coming from the diffusive processes. Analogically, a comparison between results of different simulation runs show that the deviation at tD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 decreases with an increase of D0
(compare also Figs. 12 and 13). We have also found that Dfit as a function of tD strongly depends on a. For example, for the simulated mixtures, Dfit/D0-1 for tD
0 decreases with an increase of D0
(compare also Figs. 12 and 13). We have also found that Dfit as a function of tD strongly depends on a. For example, for the simulated mixtures, Dfit/D0-1 for tD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 changes its value from a large and positive at a0/σAB
0 changes its value from a large and positive at a0/σAB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.0 (e.g.Fig. 14) to a large and negative at a0/σAB
1.0 (e.g.Fig. 14) to a large and negative at a0/σAB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.27. In a real experiment a is never determined exactly (the molecules are not spherical ones) so, we are unable to estimate even a tendency and say if the effect overestimates or underestimates the resulting values of Dfit. The curve marked with triangles down in Fig. 14 has been obtained at the conditions similar to that of the experiment of Krystkowiak and Maciejewski.17,18 The corresponding deviations at tD
1.27. In a real experiment a is never determined exactly (the molecules are not spherical ones) so, we are unable to estimate even a tendency and say if the effect overestimates or underestimates the resulting values of Dfit. The curve marked with triangles down in Fig. 14 has been obtained at the conditions similar to that of the experiment of Krystkowiak and Maciejewski.17,18 The corresponding deviations at tD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 amount to about 50% which is over two times higher than the deviation for the “idealized” values from Sec. 3.2.
0 amount to about 50% which is over two times higher than the deviation for the “idealized” values from Sec. 3.2.
The convergence in Fig. 14 seems to be very fast but as one can see the curves converge to the values different than the limit for tD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∞ and if tT is small the difference may be quite large (see, especially the curve for tT
∞ and if tT is small the difference may be quite large (see, especially the curve for tT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100). The effect occurs if tT is lower than some critical value (as an example the value is given in the description of Figs. 14). A precise analysis shows that actually, for small tT the value of Dfit systematically changes with tD and the limit does not exist. But the rate of change is sometimes very low and in a real experiment the fact that the limit has not been attained yet can be missed especially because the analyzed curve loses its stability with tD approaching tT.
100). The effect occurs if tT is lower than some critical value (as an example the value is given in the description of Figs. 14). A precise analysis shows that actually, for small tT the value of Dfit systematically changes with tD and the limit does not exist. But the rate of change is sometimes very low and in a real experiment the fact that the limit has not been attained yet can be missed especially because the analyzed curve loses its stability with tD approaching tT.
Fig. 15 presents the results of the minimization for both D and a for #5b. The shapes of the curves and the time scale are similar to that in Fig. 14 but the amplitudes are much higher in spite of D0 being about four times larger than in #8a. The most surprising result is that for the highest tT
(=2184 [15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 ps]) the deviations at tD
600 ps]) the deviations at tD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 attain nearly 100%. It means that even if the data are collected for a very long time (for #5b, tT
0 attain nearly 100%. It means that even if the data are collected for a very long time (for #5b, tT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2184
2184![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (D0tT)/σ2
(D0tT)/σ2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≈
≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 61) the contribution from the very early stage of quenching process is still important and may significantly influence the fit. This fact questions the credibility of results obtained when real experimental data are analyzed as a whole (i.e.tD
61) the contribution from the very early stage of quenching process is still important and may significantly influence the fit. This fact questions the credibility of results obtained when real experimental data are analyzed as a whole (i.e.tD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0). In the units resulting from (3.1) both D0
(=[2.5
0). In the units resulting from (3.1) both D0
(=[2.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−5 cm2 s−1]) and tT
(the minimal one
10−5 cm2 s−1]) and tT
(the minimal one![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 [720 ps]) are significantly larger than those describing the system studied by Krystkowiak and Maciejewski.17,18,33 For lower tT and D0
(as in their experiment) the deviations should be higher. Therefore, large errors discussed in their work18 may have the same origin as the inconsistencies between the SCK model and our simulations.
100 [720 ps]) are significantly larger than those describing the system studied by Krystkowiak and Maciejewski.17,18,33 For lower tT and D0
(as in their experiment) the deviations should be higher. Therefore, large errors discussed in their work18 may have the same origin as the inconsistencies between the SCK model and our simulations.
The main technical problem of fitting both parameters at once is not the convergence itself (as in the case on Fig. 14) but a lack of stability which is a consequence of the correlation between D and a (see also Fig. 10). If tT is not sufficiently larger than tD then the fitted values fluctuate with opposite phases and the amplitude of the fluctuations increases with increasing tD (i.e.tD approaching tT). This effect appears for much lower tD than the instability of the minimization with respect to one of the parameters.
4. Summary and final conclusions
In this work we have presented the results of molecular dynamics tests of the SCK model of diffusion controlled de-excitation process for spherical molecules. The simulations have been performed for various potentials describing interparticle interactions. We have found that the shape of potential has a little influence on the results thus we believe that the conclusions presented below can be generalized to other molecules of spherical or close to spherical shape. Our MD simulations were performed assuming that the reaction is instantaneous which agrees with the assumptions of the SCK model (the assumption (2.2)). As a result, we were able extract the errors coming only from the description based on the Smoluchowski equation. The agreement of the reaction radius afit and the diffusion coefficient Dfit obtained from the time dependent rate constant, k(t), with their values from simulations was considered as a qualitative measure of the model accuracy. In most cases studied here the inconsistencies appeared to be large and some times (Sec.3.3) the errors in Dfit and afit were of the same order of magnitude as the reference values. This shows that typical applications of the SCK model of fluorescence quenching process (i.e. with the assumption gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡
≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) should be treated only as a rough simplification, even if the assumption on instantaneous reaction is justified.
1) should be treated only as a rough simplification, even if the assumption on instantaneous reaction is justified.
According to results of the work a successful application of the SCK model to interpret experimental data (to extract afit and Dfit) mainly depends on possibility of discarding the data coming from the early stage of fluorescence quenching. If this condition is fulfilled (here, the “idealized” situation–Sec. 3.2) then the most important conclusions for the main region of a
(σAB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a
a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5σAB) are the following:
1.5σAB) are the following:
(i) If gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡
≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and diffusion is small then the values of Dfit/D0
1 and diffusion is small then the values of Dfit/D0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for a fixed a are almost always negative and can attain even 25%. This conclusion concerns also the SFNL model because it is asymptotically equivalent with the SCK one. For the case of a large diffusion (here, D0
1 for a fixed a are almost always negative and can attain even 25%. This conclusion concerns also the SFNL model because it is asymptotically equivalent with the SCK one. For the case of a large diffusion (here, D0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.197σ(ε/m)1/2) the maximum deviation exceeds +50%.
0.197σ(ε/m)1/2) the maximum deviation exceeds +50%.
(ii) The deviations significantly decrease if we include the information on gAB(r) into the model. However, the errors of about 10% may still occur. We expect similar improvement for the SNFL model. The inclusion of gAB(r) is much more physical than the assumption gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡
≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.
1.
(iii) The relative deviations of afit at fixed D and gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡
≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 are strongly correlated to that of Dfit at fixed a; they have the same sign and their amplitude is decreased by about 20–30%. As a consequence, the results of the minimization with respect of both D and a are usually closer to the real values than the results obtained from single parameter minimization at fixed a or D.
1 are strongly correlated to that of Dfit at fixed a; they have the same sign and their amplitude is decreased by about 20–30%. As a consequence, the results of the minimization with respect of both D and a are usually closer to the real values than the results obtained from single parameter minimization at fixed a or D.
We expect that the long time behavoiur of k(t) does not depend on a particular form of the microscopic reaction cross section and its asymptotic form should be similar to an SCK model with “effective”
k0 and a. Therefore our conclusions for errors in the “idealized” values (in particular the negative deviation in Dfit if gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡
≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) should apply to any reaction.
1) should apply to any reaction.
The results presented in Sec. 3.3 show that the SCK model fails completely for a very short time. If the distribution function of the reagents is incorporated into the model than in the considered examples (Figs. 12 and 13) significant differences in the k(t) curves are observed for times shorter than tB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≈
≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (mA/εA)1/2σAB[7 ps]. If gAB(r)
(mA/εA)1/2σAB[7 ps]. If gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡
≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 then the qualitative inconsistency between the model and simulations spreads out for times of an order of magnitude longer than tB. Therefore, if one treats the obtained experimental data as a whole (i.e.tD
1 then the qualitative inconsistency between the model and simulations spreads out for times of an order of magnitude longer than tB. Therefore, if one treats the obtained experimental data as a whole (i.e.tD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0) then the assumption gAB(r)
0) then the assumption gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡
≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 does lead to large errors in the parameters obtained from the minimization. The errors are especially high if D is small and the time of measurement is short. The example form Sec. 3.3 shows that for tT
1 does lead to large errors in the parameters obtained from the minimization. The errors are especially high if D is small and the time of measurement is short. The example form Sec. 3.3 shows that for tT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 [340 ps] and D0
100 [340 ps] and D0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.00616 [6.36
0.00616 [6.36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−6 cm2 s−1] the deviations for tD
10−6 cm2 s−1] the deviations for tD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 attain 50%. If the minimization is performed with respect both D and a, without discarding results for short times, then very high deviations occur even if D0 is not small and tT is large (100% of error for (D0tT)/σ2
0 attain 50%. If the minimization is performed with respect both D and a, without discarding results for short times, then very high deviations occur even if D0 is not small and tT is large (100% of error for (D0tT)/σ2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≈
≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 61).
61).
In this work we estimate the scale of errors when the SCK model is applied to describe a reaction which agrees as much as possible with the assumptions of the model. The spherical shapes of molecules as well as the assumption on instantaneous de-excitation (2.2) are only rough simplifications. In real experiments on fluorescence quenching the molecules are never spherical ones and the de-excitation process itself lasts for a period of time. Therefore, the real errors, especially of the “idealized” values, should be higher than the estimated here, because many potential sources of errors are not taken into account. On the other hand, due to non-instantaneous de-excitation, the contribution coming from non-diffusive processes spreads out over time and, as a result, the dependence of the parameters on tD may be less sharp than that for the SCK model (cf.Figs. 14, 15). Therefore, the influence of tD on the parameters obtained for the real systems may be weaker than that presented in the work. This fact should not influence the two general conclusions important from practical point of view. First–the SCK model fails if t is very close to 0 but the resulting errors can be decreased (however not fully eliminated) if the shape of gAB(r) is included into the model. Second–assuming gAB(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡
≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, the obtained results will be always only a rough estimation even if we fulfill all the conditions of the “idealized” situation.
1, the obtained results will be always only a rough estimation even if we fulfill all the conditions of the “idealized” situation.
The results of our work allows us to conclude that the shape of the intensity curve for very short times is the most important problem that influences the interpretation of experimental results on fluorescence quenching when the time of experiment is short. The problem can be solved in two possible ways. The first approach is to describe the quenching by a more general theory which includes the ballistic motion. The second approach is based on the fact that by analyzing the experimental data as a function of tD (in order to eliminate the dominant part of the errors coming from the neglect of non-diffusive processes) and including gAB we can decrease the errors to quite reasonable level. This approach requires sophisticated data analysis methods. We must also take into account that in a real system the gAB function is not spherical. To conclude, the second approach is less efficient (e.g. the errors are still non-negligible) and less elegant than the first one but it seems to be easier for practical implementation.
Acknowledgements
The authors are grateful to Professor A. Maciejewski and Dr J. Kubicki for introduction to the experimental problems related to fluorescence quenching and discussions.References
- M. V. Smoluchowski, Z. Phys. Chem., 1917, 92, 129 CAS.
- A. Szabo, J. Phys. Chem., 1989, 93, 6929 CrossRef CAS.
- F. C. Collins and G. E. Kimball, J. Colloid Sci., 1949, 4, 425 Search PubMed.
- R. M. Noyes, J. Chem. Phys., 1954, 22, 1349 CAS.
- H. V. Beijeren, W. Dong and L. Bocquet, J. Chem. Phys., 2001, 114, 6265 CrossRef.
- B. U. Felderhof and R. B. Jones, J. Chem. Phys., 1995, 103, 10
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 201 CrossRef CAS.
201 CrossRef CAS. - B. U. Felderhof and R. B. Jones, J. Chem. Phys., 1997, 106, 967 CrossRef CAS.
- I. V. Gopich, A. A. Kipriyanov and A. B. Doktorov, J. Chem. Phys., 1999, 110, 10
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 888 CAS.
888 CAS. - J. Sung and S. Lee, J. Chem. Phys., 1999, 111, 10
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 159 CAS.
159 CAS. - T. L. Nemzek and W. R. Ware, J. Chem. Phys., 1975, 62, 477 CrossRef CAS.
- J. R. Lakowicz, M. L. Johnson, I. Gryczynski, N. Joshi and G. Laczko, J. Phys. Chem., 1987, 91, 3277 CrossRef CAS.
- R. Das and N. Periasamy, Chem. Phys., 1989, 136, 361 CrossRef CAS.
- A. D. Scully, S. Hirayama, D. Hachisu and T. Tominaga, J. Phys. Chem., 1992, 96, 7333 CrossRef CAS.
- A. D. Scully, S. Hirayama, K. Fukishima and T. Tominaga, J. Phys. Chem., 1993, 97, 10
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 524 CAS.
524 CAS. - D. D. Eads, B. G. Dismer and G. R. Fleming, J. Chem. Phys., 1990, 93, 1136 CrossRef CAS.
- M. Sikorski, E. Krystkowiak and R. P. Steer, J. Photochem. Photobiol. A, 1998, 117, 1 CrossRef CAS.
- E. Krystkowiak and A. Maciejewski, J. Chem. Phys., 2002, 117, 2246 CrossRef CAS.
- E. Krystkowiak and A. Maciejewski, J. Chem. Phys., 2002, 117, 5802 CrossRef CAS.
- B. Cohen, D. Huppert and N. Agmon, J. Phys. Chem. A, 2001, 105, 7165 CrossRef CAS.
- H-X. Zhou and A. Szabo, J. Chem. Phys., 1990, 92, 3874 CrossRef CAS.
- W. Dong, F. Baros and J. C. Andre, J. Chem. Phys., 1989, 91, 4643 CrossRef CAS.
- H-X. Zhou and A. Szabo, J. Chem. Phys., 1991, 95, 5948 CrossRef CAS.
- J. B. Pedresen and P. Sibani, J. Chem. Phys., 1981, 75, 5368 CrossRef.
- R. M. Noyes, Prog. React. Kinet., 1961, 1, 129 Search PubMed.
- D. A. McQuarrie, Statistical Mechanics, Harper and Row, New York, 1976 Search PubMed.
- M. P. Allen and D. J. Tildesley, Computer Simulations of Liquids, Oxford University, Oxford, 1987 Search PubMed.
- L. Verlet, Phys. Rev., 1967, 159, 98 CrossRef CAS.
- J. Gorecki, Mol. Phys. Reports, 1995, 10, 48 Search PubMed.
- B. Nowakowski, J. Gorecki and A. L. Kawczynski, J. Phys. Chem., 1998, 102, 7250 Search PubMed.
- J. S. Rowlinson and F. L. Swinton, Liquids and Liquid Mixtures, Butterworth, London, 1982 Search PubMed.
- S. H. Northrup and J. T. Hynes, J. Chem. Phys., 1979, 71, 871 CrossRef CAS.
- G. T. Evans and B. Kumar, J. Chem. Phys., 1988, 90, 1804 CrossRef.
- A. Maciejewski, personal communication.
| This journal is © the Owner Societies 2004 |
