1,2-Chlorine atom migration in 3-chloro-2-butyl radicals: a computational study

Abstract

Skell’s hypothesis of bridged 2-haloalkyl radicals has been revisited using several different theoretical methods and the 3-chloro-2-butyl radical as an example.

The structure as well as several unimolecular reaction pathways of the 3-chloro-2-butyl radical 1 have been studied at several different theoretical levels (B3LYP/aug-cc-pVDZ, BHLYP/aug-cc-pVDZ, G3(ROMP2)B3). The symmetrically chlorine-bridged structure is a transition state at all levels of theory and the most favorable ground state structure is the unbridged β-chloroalkyl radical. Reaction barriers for the 1,2-chlorine migration process are higher than those for rotation around the central C–C bond. 1,2-migration of the chlorine atom is accompanied by an increase in chlorine negative charge as well as chlorine spin density. This hybrid homo-/heterolytic process is well known from rearrangement reactions in β-(dialkoxyphosphoryloxy)alkyl radicals and suggests that chlorine migration can be influenced by polar substituent effects.

---

Introduction

The 1,2-halogen migration in 2-haloethyl radicals has been studied repeatedly with experimental^1–4 and theoretical⁵ methods in order to identify the mechanism of stereochemical control observed in reactions of these species. One early hypothesis has been that of symmetrically or asymmetrically bridged radical intermediates (Scheme 1).^2,3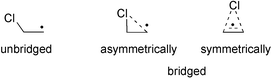

Scheme 1

Recent theoretical studies support the hypothesis of symmetrically bridged intermediates as stable stationary points for β-bromo- and β-iodoethyl radicals.^5d For β-chloro-substituted systems the situation is less clear as the symmetrically bridged β-chloroethyl radical is predicted to be a minimum by some theoretical methods and a transition state by others. All studies agree, however, that the classical unbridged β-chloroethyl radical is energetically more favorable than the bridged structure. Very little attention has been paid in all these studies to the character of the 1,2-rearrangement process, which has usually been portrayed as an essentially homolytic process. Recent studies in the field of β-(dialkoxyphosphoryloxy) radicals suggests, however, that intramolecular radical rearrangement reactions involving electronegative substituents might have substantial heterolytic character.^6,7 That this might also apply to chlorine 1,2-migration reactions is supported by recent experimental studies by Tan et al. who observed dramatic variations in the product distribution as a function of the substitution pattern in β-chloro-substituted benzyl radicals.¹ In order to address the question of charge separation for the case of 1,2-chlorine atom migration we have selected the 3-chloro-2-butyl radical 1 as a model system. Radical 1 has been generated experimentally in photobromination reactions of (S)-2-chlorobutane by Skell and coworkers, who isolated racemic 2-bromo-2-chlorobutane 2 as the main product along with minor amounts of two diastereomeric 2-bromo-3-chlorobutane trapping products 3 and 4, the latter two being essentially enantiomerically pure (Scheme 2):²

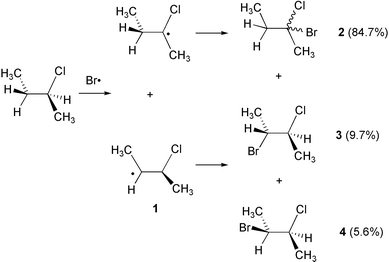Scheme 2

From these as well as earlier³ experiments it was deduced that radical 1 is present in an asymmetrically bridged form and that 1,2-chlorine migration cannot compete with either rotation around the central C–C single bond or bimolecular trapping of the radical by bromine. Alternatively, the observed stereocontrol might simply be a consequence of differential rates for rotation around the central C–C bond, the 1,2-chlorine migration process, and the radical trapping process.⁴ We are therefore studying here the structural and electronic characteristics of radical 1 as well as the chlorine 1,2-migration pathway through symmetrically bridged intermediates.

Theoretical methods

Geometry optimization has been first performed at the Becke3LYP/aug-cc-pVDZ level of theory.^8,9 Zero point vibrational energies and thermochemical corrections have been computed at this same level without any scaling. Single point calculations have then been performed using the same hybrid density functional method in combination with the all-electron aug-cc-pVTZ basis set.⁹ The energies mentioned in the text as “B3LYP/cc-pVTZ” have been obtained by combining the Becke3LYP/aug-cc-pVTZ//Becke3LYP/aug-cc-pVDZ total energies with thermochemical data obtained at the lower Becke3LYP/aug-cc-pVDZ level at 298.15K. In order to probe the influence of the density functional method on the results^10,11 all stationary points have been reinvestigated with the hybrid Becke-half-and-half-LYP density functional¹² in combination with the same basis sets as before. The results obtained after single point calculations and additional consideration of thermochemical corrections at 298.15 K are designated as “BHLYP/cc-pVTZ”. Relative energies have also been evaluated using a slightly modified G3(MP2)B3 scheme.¹³ For the sake of consistency the geometries are those obtained at Becke3LYP/aug-cc-pVDZ level and all thermochemical data has been obtained at this same level without scaling. Also, in order to avoid problems with spin contamination at the UMP2(FC) level, the large basis set calculations have been performed with the restricted open shell variant ROMP2(FC).¹⁴ Atomic charges have been calculated using the Mulliken, CHELPG,¹⁵ and NPA¹⁶ schemes. Due to the, in part, very flat potential energy surfaces all Becke3LYP calculations have utilized the pruned (99 × 590) grid supplied as “ultrafine” in Gaussian 98. All BHLYP calculations have been performed with the default “finegrid” grid size. All calculations have been performed with Gaussian 98, Rev. A.6.¹⁷

Results

Six stationary points have been identified on the potential energy surface of the 3-chloro-2-butyl radical (Scheme 3, full structural information is available as electronic supplementary information (ESI)†): The energetically most favorable, unbridged structure 1a with the terminal methyl groups in a trans orientation, a transition state for chlorine 1,2-migration 5 featuring the same orientation of the methyl groups, two transition states 6 and 7 for rotation around the central C–C bond, an unbridged 3-chloro-2-butyl radical 1b with the two terminal methyl groups in a cis orientation, and the corresponding transition state 8 for the chlorine 1,2-migration process.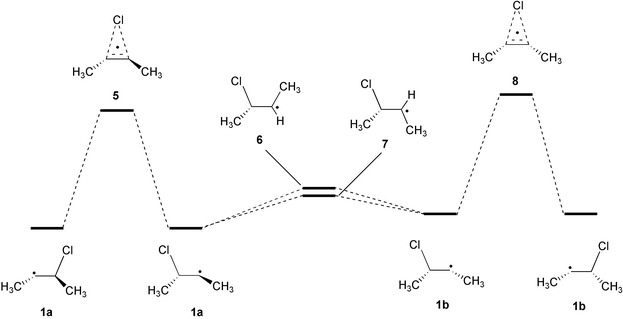

Scheme 3

Radical 1a is the energetically most favorable structure at all levels of theory and features a slightly elongated C–Cl bond of 1.95 Å, a central C–C bond of 1.46 Å, and a Cl–C–C bond angle of 107.4° (Figure 1).

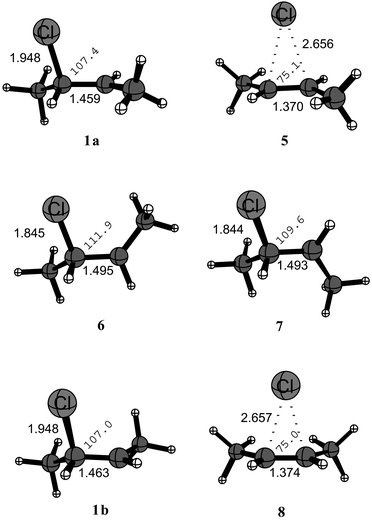Fig. 1 Stationary points in the reaction of 3-chloro-2-butyl radical 1 (Becke3LYP/aug-cc-pVDZ structures are shown).

This is in good agreement with expectation for an unbridged, β-substituted alkyl radical.^5f 1,2-Migration proceeds through symmetrically bridged structure 5 which is a transition state and not a minimum at both the B3LYP and the BHLYP level. The reaction barrier is rather low at 9.9 kJ mol⁻¹ at the B3LYP/aug-cc-pVTZ level, but significantly higher at both the G3(MP2)B3 (+29.2 kJ mol⁻¹) and the BHLYP/aug-cc-pVTZ level (+26.5 kJ mol⁻¹). See Table 1. A full comparison of absolute energies, energies corrected to 0 K, and enthalpies at 298 K is available as ESI.†

Table 1 Relative enthalpies [in kJ mol⁻¹] and imaginary frequencies [in cm⁻¹] for stationary points in the reaction of 3-chloro-2-butyl radical (1)

	B3LYP/aug-cc-pVTZ^a		G3(MP2)B3^a	BHLYP/aug-cc-pVTZ^b
	ΔH298	ν i	ΔH298	ΔH298	ν i
a B3LYP/aug-cc-pVDZ geometries. b BHLYP/aug-cc-pVDZ geometries. c B3LYP/aug-cc-pVDZ level.
1a	0.0	—	0.0	0.0	—
5	+9.87	56i	+29.19	+26.52	93i
6	+18.53	108i	+10.68	+14.89	99i
7	+16.41	99i	+8.83	+12.20	98i
1b	+5.04	—	+3.54	+4.82	—
8	+13.81	44i	+33.41	+26.75	67i

---

The structure of transition state 5 is characterized by long C–Cl distances of 2.66 Å and a rather short central C–C distance of 1.37 Å. Comparison to trans-but-2-ene 9 and the trans-but-2-ene radical cation 10 (structures available as ESI) with central C–C bond distances of 1.34 Å and 1.42 Å, respectively, suggests that the 1,2-migration process has mixed homolytic/heterolytic character, with a higher weight of the homolytic component. This interpretation is also in agreement with the charge and spin density distributions (see below). Transition state 5 is furthermore characterized through very low imaginary frequencies of only 56 cm⁻¹ (B3LYP/aug-cc-pVDZ) and 93 cm⁻¹ (BHLYP/aug-cc-pVDZ), indicating a rather flat potential energy surface in the transition state region in both cases. Rotational transition states 6 and 7 describe the interconversion of minima 1a and 1b through rotation around the central C–C bond. Transition state 6, in which the rotational motion leads to an eclipsing syn orientation of chlorine atom and the C1 methyl group, is energetically slightly less favorable than transition state 7, in which the same groups are arranged in an anti fashion. One interesting structural aspect of both transition states is the somewhat shorter C–Cl bond length of around 1.84 Å and a somewhat longer central C–C bond length of around 1.49 Å as compared to ground state 1a. These structural differences can be understood as a consequence of the hyperconjugative interaction between the singly occupied molecular orbital located at C2 and the adjacent C–Cl bond. This latter interaction is, for structural reasons, only possible in ground states 1a and 1b, but not the rotational transition states 6 and 7, and leads to lengthening of the C–Cl bond and shortening of the central C–C bond. The barriers for rotation through transition state 7 are rather low at the G3(MP2)B3 level, somewhat higher at BHLYP/aug-cc-pVTZ, and significantly higher at the B3LYP/aug-cc-pVTZ level. The same trend can be noted for rotational transition state 6. The cis-3-chloro-2-butyl radical 1b reached through transition states 6 or 7 is energetically slightly less favorable than 1a, the energy difference being similar at all three computational levels. Aside from the relative orientation of the terminal methyl groups the structural characteristics of 1b are very similar to those of 1a. Similarly, the structural characteristics of transition state 8 describing 1,2-chlorine migration starting from 1b are very similar to those of transition state 5, including long C–Cl bond distances of 2.66 Å and a central C–C bond distance of 1.37 Å. The barrier for this 1,2-migration process shows a similar method dependence to that already noted for 5.

Comparison of the barriers for the 1,2-migration process with those for rotation around the central C–C bond shows that the three computational levels employed in this study make different predictions for the two competing reaction pathways: while chlorine 1,2-migration is predicted to be more facile than rotation around the central C–C bond at the B3LYP/aug-cc-pVTZ level of theory, the reverse order is predicted by both the G3(MP2)B3 and the BHLYP/aug-cc-pVTZ levels. This conclusion is quite independent of the consideration of differences in zero point vibrational energies or thermochemical corrections and thus reflects differences in the underlying potential energy surfaces. It should also be noted that the B3LYP and G3(MP2)B3 results are based on identical molecular structures. Together with the largely similar structures obtained at the BHLYP/aug-cc-pVDZ level of theory, this rules out structural differences as the source of variable barrier heights. In line with earlier conclusions concerning results obtained at QCISD and QCISD(T) levels of theory for the 2-chloroethyl radical,^5f this suggests that the results obtained at the B3LYP level here are less reliable than those obtained at the G3(MP2)B3 or BHLYP/aug-cc-pVTZ levels.

Charge distribution

To characterize the 1,2-migration process in more detail we have collected the chlorine atomic charge as well as the unpaired spin density located at chlorine for all stationary points in Table 2. In order not to bias the results through selection of a particular population analysis scheme, partial charges have been calculated with three different approaches: the Mulliken population analysis, which may be considered to be the least flexible approach; the natural population analysis (NPA) scheme,¹⁶ which may be regarded the most robust approach; and the CHELPG scheme,¹⁵ in which partial charges are fitted to the molecular electrostatic potential. We will concentrate on the NPA values in the following, but all trends are also reproduced by the other two charge sets.

Table 2 Chlorine charges and spin densities for stationary points in the reaction of 3-chloro-2-butyl radical (1)

	B3LYP/aug-cc-pVDZ				BHLYP/aug-cc-pVDZ
	q(Cl)/e			SD(Cl)	q(Cl)/e			SD(Cl)
	(NPA)^a	(CHELPG)^a	(Mulliken)^a	(Mulliken)^a	(NPA)^b	(CHELPG)^b	(Mulliken)^b	(Mulliken)^b
a B3LYP/aug-cc-pVDZ geometries. b BHLYP/aug-cc-pVDZ geometries.
1a	−0.189	−0.276	−0.206	0.155	−0.168	−0.269	−0.187	0.120
5	−0.351	−0.345	−0.348	0.568	−0.338	−0.334	−0.331	0.589
6	−0.113	−0.237	−0.167	0.003	−0.117	−0.245	−0.165	0.003
7	−0.108	−0.228	−0.123	0.004	−0.111	−0.232	−0.117	0.006
1b	−0.189	−0.276	−0.217	0.156	−0.168	−0.263	−0.198	0.121
8	−0.352	−0.344	−0.357	0.569	−0.340	−0.334	−0.340	0.589

---

On comparison of the charges obtained at the B3LYP and BHLYP levels of theory, it is unexpectedly found that the charges hardly differ for any of the stationary points. This implies that the substantially different energetics predicted by these two DFT methods are not reflected in the charge or spin density distribution. Further analysis will therefore concentrate on the results obtained with the BHLYP functional. In ground states 1a and 1b the chlorine atom carries only a small negative charge of around −0.17e. The chlorine partial charge is further reduced in rotational transition states 6 and 7 to values around −0.12e, but increases in the 1,2-migration transition states 5 and 8 to values around −0.34e. Together with the structural characteristics, such as the C–Cl bond distances noted before, this indicates that lengthening of the C–Cl bond is accompanied by an increase in chlorine partial charge. This is, of course, the opposite of what would be expected for a purely homolytic process. Inspecting the spin density distribution calculated at the same level of theory we note that the changes in chlorine partial charge parallel those in chlorine spin density: the smallest values (close to zero) are found for rotational transition states 6 and 7 featuring the shortest C–Cl bonds while the largest spin densities are found for the 1,2-migration transition states 5 and 8. These trends support the mixed homolytic/heterolytic character of the chlorine 1,2-migration process. Considering the much larger variation in chlorine spin densities as compared to chlorine partial charge, the homolytic character is certainly dominant over the heterolytic one in this particular case. However, 1,2-migration reactions of phosphate groups in similarly small model systems have shown that the increase in negative charge of the migrating group is rather limited (around −0.13e) in the absence of effective donor substituents.^6a In light of the many examples of contact ion pair formation from suitably substituted β-(dialkoxyphosphoryloxy)alkyl radicals⁶ one may speculate, however, that a larger degree of charge separation will occur in reactions of similarly substituted β-chloroalkyl radicals.

Further characterization of the 1,2-migration reaction is possible by monitoring the chlorine partial charge along the reaction pathway (Fig. 2).

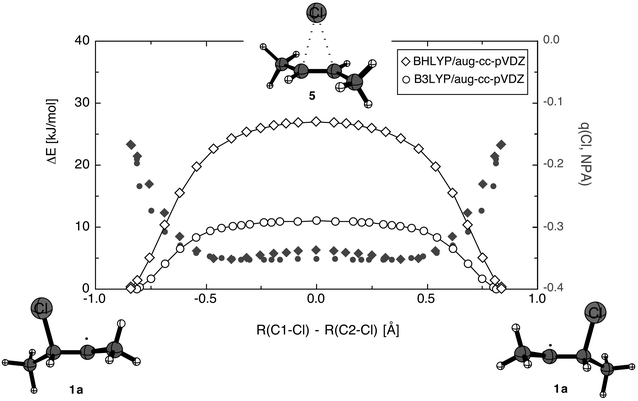Fig. 2 Variation of the chlorine atomic charge (NPA scheme) along the 1,2-migration pathway as calculated at the BHLYP/aug-cc-PVDZ (filled diamonds) and the B3LYP/aug-cc-pVDZ (filled circles) levels of theory. Relative total energies are also given in kcal mol⁻¹ at the BHLYP/aug-cc-pVDZ (open diamonds) and the B2LPY/aug-cc-pVDZ (open circles) levels.

The reaction coordinate has been chosen here as the difference in the breaking and the forming C–Cl bond distances. Starting from ground state structure 1a the potential energy surface rises quickly to reach a plateau region between reaction coordinate values of −0.5 and +0.5. The initial rise is much steeper at the BHLYP (open diamonds) than the B3LYP (open circles) level, but the plateau region is similarly flat in both cases as indicated by the very small imaginary frequencies for transition state 5 at these levels of theory. The initial rise in potential energy is accompanied by a similarly rapid rise in chlorine negative charge, which remains essentially constant in the plateau region. Quite remarkably the charge development is practically identical at the BHLYP (filled diamonds) and the B3LYP (filled circles) levels.

Conclusions

The chlorine 1,2-migration process in 2-chloro-3-butyl radical 1 proceeds through a symmetric transition state. Neither symmetrically nor asymmetrically bridged intermediates can be identified in this system. The barrier for chlorine 1,2-migration is substantially higher than that for rotation around the central C–C single bond. Analysis of the charge and spin density distribution along the 1,2-migration pathway reveals that the migrating chlorine atom carries a larger negative partial charge as well as substantially higher unpaired spin density, as is the case in the ground state radical. Such a hybrid homolytic/heterolytic process is largely similar to 1,2-migration processes in β-(dialkoxyphosphoryloxy)alkyl radicals and suggests that larger degrees of charge separation can be achieved in more highly substituted systems.

Acknowledgements

Financial support through the Fonds der Chemischen Industrie and generous allocation of computational resources by the Leibniz Rechenzentrum, Muenchen, is gratefully acknowledged.

References

1. (a) E. W. Tan and J. P. Shaw, J. Org. Chem., 1996, 61, 5635; (b) E. W. Tan, B. Chan and A. G. Blackman, J. Am. Chem. Soc., 2002, 124, 2078.
2. P. S. Skell, R. R. Pavlis, D. C. Lewis and K. J. Shea, J. Am. Chem. Soc., 1973, 95, 6735.
3. P. S. Skell, D. L. Tuleen and P. D. Readio, J. Am. Chem. Soc., 1963, 85, 2849.
4. R. V. Lloyd and D. E. Wood, J. Am. Chem. Soc., 1975, 97, 5986.
5. (a) B. Engels and S. D. Peyerimhoff, J. Mol. Struct. (THEOCHEM), 1986, 138, 59; (b) B. Engels, S. D. Peyerimhoff and P. S. Skell, J. Phys. Chem., 1990, 94, 1267; (c) M. Guerra, J. Am. Chem. Soc., 1992, 114, 2077; (d) H. Ihee, A. H. Zewail and W. A. Goddard III, J. Phys. Chem. A, 1999, 103, 6638; (e) X. Zheng and D. L. Phillips, J. Phys. Chem. A, 2000, 104, 1030; (f) P. Brana, B. Menendez, T. Fernandez and J. A. Sordo, J. Phys. Chem. A, 2000, 104, 10842; (g) P. Brana, B. Menendez, T. Fernandez and J. A. Sordo, Chem. Phys. Lett., 2000, 325, 693; (h) Z.-H. Li, K.-N. Fan and M. W. Wong, J. Phys. Chem. A, 2001, 105, 10890; (i) H. Ihee, J. Kua, W. A. Goddard III and A. H. Zewail, J. Phys. Chem. A, 2001, 105, 3623.
6. (a) D. Crich and X.-Y. Jiao, J. Am. Chem. Soc., 1996, 118, 6666; (b) M. Newcomb, J. H. Horner, P. O. Whitted, D. Crich, X. Huang, Q. Yao and H. Zipse, J. Am. Chem. Soc., 1999, 121, 10685; (c) M. Newcomb, N. Miranda, X. Huang and D. Crich, J. Am. Chem. Soc., 2000, 122, 6128; (d) B. C. Bales, J. H. Horner, X. Huang, M. Newcomb, D. Crich and M. M. Greenberg, J. Am. Chem. Soc., 2001, 123, 3623; (e) J. H. Horner and M. Newcomb, J. Am. Chem. Soc., 2001, 123, 4364; (f) M. Newcomb, N. Miranda, M. Sannigrahi, X. Huang and D. Crich, J. Am. Chem. Soc., 2001, 123, 6445.
7. H. Zipse, J. Am. Chem. Soc., 1997, 119, 2889.
8. (a) A. D. Becke, J. Chem. Phys., 1993, 98, 5648; (b) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785; (c) R. H. Hertwig and W. Koch, J. Comp. Chem., 1995, 16, 576.
9. T. H. Dunning, Jr., J. Chem. Phys., 1989, 90, 1007.
10. B. J. Lynch, P. L. Fast, M. Harris and D. G. Truhlar, J. Phys. Chem. A, 2000, 104, 4811.
11. H. Zipse and M. Bootz, J. Chem. Soc. Perkin Trans. 2, 2001, 1566.
12. A. D. Becke, J. Chem. Phys., 1993, 98, 1372.
13. A. G. Baboul, L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 1999, 110, 7650.
14. (a) D. M. Smith, B. T. Golding and L. Radom, J. Am. Chem. Soc., 1999, 121, 9388; (b) S. D. Wetmore, D. M. Smith, B. T. Golding and L. Radom, J. Am. Chem. Soc., 2001, 123, 7963.
15. C. M. Breneman and K. B. Wiberg, J. Comp. Chem., 1990, 11, 361.
16. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899.
17. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery, Jr., R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Cioslowski, J. V. Ortiz, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, C. Gonzalez, M. Challacombe, P. M. W. Gill, B. G. Johnson, W. Chen, M. W. Wong, J. L. Andres, M. Head-Gordon, E. S. Replogle and J. A. Pople, GAUSSIAN 98 (Revision A.6), Gaussian, Inc., Pittsburgh, PA, 1998.

---

Footnote

† Electronic supplementary information (ESI) available: Calculated energies and enthalpies of stationary points, full structural information, and structures of trans-but-2-ene (9) and trans-but-2-ene radical (10). See http://www.rsc.org/suppdata/ob/b2/b209981k/

---