γ Agostic C–H or β agostic Si–C bonds in La{CH(SiMe₃)₂}₃? A DFT study of the role of the ligand

Abstract

DFT calculations show that La{CH(SiMe₃)₂}₃, whose X-ray structure has previously been determined, should be considered as having a β agostic Si–C bond and not a γ agostic C–H bond. The role of the isolated ligand CH(SiMe₃)₂⁻ in agostic interactions involving an extremely electropositive metal centre is discussed. Delocalization of the electrons of the lone pair located on the C centre in the neigbouring trimethylsilyl group (negative hyperconjugation) is suggested as being important. The metal centre has an electrostatic effect which elongates preferentially the β Si–C bond of the closest methyl group and contracts the La–C–Si angle.

---

Introduction

Agostic interactions appear in a number of highly diverse unsaturated transition and lanthanide metal compounds.¹ It is normally described as an interaction of a σ X–Y bond acting as an electron-donor toward an unsaturated metal centre acting as an electron-acceptor. The agostic interaction is not only a structural curiosity but often also a key factor for reactivity. In particular, agostic C–H interactions are known to control the tacticity of polymers.² Consequently, there is considerable interest in developing an understanding of agostic interactions. It should be noted that in the original definition by Brookhart and Green,¹ the term ‘agostic’ was given to an interaction between a C–H bond part of a ligand and a metal. It was later also used for describing the interaction of a C–H bond from a molecule forming an adduct with a transition metal complex. For instance an alkane complex with a side-on bound C–H bond is often described as having an agostic C–H interaction with the metal. Indeed, there are obvious analogies between the intramolecular and intermolecular versions of the interaction although there are also some fundamental differences which could confuse some of the issues.³ One of the key differences between these two versions will be brought out in the present paper, which focuses on an intramolecular agostic interaction.

Although C–H is the most frequently observed agostic bond,¹ it is far from exclusive and other σ bonds are known to be involved in similar interactions. The next most common case is probably that of Si–H which can be agostic with various late and early transition metal or lanthanide complexes.⁴ The B–H agostic bond is also documented, but only a few cases have been reported.⁵ An M⋯H–X interaction in which the H is strongly positively charged as in N–H should not be regarded as agostic, but more as a hydrogen bond.⁶ Two different situations occur for C–X bonds where X ≠ H. When X carries a lone pair such as for NR₂, OR or halide, a short distance between X and M is frequently observed.⁷ While such situations are often described as agostic in the literature, this is not really appropriate since the metal interacts with the lone pair of X and not with the C–X σ bond. Agostic C–X bonds where X is not H and does not carry a lone pair are rarities. The reason is that there is a clear preference for a C–H bond to be agostic compared to a C–C bond when an alkyl group is in the vicinity of a metal centre. It is currently accepted that the metal centre accesses the electronic density of C–H considerably more easily than from the C–C bond which is sterically hindered by the neighbouring C–H bonds. An agostic C–C has been suggested in heavily strained systems.⁸ Nevertheless, the geometric argument of C–H bond accessibility does not convincingly explain why Si–C bonds appear to be agostic in some systems.⁹ One hypothesis is that a Si–C bond, being longer than a C–C bond, is less efficiently protected by the vicinal C–H bonds from interacting with the metal centre. Although this cannot be excluded, other factors may also be responsible for the occurrence of a Si–C agostic bond.

The energetic weakness (∼10 kcal mol⁻¹)^1c of agostic interactions derives from the fact that C–H is a very poor Lewis base even if the unsaturated metal is a reasonably strong acid. Despite the weakness of this interaction, theoretical calculations have usually been able to reproduce its presence (e.g., in olefin polymerization),^2b although earlier calculations at the Hartree–Fock level met with some difficulties.¹⁰ As expected, a weak interaction is sensitive to many factors. Steric factors have been shown to play a key role by favouring the agostic interaction.¹¹ Other effects like changes in interligand angles,^12a electron donation from other ligands in the complex,¹² or interactions between ligands such as π–π stacking¹³ can control the agostic interaction.

Interpretations different from the simple σ electron donor bond–metal electron acceptor interaction have been suggested. The α C–H agostic interaction has been suggested to originate from a reorganization of the M–C bond associated with the presence of several empty d orbitals.¹⁴ Similarly, a bent M–C bond was discussed.¹⁵ For the β agostic bond, the direct electron transfer from C–H to the metal is implicitly accepted. However, in a set of key papers, the delocalization of the electrons of the Ti–C bond into the ethyl ligand in Cl₃TiCH₂–CH₃, as well as very recently that of the Li–C bond in lithium alkyl and silyl alkyl complexes, has been shown to be important.¹⁶ It has also been suggested by the same groups of authors that the C terminus of the C–H bond appears to be the electron-donor to the metal.

As apparent from the references cited above, agostic interactions are especially frequent in early transition metal and lanthanide complexes. In this work we will discuss the case of La{CH(SiMe₃)}₃, 1 (Fig. 1).^17a The presence of three γ C–H bonds were suggested from the short non-bonded La⋯C(2) distance (3.121(9) Å) seen by X-ray diffraction.^17a Very similar features have been reported for Cr{CH(SiMe₃)₂}₃^17b and In{CH(SiMe₃)₂}₃.^17c Although rather rare, γ C–H agostic bonds have been reported.¹⁸ Low temperature X-ray and neutron diffraction of [Mg{CH(SiMe₃)₂}₂] was reported and the polymerization was interpreted as involving an intermolecular γ-methyl–metal interaction, or, more plausibly, a Si–C/Mg interaction.^17d A similar interpretation was offered for Yb{N(SiMe₃)₂}₂–{Me₂PCH₂–CH₂PMe₂}.^16a The most frequent position for an agostic bond is β to the metal. The present DFT calculations suggest the presence of a β agostic Si–C interaction and the absence of any γ C–H interaction. An interpretation of this result is offered based on the presence of a strongly polarized La–C bond and accompanying delocalization of the electron density in the bis(trimethylsilyl)methyl ligand.

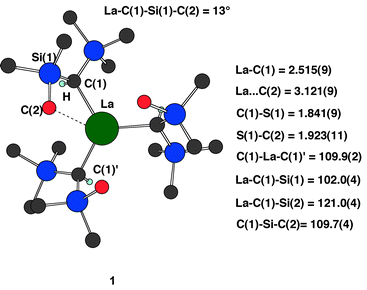Fig. 1 Structure of 1 drawn from experimental atom coordinates.^17a H atoms have been removed for clarity, carbon atoms are represented as black and red circles, the red circle represents the carbon of the key trimethylsilyl group corresponding to the long Si–C bond, La is represented by a green circle and Si by blue circles. Distances in Å and angles in degrees are from the publication and dihedral angle from the atom coordinates.^17a

Computational details

The large Relativistic Effective Core Potential (RECP), optimized by the Stuttgart–Bonn group,¹⁹ has been shown to be well adapted to represent the geometries of lanthanide complexes since 4f electrons do not participate in metal–ligand bonding.²⁰ Basis sets adapted to the RECPs augmented by a polarization f function (exp = 1.000) were used. Silicon atoms were also treated with a large core RECP in combination with the adapted basis set, augmented by a polarization d function (exp = 0.284).²¹ Carbon and hydrogen were treated with an all-electron 6-31G(d,p) basis set.²² Calculations were carried out at the DFT level of theory using the hybrid functional B3PW91.²³ The ONIOM²⁴ calculations were carried out at the B3PW91/UFF²⁵ level. Geometry optimizations were carried out without any symmetry restriction. The nature of extrema QM (B3PW91) and ONIOM (B3PW91/UFF) was verified by analytical calculations of frequency. All calculations were carried out with the Gaussian 98 suite of programs.²⁶

Results

To obtain a good understanding of complex 1, LaX₃ complexes in which X is built step by step from CH₃ to the real CH{(SiMe₃)₂} have been calculated and analyzed. The size of the real system is too large to be calculated in full with a DFT method. Therefore selected parts of the ligand have been represented at the MM level. This progressive buildup of the real ligand securely establishes the validity of the hybrid QM/MM method and helps us to analyze the bonding. This approach also permits an analysis of the role of parts of the ligands in complex 1 to be established.

The full DFT calculations

La(CH₃)₃ 2. The metal centre is pyramidal in La(CH₃)₃ (2, Fig. 2) with the C(1)–La–C(1)′ angle equal to 107°, very close to the value of 109.9(2)° in 1.^17a The La–C(1) bond length (2.498 Å) is also reasonably close to that in 1 (2.515(9) Å). Inversion of the pyramid at La requires a small energy barrier of 4.9 kcal mol⁻¹. The pyramidal geometry at La in the experimental structure is thus neither due to steric crowding associated with the presence of three bis(trimethylsilyl)methyl ligands coordinated to La nor to the agostic bonds. Probably the bulk of the real ligand in 1 is responsible for the larger C(1)–La–C(1)′ angle compared to that in 2. Remarkably, La(CH₃)₃ has no α agostic C–H bond. The pyramidal geometry at La does not favour such interaction.

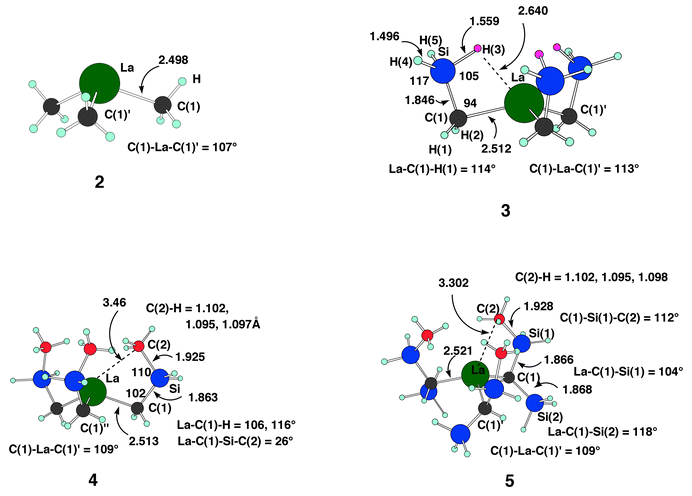Fig. 2 Optimized B3PW91 geometries for 2–5. For these structures, the colour coding for the heavy atoms is similar to that for 1. The H centres are represented by small circles in either a light blue or a pink circle. The latter corresponds to the H of SiH₃ which is elongated. Complexes 2 and 3 have C_3v symmetry and complexes 4 and 5 have C₃ symmetry. Distances are in Å and angles in degrees.

La(CH₂–SiH₃)₃ 3. The coordination at La in La(CH₂–SiH₃)₃ is similar to that in LaMe₃ (C(1)–La–C(1)′ = 113°) (3, Fig. 2). The complex has close to C_3v symmetry. The La–C(1) bond length of 2.512 Å is also only marginally longer than in La(CH₃)₃. Three β Si–H agostic bonds appear, with considerable elongation of the Si–H(3) bond length (1.559 Å) relative to the geminal non-agostic Si–H(4)(5) bond lengths (1.496 Å), in agreement with numerous β Si–H agostic interactions especially in early transition metal and lanthanide complexes.⁴ The presence of vacant coordination sites in the space opposite the La–C bonds strongly favours these interactions in 3. A closer proximity of La and Si–H is obtained by reducing the La–C(1)–Si angle down to 94° and the C(1)–Si–H(3) angle to 105°, while the other bond angles are slightly wider than the tetrahedral value. This brings H(3) 2.640 Å from La. It is interesting to note that the angular distortions of the CH₂SiH₃ ligand are stronger than in 1. In particular, the experimental La–C(1)–Si angle is reduced to only 102.0(4)°. Complex 3 is a very approximate model of the experimental system 1. However, difficulties have been noticed when SiMe₃ has been modelled by SiH₃.²⁷ For this reason we needed to study a more complete model. Before considering a more elaborate model for 1, we were able to verify that La(C₂H₅)₃ had a β C–H bond elongated by 0.043 Å compared to the C–H bond which points away from the metal. This elongation is much larger than the average elongation of C–H bond (0.02 Å) calculated in most other transition metal alkyl complexes. These La complexes thus have unusually long β agostic Si–H or C–H bonds. As expected from the larger polarizability of Si–H compared to that of C–H, the bond elongation is larger with Si than with C.

La(CH₂SiH₂Me)₃ 4. Replacing the H pointing towards La by Me in the silyl group in 3 leads to one conformation of La(CH₂SiH₂Me)₃4 adapted to represent 1 at reasonable computational cost (Fig. 2). After optimization of geometry, the Me group is still pointing towards La but avoids steric hindrance by a slight twist (dihedral angle La–C(1)–Si–C(2) = 26°) which compares reasonably well to the experimental value (13°). The complex has C₃ symmetry. To accommodate the Me group, La becomes more pyramidal (C(1)–La–C(1)′ = 109°) and the La–C(1)–Si angle is identical to that in 3. The distances within the ligand (La–C(1) = 2.513 Å; C(1)–Si = 1.863 Å; Si–C(2) = 1.925 Å) are close to those in the experimental structure 1 (Fig. 1). The angular parameters are also in remarkable agreement. This gives a non-bonded La⋯C(2) distance of 3.46 Å (3.121(9) Å in 1) with the shortest La⋯H distance of 3.06 Å and a non-elongated C(2)–H bond (1.102 Å) compared to the geminal C–H bonds of 1.095 and 1.097 Å. This model also gives two different La–C(1)–H angles (106° and 116°) in good agreement with the situation in 1. This simplified system already reproduces the experimental system very well. It should be noted, however, that the conformation described previously is not the absolute minimum. The most stable structure has the Me groups turned away from La. This structure is irrelevant to representing 1 and will not be discussed further. It illustrates the difficulties in representing the SiMe₃ group by SiH₃ in lanthanide chemistry, as noted previously.²⁷

La(CH(SiH₃)SiMeH₂)₃ 5. In 5, an H on C(1) has been replaced by SiH₃ (this Si centre is labelled Si(2) and the other one Si(1)) (Fig. 2). Not surprisingly, the La–C(1)–Si(2) angle is 118° while La–C(1)–H is 103°. By comparison with 4, the opening of the La–C(1)–Si(2) angle is thus not due to the bulk of SiH₃ since the same large angle was already present with two Hs on C(1). The other angles adjust gently compared to that in 4. The La–C(1) bond length is slightly elongated (2.521 Å) with respect to that in 4 (2.513 Å), still very close to the experimental value 2.515(9) Å. This leads to a La⋯C(2) non-bonded distance equal to 3.302 Å and a shortest La⋯H distance from Me of 2.994 Å. As in 4, the three C–H bonds of this CH₃ group are almost identical: 1.095, 1.098, 1.102 Å. Essentially the major consequence of the additional SiH₃ group in 5 is a slight flattening of the pyramidal La.

The ONIOM calculation, 6, of the experimental system 1

System 5 is the largest which could reasonably be calculated with a pure quantum method. The two additional methyl groups on the key silyl group (Si(1) in 5) and the three methyl groups on the spectator silyl ligand (Si(2) in 5) are thus introduced at the MM level. The experimental system 1 was thus calculated with ONIOM (B3PW91/UFF) calculations and the result of the calculations is shown in 6. All atoms in 6 in dark colours Fig. 3 are calculated at the B3PW91 level and the atoms in pastel colours are calculated at the UFF level. Species 6 has the quantum part of complex 5. It should be noted that groups in the MM part only modify the steric environment without changing the electronic properties of ligands. In addition, it is not possible to compare the Si–C distances within the key trimethylsilyl group since only the Si–C(2) bond length is calculated with the QM method. The focus is thus now to analyze how these additional ligands influence the structural parameters of the skeleton calculated at the QM level.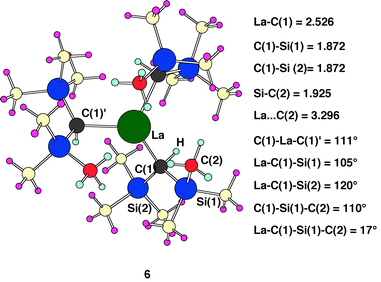

Fig. 3 Optimized ONIOM (B3PW91/UFF) geometry for 6. Dark colours similar to those in Figs. 1 and 2 represent atoms calculated at the B3PW91 level, atoms calculated at the UFF level are in pastel colours. Distances are in Å and angles in degrees.

In 6, the C(1)–La–C(1)′ angle of 111° is wider than in 5 and very close to the experimental value of 109.9(2)° in 1. The La–C(1)–Si(1) angle is constrained at 105° but not as significantly as in 1 (102.0(4)°). The C(1)–Si–C(2) angle of 110° is essentially identical to the experimental value. The calculated distances La–C(1) = 2.526 Å, C(1)–Si = 1.872 Å, Si–C(2) = 1.925 Å also compare well with the corresponding experimental values. The non-bonded La⋯C(2) distance (3.296 Å) is still marginally longer than the experimental value of 3.121(9) Å, which, however, is not surprising in the light of the fact that non-bonded distances are harder to reproduce. The metrical parameters of the calculated system essentially reproduce quantitatively the experimental system 1. A very similar structure is obtained when representing the entire spectator trimethylsilyl ligand at the MM level showing that it has mainly a steric role. The main difference is a slight increase of the La⋯C(2) distance (3.382 Å) by small changes in bond angles. The calculations thus suggest the presence of an agostic β Si–C interaction and not an agostic γ C–H interaction.

Discussion

Some of the features of the geometry of this lanthanide complex appear correctly at a very primitive level of modelling. The lanthanide centre is pyramidal for 2 with an angle between the ligands that seems to depend only marginally on the substituent on the alkyl ligand. The low energy barrier of 4.9 kcal mol⁻¹ for inversion at La for LaMe₃ is suggestive of high nonrigidity. The inversion barrier most probably considerably increases with the size of the ligands and our calculated value gives thus only a lower limit. The preferred pyramidal structure at La results from a second order Jahn–Teller distortion associated with the presence of low lying empty d_xz and d_yz orbitals. These two orbitals can also participate in the La–C bond only in a pyramidal structure (Fig. 4), whereas only d_x²−y², d_xy and d_z² are symmetry adapted to participate (in addition to the La s and p orbitals) in the La–C bonds of the trigonal planar structure. This interpretation accounts for the pyramidalization of many LaX₃ species.²⁸ This effect is similar to that discussed in accounting for the unexpected trigonal prismatic structure of WH₆, where low lying empty d orbitals create a better W–H interaction than in the octahedral geometry of this and closely related species.^28b The non-linear MgC₂ core in species like Mg(CH(SiMe₃)₂),^17d or the non-planar InC₃ core in species like In{CH(SiMe₃)₂}₃,^17c have been interpreted similarly; the participation of the empty d orbitals in the M–C bonds is larger in the non-linear or non-planar geometry.²⁹ The geometry of a large number of species having organic ligands bonded to a d⁰ metal has been discussed and is understood similarly.^29b A full discussion for the pyramidalization of LnX₃ species will be published separately,^28a since the focus of this paper is different.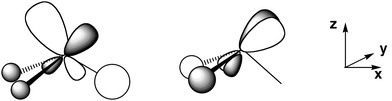

Fig. 4 Schematic representation of the bonding between the d_xz and d_yz orbitals of La and the ligands. These d orbitals would be non-bonding in a trigonal planar geometry.

Whereas an α agostic interaction does not occur in the calculated structures, the β agostic interaction is clearly prevalent. It appears in La(CH₂SiH₃)₃, 3, where Si–H is strongly elongated (1.559 Å vs. 1.496 Å for the geminal Si–H bonds) and H is at a short distance from La (2.640 Å). The angular distortions traditionally associated with the agostic interaction are present in the acute La–C(1)–Si angle (94°) and the tilt of the SiH₃ group towards La (C(1)–Si–H(3) = 105° vs. C(1)–Si–H(4)(5) = 117°). A related angular pattern (La–C(1)–Si = 104°) and bond elongation, concerning Si–C(2) (1.923 Å) compared to C(1)–Si of 1.863 Å, is found in 4. However, all angles around Si and C(2) are close to the tetrahedral values and none of the C(2)–H bonds are significantly elongated. The non-bonded La⋯C(2) distance is equal to 3.302 Å. There is thus no sign of a γ C–H agostic interaction but there is geometrical evidence for a β agostic Si–C(2) interaction. This situation is thus similar to that obtained in closely related systems where a similar proposal was made.⁹

Whereas the structural parameters of 3 may be interpreted as arising from an agostic interaction viewed in a traditional sense (electron donation from the σ bond to the metal centre), the geometrical parameters of 4 are more difficult to rationalize. It is traditionally considered that a “donation” of the electronic density of the σ bond to the electron deficient metal centre is the main component of the agostic interaction. This requires that the metal accesses the space where the electron density of the σ bond is located. This is easy for a C–H or Si–H bond, because of the spherical nature of H. As to the mechanism whereby the metal accesses the electron density of the Si–C bond without implicating the density of the C–H bonds of the terminal Me group and thus establishing C–H agostic interactions, alternative interpretations have been offered.¹⁶ As this work was being completed, a detailed study of the agostic interaction from the analysis of the electron density from neutron diffraction and theoretical calculations of an alkyl lithium complex has suggested that there was no covalent bond between Li and the terminal end of the organic chain.^16c The size and nature of the metal centre in our system do not permit such a detailed analysis. We have, however, arrived independently at similar conclusions. The geometrical changes in the alkyl chain, and in particular the significant elongation of the β bonds, are, in this system also, the result of a delocalisation of the electron density at C(1) through negative hyperconjugation. Our analysis, which takes a slightly different perspective from that of Scherer, McGrady et al.,^16c complements their work.

The bond between La and a ligand has a strong ionic component. Species 3 can thus be viewed as La³⁺ interacting with three CH₂–SiH₃⁻ ligands. The structural parameters of an isolated anion CH₂–SiH₃⁻ and the neutral molecule H₃C–SiH₃ are of interest by way of comparison. In CH₂–SiH₃⁻, the Si–H bonds are long (1.573 Å for the Si–H trans to the carbon lone pair and 1.530 Å for the two other Si–H bonds) compared to those in H₃C–SiH₃ (1.496 Å) as expected from the electron delocalization of the C lone pair into the low lying π*_SiH3 group which illustrates the negative hyperconjugation ability of the SiH₃ group. Likewise, the delocalization of the C lone pair is responsible for the elongation of the Si–C bonds in CH₂–SiMe₃⁻ (1.964 Å and 1.934 Å) compared to 1.898 Å in SiMe₄. No elongation of the C–H bond of the Me groups of SiMe₃ is found in CH₂–SiMe₃⁻ showing that hyperconjugation concerns only bonds that are β to the lone pair. If the lone pair on C is at lower energy, the electron delocalization in the β bonds is decreased and the bonds β to the carbanionic centre are shorter. This has been tested by calculating CF₂–SiH₃⁻. The electronegative F atoms lower the energies of all occupied orbitals and especially those with a strong contribution on the geminal carbanionic centre. The Si–H bond lengths of 1.564 Å and 1.513 Å may be compared to those in CH₂–SiH₃⁻, of 1.573 Å and 1.530 Å.

Elongation of bonds β to C(1) is therefore present in the isolated anion. The metal centre has, however, a role. In the free anionic ligands, the three bonds of SiH₃ or of SiMe₃ are elongated because the carbon lone pair is delocalized in the symmetry adapted linear combination of the σ*_Si–R bonds. In contrast, in 3, only the bond closer to the metal centre is elongated and the other bonds are shorter compared to those in the free anion. Thus the Si–H(3) and SiH(4)(5) bond lengths of 1.559 Å and 1.496 Å respectively may be compared with the values of 1.573 Å and 1.530 Å in CH₂–SiH₃⁻. The strong electrostatic field of the metal polarizes the electron density in the ligands, the σ*_Si–R of the bonds closer to the metal receive more density which in turn further elongates these bonds. If the C lone pair is at lower energy, the negative hyperconjugation is negligible and the agostic interaction does not occur. For instance there is no β Si–H agostic interaction in La(CF₂–SiH₃)₂; it is replaced by the stronger La⋯F interaction. This should be kept in mind for the structure of amido complexes.

An analysis of the electron density³⁰ in 4 shows no deformation of the density between La and Si–C(2) and no bonding critical point between these three atoms. There is thus no need for direct contact between La and the agostic single bond which removes all concerns about accessibility of the bond by the metal. An NBO charge analysis was carried out on 2 and on La{CH(SiH₃)₂}₃, where CH(SiH₃)₂ is a better model to evaluate the atomic charges associated with CH(SiMe₃)₂. The charge on La is 2.3 for 2 and 2.5 for La{CH(SiH₃)₂} due to the partial occupation of the 5d orbitals as also shown earlier for amido complexes; the higher charge in the latter results from the negative hyperconjugation of the SiH₃ groups.²⁰ The electrostatic field from La is sufficient to polarize the electron density within the ligand skeleton towards one of the three bonds which hyperconjugates with the C(1) sp³ lone pair. This lengthens the β bond closest to La and as a consequence shortens the two β bonds that are pointing away from the metal. The calculations show that the distances of these two Si–H β bonds in 4 are essentially that in the neutral molecule like CH₃–SiH₃. The delocalization is less marked with bonds that are less polarizable (C–C vs. Si–C) and with metals that are less electropositive (Ti vs. La) so that the effect is less marked in Cl₃Ti–C₂H₅ although already noticed.^16b A similar magnitude of lengthening of an Si–C bond has been obtained from calculations for LiCH₂–SiH₃ and LiCH₂–CH₃, when Li is exclusively bonded to one alkyl chain.^16c As shown by the experimental data, the coordination of Li to additional molecules gives a smaller lengthening of Si–C.^16c In other systems in which a highly electropositive metal is bonded to the same CH(SiMe₃)₂ group such as Mg{CH(SiMe₃)₂},^17b the geometrical features are similar to those in 1. The same interpretation is likely to be applicable.

The energy stabilization associated with the agostic interactions has been estimated for La(CH₂–SiH₃)₃ and La(CH₂–CH₃)₃ by rotating the agostic bond away from the metal. The transition states for rotation around the C(1)–Si or C(1)–C(2) bonds have been located. They correspond to a staggered orientation in one of the three ligands, the other two maintaining an eclipsed conformation. These transition states are 1.5 and 0.8 kcal mol⁻¹ above their corresponding ground states. The rotation has two effects: it annihilates the agostic interaction but it also changes the conformation of the chain from eclipsed in the agostic geometry to staggered in the transition state. The annihilation of the agostic interaction for the rotated group induces a widening of the La–C–Si angle from 94° to 112°. The narrow La–C–Si angle of 94° is a consequence of the electrostatic attraction between La and the β bond. The energy stabilization of the agostic interaction needs thus to take into account the conformational change which was calculated in the neutral systems CH₃–SiH₃ (1.5 kcal mol⁻¹), CH₃–CH₃ (2.8 kcal mol⁻¹). This leads to an estimate of around 3.6 kcal mol⁻¹ for agostic C–H, 4 kcal mol⁻¹ for agostic Si–H. The stabilization associated with the Si–C agostic interaction cannot be determined by this method, since the optimized structure is a secondary minimum on the potential energy surface and the most stable structure has an Si–H group pointing towards La. There is no reason to believe that a Si–C agostic bond will be stronger than Si–H. On average in these lanthanide complexes, the energy of the β agostic interaction barely overcomes the staggered-eclipsed energy loss. It is notably weaker than that suggested for C–H (∼10 kcal mol⁻¹) in the case of W(CO)₃L₂ (L = PCy₃).^1c

The progressive buildup of the experimental system and the use of QM/MM calculations has allowed us to establish the role of all parts of the ligands. The trimethylsilyl non-agostic group exerts mainly a steric influence on the molecule. In contrast, the two methyl groups pointing away from La cannot be replaced by H since the absolute minimum for 4 has an agostic Si–H bond in place of an agostic Si–C bond. However, the structure of the secondary minimum with the agostic Si–C bond has a geometry in good agreement with the observed parameters in complex 1. This illustrates some of the validity and limitation in modelling of ligands.

Conclusions

The DFT calculation on several models of the title molecule reveals the presence of an agostic Si–C β bond in preference to an agostic γ C–H bond. The analysis suggests that the lengthening of the β Si–C bond is due to the delocalization of the electronic density within the anionic ligand in the field of the electropositive La³⁺ ion. The delocalization accumulates electron density in the bond closest to the metal and vicinal to the atom bonded to the metal. One signature of the attraction between the electropositive centre and the β Si–C bond is the narrow La–C–Si angle. The maximum effect is thus expected for electropositive metal centres and anionic centres that do not efficiently stabilize electron density (for instance alkyl vs. amido). This effect shows that the concept of the agostic interaction covers a wide variety of effects and interactions. It is probably unwise to generalize the present results obtained for a metal centre with no electron density to the case of the less electropositive late transition metals which are also able to back-donate into C–H empty orbitals. It also shows that intramolecular and intermolecular agostic interactions may have very little in common. In the latter, the only interaction is truly that of a C–H with the metal. Paradoxically, this could be the purest example of the agostic interaction following the definition of Brookhart and Green, except of course that they specifically invoke intramolecularity.

Note added during revision

After submission of this manuscript, we were informed of a closely related DFT study³¹ of the same La complex and its Sm analog which had earlier been studied experimentally.^17a

References

1. (a) For reviews see M. L. H. Green and M. Brookhart, J. Organomet. Chem., 1983, 250, 395; M. Brookhart, M. L. H. Green and L. Wong, Prog. Inorg. Chem., 1988, 36, 1; R. H. Crabtree and D. G. Hamilton, Adv. Organomet. Chem., 1988, 28, 299; (b) for some recent publications see also W. W. Lukens, M. R. Smith III and R. A. Andersen, J. Am. Chem. Soc., 1996, 118, 1719; J. C. Gordon, G. R. Giesbrecht, J. T. Brady, D. L. Clark, D. W. Keogh, B. L. Scott and J. G. Watkin, Organometallics, 2002, 21, 127; J. M. Cole, V. C. Gibson, J. A. K. Howard, G. J. McIntyre and G. L. P. Walker, Chem. Commun., 1998, 1829; (c) K. Zhang, A. A. Gonzalez, S. L. Mukerjee, S. J. Chou, C. D. Hoff, K. A. Kubatmartin, D. Barnhart and G. J. Kubas, J. Am. Chem. Soc., 1991, 113, 9170.
2. See for instance (a) R. H. Grubbs and G. W. Coates, Acc. Chem. Res., 1996, 29, 85; (b) P. Margl, L. Deng and T. Ziegler, Organometallics, 1998, 17, 933; P. Margl, L. Deng and T. Ziegler, J. Am. Chem. Soc., 1998, 120, 5517; P. Margl, L. Deng and T. Ziegler, J. Am. Chem. Soc., 1999, 121, 154.
3. R. H. Crabtree, Angew. Chem., Int. Ed. Engl., 1993, 32, 789; C. Hall and R. N. Perutz, Chem. Rev., 1996, 96, 3125; A. E. Shilov and G. B. Shu'lpin, Chem. Rev., 1997, 97, 2879; G. J. Kubas, Transition metal σ bond and Dihydrogen complexes, Kluwer Academic/Plenum Publishers, New-York, NY, 2001.
4. (a) For late transition metal see J. J. Schneider, Angew. Chem., Int. Ed. Engl., 1996, 35, 1068; U. Schubert, Adv. Organomet. Chem., 1990, 30, 151; F. Delpech, S. Sabo-Etienne, J.-C. Daran, B. Chaudret, K. Hussein, C. J. Marsden and J.-C. Barthelat, J. Am. Chem. Soc., 1999, 121, 668; K. Hussein, C. J. Marsden, J.-C. Barthelat, V. Rodriguez, S. Conejero, S. Sabo-Etienne, B. Donnadieu and B. Chaudret, Chem. Commun., 1999, 1315; M.-F. Fan and Z. Lin, Organometallics, 1999, 18, 286; S.-H. Choi, J. Feng and Z. Lin, Organometallics, 2000, 19, 2051; U. Schubert, M. Schwarz and F. Möller, Organometallics, 1994, 13, 1554; M. D. Butts, J. C. Bryan, X.-L. Luo and G. J. Kubas, Inorg. Chem., 1997, 36, 3341; X.-L. Luo, G. J. Kubas, C. Jeffrey, C. J. Burns and C. J. Unkefer, J. Am. Chem. Soc., 1994, 116, 10 312; Z. Lin, Chem. Soc. Rev., 2002, 31, 2399; (b) for early transition metals and lanthanides see W. Bauer and P. v. R. Schleyer, J. Am. Chem. Soc., 1989, 111, 7191; D. Braga, F. Grepioni, K. Biradha and G. R. Desideraju, J. Chem. Soc., Dalton Trans., 1996, 3925; B. Goldfuss, P. V. R. Schleyer, S. Handschub, F. Hampel and W. Bauer, Organometallics, 1997, 16, 5999; W. A. Herrmann, J. Eppinger, M. Spiegler, O. Runte and R. Anwander, Organometallics, 1997, 16, 1813; J. Eppinger, M. Spiegler, W. Hieringer, W. A. Herrmann and R. Anwander, J. Am. Chem. Soc., 2000, 122, 3080; W. Hieringer, J. Eppinger, R. Anwander and W. A. Herrmann, J. Am. Chem. Soc., 2000, 122, 11 983; M. G. Klinpel, H. W. Görlitzer, M. T. Tafilposly, M. Spiegler, W. Scherer and R. Anwander, J. Organomet. Chem., 2002, 647, 236; G. Ciruelo, T. Cuenca, R. Gómez, P. Gómez-Sal and A. Martín, J. Chem. Soc., Dalton Trans., 2001, 1657; L. J. Procopio, P. J. Carroll and D. H. Berry, J. Am. Chem. Soc., 1994, 116, 177; G. I. Nikonov, P. Mountford, S. Ignatoc, J. C. Green, M. A. Leech, L. G. Kuzmina, A. G. Razuvaev, N. H. Rees, A. J. Blake, J. A. K. Howard and D. A. Lemenovski, J. Chem. Soc., Dalton Trans., 2001, 2903; G. I. Nikonov, J. Organomet. Chem., 2001, 635, 24; M. Ichiche, A. Sekiguchi, M. Takahashi and H. Sakurai, Bull. Chem. Soc. Jpn., 1999, 72, 1905; N. Peulecke, A. Ohff, P. Kosse, A. Tillack, A. Spannenberg, R. Anke, W. Baumann, V. V. Burlakov and U. Rosenthal, Chem. Eur. J., 1998, 4, 1852; W. S. Rees Jr., O. Just, H. Schumann and R. Weiman, Angew. Chem., Int. Ed. Engl., 1996, 35, 419.
5. C. Viñas, R. Nuñez, F. Teixidor, R. Kivekäs and R. Sillanpää, Organometallics, 1998, 17, 2376; M. Garcia, A. Paulo, Â. Domingos, I. Santos, K. Ortner and R. Alberto, J. Am. Chem. Soc., 2000, 122, 11 240; A. Caballero, F. Gómez-de la Torre, F. A. Jalón, B. R. Manzano, A. M. Rodríguez, S. Trofimenko and M. P. Sigalas, J. Chem. Soc., Dalton Trans., 2001, 427.
6. W. Yao, O. Eisenstein and R. H. Crabtree, Inorg. Chim. Acta, 1997, 254, 105; D. Braga, F. Grepionio, E. Tedesco, K. Biradha and G. R. Desiraju, Organometallics, 1997, 16, 1846.
7. For some recent references see A. Monge and C. Ruiz, Organometallics, 1999, 18, 3294; L. A. Watson, D. V. Yandulov and K. G. Caulton, J. Am. Chem. Soc., 2001, 123, 603; D. R. Click, B. L. Scott and J. G. Watkin, Chem. Commun., 1999, 633; G. Ujaque, F. Maseras, A. Lledós, L. Contreras, A. Pizzano, D. Rodewald, L. Sánchez, E. Carmona, A. Monge and C. Ruiz, Organometallics, 1999, 18, 3294.
8. B. Rybtchinski, S. Oevers, M. Montag, A. Vigalok, H. Rozenberg, J. M. L. Martin and D. Milstein, J. Am. Chem. Soc., 2001, 123, 9064 and references therein.
9. N. Koga and K. Morokuma, J. Am. Chem. Soc., 1988, 110, 108; W. T. Klooster, L. Brammer, C. J. Schaverein and P. H. M. Budzelaar, J. Am. Chem. Soc., 1999, 121, 1381; Y. W. Alelyanas, N. C. Baenziger, P. K. Prudence and R. F. Jordan, Organometallics, 1994, 13, 148; R. Gleiter, I. Hyla-Kryspin, S. Niu and G. Erker, Organometallics, 1993, 12, 3828; A. D. Horton and A. G. Orpen, Organometallics, 1991, 10, 3910.
10. S. Obara, N. Koga and K. Morokuma, J. Organomet. Chem., 1984, 270, C33.
11. G. Ujaque, A. C. Cooper, F. Maseras, O. Eisenstein and K. G. Caulton, J. Am. Chem. Soc., 1998, 120, 361; J. Jaffart, R. Mathieu, M. Etienne, J. E. McGrady, O. Eisenstein and F. Maseras, Chem. Commun., 1998, 2011; A. C. Cooper, E. Clot, F. Maseras, O. Eisenstein and K. G. Caulton, J. Am. Chem. Soc., 1999, 121, 97; J. Jaffart, M. Etienne, F. Maseras, J. E. McGrady and O. Eisenstein, J. Am. Chem. Soc., 2001, 123, 6000; R. Cini and A. Cavaglioni, Inorg. Chem., 1999, 38, 3751.
12. See for instance (a) M. Jiménez Tenorio, K. Mereiter, M. Carmen Puerta and P. Valerga, J. Am. Chem. Soc., 2000, 122, 11 230; (b) R. Bau, S. A. Mason, B. O. Patrick, C. S. Adams, W. B. Sharp and P. Legzdins, Organometallics, 2001, 20, 4492; D. G. Gusev, M. Madott, F. M. Dolgushin, K. A. Lyssenko and M. Y. Antipin, Organometallics, 2000, 19, 1734; J. M. Boncella, M. L. Cajigal and K. A. Abboud, Organometallics, 1996, 16, 1905.
13. E. Clot, O. Eisenstein, T. Dube, J. W. Faller and R. H. Crabtree, Organometallics, 2002, 21, 575.
14. R. J. Goddard, R. Hoffmann and E. D. Jemmis, J. Am. Chem. Soc., 1980, 102, 7667; O. Eisenstein and Y. Jean, J. Am. Chem. Soc., 1985, 107, 1177.
15. A. Haaland, W. Scherer, H. V. Volden, H. P. Verne, O. Gropen, G. S. McGrady, A. J. Downs, G. Dierker, W. A. Herrmann, P. W. Roesky and M. R. Geisberger, Organometallics, 2000, 19, 22.
16. (a) T. D. Tilley, R. A. Andersen and A. Zalkin, J. Am. Chem. Soc., 1982, 104, 3725; (b) A. Haaland, W. Scherer, K. Ruud, G. S. McGrady, A. J. Downs and O. Swang, J. Am. Chem. Soc., 1998, 120, 3762; W. Scherer, T. Priermeier, A. Haaland, H. V. Volden, G. S. McGrady, A. J. Downs, R. Boese and D. Bläser, Organometallics, 1998, 17, 4406; G. S. McGrady, A. J. Downs, A. Haaland, W. Scherer and D. C. McKean, Chem. Commun., 1997, 1547; W. Scherer, W. Hieringer, M. Spiegler, P. Sirsch, G. S. McGrady, A. J. Downs, A. Haaland and B. Pedersen, Chem. Commun., 1998, 2471; W. Scherer, P. Sirsch, M. Grosche, M. Spiegler, S. A. Mason and M. G. Gardiner, Chem. Commun., 2001, 2072; D. C. McKean, G. S. McGrady, A. J. Downs, W. Scherer and A. Haaland, Phys. Chem. Chem. Phys., 2001, 3, 2781; (c) W. Scherer, P. Sirsch, D. Shorokhov, G. S. McGrady, S. A. Mason and M. G. Gardiner, Chem. Eur. J., 2002, 8, 2324.
17. (a) P. B. Hitchcock, M. F. Lappert, R. G. Smith, R. A. Bartlett and P. P. Power, J. Chem. Soc., Chem. Commun., 1988, 1007; (b) G. K. Barker, M. F. Lappert and J. A. K. Howard, J. Chem. Soc., Dalton Trans., 1978, 734; (c) A. J. Carty, M. J. S. Gynane, M. F. Lappert, S. J. Miles, A. Singh and N. J. Taylor, Inorg. Chem., 1980, 19, 3637; (d) P. B. Hitchcock, J. A. K. Howard, M. F. Lappert, W.-P. Leung and S. A. Mason, J. Chem. Soc., Chem. Commun., 1990, 1116.
18. K. H. Den Haan, J. L. De Boer, J. H. Teuben, A. L. Spek, B. Kojic-Prodic, G. R. Hajs and R. Huis, Organometallics, 1986, 5, 1726.
19. M. Dolg, H. Stoll, A. Savin and H. Preuss, Theor. Chim. Acta, 1989, 75, 173; M. Dolg, H. Stoll, A. Savin and H. Preuss, Theor. Chim. Acta, 1993, 85, 441.
20. L. Maron and O. Eisenstein, J. Phys. Chem. A, 2000, 104, 7140.
21. A. Bergner, M. Dolg, W. Kuechle, H. Stoll and H. Preuss, Mol. Phys., 1993, 80, 1431.
22. W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257.
23. A. D. Becke, J. Chem. Phys., 1993, 98, 5648; J. P. Perdew and Y. Wang, Phys. Rev. B, 1992, 82, 284.
24. M. Svensson, S. Humbel, R. D. J. Froesee, T. Matsubara, S. Sieber and K. Morokuma, J. Phys. Chem., 1998, 100, 19 357.
25. A. K. Rappé, C. Casewitt, K. S. Colwell, W. A. Goddard and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10 024.
26. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery Jr., R. E. Stratmann, J. C. Burant, S. Daprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Cioslowski, J. V. Ortiz, A. G. Baboul, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Martin, R. L. Gomperts, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, C. Gonzalez, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, J. L. Andrés, M. Gonzalez, M. Head-Gordon, E. S. Replogle and J. A. Pople, Gaussian 98, Revision A.7, Gaussian, Inc., Pittsburgh, PA, 1998.
27. L. Maron and O. Eisenstein, New J. Chem., 2001, 25, 255.
28. (a) L. Perrin, L. Maron and O. Eisenstein, Faraday Discuss., submitted; (b) M. Kaupp, Angew. Chem., Int. Ed., 2001, 40, 3534.
29. (a) A. Demolliens, Y. Jean and O. Eisenstein, Organometallics, 1986, 5, 1457; S. K. Kang, T. A. Albright and O. Eisenstein, Inorg. Chem., 1989, 28, 1611; (b) M. Kaupp, Chem. Eur. J., 1998, 4, 1678; (c) V. Pfennig and K. Seppelt, Science, 1996, 271, 626; (d) X. Wang and L. Andrews, J. Am. Chem. Soc., 2002, 124, 5636.
30. R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Clarendon Press, Oxford, UK, 1990; R. F. W. Bader, Chem. Rev., 1992, 92, 893.
31. D. L. Clark, J. C. Gordon, P. J. Hay, R. L. Martin and R. Poli, Organometallics, 2002, 21, 5000.

---